Федеральное Агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Московский Государственный Институт Стали и Сплавов
(технологический университет)
Кафедра экономики и менеджмента
Курсовая работа по высшей математике на тему:
«Приложение интегрального и дифференциального исчисления к решению прикладных задач».
Выполнила:
Рашидуллина А.Г.
группа МЭ-07-3
Проверил(а):
Дьяченко О. Н.
Москва
2005
Задание № 1
экстремум непериодическая функция фурье
Найти наибольшее и наименьшее значения функции f(x,y)= y2
+x2
+6x+ -4y в замкнутой ограниченной области D: x2
+y2
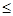 4; x+y 4; x+y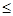 2. 2.
Теория:
I). Если из уравнения связи найти y как функция x, т.е f(x, y(x)) тогда задача сводится к отысканию наибольшего и наименьшего значения функции одной переменной на заданном отрезке.
Находим значение функции в точках, в которых выполнено необходимое условие наличия экстремумов функции (точки попадания в данную область)
Из найденных значениях выбираем наибольшее и наименьшее значения.
(x0
,y0
) – точка условного экстремума f(x;y)
Для максимума:
1. (x0
;y0
) – удовлетворяет уравнению связи 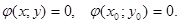
2. Существует такая окрестность точки (x0
;y0
), что для любых (х;у), таких что
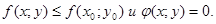
(Аналогично для минимума).
II). Нахождение точек в которых выполнено необходимое условие наличия экстремума функции методом множителей Лагранжа.
z=f(x;y), 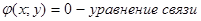 . .
1. Составляем функцию 3-х переменных 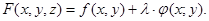
2. Для функции F находим точки в которых выполнено необходимое условие обычного экстремума:
 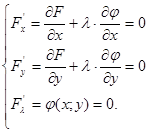
Решение.

1). Находим точки в которых выполнено необходимое условие наличия экстремума.
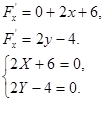 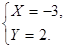
Точка (-3, 2) 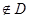 (т.е не принадлежит области определения). (т.е не принадлежит области определения).
2). Находим наибольшее и наименьшее значения на границе области.
а) 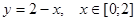
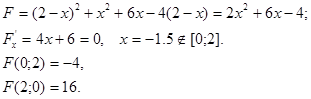
б). Находим точки в которых выполнено необходимое условие условного экстремума с помощью теоремы Лагранжа.
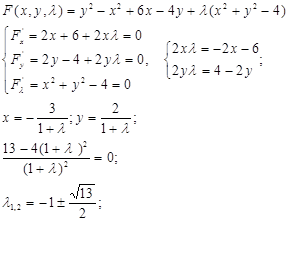
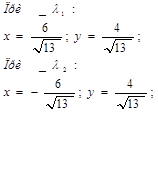
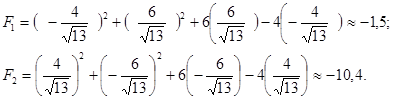 . .
| x |
y |
z |
| 0 |
2 |
-4 |
| 2 |
0 |
16 |
 |
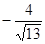 |
-1,5 |
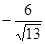 |
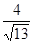 |
-10,4 |
Ответ:
zнаиб.
(2;0)=16.
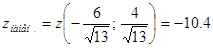
Задание № 2
Завод производит два вида продукции : А и В. Единица продукции вида А требует 2 часа на обработку деталей, 4 часов на сборку и 82 часов на упаковку. А единица продукции типа В требует соответственно 3, 12 и 6 часов. Оборудование завода позволяет потратить на эти операции соответственно 48, 168 и 144. Единица продукции первого вида даёт прибыль в размере $11, а второго - $10. Требуется составить план выпуска продукции, обеспечивающий заводу максимальную прибыль. Решить задачу двумя способами ( геометрическим методом и симплексным методом).
| На обработку деталей,час |
На сборку,час |
На упаковку, час |
Прибыль с ед. продукции |
| Продукция типа А |
2 |
4 |
8 |
11 |
| Продукция типа В |
3 |
12 |
6 |
10 |
| Завод позволяет,час |
48 |
168 |
144 |
Геометрический метод:
X-количество продукции типа А
Y-количество продукции типа В
Тогда 11X+10Y – общая выручка, максимизируя ее, получаем целевую функцию.
11X+10Y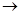 max - целевая функция, обеспечивающая заводу максимальную прибыль. max - целевая функция, обеспечивающая заводу максимальную прибыль.
Условия ограниченности времени:
2X+3Y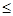 48, 48,
4X+12Y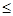 168, 168,
8X+6Y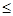 114, 114,
X>0, Y>0

 Рассмотрим вначале геометрический метод. В общем случае, он применим лишь в том случае, если ЗЛП содержит не более 2-х переменных величин (не считая самого значения целевой функции). В некоторых случаях ЗЛП с числом переменных более двух может быть сведена к ЗЛП с двумя переменными, однако здесь мы не будем касаться этих возможностей. Суть геометрического метода заключается в следующем: Рассмотрим вначале геометрический метод. В общем случае, он применим лишь в том случае, если ЗЛП содержит не более 2-х переменных величин (не считая самого значения целевой функции). В некоторых случаях ЗЛП с числом переменных более двух может быть сведена к ЗЛП с двумя переменными, однако здесь мы не будем касаться этих возможностей. Суть геометрического метода заключается в следующем:
1) На плоскости, по осям которой отложены искомые переменные величины, строится система ограничений, указанная в задаче (то есть фактически решаем графически систему неравенств). Если она не имеет решения, то соответственно ЗЛП также не имеет решения. Если имеет, то обычно мы получаем некоторый многоугольник (он может быть не замкнут). Этот многоугольник представляет собой область допустимых решения ЗЛП.
2) Находим градиент целевой функции. Он представляет собой вектор, направленный в сторону наибольшего возрастания функции.
3) Строим так называемую линию уровня. Для этого приравниваем целевую функцию какой-либо константе. Очевидно, что мы получаем прямую, перпендикулярную градиенту.
4) Возможны два варианта:
1) Целевая функция на максимум: перемещаем линию уровня параллельно самой себе в направлении градиента. Для простоты будем считать, что ЗЛП имеет единственное оптимальное решение. Тогда последняя точка, лежащая на границе области допустимых решений ЗЛП, через которую пройдет линия уровня и будет представлять собой оптимальное решение.
2) Целевая функция на минимум: все аналогично пункту 1 за исключением того, что линию уровня нужно перемещать в сторону, противоположную градиенту.
2X+3Y=4, (1)
4X+12Y=168, (2)
8X+6Y=114. (3)
В данном случае многоугольник ODABC представляет собой область допустимых решений ЗЛП. Как можно видеть из рисунка оптимальным решением ЛЗП является точка A с координатами (12;8).
На пересечении графиков (1) и (3) достигается максимальное значение функции:
Решаем систему из (1) и (3) уравнения
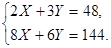
Получаем: X=12; Y=8.
Подставим в целевую функцию:
11*12+10*8=132+ 80=242.
Т.е. максимальная прибыль в 212$ будет достигаться при следующем плане выпуска 12 единиц товара А и 8 единиц товара В.
Симплексный метод:
Однако ЗЛП с двумя переменными на практике встречаются редко. В реальных задачах их число может доходить до сотен. Мощным инструментом для решения подобных задач является симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что позволяет использовать его в ЗЛП с практически любым конечным числом переменных. Здесь мы не будем останавливаться подробно на симплекс-методе. Укажем лишь основные его черты. Для его использования все ограничения задачи должны представлять собой равенства. Чтобы добиться этого обычно вводят дополнительные переменные. Симплекс-метод основан на том, что оптимальным решением ЗЛП является какая-либо вершина многогранника допустимых решений ЗЛП. Вначале выбирается произвольно любая вершина многогранника (иногда это может быть сопряжено с определенными трудностями). Затем осуществляется переход к другим вершинам до тех пор, пока не обнаруживается оптимальная. Необходимо отметить, что главной отличительной чертой симплекс-метода по сравнению с простым перебором является то, что переход к следующей вершине осуществляется в направлении роста (или падения) целевой функции. Это позволяет значительно ускорить процесс поиска оптимального решения. Решим рассмотренную ранее задачу симплекс-методом.
Решение:
11X+10Y → max
 2X+3Y 2X+3Y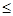 48, + U1 48, + U1
4X+12Y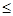 168,+ U2 168,+ U2
8X+6Y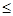 114 + U3 114 + U3
| X(11) |
Y(10) |
U1(0) |
U2(0) |
U3(0) |
F(0) |
| U1(0) |
2 |
3 |
1 |
0 |
0 |
48 |
| U2(0) |
4 |
12 |
0 |
1 |
0 |
168 |
| U3(0) |
8 |
6 |
0 |
0 |
1 |
144 |
| Инд.строка |
0 |
0 |
0 |
0 |
| U1(0) |
08.мар |
0 |
1 |
-0,2222 |
0 |
8 |
| Y(6) |
01.мар |
1 |
0 |
янв.18 |
0 |
6 |
| U3(0) |
28.мар |
0 |
0 |
-0,4444 |
1 |
36 |
| Инд.строка |
-2 |
0 |
0 |
01.мар |
0 |
36 |
| X(4) |
1 |
0 |
03.авг |
-0,0833 |
0 |
3 |
| Y(6) |
0 |
1 |
-0,125 |
01.дек |
0 |
5 |
| U3(0) |
0 |
0 |
-9,3333 |
01.мар |
1 |
8 |
| Инд.строка |
0 |
0 |
03.апр |
01.июн |
0 |
42 |
При введении дополнительных переменных получаем:
4X+4Y+0·U1
+0·U2
+0·U3
→max
4X+4Y+U1
=32
6X+18Y+U2
=108
12X+8Y+U3
=84
Процесс перебора вершин многогранника допустимых решений в поисках оптимального отразим в следующей симплекс-таблице:
a22
-разрешающий элемент
a11
-разрешающий элемент
Т.к. в индексной строке мы достигли положительного (все элементы положительны), следовательно находимся в оптимальном решении.
В итоге получаем:
X=3; Y=5; U3=8 - базисные переменные
U1=0; U2=0 - свободные переменные
Fmax = 42 – достигнута максимальная прибыл
Задание № 3
Разложить в ряд Фурье по синусам функцию f(x)=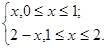 на отрезке [0;2]. на отрезке [0;2].
Теория:
Определение. Функциональный ряд вида 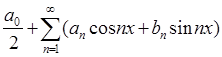
называется тригонометрическим рядом или рядом Фурье. Постоянные числа a0
, an
, и bn
(n=1,2,…) называются коэффициентами тригонометрического ряда или коэффициентами Фурье.
Если дана периодическая функция f(x) с периодом 2π, то целью применения ряда Фурье является отыскание тригонометрического ряда, сходящегося к данной функции. Таким образом, мы отыскиваем функцию, являющуюся суммой ряда в интервале (-π, π):
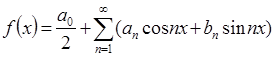 . .
При этом коэффициенты Фурье находят по формулам:
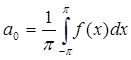 , , 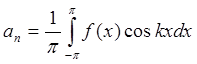 , ,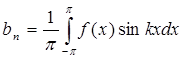
Ряд Фурье для функции с периодом 2l.
Пусть f(x) есть периодическая функция с периодом 2l, вообще говоря, отличным от 2π. Тогда при разложении ее в ряд Фурье получим формулу:
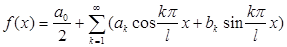 , ,
где коэффициенты a0
, an
, и bn
вычисляются по формулам:
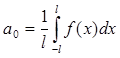 , , 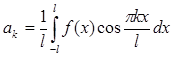 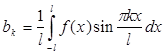
О разложении в ряд Фурье непериодической функции.
Пусть на некотором отрезке 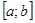 задана кусочнo-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим произвольную периодическую кусочно монотонную функцию задана кусочнo-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим произвольную периодическую кусочно монотонную функцию 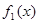 с периодом с периодом 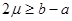 , совпадающую с функцией f(x) на отрезке , совпадающую с функцией f(x) на отрезке 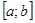 . Разложим функцию . Разложим функцию 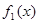 в ряд Фурье. Сумма этого ряда во всех точках отрезка в ряд Фурье. Сумма этого ряда во всех точках отрезка 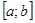 (кроме точек разрыва) совпадает с заданной функцией f(x), т.е. мы разложили функцию f(x) в ряд Фурье на отрезке (кроме точек разрыва) совпадает с заданной функцией f(x), т.е. мы разложили функцию f(x) в ряд Фурье на отрезке 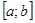 . .
Рассмотрим, далее, следующий важный случай. Пусть функция f(x) задана на отрезке [0,l]. Дополняя определение этой функции произвольным образом на отрезке [-l,0] (сохраняя кусочно монотонность), мы можем разложить эту функцию в ряд Фурье. В частности, если мы продолжим определение функции f(x) при 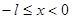 так: f(x) = так: f(x) = 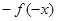 , то получим нечетную функцию, которая разлагается по синусам. (Функция f(x) “продолжена нечетным образом”). , то получим нечетную функцию, которая разлагается по синусам. (Функция f(x) “продолжена нечетным образом”).
Решение:
При разложении ряд Фурье по синусам функцию на интервале [0;2] продолжаем нечётным образом.
Доопределим функцию четным образом (симметрично относительно oy).
Найдем коэффициенты Фурье:
а0
=
аn
=0
bn
=
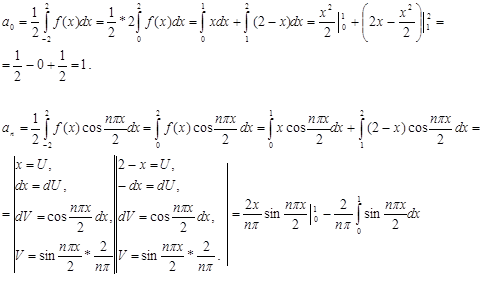
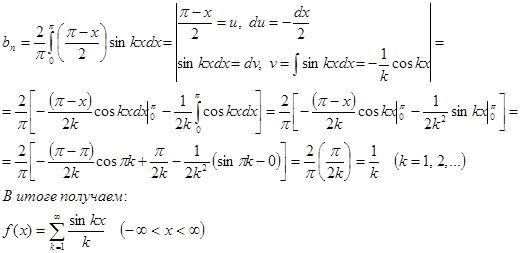
Ответ : f(x)=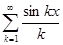 
a) Нарисовать график функции f(x) на отрезке [0;2].

b) Написать к чему сходится этот ряд Фурье в точках отрезка [0;2].
Теория:
Определение. Функция f (x) называется удовлетворяющей условиям Дирикле на сегменте [a, b], если:
1.функция непрерывна на сегменте [a, b] или же имеет на нем конечное число точек разрыва 1 рода;
2.функция кусочно-монотонна на сегменте [a, b].
Теорема Дирикле: Пусть периодическая функция f (x) с периодом 2π удовлетворяет на любом сегменте условиям Дирикле. В таком случае ряд Фурье, соответствующий этой функции, сходится во всех точках числовой оси. При этом в каждой точке непрерывности функции f (x) сумма ряда S (x) равна значению функции в этой точке. В каждой точке x0
разрыва функции сумма ряда равна среднему арифметическому предельных значений функции при x→x0
слева и справа, т.е.:
S(x) = 0,5[f(x0
+ 0)+f(x0
- 0)]
Во всех точках непрерывности функции f(x) ряд сходится к значениям функции в этих точках, т.е. S(x)=f(x) на интервале [0,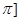 ; в точке x=0 (точка разрыва функции) ряд сходится к 0, т.к. ; в точке x=0 (точка разрыва функции) ряд сходится к 0, т.к.
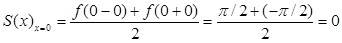
Ответ: S(0)=0
c) Нарисовать график суммы ряда на отрезке [-2;6] :
1) для четного

2) для нечетного

c) Пользуясь равенством Парсеваля, найти сумму:
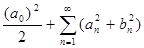
Теория:
Для функции f(x), такой, что f2
(x)ÎL(-p;p), справедливо равенство Парсеваля:
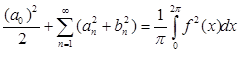
Решение:
Период рассматриваемой функции равен p, поэтому поменяем пределы интегрирования с [0;2p] на [0;p], а коэффициент 2 вынесем, тогда:
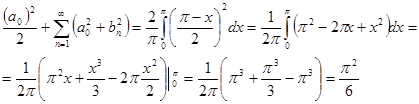
Ответ: 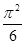
|