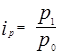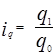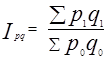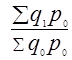КОНТРОЛЬНАЯ РАБОТА
Статистика
Задачи
ЗАДАЧА №
I
За отчётный период предприятие выработало следующее количество мыла и моющих средств по видам:
| Виды мыла и моющих средств |
Количество произведенной продукции |
| Мыло хозяйственное 72% - ной жирности |
1200 |
| Мыло хозяйственное (специальное) 60% - ной жирности |
600 |
| Мыло хозяйственное 40% - ной жирности |
350 |
| Мыло хозяйственное 80% - ной жирности |
1900 |
| Стиральный порошок 10% - ной жирности |
3000 |
Определите общее количество выработанной предприятием продукции в условно-натуральных единицах измерения. За условную единицу измерения принимается мыло 40%-й жирности
Решение:
Общее количество выработанной продукции равно
1200+600+350+1900+3000 = 7050
Так как за единицу измерения принимаем мыло 40 % -й жирности, то количество выработанной предприятиям продукции будет равно:
850 + 250+350+1550+2650 = 5650, так как
1200 - 350 = 850
600 - 350 = 250
1900 - 350 = 1550
3000 - 350 = 2650
ЗАДАЧА № 2
За отчётный год работа предприятий отрасли промышленности характеризуется следующими данными:
| Номер предприятия |
Фактически произведено продукции (тыс. шт.) |
Общая сумма затрат на производство продукции (млн. руб.) |
Себестоимость единицы продукции (тыс. руб.) |
| 1 |
9,7 |
53,86 |
5,7 |
| 2 |
9,5 |
39,78 |
6,3 |
| 3 |
5,7 |
35,94 |
6,5 |
| 4 |
11,7 |
62,74 |
5,5 |
| 5 |
4,8 |
29,24 |
6,3 |
| 6 |
9,8 |
55,30 |
5,8 |
| 7 |
4,1 |
26,90 |
6,3 |
| 8 |
6,8 |
41,74 |
5,6 |
| 9 |
11,9 |
65,00 |
6,6 |
| 10 |
4,0 |
28,96 |
7,5 |
| 11 |
4,5 |
28,70 |
6,6 |
| 12 |
4,4 |
28,91 |
6,8 |
| 13 |
4,0 |
27,00 |
10,0 |
| 14 |
6,0 |
36,88 |
6,3 |
| 15 |
10,1 |
57,10 |
5,8 |
| 16 |
11,4 |
62,25 |
5,6 |
| 17 |
3,1 |
22,30 |
7,5 |
| 18 |
2,7 |
19,00 |
7,4 |
| 19 |
8,1 |
48,10 |
6,1 |
| 20 |
6,8 |
42,98 |
6,5 |
| 21 |
6,3 |
14,62 |
6,7 |
| 22 |
1,9 |
13,42 |
7,5 |
| 23 |
7,2 |
44,83 |
6,4 |
| 24 |
6,4 |
40,42 |
6,5 |
| 25 |
8,5 |
49,66 |
6,0 |
| 26 |
9,7 |
58,56 |
6,2 |
| 27 |
8,9 |
54,66 |
6,3 |
| 28 |
6,0 |
34,00 |
6,2 |
| 29 |
2,1 |
15,10 |
7,6 |
| 30 |
10,1 |
57,10 |
5,8 |
средний процент единица измерения
С целью выявления зависимости между объёмом производственной продукции и её себестоимостью произведите аналитическую группировку по объёму производственной продукции, образовав, пять групп с равными интервалами.
По каждой группе и итогу в целом подсчитайте:
I. Число предприятий".
2. Объём произведённой продукции - всего и в среднем на одно предприятие.
3. Общую сумму затрат на производство, продукции - всего и в среднем на одно предприятие.
4. Себестоимость единицы продукции.
Решение:
1. Построим рабочую таблицу.
Найдем интервал по группам: h= 11.9 - 1.9| 5 = 2
Построим аналитическую группировку по объему производственной продукции:
| Группа |
Номера предприятий |
Объем продукции |
| 1 |
22, 29, 18,17,13,10 |
1.9, 2.1, 2.7, 3.1, 4.0, 4.0 |
| 2 |
7 12 11 5 3 14 |
4.1 4.4 4.5 4.8 5.7 6.0 |
| 3 |
28 21 24 20 8 23 |
6.0 6.3 6.4 6.8 6.8 7.2 |
| 4 |
19 25 27 2 1 26 |
8.1 8.5 8.9 9.5 9.7 9.7 |
| 5 |
6 30 15 16 4 9 |
9.8 10.1 10.1 11.4 11.7 11.9 |
| № предприятий (Группы) |
Группа предприятий по объему произведенной продукции, т. шт. |
Номера предприятий |
Объем произведенный продукции, т. шт. |
Общая сумма затрат на производство продукции, млн., руб. |
Себестоимость единицы продукции, т. руб. |
| 1 |
1 |
22 29 18 17 13 10 |
1.9 2.1 2.7 3.1 4.0 4.0 |
13.42 15.10 19.00 22.30 27.0 28.96 |
7.5 7.6 7.4 7.5 10.0 7.5 |
| 1.9 - 4.0 |
Итого: |
6 |
17.8
На одно предприятие 3
|
125.78
В среднем на одно предприятие 21
|
47.5
На одно предприятие 8
|
| 2 |
2 |
7 12 11 5 3 14 |
4.1 4.4 4.5 4.8 5.7 6.0 |
26.90 28.91 28.70 29.24 35.94 36.88 |
6.3 6.8 6.6 6.3 6.5 6.3 |
| 4.1 - 6.0 |
итого |
6 |
29.5
На одно предприятие 5
|
186.57
На одно предприятие 31
|
38.8
На одно предприятие 6.5
|
| 3 |
3 |
28 21 24 20 8 23 |
6.0 6.3 6.4 6.8 6.8 7.2 |
34.00 14.62 40.42 42.98 41.74 44.83 |
6.2 6.7 6.5 6.5 5.6 6.4 |
| 6.0 - 7.2 |
итого |
6 |
39.5
На одно предприятие 6.6
|
218.59
На одно предприятие 36.4
|
37.9
На одно предприятие 6.3
|
| 4 |
4 |
19 25 27 2 1 26 |
8.1 8.5 8.9 9.5 9.7 9.7 |
48.10 49.66 54.66 39.78 53.86 58.56 |
6.1 6.0 6.3 6.3 5.7 6.2 |
| 8.1 - 9.7 |
Всего |
6 |
54.4
На одно предприятие 9
|
304.62
На одно предприятие 51
|
36.6
На одно предприятие 6.1
|
| 5 |
5 |
6 30 15 16 4 9 |
9.8 10.1 10.1 11.4 11.7 11.9 |
55.30 57.10 57.10 62.25 62.74 65.00 |
5.8 5.8 5.8 5.6 5.5 6.6 |
| 9.8 - 11.9 |
Всего |
6 |
65
На одно предприятие 10.8
|
359.49
На одно предприятие 60
|
35.1
На одно предприятие 6
|
| Итого: |
30 |
206.2
На одно предприятие 6.9
|
1195.05
На одно предприятие 40
|
195.9
На одно предприятие 6.5
|
2. Построим зависимость между объемом произведенной продукции и ее себестоимостью.
№
Предприятий
|
Группа предприятий по объему произведенной продукции, т. шт.) |
Число
предприятий, шт
|
Объем произведенный продукции, |
Продукция за отчетный период, млн. руб |
Себестоимость единицы продукции |
| всего |
На одно предприятие |
| 1 |
1 |
6 |
17.8 |
125.78 |
21 |
47.5 |
| 2 |
2 |
6 |
29.5 |
186.57 |
31 |
38.8 |
| 3 |
3 |
6 |
39.5 |
218.59 |
36.4 |
37.9 |
| 4 |
4 |
6 |
54.4 |
304.62 |
51 |
36.6 |
| 5 |
5 |
6 |
65 |
359.49 |
60 |
35.1 |
| Итого |
5 |
30 |
206.2 |
1195.05 |
199.4 |
195.9 |
ЗАДАЧА №3
Имеются данные о работе промышленных предприятий объединения:
| Номер предприятия |
План выпуска продукции, млн. руб. |
Фактический выпуск продукции, млн. руб. |
Продукция, соответствующая мировым стандартам |
| 1 |
51,0 |
51,0 |
20,0 |
| 2 |
56,0 |
27,0 |
17,0 |
| 3 |
61,0 |
59,0 |
11,0 |
| 4 |
53,0 |
55,0 |
23,0 |
Определите средний процент выполнения плана по объединению и средний процент продукции, соответствующий мировым стандартам.
Решение:
= Фактический выпуск продукции х 100
План выпуска продукции
Х = 192/221*100 = 86.9, так как
Фактический выпуск продукции = 51.0+27.0+59.0+55.0 = 192
План выпуска продукции = 51.0+56.0+61.0+53.0 = 221 % продукции о = Продукция, соответствующая мировым стандартам соответствующий Фактический выпуск продукции мировым стандартам
% = 71/192 = 0.37*100% = 37%, так как
Продукция соответствующая мировым стандартам = 20.0+17.0+11.0+23.0 = 71
ЗАДАЧА 4
Произвести расчёт показателей вариации по группам фирм по вооруженности работников промышленно-производственными основными фондами одного из регионов России.
| Группы фирм по величине ППОФ на 1 работника, млн. руб. (Х) А |
Среднегодовая я численность ППП, в % к итогу (fi
) |
Середина интервалов
XI
2
|
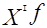
3
|
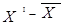 ) )
4
|
(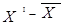 ) ) 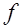
5
|
(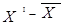 ) 2 ) 2
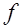
6
|
| До 1,2 |
7,7 |
| 1,3-2,2 |
12,3 |
| 2,3-3,2 |
15,0 |
| 3,3-5,2 |
23,2 |
| 5,3-10,2 |
24,7 |
| 10,3-20,2 |
10,7 |
| 20,3 и более |
6,8 |
| Итого |
100 |
Вычислите: I. Среднее арифметическое.
2. Среднее линейное отклонение.
3. Дисперсию.
4. Среднее квадратическое отклонение
Решение:
1. Среднее арифметическое
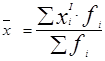 = 3*100/100 = 3 = 3*100/100 = 3
2. Среднее линейное отклонение
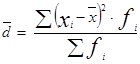 = 5*5/100 = 0.25 = 5*5/100 = 0.25
3. Дисперсия
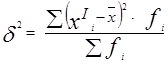 = 16*100/100 = 16 = 16*100/100 = 16
4. Среднее квадратическое отклонение
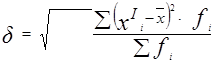
= 4*4*100/100 = 16 =4
ЗАДАЧА№
5
Имеются следующие данные о товарных запасах розничного торгового предприятия (млн. руб.).
| На 1/1 - 1993 г. |
На 1/5-1993 г. |
На 1/8 - 1993г. |
На 1/1 - 1994г. |
| 6,2 |
59,0 |
53,0 |
71,0 |
Вычислите среднегодовой товарный запас розничного торгового предприятия за 1993 год?
Решение:

У = (6.2 + 59.0) *1 + (59.0+53.0) *2 + (53.0+71.0) *3/4*4 = 65.2+224+ 372/ 16 = 41.3
ЗАДАЧА
№ 6
Имеются данные о продаже овощей на душу населения по городу в 1981 по 1989 гг (тыс. руб.)
| 1981 |
1982 |
1983 |
1984 |
1985 |
1986 |
1987 |
1988 |
1989 |
| 10,0 |
10,8 |
12,1 |
10,3 |
12,9 |
16,4 |
15,7 |
17,9 |
18,2 |
Для анализа внутригодовой динамики определите индексы сезонности с применением метода аналитического выравнивания
Решение:
| Годы |
На душу населения, тыс. руб. |
Условные обозначения периодов |
У * t |
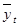 |
Ji =
|
| t |
t2
|
| 1981 |
10.0 |
-4 |
16 |
-40 |
11.3 |
0.9 |
| 1982 |
10.8 |
-3 |
9 |
-32.4 |
10.2 |
1 |
| 1983 |
12.1 |
-2 |
4 |
-24.2 |
7.8 |
1.6 |
| 1984 |
10.3 |
-1 |
1 |
-10.3 |
3.5 |
3 |
| 1985 |
12.9 |
0 |
0 |
0 |
0 |
0 |
| 1986 |
16.4 |
+1 |
1 |
16.4 |
16.4 |
1 |
| 1987 |
15.7 |
+2 |
4 |
31.4 |
7.9 |
2 |
| 1988 |
17.9 |
+3 |
9 |
53.7 |
6.0 |
3 |
| 1989 |
18.2 |
+4 |
16 |
72.8 |
4.6 |
4 |
| Итого |
124.3 |
- |
60 |
67.4 |
67.7 |
16.5 |
2. Выравнивание производится по уравнению прямой
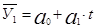
а0 =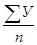 ;
а1
= ;
а1
=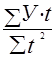 ; ;
а0
= 124.3/9 = 13.8
а1
= 67.4/60 = 1.12
У = 13.8 + 1.12 = 14.92
ЗАДАЧА
№ 7
Имеются данные о ценах и реализации товара за два месяца:
| Товары |
Март 2000 |
Апрель 2000 |
Индексы, % |
| Цена, руб (р0
). |
Количество, кг (q0
) |
Стоимость? руб. (р0
q0
) |
Цена, руб. (р1
). |
Количество, кг. (q1
) |
Стоимость, руб. (р1
q1
) |
Цен |
Физического объема продажи |
Товарооборота |
| А |
| Б |
| В |
Определить индивидуальные и общие индексы товарооборота, физического объёма проданных товаров и цен.
Решение:
I. Индивидуальные индексы:
а) цен
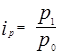
б) количества проданных товаров
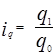
2. Общий индекс товарооборота
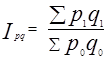
3. Общий индекс физического объёма товарооборота (количества проданных товаров) исчисляется по следующей агрегатной форме индекса Iq
= 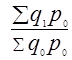
4. Общий индекс цен

5. Прирост товарооборота исчисляется как разность между числителем и знаменателем индекса товарооборота. Σ p1
q1
- Σ p0
q0
ЗАДАЧА № 8
По десяти предприятиям имеются данные о размере основных фондов и выпуске продукции:
| Размер основных фондов, млн. руб. |
6,2 |
7,3 |
5,5 |
8,8 |
5,8 |
6,6 |
5,9 |
8,3 |
7,4 |
8,7 |
| Выпуск продукции, млн. руб. |
24,5 |
19,5 |
15,5 |
11,5 |
20,0 |
17,5 |
24, 5 |
17,5 |
18,5 |
21,5 |
Рассчитайте ранговый коэффициент корреляции Спирмена.
Решение:
Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывает" и по формуле:
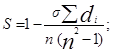
где:  квадрат разности рангов; квадрат разности рангов;
n - число наблюдений (число пар рангов)
S = 1 - (-110/10*10*10-1) = 1 - (-0.1) = 1.1 = 1
Расчёт произвести по следующей таблице
| Номера предприятий |
Размер основных фондов, млн. руб. (Х) |
Выпуск продукции, млн. руб. (У) |
Ранжирование |
di =
Nx -
Nу
|
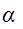 |
| Х |
У |
Nx
|
Nу
|
| 1 |
6,2 |
14,5 |
6.2 |
14.5 |
6.2 |
14.5 |
-8.3 |
| 2 |
7,3 |
19,5 |
7.3 |
19.5 |
7.3 |
19.5 |
-12.2 |
| 3 |
5,5 |
15,5 |
5.5 |
15.5 |
5.5 |
15.5 |
-10 |
| 4 |
8,8 |
11,5 |
8.8 |
11.5 |
8.8 |
11.5 |
-2.7 |
| 5 |
5,8 |
20,0 |
5.8 |
20.0 |
5.8 |
20 |
-14.2 |
| 6 |
6,6 |
17,5 |
6.6 |
17.5 |
6.6 |
17.5 |
- 10.9 |
| 7 |
5,9 |
24,5 |
5.9 |
24.5 |
5.9 |
24.5 |
-18.6 |
| 8 |
8,3 |
17,5 |
8.3 |
17.5 |
8.3 |
17.5 |
-9.2 |
| 9 |
7,4 |
18,5 |
7.4 |
18.5 |
7.4 |
18.5 |
-11.1 |
| 10 |
8,7 |
21,5 |
8.7 |
21.5 |
8.7 |
21.5 |
-12.8 |
Коэффициент Спирмена принимает любое значение в интервале (-1;1)
|
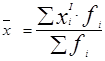 = 3*100/100 = 3
= 3*100/100 = 3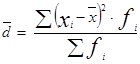 = 5*5/100 = 0.25
= 5*5/100 = 0.25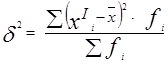 = 16*100/100 = 16
= 16*100/100 = 16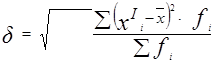

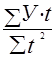 ;
;