Содержание
Введение
Глава 1. Методы решения задач на экстремумы
§1.История развития задач на экстремумы.
§2.Способы решения задач на экстремумы.
2.1 Элементарные приемы решения задач на экстремумы.
2.2 Универсальный метод решения задач на экстремум.
Глава 2.Применение уровневой дифференциации в обучении математике на примере темы «Задачи на экстремум».
§1.Дифференциация обучения.
1.1 Понятие дифференциации.
1.2 Уровневая дифференциация.
1.3 Плюсы и минусы уровневой дифференциации.
§2. Методические основы обучения решению задач на экстремумы
2.1 Задачи на экстремумы в школьном курсе математики (обзор учебников)
2.2 Методика обучения решению задач
Глава 3. Разработка факультативных занятий по теме «Решение задач на экстремум».
Занятие 1 – Тема: «Геометрический подход к решению задач на экстремумы»
Занятие 2 - Тема: «Геометрический подход к решению задач на экстремумы»
Занятие 3 - Тема: «Алгебраический подход к решению задач на экстремумы»
Занятие 4 - Тема: «Алгебраический подход к решению задач на экстремумы»
Занятие 5 - Тема: «Универсальный метод решения задач на экстремумы».
Заключение.
Библиография
Введение
С давних времен перед человеком возникают практические проблемы выбора оптимального значения некоторой величины при определенных условиях.
Как правило, в задачах подобного рода достижение некоторого результата может быть осуществлено не единственным способом и приходится отыскивать наилучший способ достижения результата.
Однако в одной и той же задаче в разных ситуациях наилучшими могут быть совершенно разные решения. Здесь все зависит от выбранного или заданного критерия. Например, каковы должны быть наилучшие очертания судна? Ответы будут разными в зависимости от того, для каких целей предназначено судно. Для разных целей различны будут и главные критерии. Критерии могут быть следующими:
1.Необходимо, чтобы при движении в воде судно испытывало наименьшее сопротивление (это главный критерий быстроходного судна)
2.Необходимо, чтобы судно было максимально устойчивым при сильном волнении и сильном ветре.
3.Необходимо, чтобы судно имело наименьшую осадку (в случае если судно предназначается для эксплуатации на мелких водоемах).
Задачи такого характера, получившие название задачи на экстремумы или задачи на оптимизацию, возникают в самых различных областях человеческой деятельности. И их роль в жизни людей действительно очень важна. Решением таких задач занимались крупнейшие математики прошлых эпох - Евклид, Архимед, Аполлоний, Герон, Тарталья, Торричелли, Ньютон и многие другие. Ведь, несмотря на все разнообразие, их объединяет одна особенность – поиск наиболее выгодного, в определенном отношениях, наиболее экономного, наименее трудоемкого, наиболее производительного. Этот поиск кратко можно назвать поиском лучшего.
Целью дипломной работы является изучение различных методов решения задач на экстремумы и адаптация их к школьному курсу математики.
Для достижения цели поставлены следующие задачи:
- подбор и изучение соответствующей теоретической и методической литературы;
- изучение элементарных (геометрических и алгебраических) методов решения задач на экстремумы;
- изучение применения методов математического анализа к решению задач на экстремумы;
- отбор теоретического материала, доступного для понимания школьниками;
- разработка факультативных занятий по изучению данной темы.
В первой главе дипломной работы рассматриваются история задач на экстремум, и различные методы решения задач на экстремумы.
Вторая глава дипломной работы посвящена изучению данной темы в школе с применением дифференцированного подхода: вводится понятие дифференциации и целесообразность использования дифференцированного подхода в обучении. Более подробно в работе рассмотрена уровневая дифференциация.
Далее в дипломной работе проведена методика обучения решению задач на экстремумы и,в частности, анализ изложения темы «задачи на экстремум» в школьных учебниках различных авторов. Были рассмотрены учебники под редакцией: Алимова Ш.А., Александрова А.Д., Погорелова А.В., Колмогорова А.Н., Башмакова М.И., Мордковича А.Г., Дорофеева Г.В., Виленкина Н.Я..
Третья глава диплома посещена разработке цикла факультативных занятий на тему: «Решение задач на экстремум», с применением дифференцированного подхода.
В заключении подведены итоги проведенной работы.
Глава 1. Методы решения задач на экстремумы
§1 История развития задач на экстремумы
Экстремальными задачами человек интересуется с античных времен. В Древней Греции уже давно (во всяком случае до VI века до н.э.) знали об экстремальных свойствах круга и шара: среди плоских фигур с одинаковым периметром наибольшую площадь имеет круг (среди пространственных фигур с одинаковой площадью поверхности (решение изопериметрической экстремальной задачи); шар имеет максимальный объем (решение изопифанной экстремальной задачи). История сохранила легенду о следующей самой древней экстремальной задаче, известной как задача Дидоны. Финикийская царевна Дидона (IX век до н.э.) решила организовать поселение на берегу понравившегося ей залива в Северной Африке. Она уговорила вождя местного племени отдать ей клочок земли, который можно охватить воловьей шкурой. Воины Дидоны разрезали шкуру на тонкие полоски, и Дидона охватила ремнем, составленным из этих полосок, участок земли на берегу залива. Так возник город Карфаген. Задача Дидоны состоит в указании формы границы участка, имеющей заданную длину, при которой площадь участка максимальна. Если знать экстремальное свойство круга, то решение получается немедленно: граница участка представляет часть окружности, имеющей заданную длину. Экстремальными задачами занимались многие античные ученые (Евклид, Архимед, Аристотель и др.). Известна следующая задача Евклида (IV век до н.э.): в заданный треугольник ABC вписать параллелограмм ADEF наибольшей площади. Нетрудно доказать, что решением этой задачи является параллелограмм, вершины D, E, F которого делят соответствующие стороны треугольника пополам.
После гибели античной цивилизации научная жизнь в Европе стала возрождаться только в XV веке. Задачи на экстремумы оказались среди тех, которыми интересовались лучшие умы того времени. Если в античные времена задачи на экстремумы исследовались только геометрическими методами и каждая задача для своего решения требовала специфического приема, то в XVII веке появились общие методы изучения задач на экстремумы, которые привели к созданию дифференциального и интегрального исчислений. Первые элементы математического анализа были созданы И. Кеплером (1615 год), который так описывает появление своего открытия: "Мне как хорошему хозяину следовало запастись вином. Я купил его несколько бочонков. Через некоторое время пришел продавец - измерить вместимость бочонков, чтоб назначить цену на вино. Для этого он опускал в каждый бочонок железный прут и, не прибегая ни к какому вычислению, немедленно объявлял, сколько в бочке вина". После размышлений Кеплер открыл секрет такого простого способа измерения объема бочек. Оказалось, что бочары за долгую историю научились изготавливать бочки такой формы, при которой они имели наибольший объем при заданной длине мокрой части прута. А поскольку в окрестности максимума значения функции изменяются мало (в этом суть открытия И. Кеплера), то торговец вина почти не ошибался при объявлении объема бочки по одному измерению.
Открытое И. Кеплером основное свойство экстремумов было затем оформлено в виде теоремы сначала П. Ферма (для многочленов), потом И. Ньютоном и Г. В. Лейбницем для произвольных функций и носит теперь название теоремы Ферма, согласно которой в точке экстремума x0 непрерывной функции f (x) производная функции равна нулю:
С тех пор исследование функций с помощью анализа бесконечно малых величин стало одним из мощнейших математических методов и привело к созданию современного математического анализа.
§2 Способы решения задач на экстремумы
Различны и многообразны приёмы и методы решения задач на экстремумы, как аналитические (перебора, оценки, неравенств и др.) так и геометрические (преобразование плоскости, оценка, перебор…). Каждый метод по-своему уникален и неповторим. Эти приёмы можно отнести к элементарным, т.к. они не предполагают применения математического анализа, а ограничиваются алгебраическим или геометрическим подходом к решению задачи на экстремум. Каждый их таких элементарных приемов является мостиком к решению не большого класса задач на экстремум, но методически для нас важен тем, что актуализирует знания учащихся из области алгебры или геометрии. Кроме того, применение этих методов для ряда задач будет более рационально, чем использование инструментов математического анализа, ибо незачем "стрелять из пушки по воробьям".
В отличии от элементарных приёмов, использование производной даёт нам метод действительно универсальный. Который можно применять для решения всего этого широкого спектра задач.
В этом разделе рассмотрены основные методы решении задач на экстремумы и их применение при решении конкретных задач.
2.1 Элементарные приемы решения задач на экстремумы
Геометрический подход к решению задач
Метод преобразования плоскости
В качестве одного из основных методов решения геометрических задач на экстремумы используется метод преобразования плоскости. Суть метода заключается в следующем.
Пусть требуется найти экстремум элемента х фигуры F, однозначно определенного элементами x,аi,i = 1,2,...,n.
Метод нахождения экстремума:
1) Элементу х зададим определенное значение х = С и решим задачу на построение фигуры Fпо заданным элементам х и аi.
2) Решив эту задачу, считаем элемент с перемещением. Затем, применяя те или иные преобразования плоскости, замечаем те особенности, которые возникают при достижении элементом х максимального или минимального значения.
Выделение указанной особенности позволяет сделать заключение об экстремуме элемента х фигуры F.
Посмотрим применение метода при решение конкретной задачи.
Пример 1:
Среди всех возможных треугольников с данным основанием а и противолежащим углом α найти треугольник, имеющий медиану максимальной длины.
Решение:
1)Обозначим длину медианы АК = х (рис.8). Пусть х = та (определенное число) и решим задачу: построить треугольник ABCпо данному углу А = α, противолежащей стороне а и медиане та

2) Решив эту задачу (используя методы построения), считаем длину медианы та переменной и замечаем особенности, возникающие при достижении медианой максимального значения.
3) Если точка А перемещается по окружности, то ВС и угол BACостаются постоянными, и длина медианы изменяется в пределах: А2К <та < А1 К.
4) Значит, из всех треугольников с данным основанием и противолежащим углом равнобедренный треугольник имеет наибольшую медиану.
Пример 2:
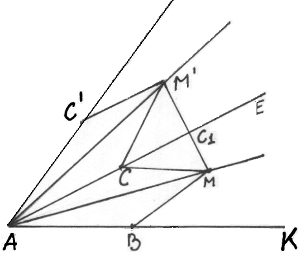
На плоскости нарисован угол A<900, внутри него задана точка М. Укажите на сторонах угла такие точки В и С, чтобы выполнялись условия: АВ = АС и сумма МВ+МС принимала наименьшее значение.
Решение:
Используем общие рассуждения метода преобразования плоскости. Неизвестный элемент в этой задаче представляет сумму MB + МС, т.е. х = МВ+ МС. Численное значение элемента х зависит от определения места расположения двух точек В и С.
Но так как граничного значения элемента х не видно, то решение задачи нужно свести к определению одной точки.
С этой целью применим поворот плоскости вокруг точки А на угол А=α. Точка В перейдет в точку С, точка С в С', точка М в М'. Теперь легко заметить, что численное значение х= МС+МВ = МС +М'С зависит только от расположения точки С, которая определит граничное значение элемента х = МС+М'С, и если C1=MM' AE, то M'C1 + MС1 = М M'. Но MB = М'С, поэтому min (МС + MB) = ММ1, где М'= RαА(М). AE, то M'C1 + MС1 = М M'. Но MB = М'С, поэтому min (МС + MB) = ММ1, где М'= RαА(М).
Пример 3:
Дан треугольник АВС и внутри него две точки в и Е. Как кратчайшим путем пройти из одной точки в другую, побывав на каждой стороне треугольника?
Решение:

Выполним следующее построение. Построим точки D1 и Е1, симметричные в и Е относительно АС и ВС. Построим также точку D2, симметричную D1 относительно АВ. Проведем отрезок D2Е1 и построим ломаную DMKLE. Длина ее равна длине отрезка D2Е1. Легко сообразить, что всякий иной путь из в в Е, с тем же порядком захода на стороны данного треугольника, будет длиннее. Но можно было бы порядок захода на стороны треугольника избрать иной (выполнив такие же построения). Всего таких ломаных линий, как DMKLE, получится три. Останется выбрать из них имеющую наименьшую длину, для чего достаточно сравнить три таких отрезка, как D2E1.
Метод перебора.
При решении геометрических задач на экстремумы в школе встречаются задачи, решение которых представляет собой выборку на конечном множестве объектов. Метод решения этих задач не является универсальным, так как он связан с решением задач, в которых рассматривается конечное множество фигур или фигура с размерами, выраженными натуральными числами. Однако роль этого метода очень важна, он воспитывает практические навыки учащихся, развивает потребность в нахождении оптимального результата оптимальной модели.
Рассмотрим задачу, в которой нахождения наибольшего (наименьшего) значения зависит от взаимного расположения фигур.
Пример 1: Из листов материала прямоугольной формы размером 60x130 мм выкроить заготовки двух типов, в таком количестве:
| Тип заготовок |
Размер заготовки |
Число штук |
| М |
2x3 мм |
150 |
| В |
4x5 мм |
50 |
Определите минимальный процент отходов.
Решение:
Эта задача играет важную иллюстративную роль. Она позволяет разъяснить учащимся характер задачи рационального раскроя промышленных материалов и основные методические приемы, которые нужны при их решении.
С целью облегчения поисков решения данной задачи следует предложить учащимся исходные данные листа материала и заготовок с соответствующим масштабом на рисунке. Далее нетрудно видеть, что каждый лист материала можно раскроить различными способами, получая при этом большее или меньшее количество заготовок. Приведем возможные способы раскроя листа материала
1 способ:
2 способ:
3 способ:
4 способ:
5 способ:
6 способ:
И посчитаем в каждом случае потери материала при каждом раскрое. Это дает возможность рассмотреть все возможности варианты раскроя и выбрать наилучший. На этом пути приходится встречаться с методом перебора. Результаты рассуждений целесообразно свести в таблицу, из которой легко сделать вывод об оптимизационном расходе материала
| Способ |
1 |
2 |
3 |
4 |
5 |
6 |
| Количество заготовок типа М |
9 |
5 |
6 |
1 |
0 |
13 |
| Количество заготовок типа В |
1 |
2 |
2 |
3 |
3 |
0 |
| Потери площади в кв. ед. |
4 |
8 |
2 |
12 |
18 |
0 |
Оптимальный план раскроя состоит в том, что 25 листов материала нужно раскроить способом 3, при этом потеря материала будет минимальной, то есть 2,6 %.
Достаточно изменить число заготовок и задача станет более сложной, тогда она может быть предложена учащимся для индивидуальной работы.
Пример 2: (Задача о наименьшей площади.)
Дан угол и точка внутри него. Требуется провести через эту точку прямую, отсекающую от угла треугольник наименьшей площади.
Решение.
Покажем, что искомая прямая обладает тем свойством, что отрезок ее, лежащий внутри угла, делится заданной точкой пополам. Такую прямую нетрудно построить. Можно, например, соединить заданную точку М с вершиной А, на продолжении отрезка [AM] отложить отрезок [MA'], равный по длине отрезку [AM], и провести через точку А' прямую параллельно АС. Пусть D- точка пересечения этой прямой и стороны АВ. Тогда, как легко понять, прямая, соединяющая точку в с точкой М и пересекающая АС в точке Е, обладает тем свойством, что |DM| = |ME| (ибо треугольники

MDA'и МЕА равны)
Искомая прямая построена. Возможны и другие способы построения.
Докажем теперь, что построенная прямая

действительно является искомой. Для этого проведем какую-нибудь еще прямую D'E'. Пусть для определенности точка Е' лежит вне Е. тогда площадь треугольника AE'D' равна площади треугольника AED минус площадь треугольника EME' и плюс площадь треугольника MDD'. Обозначим через F точку пересечения прямой DA' с прямой D'E'. Тогда треугольники EME' и MDF равны. Но второй из этих треугольников содержится в треугольнике DD'M. Из сказанного вытекает, что площадь треугольника ADE меньше площади треугольника AD'E'.
Пример 3.
В шар радиуса R вписан конус, осевое сечение которого – равносторонний треугольник. Определить, между какими пределами может изменяться разность площадей двух сечений, из которых первое (КGFD) получается в результате пересечения шара плоскостью, параллельной основанию конуса, а второе(NPF) – в результате пересечения конуса той же плоскостью.
Решение.
Площади обоих сечений равны нулю в том случае, когда проводимая плоскость касается шара в точке В (вершина конуса). Площади обоих сечений будут равны, когда проводима плоскость совпадает с плоскостью основания конуса. Когда же проводимая плоскость занимает промежуточное положение между положениями рассмотренными выше, то площади сечений шара и конуса не равны. Итак, разность S площадей сечений шара и конуса изменяется от нуля до нуля, переходя через максимум, который мы определим.
S=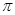 ( MK2- MN2 ); OB=R; MB=x; ( MK2- MN2 ); OB=R; MB=x;
MK2 = OK2 – OM2 = R2- (R - x)2 = 2Rx – x2/
Так как ∆ АВС равносторонний по условию и АС || NP, то и ∆ NBP также равносторонний, следовательно, MN2 = 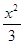 . .

Следовательно S= 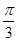 2x (3R – 2x), 2x (3R – 2x),
которое будет максимально, когда максимально S1= 2x(3R- 2x). Так как сумма множителей 2x + 3R - 2x = 3R, то S1 максимально, когда 2х= 3R- 2х, т.е. х= ¾R. Следовательно, максимальное значение S равно  . .
Метод оценки.
Суть метода состоит в следующем. Рассматривается конкретная геометрическая фигура F, выделяется одна или несколько величин, которые характеризуют данную фигуру. Требуется оценить выделенную величину или совокупность величин, то есть доказать, что величина Z удовлетворяет одному из неравенств вида: Z<Mили Z>m, (1) где т и М определяются условием задачи.
Для решения задачи требуется установить справедливость одного из неравенств (1), то есть доказать, что для каждого Z, принадлежащего одному из неравенств (1), фигура Fсуществует и ни для одного числа Z, не удовлетворяющего неравенству, фигура Fне существует. Заключительным этапом решения задачи является определение экстремальных значений т и М.
Задачи, имеющиеся в учебниках геометрии, чаще всего решаются методом оценки.
Пример 1:
Примером может послужить такая задача.
Расстояние от пункта А до В 4 км, а от В до С в двое больше. Какое наибольшее и наименьшее расстояние может быть от пункта А до пункта С.
Решение:
Расстояние АС зависит от места расположения точки С. Так как расстояние ЕС постоянное, то точка С принадлежит точкам окружности с

R = BC, В - центр. Легко заметить какие граничные значения может принимать АС,4 = АС2 < AСi <АВ + BCi= 12.
Отсюда, наибольшее: [АСi] = 12км;
наименьшее: [АСi ] = 4 км.
Искомыми точками Сi являются концы диаметра длиной 16 км с центром окружности в точке В.
Пример 2:
На озере, имеющем форму круга, расположен объект длиной ОА. В каком месте на берегу должен остановиться наблюдатель, чтобы наилучшим образом рассмотреть объект ОА (О - центр круга)?
Решение:
Пусть М - произвольная точка окружности k. Ставится задача оценить величину угла AMiO.
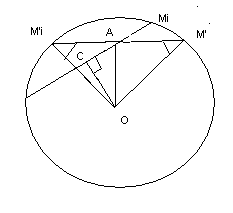
Если M k, а С k, а С  МiА и МiА МiА и МiА  ОС, то ОС, то
0° < АМiO < AM'О так как ОС ≤ ОА.
Задача имеет два решения:
max( AMiO) = AMiO) = AM'О= AM'О=  AM'iО, AM'iО,
где ОА  M'M'i M'M'i
Пример 3:
Рассмотрим еще задачу об экономном расходовании материалов. Попытаемся установить, для какой крыши (двускатной или четырехскатной) потребуется больше кровельного материала.
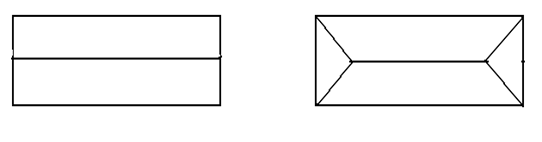
Решение:
Будем считать, что оба ската двускатной крыши наклонены к горизонтальной плоскости под углом φ, скаты 1 и 2 четырехскатной крыши – под тем же углом φ, а 3 и 4 – под углом α. При этих предположениях и указанных на чертеже размерах площадь двускатной крыши будет равна  , а четырехскатной - , а четырехскатной -  . Для сравнения этих площадей рассмотрим разность их . Для сравнения этих площадей рассмотрим разность их  . Здесь b>0, m>0, 0<α<900 и 0<φ<900. Поэтому при α<φ получим S2-S1<0, при α=φ будем иметь S2-S1=0, а при α>φS2-S1<0. Следовательно, если все скаты как двускатной, так и четырехскатной крыш будут одинаково наклонены к горизонтальной плоскости, то кровельного материала понадобится одинаково на обе крыши. Если же скаты 3 и 4 четырехскатной крыши будут иметь больший угол наклона, чем скаты 1 и 2, то для четырехскатной крыши кровельного материала понадобится больше, чем для двускатной, а при меньшем угле – меньше. . Здесь b>0, m>0, 0<α<900 и 0<φ<900. Поэтому при α<φ получим S2-S1<0, при α=φ будем иметь S2-S1=0, а при α>φS2-S1<0. Следовательно, если все скаты как двускатной, так и четырехскатной крыш будут одинаково наклонены к горизонтальной плоскости, то кровельного материала понадобится одинаково на обе крыши. Если же скаты 3 и 4 четырехскатной крыши будут иметь больший угол наклона, чем скаты 1 и 2, то для четырехскатной крыши кровельного материала понадобится больше, чем для двускатной, а при меньшем угле – меньше.
Алгебраический подход к решению задач
Встречаются такие задачи на отыскание наибольшей и наименьшей величины, которые оптимальнее всего решать методами элементарной математики.
Использование квадратичной функции
При решении задач этим методом мы будем опираться на следующую теорему:
Теорема 1. Функция ах2 + вх + с при а>0 имеет наименьшее значение, равное (4ас-b2)/4, и при а<0 - наибольшее значение, равное тоже (4ас-b2)/4. Эти наименьшие и наибольшие значения получаются при х = - b/2а.
Доказывается эта теорема с помощью выделения полного квадрата. Приведем примеры.
Пример:
Найти наименьшее значение функции
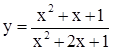
и построить ее график.
Поиски решения.
Данную функцию можно изобразить аналитически так:

Отсюда видно, что при х = -1 она теряет смысл, а при всех других действительных значениях х принимает только положительные значения. Следовательно, ее наименьшим значением может быть только положительное число. Обнаружить это наименьшее значение непосредственно не представляется возможным. Поэтому надо обратиться к каким-то целенаправленным преобразованиям данного аналитического изображения функции.
Решение:
Очевидно, что

Обозначив дробь 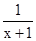 буквой u, получим: буквой u, получим:

Искомое наименьшее значение равно  и получается оно при и получается оно при  т.е. при т.е. при
х = 1
Перейдем к построению графика данной функции. Составим таблицу нескольких значений х и у, пользуясь формулой

| х |
-3 |
-2 |
-3/2 |
-1 |
-1/2 |
0 |
1 |
2 |
3 |
… |
| у |
7/4 |
3 |
7 |
Х |
3 |
1 |
3/4 |
7/9 |
13/16 |
… |
Если аргумент х будет приближаться к -1 (слева или справа), то у будет неограниченно возрастать.
Теперь посмотрим, как будет вести себя у, когда х станет стремиться к плюс бесконечности или минус бесконечности. Очевидно, что
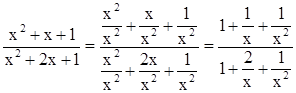
Отсюда видно, что при стремлении х к бесконечности у стремится к 1.
Пример 2:
Требуется соорудить канал с поперечным сечением ABDC, где АВ=CD, АВ и CD перпендикулярны к BD. Сумма длин АВ, ВD и СD должны быть равной Р метрам.
Спрашивается, какими надо сделать ширину и глубину канала, чтобы площадь его поперечного сечения, т.е. площадь прямоугольника с вершинами в точках А, В, С, D, оказалась бы наибольшей?
Поиски решения.
Поскольку мы еще не знаем, какими надо сделать глубину и ширину канала, то естественно обозначить эти переменные какими-либо подходящими буквами. Например, положить АВ = х и BD = у. Далее надо выразить через х и у ту величину, наибольшее значение которой нам надо найти, т.е. площадь сечения канала. Эта площадь выразится произведением ху, т.е. будет зависеть от двух переменных величин х и у. Но наше исследование облегчится, если нам удастся выразить площадь в зависимости только от одной переменной. Очевидно, что в данном случае это сделать легко, т.к. по условию задачи 2х + у = Р.
Решение.
Пусть АВ = х, тогда и CD = х, а BD = P - 2x. Площадь сечения будет равна х (Р - 2х). Задача сводится к определению наибольшего значения функции х (Р - 2х), которая представляет собой многочлен второй степени, имеющий вид -2х2+Рх. Очевидно, что
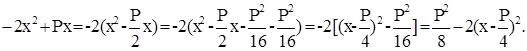
Отсюда видно, что наибольшая площадь получится в том случае, когда мы сделаем глубину канала х = Р/4. Тогда окажется ширина у равной Р/2, а наибольшая площадь равной Р2/8.
Пример 3:
Найти наименьшее и наибольшее значение функции y=4x+6|x-2|-x2 на отрезке [-1;3].
Решение:
y=-( x2-4x+4-4)+ 6|x-2|=-(x-2)2 +6|x-2|+4. Так как а2=|а|2, то
y= -|x-2|2+6|x-2|+4. Пусть t=|x-2|. Поскольку -1 ≤ х ≤ 3, то 0 ≤ t ≤ 3. При этом y=-t2+6t+4 возрастает и, следовательно,
miny(t)=y(0)=4, maxy(t)=y(3)=13.
[0;3] [0;3]
Если t=0, то x=2. Если t=3, то |x-2|=3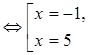
Но по условию х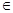 [-1;3], поэтому остается только значение х=-1. [-1;3], поэтому остается только значение х=-1.
Ответ: miny(х)=y(2)=4, maxy(х)=y(-1)=13.
[-1;3] [-1;3]
Оценок и неравенств
Теорема 2.
Функция х + 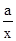 , где а > 0 и x > 0, имеет наименьшее значение равное 2 , где а > 0 и x > 0, имеет наименьшее значение равное 2 . Это наименьшее значение получается при х = . Это наименьшее значение получается при х =  . .
 или или 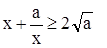 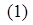
Очевидно, что  . .
Отсюда следует, что наименьшее значение получается при х – 2 =  , т.е. при х = 6, а само наименьшее значение равно 10. , т.е. при х = 6, а само наименьшее значение равно 10.
Теорема 3.
Если сумма двух положительных переменных величин постоянна, то произведение этих переменных имеет наибольшее значение, когда оба сомножителя принимают одинаковые значения.
Доказательство.
Пусть х и у - положительные переменные величины и пусть х + у = с, где с - постоянная величина. Применяя неравенство о среднем арифметическом и среднем геометрическом, получим:
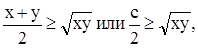 или, наконец, или, наконец, 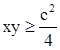
Отсюда очевидно, что наибольшее значение произведения ху равно с2/4 и получается оно при х = у.
Теорема 4.
Если сумма n положительных переменных величин постоянна, то произведение этих переменных имеет наибольшее значение, когда все эти переменные принимают одинаковые значения. (Эта теорема является обобщением теоремы 3.)
Доказательство.
Пусть х1, х2, …, хn - положительные переменные величины и пусть х1 + х2 + … + хn = с, где с - постоянна. По теореме Коши о среднем арифметическом и среднем геометрическом имеем:

Отсюда х1х2…хn≤(с/n)n ( здесь знак равенства имеет место тогда и только тогда, когда х1 = х2 = …= хn). Следовательно, наибольшее значение произведения х1х2…хn равно (c/n)n и получается оно при х1 = х2 = …= хn. Теорема доказана.
Пример 1:
Найти наибольшее значение функции х4(32-х4).
Поиски решения.
Данная функция принимает отрицательные значения при 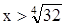 , а при , а при  -положительные. Поскольку ее наибольшее значение надо искать среди значений х меньших , чем -положительные. Поскольку ее наибольшее значение надо искать среди значений х меньших , чем 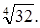
Если мы положим х4 = у, то задача сведется к нахождению наибольшего значения многочлена второй степени, имеющего вид:
- у2 +32у.
Однако если проявить наблюдательность и заметить, что сумма множителей х4 и (32 - х4) является величиной постоянной, то можно воспользоваться теоремой 3 и решить задачу проще.
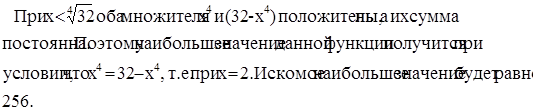
Пример 2:
Найти наибольшее значение функции 3х2 - 2х3 при 0<х<3/2.
Поиски решения.
Во-первых, выясним, почему здесь на независимую переменную х наложены ограничения. Если допустить, что х<0, то данная функция не будет иметь наибольшего значения, так как она будет неограниченно возрастать при неограниченном возрастании абсолютной величины аргумента х, принимающего отрицательные значения. Например, при х = -1000 значение данной функции будет равно 3 10002 + 2 10003. Если же допустить, что х>3/2, то окажется, что 3х2 - 2х3<0. При значениях же х, заключенных между нулем и числом 3/2, все значения данной функции будут положительными. Поэтому наибольшее значение надо искать при таких значениях х, которые удовлетворяют неравенствам 0<х<3/2.
Если мы запишем нашу функцию в виде х2 (3 - 2х), то увидим, к сожалению, что сумма сомножителей х2 и (3 - 2х) не постоянна. И вот тут-то надо проявить изобретательность и записать данную функцию в виде произведения трех сомножителей, а именно так: х х (3 - 2х).
Решение. Очевидно, что 3х2 - 2х3 = х2(3 - 2х) = х х (3 - 2х).
При условиях нашей задачи в последнем произведении все три множителя положительны и их сумма равна 3, т.е. является величиной постоянной.
По теореме 4 наша функция будет иметь наибольшее значение при условии, что х = х = 3 - 2х, т.е. при х = 1. И само наибольшее значение нашей функции будет равно тоже 1. Если мы положим, например, х = 5/4, то значение нашей функции окажется равным 25/32, т.е. окажется меньшим единицы.
Пример 3:
Найти наибольшее значение функции 
y=4 на интервале (-∞; на интервале (-∞;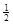 ). ).
Решение:
y=4 = =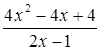 = = =2x-1+ =2x-1+ . .
Так как по условию х<1/2, то 2х-1<0 и  <0. Воспользуемся неравенством | at+b/t | ≥2 <0. Воспользуемся неравенством | at+b/t | ≥2
для случая t<0. Тогда y=2х-1+ ≤-2 ≤-2 , причем знак неравенства достигается тогда и только тогда, когда , причем знак неравенства достигается тогда и только тогда, когда
2х-1=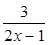 , и 2х-1<0 . , и 2х-1<0 .
И последней системы находим х=
Ответ: maxy(x)=y( )=-2 )=-2
(-∞;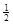 ) )
2.2 Универсальный метод решения задач на экстремумы
Мы рассмотрели довольно много задач на нахождение экстремумов. Те приемы, которыми мы решали эти задачи, оказались весьма разнообразными и порой, довольно искусственными. Дело обстоит так, что почти для каждой задачи на экстремум приходилось «изобретать» подходящий для нее прием. Возникает поэтому вопрос: а нет ли достаточно общего приема решения задач на экстремумы? Такой прием есть. Его дает математический анализ.
Общий прием решения задач на экстремум опирается на теорему Ферма.
Если функция у = f(х) (имеющая локальную производную) при х = х0 принимает локальный максимум или минимум, то производная от этой функции при х = х0 обращается в 0.
Геометрически это означает, что касательная к графику функции в соответствующей точке его параллельна оси х-ов

Теорема Ферма очень наглядна. И все же докажем ее.
Пусть х0 - точка максимума функции у = f(x), т.е. при х = х0 эта функция принимает наибольшее значение. Дадим х0 достаточно малое приращение h. Новое значение аргумента х0 + h будет достаточно близким к х0, и т.к. при х = х0 данная функция имеет максимум, то f(x0+h)-f(x0)≤0. Поэтому
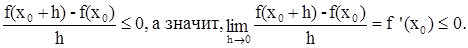
Если же дать х0 отрицательное приращение (достаточно малое по абсолютной величине), то получим:
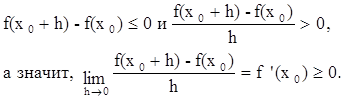
Оказалось, что одно и то же число f '(x0) не положительно и неотрицательно. Это означает, что это число равно 0, т.е. f '(x0) = 0. Рассуждения в случае минимума аналогичны.
Чему же учит нас теорема Ферма? Она учит нас тому, что значения аргумента, при которых данная функция f(x) имеет локальные минимумы, следует искать среди корней уравнения f '(x) = 0. Она выражает необходимое условие экстремума:
Для того чтобы функция (имеющая производную) имела при х = х0 максимум или минимум, необходимо, чтобы производная при этом значении х была равна 0.
Необходимо, но не достаточно! Производная может быть равна 0, и все же при этом значении х функция экстремума может и не иметь. Так, например, производная функции у = х3 (у' = 3х2) при х = 0 обращается в 0, но эта функция при х = 0 экстремума не имеет (рис.2). Значит, уравнение f '(х) = 0 дает лишь «подозрительные» на экстремум значения х.
Как же из этих «подозрительных» значений выделить те, при которых рассматриваемая функция действительно имеет экстремумы?
Как для выделенных значений установить вид экстремума?
По этим вопросам мы ограничимся соображениями, источником которых является наглядность. Рассмотрим рисунок, на котором изображены максимум и минимум функции у = f(x). По этому рисунку установим, какие по знаку значения принимает производная функция f '(x) для значений х, достаточно близких к х0, меньших и больших его. Если при х = х0 данная функция имеет максимум, то для значений х, меньших х0, но достаточно близких к х0, производная будет положительна, а для больших- отрицательна, т.к. в первом случае касательная к графику функции образует с положительным направлением оси х-ов острый угол, а во втором- тупой.
Если же при х = х0 функция принимает минимальное значение, то получается наоборот. Таким образом, будет ли «подозрительная» точка х0 точкой экстремума и, если будет, то какого именно (максимума или минимума), зависит от значений, принимаемых в достаточной близости слева и справа от точки х0 производной функцией. Все возможные случаи можно записать в следующей таблице.
| х0+Δх, Δх<0 |
х0 |
х0+Δх |
Поведение f(x) |
f '(x)
f '(x)
f '(x)
f '(x)
|
+
-
+
-
|
0
0
0
0
|
-
+
+
-
|
максимум
минимум
возрастает (экстремума нет)
убывает (экстремума нет)
|
Вот этой таблицей и можно пользоваться при решении задач на экстремумы.
Но можно из этой таблицы сделать новые выводы и пользоваться ими. Вот о каких выводах идет речь. В случае максимума с возрастанием х и переходом через значение х0 производная убывает, поэтому производная от этой производной(т.е. производная второго порядка) отрицательна. В случае минимума производная при переходе х через х0 возрастает, а значит, производная второго порядка положительна. Поэтому если в «подозрительной» точке х0 производная второго порядка f ''(x0) отрицательна, то в этой точке данная функция имеет максимум, если же f ''(x0) положительна, то функция принимает минимальное значение.
Чтобы проиллюстрировать рассмотренный общий прием решения задач на экстремумы, рассмотрим пример.
Пример 1: (Задача о прямоугольнике наибольшей площади)
Из куска стекла, имеющего указанные форму и размеры, нужно вырезать прямоугольную пластину наибольшей площади.
Решение.
Площадь пластины S = xy. За независимую переменную примем х (0<х≤100). Тогда из подобия треугольников АВЕ и СDЕ следует:
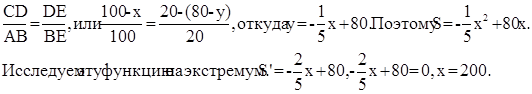
Найденное значение х выходит из промежутка изменения х. Поэтому внутри этого промежутка стационарных точек нет. Значит, наибольшее значение S принимает в одном из концов промежутка, а именно при х = 100 (мм), а тогда у = 60 (мм) и S = 6000 (мм2).
Пример 2: (Задача о скорости течения воды в трубе)
По трубе, сечение которой круг с радиусом r, течет вода. Известно, что скорость течения пропорциональна так называемому гидравлическому радиусу профиля сечения (заполненного водой). Гидравлическим же радиусом профиля называется отношение площади профиля к длине смоченного (подводного) периметра профиля. При каком заполнении трубы водой скорость течения (при неизменных других условиях) будет наибольшей?
Решение:
Воспользуемся обозначениями: α - центральный угол сегмента заполнения трубы водой (в радианах), F- площадь этого сечения и R- гидравлический радиус. Тогда площадь сегмента OABC равна ½ r2α, а площадь треугольника AOB равна

Поэтому

Смоченный периметр равен rα, а значит,
R=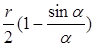
Эта формула будет верна и в том случае, когда α будет больше π. Вообще, α может меняться от 0 до 2π.
Найдем R'и составим уравнение для нахождения критических значений α. Получаем

но α ≠ 0, поэтому sinα - αcosα = 0, или tgα = α. Полученное уравнение может быть решено графически. Единственный корень его α ≈ 4,5, или α ≈ 2580.
Нетрудно сообразить, что производная от R, равная
при переходе через α ≈ 4,5, меняет знак с + на -. Значит, при α ≈ 2580 скорость течения будет наибольшей.
Пример 3:(Задача о наибольшем количестве теплоты).
Рассматривая основной метод решения задач на экстремум, мы ограничивались функциями, имеющими во всех точках области определения производную. Но экстремум может достигаться функцией и в такой внутренней точке области определения, где производная не существует. Такими точками являются точки излома графика, угловые точки и, в частности, может быть точки, разделяющие график на части, задаваемые разными формулами. Приведем пример.
На электроплитке кипятится чайник. Установить, когда он обладает наибольшим количеством теплоты.
Для облегчения решения будем считать коэффициент полезного действия плитки равным 100 %. Отсчет времени проведем с момента, когда чайник был поставлен на плитку. Пусть в этот момент чайник обладал q калориями теплоты. Количество теплоты (в калориях), выделенное плиткой, выражается функцией Q = 0,24J2Rt, где J- сила тока в амперах, R- сопротивление в Омах и t- время нагревания в секундах, а количество теплоты в чайнике в момент времени t равно q + 0,24J2Rt. Когда чайник закипит (в момент времени t0), вода начнет испаряться. Известно, что на образование одного грамма пара уходит 539 калорий. За одну секунду плитка выделит теплоты 0,24J2R калорий, которая идет полностью на парообразование. Поэтому за 1 секунду выкипает
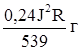
воды, и с ней уносится из чайника
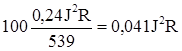
калорий (множитель 100 здесь появляется потому, что температура кипящей воды 1000 С). Если t > t0, то выкипевшая вода унесет из чайника 0,041J2R(t - t0) калорий и останется q + 0,24J2Rt0 - 0,041J2R(t - t0) = -0,041J2Rt + q + 0,281J2Rt0 калорий. Значит, количество теплоты в чайнике выражается функцией

График этой функции состоит из двух прямолинейных участков. Угловой точкой его является точка А, в которой функция не имеет производной. По графику видно, что рассматриваемая функция имеет максимум при t = t0, равный 0,24J2Rt0 + q.
Подведем итог. Для разыскания экстремальных значений функции нужно прежде всего найти все локальные экстремумы. С этой целью нужно найти все стационарные точки, для каждой из них воспользоваться достаточными условиями минимума и максимума и вычислить экстремум в этих точках. Далее нужно вычислить значение функции в точках (если функция в них определена), где не существует производная от данной функции. Из всех найденных таким образом значений функции надо выбрать наибольшее и наименьшее.
Можно поступать и иначе. Сначала вычислить значения рассматриваемой функции во всех “подозрительных” (в отношении существования экстремумов) точках: стационарных, концевых и где не существует производная. Наибольшее и наименьшее из этих чисел и будут искомыми наибольшим и наименьшим значениями функции.
Глава 2. Применение уровневой дифференциации в обучении математики на примере темы «Задачи на экстремумы»
§1 Дифференциация обучения
1.1 Понятие дифференциации
Обучение всех школьников по единым программам не позволяет ребенку получить образование на уровне своих возможностей. Для кого-то оказывается непосильным даже средний уровень требований, а кто-то, наоборот, недополучает знаний.
Введем понятие дифференциации. Это слово происходит от латинского differentia - различие, разделение. Что же разделяется в процессе обучения? Разделяются, а точнее, выделяются отдельные группы учащихся, обучение которых строится по-разному.
Для чего выделяются эти группы? Ответив на данный вопрос, мы определим цели дифференциации.
В условиях классно-урочной системы, без введения дифференциации процесс обучения, организуется одинаково для всех учащихся и оказывается, по-разному эффективен для них. Общие интеллектуальные способности учеников разные, разная у них и обучаемость кто-то может очень быстро усвоить новый материал, кому-то нужно гораздо больше времени, большее число повторений для закрепления его, для кого-то предпочтительнее слуховое восприятие новой информации, для кого-то зрительное. Есть ученики, обладающие хорошо развитым логическим мышлением и хорошо усваивающие предметы естественно-математического цикла, но не испытывающие склонности и интереса к гуманитарным дисциплинам. А есть ученики с хорошо развитым образным мышлением, глубоко чувствующие, но... не любящие математику, физику, химию. Конечно, можно учить столь разных индивидов одинаково, но качество образовательного процесса, естественно, снизится.
Дифференциация обучения позволяет организовать учебный процесс на основе учета индивидуальных особенностей личности, обеспечить усвоение всеми учениками содержания образования, которое может быть различным для разных учащихся, но с обязательным для всех выделением инвариантной части. При этом каждая группа учеников, имеющая сходные индивидуальные особенности, идет своим путем. Процесс обучения в условиях дифференциации становится максимально приближенным к познавательным потребностям учеников, их индивидуальным особенностям.
Немаловажной задачей процесса обучения является развитие ученика: его интеллектуальной, эмоционально-ценностной, волевой сфер. Организуя дифференцированное обучение, мы усиливаем развивающие функции процесса обучения: например, в естественно-математических классах будет обращаться внимание на развитие таких мыслительных операций ученика, как анализ, синтез, выявление закономерностей и т.п., таких элементов творческой деятельности, как видение и формулирование проблемы, выдвижение гипотез, их проверка и т.д. В гуманитарных классах больше внимания будет уделено развитию образного мышления, выразительности речевых средств и т.д. В классе коррекционно-развивающего обучения на первый план выступят задачи развития тех школьно-значимых функций, которые не достаточно развиты у ученика.
Таким образом, цель дифференциации процесса обучения - обеспечить каждому ученику условия для максимального развития его способностей, склонностей, удовлетворения познавательных потребностей и интересов в процессе усвоения им содержания общего образования.
Указанная формулировка целей дифференциации свидетельствует, что характерным для нашего понимания дифференциации является выделение ее направленности на максимальное развитие каждого ученика, создание ему комфортных условий образовательного процесса. Дифференциация не направлена на селекцию детей и отбор самых талантливых с предоставлением им наиболее благоприятных условий развития. В условиях дифференциации педагог так видоизменяет процесс обучения, чтобы и менее способные дети смогли максимально развить свои способности и склонности и успешно освоить инвариантное содержание образования.
Учитывая все вышесказанное, в понимании дифференциации можно выделить три основных аспекта:
1.Учет индивидуальных особенностей учащихся.
2.Группирование учеников на основании этих особенностей.
3.Вариативность учебного процесса в группах.
Любые ли особенности нужно учитывать при дифференциации? Конечно же, нет, только те, которые важны для организации процесса обучения. Например, цвет глаз или волос ребенка учитываться не будут, тогда как скорость протекания нервных процессов, преобладающий тип памяти, сформированность интеллектуальных операций - в условиях дифференциации учитываются.
Рассмотрим кратко те особенности, которые следует учитывать в первую очередь при дифференциации учебной работы.
Сюда относится, прежде всего, уровень умственного развития учащегося. Это понятие включает предпосылки к учению (обучаемость - способность достигать в более короткий срок более выгодного уровня усвоения) и приобретенные знания (обученность).
К понятию обучаемости близко понятие общих умственных способностей. Под ними обычно понимается комплекс способностей, требуемых для осуществления учащимися учебной деятельности. Сюда относится способность запоминать материал, способность проведения логических операций, способность творческого мышления.
С умственными способностями тесно связана способность учащихся самостоятельно усваивать, знания, предполагающая наличие у них соответствующих интеллектуальных умений.
Следующей важной особенностью является скорость усвоения - комплексное явление, существенный показатель которого не столько скорость запоминания, сколько темп обобщений.
Кроме умственных способностей в учебной работе проявляются и специальные особенности, а также одаренность детей (прирожденные задатки для формирования способностей).
Школьные программы построены так, что все последующее опирается на уже пройденное, усвоенное. На каждом этапе обучения приобретаются соответствующие знания, вырабатываются определенные умения и навыки. Умственные способности представляют собой потенциальные возможности для учения, полученные же знания, являются базой для реализации способностей. При обучении предмету следует учитывать также индивидуальные различия в знаниях. Эти различия могут быть вызваны тем, что кто-то из учащихся может владеть предметом (например, школьник дополнительно обучается в музыкальной или художественной школе).
Кроме личностных психологических факторов на учебный процесс свое влияние оказывают:
- социальные факторы (статус ученика в классе, домашняя обстановка);
- состояние здоровья ребенка. Болезни, в зависимости от их характера, оказывают на учащегося временное или постоянное отрицательное воздействие, снижают его трудоспособность; и многое другое.
Резюмируя сказанное, можно выделить следующие обобщенные особенности учащихся, которые в первую очередь следует учитывать при индивидуализации учебной работы:
1) обучаемость, т.е. общие умственные способности, а также специальные способности;
2)учебные умения;
3)обученность, которая состоит как из программных, так и внепрограммных знаний, умений и навыков;
4)познавательные интересы;
5)социальные факторы.
Обратимся к практике дифференциации, которая в настоящее время представлена множеством различных проявлений, попытаемся их систематизировать.
Конкретные проявления дифференциации мы называем формами дифференцированного обучения, которые могут быть объединены в виды и реализовываются на различных уровнях.
Виды дифференциации определяются, исходя из тех индивидуально-типологических особенностей учащихся, которые в данном случае учитываются.
Традиционно выделяются следующие виды дифференцированного обучения: по общим и специальным способностям, по интересам, склонностям, по проектируемой профессии.
Понимание дифференциации по общим способностям предполагает учет уровня общих способностей учащихся, т.е. низкий уровень их развития и будет являться основанием для дифференциации по неспособностям.
К традиционным видам дифференциации в настоящее время добавилась дифференциация по национальному признаку, когда создаются специальные школы для детей различные национальностей, например в г. Москве — это армянские, грузинские, еврейские школы (сейчас они называются школами с этнокультурным компонентом); по религиозной принадлежности — православные школы, есть школа ведической культуры «Гурукула»; по социальному и имущественному положению родителей — в некоторых негосударственных образовательных учреждениях могут учиться только дети обеспеченных родителей, т.к. велика плата за образование.
Дифференциация может осуществляться на различных уровнях. Обычно выделяют три уровня:
I-й микроуровень, когда различный подход осуществляется к отдельным группам детей внутри класса. Этот уровень дифференциации иногда называется внутренней или внутриклассной.
II-й мезоуровень – уровень школы, когда дифференциация осуществляется внутри школы между отдельными классами, профилями, направлениями.
III-й макроуровень - дифференциация между школами, создание различных типов школ. Второй и третий уровень представляют собой дифференциацию внешнюю.
Разновидностью внутриклассной дифференциации по общим способностям является уровневая дифференциация. Остановимся на ней белее подробно.
1.2 Уровневая дифференциация
Очень плотно уровневой дифференциацией занимались Г.В. Дорофеев, В.В. Фисов и др. Организацию учебного процесса с учетом уровневой дифференциации они назвали разноуровневым обучением. Оно выражалось в том, что, обучаясь в одном классе, по одной программе и учебнику, школьники могут усваивать материал на разных уровнях. Определяющем при этом является уровень обязательной подготовки. Его достижение свидетельствует о выполнении учеником минимально необходимых требований к усвоению содержания. На его основе формируются более высокие уровни овладения материалом.
При такой дифференциации учитель четко выделяет содержание учебного материала, который ученики должны усвоить, занимаясь на том или ином уровне, и перед началом изучения темы должен познакомить учеников с результатами которых они должны достичь (т.е. с планируемыми результатами обучения).
В основе данного вида дифференциации лежат не только общие способности учеников, но и их интересы. Ученик может выбрать минимальный уровень изучения предмета не потому что не способен изучить его глубже, а потому что его интересы лежат в другой познавательной области.
Предлагая обязательные результаты обучения, их авторы исходили из того, что в процессе обучения учителя всегда ориентировались на максимум содержания материала. Если ученик полностью осваивал этот максимум, его знания оценивались 5 баллами, если был незначительные пробелы или неточности - 4 баллами и т.д. Добросовестный ученик был ориентирован именно на максимум знаний и изо всех сил старался его усвоить. Это вызывало у него перегрузку, так как на максимум знаний надо было усвоить по всем предметам.
Авторы идеи уровневой дифференциации предложил перейти в процессе обучения от ориентации на максимум содержания к ориентации на его минимум. При этом необходимым является четкое определение того минимума, которым должен овладеть ученик и без которого он не сможет двигаться дальше в изучении данного предмета. Это минимальный уровень общих требований, который задается в виде перечня понятий, законов, закономерностей, которые ученик должен уметь решать. Определяется также содержание, которое необходимо усвоить ученику на повышенных уровнях.
Каждый ученик получает право и возможность самостоятельно определять, на каком уровне он усвоит учебный материал. Важно, что бы этот уровень не был ниже уровня обязательной подготовки.
Авторы концепции уровневой дифференциации выдвинули ряд условий, выполнение которых необходимо для успешного и эффективного ее осуществления:
1) Выделенные уровни усвоения материала и в первую очередь обязательные результаты обучения должны быть открытыми для учащихся.
Если цели известны и посильны ученику, а их достижения поощряется, то подросток стремится к их выполнению, т. е. формируются положительные мотивы учения, сознательное отношение к учебной работе; можно привлечь самооценку ученика для организации дифференцированной работы.
2) Наличие определенных «ножниц» между уровнем требований и уровнем обучения. Уровень требования должен быть в целом существенно выше, чем обязательный уровень усвоения материала. То есть уровневая дифференциация осуществляется не за счет того, что одним ученикам дают меньше, а другим больше, а в силу того, что, предлагая ученикам, одинаковый объем материала, предъявляют различные уровни требований к его усвоению. В силу этого ученик должен иметь учебник, в котором были бы предусмотрены (и явно выделены) все уровни усвоения материала (в том числе и минимально обязательные).
3) В обучении должна быть обеспечена последовательность в продвижении ученика по уровням. То есть не следует предъявлять более высоких требований тем учащимся, которые не достигли уровня обязательной подготовки, но при этом не следует необоснованно задерживать остальных на этом этапе.
4) Содержание контроля и оценка должны отражать принятый уровневый подход. Контроль должен предусматривать проверку достижения всеми учащимися обязательных результатов обучения как государственных требований, а также дополняться проверкой усвоения материала на более высоких уровнях. При этом достижении обязательных результатов целесообразно оценивать «зачтено» - «не зачтено», для более высоких уровней
5) целесообразно соответствующую шкалу оценивания (например, отметка «4», «5»).
6) Добровольность в выборе уровня усвоения и отчетности.
Эти идеи легли в основу проекта стандарта школьного образования, в котором требование к математической подготовке школьников задается на двух уровнях: уровне обязательной подготовки и уровне, условно названном, уровнем возможностей. Уровень обязательной подготовки характеризует тот минимум, который должны получить все учащиеся и определяет нижнюю допустимую границу результатов математического образования. Уровень возможностей характеризует результаты, к которым могут стремиться и достичь учащиеся, изучающие общеобразовательный курс.
Таким образом, введение стандарта полностью соответствует концепции уровневой дифференциации, предполагая наличие хотя бы двух уровней овладения материалом: обязательного и повышенного. Однако, количество уровня овладения материалом может быть увеличено. В работах современных авторов обычно идет речь, как минимум, о трех (и более) уровнях.
На сегодняшний день в дидактических и методических исследованиях разработаны различные подходы к выделению основных уровней учебного материала. Обычно методисты выделяют 3 уровня усвоения знаний по математике: - общекультурный, прикладной и творческий.
Они считают, что для учеников, овладевших первым уровнем, математика является лишь элементом общего развития, и в их дальнейшей производственной деятельности будет использоваться в незначительном объеме. Для учащихся второго уровня математика будет важным инструментом в их профессиональной деятельности. Учащиеся третьего уровня выберут математику(или близкие к ней области знания ) в качестве основы своей будущей деятельности. Поэтому для учащихся первого уровня «существенно овладение общей математической культурой », для учащихся второго уровня «существенны не только знания о математических фактах, навыки логического мышления, пространственные представления, но и прочные навыки решения математических задач». Учащиеся третьего уровня должны творчески овладеть основами математики.
1.3 Плюсы и минусы уровневой дифференциации
Традиционные программы, учебные планы, учебники и дидактические средства, требования, методы и формы, являясь одинаковыми для всех школьников, отодвигают на задний план изучение и учет индивидуальных особенностей. Сегодня во многих школах страны уже в первом классе учащихся распределяют по классам (потокам) возрастной нормы, ускоренного обучения, повышенного индивидуального внимания, коррекции, выравнивания. Правда, такой подход, особенно ранняя дифференциация, вызывает немало нареканий. Считают, что разделение на потоки вызывает снобизм у сильных учащихся и чувство неуверенности и собственной неполноценности у слабых. Жесткая дифференциация учащихся на способных, средних и слабых с последующим длительным пребыванием в разных по содержанию и методам обучения классах, имеет не только плюсы, но и существенные минусы.
Смысл уровневой дифференциации заключается в том, чтобы адаптировать учебный процесс к познавательным возможностям каждого ученика, предъявить соответствующие уровню его развития требования, программы, учебники, методы и формы обучения. Почти каждый ребенок идет в школу с большим желанием учиться, однако очень скоро у значительной части школьников это желание пропадает, учеба превращается в тяжелую повинность. Причина очевидна: им предложены такие условия обучения и предъявлены такие требования, которые превышают уровень их развития. Этого можно избежать, если с первых школьных лет каждый ребенок окажется в однородной среде, в которой он чувствует себя комфортно, а учеба сопровождается успехом. Но проведение уровневой дифференциации уже в начальной школе должно быть обставлено одним непременным условием: потоки (группы) должны быть динамическими, то есть на определенном этапе обучения наиболее успевающие или, напротив, неуспевающие учащиеся должны своевременно переводиться в классы соответствующего уровня.
§2 Методические основы обучения решению задач на экстремумы
2.1 Задачи на экстремумы в школьном курсе математики (обзор учебников)
Задачи на экстремумы в курсе алгебры 7-9 классов.
В основном, в школьных учебниках алгебры встречаются такие задачи, в которых с помощью известных методов приходят к однозначному ответу, удовлетворяющему условиям задачи.
Решение задач на экстремумы проходит в два этапа:
- на первом этапе текст задачи переводится на математический язык в виде функции, которая допускает много или бесконечно много решений;
- на втором этапе по тем или иным признакам, определяется какое из решений задачи наиболее выгодно.
Посмотрим решение задач на экстремумы на примерах учебников
А.Г. Мордковича и Ш.А.Алимова.
Сначала рассмотрим серию учебников под редакцией А.Г. Мордковича,
Т.Е. Мишустина, Е.Е. Тульчинской.
В 7 классе учащиеся первый раз сталкиваются с задачами на экстремум при изучении координатной прямой. Здесь им приходится решать задачи на нахождение наибольшего и наименьшего числа на взятом промежутке, нахождение наибольших и наименьших значений функций на отрезке.
В 8 и 9 классах учащиеся продолжают сталкиваться с задачами на нахождение наибольшего и наименьшего значения при изучении квадратичной функции, функции у= , у= , у=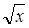 (8 класс) и при изучении темы «Неравенства» (9 класс). Здесь ученикам приходится решать задачи, как на нахождение наименьшего числа удовлетворяющего системе уравнений, нахождение наименьшего и наибольшего значения функций вида у= (8 класс) и при изучении темы «Неравенства» (9 класс). Здесь ученикам приходится решать задачи, как на нахождение наименьшего числа удовлетворяющего системе уравнений, нахождение наименьшего и наибольшего значения функций вида у=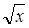 на отрезке. на отрезке.
В серии учебников под редакцией Ш.А.Алимова, Ю.М. Колягина и др. курс алгебры 7-9 классов построен иначе, в этой серии с задачами на экстремум учащиеся сталкиваются только в 7 и 8 классах при изучении квадратичной функции, неравенств и систем уравнений с 2 неизвестными.
Задачи на экстремумы в курсе алгебры 10-11 классов.
Фактически все задачи на экстремумы, с которыми учащимся приходится сталкиваться в курсе алгебры 10-11 классах, решаются основным методом - с помощью производной.
В учебнике «Алгебра и начала анализа », под редакцией А. Н. Колмогорова, производной и ее применению уделена одна из самых больших глав. Авторы сначала дают понятие производной, рассматривают правила ее вычисления, а после этого в учебники приведены различные задачи на отыскание наибольшего и наименьшего значения.
В учебниках «Алгебра и начала анализа» для 10 и 11 классов под редакцией
Н.Я. Виленкина, производной тоже уделено много времени, но учащимся предлагаются задачи более высокого уровня сложности (учебник рекомендован для школ и классов с углубленным изучением математики).
Если говорить о серии учебников под редакцией А.Г. Мордковича, Т.Е. Мишустина, Е.Е. Тульчинской, то мы видим, что, начиная с 7 класса общеобразовательной школы, учащиеся приступают к знакомству с экстремальными задачами. Это происходит при изучении координатной прямой, задач на нахождение наибольшего и наименьшего числа на взятом промежутке, задач на нахождение наибольших и наименьших значений функций на отрезке. В 8-9 классе к уже полученным знаниям, навыкам и умениям добавляются задачи на нахождение наименьшего числа удовлетворяющего системе уравнений, нахождение наименьшего и наибольшего значения функций вида у=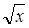 на отрезке. на отрезке.
Отметим, что также есть учебный курс алгебры, выстроенный иначе. Он представлен в серии учебников под редакцией Ш.А.Алимова, Ю.М. Колягина и др. Следуя этому курсу, учащиеся сталкиваются с задачами на экстремум в 7 и 8 классах при изучении квадратичной функции, неравенств и систем уравнений с 2 неизвестными
В 10-11 классах общеобразовательной школы учащиеся знакомятся с еще одним методом решения задач на экстремумы - с помощью производной. К слову, в учебнике «Алгебра и начала анализа» под редакцией А. Н.Колмогорова, для изучения производной и ее применения автор отводит одну из самых больших глав.
В учебнике «Алгебра и начала анализа» для 10 и 11 классов под редакцией Н.Я..Виленкина производной также уделяется немало времени, но предлагаются задачи более высокого уровня сложности, поскольку данный учебник рекомендован для специализированных математических школ или классов.
2.2 Методика обучения решению задач
Для того чтобы учащийся понимал, как решать задачу, он должен в первую очередь понимать, что такое задача.
Задача — проблемная ситуация с явно заданной целью, которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, т.е. то, что требуется сделать.
Поиск решения задачи можно представить в виде плана, выполняя который мы прейдем к нужному результату:
1. Понять предложенную задачу.
2. Найти путь от неизвестного к данным, если нужно, рассмотрев промежуточные задачи (анализ).
3. Реализовать найденную идею решения (синтез).
4. Проверка решения.
Теперь давайте рассмотрим каждый из этих пунктов более подробно:
1. В первом пункте нам предстоит ответить на множество вопросов: Что гласит задача? Что дано? Что нужно найти? Определено ли неизвестное данными задачи, или они недостаточны, или же чрезмерны? Нельзя ли найти связь между данной задачей и какой-нибудь задачей с известным решением? Или задачей, решающейся проще, а может быть и сразу? Ответив на эти вопросы мы сможем разобраться в деталях задачи, которые впоследствии, вероятно, будут играть определённую роль.
2. Сформулировать отношение (или отношения) между неизвестным и данными. Преобразовать неизвестные элементы. Попытаться ввести новые неизвестные, более близкие к данным задачи. Преобразовать данные элементы. Попытаться получить, таким образом, новые элементы, более близкие к искомым неизвестным.
3. Выполнение во всех деталях тех алгебраических или геометрических действий, которые вы предварительно сочли выполнимыми. Проверяя правильность каждого шага либо при помощи логических рассуждений, либо при помощи интуитивных рассмотрений, либо, если это возможно, обоими способами. Если задача сложная, можно разбить её на «большие» и «малые» шаги, разделяя каждый большой шаг на несколько малых. Тем самым мы сможем добиться решения, каждый шаг которого будет, без сомнения правилен.
4.Проверяя решение задачи нам вновь приходится ответить на некоторые вопросы: Правдоподобен ли результат? Нет ли другого пути, ведущего к полученному результату, более прямому? Какие результаты ещё можно получить на том же пути? Ответив на эти вопросы мы возможно сможем найти новое, лучшее решение, можем обнаружить новые интересные факты.
Таким образом, решая задачу мы даём ответ на вопрос этой задачи, но во время поиска этого решения нам нужно дать ответ на другие вопросы возникающие во время работы с задачей.
Итак, вернёмся к задачам на отыскание экстремальных значений функции на промежутках. Из обзора школьных учебников учебников можно сделать вывод, что знакомство с задачами на экстремум начинается с решения задач на нахождение наименьшего и наибольшего числа на взятом промежутке, либо значения функции на отрезке. Постепенно задача усложняется, появляются задачи на вычисление наименьшего числа удовлетворяющего системе уравнений, нахождение наименьшего и наибольшего значения квадратичных функций. И уже в 10 – 11 классах после знакомства с производными, ученики начинают решать задачи на нахождение наибольшего и наименьшего значения сложных степенных функций, решать прикладные задачи.
Требования стандарта образования к умениям и навыкам учащихся гласят, что учащиеся должны уметь:
- вычислять производные и первообразные элементарных функций, используя справочные материалы;
- исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
- вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Исходя из требований стандарта можно сделать вывод, что учащиеся должны владеть элементарными навыками математического моделирования и в частности, уметь применять математический аппарат при решении задач на отыскание наибольших и наименьших значений различных величин при заданных условиях. Таким образом реализуется прикладная направленность обучения математике и осуществляются межпредметные связи с другими дисциплинами. В первую очередь учащиеся должны владеть универсальным методом решения задач на оптимизацию, методом, включающим в себя построение некоторой функции и отыскание ее экстремумов с помощью производной. Алгоритм решения задач этим методом включает в себя три основных этапа:
Первый этап. Составление математической модели:
1. Анализ условий задачи, выделение оптимизируемой величины, т.е. величины, о наибольшем или наименьшем значении которой идет речь. Обозначьте ее буквой у (или S, R, V - в зависимости от фабулы).
2. Одна из участвующих в задаче неизвестных величин, через которую сравнительно не трудно выразить оптимизируемую величину, принимают за неизвестную переменную и обозначают её буквой х (или какой либо другой буквой). Установка реальных границ изменения неизвестной переменной, в соответствии с условиями задачи.
3. Исходя из условия задачи, выразить у через х. Математическая модель задачи представляет собой функцию у=f(х) с областью определения Х, которую нашли на втором шаге.
Второй этап. Работа с составленной моделью.
На этом этапе для функции у=f(х), х Х находится унаим или унаиб в зависимости от того, что требуется в условии задачи. Х находится унаим или унаиб в зависимости от того, что требуется в условии задачи.
Третий этап. Ответ на вопрос задачи.
Получение конкретного ответа на вопрос задачи, опираясь на результаты, полученные на этапе
работы с моделью.
Помимо универсального метода решения задач на экстремумы, полезно было бы познакомить учащихся и с методами решения этих задач, опирающимися на сведения из элементарной математики (метод перебора, метод преобразования плоскости, метод оценок и неравенств). Эти методы предполагают алгебраический или геометрический подход к решению задачи, тем самым актуализируя знания учащихся из курса алгебры и геометрии и развивая их математическую интуицию.
Таким образом, в понятие задачи на экстремумы входит очень широкий спектр задач, весьма разнообразных по уровню сложности, а значит, в этом задачном материале возможно и весьма полезно провести уровневую дифференциацию таких задач. Т.е. распределить предъявляемые учащимся задачи по уровням сложности и использовать эту дифференциацию при проведении практических занятий с учащимися.
Глава 3. Разработка факультативных занятий по теме: «Решение экстремальных задач»
Еще на рубеже XIX и XX веков некоторые педагоги поняли, что преподавание в общеобразовательной школе какого-либо предмета по обязательной единой общегосударственной программе становится существенно более успешным, если его дополнить циклом не обязательных для учащихся, предназначенных только для желающих, внепрограммных групповых занятий.
Такие занятия должны были, прежде всего, учитывать «местные» условия, а именно: реальные и потенциальные запросы и интересы конкретного коллектива учащихся данного класса, и отдельно каждого ученика.
Так возникла идея факультативных занятий в школе.
Хорошо поставленные факультативы обеспечивают высокое качество знаний, повышаю уровень общего развития учащихся, стимулируют учебную деятельность и повышают интерес к предмету.
Задача факультатива состоит в том, чтобы в результате посещения занятий ученик углублял знания, полученные на уроках, совершенствовал умения и навыки, развивал мыслительные и творческие способности.
При проведении факультатива необходимо установить оптимальное сочетание теоретической и практической частей.
Очень важным является проведение факультатива в 11 классе, целью которого является подготовка учащихся к сдаче ЕГЭ.
Разработка факультативных занятий по теме:
«Решение задач на экстремум».
Занятие 1
Тема:«Геометрический подход к решению задач на экстремумы».
Тип: Комбинированный урок.
Цели:
Обучающая: изучение метода преобразования плоскости для решения экстремальных задач.
Развивающая: развитие мыслительной деятельности, создать условия для продвижения учащихся в интеллектуальном развитии.
Воспитательная: воспитание интереса к математике, воспитание эмоционально-положительной направленности на практическую деятельность..
Задачи: вспомнить понятие «экстремальная задача», дать понятие метода преобразования плоскости, рассмотреть применения метода при решении задач.
Оборудование: доска, мел, карточки с заданиями.
План урока
| Содержание |
Методы и приемы |
Время |
1. Орг. момент
Сообщение цели урока
|
Инструктаж учителя |
3 мин |
2. Изучение нового материала
1.Суть метода преобразования плоскости.
2. Пример решения задачи методом преобразованием плоскости.
|
Лекция
(объяснительно-иллюстра–тивный с элементами проблемного изложения)
Учащиеся конспектируют, задают вопросы.
|
20 мин |
| 3. Закрепление пройденного материала. |
Учитель предлагает учащимся задачи для самостоятельного решения. Учащиеся самостоятельно решают задачи своего уровня сложности (репродуктивный, частично-поисковый) |
29 мин |
| 4. Подведение итогов |
беседа |
3 мин |
| 5. Запись домашнего задания |
Инструкция учителя
(репродуктивный)
|
5 мин |
Ход урока:
| Деятельность учителя |
Деятельность учащихся |
I. Орг. момент.
Здравствуйте, садитесь.
Откройте тетради, запишите число.
Сегодня мы с вами начинаем изучение темы "Решение задач на экстремум". На занятиях по этой теме мы рассмотрим решения задач на нахождение наибольших и наименьших величин различными методами. Начнем мы с геометрических методов, сегодня мы рассмотрим метод преобразования плоскости.
Но сначала давайте вспомним, какие задачи называют экстремальными, и где в повседневной жизни мы с ними встречаемся?
Конечно, с нахождением максимальных и минимальных значений, наиболее выгодных условий и т.д. – т.е. с нахождением (выбором) лучшего мы сталкиваемся постоянно.
И очень часто лучший вариант не очевиден. В его нахождении помогает математика. Существует много решения таких задач, начнем с преобразования плоскости.
|
Садятся
Выполняют инструкции учителя, слушают, задают вопросы.
Высказывают свои предположения.
Слушают учителя.
|
II. Лекция.
1. Суть метода преобразования плоскости.
В качестве одного из основных подходов решения геометрических экстремальных задач используется метод преобразования плоскости. Суть метода заключается в следующем.
Пусть требуется найти экстремум элемента х фигуры F, однозначно определенного элементами x,аi,i = 1,2,...,n.
Метод нахождения экстремума:
3) Элементу х зададим определенное значение х = С и решим задачу на построение фигуры Fпо заданным элементам х и аi.
4) Решив эту задачу, считаем элемент с перемещением. Затем, применяя те или иные преобразования плоскости, замечаем те особенности, которые возникают при достижении элементом х максимального или минимального значения.
Выделение указанной особенности позволяет сделать заключение об экстремуме элемента х фигуры F.
Посмотрим применение метода при решение конкретной задачи.
2. Пример решения задачи методом
преобразованием плоскости.
Решим следующую задачу: построить прямую, проходящую через вершину А треугольника ABC, так, чтобы сумма расстояний до нее от вершин В и С была наибольшей.
Сначала построим треугольник АВС. Через вершину А проведем произвольную прямую EF .

Из точек В и С опустим перпендикуляры KBи CNна
EF. Если КВ=х, CN=y, то расстояние
KB+CN=x+y. Построим точку
B}=ZA(B) и точку K1=ZA(K), тогда
х + у = KB + GN = К1В1 + CN< В1 C1, так как В 1 К 1 ≤ В 1 М и СN≤ CM где М- точка пересечения прямой EFи отрезка В{С.
Мысленно вращая прямую EF вокруг точки А так, чтобы точка М перемещалась по В 1С от точки В1 до точки C1 замечаем, что х + у ≤В1 С. Знак равенства имеет место в случае, когда EF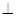 В1 С. В1 С.
Если прямую EFмысленно поворачивать дальше вокруг точки А, то точка М будет перемещаться по отрезку ВС от точки С до точки В, а сумма х + у < ВС. Знак равенства достигается тогда, когда EF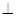 ВС. ВС.
|
Ученики конспектируют, задают вопросы
Слушают учителя, записывают решения в тетрадь, задают возникающие вопросы.
|
III Закрепление пройденного материала.
Сейчас возьмите карточки с заданиями своего уровня и решите предложенные там задачи.
Учитель следит за тем, что бы все работали, отвечает на возникающие вопросы. Если какая-та задача вызывает у многих затруднения, ее (полностью или частично) прорешивают на доске.
|
Учащиеся берут карточки с задании-
ями и преступаю к решению задач. Если возникают трудности, они обращаются за по-
мощью к учителю.
|
IV Подведение итогов
Итак, сегодня мы с вами изучили один из методов решения экстремальных задач, рассмотрели применение этого метода при решении задач.
Какие у вас есть вопросы по пройденному сегодня материалу? (отвечает на вопросы, если они есть)
|
Задают вопросы, которые остались непонятными.
|
V Запись домашнего задания
Домашнее задание: посмотреть конспект сегодняшнего занятия, дорешать 2 задачу.
|
Записывают. |
Задачи предлагаемые учащимся.
Iуровень сложности.
Задача 1.
В каком месте следует построить мост MN через реку, разделяющую деревни А и В, чтобы путь AMNB был кратчайшим? (Берега реки считаются параллельными прямыми, мост перпендикулярен берегам).
Решение:

Заметим, что длина отрезка MN не зависит от положения точки М на прямой а, а вектор v = MNопределяется лишь прямыми а и b. Поэтому надо найти такое положение точки М, чтобы сумма AM+NB была наименьшей. Пока отрезки AM и NB удалены друг от друга. Поэтому переведем отрезок AM в положение A'Nпараллельным переносом на вектор v.
| Если переносить другую точку, то тогда точки А, М, В' должны принадлежать одной прямой, (рис.). |
Получим ломаную A'NB. И теперь становится ясно, что длина ломаной A'NB, а значит и длина пути AMNB будет наименьшей в том случае, когда точки А', N, В лежат на одной прямой. Итак, N - точка пересечения отрезка А'В с прямой Ь, а М - проекция N на прямую а.
Тогда М - точка пересечения отрезка АВ' с прямой а, а N - проекция М на прямую b .
Вся трудность задачи заключается в том, чтобы заметить особенности, при которых искомая ломаная может принять наименьшую длину.
Задача 2.
Среди всех трапеций с заданной высотой 3 см и диагоналями длиной 6 см и 5 см найдите трапецию максимальной (минимальной) площади. Вычислите
площадь.
Решение:
SABCD =  · h = · h =  h = S∆ACD1= const. SABCD= S∆ACD1= ½ ( h = S∆ACD1= const. SABCD= S∆ACD1= ½ ( ) · 3 ) · 3
задача экстремум дифференциация математика
Нетрудно заметить, что параллельные перенос чаще всего используется в тех случаях, когда объектом задачи является трапеция, параллелограмм и другие четырехугольники с параллельными сторонами.
Задача 3.
Две деревни А и В находятся по одну сторону от прямого шоссе а. В какой точке С на шоссе а надо установить остановку автобуса, чтобы сумма расстояний АС + СВ была кратчайшей?
Решение:
Построим точку В, симметричную точке В, относительно прямой а. Для любой точки Упрямой аВХ = ВХ. Поэтому АХ+ХВ = АХ+ ХВ. Ясно, что сумма АХ + ХВ/ становится кратчайшей, когда Xпопадает в точку пересечения отрезка АВ! с прямой а. Эта точка С и дает решение задачи.
 В В

II уровень сложности.
Задача 1.
Объекты А, В и С расположены между двумя прямолинейными путями l1 и l2 (рис.). Соединить эти объекты между собой замкнутой дорогой кратчайшей длины с выходом на прямолинейные пути.
Решение:

Построим В' =  (В), С = S (В), С = S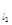 (C); AC/ пересекает 12 в точке D, а АВ' пересекает l1 в точке К (рис.). (C); AC/ пересекает 12 в точке D, а АВ' пересекает l1 в точке К (рис.).
Ломанная AKBCDA имеет наименьшую длину.
Задача 2.
Дан угол и две точки С и в внутри него. Найти точки А и В на сторонах угла так, чтобы сумма длин СА + АВ + BD, была наименьшей.
Решение:
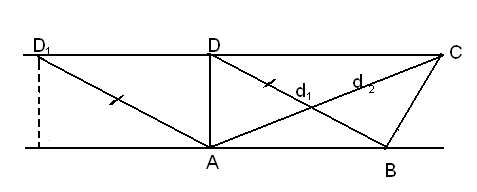
Выполним следующее построение.  Построим d1 и С1 симметричные в и С относительно сторон KLи LM. Проведем отрезок D1C1 и ломаную CABD. Длина ее равна длине отрезка D1C1. Нетрудно понять, что иной путь из С в в с тем же порядком захода на стороны угла будет длиннее. Построим d1 и С1 симметричные в и С относительно сторон KLи LM. Проведем отрезок D1C1 и ломаную CABD. Длина ее равна длине отрезка D1C1. Нетрудно понять, что иной путь из С в в с тем же порядком захода на стороны угла будет длиннее.
Задача 3.

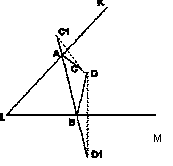
В квадрат, диагональ которого равна d, вписан произвольный четырехугольник ABCD. Доказать, что минимальный периметр четырехугольника равен 2d.
Решение:
Пусть MN=dL1=SNC(L) и K1=SMD(K); CL=CL1 и KD=K1D, KD+DC+CL=K1D+DC+CL1≥MN так как  K1MK= K1MK= LNL1=90◦. LNL1=90◦.
Пусть MN=d . L1=SNC(L) и K1=SMD(K);
CL=CL1 и KD=K1D,
KD+DC+CL=K1D+DC+CL1≥MN так
как  K1MK= K1MK= LNL1=90◦. LNL1=90◦.
Аналогично можно доказать, что LB + АВ + АК > MN
PABCD=AD+AB+BC+CD = (AK+AB+BL) + (LC+CD+DK) ≥ 2MN ≥ 2d
Pmjn = 2d, если ABCD - прямоугольник.
III уровень сложности.
Задача 1.
По разные стороны от полотна железной дороги АВ расположены два завода М и N. Где нужно построить на железной дороге платформу CD длиной а так, чтобы общая длина дороги MCDN была наименьшей?
А если заводы М и N расположены по одну cторону от железной дороги АВ?
Решение:
Получим ММ1 параллельным переносом на вектор CD. MCDN-min;
MCDN=MM1DNMM1DN - min <=> M1, D, N принадлежат одной прямой.
Если же М и N расположены по одну сторону от прямой АВ. M1
симметрична М относительно прямой АВ.
ММ2 получен параллельным переносом на вектор CD
MCDN-min
MCDN=MiM2DN
M{M2DN - min <=> M2, D, N принадлежат одной прямой.
Задача 2

Дан угол и точка С внутри него. Найти точки А и В на сторонах угла так, чтобы периметр треугольника ABCбыл наименьшим.
Решение:
Возьмем произвольный ∆СА 1В1, две вершины которого, лежат соответственно на сторонах угла KLи LM, а третьей служит точка С.
Построим точки Е и Р, симметричные точке С относительно сторон угла KLи LMи соединим отрезками прямой эти точки соответственно с вершинами А1 и В1 треугольника. Так как нас интересует треугольник с наименьшим периметром, а наименьшим будет периметр, равный длине отрезка ЕР. Поэтому вершины треугольника А и В искомого треугольника определяются как точки пересечения прямой ЕР со сторонами данного угла.
Занятие 2
Тема: «Геометрический подход к решению задач на экстремумы».
Тип: Комбинированный урок
Цели:
Обучающая: изучение различных геометрических методов решения экстремальных задач, обучение решению задач с использованием этих методов.
Развивающая: Развитие критичности мышления, делать выводы, обобщать; развитие навыков самостоятельной работы.
Воспитательная: воспитание личной ответственности за результаты своей работы, активной жизненной позиции, умения ставить и достигать цели.
Задачи: Рассмотреть различные геометрические методы решения экстремальных задач, показать на примерах их использование при решении задач.
Оборудование: доска, мел, карточки с заданиями.
План урока
| Содержание |
Методы и приемы |
Время |
1. Орг. момент
Сообщение цели урока
|
Инструктаж учителя |
3 мин |
2. Изучение нового материала
1.Обзор различных
геометрических методов
решения экстремальных
задач.
2. Пример решения задачи.
|
Лекция
(объяснительно-иллюстра–тивный с элементами
проблемного изложения)
Учащиеся конспектируют,
задают вопросы.
|
20 мин |
3. Закрепление пройденного материала. (Учитель предлагает учащимся задачи для
самостоятельного решения).
|
Учащиеся самостоятельно
решают задачи своего уровня сложности (репродуктивный, частично-поисковый)
|
29 мин |
| 4. Подведение итогов |
беседа |
3 мин |
| 5. Запись домашнего задания |
Инструкция учителя
(репродуктивный)
|
5 мин |
Ход урока:
| Деятельность учителя |
Деятельность учащихся |
I. Орг. момент.
Здравствуйте, садитесь.
Откройте тетради, запишите число.
Сегодня мы с вами продолжаем изучение темы "Решение экстремальных задач геометрическим подходом".
Но прежде чем перейти к изучению новых способов решения экстремальных задач я хотел бы узнать, возникли ли какие-нибудь вопросы при выполнении домашней работы? Может у кого-то возникли трудности при решении какой-нибудь задачи?
Слушает детей, возможно частично прорешивают какую-то задачу у доски.
|
Садятся
Выполняют инструкции учителя, слушают, задают вопросы.
Задают возникшие вопросы.
|
II. Лекция.
1.Обзор различных геометрических методов
решения экстремальных задач.
На прошлом занятии мы с вами решали различные экстремальных задач. Какой метод мы использовали при решении этих задач? В чем его суть?
Вы совершенно правы, мы решали задачи методом преобразования плоскости. Но задачи на экстремум решаются не только преобразованием плоскости. Есть еще очень много геометрических подходов к решению экстремальных задач, самые используемые из них метод перебора и оценки. Сегодня мы будем решать экстремальные задачи, используя эти методы.
Посмотрим на примере.
2. Пример решения задачи
Решим задачу:
Дан прямоугольный параллелепипед ABCDEFGJ, в котором AB=AE=12, AD=30.
Точка М расположена на грани АВFE на расстоянии 1 от середины АВ и на равных расстояниях от А и В. Точка N принадлежит грани DCGJ и расположена симметрично точки М относительно центра АВСDEFGJ. Найти длину кратчайшего пути по поверхности параллелепипеда между точками М и N.
Учитель с помощью детей решает задачу у доски, объясняя учащимся свои выкладки.
Решение:
Рассмотрим следующие варианты:
1. Пусть путь пересекает EF и GJ. Длина кратчайшего пути в этом случае равна 11+30+1=42.
2. Пусть путь последовательно пересекает ребра BF, FG, GJ. Сделаем развертку. Обозначим точки на развертки так же, как и на параллелепипеде. По теореме Пифагора MN=(MK2 +NK2)1|2 =(372+172)1|2=16581|2.
3. Путь последовательно пресекает ребра АВ, ВС,FG,GJ. Сделаем развертку. Длина кратчайшего пути в этом случае: MN= (MK2+NK2)1|2=(242+322)1|2=40. Этот путь и оказывается кратчайшим, т.к. его длина равна 40.

|
Ученики слушают, отвечают на вопросы.
Конспектируют, задают вопросы.
Слушают учителя, записывают решения в тетрадь, задают возникающие вопросы.
|
III Закрепление пройденного материала.
Сейчас возьмите карточки с заданиями своего уровня и решите предложенные там задачи.
Учитель следит за тем, что бы все работали, отвечает на возникающие вопросы. Если какая-та задача вызывает у многих затруднения, ее (полностью или частично) прорешивают на доске.
|
Учащиеся берут карточки с
заданиями и
преступаю к
решению задач.
Если возникают
трудности, они
обращаются за
помощью к
учителю.
|
IV Подведение итогов
Итак, сегодня мы с вами рассмотрели еще два метода решения экстремальных задач и их приминение..
Какие у вас есть вопросы по пройденному сегодня материалу? (отвечает на вопросы, если они есть)
|
Задают вопросы, которые остались непонятными.
|
VЗапись домашнего задания
Домашнее задание: посмотреть конспект сегодняшнего занятия, дорешать задачки своей карточки.
|
Записывают. |
Задачи предлагаемые учащимся.
Iуровень сложности.
Задача 1.

На стороне ВС треугольника ABC найти точку в так, чтобы отрезок AD имел:
а) наибольшую длину;
б) наименьшую длину.
Решение:
а) Пусть di - произвольная внутренняя точка ВС
и АВ > АС. Так как  AD1B> AD1B>  C> C> B, то AB >ADl. B, то AB >ADl.
Следовательно, отрезок AD имеет наибольшую длину, если он совпадает со стороной АВ. Если АВ = АС, то имеем два решения: стороны АВ и АС.
б) Пусть в треугольнике ABC ни один из углов В и С не тупой. Тогда основание высоты, проведенной из вершины А находится на стороне ВС и отрезок AD имеет наименьшую длину, если AD BC. BC.
Пусть теперь угол С тупой. В этом случае основание Н высоты АН треугольника лежит на продолжении стороны ВС за точку С. Так как наклонная А С меньше всякой другой наклонной AD1 с основанием на ВС, то отрезок AD имеет наименьшую длину, если он совпадает со стороной АС треугольника.

Задача 2.
Прямая MN отсекает от данного угла А треугольник данной площади Q (М и N - точки на сторонах угла А). При каком условии отрезок MN имеет наименьшую длину, и какова эта длина?
Решение:
Обозначив отрезки AM и ANсоответственно через х и у, по теореме косинусов получим:

MN2 = x2 + y2 - 2xycosA = (x-y)2 + 2xy (1-cosA) = (x-y)2 + 4 Q tg
так как ½ xysin А = Q.
Следовательно, при х= у (AM = AN) отрезок имеет наименьшую длину, равную  . .
Задача 3.
Под каким углом к берегу нужно направить лодку, что бы за время ее переправки лодку как можно меньше снесло течением, если скорость течения 6 км/ч, а собственная скорость лодки – 3 км/ч.
Решение.
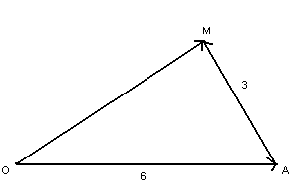
Необходимо направить лодку так, чтобы ее абсолютная скорость (относительно берегов) составляла, возможно, больший угол с берегом.
Пусть вектор  - скорость лодки относительно воды. Сумма - скорость лодки относительно воды. Сумма  + +  = =  дает абсолютную скорость лодки (относительно берегов). Длина вектора дает абсолютную скорость лодки (относительно берегов). Длина вектора
 =3 и его можно направить в любую сторону. Множество возможных положений точки М – окружность радиуса 3 с центром в точке А. =3 и его можно направить в любую сторону. Множество возможных положений точки М – окружность радиуса 3 с центром в точке А.
Из всех векторов  наибольший угол с берегом составляет наибольший угол с берегом составляет 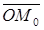 , направленный по касательной к окружности. Получаем прямоугольный треугольник, у которого катет вдвое меньше гипотенузы. У такого треугольника угол равен 600. , направленный по касательной к окружности. Получаем прямоугольный треугольник, у которого катет вдвое меньше гипотенузы. У такого треугольника угол равен 600.
II уровень сложности.
Задача 1.
Какой из всех параллелограммов с заданными диагоналями а и b имеет наибольшую площадь?
Решение:

Граничное значение переменной площади S параллелограмма ABCD непосредственно заметить трудно, но если эту переменную площадь выразить формулой
S = АС• DK= ah, то легко заметить, что S = ah ≤ ab, так как h ≤  . .
Если использовать формулу S = abs'ma, то наибольшую площадь S нетрудно найти, граничное значение sin а хорошо известно.

Задача 2.
Расстояние от пункта А до пункта В 4 км, а от пункта В до пункта С вдвое больше. Какое наибольшее и наименьшее расстояние может быть от пункта А до пункта С?
Решение:
Расстояние АС зависит от места расположения
точки С. Так как расстояние ВС постоянное, то точка С
принадлежит точкам окружности с R = ВС, В - центр. Легко заметить, какие граничные значения может принимать АС, т.е.
4 = АСг < ACi < AB + BCi = 12.
Отсюда, max [AСi] = 12 km
min [ACi] = 4 km
Искомыми точками Ci являются концы диаметра длиной 16 км с центром окружности в пункте В.
Задача 3.
Данный треугольник ABC разделить отрезком наименьшей длины на две равновеликие части.

Решение:
Пусть а<b<с, тогда с < а + b < 2b, т.е. b<c<2b. Как показано выше, длина наименьшего отрезка MN, отсекающего от данного треугольника ABC треугольник площади 1/2 S с углом А, равна 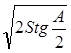 . Отрезок MN и является искомым, так как он меньше наименьших отрезков, отсекающих треугольники с углами В и С: . Отрезок MN и является искомым, так как он меньше наименьших отрезков, отсекающих треугольники с углами В и С:
Таким образом, на сторонах наименьшего угла А треугольника ABC
нужно построить точки М и N так, чтобы АМ= AN= . .
III уровень сложности.
Задача 1.
На сторонах АВ и АС треугольника ABC найти соответственно точки М и N так, чтобы треугольник ABC делился отрезком MN на две равновеликие части и чтобы отрезок MN имел наименьшую длину.
Решение:
Пусть MN - искомый отрезок. Обозначим площадь треугольника ABC через S,

тогда площадь треугольника AMN равна  S. S.
AM = AN и MN = 
Выразим отрезок AM через стороны b и с треугольника ABC. Так как площадь треугольника AMN составляет половину площади треугольника
ABC, то АМ2 sin А=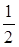 bcsinA, откуда AM = bcsinA, откуда AM =  . .
По условию точки M и N должны лежать на сторонах АВ и АС треугольника. Значит, полученное выражение для AM является решением задачи
лишь при условии, что  не больше каждой из сторон b и с треугольника. не больше каждой из сторон b и с треугольника.
Пусть b ≤ с, тогда ≤ b в том и только в том случае, если с ≤ 2b. ≤ b в том и только в том случае, если с ≤ 2b.
Итак, если b < с < 2b, то на сторонах АВ и АС треугольника ABC строим
точки М и N такие, что AM=AN =  . .
Нетрудно показать, что если с > 2b, то искомым отрезком является медиана треугольника, проведенная к стороне с, причем длина этой медианы
более  . .
Задача 2.
На какое наименьшее число треугольных пирамид (тетраэдров) можно разбить куб?
Решение.

Куб ABCDA1B1C1D1 можно разбить на 5 тетраэдров: если отсечь от него тетраэдры BACВ1 и DACD1, A1B1D1А и C1B1D1С, то останется еще пятый тетраэдр ACB1D1. Он правильный. Попробуем установить, что меньше чем на 5 тетраэдров куб разбить нельзя. Допустим, что куб ABCDA1B1C1D1 разбит на некоторое число тетраэдров.
При этом грань АВСD куба разбивается на части, являющиеся гранями не менее чем двух тетраэдров (квадрат АВСD может быть разбит на 2 или большее число треугольников ), причем сумма площадей оснований этих тетраэдров равна a2, а высота каждого из них не больше а, поэтому объемов примыкающих к грани АВСD тетраэдров разбиения не превосходит 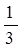 а2 а= а2 а= . .
Аналогично этому к грани A1B1C1D1 куба примыкает не менее двух тетраэдров, причем общий объем этих тетраэдров также не превосходит 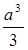 . .
Так как ни один тетраэдр не может одновременно иметь граней, являющихся частью квадрата АВСD и частью квадрата A1B1C1D1 (ведь никакой тетраэдр не имеет параллельных граней!), то мы уже имеем не менее 4 тетраэдров, причем общее число тетраэдров не превышает 2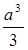 , то есть меньше объема а3. Отсюда и вытекает, что число тетраэдров не может быть меньше пяти. , то есть меньше объема а3. Отсюда и вытекает, что число тетраэдров не может быть меньше пяти.

Задача 3.
В шар радиуса R вписан конус, осевое сечение которого – равносторонний треугольник. Определить, между какими пределами может изменяться разность площадей двух сечений, из которых первое (КGFD) получается в результате пересечения шара плоскостью, параллельной основанию конуса, а второе(NPF) – в результате пересечения конуса той же плоскостью.
Решение.

Площади обоих сечений равны нулю в том случае, когда проводимая плоскость касается шара в точке В (вершина конуса). Площади обоих сечений будут равны, когда проводима плоскость совпадает с плоскостью основания конуса. Когда же проводимая плоскость занимает промежуточное положение между положениями рассмотренными выше, то площади сечений шара и конуса не равны. Итак, разность S площадей сечений шара и конуса изменяется от нуля до нуля, переходя через максимум, который мы определим.
S=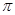 ( MK2- MN2 ); OB=R; MB=x; ( MK2- MN2 ); OB=R; MB=x;
MK2 = OK2 – OM2 = R2- (R - x)2 = 2Rx – x2/
Так как ∆ АВС равносторонний по условию и АС || NP, то и ∆ NBP также равносторонний, следовательно, MN2 = 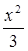 . .
Следовательно S=  2x (3R – 2x), 2x (3R – 2x),
которое будет максимально, когда максимально S1= 2x(3R- 2x). Так как сумма множителей 2x + 3R - 2x = 3R, то S1 максимально, когда 2х= 3R- 2х, т.е.
х= ¾R. Следовательно, максимальное значение S равно 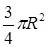 . .
Занятие 3
Тема: «Алгебраический подход к решению задач на экстремумы».
Тип: Комбинированный урок.
Цели:
Обучающая: Отработка и совершенствование навыков решения экстремальных задач аналитическими методами.
Развивающая: Развитие мышления в процессе перевода словесной информации в математические символы, развитие ответственности и добросовестности во время индивидуальной работы.
Воспитательная: воспитание объективного отношения к результатам своей работы, эстетическое восптание..
Задачи: обзор методов решения экстремальных задач – геометрических и аналитических, рассмотрения аналитического метода решения задач с использованием квадратичной функции. Рассмотрение конкретных задач, решаемых этим методом.
Оборудование: доска, мел, карточки с заданиями.
План урока
| Содержание |
Методы и приемы |
Время |
1. Орг. момент
Сообщение цели урока
|
Инструктаж учителя |
3 мин |
2. Изучение нового материала
1.Суть метода.
2.Пример решения задачи
методом перебора.
3.Решение задачи с использованием квадратичной функции.
|
Лекция
(объяснительно-иллюстра–тивный с элементами
проблемного изложения)
Учащиеся конспектируют, задают вопросы.
|
29 мин |
| 3.Закрепление пройденного материала. |
Учитель предлагает
учащимся задачи для
самостоятельного решения. Учащиеся самостоятельно решают задачи своего уровня сложности (репродуктивный, частично-поисковый)
|
23 мин |
| 4.Подведение итогов |
беседа |
2 мин |
| 5.Запись домашнего задания |
Инструкция учителя
(репродуктивный)
|
3 мин |
Ход урока:
| Деятельность учителя |
Деятельность
учащихся
|
I. Орг. момент.
Добрый день.
На протяжении последних двух занятий мы с вами решали задачи на нахождение наибольших и наименьших величин геометрическим подходом.
Какие методы мы использовали?
Сегодня мы рассмотрим алгебраические подходы к решения экстремальных задач.
|
Садятся
Слушают учителя, отвечают на его вопросы.
|
II.Лекция.
1.Суть метода.
Как и геометрических, алгебраических подходов очень много, сегодня мы рассмотрим два из них: метод перебора и использование квадратичной функции.
В практике часто встречаются экстремальные задачи, при решении которых получается одно уравнение с несколькими переменными, заданными на множестве целых неотрицательных чисел. Решение таких задач сводится к исследованию линейной функции.
2.Пример решения задачи методом перебора.
Примером может послужить такая задача:
Содержание витамина С в 1 кг фруктов и стоимость 1 кг заданы следующей таблицей:
| Фрукты |
Витамин С (кг) |
Стоимость(у.е.) |
Вишни
Абрикосы
|
150
75
|
0,3
0,4
|
Обозначим количество килограммов вишни через х, а количество килограммов абрикосов – через у. Тогда решение задачи сводится к нахождению min(0,3 x + 0,4y), если 150 х + 75у =75, где х < 0,25.
min (0,3 x + 0,4 – 0,8 x ) = min (- 0,5x + 0,4) = 0,275.
В дневной рацион следует включать 0,25 кг. Вишни и 0,5 кг. Абрикосов.
При решении задач квадратичной функции мы будем опираться на следующую теорему:
Теорема:
Функция ах2 + вх + с при а>0 имеет наименьшее значение, равное (4ас-b2)/4, и при а<0 - наибольшее значение, равное тоже (4ас-b2)/4. Эти наименьшие и наибольшие значения получаются при х = - b/2а.
3.Решение задачи с использованием квадратичной функции.
Найти наименьшее значение функции

и построить ее график. Поиски решения. Данную функцию можно изобразить аналитически так:
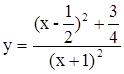
Отсюда видно, что при х = -1 она теряет смысл, а при всех других действительных значениях х принимает только положительные значения. Следовательно, ее наименьшим значением может быть только положительное число. Обнаружить это наименьшее значение непосредственно не представляется возможным. Поэтому надо обратиться к каким-то целенаправленным преобразованиям данного аналитического изображения функции.
Решение:
Очевидно, что
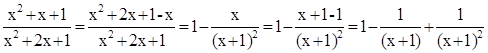
Обозначив дробь  буквой u, получим: буквой u, получим:
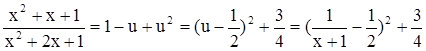
Искомое наименьшее значение равно 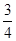 и получается оно при и получается оно при 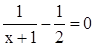 т.е. при т.е. при
х = 1
Перейдем к построению графика данной функции. Составим таблицу нескольких значений х и у, пользуясь формулой

| х |
-3 |
-2 |
-3/2 |
-1 |
-1/2 |
0 |
1 |
2 |
3 |
… |
| у |
7/4 |
3 |
7 |
Х |
3 |
1 |
3/4 |
7/9 |
13/16 |
… |
Если аргумент х будет приближаться к -1 (слева или справа), то у будет неограниченно возрастать.
Теперь посмотрим, как будет вести себя у, когда х станет стремиться к плюс бесконечности или минус бесконечности. Очевидно, что

Отсюда видно, что при стремлении х к бесконечности у стремится к
|
Ученики конспектируют, задают вопросы
Слушают учителя,
записывают решение в тетрадь, задают
возникающие вопросы.
|
IIIЗакрепление пройденного материала.
Сейчас возьмите карточки с заданиями своего уровня и
решите предложенные там задачи.
Учитель следит за тем, что бы все работали, отвечает на возникающие вопросы. Если какая-та задача вызывает у многих затруднения, ее (полностью или частично) прорешивают на доске.
|
Учащиеся берут карточки с заданиями и преступаю к решению задач. Если возникают трудности, они обращаются за помощью к учителю. |
IVПодведение итогов
Итак, сегодня мы с вами рассмотрели еще два метода решения экстремальных задач и их применение.
Какие у вас есть вопросы по пройденному сегодня материалу? (отвечает на вопросы, если они есть)
|
Задают вопросы, которые остались непонятными.
|
VЗапись домашнего задания
Домашнее задание: посмотреть конспект сегодняшнего занятия, дорешать задачки своей карточки.
|
Записывают. |
Задачи предлагаемые учащимся.
I уровень сложности.
Задача 1.
В швейном цехе имеется 164 м ткани. На шитье одного халата требуется 4 м. ткани, а одной пижамы – 3 м. Сколько следует изготовить халатов и пижам для получения наибольшей прибыли от реализации продукции, если халат стоит 7 руб., а пижама – 6 руб.? Известно, что халатов требуется изготовить не менее 14 шт.
Решение.
Пусть в швейном цехе изготовлено х халатов и у пижам. Тогда решение задачи сводится к нахождению max(7x + 6y), если 4х + 3у =1 64.
max(7x + 6y) = max (328- x) = 314 , где x≥ 14.
Для получения наибольшей прибыли следует изготовить 14 халатов и 36 пижам.
Задача 2.
Требуется соорудить канал с поперечным сечением ABDC, где АВ=CD, АВ и CD перпендикулярны к BD. Сумма длин АВ, ВD и СD должны быть равной Р метрам.
Спрашивается, какими надо сделать ширину и глубину канала, чтобы площадь его поперечного сечения, т.е. площадь прямоугольника с вершинами в точках А, В, С, D, оказалась бы наибольшей?
Поиски решения. Поскольку мы еще не знаем, какими надо сделать глубину и ширину канала, то естественно обозначить эти переменные какими-либо подходящими буквами. Например, положить АВ = х и BD = у. Далее надо выразить через х и у ту величину, наибольшее значение которой нам надо найти, т.е. площадь сечения канала. Эта площадь выразится произведением ху, т.е. будет зависеть от двух переменных величин х и у. Но наше исследование облегчится, если нам удастся выразить площадь в зависимости только от одной переменной. Очевидно, что в данном случае это сделать легко, т.к. по условию задачи 2х + у = Р.
Решение.
Пусть АВ = х, тогда и CD = х, а BD = P - 2x. Площадь сечения будет равна х (Р - 2х). Задача сводится к определению наибольшего значения функции х (Р - 2х), которая представляет собой многочлен второй степени, имеющий вид -2х2+Рх. Очевидно, что
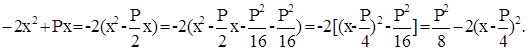
Отсюда видно, что наибольшая площадь получится в том случае, когда мы сделаем глубину канала х = Р/4. Тогда окажется ширина у равной Р/2, а наибольшая площадь равной Р2/8.
Задача 3.
Найти наибольшее и наименьшее значения функции y = 9x – 2∙3 x на отрезке [-1; 2].
Решение.
Пусть t= 3x. Так как -1 ≤ x ≤ 2, то  , у= t2 – 2t. Таким образом, решение задачи сводится к вычислению наибольшего и наименьшего значений квадратичной функции , у= t2 – 2t. Таким образом, решение задачи сводится к вычислению наибольшего и наименьшего значений квадратичной функции
у = t2 – 2t на отрезке [ ; 9]. Абсцисса t0 вершины параболы, являющейся графиком э той функции , равна 1, ветви параболы направлены вверх. Так как t0 є [ ; 9]. Абсцисса t0 вершины параболы, являющейся графиком э той функции , равна 1, ветви параболы направлены вверх. Так как t0 є [ ; 9], то miny(t) =y (1) = - 1, а максимальное значение достигается на том конце отрезка, который наиболее удален от t0 , т.е. maxy(t) = y(9) = 63. Если t = 1, то х = 0, если t= 9, то х =2. Поэтому maxy(x) = y(2) = 63, miny(x) = y(0) = - 1. ; 9], то miny(t) =y (1) = - 1, а максимальное значение достигается на том конце отрезка, который наиболее удален от t0 , т.е. maxy(t) = y(9) = 63. Если t = 1, то х = 0, если t= 9, то х =2. Поэтому maxy(x) = y(2) = 63, miny(x) = y(0) = - 1.
II уровень сложности.
Задача 1.
Предполагается, что рацион составляется из двух видов кормов - сена и концентратов. В таблице приведены числовые данные о суточной потребности одного животного в питательных веществах и о себестоимости кормов в данном хозяйстве:
| Виды кормов |
Содержание в 1 кг. Кормов кормовых единиц |
Себестоимость 1 кг(в руб.) |
| Сено |
0,5 |
1,5 |
| Концентраты |
1,0 |
2,5 |
| Суточная потребность на одного животного |
20 |
- |
Требуется найти самый дешевый рацион, если ежедневный рацион кормления сельскохозяйственных животных должен включать не менее 16 кг. сена.
Решение.
Пусть ежедневный рацион кормления состоит из х кг. сена и у кг. концентратов. Тогда ежедневный рацион содержит (0,5 х + у) кормовых единиц, себестоимость которого равна (1,5 х + 2,5 у).
Решение задачи сводится к нахождению min (1,5 х + 2,5 у), если 0,5 х + у =20.
min (1,5 х + 2,5(20 – 0, 5х )) = min (0,25 х + 50) = 54.
Задача 2.
Найти наибольшее значение функции f = х4 (32-х4).
Решение:
Поиски решения.
Данная функция принимает отрицательные значения
при 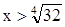 , а при , а при 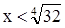 - положительные. Поскольку ее наибольшее значение надо искать среди значений х меньших, чем - положительные. Поскольку ее наибольшее значение надо искать среди значений х меньших, чем  . .
Если мы положим х4 = у, то задача сведется к нахождению наибольшего значения многочлена второй степени, имеющего вид:
- у2 +32у.
Однако если проявить наблюдательность и заметить, что сумма множителей х4 и (32 - х4) является величиной постоянной, то можно воспользоваться теоремой 3 и решить задачу проще.

Задача 3.
Найти наибольшее и наименьшее значения функции у=6  - 2х на отрезке [2 ; 8] . - 2х на отрезке [2 ; 8] .
Решение.
Пусть t =  . Так как 2 ≤ х ≤ 8 , то 1 ≤ t ≤ . Так как 2 ≤ х ≤ 8 , то 1 ≤ t ≤ 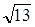 . При этом 2х = t2 + 3, откуда . При этом 2х = t2 + 3, откуда
y=6 t - t2 –3. Таким образом, решение задачи сводится к вычислению наибольшего и наименьшего значений квадратичной функции на отрезке.
Графиком этой функции является парабола, ветви которой направлены вниз, абсцисса t0 вершины параболы, равна 3. Так как t0 є [1; 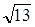 ] , то maxy(t) =y (3) =6, а наименьшее значение достигается в том из концов отрезка который наиболее удален от t0, т.е. ] , то maxy(t) =y (3) =6, а наименьшее значение достигается в том из концов отрезка который наиболее удален от t0, т.е.
miny(t) =y (1) = 2.
Если t = 3, то х = 6, если t= 1, то х =2. Поэтому maxy(x) = y(6) = 6, miny(x) = y(2) = 2.
III уровень сложности.
Задача 1.
Завод должен переслать заказчику 1100 деталей. Детали упаковывают в ящики трех видов.6 по 70, 40 и 25 деталей в каждый. Стоимость пересылки одного ящика каждого вида соответственно равна 20 руб., 10 руб. и 7 руб. Сколько ящиков и какого вида должен использовать завод , чтобы стоимость пересылки была наименьшей.
Решение.
Оценим, в каком из ящиков пересылка одной детали будет наиболее дешевой: в первом  руб., во втором руб., во втором  руб., в третьем руб., в третьем  руб. Поскольку руб. Поскольку 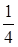 < <  , то выгоднее пересылать детали в ящиках по 40 штук, менее выгодно- по 25 штук, наименее выгодно – по 70 штук. , то выгоднее пересылать детали в ящиках по 40 штук, менее выгодно- по 25 штук, наименее выгодно – по 70 штук.
Но 1100 деталей в ящики по 40 штук полностью вместить нельзя. Следовательно, необходимо найти максимальное количество деталей, которые можно переслать в ящиках по 40 деталей.
Максимальное количество стоит искать среди чисел, близких к 1100 и кратных 40, т.е. среди чисел, 1080, 1040, 1000 и т.д. Первые два числа не подходят, т.к. останется в первом случае 20, а во втором -60 деталей; в третьем случае останется 100 деталей, которыми можно загрузить 4 ящика по 25 деталей.
Можно подсчитать, что в этом случае затраты на пересылку составят 10 ∙ 25 + 4 ∙ 7 =278 руб. А если, например, отправить 10 ящиков по 70 деталей и 16 ящиков по 25 деталей, то затраты составят 312 руб..
Задача 2.
Найти наименьшее и наибольшее значение функции y=4x+6|x-2|-x2 на отрезке
[-1;3].
Решение:
y=-( x2-4x+4-4)+ 6|x-2|=-(x-2)2 +6|x-2|+4. Так как а2=|а|2, то y=
-|x-2|2+6|x-2|+4. Пусть t=|x-2|. Поскольку -1 ≤ х ≤ 3, то 0 ≤ t ≤ 3. При этом y=-t2+6t+4 возрастает и, следовательно,
miny(t)=y(0)=4, maxy(t)=y(3)=13.
[0;3] [0;3]
Если t=0, то x=2. Если t=3, то |x-2|=3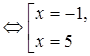
Но по условию х [-1;3], поэтому остается только значение х=-1. [-1;3], поэтому остается только значение х=-1.
Ответ: miny(х)=y(2)=4, maxy(х)=y(-1)=13.
[-1;3] [-1;3]
Задача 3.
Найти наименьшее и наибольшее значения функции у=2sinx – cos 2x +cos2 x.
Решение.
Так как
cos 2x = 1 -2 sin2 x, cos2 x = 1- sin2 x, тоy= sin2 x+ 2 sin x. Пустьt =sin x, -1 ≤ t ≤ 1.
Тогда, решение задачи сводится к вычислению наибольшего и наименьшего значений квадратичной функции на отрезке.
Графиком этой функции является парабола, ветви которой направлены вверх, абсцисса t0 вершины параболы, равна - 1. Так как t0 є [- 1;1] , то maxy(t) =y (1) =3, miny(t) =y (-1) = -1.
Если t = 1, то sinx = 1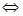 x = x = 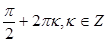 . Если t= - 1, то . Если t= - 1, то
sin х = -1 n, n n, n Z. Поэтому maxy(x) = 3, miny(x) = - 1. Z. Поэтому maxy(x) = 3, miny(x) = - 1.
Занятие 4
Тема: «Алгебраический подход к решению задач на экстремумы».
Тип: Комбинированный урок.
Цели:
Обучающая: Обучить способу решения экстремальных задач различными аналитическими методами, совершенствование навыков решения экстремальных задач аналитическими методами.
Развивающая: дать возможность учащимся убедится в том, на сколько развиты их возможности и над чем нужно поработать.
Воспитательная: воспитание потребности и умения работать в коллективе для решения совместных задач, активной жизненной позиции, умения ставить и достигать цели.
Задачи: Рассмотреть различные аналитические методы решения экстремальных задач, и их применение при решении конкретных задач; закрепление умений и навыков решения экстремальных задач аналитическими методами.
Оборудование: доска, мел, карточки с заданиями.
План урока
| Содержание |
Методы и приемы |
Время |
1.Орг. момент
Сообщение цели урока
|
Инструктаж учителя |
3 мин |
2.Изучение нового
материала
1.Суть метода.
2.Пример решения
задачи c
использованием
неравенств.
|
Лекция
(объяснительно-иллюстра–тивный с элементами
проблемного изложения)
Учащиеся конспектируют, задают вопросы.
|
20 мин |
| 3.Закрепление пройденного материала. |
Учитель предлагает
учащимся задачи для
самостоятельного решения.
Учащиеся самостоятельно
решают задачи своего
уровня сложности
(репродуктивный, частично-поисковый)
|
31 мин |
| 4.Подведение итогов |
беседа |
2 мин |
| 5.Запись домашнего задания |
Инструкция учителя
(репродуктивный)
|
4 мин |
Ход урока:
| Деятельность учителя |
Деятельность учащихся |
I.Орг. момент.
Добрый день.
На прошлом занятии мы в вами начали изучать алгебраические подходы к решению задач на экстремумы. Сегодня мы рассмотрим еще один подход - использование стандартных неравенств.
|
Садятся.
Слушают учителя,
отвечают на его
вопросы.
|
II. Лекция.
1.Суть метода.
Напомним, что для любых двух неотрицательных чисел а и в справедливо неравенство, называемое неравенством между средним арифметическим и средним геометрическим этих чисел (неравенство Коши):
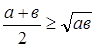 . .
Важным следствием неравенства Коши является следующее: для любых двух положительных чисел а и в и любого отличного от нуля действительного числа t
 ≥ 2 ≥ 2 . Причем знак неравенства достигается в том и только том случае, когда at=b/t, т.е. t2=b/a. . Причем знак неравенства достигается в том и только том случае, когда at=b/t, т.е. t2=b/a.
2.Пример решения задачи.
Найти наибольшее значение функции 
y=4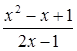 на интервале (-∞; на интервале (-∞; ). ).
Решение:
y=4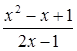 = = = = =2x-1+ =2x-1+ . Так как по условию х<1/2, то 2х-1<0 и . Так как по условию х<1/2, то 2х-1<0 и  <0. Воспользуемся неравенством | at+b/t | ≥2 <0. Воспользуемся неравенством | at+b/t | ≥2
для случая t<0. Тогда y=2х-1+ ≤-2 ≤-2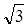 , причем знак неравенства достигается тогда и только тогда, когда , причем знак неравенства достигается тогда и только тогда, когда
 2х-1= 2х-1= , и 2х-1<0 . , и 2х-1<0 .
И последней системы находим х=
Ответ: maxy(x)=y( )=-2 )=-2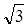
(-∞; ) )
|
Ученики конспектируют, задают вопросы
Слушают учителя, записывают решение в тетрадь, задают
возникающие вопросы.
|
III Закрепление пройденного материала.
Сейчас возьмите карточки с заданиями своего уровня и решите предложенные там задачи.
Учитель следит за тем, что бы все работали, отвечает на возникающие вопросы. Если какая-та задача вызывает у многих затруднения, ее (полностью или частично) прорешивают на доске.
|
Учащиеся берут
карточки с
заданиями и
преступают к
решению задач.
Если возникают
трудности, они
обращаются за
помощью к
учителю.
|
IVПодведение итогов
Итак, сегодня мы с вами рассмотрели еще два метода решения экстремальных задач и их применение.
Какие у вас есть вопросы по пройденному сегодня материалу? (отвечает на вопросы, если они есть)
|
Задают вопросы, которые остались непонятными.
|
VЗапись домашнего задания
Домашнее задание: посмотреть конспект сегодняшнего занятия, дорешать задачи своей карточки.
|
Записывают. |
Задачи предлагаемые учащимся.
I уровень сложности.
Задача 1.
Найдите прямоугольник наименьшего периметра, ограничивающий заданную площадь.
Решение.
В данном случае площадь S= xy постоянна. Следовательно, p= x+y достигает наименьшего значения, если х + у = 2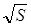 . Таким прямоугольником является квадрат со стороной . Таким прямоугольником является квадрат со стороной 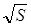 , периметр его 4 , периметр его 4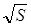 . .
Задача 2.
Найти наименьшее значение функции у = х +  , при х > 2. , при х > 2.
Решение.
Очевидно, что

Отсюда следует, что искомое наименьшее значение получается при х-2 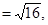 при при
х = 6, а само искомое значение равно 
Задача 3.
Найти наибольшее значение функции
y= . .
Решение.
Заметим, что D(y) = [0; 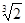 ]. При х ]. При х  [0; [0; 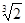 ] выполнены, очевидно, неравенства х3 ≥ 0, 2 – х3 ≥0. ] выполнены, очевидно, неравенства х3 ≥ 0, 2 – х3 ≥0.
Применим неравенство Коши :
y= ≤ ≤ 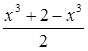 =1. =1.
Поэтому у ≤ 1, причем знак равенства достигается, лишь если
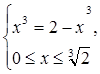 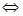 х =1. х =1.
maxy(x) = y(1) = 1.
II уровень сложности.
Задача 1.
Требуется сделать коробку, объем которой должен равняться 108 см3. Коробка открыта сверху и имеет квадратное дно. Каковы должны быть размеры ее, чтобы на ее изготовление пошло наименьшее количество материала?
Решение.
Длину стороны основания обозначим через х см., а высоту коробки – у см.(х>0, y>0). Тогда ее объем V= x2y. Учитывая, что V= 108 см3, имеем x2y = 108 => у= . .
Пусть S-площадь поверхности коробки:
S= x2+4xy = x2+4x = x2+ = x2+ 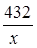 . .
Представим выражение для S следующим образом:
S = x2 + 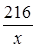 + + 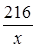 . .
Произведение x2 + 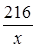 + + 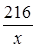 равно 2162. Следовательно, S достигает наименьшего значения, если х2= равно 2162. Следовательно, S достигает наименьшего значения, если х2= 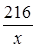 , т.е. х3 = 216 => х =6 => y = 3. , т.е. х3 = 216 => х =6 => y = 3.
Тогда = 108 (см 2).
Задача 2.
Найти наименьшее значение функции y=32х – 1 + 4∙33 – 2х.
Решение.
Так как 3t и 4∙ 3z положительные при любых действительных значениях t и z, то, применив неравенство Коши, получим
У=32х – 1 + 4∙33 – 2х ≥ 2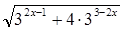 =2 =2 =12. =12.
Таким образом, у(х) ≤ 12 при любом действительном х, причем знак равенства достигается, лишь, если
32х – 1=4∙33 – 2х 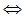 34х – 4 =4 34х – 4 =4 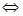 х= х=  . .
miny(x) = y( ) =12. ) =12.
Задача3.
Найти наибольшее значение функции у=4 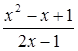 на интервале (-∞ ; на интервале (-∞ ;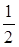 ) . ) .
Решение.
у=4 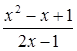 = =
Так как по условию х< , то 2х – 1 <0 и , то 2х – 1 <0 и  <0. <0.
maxy(x) = y( ) = -2 ) = -2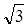 . .
III уровень сложности.
Задача 1.
При небрежной транспортировке рулонов типографской бумаги на их поверхности появляются трещины, в результате чего образуется так называемый бумажный срыв, идущий в отходы. Очевидно, что эти отходы тем меньше, чем меньше полная поверхность рулона при данном его объеме. Необходимо исследовать, при каком соотношении между диаметром и длиной(т.е. образующей) рулона срыв бумаги будет наименьшим.
Решение.
Задача сводится к нахождению такого соотношения между радиусом R основания и высоты Н цилиндра, чтобы при данном объеме цилиндра его полная поверхность имела наименьшее значение.
Имеем : S= 2π RH + 2π R2, H= . .
Поэтому
S =  +2πR2 = +2πR2 = 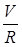 + +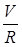 + 2πR2 . + 2πR2 .
Надо найти наименьшее значение суммы трех положительных слагаемых 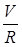 + +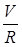 + 2πR2, произведение которых + 2πR2, произведение которых 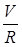 ∙ ∙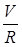 2πR2= 2πV2 неизменно при данном постоянном значении V. Поэтому Sдостигает тогда и только тогда, когда 2πR2= 2πV2 неизменно при данном постоянном значении V. Поэтому Sдостигает тогда и только тогда, когда 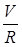 =2πR2, т.е. когда =2πR2, т.е. когда 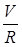 =2πR3. =2πR3.
H=  = =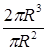 =2R. =2R.
Задача 2.
Найти наименьшее значение функции у = на интервале (13/6 π ; 17/6 π). на интервале (13/6 π ; 17/6 π).
Решение.
у = =2sinx + 1+ =2sinx + 1+ =2 sinx – 1+ =2 sinx – 1+ 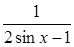 +2. +2.
По условию, 13/6 π < x < 17/6 π , т.е.  + 2π < x < + 2π < x < 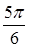 + 2π, откуда + 2π, откуда
sinx > ½.
Y = 2sinx - 1 +  +2 ≥ 2 +2 ≥ 2 +2 =4. +2 =4.
Таким образом, у ≥ 4, причем знак равенства достигается тогда и только тогда , когда

C учетом того, что 13/6 π < x < 17/6 π, получим х = 
miny= 4.
Задача 3.
Найти наименьшее значение функции
y=| x2 – x| + |x + 1|.
Решение.
y=| x2 – x| + |x + 1|≥ |x2 – x + x +1| =|x2 + 1| = x2 + 1≥ 1.
Таким образом, у≥1, причем знак равенства достигается только в том случае, когда одновременно выполнены равенства
| x2 – x| + |x + 1| = |x2 + 1| и x2 + 1=1, откуда x=0.
miny(x) = y(0) =1.
Занятие 5
Тема: «Универсальный метод решения задач на экстремумы».
Тип: Комбинированный урок.
Цели:
Обучающая: отработка и совершенствование навыков решения экстремальных задач с помощью производной, обобщить материал по теме «Решение экстремальных задач».
Развивающая: развитие волевых качеств, воспитание желание самосовершенствования, развитие навыков самостоятельной работы.
Воспитательная: воспитание интереса к математике, воспитание эмоционально-положительной направленности на практическую деятельность.
Задачи: повторить методику решения задач на максимум и минимум с помощью производной, прорешать основные типы задач на использование этого метода.
Оборудование: доска, мел, карточки с заданиями.
План урока
| Содержание |
Методы и приемы |
Время |
1. Орг. момент
Сообщение цели урока
|
Инструктаж учителя |
7 мин |
2. Изучение нового материала
1.Суть метода.
2. Пример решения
задачи с помощью
дифференцирования.
|
Лекция
(объяснительно-иллюстра–тивный с элементами
проблемного изложения)
Учащиеся конспектируют, задают вопросы.
|
16 мин |
| 3.Закрепление пройденного материала. |
Учитель предлагает учащимся задачи для самостоятельного решения. Учащиеся самостоятельно решают задачи своего уровня сложности (репродуктивный, частично-поисковый) |
31 мин |
| 4. Подведение итогов |
беседа |
2 мин |
| 5. Запись домашнего задания |
Инструкция учителя
(репродуктивный)
|
4 мин |
Ход урока:
| Деятельность учителя |
Деятельность учащихся |
I. Орг. момент.
Здравствуйте, садитесь.
На протяжении нескольких занятий мы с вами решаем экстремальные задачи. Мы рассмотрели довольно много задач на нахождение экстремумов. Те приемы, которыми мы решали эти задачи, оказались весьма разнообразными и порой довольно искусственными. Дело обстоит так, что почти для каждой задачи на экстремум приходилось «изобретать» подходящий для нее прием. Возникает поэтому вопрос: а нет ли достаточно общего приема решения задач на экстремумы? Такой прием есть. Его дает математический анализ.
|
Садятся.
Слушают учителя, отвечают на его вопросы.
|
II. Лекция.
1. Суть метода.
Общий прием решения задач на экстремум опирается на теорему Ферма.
Если функция у = f(х) (имеющая локальную производную) при х = х0 принимает локальный максимум или минимум, то производная от этой функции при х = х0 обращается в 0.
Геометрически это означает, что касательная к графику функции в соответствующей точке его параллельна оси х-ов.
Чему же учит нас теорема Ферма? Она учит нас тому, что значения аргумента, при которых данная функция f(x) имеет локальные минимумы, следует искать среди корней уравнения f '(x) = 0. Она выражает необходимое условие экстремума:
Для того чтобы функция (имеющая производную) имела при х = х0 максимум или минимум, необходимо, чтобы производная при этом значении х была равна 0.
Необходимо, но не достаточно! Производная может быть равна 0, и все же при этом значении х функция экстремума может и не иметь. Так, например, производная функции у = х3 (у' = 3х2) при х = 0 обращается в 0, но эта функция при х = 0 экстремума не имеет (рис.2). Значит, уравнение f '(х) = 0 дает лишь «подозрительные» на экстремум значения х.
Как же из этих «подозрительных» значений выделить те, при которых рассматриваемая функция действительно имеет экстремумы?
Как для выделенных значений установить вид экстремума?
По этим вопросам мы ограничимся соображениями, источником которых является наглядность. Рассмотрим рисунок, на котором изображены максимум и минимум функции у = f(x). По этому рисунку установим, какие по знаку значения принимает производная функция f '(x) для значений х, достаточно близких к х0, меньших и больших его. Если при х = х0 данная функция имеет максимум, то для значений х, меньших х0, но достаточно близких к х0, производная будет положительна, а для больших- отрицательна, т.к. в первом случае касательная к графику функции образует с положительным направлением оси х-ов острый угол, а во втором- тупой.
Если же при х = х0 функция принимает минимальное значение, то получается наоборот. Таким образом, будет ли «подозрительная» точка х0 точкой экстремума и, если будет, то какого именно (максимума или минимума), зависит от значений, принимаемых в достаточной близости слева и справа от точки х0 производной функцией. Все возможные случаи можно записать в следующей таблице.
| х0+Δх, Δх<0 |
х0 |
х0+Δх |
Поведение f(x) |
f '(x)
f '(x)
f '(x)
f '(x)
|
+
-
+
-
|
0
0
0
0
|
-
+
+
-
|
максимум
минимум
возрастает (экстремума нет)
убывает (экстремума нет)
|
Вот этой таблицей и можно пользоваться при решении задач на экстремумы.
Но можно из этой таблицы сделать новые выводы и пользоваться ими. Вот о каких выводах идет речь. В случае максимума с возрастанием х и переходом через значение х0 производная убывает, поэтому производная от этой производной(т.е. производная второго порядка) отрицательна. В случае минимума производная при переходе х через х0 возрастает, а значит, производная второго порядка положительна. Поэтому если в «подозрительной» точке х0 производная второго порядка f ''(x0) отрицательна, то в этой точке данная функция имеет максимум, если же f ''(x0) положительна, то функция принимает минимальное значение.
Чтобы проиллюстрировать рассмотренный общий прием решения задач на экстремумы, рассмотрим пример.
2. Пример решения задачи.
Пример: (Задача о прямоугольнике наибольшей площади)
Из куска стекла, имеющего указанные форму и размеры, нужно вырезать прямоугольную пластину наибольшей площади.
Площадь пластины S = xy. За независимое переменное примем х(0<х≤100). Тогда из подобия треугольников АВЕ и СDЕ следует:
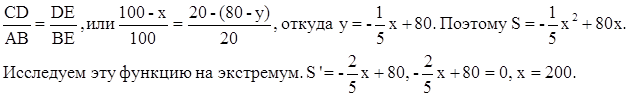 Найденное значение х выходит из промежутка изменения х. Поэтому внутри этого промежутка стационарных точек нет. Значит, наибольшее значение S принимает в одном из концов промежутка, а именно при х = 100 (мм), а тогда у = 60 (мм) и S = 6000 (мм2). Найденное значение х выходит из промежутка изменения х. Поэтому внутри этого промежутка стационарных точек нет. Значит, наибольшее значение S принимает в одном из концов промежутка, а именно при х = 100 (мм), а тогда у = 60 (мм) и S = 6000 (мм2).
|
Ученики конспектируют, задают вопросы
Слушают учителя, записывают решение в
тетрадь, задают возникающие вопросы.
|
III Закрепление пройденного материала.
Сейчас возьмите карточки с заданиями своего уровня и решите предложенные там задачи.
Учитель следит за тем, что бы все работали, отвечает на возникающие вопросы. Если какая-та задача вызывает у многих затруднения, ее (полностью или частично) прорешивают на доске.
|
Учащиеся берут карточки с заданиями и
Преступают к
решению задач. Если возникают трудности, они обращаются за помощью к учителю.
|
IV Подведение итогов
Итак, сегодня мы с вами рассмотрели еще два метода решения экстремальных задач и их применение.
Какие у вас есть вопросы по пройденному сегодня материалу? (отвечает на вопросы, если они есть)
|
Задают вопросы, которые остались непонятными |
VЗапись домашнего задания
Домашнее задание: посмотреть конспект сегодняшнего занятия, дорешать задачи своей карточки.
|
Записы-вают. |
Задачи предлагаемые учащимся.
I уровень сложности.
Задача 1.
Требуется огородить забором прямоугольный участок земли площадью 294 м2 и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора будет наименьшей?
Решение:
Пусть х и у – линейные размеры участка в метрах, тогда площадь участка есть 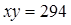 , откуда , откуда 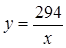 . длина всего забора выразится функцией . длина всего забора выразится функцией
 причем по смыслу задачи x>0. причем по смыслу задачи x>0.
Далее имеем  откуда откуда  при при 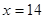 (поскольку x>0). Если 0<x<14, то (поскольку x>0). Если 0<x<14, то  ; если же x>14, то ; если же x>14, то  ; поэтому x=14 есть точка минимума функции ; поэтому x=14 есть точка минимума функции  . в результате получаем, что x=14, у=21. . в результате получаем, что x=14, у=21.
Ответ: x=14, у=21.
Задача2.
Число 81 разбить на 3 положительных сомножителя так, чтобы два из них относились как два к одном у, а сумма трех сомножителей была наименьшей.
Решение:
Обозначим первое слагаемое за х. Тогда второе слагаемое выразится как 2х, а третье 81/2х2. Найдем сумму слагаемых S. S=3х+81/2х2. Найдем наименьшее значение функции S. Для этого найдем производную S'=3-81/х3=0 => х=3- минимальное значение функции. Тогда второе число 6, третье число 4,5.
Задача3.
Из квадратного листа железа со стороной а, надо изготовить открытую сверху коробку, вырезав по углам квадратики и загнув образовавшиеся кромки, чтобы ее объем был максимальным.
Решение:
Обозначим через х длину стороны основания коробки. Тогда длины сторон вырезанных квадратиков равны S (а -х), а объем коробки равен S (а –х)х2 на интервале (0, а). Таким образом задачу мы свели к следующей задачи: найти наибольшее значение функции V(x)=1/2(a - x)x2 на интервале (0, а). Находим критические точки функции : V/ (x) = ax – 3/2 x2, ax – 3/2 x2=0, т.е. х=0 или х=2/3 а V(2/3а) =1/2(a -2/3a)(2/3a)2= 2/27 a3. Т.к. V(0)=0 и V(a) =0, своего наибольшего значения на отрезке функция достигает при х =2/3а, т.е. maxV(x) =2/27 a3.
Полученный результат означает, что максимальный объем имеет коробка со стороной основания 2/3 а.
II уровень сложности
Задача 1.
В прямоугольный треугольник с гипотенузой 24 см и углом  вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей? вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей?
Решение:
По условию, АВ=24см,  , откуда , откуда 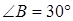 . Пусть . Пусть  и и 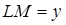 - линейные размеры прямоугольника MNKL (в сантиметрах). Выразим - линейные размеры прямоугольника MNKL (в сантиметрах). Выразим 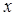 через через 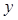 . .
Из  : : 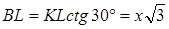 ; из ; из  : : 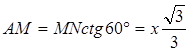 ;тогда ;тогда 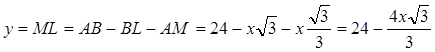 . .
Площадь прямоугольника MNKL выразится функцией
 . .
Далее имеем  , откуда , откуда 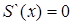 при при  . Если . Если 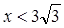 , то , то 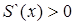 , а если , а если 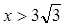 , то , то  , т.е. , т.е. 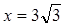 – точка максимума функции – точка максимума функции 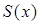 . Итак, длины сторон искомого прямоугольника равны . Итак, длины сторон искомого прямоугольника равны  см и см и  см. см.
Ответ:  и 12 см. и 12 см.
Задача 2.
Из пункта А на прогулку вышел пешеход со скоростью 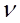 км/ч. После того как он отошел от А на 6 км, из А следом за ним выехал велосипедист, скорость которого была на 9 км/ч больше скорости пешехода. Когда велосипедист догнал пешехода, они повернули назад и возвратились вместе в А со скоростью 4 км/ч. При каком значении км/ч. После того как он отошел от А на 6 км, из А следом за ним выехал велосипедист, скорость которого была на 9 км/ч больше скорости пешехода. Когда велосипедист догнал пешехода, они повернули назад и возвратились вместе в А со скоростью 4 км/ч. При каком значении  время прогулки окажется наименьшим? время прогулки окажется наименьшим?
Решение:
Время, за которое велосипедист догонит пешехода, составит  . До встречи пешеход находился в пути . До встречи пешеход находился в пути  и прошел и прошел 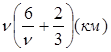 . Этот же путь они преодолели обратно с одинаковой скоростью 4 км /ч и затратили время . Этот же путь они преодолели обратно с одинаковой скоростью 4 км /ч и затратили время  Тогда время, затраченное пешеходом на всю прогулку, выразится функцией Тогда время, затраченное пешеходом на всю прогулку, выразится функцией

где 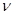 >0. >0.
Находим 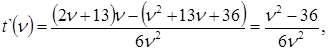
откуда  при при 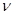 =6. Легко установить, что =6. Легко установить, что 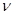 =6 – точка минимума функции =6 – точка минимума функции  . .
Итак, пешеход затратит на прогулку наименьшее время, если первоначально будет идти со скоростью 6 км/ч.
Ответ: 6 км/ч
Задача 3.
Площадь прямоугольного треугольника 16 см2 какими должны быть длины сторон треугольника, чтобы сумма площадей квадратов построенных на его сторонах была наименьшей?
Решение:
Обозначим один из катетов треугольника за х, тогда второй равен  из теоремы Пифагора находим третью сторону - из теоремы Пифагора находим третью сторону - 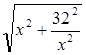 . Тогда искомая функция: . Тогда искомая функция:
у =х2+ 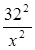 + х2+ + х2+  , ,
исследуя эту функцию находим miny=4 . Откуда получаем искомые стороны треугольника: 4 . Откуда получаем искомые стороны треугольника: 4 ; 4 ; 4 ; 8. ; 8.
III уровень сложности.
Задача 1.
Каков должен быть радиус основания открытого цилиндрического бака , имеющего приданном объеме V наименьшую площадь основания?
Решение:
S=2πRH+ πR2, V= πR2H,  H= H= 
S=2πR + 2πR2 = + 2πR2 = + πR2 , S/=- + πR2 , S/=-  + πR; + πR;
S/=0; 2πR= , V = πR3 , V = πR3   R = R =
Задача 2.
Найти длину боковой стороны трапеции имеющей наименьший периметр среди всех равнобедренных трапеций с заданной площадью, углом между боковой стороной и нижним основанием.
Решение:
Пусть высота трапеции – х.
Тогда: 
Из  : : 
По условию  ; ;
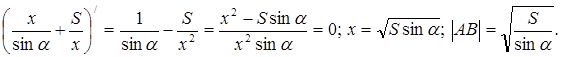
Покажем, что при этих условиях периметр минимальный 
а) пусть  , тогда , тогда 
б) пусть 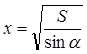 , ,
тогда 
Т.к. 
Ответ:  . .
Задача 3.
Лодка М находится на расстоянии 3 км от ближайшей точки А берега. Пассажир лодки желает достигнуть точки В, находящейся на берегу на расстоянии 5 км. от А. Лодка движется со скоростью 4 км/ч , а пассажир, выйдя из лодки, может пройти в час 5 км. К какому пункту берега должна прибыть лодка, чтобы пассажир достиг В в кратчайшее время?
Решение:
t= 
Пусть АО = х. Тогда ОВ = 5 – х и t=
t/(x) = - - 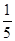 , ,  = = 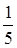 , x =4. , x =4.
Ответ: 4км, 1км.
Анализ.
Часть занятий факультатива была опробированна на учащихся 11 класса общеобразовательной школы.
Проведенные занятия показали, что наиболее легким для учащихся является основной метод решения экстремальных задач, но наибольший интерес вызывают задачи прикладного характера. Ребята с удовольствием решали предложенные задачи, а дифференцированный подход позволил каждому, самостоятельно, находить решения задач, используя различные методы и приемы.
Данный факультатив стимулирует интерес учащихся к математике, дает возможность ребятам убедиться в том, насколько развиты их возможности и над чем необходимо поработать, формирует культуру, интеллектуальное развитие и совершенствование.
Заключение
Задачи на максимум и минимум часто встречаются как в науке, так и в повседневной жизни человека. Своей распространенностью они обязаны тому, что при решении задач мы находим наиболее выгодный из имеющихся вариантов.
При подготовки дипломной работы была изучена литература по данной теме, исторические задачи и их решения.
Также были рассмотрены алгебраические и геометрические подходы к решению задач на экстремум.
Во второй главе дипломной работы рассмотрены проблемы дифференцированного обучения на уроках и приведена разработка факультатива на тему «Решение задач на экстремум».
Целью дипломной работы являлось изучение различных методов решения экстремальных задач и адаптация их к школьному курсу математики. Считаю, что задачи выполнены, цель достигнута.
Библиография
1. Александров, А.Д. Геометрия 7 - 9 кл.: Учеб. для общеобразоват. учеб. заведений [Текст] / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– М.: Просвещение, 2003.
2. Александров, А.Д. Геометрия: 10 - 11 кл. [Текст] / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– М.: Просвещение, 1998.
3. Александров, А.Д. Геометрия: 10-11 кл.: Учеб. для общеобразоват. учеб. заведений [Текст] / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– М.: Просвещение, 1998.
4. Александров, А.Д. Геометрия: 10-11 кл.: Учеб. для общеобразоват. учеб. заведений [Текст] / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– М.: Просвещение, 2003.
5. Алексеев, Н.А. Психолого-педагогические проблемы развивающего дифференцированного обучения: Монография. [Текст] / Н.А. Алексеев.– Челябинск: Факел, 1995.
6. Алимов, Ш.А. Алгебра: 7 кл.: Учеб. для общеобразоват. учеб. заведений [Текст] / Ш.А. Алимов, Ю.М. Колягин и др.– М.: Просвещение, 2002.
7. Алимов, Ш.А. Алгебра: 8 кл.: Учеб. для общеобразоват. учеб. заведений [Текст] / Ш.А. Алимов, Ю.М. Колягин и др.– М.: Просвещение, 2001.
8. Алимов, Ш.А. Алгебра: 9 кл.: Учеб. для общеобразоват. учеб. заведений [Текст] / Ш.А. Алимов, Ю.М. Колягин и др.– М.: Просвещение, 2002.
9. Давыдов, В.В. Виды обобщения в обучении (логико-психологические проблемы построения учебных предметов). [Текст] / В.В. Давыдов.– М.: Педагогика, 1972.
10. Иванова, Л.М. Дифференцированный подход при обучении. [Текст] / Л.М. Иванова.– М., 1998.
11. Методика преподавания математики в средней школе. Частные методики [Текст] / Ю.М. Колягин, Г.Л. Луканкин, Е.Л. Мокрушин и др.– М.: Просвещение, 1977.
12. Методика преподавания математики в средней школе: Учебное пособие [Текст] / Ю.М. Колягин, В.А. Оганесян, В.Я. Саннинский, Г.Л. Луканкин.– М., 1975..
13. Мордкович, А.Г. Алгебра и начала анализа. 10 - 11 кл.: Методическое пособие для учителя. [Текст] / А.Г. Мордкович.– М.: Мнемозина, 2002.
14. Мордкович, А.Г. Алгебра: 7 кл.: задачник для общеобразоват. учеб. заведений. [Текст] / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская – М.: Мнемозина, 2003.
15. Мордкович, А.Г. Алгебра: 8 кл.: задачник для общеобразоват. учеб. заведений. [Текст] / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская – М.: Мнемозина, 2003.
16. Мордкович, А.Г. Алгебра: 9 кл.: задачник для общеобразоват. учеб. заведений. [Текст] / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.– М.: Мнемозина, 2003.
17. Окунев, А.Л. Развитие у учащихся способности наблюдать и анализировать [Текст] / А.Л. Окунев // Математика в шк.– 1982.– № 5.– 23С.
18. Осмоловская, И.М. Организация дифференцированного обучения в современной общеобразовательной школе [Текст] / И.М. Осмоловская.– М.: Ин-т практич. психологии, 1998.
19. Осмоловская, И.М. Организация дифференцированного обучения в современной общеобразовательной школе. :пособие для учителей [Текст] / И.М. Осмоловская.– М.: Просвещение, 1997.
20. Письменный, Д.Т. Математика для старшеклассников[Текст] / Д.Т. Письменный.– М.: Айрис, 1996.
21. Погорелов, А.В. Геометрия 10-11класс: Учеб. для общеобразоват. учеб. заведений [Текст] / А.В. Погорелов.– М.:Просвещение,1993.
22. Пойа, Д. Как решать задачу: пособие для учителей [Текст]: пер. с англ. / под редакцией Ю.М. Гайдука.– М.: Гос. учеб. – пед. изд-во МП РСФСР, 1959.
23. Потапов, А.С. Дифференциация обучения с учетом психологических особенностей [Текст] / А.С. Потапов.– М.: Просвещение, 1989.
24. Потапов, А.С. Дифференциация обучения с учетом психологических особенностей. :пособие для учителей [Текст] / А.С. Потапов.– М. Просвещение, 1989.
25. Саранцев, Г.И. Методика обучения математике в средней школе: Учеб. пособие для студ. математических спец. пед вузов и ун-тов. [Текст] / Г.И. Саранцев.– М.: Просвещение, 2002.
26. Учебные стандарты школ России: в 2 кн. Кн.2: Математика. Естественно - научные дисциплины [Текст] / Под ред. В.С. Леднева, Н.Д. Никандрова, М.Н. Лазутовой.– М.: Сфера: Прометей, 1998.
27. Шарыгин, И.Ф. Факультативный курс по математике – 10 кл.: пособие для учителей [Текст] / И.Ф. Шарыгин.– М.: Просвещение, 1989.
28. Шарыгин, И.Ф. Факультативный курс по математике - 11 кл.: пособие для учителей [Текст] / И.Ф. Шарыгин.– М.: Просвещение, 1992.
|