Контрольная работа: Сглаженная поверхность для границы трех атомов в пространстве
|
Название: Сглаженная поверхность для границы трех атомов в пространстве Раздел: Рефераты по информатике, программированию Тип: контрольная работа | |
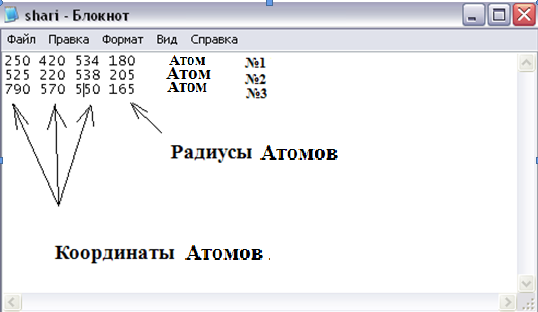
Федеральное агентство по образованию РФ ГОУ ВПО «Волгоградский государственный университет» Факультет математики и информационных технологий Кафедра ПМП Семестровая работа на тему:«Сглаженная поверхность для границы трёх атомов в пространстве» Выполнил: студент группы ПМб-091 Орлов А.А. Научный руководитель: Чернышев И.В. Волгоград 2011Содержание Введение Постановка задачи Метод (схема) решения поставленной задачи Заключение К задаче о построении сглаженной поверхности в пространстве сводится задача вычисления эффективных значений объема и поверхности молекул, при котором молекула моделируется областью с гладкой границей, представляющей из себя объеденение сферических фрагментов. Например для вычисления объема полости, занимаемой молекулой солюта в растворе, а также величины возникающей при этом поверхности раздела, что является необходимым звеном в построении количественных моделей взаимодействия растворенного вещества с растворителем. Идея предлагаемого геометрического метода сглаживания формы молекулы состоит в том, что граница молекулы представляется в виде поверхности, у которой радиус кривизны вогнутых частей в любой точке не меньше некоторого заданого значения. Этим радиусом скругления может быть, например, эффективный радиус молекул некоторого химического соеденинения, учавствующего во взаимодействии с рассматриваемой молекулой. В данной работе необходимо построить сглаженную поверхность для заданных 3-х атомов и радиусу большого атома. Постановка задачи Задача построения поверхности заключаетя в создании алгоритма с помощью которого, по заданым координатам и радиусам 3-х атомов, а также радиусу атома, касающегося их, можно построить сглаженную поверхность для границы данных атомов в пространстве. Метод (схема) решения поставленной задачи 1. Программа считывает данные с файла shari.txt
Далее вычисляются координаты центра атома, который касается 3-х 2. остальных. Координаты центра атома радиуса RS , касающегося трех атомов с центрами в точках Oi (xi ,yi ,zi ), Oj (xj ,yj ,zj ), Ok (xk ,yk ,zk ) определяются следующими формулами:
где
Для сокращения записи использованы обозначения
3. Вычисляютя координаты точек касания большого атома с 3-мя остальными. Для каждой точки касания необходимо выполнение 3-х условий: A. Точка касания принадлежит большому атому. Б. Точка касания принадлежит атому с которым касается большойй. В. Точка касания принадлежит каноническому уравнению прямой, которое составленно по координатам центра большого атома и координатам центра атома, которого касается большой атом: (Xkosn - Xc)2 + (Ykosn - Yc)2 + (Zkosn - Zc)2 =Rc2 (Xkosn - Xn)2 + (Ykosn - Yn)2 + (Zkosn - Zn)2 =Rn2
Xc – Xn Yc – Yn Zc – Zn Где N=1, 2, 3 соответственно. Xc,Yc,Zc – координаты большого атома. Xkosi ,Ykosi ,Zkosi ,– координаты точки касания i-го атома и большого атома. Решая данную ситему находим координаты точек касания.
X – X1 Y – Y1 Z – Z1 X2 – X1 Y2 – Y1 Z2 – Z1 = 0 Xc – X1 Yc – Y1 Zc – Z1
X – X1 Y – Y1 Z – Z1 X3 – X1 Y3 – Y1 Z3 – Z1 = 0 Xc – X1 Yc – Y1 Zc – Z1
X – X2 Y – Y2 Z – Z2 X3 – X2 Y3 – Y2 Z3 – Z2 = 0 Xc – X2 Yc – Y2 Zc – Z2 Далее находим точки пересечения каждой плоскости с поверхностью большого атома. (X - Xc)2 + (Y - Yc)2 + (Z - Zc)2 =Rc2 При этом должно выполнятся условие: Xkosi <= X <= Xkosj Если Xkosi < Xkosj Xkosj <= X <= Xkosi Если Xkosj < Xkosi Где (i=1,j=2) (i=1,j=3) (i=2,j=3) 5) В результате работы программа строит: A) 3 атома по координатам считанным с файла shari.txt Б) Атом с радиусом Rc считанным с клавиатуры, который касается 3-х остальных. В) Сглаженную поверхность. Г) Оси координат.
После поворота системы шаров на угол 900 вокруг оси X=x[1]+x[2]+x[3]
Заключение Задачей данной семестровой работы являлась построение алгоритма, с помощью которого строится сглаженная поверхность для границы трех атомов в пространстве. Итогом работы можно считать приложение для ОС Windows, которое по заданным координатам и радиусам 3-х атомов, а также радиусу большого атома строит сглаженную поверхность. Приложение Текст программы имитации движения частиц в пористой среде для ОС Windows . алгоритм сглаженная поверхность атом #include<stdio.h> #include<stdlib.h> #include<graphics.h> #include<math.h> #define ESC 27 #define DOWN 80 #define UP 72 #define ENTER 13 int x[4],y[4],z[4],r[4],Rc,raz=0,kol_vr; int skok=1,schit=0; double aj,bj,cj,ak,bk,ck,Ris,Rjs,Rks,p[5],alp1,alp2,alp3,al1,al2,al3,al4,alp4;; double Xc,Yc,Zc,dj,dk,sin_a,sin_b,Xvr,Zvr,R1,R2,R3,R4,ugol[1500],Rad[1500],XX[1500],YY[1500],ZZ[1500]; double Bx,By,Bz,Cx,Cy,Cz,A,sum[3]; double Xkos1,Ykos1,Zkos1,yc1,xc1,zc1,XYc1,ZYc1,M1,M2; double Xkos2,Ykos2,Zkos2,yc2,xc2,zc2,XYc2,ZYc2,M3,M4; double Xkos3,Ykos3,Zkos3,yc3,xc3,zc3,XYc3,ZYc3,M5,M6; void dano(void) { FILE *f=fopen("shari.txt","r"); int i; printf("KOORDINATI 3 SFER I IH RADIUSI\n"); for(i=1;i<=3;i++) { printf("X%d=",i);fscanf(f,"%d",&x[i]);printf("%d\n",x[i]); printf("Y%d=",i);fscanf(f,"%d",&y[i]);printf("%d\n",y[i]); printf("Z%d=",i);fscanf(f,"%d",&z[i]);p[i]=z[i];printf("%d\n",z[i]); printf("R%d=",i);fscanf(f,"%d",&r[i]);printf("%d\n",r[i]); } Zvr=(z[1]+z[2]+z[3])/3; Xvr=(x[1]+x[2]+x[3])/3; R1=(sqrt((x[1]-Xvr)*(x[1]-Xvr)+(z[1]-Zvr)*(z[1]-Zvr))); R2=(sqrt((x[2]-Xvr)*(x[2]-Xvr)+(z[2]-Zvr)*(z[2]-Zvr))); R3=(sqrt((x[3]-Xvr)*(x[3]-Xvr)+(z[3]-Zvr)*(z[3]-Zvr))); double x1,x2,y1,y2; x1=x[1]-Xvr;x2=R1;y1=z[1]-Zvr;y2=0; alp1=(x1*x2+y1*y2)/((sqrt(x1*x1+y1*y1)))/(sqrt(x2*x2+y2*y2)); al1=acos(alp1)*180/M_PI; x1=x[2]-Xvr;x2=R2;y1=z[2]-Zvr;y2=0; alp2=(x1*x2+y1*y2)/((sqrt(x1*x1+y1*y1)))/(sqrt(x2*x2+y2*y2)); al2=acos(alp2)*180/M_PI; x1=x[3]-Xvr;x2=R3;y1=z[3]-Zvr;y2=0; alp3=(x1*x2+y1*y2)/((sqrt(x1*x1+y1*y1)))/(sqrt(x2*x2+y2*y2)); al3=acos(alp3)*180/M_PI; printf("vvedite radius bolshogo shara\n"); scanf("%d",&Rc); initwindow (1024,860); } int stroim(void) { int i,k,j;double max; max=p[1]; for(i=1;i<=4;i++) {if (p[i]>=max) {max=p[i];k=i;}} for(i=1;i<4;i++) { if (z[i]==max) {p[k]=-1;return i;} } p[4]=-1; return 4; } void risuem(void) { setcolor(7); setlinestyle(0,0,1); char st1[5]; char st2[5]; char st3[5]; xc1=Xc-x[1];xc2=Xc-x[2];xc3=Xc-x[3]; yc1=Yc-y[1];yc2=Yc-y[2];yc3=Yc-y[3]; zc1=Zc-z[1];zc2=Zc-z[2];zc3=Zc-z[3]; XYc1=(-xc1*y[1]+yc1*x[1])/yc1;XYc2=(-xc2*y[2]+yc2*x[2])/yc2;XYc3=(-xc3*y[3]+yc3*x[3])/yc3; ZYc1=(-zc1*y[1]+yc1*z[1])/yc1;ZYc2=(-zc2*y[2]+yc2*z[2])/yc2;ZYc3=(-zc3*y[3]+yc3*z[3])/yc3; M1=((Rc*Rc)-(Xc*Xc+Yc*Yc+Zc*Zc))/(-2); M2=((r[1]*r[1])-(x[1]*x[1]+y[1]*y[1]+z[1]*z[1]))/(-2); M3=((r[2]*r[2])-(x[2]*x[2]+y[2]*y[2]+z[2]*z[2]))/(-2); M4=((r[3]*r[3])-(x[3]*x[3]+y[3]*y[3]+z[3]*z[3]))/(-2); Ykos1=(M1-M2-XYc1*Xc+XYc1*x[1]-ZYc1*Zc+ZYc1*z[1])/(xc1*Xc/yc1-xc1*x[1]/yc1+(Yc-y[1])+zc1*Zc/yc1-zc1*z[1]/yc1); Ykos2=(M1-M3-XYc2*Xc+XYc2*x[2]-ZYc2*Zc+ZYc2*z[2])/(xc2*Xc/yc2-xc2*x[2]/yc2+(Yc-y[2])+zc2*Zc/yc2-zc2*z[2]/yc2); Ykos3=(M1-M4-XYc3*Xc+XYc3*x[3]-ZYc3*Zc+ZYc3*z[3])/(xc3*Xc/yc3-xc3*x[3]/yc3+(Yc-y[3])+zc3*Zc/yc3-zc3*z[3]/yc3); Xkos1=Ykos1*xc1/yc1+XYc1;Xkos2=Ykos2*xc2/yc2+XYc2;Xkos3=Ykos3*xc3/yc3+XYc3; Zkos1=Ykos1*zc1/yc1+ZYc1;Zkos2=Ykos2*zc2/yc2+ZYc2;Zkos3=Ykos3*zc3/yc3+ZYc3; line(40,600,200,600);line(40,640,200,640);line(40,680,200,680);line(40,720,200,720);line(40,760,200,760); line(80,640,80,800);line(120,640,120,800);line(160,640,160,800);line(200,600,200,800); outtextxy(53,618,"ТОЧКИКАСАНИЯ"); outtextxy(47,655,"АТОМ");outtextxy(87,655,"¹1");outtextxy(127,655,"¹2");outtextxy(167,655,"¹3"); outtextxy(45,695,"Xkos");outtextxy(45,735,"Ykos");outtextxy(45,775,"Zkos"); sprintf(st1,"%.1f",Xkos1);sprintf(st2,"%.1f",Xkos2);sprintf(st3,"%.1f",Xkos3); outtextxy(81,695,st1);outtextxy(121,695,st2);outtextxy(161,695,st3); sprintf(st1,"%.1f",Ykos1);sprintf(st2,"%.1f",Ykos2);sprintf(st3,"%.1f",Ykos3); outtextxy(81,735,st1);outtextxy(121,735,st2);outtextxy(161,735,st3); sprintf(st1,"%.1f",Zkos1);sprintf(st2,"%.1f",Zkos2);sprintf(st3,"%.1f",Zkos3); outtextxy(81,775,st1);outtextxy(121,775,st2);outtextxy(161,775,st3); setlinestyle(0,0,1); p[4]=Zc; int q=0,i,j,svet=4; double h=Rc; for(q=1;q<=4;q++) { i=stroim(); if (i==4) { setcolor(15); if (raz!=0) setlinestyle(3,0,1); circle(Xc+40,800-Yc,Rc); ellipse(Xc+40,800-Yc,180,360,Rc,Rc/2); ellipse(Xc+40,800-Yc-Rc/2,180,360,Rc-(Xc+Rc-(sqrt(Rc*Rc-(Rc/2)*(Rc/2))+Xc))-2,Rc/4); ellipse(Xc+40,800-Yc+Rc/2,180,360,Rc-(Xc+Rc-(sqrt(Rc*Rc-(Rc/2)*(Rc/2))+Xc))-2,Rc/4); setlinestyle(1,0,1); ellipse(Xc+40,800-Yc,0,180,Rc,Rc/2); ellipse(Xc+40,800-Yc-Rc/2,0,180,Rc-(Xc+Rc-(sqrt(Rc*Rc-(Rc/2)*(Rc/2))+Xc))-2,Rc/4); ellipse(Xc+40,800-Yc+Rc/2,0,180,Rc-(Xc+Rc-(sqrt(Rc*Rc-(Rc/2)*(Rc/2))+Xc))-2,Rc/4); if (raz==0) setlinestyle(0,0,1); } if (i!=4) { if (raz==0) { setcolor(0);setfillstyle(0,0); pieslice(x[i]+40,800-y[i],0,360,r[i]); setcolor(svet);setlinestyle(0,0,1); } setcolor(svet); setcolor(10); char er[15]; sprintf(er,"ñôåðà ¹%d",i); circle(x[i]+40,800-y[i],r[i]);outtextxy(x[i]+40,800-y[i],er); ellipse(x[i]+40,800-y[i],180,360,r[i],r[i]/2); ellipse(x[i]+40,800-y[i]-r[i]/2,180,360,r[i]-(x[i]+r[i]-(sqrt(r[i]*r[i]-(r[i]/2)*(r[i]/2))+x[i]))-2,r[i]/4); ellipse(x[i]+40,800-y[i]+r[i]/2,180,360,r[i]-(x[i]+r[i]-(sqrt(r[i]*r[i]-(r[i]/2)*(r[i]/2))+x[i]))-2,r[i]/4); setlinestyle(3,0,1); ellipse(x[i]+40,800-y[i],0,180,r[i],r[i]/2); ellipse(x[i]+40,800-y[i]-r[i]/2,0,180,r[i]-(x[i]+r[i]-(sqrt(r[i]*r[i]-(r[i]/2)*(r[i]/2))+x[i]))-2,r[i]/4); ellipse(x[i]+40,800-y[i]+r[i]/2,0,180,r[i]-(x[i]+r[i]-(sqrt(r[i]*r[i]-(r[i]/2)*(r[i]/2))+x[i]))-2,r[i]/4); if (raz==0) setlinestyle(0,0,1); if (svet==2) svet=14; else svet=svet-2; } } raz=raz+1; for(i=1;i<=3;i++) {p[i]=z[i];} p[4]=Zc; if (raz==1) risuem(); } void sechen(void) { setcolor(7); setlinestyle(0,0,2); double xp,yp,pol1,pol2,mon=0; double x1,x2,y1,y2; int i,smen=0,nt; int Xmen; double stat1,stat2,stat3,stat4,pl; double AD,CB,ADY,DISC,ABD,AC,ABX; double at,bt,ct,Yris1,Zris1,Yris2,Zris2,gr1,gr2,Xris1,Xris2; for(i=0;i<3;i++) { if (i==0) { if (abs(Xkos3-Xkos1)>abs(Ykos3-Ykos1)) { if (Ykos1>Ykos3) {pol2=Ykos1;pol1=Ykos3;} else {pol2=Ykos3;pol1=Ykos1;} smen=1; if (Xkos1>Xkos3) {gr1=Xkos3;gr2=Xkos1;} else {gr1=Xkos1;gr2=Xkos3;} } else { if (Xkos1>Xkos3) {pol2=Xkos1;pol1=Xkos3;} else {pol2=Xkos3;pol1=Xkos1;} smen=2; if (Ykos1>Ykos3) {gr1=Ykos3;gr2=Ykos1;} else {gr1=Ykos1;gr2=Ykos3;} } stat1=(Ykos3-Ykos1)*(Zc-Zkos1)-(Yc-Ykos1)*(Zkos3-Zkos1); stat2=(Zkos3-Zkos1)*(Xc-Xkos1)-(Xkos3-Xkos1)*(Zc-Zkos1); stat3=(Xkos3-Xkos1)*(Yc-Ykos1)-(Xc-Xkos1)*(Ykos3-Ykos1); stat4=-(Xkos1*stat1+Ykos1*stat2+Zkos1*stat3); } if (i==1) { if (abs(Xkos2-Xkos1)>abs(Ykos2-Ykos1)) { if (Ykos1>Ykos2) {pol2=Ykos1;pol1=Ykos2;} else {pol2=Ykos2;pol1=Ykos1;} smen=1; if (Xkos1>Xkos2) {gr1=Xkos2;gr2=Xkos1;} else {gr1=Xkos1;gr2=Xkos2;} } else { if (Xkos1>Xkos2) {pol2=Xkos1;pol1=Xkos2;} else {pol2=Xkos2;pol1=Xkos1;} smen=2; if (Ykos1>Ykos2) {gr1=Ykos2;gr2=Ykos1;} else {gr1=Ykos1;gr2=Ykos2;} } stat1=(Ykos2-Ykos1)*(Zc-Zkos1)-(Yc-Ykos1)*(Zkos2-Zkos1); stat2=(Zkos2-Zkos1)*(Xc-Xkos1)-(Xkos2-Xkos1)*(Zc-Zkos1); stat3=(Xkos2-Xkos1)*(Yc-Ykos1)-(Xc-Xkos1)*(Ykos2-Ykos1); stat4=-(Xkos1*stat1+Ykos1*stat2+Zkos1*stat3); } if (i==2) { if (abs(Xkos3-Xkos2)>abs(Ykos3-Ykos2)) { if (Ykos2>Ykos3) {pol2=Ykos2;pol1=Ykos3;} else {pol2=Ykos3;pol1=Ykos2;} smen=1; if (Xkos2>Xkos3) {gr1=Xkos3;gr2=Xkos2;} else {gr1=Xkos2;gr2=Xkos3;} } else { if (Xkos2>Xkos3) {pol2=Xkos2;pol1=Xkos3;} else {pol2=Xkos3;pol1=Xkos2;} smen=2; if (Ykos2>Ykos3) {gr1=Ykos3;gr2=Ykos2;} else {gr1=Ykos2;gr2=Ykos3;} } stat1=(Ykos3-Ykos2)*(Zc-Zkos2)-(Yc-Ykos2)*(Zkos3-Zkos2); stat2=(Zkos3-Zkos2)*(Xc-Xkos2)-(Xkos3-Xkos2)*(Zc-Zkos2); stat3=(Xkos3-Xkos2)*(Yc-Ykos2)-(Xc-Xkos2)*(Ykos3-Ykos2); stat4=-(Xkos2*stat1+Ykos2*stat2+Zkos2*stat3); } mon=0;nt=0; while (gr1<=gr2) { if (smen==1) {CB=stat3/stat2; AD=(-stat1*gr1)/stat2-(stat4/stat2); ADY=(AD-Yc); at=(CB*CB+1); bt=(-2)*(ADY*CB+Zc); ct=(ADY*ADY+Zc*Zc+(gr1-Xc)*(gr1-Xc)-Rc*Rc); DISC=(bt/2)*(bt/2)-at*ct; { if (DISC>=0) { setcolor(9); Zris2=((-bt/2)+sqrt(DISC))/at; Zris1=((-bt/2)-sqrt(DISC))/at; Yris1=AD-CB*Zris1; Yris2=AD-CB*Zris2; YY[schit]=Yris2; ZZ[schit]=Zris2; XX[schit]=gr1; Rad[schit]=(sqrt((XX[schit]-Xvr)*(XX[schit]-Xvr)+(ZZ[schit]-Zvr)*(ZZ[schit]-Zvr))); x1=XX[schit]-Xvr;x2=Rad[schit];y1=ZZ[schit]-Zvr;y2=0; ugol[schit]=acos((x1*x2+y1*y2)/((sqrt(x1*x1+y1*y1)))/(sqrt(x2*x2+y2*y2)))*180/M_PI; schit++; // if (Yris2>pol1 && Yris2<pol2) {if (mon==0) {xp=gr1;yp=Yris2;mon++;} else {line(xp+40,800-yp,gr1+40,800-Yris2);mon=0;} circle(gr1+40,800-Yris2,2); } gr1=gr1+1; } } } if (smen==2) { ABD=(-stat2*gr1)/stat1-stat4/stat1; AC=stat3/stat1; ABX=ABD-Xc; at=(AC*AC+1); bt=(-2)*(ABX*AC+Zc); ct=(ABX*ABX+Zc*Zc+(gr1-Yc)*(gr1-Yc)-Rc*Rc); DISC=(bt/2)*(bt/2)-at*ct; if (DISC>=0) { setcolor(9); Zris2=((-bt/2)+sqrt(DISC))/at; Zris1=((-bt/2)-sqrt(DISC))/at; Xris1=ABD-AC*Zris1; Xris2=ABD-AC*Zris2; YY[schit]=gr1; ZZ[schit]=Zris2; XX[schit]=Xris2; Rad[schit]=(sqrt((XX[schit]-Xvr)*(XX[schit]-Xvr)+(ZZ[schit]-Zvr)*(ZZ[schit]-Zvr))); x1=XX[schit]-Xvr;x2=Rad[schit];y1=ZZ[schit]-Zvr;y2=0; ugol[schit]=acos((x1*x2+y1*y2)/((sqrt(x1*x1+y1*y1)))/(sqrt(x2*x2+y2*y2)))*180/M_PI; schit++; {if (mon==0) {xp=Xris2;yp=gr1;mon++;} else {line(xp+40,800-yp,40+Xris2,800-gr1);mon=0;} circle(Xris2+40,800-gr1,2); } gr1=gr1+1; } } } } double rk=0.0,pc; if (Xkos1>rk) {rk=Xkos1;pc=Ykos1;} if (Xkos1>rk) {rk=Xkos2;pc=Ykos2;} if (Xkos1>rk) {rk=Xkos3;pc=Ykos3;} setcolor(15); setlinestyle(1,0,1); line(Xc+40,800-Yc,x[1]+40,800-y[1]); line(Xc+40,800-Yc,x[2]+40,800-y[2]); line(Xc+40,800-Yc,x[3]+40,800-y[3]); setlinestyle(0,0,1); } void raschet(void) { int i,kol=0; aj=x[2]-x[1]; bj=y[2]-y[1]; cj=z[2]-z[1]; ak=x[3]-x[1]; bk=y[3]-y[1]; ck=z[3]-z[1]; Ris=(r[1]+Rc)*(r[1]+Rc); Rjs=(r[2]+Rc)*(r[2]+Rc); Rks=(r[3]+Rc)*(r[3]+Rc); dj=(0.5*(Ris-Rjs+(aj*aj)+(bj*bj)+(cj*cj))); dk=(0.5*(Ris-Rks+(ak*ak)+(bk*bk)+(ck*ck))); A=(aj*bk-ak*bj)*(aj*bk-ak*bj)+(bj*ck-bk*cj)*(bj*ck-bk*cj)+(cj*ak-ck*aj)*(cj*ak-ck*aj); Bx=(dj*bk-dk*bj)*(aj*bk-ak*bj)+(dj*ck-dk*cj)*(aj*ck-ak*cj); By=(dj*ck-dk*cj)*(bj*ck-bk*cj)+(dj*ak-dk*aj)*(bj*ak-bk*aj); Bz=(dj*ak-dk*aj)*(cj*ak-ck*aj)+(dj*bk-dk*bj)*(cj*bk-ck*bj); Cx=(dj*bk-dk*bj)*(dj*bk-dk*bj)+(dj*ck-dk*cj)*(dj*ck-dk*cj)-Ris*(bj*ck-bk*cj)*(bj*ck-bk*cj); Cy=(dj*ck-dk*cj)*(dj*ck-dk*cj)+(dj*ak-dk*aj)*(dj*ak-dk*aj)-Ris*(cj*ak-ck*aj)*(cj*ak-ck*aj); Cz=(dj*ak-dk*aj)*(dj*ak-dk*aj)+(dj*bk-dk*bj)*(dj*bk-dk*bj)-Ris*(aj*bk-ak*bj)*(aj*bk-ak*bj); if ((Bx*Bx-A*Cx)<0) kol++; if ((By*By-A*Cy)<0) kol++; if ((Bz*Bz-A*Cz)<0) kol++; if (kol!=0) {printf("SPHERA RADIUSA %d NE MOZHET ODNOVREMENNO KASATSJA 3 DANNIH SPHER",Rc);system("PAUSE");exit(1);} Xc=double(x[1])+(Bx+sqrt((Bx*Bx-A*Cx)))/A; double dg1,dg2,dg3; double xc1,yc1,zc1,xc2,yc2,zc2,xc3,yc3,zc3,pc1,pc2,pc3; int nom; int j=1; while (j<1500) { Yc=j; Zc=sqrt((r[1]+Rc)*(r[1]+Rc)-(x[1]-Xc)*(x[1]-Xc)-(y[1]-Yc)*(y[1]-Yc))+z[1]; nom=0; xc1=(Xc-double(x[1]))*(Xc-double(x[1])); yc1=(Yc-double(y[1]))*(Yc-double(y[1])); zc1=(Zc-double(z[1]))*(Zc-double(z[1])); xc2=(Xc-double(x[2]))*(Xc-double(x[2])); yc2=(Yc-double(y[2]))*(Yc-double(y[2])); zc2=(Zc-double(z[2]))*(Zc-double(z[2])); xc3=(Xc-double(x[3]))*(Xc-double(x[3])); yc3=(Yc-double(y[3]))*(Yc-double(y[3])); zc3=(Zc-double(z[3]))*(Zc-double(z[3])); dg1=sqrt(xc1+yc1+zc1)-double(r[1])-Rc; dg2=sqrt(xc2+yc2+zc2)-double(r[2])-Rc; dg3=sqrt(xc3+yc3+zc3)-double(r[3])-Rc; if (abs(int(dg1))<=1) nom++; if (abs(int(dg2))<=1) nom++; if (abs(int(dg3))<=1) nom++; if (nom==3) {break;} Zc=z[1]-sqrt((r[1]+Rc)*(r[1]+Rc)-(x[1]-Xc)*(x[1]-Xc)-(y[1]-Yc)*(y[1]-Yc)); nom=0; xc1=(Xc-double(x[1]))*(Xc-double(x[1])); yc1=(Yc-double(y[1]))*(Yc-double(y[1])); zc1=(Zc-double(z[1]))*(Zc-double(z[1])); xc2=(Xc-double(x[2]))*(Xc-double(x[2])); yc2=(Yc-double(y[2]))*(Yc-double(y[2])); zc2=(Zc-double(z[2]))*(Zc-double(z[2])); xc3=(Xc-double(x[3]))*(Xc-double(x[3])); yc3=(Yc-double(y[3]))*(Yc-double(y[3])); zc3=(Zc-double(z[3]))*(Zc-double(z[3])); dg1=sqrt(xc1+yc1+zc1)-double(r[1])-Rc; dg2=sqrt(xc2+yc2+zc2)-double(r[2])-Rc; dg3=sqrt(xc3+yc3+zc3)-double(r[3])-Rc; if (abs(int(dg1))<=1) nom++; if (abs(int(dg2))<=1) nom++; if (abs(int(dg3))<=1) nom++; if (nom==3) {break;} j++; } R4=(sqrt((Xc-Xvr)*(Xc-Xvr)+(Zc-Zvr)*(Zc-Zvr))); double x1,x2,y1,y2; x1=Xc-Xvr;x2=R4;y1=Zc-Zvr;y2=0; alp4=(x1*x2+y1*y2)/((sqrt(x1*x1+y1*y1)))/(sqrt(x2*x2+y2*y2)); al4=acos(alp4)*180/M_PI; printf("Xc=%10.10f\n",Xc); printf("Yc=%10.10f\n",Yc); printf("Zc=%10.10f\n",Zc); xc1=Xc-x[1];xc2=Xc-x[2];xc3=Xc-x[3]; yc1=Yc-y[1];yc2=Yc-y[2];yc3=Yc-y[3]; zc1=Zc-z[1];zc2=Zc-z[2];zc3=Zc-z[3]; XYc1=(-xc1*y[1]+yc1*x[1])/yc1;XYc2=(-xc2*y[2]+yc2*x[2])/yc2;XYc3=(-xc3*y[3]+yc3*x[3])/yc3; ZYc1=(-zc1*y[1]+yc1*z[1])/yc1;ZYc2=(-zc2*y[2]+yc2*z[2])/yc2;ZYc3=(-zc3*y[3]+yc3*z[3])/yc3; M1=((Rc*Rc)-(Xc*Xc+Yc*Yc+Zc*Zc))/(-2); M2=((r[1]*r[1])-(x[1]*x[1]+y[1]*y[1]+z[1]*z[1]))/(-2); M3=((r[2]*r[2])-(x[2]*x[2]+y[2]*y[2]+z[2]*z[2]))/(-2); M4=((r[3]*r[3])-(x[3]*x[3]+y[3]*y[3]+z[3]*z[3]))/(-2); Ykos1=(M1-M2-XYc1*Xc+XYc1*x[1]-ZYc1*Zc+ZYc1*z[1])/(xc1*Xc/yc1-xc1*x[1]/yc1+(Yc-y[1])+zc1*Zc/yc1-zc1*z[1]/yc1); Ykos2=(M1-M3-XYc2*Xc+XYc2*x[2]-ZYc2*Zc+ZYc2*z[2])/(xc2*Xc/yc2-xc2*x[2]/yc2+(Yc-y[2])+zc2*Zc/yc2-zc2*z[2]/yc2); Ykos3=(M1-M4-XYc3*Xc+XYc3*x[3]-ZYc3*Zc+ZYc3*z[3])/(xc3*Xc/yc3-xc3*x[3]/yc3+(Yc-y[3])+zc3*Zc/yc3-zc3*z[3]/yc3); Xkos1=Ykos1*xc1/yc1+XYc1;Xkos2=Ykos2*xc2/yc2+XYc2;Xkos3=Ykos3*xc3/yc3+XYc3; Zkos1=Ykos1*zc1/yc1+ZYc1;Zkos2=Ykos2*zc2/yc2+ZYc2;Zkos3=Ykos3*zc3/yc3+ZYc3; } void osi(void) { int i,s=40; char st[14]; setcolor(15); line(40,40,40,800); line(40,800,1000,800); for(i=60;i<1000;i=i+20) {line(i,798,i,802);} for(i=80;i<1000;i=i+40) { sprintf(st,"%d",s); outtextxy(i-7,810,st); s=s+40;} line(1000,800,985,795); line(1000,800,985,805); for(i=60;i<800;i=i+20) {line(38,i,42,i);} line(40,40,35,55); line(40,40,45,55); s=40; for(i=760;i>40;i=i-40) { sprintf(st,"%d",s); outtextxy(10,i-7,st); s=s+40; } outtextxy(25,790,"0"); } void menu() { int c=-1,i; while(c!=ESC) { c=getch(); if (c==DOWN) { int re=0; floodfill(10,10,3); al1=al1+5;al2=al2+5;al3=al3+5;al4=al4+5; z[1]=Zvr+R1*sin(al1*M_PI/180); x[1]=Xvr+R1*cos(al1*M_PI/180); z[2]=Zvr+R2*sin(al2*M_PI/180); x[2]=Xvr+R2*cos(al2*M_PI/180); z[3]=Zvr+R3*sin(al3*M_PI/180); x[3]=Xvr+R3*cos(al3*M_PI/180); Zc=Zvr+R4*sin(al4*M_PI/180); Xc=Xvr+R4*cos(al4*M_PI/180); raz=0;osi();risuem(); setcolor(9); for(i=0;i<schit;i++) { ugol[i]=ugol[i]+5; XX[i]=Xvr+Rad[i]*cos(ugol[i]*M_PI/180); circle(XX[i]+40,800-YY[i],2); } setcolor(15); setlinestyle(1,0,1); line(Xc+40,800-Yc,x[1]+40,800-y[1]); line(Xc+40,800-Yc,x[2]+40,800-y[2]); line(Xc+40,800-Yc,x[3]+40,800-y[3]); setlinestyle(0,0,1); } if (c==UP) { floodfill(10,10,3); al1=al1-5;al2=al2-5;al3=al3-5;al4=al4-5; z[1]=Zvr+R1*sin(al1*M_PI/180); x[1]=Xvr+R1*cos(al1*M_PI/180); z[2]=Zvr+R2*sin(al2*M_PI/180); x[2]=Xvr+R2*cos(al2*M_PI/180); z[3]=Zvr+R3*sin(al3*M_PI/180); x[3]=Xvr+R3*cos(al3*M_PI/180); Zc=Zvr+R4*sin(al4*M_PI/180); Xc=Xvr+R4*cos(al4*M_PI/180); raz=0;osi();risuem(); setcolor(9); for(i=0;i<schit;i++) { ugol[i]=ugol[i]-5; XX[i]=Xvr+Rad[i]*cos(ugol[i]*M_PI/180); circle(XX[i]+40,800-YY[i],2); } setcolor(15); setlinestyle(1,0,1); line(Xc+40,800-Yc,x[1]+40,800-y[1]); line(Xc+40,800-Yc,x[2]+40,800-y[2]); line(Xc+40,800-Yc,x[3]+40,800-y[3]); setlinestyle(0,0,1); } }} int main() { dano(); raschet(); osi(); risuem(); sechen(); menu(); getch(); return 0; } |
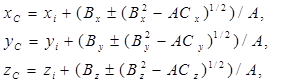
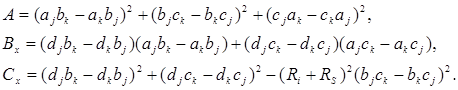
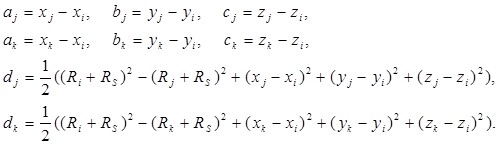
 Д) Таблицу содержащую координаты точек касания большого атомоа с другими 3-мя атомами.
Д) Таблицу содержащую координаты точек касания большого атомоа с другими 3-мя атомами. Z=z[1]+z[2]+z[3]
Z=z[1]+z[2]+z[3]