|
В современных условиях управленческие решения должны приниматься лишь на основе тщательного анализа имеющейся информации. Для решения подобных задач предназначен аппарат прикладной статистики, составной частью которого являются статистические методы прогнозирования. Эти методы позволяют выявить закономерности на фоне случайностей, сделать обоснованные прогнозы и выявить вероятность их выполнения.
При рассмотрении классической модели регрессии характер экспериментальных данных не имеет принципиального значения. Методы исследования моделей, основанных на данных пространственных выборок и временных рядов, существенно отличаются. Это можно объяснить тем, что наблюдения во временных рядах нельзя считать независимыми.
Прогнозирование – это оценка на основе глубокого анализа тенденций развития социально-экономических явлений и их взаимосвязей. Процесс прогнозирования предполагает выявление возможных альтернатив развития в перспективе для обоснованного их выбора и принятия оптимального решения.
Экономическое прогнозирование невозможно без хорошего знания изучаемого явления и владения различными методами обработки динамических рядов, которые в каждом отдельном случае помогли бы обнаружить общую закономерность изменения, периодичность в повышении или снижении уровней (если она имеет место), корреляцию между отдельными рядами.
Для анализа данных целесообразно рассчитывать показатели: абсолютные приросты (изменения) уровней; темпы роста; темпы прироста (снижения) уровней.
Для обобщающей характеристики динамики исследуемого явления за ряд периодов использовались средние показатели: средний темп роста, средний темп прироста, средний абсолютный прирост.
Целью курсовой работы являлось приобретение практических навыков поиска и систематизации собранного материала для статистического исследования.
Для реализации поставленной цели в дипломной работе будут решены следующие задачи:
1) графический анализ данных об объеме рынка бытовой техники;
2) содержательный анализ данных об объеме рынка бытовой техники;
3) анализ данных об объеме рынка бытовой техники на основе методов прогнозирования;
4) задача прогнозирования на 2009 г., проверка адекватности и точности прогноза и анализ ситуации на рынке бытовой техники г. Уфа в 2009 г;
5) выбор наилучшего метода прогнозирования;
6) задача прогнозирования на 2010 г.;
7) сформулированы выводы.
1.1 Экономические процессы и их прогнозирование
графический анализ прогнозирование
Одним из наиболее сложных этапов прогнозирования, который отнимает много времени и сил, является сбор обоснованных и достоверных данных. Точность любого прогноза ограничивается достоверностью тех данных, на которых он построен. Наиболее сложные модели прогнозирования не сработают, если они будут применяться к недостоверным данным [1, С.85].
Для оценки, будут ли имеющиеся данные полезны для решения поставленной задачи, можно использовать следующие четыре принципа:
1) данные должны быть достоверными и точными. Необходимо позаботиться о том, чтобы данные были получены из достоверного источника, и обратить внимание на то, чтобы они имели требуемую точность;
2) данные должны быть значимыми. Данные должны отражать те обстоятельства, для анализа которых они будут использоваться;
3) данные должны быть согласованными. Если обстоятельства, в отношении которых данные собирались, изменились, необходимо внести корректировки, направленные на сохранение согласованности новых данных с исторически сложившейся структурой;
4) данные должны собираться через определенные интервалы времени. Данные, собранные и подытоженные в строгом хронологическом порядке, представляют наибольший интерес для целей прогнозирования.
Для создания прогнозов представляют интерес два типа данных. К первому типу относят данные, собранные в фиксированный момент времени. Это может быть конкретный час, день, неделя, месяц или квартал. Второй тип представляют данные наблюдений, произведенных с течением времени. Кросс-секционными данными называются наблюдения, собранные в фиксированный момент времени [2, С.85]. Задача состоит в изучении таких данных с последующей экстраполяцией или последующим распространением полученных взаимоотношений на большую генеральную совокупность.
1.2.1 Временные ряды и их компоненты
Совокупность наблюдений величины 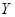 , выполненных в течение некоторого промежутка времени, называют данными временного ряда или просто временным рядом. Чаще всего наблюдения регистрируются через постоянные промежутки времени. В общем случае временные ряды не представляют собой случайную выборку и требуют специальных методов для их исследования. Наблюдения во временных рядах, как правило, зависят друг от друга (автокоррелируют). Эта зависимость образует модель изменения или поведения данных, которую можно использовать для предсказания их будущих значений, а это, в свою очередь, может значительно помочь руководству в управлении деловыми операциями [3, С.180]. , выполненных в течение некоторого промежутка времени, называют данными временного ряда или просто временным рядом. Чаще всего наблюдения регистрируются через постоянные промежутки времени. В общем случае временные ряды не представляют собой случайную выборку и требуют специальных методов для их исследования. Наблюдения во временных рядах, как правило, зависят друг от друга (автокоррелируют). Эта зависимость образует модель изменения или поведения данных, которую можно использовать для предсказания их будущих значений, а это, в свою очередь, может значительно помочь руководству в управлении деловыми операциями [3, С.180].
Декомпозиция
Один из методов анализа данных временных рядов включает попытку определить составляющие факторы, которые влияют на каждое значение временного ряда. Подобная процедура идентификации называется декомпозицией. Каждая компонента идентифицируется отдельно. Затем вклады каждой компоненты комбинируются с целью получения прогнозов будущих значений временных рядов.
Рассмотрение методов декомпозиции начинается с четырех компонент временных рядов – это трендовая, циклическая, сезонная и нерегулярная (или случайная) компоненты.
1. Тренд. Тренд – это компонента, представляющая основной рост (или спад) во временном ряду. Компонента тренда обозначается буквой 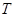 . .
2. Цикличность. Циклическая компонента – это последовательность волнообразных флуктуации или циклы длительностью более одного года. Изменение экономических условий обычно происходит циклически. Циклическая компонента обозначается буквой 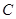 . .
3. Сезонность. Сезонные изменения обычно присутствуют в квартальных, месячных или недельных данных. Под сезонными вариациями понимаются изменения с более или менее стабильной структурой, имеющие годовую цикличность и повторяющиеся из года в год. Сезонная компонента обозначается буквой 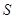 . .
4. Нерегулярность. Нерегулярная компонента включает непредсказуемые или случайные флуктуации. Нерегулярная компонента обозначается буквой 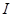 . .
Двумя простейшими моделями, связывающими наблюдаемую величину временного ряда (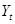 ) с компонентами тренда ( ) с компонентами тренда ( ), сезонности ( ), сезонности (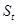 ) и нерегулярности ( ) и нерегулярности (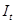 ), являются модель аддитивных компонент ), являются модель аддитивных компонент
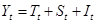 (1.1) (1.1)
и модель мультипликативных компонент.
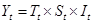 . (1.2) . (1.2)
Модель аддитивных компонент применима в тех случаях, когда анализируемый временной ряд имеет приблизительно одинаковые изменения на протяжении всей длительности ряда. Иными словами, все значения ряда существенно убывают в пределах полосы постоянной ширины, центрированной на уровне тренда.
Модель мультипликативных компонент эффективнее в тех ситуациях, когда изменение временной последовательности увеличивается с ростом уровня.
Тренд
Тренд представляет собой долговременные изменения во временных рядах, которые иногда можно описать с помощью прямой линии или гладкой кривой. Если грубо представить тренд в виде прямой линии, т.е. если рост или спад похожи на прямую линию, то она описывается следующим уравнением:
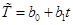 , (1.3) , (1.3)
где
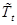 – это расчетное значение тренда в момент времени – это расчетное значение тренда в момент времени 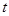 . .
Символ 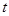 используется для независимой переменной, представляющей время и обычно принимающей целочисленные значения 1,2,3,..., соответствующие последовательным периодам времени. Коэффициент наклона используется для независимой переменной, представляющей время и обычно принимающей целочисленные значения 1,2,3,..., соответствующие последовательным периодам времени. Коэффициент наклона 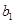 является средним ростом или спадом является средним ростом или спадом 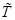 для любого возрастания во времени за один период. для любого возрастания во времени за один период.
Прогноз тренда
Пусть прогноз величины 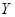 на на 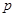 шагов вперед делается в момент времени шагов вперед делается в момент времени 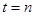 (конец последовательности), при этом для прогнозирования используется трендовая модель. Период времени, на который делается прогноз, – в данном случае это (конец последовательности), при этом для прогнозирования используется трендовая модель. Период времени, на который делается прогноз, – в данном случае это 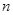 – называется началом предсказания. Значение – называется началом предсказания. Значение 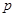 именуется дальностью прогнозирования. Для модели линейного тренда можно сделать прогноз, вычисляя значения по уравнению именуется дальностью прогнозирования. Для модели линейного тренда можно сделать прогноз, вычисляя значения по уравнению 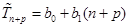 . .
В исходных данных нам представлен интервальный ряд с равноотстоящими уровнями во времени [4, C.51]. Поэтому для определения среднего уровня ряда можно воспользоваться следующей формулой:
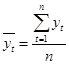 , (1.4) , (1.4)
где
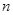 – длина временного ряда, то есть число уровней. – длина временного ряда, то есть число уровней.
Для количественной оценки динамики явлений применяются следующие основные аналитические показатели:
1) абсолютный прирост;
2) темпы роста;
3) темпы прироста.
Причем каждый из перечисленных показателей может быть трех видов:
1) цепной;
2) базисный;
3) средний.
Абсолютный прирост характеризует изменение показателя за определенный промежуток времени и находится по формуле:
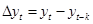 , (1.5) , (1.5)
где
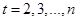 , ,
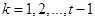 . .
Причем, если 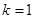 , то можно найти цепной абсолютный прирост: , то можно найти цепной абсолютный прирост:
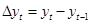 . (1.6) . (1.6)
Если  , то можно найти базисный абсолютный прирост относительно начального уровня: , то можно найти базисный абсолютный прирост относительно начального уровня:
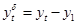 . (1.7) . (1.7)
Средний абсолютный прирост – это обобщающая характеристика скорости изменения исследуемого показателя во времени (скорость – это прирост в единицу времени):
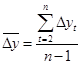 , (1.8) , (1.8)
где
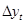 – цепной абсолютный прирост – цепной абсолютный прирост
Темп роста характеризует отношение двух сравниваемых уровней ряда и определяется по формуле:
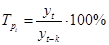 . (1.9) . (1.9)
Цепной темп роста:
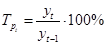 . (1.10) . (1.10)
Базисный темп роста относительно начального уровня:
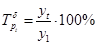 . (1.11) . (1.11)
Средний темп роста – обобщающая характеристика динамики, отражающая интенсивность изменения уровней ряда. Эта величина показывает, сколько в среднем процентов составляет последующий уровень от предыдущего на всем периоде наблюдения. Показатель находится по формуле:
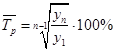 . (1.12) . (1.12)
Темп прироста характеризует абсолютный прирост в относительных величинах. Данный показатель показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Для расчета этой величины необходимо воспользоваться следующей формулой:
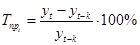 . (1.13) . (1.13)
Цепной темп прироста:
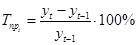 . (1.14) . (1.14)
Базисный темп прироста относительно начального уровня:
 . (1.15) . (1.15)
Средний темп прироста:
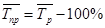 . (1.16) . (1.16)
1.2.3 Проверка гипотезы о наличии тренда (критерий Фостера-Стюарта, критерии серий)
Если присутствие тренда во временном ряду прослеживается нечетко, то прежде чем перейти к дальнейшему анализу, нужно выяснить, существует ли тенденция в исследуемом процессе [5, C.101]. Основные подходы к решению этой проблемы основаны на проверке статистических гипотез. Критерии выявления компонент ряда основаны на проверке гипотезы о случайности ряда (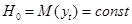 ). ).
Существует множество критериев, которые отличаются мощностью и сложностью. К таким критериям можно отнести критерии серий и критерий Фостера-Стюарта. Критерии серий делятся на критерий серий, основанный на медиане выборки, и критерий «нисходящих» и «восходящих» серий.
Введем 2 гипотезы:
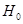 – тренда нет; – тренда нет;
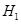 – тренд присутствует. – тренд присутствует.
Критерий Фостера-Стюарта
Проверка гипотезы осуществляется в несколько этапов:
1) Для начала определяем вспомогательные характеристики 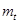 и и 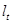 : :
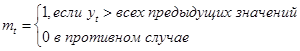
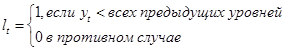 . .
2) Вычисляем . Эта величина может принимать значения: –1,0,1. . Эта величина может принимать значения: –1,0,1.
3) 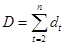 . .
4)
5) Применяем критерий Стьюдента:
 , (1.17) , (1.17)
где
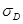 – среднее квадратическое отклонение величины – среднее квадратическое отклонение величины 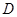 . .
Если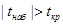 , то гипотеза об отсутствии тренда отвергается. , то гипотеза об отсутствии тренда отвергается.
Критерии серий:
1)
Критерий «восходящих» и «нисходящих» серий.
Образуем последовательность  из «+» и «-» по следующему правилу [6, C.59]: из «+» и «-» по следующему правилу [6, C.59]:
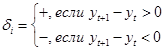 , ,
где
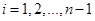 . .
В случае если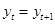 , учитывается лишь одно значение. , учитывается лишь одно значение.
Далее необходимо подсчитать число серий 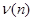 и протяженность самой длинной серии и протяженность самой длинной серии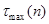 и проверить выполнение неравенств: и проверить выполнение неравенств:
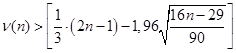 , (1.18) , (1.18)
 , (1.19) , (1.19)
где
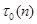 – табличное значение. – табличное значение.
Если оба неравенства выполняются, то принимается гипотеза 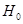 при уровне значимости при уровне значимости 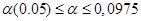 . .
2)
Критерий серий, основанный на медиане выборки.
Строим ранжированный ряд: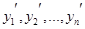 , где , где 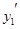 – наименьшее значение из – наименьшее значение из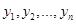 . .
Определим медиану полученного вариационного ряда:
если 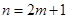 , то , то  , ,
если 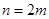 , то , то 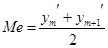 . .
Следующий шаг – это образование последовательности  из «+» и «-» по правилу: из «+» и «-» по правилу:
 . .
Если 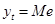 , то это значение пропускается. , то это значение пропускается.
Далее необходимо подсчитать число серий 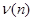 в совокупности в совокупности  , где под серией понимается последовательность подряд идущих плюсов или минусов. Один плюс или минус тоже считается серией. , где под серией понимается последовательность подряд идущих плюсов или минусов. Один плюс или минус тоже считается серией.
При отсутствии системной составляющей протяженность самой длинной серии не должна быть слишком большой, а число серий слишком маленьким, то есть:
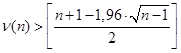 , (1.20) , (1.20)
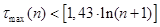 . (1.21) . (1.21)
Если хотя бы одно из неравенств нарушается, то гипотеза 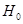 отвергается с вероятностью ошибки отвергается с вероятностью ошибки 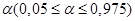 , то есть подтверждается наличие неслучайной составляющей, зависящей от , то есть подтверждается наличие неслучайной составляющей, зависящей от 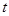 . .
1.2.4 Анализ структуры временного ряда с использованием коэффициента автокорреляции
При наличии тенденции и периодических колебаний значений каждого последующего уровня ряда зависит от предыдущих [7, C.79].
Коэффициент автокорреляции находится по следующей формуле:
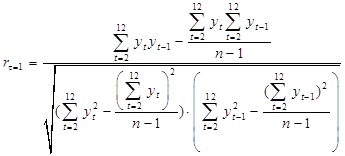 . (1.22) . (1.22)
Аналогично находятся остальные коэффициенты:
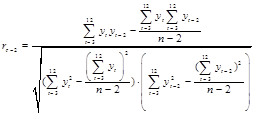 . (1.23) . (1.23)
Проверим значимость коэффициента автокорреляции. Для этого введем две гипотезы:
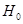 : : 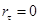
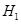 : : 
 находится по таблице критических значений находится по таблице критических значений 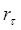 отдельно для отдельно для 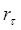 >0 и >0 и 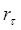 <0. Причем, если | <0. Причем, если |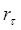 |>| |>| |, то принимается гипотеза |, то принимается гипотеза 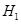 , то есть коэффициент значим. Если | , то есть коэффициент значим. Если |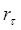 |<| |<| |, то принимается гипотеза |, то принимается гипотеза 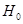 и коэффициент автокорреляции незначим. Если коэффициент автокорреляции достаточно велик, то проверять его значимость необязательно. и коэффициент автокорреляции незначим. Если коэффициент автокорреляции достаточно велик, то проверять его значимость необязательно.
Распространенным приемом при выявлении и анализе тенденции временного ряда является его сглаживание [8, C.114]. Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые в меньшей мере подвержены колебаниям. Это способствует более четкому проявлению тенденции развития.
Скользящие средние позволяют сгладить как случайные, так и периодические колебания и выявить тенденцию в развитии процесса, поэтому они служат важным инструментом при фильтрации компонент временного ряда. Иногда скользящие средние применяют как предварительный этап перед моделированием тренда с помощью процедур аналитического подхода [9, C.84].
Процедура сглаживания приводит к устранению периодических колебаний во временном ряду, если длина интервала берется равной или кратной периоду колебаний.
Поэтому для устранения сезонных колебаний часто требуется использовать 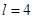 или или 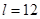 . .
Если 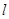 - четное число, то первое и последнее наблюдения на активном участке берутся с половинными весами. Активный участок сглаживания – наблюдения, которые берутся для расчета среднего значения. - четное число, то первое и последнее наблюдения на активном участке берутся с половинными весами. Активный участок сглаживания – наблюдения, которые берутся для расчета среднего значения.
Для четырехчленной скользящей средней используется следующая формула:
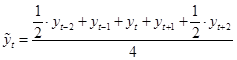 .(1.24) .(1.24)
Аналогично находятся остальные сглаженные значения.
Недостатком метода скользящей средней является потеря первых и последних уровней ряда. Причем потеря последних уровней ряда является существенным недостатком, так как свежие значения обладают наибольшей информационной ценностью.
Одним из приемов восстановления пропущенных уровней является последовательное прибавление среднего абсолютного прироста 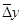 на последнем активном участке к последнему сглаженному значению. Для восстановления используется формула: на последнем активном участке к последнему сглаженному значению. Для восстановления используется формула:
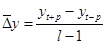 . (1.25) . (1.25)
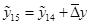 . (1.26) . (1.26)
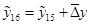 . (1.27) . (1.27)
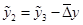 . (1.28) . (1.28)
 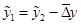 . (1.29) . (1.29)
1.3 Методы прогнозирования на основе временных рядов
Основным фактором, влияющим на выбор метода прогнозирования, является идентификация и четкое понимание реальных моделей, присутствующих в данных. Если в них удастся распознать тренд, циклическую или сезонную модель, это существенно облегчит поиск эффективного метода экстраполирования [10, C.51].
Аппарат прогнозирования для стационарных данных
Прогнозирование стационарного ряда в своей простейшей форме включает в себя использование его предыстории для оценки среднего значения, которое затем становится прогнозом на будущие периоды. Более сложная техника состоит в уточнении оценки с использованием вновь поступившей информации. Эти методы полезны, когда начальные оценки ненадежны или когда постоянство среднего значения под вопросом.
Методы прогнозирования, которые могут применяться по отношению к стационарным рядам, включают в себя наивные методы, методы простого усреднения, скользящие средние, простое экспоненциальное сглаживание и методы авторегрессионого скользящего среднего (методы Бокса-Дженкинса).
Аппарат прогнозирования для данных, имеющих тренд
Ряд, обладающий трендом, ранее был определен как ряд, содержащий долгосрочную компоненту, которая отражает постоянное возрастание или убывание значений ряда в течение продолжительного периода времени. Наличие тренда типично для временных рядов экономических показателей [11, C.124].
Аппарат прогнозирования, который должен использоваться для прогнозирования рядов, имеющих тренд, – это метод скользящих средних, метод линейного экспоненциального сглаживания Хольта, простая регрессия, возрастающие кривые, экспоненциальные модели и методы авторегрессионых интегрированных скользящих средних (методы Бокса-Дженкинса).
Измерение ошибки прогноза
Основные обозначения, используемые в прогнозировании [12, C.55]:
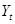 – значение временного ряда в момент – значение временного ряда в момент 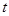 . .
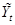 – прогноз значения – прогноз значения 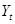 . .
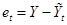 – погрешность или ошибка прогноза. – погрешность или ошибка прогноза.
Разработано несколько методов оценки ошибок, присущих отдельным методам прогнозирования. Большинство этих методов состоит в усреднении некоторых функций от разностей между действительным значением и его прогнозом.
Ошибкой прогноза является разность между действительным значением и его прогнозом.
В одном из способов оценки метода прогнозирования используется суммирование абсолютных ошибок. Среднее абсолютное отклонение (MeanAbsoluteDerivation, MAD) измеряет точность прогноза, усредняя величины ошибок прогноза (абсолютные значения каждой ошибки).
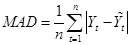 . (1.30) . (1.30)
Среднеквадратическая ошибка (МеаnSquaredError, MSE) – это другой способ оценки метода прогнозирования. Каждая ошибка или погрешность возводится в квадрат; эти величины затем суммируются и делятся на количество наблюдений. Поскольку каждое значение отклонения возводится в квадрат, этот метод подчеркивает большие ошибки прогноза.
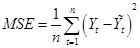 . (1.31) . (1.31)
Иногда предпочтительнее вычислять не абсолютные величины ошибок, а их процентное отношение. Средняя абсолютная ошибка в процентах (MeanAbsolutePercentage Еггог, МАРЕ) вычисляется путем отыскания абсолютной ошибки в каждый момент времени и деления ее на действительно наблюдаемое значение (в этот момент времени) с последующим усреднением полученных абсолютных процентных ошибок. Этот подход полезен в том случае, когда размер или значение прогнозируемой величины важны в оценке точности прогноза. МАРЕ подчеркивает, насколько велики ошибки прогноза в сравнении с действительными значениями ряда.
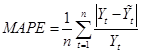 . (1.32) . (1.32)
Часто необходимо определить, является ли метод прогнозирования смещенным (полученный прогноз постоянно оказывается заниженным или завышенным) [13, C.78]. В этих случаях используется средняя процентная ошибка (MeanPercentage Еггог, МРЕ). Она вычисляется посредством нахождения ошибки в каждый момент времени и деления ее значения на действительное значение в этот момент времени с последующим усреднением полученных процентных выражений ошибок.
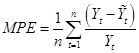 . (1.33) . (1.33)
Часть решения о выборе соответствующего метода прогнозирования состоит в определении того, дает ли данный метод достаточно малые ошибки прогноза. Действительно, естественно ожидать, что правильно подобранный метод будет давать относительно малые ошибки прогноза.
Определенные выше четыре способа оценки точности прогноза используются для следующих целей:
1) сравнение точности двух различных методов;
2) оценка полезности и надежности метода;
3) отыскание оптимального метода.
1.3.1 Метод экспоненциального сглаживания с учетом тренда
В 1957 г. Хольт разработал метод экспоненциального сглаживания, получивший название двухпараметрического метода Хольта. В этом методе учитывается локальный линейный тренд, присутствующий во временных рядах [14, C.117].
Если во временных рядах имеется тенденция к росту, то вместе с оценкой текущего уровня необходима и оценка наклона. В методике Хольта значения уровня и наклона сглаживаются непосредственно, при этом используются различные постоянные сглаживания для каждого из них. Эти постоянные сглаживания позволяют оценить текущий уровень и наклон, уточняя их всякий раз, когда появляются новые наблюдения. Одним из преимуществ методики Хольта является ее гибкость, позволяющая выбирать соотношение, в котором отслеживаются уровень и наклон.
Ниже приведены три уравнения, составляющие метод Хольта.
1. Экспоненциально сглаженный ряд или оценка текущего уровня:
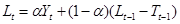 . (1.34) . (1.34)
2. Оценка тренда:
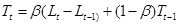 . (1.35) . (1.35)
3. Прогноз нар периодов вперед:
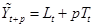 , (1.36) , (1.36)
где
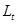 – новая сглаженная величина; – новая сглаженная величина;
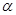 – постоянная сглаживания для данных ( – постоянная сглаживания для данных (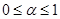 ); );
 – новое наблюдение или реальное значение ряда в период – новое наблюдение или реальное значение ряда в период 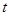 ; ;
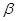 – постоянная сглаживания для оценки тренда ( – постоянная сглаживания для оценки тренда (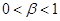 ); );
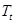 – оценка тренда; – оценка тренда;
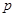 – количество периодов вперед, на которое делается прогноз; – количество периодов вперед, на которое делается прогноз;
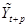 – прогноз на – прогноз на 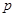 периодов вперед. периодов вперед.
Постоянная 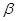 нужна для сглаживания оценки тренда. нужна для сглаживания оценки тренда.
Постоянные 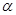 и и 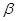 выбираются субъективно или путем минимизации ошибки прогнозирования, например значения MSE. Чем большие значения весов будут взяты, тем более быстрый отклик на происходящие изменения будет иметь место. выбираются субъективно или путем минимизации ошибки прогнозирования, например значения MSE. Чем большие значения весов будут взяты, тем более быстрый отклик на происходящие изменения будет иметь место.
Для минимизации значения MSE нужно создать сетку значений 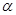 и и 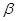 (т.е. все комбинации (т.е. все комбинации 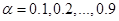 и и 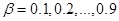 ) и выбрать ту комбинацию, которая даст меньшее значение MSE. ) и выбрать ту комбинацию, которая даст меньшее значение MSE.
Для того чтобы воспользоваться алгоритмом уравнения (1.34), нужно иметь набор из начальных величин и тренда. Одно из возможных решений состоит в том, чтобы первую оценку положить равной первому наблюдению. При этом тренд будет равен нулю. Другое решение – это определить начальное значение как среднее для первых пяти или шести наблюдений. Тогда тренд можно оценить наклоном линии, образованной этими пятью или шестью точками.
1.3.2 На основе аддитивной модели
Фактическое значение = трендовое значение + сезонная вариация + ошибка.
На первом шаге нужно исключить влияние сезонной вариации, воспользовавшись методом скользящей средней. Далее необходимо провести десезонализацию данных.
Уравнение линии тренда:
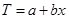 . (1.37) . (1.37)
Ошибки вычисляются с помощью формул (1.30, 1.31).
1.3.3 На основе мультипликативной модели
Фактическое значение = трендовое значение * сезонная вариация * ошибка. Значения сезонной вариации – это доли. Число сезонов равно 4.
На первом шаге нужно исключить влияние сезонной вариации, воспользовавшись методом скользящей средней. Далее необходимо провести десезонализацию данных.
Уравнение линии тренда:
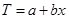 . (1.38) . (1.38)
Ошибки вычисляются с помощью формул (1.30, 1.31).
1.3.4 Использование индексов
Расчёт производится путём деления суммарного годового объема рынка бытовой техники на суммарный объем прошлого года, усреднении этого индекса и умножении его на данные последнего рассматриваемого года.
1.3.5 Оценка адекватности и точности модели
Одной из наиболее эффективных оценок адекватности модели является коэффициент детерминации, который рассчитывается по формуле (1.39) [15, C.94]:
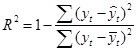 (1.39) (1.39)
Рассчитывается коэффициент детерминации и делается вывод об адекватности модели.
Рынок бытовой техники является одним из самых крупных в России, и в частности в г. Уфа. Его доля в потребительском секторе составляет почти 50% [16].
Сегмент крупногабаритной бытовой техники является самым крупным сегментом рынка в г. Уфа. К нему относятся стиральные машины, холодильники, морозильники, кухонные плиты и панели, посудомоечные машины. Чайники, пылесосы, утюги и микроволновые печи относятся к сегменту мелкой бытовой техники.
В данной курсовой работе рассматриваются квартальные данные об объемах продаж всей бытовой техники в г. Уфа.
2.1 Графический анализ данных об объеме
рынка бытовой техники
Исходные данные, полученные для анализа, охватывают период 2003-2009 гг. и включают объем рынка бытовой техники г. Уфа в денежном эквиваленте (руб.)
Таблица 2.1Объем рынка бытовой техники г. Уфа
| Квартал |
2009 г. |
2008 г. |
2007 г. |
2006 г. |
2005 г. |
2004 г. |
2003 г. |
| 1 |
1823014 |
1747589 |
1395473 |
1110683 |
892901 |
712300 |
582790 |
| 2 |
1900147 |
1754871 |
1400217 |
1115879 |
898787 |
720458 |
589787 |
| 3 |
1958799 |
1768796 |
1421587 |
1135897 |
914525 |
734879 |
602547 |
| 4 |
1982140 |
1789797 |
1447879 |
1150121 |
922145 |
739528 |
605458 |
Суммарный объем рынка бытовой техники г. Уфа за 2003-2009 гг. представлен на рис. 2.1.
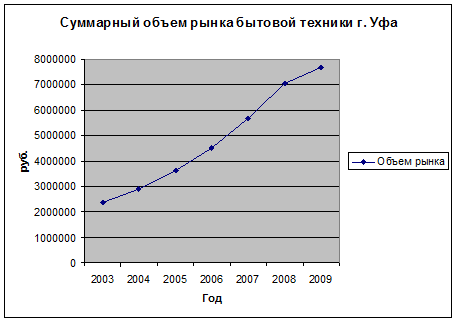
Рис. 2.1. Суммарный объем рынка бытовой техники
Графический анализ квартальных данных за 7 лет представлен на рис. 2.2.
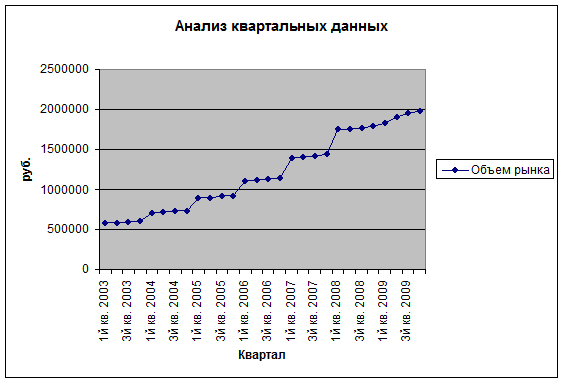
Рис. 2.2. Анализ квартальных данных
На основе графического анализа исходного временного ряда можно сформулировать допущение о тенденции увеличения объемов рынка бытовой техники в течение последних семи лет.
2.2 Содержательный анализ данных об объеме
рынка бытовой техники
2.2.1 Основные показатели динамики для временного ряда годовых данных
Рассчитаем показатели динамики на основе формул (1.4-1.16):
Таблица 2.2 Показатели динамики
Средний уровень ряда, 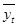 |
1207821 |
Цепной абсолютный прирост, 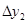 |
6997 |
Базисный абсолютный прирост, 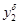 |
6997 |
Средний абсолютный прирост, 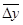 |
51828 |
Цепной темп роста, 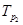 |
101% |
Базисный темп роста, 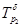 |
101% |
Средний темп роста, 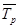 |
147% |
Цепной темп прироста, 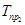 |
1% |
Базисный темп прироста, 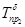 |
1% |
Средний темп прироста, 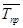 |
47% |
Объем рынка бытовой техники изменяется со скоростью 51828 руб. в год. В последние годы спрос смещается в сторону аудио- и видеотехники. Причиной этому стало удовлетворение потребности покупателей в приобретении товаров первой необходимости (чайников, утюгов, пылесосов) [17].
Представим все статистические показатели динамики в виде таблицы (Приложение 1).
Найдем сглаженные значения, воспользовавшись формулой (1.24):
Полученные результаты сведем в таблицу 2.3.
Таблица 2.3 Сглаженные значения
| № квартала |
Объем рынка |
Сглаженные значения |
Отклонения, % |
| 1 |
582790 |
546579 |
6,2 |
| 2 |
589787 |
578957 |
1,8 |
| 3 |
602547 |
611334 |
1,5 |
| 4 |
605458 |
643857 |
6,3 |
| 5 |
712300 |
676732 |
5,0 |
| 6 |
720458 |
710033 |
1,4 |
| 7 |
734879 |
749366 |
2,0 |
| 8 |
739528 |
794233 |
7,4 |
| 9 |
892901 |
838980 |
6,0 |
| 10 |
898787 |
884262 |
1,6 |
| 11 |
914525 |
934312 |
2,2 |
| 12 |
922145 |
988672 |
7,2 |
| 13 |
1110683 |
1043480 |
6,1 |
| 14 |
1115879 |
1099648 |
1,5 |
| 15 |
1135897 |
1163744 |
2,5 |
| 16 |
1150121 |
1234885 |
7,4 |
| 17 |
1395473 |
1306138 |
6,4 |
| 18 |
1400217 |
1379069 |
1,5 |
| 19 |
1421587 |
1460304 |
2,7 |
| 20 |
1447879 |
1548650 |
7,0 |
| 21 |
1747589 |
1636383 |
6,4 |
| 22 |
1754871 |
1722524 |
1,8 |
| 23 |
1768796 |
1774691 |
0,3 |
| 24 |
1789797 |
1802279 |
0,7 |
| 25 |
1823014 |
1844189 |
1,2 |
| 26 |
1900147 |
1891982 |
0,4 |
| 27 |
1958799 |
1940068 |
1,0 |
| 28 |
1982140 |
1988154 |
0,3 |
Рассчитаем средний абсолютный прирост, воспользовавшись формулой (1.25):
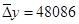 (для последних членов). (для последних членов).
Рассчитаем восстановленные пропущенные уровни с помощью формул (1.26-1.29):
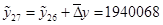 ; ;
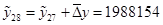 . .
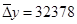 (для первых членов). (для первых членов).
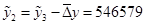 ; ;
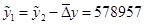 . .
Теперь изобразим на графике сглаживающую линию:
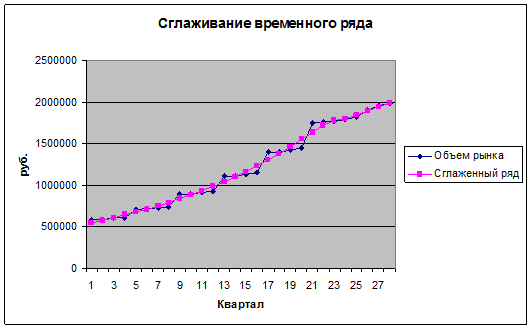
Рис. 2.3. Сглаживание временного ряда
На рынке бытовой техники г. Уфа в 2009 году произошел спад. Снижение объемов продаж произошло повсеместно по России в связи с экономическим кризисом.
Среди причин кризисных тенденций, повлекших снижение объемов рынка, можно назвать:
1) снижение темпов увеличения доходов;
2) безработица;
3) снижение объемов кредитования;
4) замедление темпов строительства.
В 2009 году основные продажи техники осуществились за счет замены устаревших товаров, а не покупки дополнительной техники [18].
Существенное снижение объемов продаж произошло в сегменте дополнительных видов бытовой техники, например, микроволновых печей.
На основе материала, изложенного в разделе 1, тренд описывается как долгосрочная компонента, отражающая возрастание или убывание временного ряда в течение длительного периода времени.
На основе графического анализа исходного временного ряда (рис. 2.1) можно сформулировать допущение о наличии тренда. Проверим это допущение с помощью гипотез.
В таблице 3.1 представлены квартальные данные по объему рынка бытовой техники за 2006, 2007 и 2008 гг.
Таблица 3.1Квартальные данные по объему рынка бытовой техники
| Квартал |
2009 г. |
2008 г. |
2007 г. |
2006 г. |
2005 г. |
2004 г. |
2003 г. |
| 1 |
1823014 |
1747589 |
1395473 |
1110683 |
892901 |
712300 |
582790 |
| 2 |
1900147 |
1754871 |
1400217 |
1115879 |
898787 |
720458 |
589787 |
| 3 |
1958799 |
1768796 |
1421587 |
1135897 |
914525 |
734879 |
602547 |
| 4 |
1982140 |
1789797 |
1447879 |
1150121 |
922145 |
739528 |
605458 |
Введем 2 гипотезы:
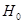 – данные об объеме рынка бытовой техники временного ряда тренда не имеют; – данные об объеме рынка бытовой техники временного ряда тренда не имеют;
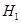 – данные об объеме рынка бытовой техники временного ряда тренда имеют. – данные об объеме рынка бытовой техники временного ряда тренда имеют.
3.1.1 Критерий Фостера-Стюарта
Проверим гипотезу о наличии тренда с помощью критерия Фостера-Стюарта. Для этого заполним вспомогательную таблицу.
Таблица 3.2 Вспомогательная таблица
| t |
yt |
mt |
lt |
d |
| 1 |
582790 |
- |
- |
- |
| 2 |
589787 |
1 |
0 |
1 |
| 3 |
602547 |
1 |
0 |
1 |
| 4 |
605458 |
1 |
0 |
1 |
| 5 |
712300 |
1 |
0 |
1 |
| 6 |
720458 |
1 |
0 |
1 |
| 7 |
734879 |
1 |
0 |
1 |
| 8 |
739528 |
1 |
0 |
1 |
| 9 |
892901 |
1 |
0 |
1 |
| 10 |
898787 |
1 |
0 |
1 |
| 11 |
914525 |
1 |
0 |
1 |
| 12 |
922145 |
1 |
0 |
1 |
| 13 |
1110683 |
1 |
0 |
1 |
| 14 |
1115879 |
1 |
0 |
1 |
| 15 |
1135897 |
1 |
0 |
1 |
| 16 |
1150121 |
1 |
0 |
1 |
| 17 |
1395473 |
1 |
0 |
1 |
| 18 |
1400217 |
1 |
0 |
1 |
| 19 |
1421587 |
1 |
0 |
1 |
| 20 |
1447879 |
1 |
0 |
1 |
| 21 |
1747589 |
1 |
0 |
1 |
| 22 |
1754871 |
1 |
0 |
1 |
| 23 |
1768796 |
1 |
0 |
1 |
| 24 |
1789797 |
1 |
0 |
1 |
| 25 |
1823014 |
1 |
0 |
1 |
| 26 |
1900147 |
1 |
0 |
1 |
| 27 |
1958799 |
1 |
0 |
1 |
| 28 |
1982140 |
1 |
0 |
1 |
Проверка гипотезы:
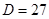 . .
Воспользуемся формулой (1.27):
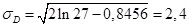
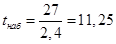
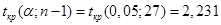
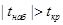 , то есть , то есть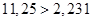 , следовательно гипотеза , следовательно гипотеза 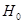 отвергается, тренд есть. отвергается, тренд есть.
Проверим гипотезу о наличии тренда с помощью критерия «восходящих» и «нисходящих» серий.
Образуем последовательность 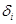 из «+» и «-»: из «+» и «-»:
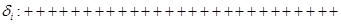
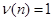 , ,
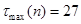
Проверим выполнение неравенств (1.18), (1.19):
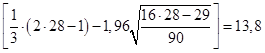
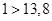 , то есть первое неравенство не выполняется. , то есть первое неравенство не выполняется.
Следовательно, гипотеза об отсутствии тренда отвергается, то есть в объеме продаж бытовой техники присутствует тенденция.
Проверим гипотезу о наличии тренда с помощью критерия серий, основанного на медиане выборки.
Строим ранжированный ряд:
 582790, 589787, 602547, 605458, 712300, 720458, 734879, 739528, 892901, 898787, 914525, 922145, 1110683, 1115879, 1135897, 1150121, 1395473, 1400217, 1421587, 1447879, 1747589, 1754871, 1768796, 1789797, 1823014, 1900147, 1958799, 1982140. 582790, 589787, 602547, 605458, 712300, 720458, 734879, 739528, 892901, 898787, 914525, 922145, 1110683, 1115879, 1135897, 1150121, 1395473, 1400217, 1421587, 1447879, 1747589, 1754871, 1768796, 1789797, 1823014, 1900147, 1958799, 1982140.
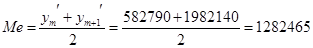
Образуем последовательность 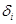 из «+» и «-»: из «+» и «-»:
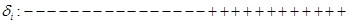
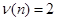

Проверим выполнение неравенств (1.30), (1.31):
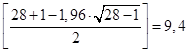

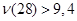
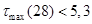
Как видно, ни одно из неравенств системы не выполняется. Это говорит о том, что в объеме рынка бытовой техники подтверждается наличие неслучайной составляющей, зависящей от 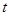 . .
Проанализируем структуру временного ряда с использованием коэффициента автокорреляции.
Воспользовавшись формулой (1.22), найдем коэффициенты корреляции.
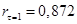 – коэффициент автокорреляции первого порядка, так как сдвиг во времени – коэффициент автокорреляции первого порядка, так как сдвиг во времени 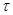 равен единице ( равен единице (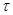 -лаг). -лаг).
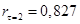 – коэффициент автокорреляции второго порядка. – коэффициент автокорреляции второго порядка.
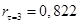 – коэффициент автокорреляции третьего порядка. – коэффициент автокорреляции третьего порядка.
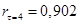 – коэффициент автокорреляции четвертого порядка. – коэффициент автокорреляции четвертого порядка.
Таким образом, мы видим, что самым высоким является коэффициент автокорреляции четвертого порядка. Это говорит о том, что во временном ряде присутствуют сезонные колебания с периодичностью в четыре квартала.
В нашем случае коэффициент автокорреляции достаточно велик, и проверять его значимость необязательно.
На основе имеющихся квартальных данных за период 2003-2009 гг., прогноз будет построен на 2010 г. Сравнить полученный прогноз с реальными показателями (первый, второй и третий кварталы) не представляется возможным ввиду отсутствия данных за 2010 г. [19].
Проанализировав данные об объеме рынка бытовой техники г. Уфа графически и содержательно, можно сделать вывод о факторах, определяющих развитие рынка:
· pocт peaльныx дoxoдoв нaceлeния;
· рост потребительского кредитования;
· рост жилищного строительства.
На основе материала, изложенного в пункте 1.3, были построены прогнозы на 2009 г. методами экспоненциального сглаживания с учетом тренда, на основе аддитивной модели, мультипликативной модели и с использованием индексов.
Сравнение полученных данных представлено в таблице 4.1.
Таблица 4.1 Сравнение прогнозных и реальных значений
| Реальные значения |
Прогноз |
| Экспоненциальное сглаживание |
Аддитивная модель |
Мультипликативная модель |
С использованием индексов |
| 1747589 |
1853982 |
1823281 |
1929637 |
1777767 |
| 1754871 |
1915300 |
1867596 |
1916210 |
1789130 |
| 1768796 |
1976618 |
1914558 |
1898126 |
1781820 |
| 1789797 |
2037936 |
1959756 |
1875383 |
1858792 |
В таблицах 4.2, 4.3 представлен сравнительный анализ ошибок прогнозирования при различных методах.
Таблица 4.2 Ошибки прогнозных значений в процентах
| Прогноз |
| Экспоненциальное сглаживание |
Аддитивная модель |
Мультипликативная модель |
С использованием индексов |
| 6,09 |
4,33 |
10,42 |
1,73 |
| 9,14 |
6,42 |
9,19 |
1,95 |
| 11,75 |
8,24 |
7,31 |
0,74 |
| 13,86 |
9,50 |
4,78 |
3,85 |
| max |
13,86 |
9,50 |
10,42 |
3,85
|
| среднее |
10,21 |
7,12 |
7,93 |
2,07
|
Таблица 4.3 Ошибки прогнозных значений в процентах
| Прогноз |
| Экспоненциальное сглаживание |
Аддитивная модель |
Мультипликативная модель |
С использованием индексов |
| MAD |
30116 |
21006 |
23263 |
6102
|
| MSE |
5909154885 |
2857036140 |
3467625716 |
292264866
|
| MAPE |
0,01702 |
0,01070 |
0,01239 |
0,00322
|
Таким образом, наименьшие ошибки получены при прогнозировании с помощью использования индексов.
4.2 Выбор наилучшего метода прогнозирования
На рис 4.1 представлены графики прогнозов различными методами.
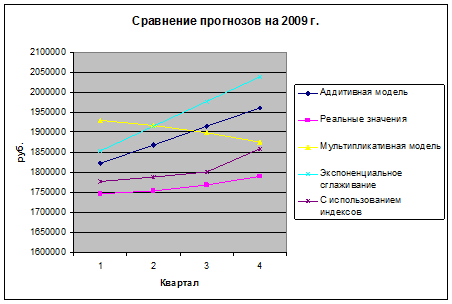
Рис. 4.1. Сравнение прогнозов на 2009 г.
Наиболее точный прогноз получен с помощью использования индексов. При прогнозе данным методом ошибки минимальны.
В 2009 году ситуация на рынке бытовой техники ухудшилась. В основном снижение продаж коснулось рынка стиральных машин, встраиваемой техники, кондиционеров и телевизоров [20].
Полученный различными методами прогноз объема рынка бытовой техники г. Уфа необходимо оценить.
Для эффективной оценки адекватности моделей, позволяющих спрогнозировать объем рынка, рассчитаем коэффициенты детерминации по формуле (1.55):
Таблица 4.4 Коэффициенты детерминации
| Метод прогнозирования |
Коэффициент детерминации |
| Метод Хольта |
0,768 |
| Аддитивная модель; |
0,825 |
| Мультипликативная модель |
0,771 |
| Прогноз с использованием индексов. |
0,974 |
Наиболее высокий коэффициент детерминации у модели с использованием индексов, что говорит об адекватности этой модели.
Прогноз на 2010 г. построен с помощью наиболее точного и адекватного метода – с помощью индексов. Результаты представлены на рис. 4.2.
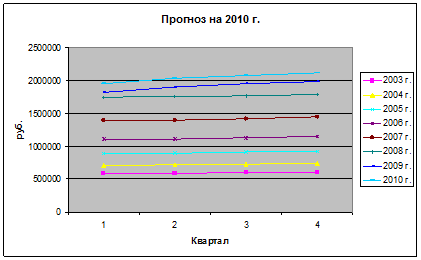
Рис. 4.2. Прогноз на 2010 г.
Таблица 4.5 Прогнозные значения на 2010 г.
| Квартал |
Прогнозные значения |
| I |
1953724 |
| II |
2036834 |
| III |
2073799 |
| IV |
2120464 |
На основе данного прогноза можно сделать вывод, что на рынке бытовой техники г. Уфа в 2010 г. ожидается увеличение объемов продаж.
Прогнозируемый годовой объем продаж за 2010 г. составит 8 184 821 руб.
В ходе написания курсовой работы приобретены практические навыки поиска и систематизации собранного материала для статистического исследования, исследованы теоретические и прикладные аспекты прогнозирования на основе временных рядов.
Результаты применены к материалам рынка бытовой техники г. Уфа за 2010 г. В данной работе сделан графический и содержательный анализ данных, выявлена динамика основных показателей за 7 лет, разработана процедура прогнозирования, получен прогноз на 2010 г. Также оценена и проверена адекватность моделей и сделан вывод о том, что наиболее эффективный прогноз получен с помощью использования индексов.
В курсовой работе решены следующие задачи:
1) подготовка обзоров методов прогнозирования;
2) графический анализ данных об объеме рынка бытовой техники;
3) содержательный анализ данных об объеме рынка бытовой техники;
4) анализ данных об объеме рынка бытовой техники на основе методов прогнозирования;
5) задача прогнозирования на 2009 г., проверка адекватности и точности прогноза и анализ ситуации на рынке бытовой техники г. Уфа в 2009 г;
6) выбор наилучшего метода прогнозирования;
7) построение прогноза на 2010 г. и расчет прогнозируемого объема продаж
8) построение прогноза на 2008 г. и проверка адекватности и точности прогноза;
9) построение прогноза на 2009 г. и анализ ситуации на предприятии в 2009 г.;
10) выбор наилучшего метода прогнозирования;
11) построение прогноза на 2010 г. и расчет прогнозируемого дохода.
В курсовой работе сформулированы выводы о том, что прогнозируемый объем продаж в 2010 г. составит 8 184 821 руб.
1. Кендэл М. Временные ряды / М. Кендэл. М.: Финансы и статистика, 1981. 199 с.
2. Ханк Д. Бизнес-прогнозирование / Д Ханк, А. Райтс, Д. Уичерн. М: Издательство «Вильямс», 2003. 656 с.
3. Просветов Г.И. Управленческий учет. Задачи и решения / Г.И. Просветов. М: Издательство РДЛ, 2006. 272 с.
4. Боровиков В.П. Популярное введение в программу STATISTICA / В.П. Боровиков. М.: Финансы и статистика, 2003. 267 с.
5. Боровиков В.П. Прогнозирование в системе STATISTICA / В.П. Боровиков, Г.И. Ивченко. М.: Финансы и статистика, 2000. 277 с.
6. Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов / Ю.П. Лукашин. М: Издательство РДЛ, 2007. 182 с.
7. Михайлов Д.С. Аналитические технологии для прогнозирования и анализа данных / Д.С. Михайлов. М.: Финансы и статистика, 2001. 199 с.
8. Орлов А.И. Прогнозирование / А.И. Орлов. М.: Финансы и статистика, 2003. 189 с.
9. Веснин В.Р. Прогнозы и прогнозирование / В.Р. Веснин. М: Триада 2000. 212 с.
10. Джонстон Д. Эконометрические методы / Д. Джонстон. М.: Статистика, 1980, 210 с.
11. Доугерти К. Введение в эконометрику / К. Доугерти. М.: Инфра-М, 1997. 251 с.
12. Кремер Н.Ш. Эконометрика: Учебник для ВУЗов / Н.Ш. Кремер, Б.А. Путко. М.: ЮНИТИ-ДАНА, 2003, 311 с.
13. Кандаурова Г.А. Прогнозирование и планирование в экономике / Г.А. Кандаурова. Интерпрессервис, Современная школа, 2005. 480 с.
14. Павленко В.Н. Временные ряды / В.Н. Павленко, А.М. Набиев, Е.А. Постников, М.А. Хрыкина. Санкт-Петербург: РГГМУ, 2007. 57 с.
15. Гамбаров Г.М. Статистическое моделирование и прогнозирование / Г.М.
16. Исследования рынка – Режим доступа: http://marketing.rbc.ru/
17. Официальный сайт консалтинговой компании MostMarketing– Режим доступа: http://www.m-marketing.ru/
18. Пресс-релиз – Режим доступа: http://press-release.com/
19. Информационный сайт города Уфы – Режим доступа: http://webufa.ru/
20. Информационный строительный портал – Режим доступа: http://restko.ru/
| t |
Yt |
Абсолютный прирост, минуты |
Темп роста, % |
Темп прироста, % |
| Цепной |
Базисный |
Цепной |
Базисный |
Цепной |
Базисный |
| 1 |
582790 |
- |
- |
- |
- |
- |
- |
| 2 |
589787 |
6997 |
6997 |
101 |
101 |
1 |
1 |
| 3 |
602547 |
12760 |
19757 |
102 |
103 |
2 |
3 |
| 4 |
605458 |
2911 |
22668 |
100 |
104 |
0 |
4 |
| 5 |
712300 |
106842 |
129510 |
118 |
122 |
18 |
22 |
| 6 |
720458 |
8158 |
137668 |
101 |
124 |
1 |
24 |
| 7 |
734879 |
14421 |
152089 |
102 |
126 |
2 |
26 |
| 8 |
739528 |
4649 |
156738 |
101 |
127 |
1 |
27 |
| 9 |
892901 |
153373 |
310111 |
121 |
153 |
21 |
53 |
| 10 |
898787 |
5886 |
315997 |
101 |
154 |
1 |
54 |
| 11 |
914525 |
15738 |
331735 |
102 |
157 |
2 |
57 |
| 12 |
922145 |
7620 |
339355 |
101 |
158 |
1 |
58 |
| 13 |
1110683 |
188538 |
527893 |
120 |
191 |
20 |
91 |
| 14 |
1115879 |
5196 |
533089 |
100 |
191 |
0 |
91 |
| 15 |
1135897 |
20018 |
553107 |
102 |
195 |
2 |
95 |
| 16 |
1150121 |
14224 |
567331 |
101 |
197 |
1 |
97 |
| 17 |
1395473 |
245352 |
812683 |
121 |
239 |
21 |
139 |
| 18 |
1400217 |
4744 |
817427 |
100 |
240 |
0 |
140 |
| 19 |
1421587 |
21370 |
838797 |
102 |
244 |
2 |
144 |
| 20 |
1447879 |
26292 |
865089 |
102 |
248 |
2 |
148 |
| 21 |
1747589 |
299710 |
1164799 |
121 |
300 |
21 |
200 |
| 22 |
1754871 |
7282 |
1172081 |
100 |
301 |
0 |
201 |
| 23 |
1768796 |
13925 |
1186006 |
101 |
304 |
1 |
204 |
| 24 |
1789797 |
21001 |
1207007 |
101 |
307 |
1 |
207 |
| 25 |
1823014 |
33217 |
1240224 |
102 |
313 |
2 |
213 |
| 26 |
1900147 |
77133 |
1317357 |
104 |
326 |
4 |
226 |
| 27 |
1958799 |
58652 |
1376009 |
103 |
336 |
3 |
236 |
| 28 |
1982140 |
23341 |
1399350 |
101 |
340 |
1 |
240 |
|