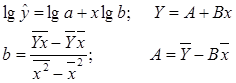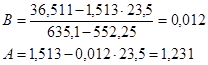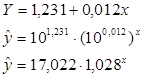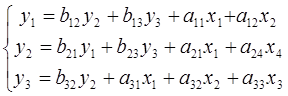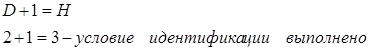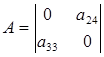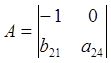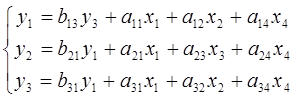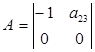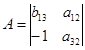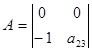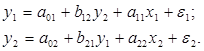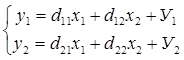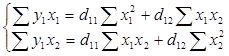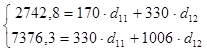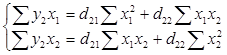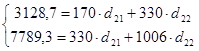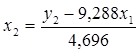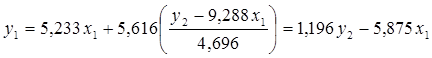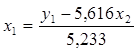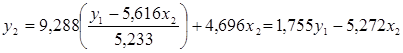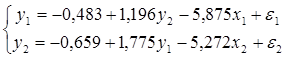Контрольная работа: Уравнения линейной регрессии

Министерство образования и науки РФ

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Филиал в г. Туле

Контрольная работа

по дисциплине «Эконометрика»

Тула - 2010 г.

Содержание

Задача 1

Задача 2 (а, б)

Задача 2 в

Задача 1

По предприятиям легкой промышленности получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (Х, млн. руб.) табл. 1.

Табл. 1.1.

Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

3. Проверить выполнение предпосылок МНК.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора Х составит 80% от его максимального значения.

7. Представить графически: фактические и модельные значения Y, точки прогноза.

8. Составить уравнения нелинейной регрессии:

гиперболической;

степенной;

показательной.

Привести графики построенных уравнений регрессии.

9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Решение

1. Линейная модель имеет вид:

Параметры уравнения линейной регрессии найдем по формулам

Расчет значения параметров представлен в табл. 2.

Табл. 1.2.

t	y	x	yx
1	43	33	1419	1089	42,236	0,764	0,584	90,25	88,36	0,018
2	27	17	459	289	27,692	-0,692	0,479	42,25	43,56	0,026
3	32	23	736	529	33,146	-1,146	1,313	0,25	2,56	0,036
4	29	17	493	289	27,692	1,308	1,711	42,25	21,16	0,045
5	45	36	1620	1296	44,963	0,037	0,001	156,25	129,96	0,001
6	35	25	875	625	34,964	0,036	0,001	2,25	1,96	0,001
7	47	39	1833	1521	47,69	-0,69	0,476	240,25	179,56	0,015
8	32	20	640	400	30,419	1,581	2,500	12,25	2,56	0,049
9	22	13	286	169	24,056	-2,056	4,227	110,25	134,56	0,093
10	24	12	288	144	23,147	0,853	0,728	132,25	92,16	0,036
∑	336	235	8649	6351	12,020	828,5	696,4	0,32
Средн.	33,6	23,5	864,9	635,1

Определим параметры линейной модели

Линейная модель имеет вид

Коэффициент регрессии показывает, что выпуск продукции Y возрастает в среднем на 0,909 млн. руб. при увеличении объема капиталовложений Х на 1 млн. руб.

2. Вычислим остатки , остаточную сумму квадратов , найдем остаточную дисперсию по формуле:

Расчеты представлены в табл. 2.

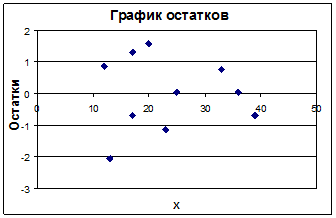
Рис. 1. График остатков ε.

3. Проверим выполнение предпосылок МНК на основе критерия Дарбина-Уотсона.

Табл. 1.3.

0,584
2,120	0,479
0,206	1,313
6,022	1,711
1,615	0,001
0,000	0,001
0,527	0,476
5,157	2,500
13,228	4,227
2,462	0,728
31,337	12,020

d1=0,88; d2=1,32 для α=0,05, n=10, k=1.

,

значит, ряд остатков не коррелирован.

4. Осуществим проверку значимости параметров уравнения на основе t-критерия Стьюдента. (α=0,05).

для ν=8; α=0,05.

Расчет значения произведен в табл. 2. Получим:

Так как , то можно сделать вывод, что коэффициенты регрессии a и b с вероятностью 0,95 значимы.

5. Найдем коэффициент корреляции по формуле

Расчеты произведем в табл. 2.

Значит,. Т.о. связь между объемом капиталовложений Х и выпуском продукции Y можно считать тесной, т.к. .

Коэффициент детерминации найдем по формуле . Значит, вариация объема выпуска продукции Y на 98,4% объясняется вариацией объема капиталовложений X.

Проверим значимость уравнения регрессии с помощью F-критерия Фишера

Fтаб=5,32, т.к. k1=1, k2=8, α=0,05

т.к. F значительно больше Fтабл, то можно сделать вывод, что уравнение регрессии с вероятностью 95% статистически значимо.

Оценим точность модели на основе использования средней относительной ошибки аппроксимации.

Расчеты произведены в табл. 2.

,

значит, линейную модель можно считать точной, т.к. Е<5%/

6. С помощью линейной модели осуществим прогноз Y при α=0,1 и х=0,8хmax

Определим границы прогноза. t0,1;8=1,86

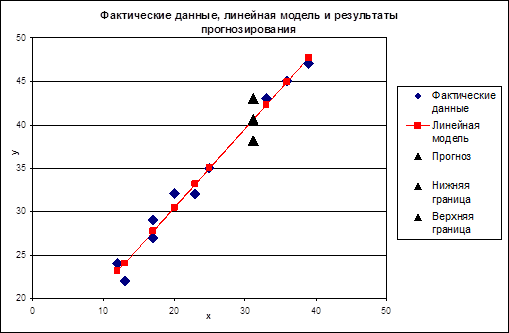
Найдем границы интервала:

7. Представим графически фактические и модельные значения Y, точки прогноза.

Рис. 2. Фактические данные, линейная модель и результаты прогнозирования.

8. а) Составим уравнение гиперболической модели. Гиперболическая модель имеет вид

;

Проведем линеаризацию переменной путем замены .

Расчеты произведем в табл. 3.

Модель имеет вид:

Табл.1.4.

t	y	x	Х	уХ
1	43	33	0,030	1,290	0,001	36,870	6,130	37,577	0,143
2	27	17	0,059	1,593	0,003	32,135	-5,135	26,368	0,190
3	32	23	0,043	1,376	0,002	34,683	-2,683	7,198	0,084
4	29	17	0,059	1,711	0,003	32,135	-3,135	9,828	0,108
5	45	36	0,028	1,260	0,001	37,289	7,711	59,460	0,171
6	35	25	0,040	1,400	0,002	35,260	-0,260	0,068	0,007
7	47	39	0,026	1,222	0,001	37,644	9,356	87,535	0,199
8	32	20	0,050	1,600	0,003	33,600	-1,600	2,560	0,050
9	22	13	0,077	1,694	0,006	29,131	-7,131	50,851	0,324
10	24	12	0,083	1,992	0,007	28,067	-4,067	16,540	0,169
∑	336	235	0,495	15,138	0,029	297,985	1,445
Средн	33,6	23,5	0,050	1,514	0,003

Найдем индекс корреляции по формуле

,

значит, связь между объемом капиталовложений Х и выпуском продукции Y можно считать тесной, т.к. .

Индекс детерминации найдем по формуле . Значит, вариация объема выпуска продукции Y на 57,2% объясняется вариацией объема капиталовложений X.

Проверим значимость уравнения на основе F-критерия Фишера.

F>Fтабл (10,692>5,32),

значит, уравнение статистически значимо.

Оценим точность модели на основе средней относительной ошибки аппроксимации.

,

значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 14,45%.

8. б) Построим степенную модель, которая имеет вид

Проведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Расчет неизвестных параметров произведем в табл. 5.

Табл. 1.5.

t	y	x	Y	Х	YХ
1	43	33	1,633	1,519	2,481	2,307	42,166	0,834	0,696	0,019
2	27	17	1,431	1,23	1,760	1,513	27,930	-0,930	0,865	0,034
3	32	23	1,505	1,362	2,050	1,855	33,697	-1,697	2,880	0,053
4	29	17	1,462	1,23	1,798	1,513	27,930	1,070	1,145	0,037
5	45	36	1,653	1,556	2,572	2,421	44,507	0,493	0,243	0,011
6	35	25	1,544	1,398	2,159	1,954	35,488	-0,488	0,238	0,014
7	47	39	1,672	1,591	2,660	2,531	46,775	0,225	0,051	0,005
8	32	20	1,505	1,301	1,958	1,693	30,896	1,104	1,219	0,035
9	22	13	1,342	1,114	1,495	1,241	23,644	-1,644	2,703	0,075
10	24	12	1,380	1,079	1,489	1,164	22,498	1,502	2,256	0,063
∑	336	235	15,127	13,380	20,422	18,192	12,296	0,346
Cредн	33,6	23,5	1,513	1,338	2,042	1,819

Получим

Перейдем к исходным переменным путем потенцирования данного уравнения.

Найдем индекс корреляции.

,

значит, связь между объемом капиталовложений Х и выпуском продукции Y тесная, т.к. .

Индекс детерминации найдем по формуле . Значит, вариация объема выпуска продукции Y на 98,2% объясняется вариацией объема капиталовложений X.

Проверим значимость уравнения на основе F-критерия Фишера.

F>Fтабл (436,448>5,32), значит, уравнение статистически значимо.

Оценим точность модели на основе средней относительной ошибки аппроксимации.

,

значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 3,46%. Модель точная.

8. в) Составим показательную модель, уравнение которой имеет вид:

Проведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Табл. 1.6.

t	y	x	Y	Yx
1	43	33	1,633	53,889	1089	42,343	0,657	0,432	0,015
2	27	17	1,431	24,327	289	27,220	-0,220	0,048	0,008
3	32	23	1,505	34,615	529	32,126	-0,126	0,016	0,004
4	29	17	1,462	24,854	289	27,220	1,780	3,168	0,061
5	45	36	1,653	59,508	1296	46,001	-1,001	1,002	0,022
6	35	25	1,544	38,600	625	33,950	1,050	1,102	0,030
7	47	39	1,672	65,208	1521	49,974	-2,974	8,845	0,063
8	32	20	1,505	30,100	400	29,571	2,429	5,900	0,076
9	22	13	1,342	17,446	169	24,374	-2,374	5,636	0,108
10	24	12	1,380	16,560	144	23,710	0,290	0,084	0,012
∑	336	235	15,127	365,107	6351	26,233	0,399
Средн	33,6	23,5	1,513	36,511	635,1

Перейдем к исходным переменным, выполнив потенцирование уравнения.

Найдем индекс корреляции.

,

значит, связь между объемом капиталовложений Х и выпуском продукции Y тесная, т.к. .

Индекс детерминации найдем по формуле . Значит, вариация объема выпуска продукции Y на 96,2% объясняется вариацией объема капиталовложений X.

Проверим значимость уравнения на основе F-критерия Фишера.

F>Fтабл (202,528>5,32),

значит, уравнение статистически значимо.

Оценим точность модели на основе средней относительной ошибки аппроксимации.

,

значит, расчетные значения ŷ для гиперболической модели отличаются от фактических значений на 3,99%. Модель точная.

9. Сравним полученные модели.

Табл. 1.7.

Модель регрессии			F-критерий
Линейная	0,992	0,984	492	3,2
Гиперболическая	0,756	0,572	10,692	14,45
Степенная	0,991	0,982	436,448	3,46
Показательная	0,981	0,962	202,528	3,99

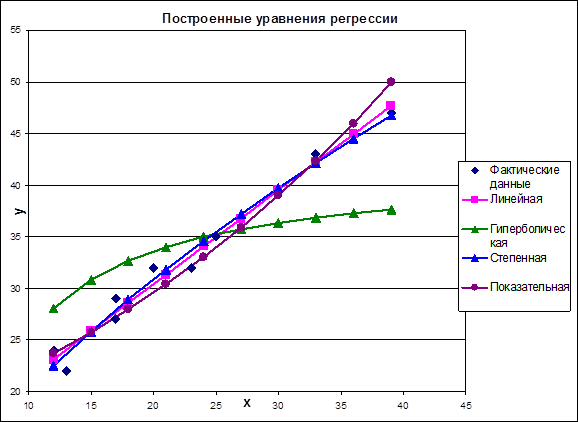
Наилучшей моделью является линейная модель (по максимуму критерия корреляции, детерминации, F-критерия и минимальной средней ошибке аппроксимации).

Рис. 3. Построенные уравнения регрессии.

Задача 2 (а, б)

Для каждого варианта даны по две СФМ, которые записаны в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.

Табл. 2.1.

Решение

a) CФМ имеет вид:

Проверим систему на идентифицируемость. Для этого проверим каждое уравнение системы на выполнение необходимого и достаточного условия идентификации.

1) В 1-м уравнении 3 эндогенные переменные y1, y2, y3 (Н=3). В нем отсутствуют экзогенные переменные х3, х4 (D=2). Необходимое условие идентификации

Для проверки на достаточное условие идентификации составим матрицу из коэффициентов при отсутствующих переменных.

Составим матрицу из коэффициентов

Определитель матрицы не равен 0, ранг равен 2. достаточное условие идентификации выполняется и 1-е уравнение точно идентифицируемо.

2) Во 2-м уравнении 3 эндогенные переменные y1, y2, y3 (Н=3); отсутствуют экзогенные х2, х3 (D=2).

2+1=3 — необходимое условие идентификации выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при отсутствующих переменных.

Определитель не равен 0, ранг матрицы равен 2, достаточное условие идентификации выполняется. 2-е уравнение точно идентифицируемо.

3) В 3-м уравнении 2 эндогенные переменные y2, y3 (Н=2); отсутствует 1 экзогенная х4 (D=1).

1+1=2 — необходимое условие идентификации выполняется.

Составим матрицу из коэффициентов при отсутствующих переменных.

Определитель не равен 0, ранг матрицы равен 2-м, достаточное условие идентификации выполняется. 3-е уравнение точно идентифицируемо.

Т.о, если все 3 уравнения идентифицируемы, то и СФМ идентифицируема.

б) СФМ имеет вид:

Проверим систему на идентифицируемость, для этого проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.

1) В 1-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1).

Составим матрицу из коэффициентов при отсутствующих переменных.

Достаточное условие не выполнено, уравнение не идентифицируемо.

2) Во 2-м уравнении 2 эндогенных переменных y1, y2 (Н=2). Отсутствующая экзогенная переменная х2 (D=1). Необходимое условие D+1=H выполняется.

Составим матрицу из коэффициентов при отсутствующих переменных.

Необходимое условие идентификации выполняется. 2-е уравнение точно идентифицируемо.

3) В 3-м уравнении 2 эндогенных переменных y1, y3 (Н=2); отсутствующая экзогенная переменная х3 (D=1). Необходимое условие D+1=H выполняется. Составим матрицу из коэффициентов при отсутствующих переменных.

Достаточное условие не выполняется. 3-е уравнение не идентифицируемо.

Т.к. 1-е и 3-е уравнения не идентифицируемы, то и вся СФМ не является идентифицируемой.

Ответ: а) СФМ идентифицируема; б) СФМ не является идентифицируемой.

Задача 2 в

По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида:

Табл. 2.2.

Решение

Структурную модель преобразуем в приведенную форму модели.

Для нахождения коэффициентов первого приведенного уравнения используем систему нормальных уравнений.

Расчеты произведем в табл. 2.3.

Табл. 2.3.

n	y1	y2	x1	x2
1	77,5	70,7	1	12	77,5	1	12	930	144	70,7	848,4
2	100,6	94,9	2	16	201,2	4	32	1609,6	256	189,8	1518,4
3	143,5	151,8	7	20	1004,5	49	140	2870	400	1062,6	3036
4	97,1	120,9	8	10	776,8	64	80	971	100	967,2	1209
5	63,6	83,4	6	5	381,6	36	30	318	25	500,4	417
6	75,3	84,5	4	9	301,2	16	36	677,7	81	338	760,5
∑	557,6	606,2	28	72	2742,8	170	330	7376,3	1006	3128,7	7789,3
средн.	92,933	101,033	4,667	12

Подставив полученные значения в систему нормальных уравнений.

Решение этих уравнений дает значения d11=5,233; d12=5,616.

1-e уравнение ПФМ имеет вид:

Для нахождения коэффициентов d2k второго приведенного уравнения используем следующую систему нормальных уравнений

Расчеты произведем в табл. 2.3.

Подставив полученные значения в систему нормальных уравнений, получим

Решение этой системы дает значения d21=9,288; d22=4,696.

2-е уравнение ПФМ имеет вид

Для перехода от ПФМ к СФМ найдем х2 из второго уравнения.

Подставив это выражение в 1-е уравнение, найдем структурное уравнение.

т.о. b12=1,196; a11=-5,875.

Найдем х1 из 1-го уравнения ПФМ

Подставив это выражение во 2-е уравнение ПФМ, найдем структурное уравнение.

т.о. b21=1,775; a22=-5,272

Свободные члены СФМ находим из уравнений

линейныйрегрессия детерминация аппроксимация квадрат

Ответ: окончательный вид СФМ таков
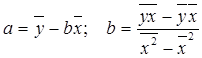
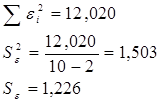
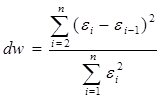
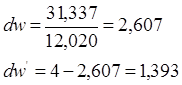
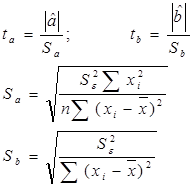
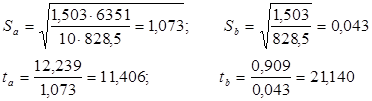
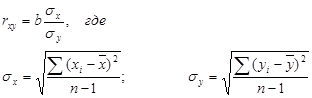
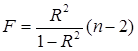
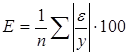
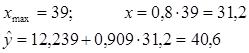
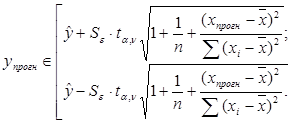
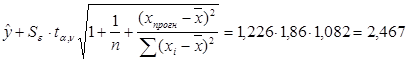
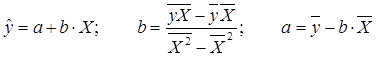
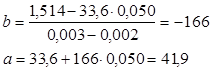
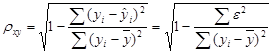
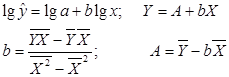
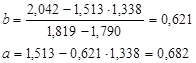
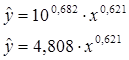
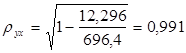