МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ЧЕРКАСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
ІМЕНІ БОГДАНА ХМЕЛЬНИЦЬКОГО
АЛГОРИТМ КЕННЕТА-ДЖЕКСОНА ДЛЯ ОПИСУ ФАЗОВИХ ПЕРЕТВОРЕНЬ У БІНАРНИХ СПЛАВАХ. ОПИС ДИФУЗІЇ
Галузь знань 0402 фізико-математичні науки
Напрям підготовки 6.040203 Фізика
Курсова робота
студентки 4 курсу факультету ФМ та КІС
денної форми навчання
Науковий керівник – кандидат фіз.-мат. наук
доцент кафедри фізики
Ковальчук А.О
ЧЕРКАСИ-2010р.
ЗМІСТ
ВСТУП
РОЗДІЛ 1. ПОНЯТТЯ ПРО ФАЗОВІ ПЕРЕХОДИ
РОЗДІЛ 2. ДИФУЗІЯ У СПЛАВАХ
2.1 Поняття дифузії
2.2 Механізми дифузії
2.3 Переміщення атомів на великі відстані
2.4 Кореляційний множник
2.5 Перший закон Фіка
2.6 Взаємна дифузія. Ефект Кіркендаля
РОЗДІЛ 3. АЛГОРИТМ КЕННЕТА-ДЖЕКСОНА ДЛЯ ОПИСУ ФАЗОВИХ ПЕРЕТВОРЕНЬ У БІНАРНИХ СПЛАВАХ
3.1 Модель
3.2 Вільна енергія Гіббса для твердого розчину
3.3 Фазова діаграма регулярного розчину
3.4 Енергія площини
3.5 Стрибкоподібний інтерфейс в 1D
3.6 Малоамплітудні синусоїдальні збурення в 1D
РОЗДІЛ 4. ХІМІЧНІ ПОТЕНЦІАЛИ
4.1 Хімічні потенціали в 1D
4.2 Хімічні потенціали в 2D
4.3 Хімічні потенціали в 3D
РОЗДІЛ 5. РІЗНИЦЕВІ РІВНЯННЯ ДЛЯ ДИФУЗІЇ
5.1 Дифузійні потоки базовані, на активностях
5.2 Різницеві рівняння для дифузії в 1D
5.3 Рівння в кінцевих різницях для дифузії в 2D
5.4 Різницеві рівняння для дифузії в 3D
5.5 Безрозмірний час
ВИСНОВОК
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Актуальність дослідження. У даній роботі розглядається новий алгоритм для опису фазових перетворень у бінарних сплавах, де описується дифузія сплавів і моделюється у 2D вимірі.
Цей спосіб дозволяє прослідкувати зміну дифузії при різних температурах, концентраціях, і заданих різних енергетичних потенціалах. Тобто, цей спосіб дуже зручно використовувати при моделюванні.
Мета і завдання дослідження. Описати дифузію сплавів і застосувати теоретичні викладки для даного алгоритму.
Об’єкт дослідження. Бінарні сплави під час фазового розподілу.
Предмет дослідження. Дифузійні процеси в бінарних сплавах.
Методи дослідження. Моделювання у середовищі програмування Delphiза допомогою алгоритму Кеннета-Джексона. Опрацювання теоретичного матеріалу.
Практичне значення одержаних результатів. Процеси дифузії, прослідковані у даній роботі, що відбуваються у бінарних сплавах під час фазового розпаду відіграють вирішальну роль у багатьох новітніх технологіях. На практиці дані знання можуть використовуватися у металургії, металообробці, створенні напівпровідникових та інтегральних схем, захисних покрить, тонких плівок.
РОЗДІЛ 1
ПОНЯТТЯ ПРО ФАЗОВІ ПЕРЕХОДИ
Фазовий перехід (фазове перетворення) в термодинаміці – це перехід речовини з однієї термодинамічної фази в іншу при зміні зовнішніх умов. З точки зору руху системи по фазовій діаграмі при зміні її інтенсивних параметрів (температури, тиску і т.т.), фазовий перехід відбувається, коли система перетинає лінію, що розділяє дві фази. Оскільки різні термодинамічні фази описуються різними рівняннями станів, то завжди можна знайти величину, яка стрибкоподібно змінюється при фазовому переході.
Оскільки поділ на термодинамічні фази – більш детальна класифікація станів, ніж класифікація за агрегатними станами речовини, то далеко не кожен фазовий перехід супроводжується зміною агрегатного стану. Проте, будь-яка зміна агрегатного стану є фазовим переходом.
Найчастіше розглядаються фазові переходи при зміні температури, але при сталому тиску (як правило в 1 атмосферу). Саме тому часто вживають терміни «точка» (а не лінія) фазового переходу, температура плавлення і т.д. Звісно, фазовий перехід може відбуватися і при зміні тиску, і при сталій температурі і тиску, але при зміні концентрації компонентів (наприклад, поява кристалів солі в розчині, що досягнув насичення).
Розрізняють фазові переходи двох родів.
При фазовому переході першого роду стрибкоподібно змінюються основні, початкові екстенсивні параметри: питомий об’єм, кількість накопиченої внутрішньої енергії, концентрації компонентів. Підкреслимо: мається на увазі стрибкоподібні зміни цих величин при зміні температури, тиску, а не стрибкоподібні зміни в часі.
Найпоширеніші приклади фазових переходів першого роду:
- плавлення і кристалізація;
- випаровування і конденсація;
- сублімація та десублімація.
При фазовому переході другого роду густина і внутрішня енергія не змінюються, тому неозброєним оком такий фазовий перехід може бути непомітним. Однак, стрибкоподібних змін зазнають похідні по температурі та тиску: теплоємність, коефіцієнт теплового розширення і т.д.
Фазові переходи другого роду відбуваються в тих випадках, коли змінюється симетрія будови речовини (симетрія може повністю зникнути або понизитися). Опис фазового переходу другого роду як наслідок зміни симетрії дається в теорії Ландау. В теперішній час прийнято говорити не про зміну симетрії, а про появу в точці переходу параметру порядку, рівного нулю в менш впорядкованій фазі і що змінюється від нуля (в точці переходу) до ненульових значень в більш впорядкованій фазі.
Найбільш поширені приклади фазових переходів другого роду:
- перехід системи через критичну точку;
- перехід парамагнетик-феромагнетик або парамагнетик-антиферомагнетик (параметр порядку – намагніченість);
- перехід металів і сплавів в стан надпровідності (параметр порядку – густина надпровідного конденсату);
- перехід рідкого гелію в надтекучий стан (параметр порядку – густина надтекучої компоненти);
- перехід аморфних матеріалів в склоподібний стан;
- впорядкування сплавів.
Сучасна фізика досліджує також системи, що володіють фазовими переходами третього або вищого роду.
Останнім часом широкого поширення набуло поняття квантового фазового переходу, тобто фазового переходу, що керується не класичними тепловими флуктуаціями, а квантовими, які існують навіть при абсолютному нулі температур, де класичний фазовий перехід не може реалізуватися внаслідок теореми Нернста.
РОЗДІЛ 2 ДИФУЗІЯ У СПЛАВАХ
2.1 Поняття дифузії
Розглянемо явища міграції атомів в твердих тілах та перебудову структури твердих тіл зі зміною температури, концентрацій та інших параметрів. Ці процеси відіграють вирішальну роль у металургії, металообробці, створенні напівпровідникових та напівпровідних матеріалів, інтегральних схем, захисних покрить, тонких плівок.
Термодинаміка відповідає на два питання – чому даний процес відбувається , і чим він мусить завершитися.
Кінетика визначає як швидко буде протікати процес, і які проміжні стадії він пройде. Саме кінетика і вивчає явище дифузії.
Воно було відкрито в твердих тілах Робертом Аустеном у 1896 році, коли він спостерігав взаємну дифузію між золотом і свинцем. За останні сто років уявлення про дифузію значно збагатилися, але ще далекі від завершення.
Дифузія – це процес перерозподілу концентрацій атомів у просторі шляхом хаотичної, тобто, теплової міграції. Причин дифузії з точки зору теплової термодинаміки може бути дві – ентропійна (завжди) та енергетична (іноді). Ентропійна причина – це збільшення хаосу (і його міри – ентропії) при перемішуванні атомів різного сорту. Енергетична причина сприяє утворенню сплаву, коли вигідніше бути поруч атомам різного сорту, та дифузійному розпаду, коли вигідніше бути поруч односортним атомам.
2.2 Механізми дифузії
Велика щільність розташування атомів у твердих тілах та особливо їх періодична структура робить питання про спосіб міграції нетривіальним. Проблема в тому, що дифузія відбуваються найчастіше зі збереженням дальнього порядку, зокрема, періодичності гратки.
Тобто міграцію атомів в ідеальних кристалах можна уявити як обмін між вузлами гратки. Такий обмін може відбуватися квантованим способом (тунельний ефект), для якого немає можливості і потреби слідкувати за траєкторіями. Якщо атоми достатньо масивні, щоб можна було знехтувати їх хвильовими властивостями, то в принципі обмін можливий класичним способом як корельовано повертання пари атомів навколо спільного центру. Зрозуміло, що на таку процедуру потрібна досить значна в атомних масштабах втрата енергії. Тому природа знаходить значно ефективніші механізми, такі, як вакансійний, міжвузільний та механізм витіснення.
Для реалізації вакансійного механізму потрібна наявність вакансій. Міграція вакансій відбувається шляхом переходу в незайнятий вузол одного з сусідніх атомів. Відповідно атом може здійснити дифузійний скачок за умови, що поруч з ним опиниться вакансія. Оскільки вакансії досить рухливі, то для забезпечення перемішування на макрорівні при температурі, близькій до температури плавлення, достатньо однієї вакансії на кілька тисяч атомів.
Міжвузільний механізм – це переходи атома з одного міжвузілля в інше. Для такого переходу мігруючому атому потрібно «протиснутися» через ворота, утворені сусідніми атомами. (рис. 2.2.1), тому міжвузьльний механізм характерний для водню, вуглецю та інших легких елементів.
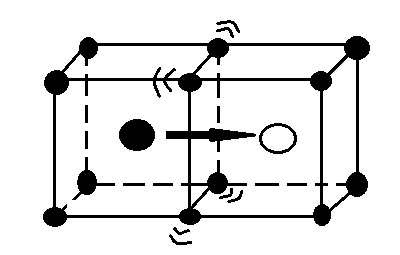
Рис.2.2.1 «Протиск» атома через ворота, утворені сусідніми
В міжвузіллі можуть знаходитися і важкі домішкові атоми або власні атоми, отримані за механізмом Френкеля або імплантовані ззовні. При цьому вони значно деформують решітку навколо себе, розсовуючи сусідів. Тому для власних атомів більш імовірний механізм витіснення, тобто дефекту легше витіснити найближчого сусіда у міжвузілля і стати на його місце, ніж протискуватися через ворота у сусіднє міжвузілля. За таким механізмом мігрує міжвузільний дефект, але на кожному кроці він реалізується різними атомами, на відміну від одного й того самого мігруючого атома у міжвузільному механізмі. У кожному акті витіснення різниця між атомом у вузлі та дефектом дещо умовна, оскільки решітка деформована і саме поняття вузла стає неоднозначним. Остаточно можна визначити механізм дифузії в даному вузлі, коли дефект перейде у наступне міжвузілля, а атоми релаксують до рівноважних положень.
Рух атома, що межує з вакансією, аналогічний процесу дифузії по міжвузіллях. Атом υ разів за секунду «ударяється» об бар’єр. Відносна частка часу, на протязі якого атом має енергію, достатня для подолання цього бар’єру, рівна 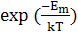 , де , де 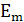 - висота бор’єру. Але в цей розрахунок повинен ввійти додатковий фактор, який враховує, що вакансія, яка наближається до втома існує в даному вузлі решітки лише малий проміжок часу. Вона визначається як - висота бор’єру. Але в цей розрахунок повинен ввійти додатковий фактор, який враховує, що вакансія, яка наближається до втома існує в даному вузлі решітки лише малий проміжок часу. Вона визначається як 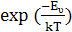 , де , де 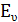 - енергія утворення вакансії. - енергія утворення вакансії.
Частота стрибків атома буде рівна
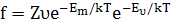
Де Z – кількість рівноцінних сусідніх вузлів.
Частота ж сильно залежить від температури. Для таких металів, як мідь, срібло, залізо, обидві енергії 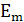 і і 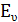 рівні приблизно 1 еВ. Тому для цих металі частота набагато менша частоти стрибків при типовій дифузії по міжвузілля (за однакових умов). рівні приблизно 1 еВ. Тому для цих металі частота набагато менша частоти стрибків при типовій дифузії по міжвузілля (за однакових умов).
Крім описаних механізмів дифузії існує багато інших – краудіонний, релаксаційний (локальне плавлення), кільцевий та інші.
2.3 Переміщення атомів на великі відстані
Розрахуємо зміщення атома після того, як він зробив певну кількість стрибків. Всі стрибки мають однакову довжину (вони рівні міжатомній відстані) і відбуваються в решітці з високим степенем симетрії. Але припустимо, що рух атома в різних можливих кристалографічних напрямках хаотичний. Атоми можуть перескакувати вперед, назад, вгору і донизу. Тому ніколи не можна передбачити, яку результуючу траєкторію здійснить атом після певної кількості стрибків. З певною точністю можна визначити лише зміщення, усереднене по багатьох дифундуючи атомах.
Найпростіше виконати такий розрахунок для випадку руху атомів тільки в одному вимірі (вздовж прямої). Припустимо, що в початковий момент часу атом знаходиться в точці 0. Тоді він виконує послідовні стрибки довжиною в кожен. (рис. 2.3.1).

Рис.2.3.1 Координати нових розміщень атомів для одновимірних хаотичних стрибків
Напрямок кожного стрибка хаотичний; він не залежить від будь-яких попередніх подій. Результуюча відстань Х, яку пройде атом після n стрибків, рівна алгебраїчній сумі всіх окремих стрибків:
 , ,
де 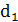 - довжина першого стрибка, - довжина першого стрибка,  - довжина n-го стрибка. Відстань Х відповідає добутку довжини стрибка в на певний множник, при чому ця відстань може бути додатною, від’ємною і рівною нулю. Насправді середня величина Х після багатьох атомних стрибків в точності рівна нулю, хоча діапазон зміни Х лежить в межах від +nd до –nd. Це середнє є алгебраїчним, і те що вона рівна нулю говорить, що додатній напрямок стрибків не має переваг над від’ємним. Але існують і такі середні значення, які не рівні нулю. До них відносяться, середнє квадратичне, яке є мірою загальної відстані, пройденої атомом від початкового положення. - довжина n-го стрибка. Відстань Х відповідає добутку довжини стрибка в на певний множник, при чому ця відстань може бути додатною, від’ємною і рівною нулю. Насправді середня величина Х після багатьох атомних стрибків в точності рівна нулю, хоча діапазон зміни Х лежить в межах від +nd до –nd. Це середнє є алгебраїчним, і те що вона рівна нулю говорить, що додатній напрямок стрибків не має переваг над від’ємним. Але існують і такі середні значення, які не рівні нулю. До них відносяться, середнє квадратичне, яке є мірою загальної відстані, пройденої атомом від початкового положення.
Середнє значення 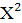 (позначається (позначається 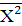 ) буде рівне ) буде рівне
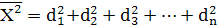
Це співвідношення зручніше записати у вигляді
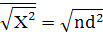
Тобто це означає, що потрібна велика кількість стрибків, щоб значення Х мали достатню величину.
Запишемо це рівняння в іншій формі. Кількість стрибків n виразимо, як добуток стрибків f і часу t, необхідного для здійснення n атомних стрибків
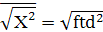 (*) (*)
Параметр  залежить від властивостей матеріалу і від температури. залежить від властивостей матеріалу і від температури.
В 1D коефіцієнт дифузії Dвизначається як
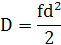
Підставивши у формулу (*) це значення отримаємо
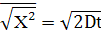 (**) (**)
Середньоквадратична відстань, яку проходить дуфундуючий атом, змінюється пропорційно кореню квадратному із часу. Коефіцієнт ½ введений у рівняння для коефіцієнту дифузії для того, щоб узгодити його з рівнянням (**).
Зазвичай атоми роблять стрибки в усіх трьох напрямках. Тому можна розрахувати середньоквадратичне радіальне зміщення
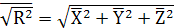 в будь-якому напрямку від початкової точки в будь-якому напрямку від початкової точки
Тоді
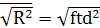 , ,
де f – частота, з якою атом змінює свій напрям в решітці. В багатьох таких задачах цікавим є результуюче дифузійне переміщення відносно певної координати, хоча атом здійснює стрибки і в інших напрямках. За умовами симетрії 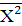 рівне рівне
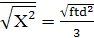 (***) (***)
Тому «трьохвимірний» коефіцієнт дифузії визначається так
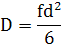
Щоб встановити залежність коефіцієнта дифузії від температури використаємо вираз для частоти. Для кубічних кристалів отримаємо:

Усі параметри перед експонентою зазвичай об’єднують в один коефіцієнт  , а сумарну енергію позначають Q: , а сумарну енергію позначають Q:
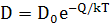
Величина  - частотний фактор, а Q – енергія активації. - частотний фактор, а Q – енергія активації.
Опишемо дифузію ансамбля незалежних частинок, які розподілені в просторі з початковою концентрацією 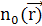 . Концентрацію цих частинок у довільний момент часу tможна виразити через наступний інтеграл . Концентрацію цих частинок у довільний момент часу tможна виразити через наступний інтеграл
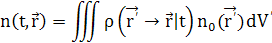
Легко переконатися, що розподіл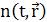 підкоряється такому ж рівнянню, як і імовірність переходів підкоряється такому ж рівнянню, як і імовірність переходів

Це і є рівняння дифузії – другий закон Фіка, запропонований ним у 1855 році.
2.4 Кореляційний множник
Легкий домішковий атом дифундує по міжвузіллях або вакансія рухається по вузлах не корельовано, тобто кожен наступний крок не залежить від попереднього. Для дифузії, як ми вже знаємо, за вакасійним механізмом все не так. Атом може здійснити скачок, але відразу після скачка він «пам’ятає», що позаду нього є вакансія і найімовірнішим для атома буде скачок назад. Отже
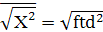 , ,
де 
Для випадку N>> 1 можна показати, що величина fвід N не залежить.
Величина f у такій інтерпретації називається кореляційним множником, і є свого роду коефіцієнтом корисної дії атомних скачків.
Для кристалу з кубічною симетрією він буде рівний
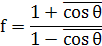
де 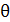 - кут між напрямами двох послідовних скачків атома. - кут між напрямами двох послідовних скачків атома.
Кореляційний множник дуже важливий в дифузії сплавів, особливо сильновпоядкованих. Тут хаотична міграція стає настільки невигідною (руйнує порядок), що кореляційний множник для механізму скачків у першу координаційну сферу прямує до нуля.
2.5 Перший закон Фіка
Розглянемо дифузію за вакансійним механізмом мічених атомів сорту А* в чистому кристалі, що складається з атомів того ж сорту. Нехай для конкретності кристал має ГЦК-структуру, а градієнт концентрації створений у напрямі <100> (вздовж ребра куба стороною а). Міжплощинна відстаньdдля цього напрямку дорівнює а/2. Виберемо уявну площину з координатою х посередині між двома сусідніми атомними площинами з координатами x-d/2, x+d/2. Нехай 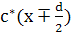 - атомні концентрації (частки) мічених атомів у відповідних площинах. Скачки мічених атомів відбуваються шляхом обміну з вакансіями, концентрація яких (а значить, імовірність появи у сусідньому вузлі) вважається постійною - атомні концентрації (частки) мічених атомів у відповідних площинах. Скачки мічених атомів відбуваються шляхом обміну з вакансіями, концентрація яких (а значить, імовірність появи у сусідньому вузлі) вважається постійною 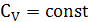 . .
Густину потоку мічених атомів через площину х знаходимо як різницю частоти скачків у двох напрямках з урахуванням кореляції
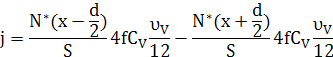
Тут  - кількість мічених атомів у площині - кількість мічених атомів у площині 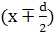 , ,
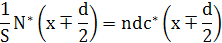
4 – кількість можливих напрямків скачків через площину х з даного вузла;
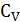 – імовірність мати вакансію у сусідньому вузлі; – імовірність мати вакансію у сусідньому вузлі;
 – частота скачків вакансії; – частота скачків вакансії;
1/12 – імовірність обміну вакансії з даним атомом (12 – кількість сусідніх вузлів);
f - кореляційний множник.
Розкладаючи 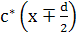 в ряд Тейлора і нехтуючи вищими порядками малості, маємо в ряд Тейлора і нехтуючи вищими порядками малості, маємо
 , ,
де h=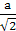 - довжина елементарного скачка (відстань до найближчого сусіда) в ГЦК-решітці. Таким чином отримаємо закон дифузії (першого закону Фіка) з коефіцієнтом дифузії - довжина елементарного скачка (відстань до найближчого сусіда) в ГЦК-решітці. Таким чином отримаємо закон дифузії (першого закону Фіка) з коефіцієнтом дифузії
фазовий дифузійний бінарний сплав
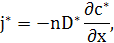
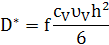
2.6 Взаємна дифузія. Ефект Кіркендаля
У 1947 році був проведений дослід, що показав існування зв’язку між дифузійними процесами та необоротною деформацією твердих тіл. Відпалювався зразок розчину цинку в решітці міді. На границях мідь-α-латунь з обох боків дифузійною зваркою були зафіксовані інертні маркери – дротинки з тугоплавкого матеріалу (молібден, вольфрам), дифузійною взаємодією яких з міддю і цинком при температурі відпалювання знехтували. При відпалюванні, крім взаємопроникнення матеріалів та згладжуванням концентраційних профілів, був помічений зсув маркерів в бік α-латуні за параболічним законом  . Тут потрібно врахувати: . Тут потрібно врахувати:
1) імовірність обміну вакансії з атомами різного сорту різна, тому компоненти сплаву мають різну рухливість (парціальний коефіцієнт дифузії);
2) різна рухливість компонентів приводить до виникнення потоку вакансій в бік більш рухливого компоненту з наступним розбиранням вакансіями атомних площин і відповідним зсувом решітки.
У системі відліку, пов’язаній з кристалічною решіткою
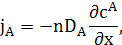
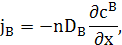
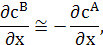

У лабораторній системі відліку потоки повинні бути рівними за величиною та протилежні за напрямком
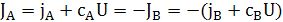
Звідси швидкість течії решітки 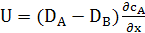
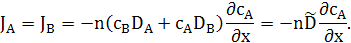
Таким чином, швидкість течії решітки визначається різницею рухливостей компонентів та градієнтом концентрації, а потоки в лабораторній системі відліку мають вигляд першого закону Фіка з коефіцієнтом дифузії 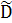 , хоча, насправді взаємна дифузія є результатом накладання течії решітки на дифузійну міграцію. , хоча, насправді взаємна дифузія є результатом накладання течії решітки на дифузійну міграцію.
РОЗДІЛ 3. АЛГОРИТМ КЕННЕТА-ДЖЕКСОНА ДЛЯ ОПИСУ ФАЗОВИХ ПЕРЕТВОРЕНЬ У БІНАРНИХ СПЛАВАХ
3.1 Модель
Розглядається система бінарного сплаву А+В в наближеній моделі регулярних розчинів, тобто:
а) взаємодія атомів розраховується в наближенні першої координаційної сфери;
б) взаємодія між атомами описується потенціалами парної взаємодії (φAA
, φAB
, і φBB
), які не залежать від концентрації та температури;
в) ентропія регулярного розчину вважається тільки конфігураційною, тобто описується лише той хаос, що пов’язаний з розміщенням атомів різного сорту по вузлах решітки, і не враховується хаос, пов’язаний з коливаннями атомів (вібраційна ентропія).
Прагнення термодинамічних систем до встановлення рівноваги за складом кількісно характеризується величиною, яка називається хімічним потенціалом. Хімічні потенціали компонентів сплаву обчислюються за допомогою вільної енергії Гібса (потенціалу Гібса), яку можна розуміти як повну хімічну енергію системи. Хімічні потенціали зумовлюють підтримання потоків речовини (дифузійних потоків), які обчислюються за допомогою активностей. Активність компонентів розчину – це ефективна концентрація компонентів з врахуванням різних взаємодій між ними в розчині, тобто з врахуванням відхилення поведінки системи від моделі ідеального розчину. Різницеві рівняння дифузійних потоків описують процес дифузії. Через те, що дифузійні потоки залежать від хімічних потенціалів сусідніх вузлів, які в свою чергу залежать від атомів сусідніх до них, ми практично отримуємо різницеві рівняння четвертого порядку. Для температур та концентрацій які сильно відрізняються від двофазної області ці рівняння перетворюються на стандартні рівняння дифузії.
3.2 Вільна енергія Гіббса для твердого розчину
Ми припустили, що враховується взаємодія атомів лише з першої координаційної сфери, і взаємодія між атомами описується потенціалами парної взаємодії між атомами відповідних сортів у вузлах решітки (φAA
, φAB
, і φBB
). Використовуючи φAA
, φAB
, і φBB
, ми можемо визначити енергію змішування, яка також відома як параметр регулярного розчину (Ω)
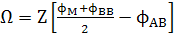 (1) (1)
де Z – це координаційне число, тобто кількість атомів, найближчих до даного атома в кристалі. Для будь-якого розподілу атомів в бінарному сплаві потенціали парних взаємодій найближчих сусідів можна визначити через Х( імовірність пари типу А-В знаходитись у двох сусідніх вузлах), тоді NZX– кількість пар АВ в суміші з N атомів. Тоді вільна енергія Гібса бінарного сплаву дорівнює:
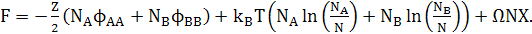 (2) (2)
NA
і NB
- кількість атомів двох видів, і N=NA
+NB
. Перший доданок – енергія ідеального сплаву (енергетичний доданок), другий – ентропія змішування, і останній – додаткова енергія неідеального сплаву. Це рівняння справедливе для будь-яких конфігурацій атомів. Для регулярних розчинів, припущено що А і В атоми рандомно розподілені, тоді Х, який залежить від розподілу атомів, дорівнює CA
CB
, де СА
=NA
/N, і CB
=NB
/N.
Для ідеального розчину, Ω=0, або (φAA
+φBB
)/2= φA
B
.
Для Ω>0, формування пар АА і ВВ знижує загальну енергію, так що сплав прямує до фази розпаду, атоми А кластеруються разом, а атоми В теж кластеруються разом.
Для Ω<0, формування пар АВ зменшує загальну енергію, так що сплав упорядковується. Це така порада для контролю за утворенням структур.
3.3 Фазова діаграма регулярного розчину
Припущено, що в регулярному розчині атоми рандомно розподілені, так що Х=С(1-С), де С=СВ
, СА
=1-С. Гранична фаза дорівнює
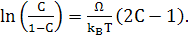 (3) (3)
Критична точка при С=1/2 і Т=ТС
, тоді kB
TC
=Ω/2.
Для фази розділу, границя спінодальної області дорівнює
C(1-C)=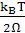 (4) (4)
Фазова діаграма регулярного розчину зображена на рис.3.3.1.
Впорядкування відбувається для від’ємних величин Ω. Концентрації атомів сорту А та В дорівнюють СА
, СВ
, відповідно, або С та 1-С, тоді
Х=(С2
+(1-С)2
)/2

Рис.3.3.1 Фазова діаграма для регулярного розчину
3.4 Енергія площини
В цьому підрозділі аналізуються атомні площини, що розташовані паралельно. Ми припускаємо, що атоми рандомно розподілені в кожній площині, і що середня концентрація змінюється від площини до площини. Розташування кожної площини визначається однією просторовою змінною,z.
Як показано в рівнянні (2), вільна енергія може бути оцінена якщо ZX (кількість пар АВ на атом) відоме. ТодіΩХ робить внесок енергії у вільну енергію Гібса, як показано в рівнянні (2).
Кожен атом має Z найближчих сусідів, і ми припускаємо, що ζз них – найближчі сусіди з верхньої площини, і ζ– найближчі сусіди з нижньої площини, тоді (Z - 2ζ) – найближчі сусіди в цій самій площині. С(z) – концентрація атомів сорту В в площині при z , і 1 - С(z) - концентрація атомів сорту А. Тоді загальна кількість пар АВ для вузлів площини zдорівнює кількості пар АВ з інших вузлів в цій самій площині, плюс кількість пар АВ між концентрацією атомів А типу в площині z і концентрацією В атомів в площині z+d і z-d, плюс кількість пар АВ між концентрацією атомів В сорту в площині z і концентрації А в площині z+d і z-d.
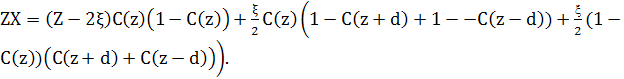 (5) (5)
Зведення подібних доданків
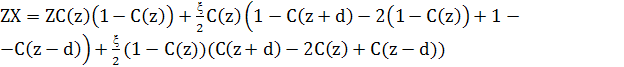 (6) (6)
Тоді
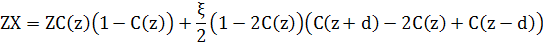
Перший доданок в рівнянні (7) тепер є кількістю зв’язків АВ в рівномірному рандомному сплаві. Другий доданок – поправка для кількості зв’язків АВ якщо структура не рівномірна.
3.5 Стрибкоподібний інтерфейс в 1D
Для ступінчатої зміни концентрації складу, при якій концентрації двох суміжних площин різні, але концентрації рівномірні вздовж цих площин, всі віддалені від інтерфейсу площини мають об’ємну вільну енергію. Позначаючи концентрації обох боків інтерфейсу C1
і C2
, кількість пар АВ площини біля інтерфейсу дорівнює:
Для поверхні 1 площини інтерфейсу
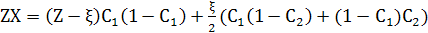 (8) (8)
Для поверхні 2 площини інтерфейсу
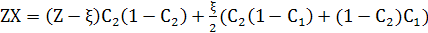 (9) (9)
Додаємо (8) та (9)
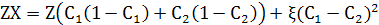 (10) (10)
Перший доданок – кількість пар АВ, якщо два шари біля інтерфейсу були об’ємними, другий – поправка відповідно до інтерфейсу. Подібний вираз був виведений Беккером який назвав другий доданок вільною енергією одиниці поверхні розділу фаз (міжфазовий натяг).
Для альтернативних шарів двох різних концентрацій, розділених стрибкоподібним інтерфейсам, як на рис.3.5.1, де інтерфейси на n/2 атомних відстанях один від одного, тоді λ=nd, повна енергія на атом одного періоду n атомів дорівнює
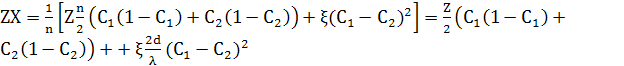 (11) (11)
Використовуючи С0
=(С1
+С2
)/2, і С1
–С2=
ΔC, це перетворюється в
 (12) (12)
Ця форма використовувалася Хіллертом. Він встановив, що вона була справедлива лише коли інтерфейси були добре розвинені на пізніших стадіях спінодального розпаду. Другий доданок схожий на «градієнт енергії» представлений Каном і Хілліардом.
3.6 Малоамплітудні синусоїдальні збурення в 1D
Вільна енергія малоамплітудного синусоїдального збурення може бути оцінена за рівнянням (7) для розподілу компонент структури у вигляді:
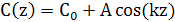 (13) (13)

Рис.3.5.1 Послідовність стрибкоподібних інтерфейсів
Підставляючи це в рівняння (7), отримаємо
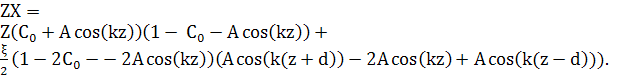 (14) (14)
Зводячи подібні доданки, і використовуючи
cos(k(z+d))+cos(k(z−d))=2cos(kz)cos(kd), рівняння (14) матиме вигляд:
 (15) (15)
Інтегрування по z, це перетворить в
 (16) (16)
Повна вільна енергія отримана підставлянням рівняння (16) в рівняння (2)
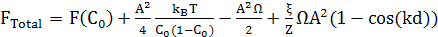 (17) (17)
Використовуючи наближення cos(kd)≈1−k2d2/2 це рівняння стає ідентичним до коефіцієнта градієнта енергії К, виведеного Каном і Хілліардом для синусоїдальних збурень в сталому розчині
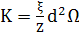 (18) (18)
РОЗДІЛ 4 ХІМІЧНІ ПОТЕНЦІАЛИ
4.1 Хімічні потенціали в 1D
Підставляючи рівняння (6) в рівняння (2), та виражаючи вільну енергію через кількість атомів кожному шарі, ми отримаємо для шару z
 (19) (19)
де W=Ω/Z, NA
(z)+NB
(z)=N(z) і 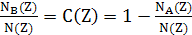
Відповідні хімічні потенціали
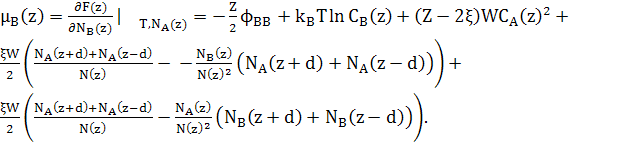 (20) (20)
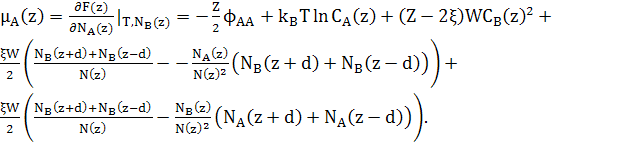 (21) (21)
При розрахунках хімічних потенціалів, необхідно включити зміну енергії сусідніх шарів відповідно до змін концентрації шару z.
Відмітимо, що
 (22) (22)
Хімічні потенціали можуть бути записані як
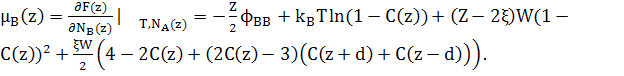 (23) (23)
 (24) (24)
4.2 Хімічні потенціали в 2D
Вільна енергія атомів квадратної решітки в 2D дорівнює
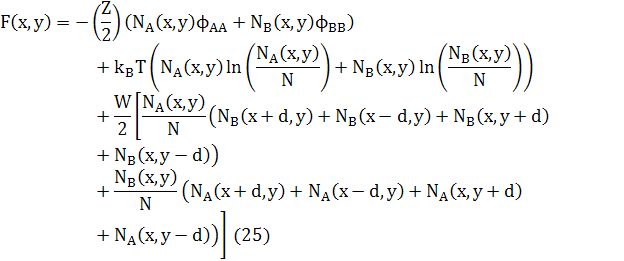
Відповідні хімічні потенціали дорівнюють
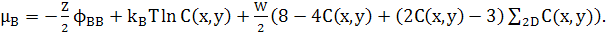 (26) (26)
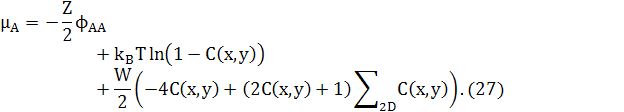
де
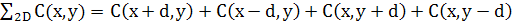 (28) (28)
є сумою концентрацій сусідніх атомів х,у.
4.3 Хімічні потенціали в 3D
Вільна енергія атомів простої кубічної решітки в дорівнює
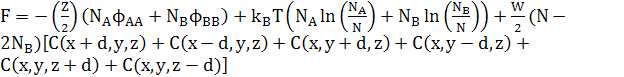 (29) (29)
Зауважимо, що останній доданок в обох рівняннях (25) і (29) може бути перетворений в доданок другої похідної, відніманням ZWNC(1−C). Це дасть стандарту форму для вільної енергії твердого розчину плюс доданок другої похідної для змін концентрацій. Відповідні хімічні потенціали в 3D
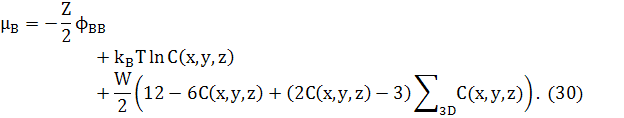
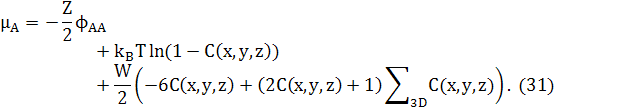
де
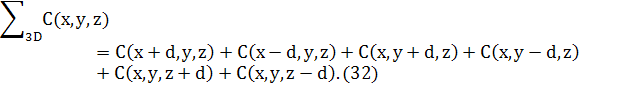
РОЗДІЛ 5
РІЗНИЦЕВІ РІВНЯННЯ ДЛЯ ДИФУЗІЇ
5.1 Дифузійні потоки, базовані на активностях
Потік атомів з вузла Ji
дорівнює частоті, помноженій на коефіцієнт Больцмана, що містить різницю між хімічним потенціалом чистого компонента (μj
*
) та дійсним значенням хімічного потенціалу j-го компонента (μj
).
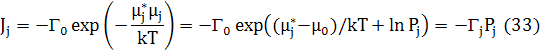
Pj=exp((μj−μj0)/kT) - активність j компонент. Г0
– звичайно береться як дебаївська частота, і відхилення від цієї частоти зосереджуються в ентропії та енергії активованого стану. μj
0
містить доданки ϕjj
в хімічних потенціалах, які включені в Γj
,
щоб давати енергію активації для дифузії. Для ідеального розчину Pj
=Cj
і отже рівняння (33) зменшує до нормальної концентрації потік що рухається. Результуюча потоків в вузол виражається різницею між повним потоком з вузлів до всіх її сусідів, і повним потоком в вузол від сусідів.
Як видно з рівняння(33), активність P збільшується зі зниженням температури. Це означає, що для постійної Γ, яку ми використаємо в наших розрахунках, потоки збільшуються з пониженням температури. Однак, беручи до уваги температурну залежність Γ, потоки зменшуються зі зниженням температури, так що результуюча енергія активації для дифузії буде меншою, ніж це було отримано з вимірів далеких від критичної точки.
Якщо система не перебуває в рівновазі, потоки двох видів, JA
і JB
будуть відрізнятися, оскільки хімічний потенціал для кожного з двох видів на кожній ділянці різний. Так як швидкість, з якою атом А міняється місцем з атомом B повинна бути такою ж, як швидкість зміни місця атома B з атомом А, то Γ є однаковою для обох типів.
Даркен розробив рівняння для дифузії, де потоки двох видів різні через введення вакансій в якості третьої компоненти. Дифузійні потоки залежать від активностей, та результуюча дифузія була отримана шляхом усереднення коефіцієнтів активності. Дифузія впливає на градієнти концентрацій, і тому процес дифузії описується стандартними диференціальними рівняннями другого порядку. Усереднення коефіцієнтів активності, як це було зроблено Даркеном, не призводить до правильної структури фаз, а усереднення потоків призводить. Даркен не розглянув можливість від’ємної ефективної дифузії, що може призвести до розпаду.
5.2 Різницеві рівняння для дифузії в 1D
Різницеві рівняння для дифузії в 1D будуть записані в звичайному вигляді, але з використанням усереднення потоків двох видів. Потік атомів А у напрямку, протилежному потоку атомів B, тому потоки просумовані зі збереженням знака потоку атомів А.

де D=d2
Γ/6, d- міжплощинний інтервал, і
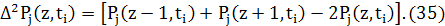
Тут в - є дифузія в одиницях довжина2
/час, в - міжплощинний інтервал, а Δt - збільшення часу між ітераціями. Хоча структури тут описані одномірною змінною, ця модель є тривимірною, з площинними змінними структури що описані однією змінною. Для того, щоб зробити результати 1D
співрозмірними з 3D результатами ми вирішили включити стрибки у площині в стрибок швидкості, і, отже, стрибок швидкості в будь якому одному напрямку дорівнює 1/6 від загальної швидкості стрибка.
Рівняння такого типу не можуть бути вирішені аналітично, але вони можуть бути легко обчислені чисельно.
5.3 Рівння в кінцевих різницях для дифузії в
2D
Як і для 1Dрізницеве рівняння для дифузії може бути записане в звичайній формі використовуючи усереднення двох потоків.
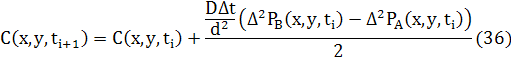
де
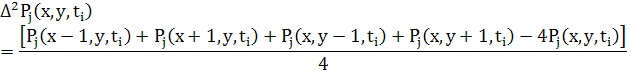
5.4 Різницеві рівняння для дифузії в 3D
Як і для 1D і 2D, різницеве рівняння для дифузії може бути записане в звичайній формі з використання усереднення двох потоків
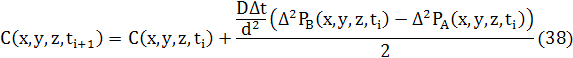
де
 (40) (40)
Коли параметр регулярного розчину, Ω = WZ, дорівнює нулю, ці диференціальні рівняння зводяться до стандартних рівнянь дифузії.
5.5 Безрозмірний час
Безрозмірний час, τ, дорівнює


Рис.3.Логарифм зростання амплітуди синусоїдального збурення в часі
Для окремих випадків, множення на d2
/D буде перетворювати τ в реальний час.
ВИСНОВОК
У даній роботі ми описали процес дифузій у сплавах. Застосували наші теоретичні знання при розгляді алгоритму Кеннета-Джексона та спробували практично його використати.
Найближчі сусідні взаємодії в роботі інтерпретувалися в нові рівняння, які описують дифузійні процеси під час фазових перетворень і впорядкувань. Дифузійні потоки виникають від хімічних рухливостей, що дають хімічні потенціали. Ці результати знаходяться у четвертій похідній рівняння в кінцевих різницях, що описує рух атомів під час фазових перетворень і впорядкувань. Результати цих рівнянь використовують для опису очікуваних змін в мікроструктурах, що часто зображалися тільки на малюнках. У метастабільному регіоні між спінодальною і фазовою межею існують досить великі флуктуації, що генерують фазові перетворення у процесах утворення ядра. У єдиному фазовому регіоні за межами двофазного поля є критичне зниження швидкості. Далеко від критичної ділянки, вирівнювання стають стандартними дифузійними рівняннями, де процес супроводжується тільки ентропією. Чисельні розрахунки описують тимчасові зміни в мікроструктурах протягом спінодального розпаду і впорядкування. Спостерігалося поширення нестійкості у спінодальних регіонах, і їх швидкості були визначені. Під час складніших перетворень між атомними сортами очікується зміна тільки певних деталей, а не істотної цифри їх поведінки.
Очікується, що метод може бути застосований до багатьох ситуацій, де є взаємодія між об’ємними елементами. Рівняння можуть описувати стрибкоподібну дифузію, також і впорядкування, і можуть вирішувати задачі Стефана для зросту розпаду.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Kenneth A. Jackson .Diffusion during phase separation Journal of NonCrystalline Solids 365. – 2010. – pg. 1109-1130.
2. Уэрт Ч., Томсон Р. Физика твердого тела Перевод с английского Пахамова А.С. – М.: Издательство «Мир», 1969. – 560 с.
3. Гусак А.М., В.Г. Гриценко, Т.В. Запорожець. Статистична фізика – основні положення та моделі. –Черкаси: ЧДУ,1998. –288с.
4. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – 793 с.
5. Сивухин Д.В. Общий курс физики. Том 2: Термодинамики и молекулярная физика. – М.: Наука, 1975. – 554 с.
6. Румер Ю.Б., Рывкин М.Ш. Термодинамика. Статистическая физика и Кинетика. – М.: Наука, 1977. – 553 с.
|