Муниципальное Образовательное Учреждение

Гимназия № 26

Реферат

Геометрия

Основные виды многогранников и их свойства

Выполнила:

Ученица 9-1 класса

Байсакова Ляззат

Преподаватель:

Сысоева Елена Алексеевна

Челябинск

План

Введение

Многогранная поверхность. Многогранник

Пирамида

Призма

Параллелепипед

Объем тела

Заключение

Список используемой литературы

Введение

До настоящего времени в курсе геометрии мы занимались планиметрией - изучали свойства плоских геометрических фигур, то есть фигур, полностью расположенных в плоскости. Но большинство окружающих нас предметов не являются полностью плоскими, они расположены в пространстве. Раздел геометрии, в котором изучают свойства фигур в пространстве, называется стереометрией ( от др. греч. στερεός, "стереос" - "твёрдый, пространственный" и μετρέω - "измеряю").

Основными фигурами в пространстве являются точка , прямая и плоскость . Наряду с данными простейшими фигурами в стереометрии рассматриваются геометрические тела и их поверхности. При изучении геометрических тел, пользуются изображениями на чертеже.

Рисунок 1 Рисунок 2

На рисунке 1 изображена пирамида, на рисунке 2 - куб. Данные геометрические тела называются многогранниками. Рассмотрим некоторые виды и свойства многогранников.

Многогранная поверхность. Многогранник

Многогранной поверхностью называют объединение конечного числа плоских многоугольников такое, что каждая сторона любого из многоугольников является в то же время стороной другого (но только одного) многоугольника, называемого смежным с первым многоугольником.

От любого из многоугольников, составляющих многогранную поверхность, можно дойти до любого другого, двигаясь по смежным многоугольникам.

Многоугольники, составляющие многогранную поверхность, называются ее гранями; стороны многоугольников называются ребрами, а вершины - вершинами многогранной поверхности.

На рис.1 изображены объединения многоугольников, удовлетворяющие указанным требованиям и являющиеся многогранными поверхностями. На рис.2 изображены фигуры, не являющиеся многогранными поверхностями.

Многогранная поверхность делит пространство на две части - внутреннюю область многогранной поверхности и внешнюю область. Из двух областей внешней будет та, в которой можно провести прямые, целиком принадлежащие области.

5 Объединение многогранной поверхности и ее внутренней области называют многогранником. При этом многогранную поверхность и ее внутреннюю область называют соответственно поверхностью и внутренней областью многогранника. Грани, ребра и вершины поверхности многогранника называют соответственно гранями, ребрами и вершинами многогранника.

Пирамида

Многогранник, одна из граней которого - произвольный многогранник, а остальные грани - треугольники, имеющие одну общую вершину, называется пирамидой.

Многоугольник называется основанием пирамиды, а остальные грани (треугольники) называются боковыми гранями пирамиды.

Различают треугольные, четырехугольные, пятиугольные и т.д. пирамиды в зависимости от вида многоугольника, лежащего в основании пирамиды.

Треугольную пирамиду также называют тетраэдром. На рис.1 изображена четырехугольная пирамида SABCD с основанием ABCD и боковыми гранями SAB, SBC, SCD, SAD.

Стороны граней пирамиды называются ребрами пирамиды. Ребра, принадлежащие основанию пирамиды, называют ребрами основания, а все остальные ребра - боковыми ребрами. Общая вершина всех треугольников (боковых граней) называется вершиной пирамиды (на рис.1 точка S - вершина пирамиды, отрезки SA, SB, SC, SD - боковые ребра, отрезки АВ, ВС, CD, AD - ребра основания).

Высотой пирамиды называется отрезок перпендикуляра, проведенного из вершины пирамиды S к плоскости основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра). На рис.1 SO - высота пирамиды.

Правильная пирамида. Пирамида называется правильной, если основанием пирамиды является правильный многоугольник, а ортогональная проекция вершины на плоскость основания совпадает с центром многоугольника, лежащего в основании пирамиды.

Все боковые ребра правильной пирамиды равны между собой; все боковые грани - равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой этой пирамиды. На рис.2 SN - апофема. Все апофемы правильной пирамиды равны между собой.

Призма

Многогранник, две грани которого - равные n -угольники, лежащие в параллельных плоскостях, а остальные n граней - параллелограммы, называетсяn -угольной призмой.

многогранник пирамида призма параллелепипед

Пару равных n -угольников называют основаниями призмы. Остальные грани призмы называют ее боковыми гранями, а их объединение - боковой поверхностью призмы. На рис.1 изображена пятиугольная призма.

Стороны граней призмы называют ребрами, а концы ребер - вершинами призмы. Ребра, не принадлежащие основанию призмы, называют боковыми ребрами.

Призму, боковые ребра которой перпендикулярны плоскостям оснований, называют прямой призмой. В противном случае призма называется наклонной.

Отрезок перпендикуляра к плоскостям оснований призмы, концы которого принадлежат этим плоскостям, называют высотой призмы.

Прямая призма, основанием которой является правильный многоугольник, называется правильной призмой.

Параллелепипед

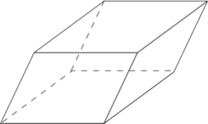
Параллелепипед - шестигранник, противоположные грани которого попарно параллельны. Параллелепипед имеет 8 вершин, 12 рёбер; его грани представляют собой попарно равные параллелограммы.

Параллелепипед называется прямым, если его боковые ребра перпендикулярны к плоскости основания (в этом случае 4 боковые грани - прямоугольники); прямоугольным, если этот параллелепипед прямой и основанием служит прямоугольник (следовательно, 6 граней - прямоугольники);

Параллелепипед , все грани которого квадраты, называется кубом.

Объём Параллелепипед равен произведению площади его основания на высоту.

Объем тела

Каждый многогранник имеет объем, который можно измерить с помощью выбранной единицы измерения объемов. За единицу измерения объемов принимают куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называется кубическим сантиметром . Аналогично определяется кубический метр и кубический миллиметр , и т.д.

В процессе измерения объемов при выбранной единице измерения объем тела выражается положительным числом, которое показывает, сколько единиц измерения объемов и ее частей укладывается в этом теле. Число, выражающее объем тела, зависит от выбора единицы измерения объемов. Поэтому единица измерения объемов указывается после этого числа.

Основные свойства объемов:

1. Равные тела имеют равные объемы.

2. Если тело составлено из нескольних тел, то его объем равен сумме объемов этих тел.

Для нахождения объемов тел в ряде случаев удобно пользоваться теоремой, получившей название принцип Кавальери .

Принцип Кавальери состоит в следующем: если при пересечении двух тел любой плоскостью, параллельной некоторой заданной плоскости, получаются сечения равной площади, то объёмы тел равны между собой.

Заключение

Итак, многогранники изучает раздел геометрии под названием стереометрия. Многогранники бывают разных видов (пирамида, призма и т.д.) и имеют разные свойства. Также, следует отметить, что многогранники в отличие от плоских фигур имеют объем и располагаются в пространстве.

Большинство окружающих нас предметов находятся в пространстве, и изучение многогранников помогает нам составить представление об окружающей нас реальности с точки зрения геометрии.

Список используемой литературы

1. Геометрия. Учебник для 7-9 классов.

2. Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина.

3. Википедия

4. Math.ru

5. Словарь

6. Fizmatik.ru