Введение
Транспорт – это система средств, предназначенных для организации и осуществления перевозки людей и грузов с определенными целями. Из приведенного определения следует, что проблема транспорта включает большой круг вопросов. Несмотря на то, что для решения этих вопросов могут быть использованы самые различные методы, есть все основания полагать, что в данном случае наиболее эффективными окажутся методы исследования операций. Транспортная сеть предоставляет исследователям систем широкое поле деятельности, где они могут продемонстрировать возможности методов исследования операций при изучении как отдельных аспектов указанной проблемы, так и проблем, возникающих при рассмотрении транспортной сети как подсистемы общей городской системы.
По мере повышения сложности транспортных сетей, которое сопровождается возрастанием роли проблем обеспечения их надежности, во многих странах растет и интерес к транспорту как к объекту исследования. Например, люди, занимающиеся проблемой перевозки грузов, не только прекрасно понимают необходимость создания хороших транзитных систем и связанные с этим выгоды (более эффективное использование энергии, оживление и восстановление деловой части города и т.п.), но и невозможность их реализации без специальных исследований. В настоящее время на многих промышленных предприятиях распределение потоков продукции анализируется с использованием системного подхода и при этом используются существующие зависимости между отдельными элементами системы распределения продукции. Результаты такого анализа часто оказываются совершенно поразительными с точки зрения громадной экономики, к которой они приводят.
При изучении проблем транспорта необходимо помнить, что он не представляет собой изолированную систему, а тесно связан с другими системами. В общем случае транспорт можно рассматривать как средство достижения некоторой цели, которая формируются в рамках другой системы. Например, перевозка грузов внутри предприятия и между предприятиями является лишь частью всей системы распределения продукции и в то же время тесно взаимодействует с такими подсистемами, как управление производственными запасами, обработка заказов, производство, обработка информации и общее управление предприятием. Если обратиться к городской транспортной системе, включающей сложную сеть улиц и магистралей, системы транзитной перевозки грузов, скоростного проезда автомобилей и т. Д., то недостаточно отметить, что эта система выполняет функции обеспечения других городских систем (экономической, социальной, политической и культурной). Необходимо также со все определенностью подчеркнуть, что транспортная подсистема является неотъемлемой органической частью общегородской системы. При этом важно иметь ввиду, что планирование работы транспорта должно обязательно включать исчерпывающий анализ взаимодействия транспортной подсистемы города с другими его подсистемами.
Разработаны методы и модели прогнозирования грузовых и пассажирских перевозок на различных видах транспорта. Минимальным объектом прогнозирования является направление перевозок. Разработанные методы и модели позволяют прогнозировать перевозки в случае усеченных наблюдений, отсутствия статистических данных по прогнозируемому показателю, учитывать в будущем действие факторов, которые не действовали ранее, делать оценки степени неудовлетворенности спроса на перевозки.
Цель работы – изучить моделирование прогнозирования потребностей как средство повышения эффективности работы транспортных сетей.
транспорт модель прогнозирование потребность
1. Теоретические основы моделирования прогнозирования потребностей как средства повышения эффективности работы транспортных сетей
1.1 Математическое моделирование
Математической моделью операции называется формальные соотношения, устанавливающие связь принятого критерия эффективности с действующими факторами операции. Чтобы построить математическую модель, необходимо оценить количественно проявления рассматриваемых факторов и указать группы рассматриваемых параметров, формально представляющие эти факторы.
Математические модели могут иметь вид формул, систем уравнений или неравенств, а также таблиц, числовых последовательностей, геометрических образов, отражающих зависимость между критерием эффективности операции и теми параметрами, которые представляют учтенные действующие факторы [8].
При построении модели (как математической так и физической) можно выделить следующие основные этапы.
1. Постановка цели моделирования. определение набора четко сформулированных согласованных и реализуемых целей - существенное условие успешного моделирования.
2. Анализ реальной системы, процесса или явления с целью формирования модели. Для анализа система разбивается на составляющие части (реальные и воображаемые), которые ограничиваются от окружающих факторов.
При этом ограниченная система должна обладать всеми свойствами, присущими ей в реальной действительности. Кроме того, система, составленная из совокупности составляющих ее частей, должна представлять единое целое.
3. Структуризация и построение модели. При физическом моделировании это может быть макет моделируемой системы. При имитационном моделировании это будет моделирующий алгоритм. Аналитическая модель будет записана в виде математических соотношений.
4. Верификация модели состоит в проведении исследования с помощью отладочных и проверочных тестов, предназначенных для выявления ошибок в структуре модели. Верификация может закончиться неудачно даже и в случаях правильной ее структуризации. В этом случае говорят об ошибке 1-го рода (отбрасывается приемлемый вариант). Возможны ошибки 2-го рода, когда принимается ошибочный вариант. Любые ошибки, выявленные на этом этапе верификации приводят к возвращению на этап структуризации.
5. Оценка пригодности модели проводится сравнением откликов проверенной модели с соответствующими откликами или изменениями, снятыми с реальной системы. Это значит, что экспериментирование может проводится как с моделью, так и с моделируемой системой. Если реальная система недоступна для экспериментирования, то обращаются к неформальным приемам, используют известные характеристики. Расхождения откликов модели и реальной системы свидетельствуют об ошибках на стадии анализа, т.е. необходимо вернуться к просмотру результатов 2-го этапа [7].
6. Планирование эксперимента. На проверенной модели возможна постановка экспериментов для получения новой информации о моделируемой системе.
7. Обработка результатов эксперимента, формирование на основе выводов и оформление соответствующей документации на прием модели пользователем.
Рассмотрим принципы построения математических моделей. Основными объектами исследования операций являются аналитические математические модели (в дальнейшем просто математические модели). При этом необходимо отметить, что построение математической модели изучаемого процесса или явления не означает еще, что построена задача исследования операций. С помощью одной модели можно исследовать, изучать разные операции. Только постановка и формализация цели операции, в результате которой формулируется оптимизационная задача, однозначно определяет задачу исследования операций [3].
Построение математической модели - это искусство, поэтому нет строгого алгоритма, который был бы пригоден для построения любой модели. Можно лишь выделить ключевые моменты этого построения [13].
1. Составление математической модели начинается с выбора переменных, совокупность числовых значений которых однозначно определяет один из вариантов процесса. Эти переменные называются параметрами задачи или элементами решения. Следует иметь в виду, что иной раз от удачного выбора этих переменных зависит простота модели и, следовательно, удобство дальнейшего анализа.
2. После выбора переменных составляются ограничения, которым должны удовлетворять эти переменные. При этом нужно следить, чтобы в модель были включены все ограничительные условия, и в то же время, чтобы не было ни одного лишнего или записанного в более жесткой, чем требуется условиями задачи, форме.
3. Составляется целевая функция, которая в математической форме, отражает критерий эффективности выбора лучшего варианта, другими словами, ставится цель операции на модели, полученной во втором пункте.
Классификация математических моделей может проводиться с различных точек зрения. В зависимости от этого получаются различные типы моделей.
1. Если в основе классификации лежат соотношения, которые выражают зависимости между состояниями системы и параметрами системы, то выделяют:
а) детерминированные модели - состояние системы в заданный момент времени однозначно определяется через параметры системы.
b) стохастические модели - однозначно определяются лишь распределения вероятностей для состояний системы при заданных распределениях вероятностей для начальных условий.
2. Если параметры задачи принимают дискретные значения (причем дискретность может быть любой природы: от целочисленного значения до произвольного набора значений), то говорят о дискретной модели. Непрерывная модель в случае непрерывных значений параметров задачи.
3. Одноэкстремальной моделью называется математическая модель задачи, имеющей один критерий эффективности. Если задача исследования операций имеет несколько критериев эффективности, то соответствующая модель называется многоэкстремальной моделью.
4. Задачей линейного программирования называется математическая модель, в которой функция и ограничения выражаются линейными функциональными зависимостями. Если среди функциональных зависимостей есть хотя бы одна нелинейная, то математическая модель будет задачей нелинейного программирования. Если функциональные зависимости - выпуклые функции, то имеет место задача выпуклого программирования. Если целевая функция является квадратичной функцией, а ограничения - линейные функции то получается задача квадратичного программирования [11].
1.2 Прогнозирование
Можно выделить два вида прогнозируемых характеристик системы, зависящих от времени: переменные состояния и переменные интенсивности. Переменная состояния
определяется периодически, и ее значение в течение небольшого интервала временизависит от времени, прошедшего с момента начала наблюдения. Переменная интенсивности
также определяется периодически, но ее значение пропорционально времени, прошедшему с момента предыдущего наблюдения. Такие характеристики системы, как температура, скорость, число подписчиков па журнал или цена, являются примерами переменных состояния. В качестве примера переменной интенсивности можно привести количество выпавших осадков, количество проданных экземпляров или спрос. Если переменная состояния характеризует количество, то переменная интенсивности - скорость его изменения [2].
Процессы прогнозирования переменных состояния и интенсивности отличаются друг от друга следующими особенностями:
· если измерения характеристик системы проводятся через разные интервалы времени, то величину интервала необходимо учитывать при оценке переменных интенсивности, в то время как при оценке переменных состояния эта величина не имеет значения;
· так как прогнозы обычно осуществляются для нескольких последовательных интервалов времени в пределах некоторого времени упреждения, по истечении которого становятся важными результаты реализации принятых решений, то правильный прогноз переменной состояния должен определять ее значение в конце времени упреждения, а прогноз переменной интенсивности должен представлять собой сумму прогнозов па протяжении времени упреждения;
· функция распределения во времени вероятностей ошибок прогноза для переменной состояния должна соответствовать функции распределения вероятностей ошибок в исходных данных, тог да как для переменной интенсивности закон распределения вероятностей ошибок прогноза во времени стремится к нормальному при любом законе распределения вероятностей ошибок в исходных данных, поскольку эти ошибки представляют собой сумму ошибок прогноза в отдельные интервалы времени.
Временные интервалы пересмотра и уточнения прогноза
Величина промежутков времени между измерениями входных переменных системы с целью проверки и уточнения ранее сделанных прогнозов о выходных переменных зависит главным образом от длительности времени упреждения и наибольшей частоты циклических изменений в системе, которые должна отражать модель. Поэтому временные интервалы пересмотров прогнозов могут из меняться в широких пределах и измеряются, например, как часа ми, так и годами. Однако эти интервалы должны быть достаточно велики, чтобы обеспечивалась вероятность осуществления ожидаемых изменений системы.
В течение времени упреждения прогноз чаще всего проверяется один-два раза, но иногда возникает необходимость увеличить количество проверок до десяти. Так, прогнозируемые сроки возобновления лесозаготовок па участке леса с периодом восстановления 80 лет могут уточняться один раз в десятилетие, а изменение потребления электроэнергии в данной местности в зависимости от погодных условий можно наблюдать каждый час.
Когда имеют место какие-то периодические процессы, как, например, при месячных изменениях температуры или изменениях объема корреспонденции, получаемой почтовым отделением в течение недели, частота наблюдений должна быть по крайней мере вдвое больше частоты изучаемого процесса. Очевидно, что наблюдения с интервалами в один месяц не будут способствовать правильной организации работы почты по понедельникам в отличие от ее работы по средам, а наблюдения с интервалами в сутки не дадут возможности обнаружить различие в интенсивностях работы первой и второй смен.
Если случайная ошибка при определении входных переменных велика по сравнению с измеряемой величиной, интервал уточнения прогноза для переменной интенсивности целесообразно увеличить, усредняя таким образом случайную ошибку. Однако для переменной состояния в аналогичном случае интервал уточнения прогноза лучше уменьшить, что позволяет для выделения полезно го сигнала использовать соответствующие методы фильтрации [1].
1.3 Прогнозирование потребностей в перевозках людей и грузов
Прогнозирование потребностей в каких-либо перевозках должно быть основано на исследовании, включающем анализ следующих восьми элементов транспортной системы:
пункт отправления
пункт назначения
объем перевозок
вид транспорта
транспортная линия
объект перевозки
расписание перевозок
характеристика времени осуществления перевозок
Объектами перевозок могут быть люди и грузы (табл.1).
Табл. 1.
Элементы транспортной системы
|
Характер информации, используемой при анализе |
| Государственный сектор |
Частный сектор |
| Пункт отправления (откуда) |
Место жительства |
Оптовые базы или магазины розничной торговли |
| Пункт назначения (куда) |
Общественные предприятия, биржи труда, торговые центры, центры развлечений и отдыха, правительственные учреждения |
Заводы, склады, центры распределения продукции, сырьевые базы |
| Транспортная линия (каким путем) |
Скоростные магистрали, дороги и улицы, транзитные магистрали, железные дороги |
Магистрали, связывающие штаты; внутренние дороги штатов; воздушные, речные и морские линии; железные дороги |
| Объект перевозки (кто, что) |
Рабочие, служащие и школьники; покупатели; престарелые и инвалиды |
Грузы всевозможных видов и габаритов |
| Вид транспорта (на чем) |
Автомобиль, автобус, велосипед |
Собственный или арендованный грузовой транспорт; самолет, корабль, поезд |
| Объем перевозок (сколько) |
Средний ежедневный объем перевозок по воздушным линиям |
Вес или друга количественная величина характеристика груза; полностью или не полностью загруженное транспортное средство (железнодорожная платформа, автомобиль и т.д.) |
| Расписание перевозок (когда) |
Расписание работы рабочих и служащих, характерное время закупок для домохозяек, школьное расписание, время наступления отдельных событий |
Режим работы транспортного средства, определяемы диспетчером или заранее составленным расписанием |
| Характеристика времени осуществления перевозок |
Часы пик, сезон или период межсезонья |
Период отправления грузов, период межсезонья |
В производственной сфере основу исследования составляют потребности в перевозках, характеризуемые грузопотоками, в то время как в непроизводственной – потребности в перевозках пассажиров, характеризуемые пассажиропотоками. Прогноз может разрабатываться как для периода времени, равного всего лишь одному дню (например, при составлении производственных расписаний), так и для периода времени до 20 лет (например, при проектировании скоростной системы транзитных перевозок). Выбор наиболее желательного варианта решения при анализе транспортных систем осуществляется с учетом ожидаемого поведения больших групп людей, имеющих общие интересы.
В общем виде характерные особенности организации перевозок людей и грузов состоят в следующем. Рост потребностей в перевозках грузов стимулируется развитием промышленного производства, которое определяется совокупной потребностью общества в товарах. Поэтому выбором пункта погрузки, способа перевозки, маршрута и составлением расписания перевозок занимается соответствующая транспортная организация, связанная с промышленностью. С другой стороны, перевозки общественным транспортом обуславливаются потребностью в перемещении населения из одной точки города в другую, причем выбор одного варианта передвижения из нескольких возможных осуществляется самим пассажиром. Органы городского управления, по существу, не оказывают влияния на работу транспортной сети, если не считать, например, таких действий, как запреты на движение определенных транспортных средств в некоторых районах города. В то же время эти органы неявным образом контролируют проектирование и составление расписания работы общественных транспортных систем, а также формируют принципы распределения земельных участков для развития транспорта. Хотя решение обоих указанных вопросов может оказать существенное влияние на организацию перевозок, важно подчеркнуть, что органы городского управления не ставят целью непосредственно контролировать, где, когда и как перемещается пассажир. Потребность в таком перемещении носит случайный характер, что существенным образом затрудняет прогнозирование развития городских транспортных сетей.
Мало того, что потребности в перевозках носят стохастический характер, для отдельных моментов времени их просто трудно определить, так как для этого необходимо было бы провести исследование перемещений больших групп населения. Целесообразность получения такой информации должна подвергаться всесторонней оценке, так как затраты на ее получение могут достигать сотен тысяч долларов. Кроме того, в столь обширных исследованиях качество информации может весьма невысоким из-за отсутствия непосредственного контроля за сборщиками информации [9].
При прогнозировании потребностей в перевозках часто используется метод множественной регрессии. Так, на основе уравнения множественной регрессии, учитывающего такие показатели, как валовый национальный продукт, национальный научно-технический уровень, объемы грузопотоков, коэффициент промышленного роста и ряд других, были предсказаны объемы воздушных грузовых перевозок и, как следствие, необходимые для этого объемы производства транспортных самолетов. Коэффициенты регрессии в этом случае определялись на основе исходных данных стандартным методом наименьших квадратов. При исследовании транспортных перевозок чикагского региона применение регрессии, учитывающей такие показатели, как количество владельцев автомобилей и плотность населения, позволило довольно точно оценить количество поездок, приходящихся на одну семью. В этом исследовании использовались методы нелинейной интерполяции, в частности полиномы и функции Гаусса для интерполяции нелинейных временных зависимостей числа автобусных и автомобильных поездок, приходящихся на одного жителя.
Более сложным и потому реже используемым методом прогнозирования является факторный анализ. Этот метод состоит в комбинировании большого числа входных переменных в существенно меньшее число групп, включающих сильно коррелирующие переменные. Иногда данный метод используется перед применением регрессионного анализа, благодаря чему последний становится более эффективным.
При прогнозировании потребностей в перевозках людей и грузов возможно также применение имитационных моделей, реализованных на ЭВМ. Обсуждение некоторых наиболее значительных имитационных моделей будет дано при рассмотрении одного из следующих этапов общей схемы исследования. Основное назначение данной модели состоит в предсказании требований к оборудованию летательных аппаратов (прогноз выполняется на срок до 10 лет путем обработки данных о функционировании авиалиний США за предыдущий десятилетний период). Хотя первоначально эта модель предназначалась для предсказания конъюнктуры рынка, тем не менее оказалось возможным прогнозировать тенденции изменения характеристик воздушного транспорта (например, необходимость в новых системах авиалиний, рост объемов перевозок и их стоимости, развитие средств обслуживания пассажиров, улучшение перевозки багажа и грузов, технического обслуживания самолетов, а также общей стоимости системы воздушных сообщений). Метод имитационного моделирования оказался наиболее подходящим для решения задачи, поставленной фирмой Lockheedи имевшей целью формирование требований к развитию большого числа различных авиалиний США.
Для руководителей какой-то определенной авиакомпании вполне естественным является желание предсказать те требования, которым должна отвечать эта авиакомпания, чтобы в будущем выстоять в конкурентной борьбе (возможно, при таком анализе некоторые конкуренты будут выделены особо). С помощью упомянутой модели можно решить эту задачу практически для любой авиакомпании США. Решение осуществляется путем сведения некоторого числа частных требований, составленных сточки зрения отдельной авиакомпании в общую систему требований с последующей конкретизацией оценок, полученных в такой укрупненной модели. Другими словами, данный подход позволяет получать детальный обзор взаимосвязанных характеристик отдельных авиакомпаний. Подобные возможности рассматриваемой модели являются уникальными, и, видимо, имеет смысл попытаться разобрать аналогичные модели и для других видов транспорта, таких, как грузовой автомобильный, железнодорожный и морской транспорт.
Рассмотрим теперь более подробно методы прогнозирования применительно к городскому транспорту. Используемые в данном случае так называемые модели распределения поездок включают в себя модели развития, конфликтующих возможностей, равных возможностей, предпочтений и притяжения. Эти модели построены на различных теоретических предположениях относительно того, каким образом локализация пунктов отправления и назначения, объем перевозок и другие элементы транспортной системы взаимосвязаны с остальными выходными переменными. В качестве последних выступают такие параметры, как планируемый рост тарифов, коэффициенты реальной занятости, расположение торговых зон или зон развлечений и отдыха, пространственное и временное разделение различных городских территорий, факторы привлекательности тех или иных районов города.
Локализация пунктов отправления и назначения может быть определена после разбиения всей городской территории на зоны. Объем перевозок обычно выражается числом поездок, приходящихся либо на одного человека, либо на одно транспортное средство. Общепринятой классификацией поездок в зависимости от пункта назначения является следующая: поездки домой, на работу, в школу, в места отдыха, развлечений, проведения общественных мероприятий, а также регулярные и нерегулярные поездки, связанные с покупкой товаров.
Модели развития позволяют определить будущее распределение поездок между различными парами выделенных зон на основе исходных данных о количестве выездов и въездов для отдельных зон и количестве поездок между различными парами зон. Прогнозируемые значения выходных переменных получаются из известных (на момент составления прогноза) значений с помощью коэффициента развития, который представляет собой оценку ожидаемых изменений в плотности населения и в степени использования территорий рассматриваемых зон. На основе модели развития разработано несколько методов анализа городского транспорта, среди них – методы постоянного коэффициента развития, среднего коэффициента развития, здравого смысла и так называемый детройтский метод. Однако наиболее тщательно разработанным и поэтому широко распространенным является метод Фратера.
Основное предположение, используемое в методе Фратера, состоит в том, что количество поездок из i
-той зоны в j
-ю для некоторого будущего момента времени пропорционально исходному числу всех выездок из i
-той зоны, умноженному на коэффициент развития j
-той зоны. Общее соотношение, используемое в методе Фратера, имеет следующий вид:
 
В этом и следующем выражениях приняты такие обозначения:  - прогнозируемое количество поездок между i
-той и j
-той зонами, обуславливаемое развитием i
-той зоны; - прогнозируемое количество поездок между i
-той и j
-той зонами, обуславливаемое развитием i
-той зоны;  - прогнозируемое количество поездок между i
-той и j
-той зонами, обуславливаемое развитием j
-той зоны (величину - прогнозируемое количество поездок между i
-той и j
-той зонами, обуславливаемое развитием j
-той зоны (величину  можно получить из формулы для можно получить из формулы для  , если в правой части этой формулы индексы i
и j
поменять местами); , если в правой части этой формулы индексы i
и j
поменять местами);  - исходное число всех поездок между i
-той и j
-той зонами; - исходное число всех поездок между i
-той и j
-той зонами;  - коэффициент развития для зоны с номером х
, где х
принимает множество значений, соответствующих всем рассматриваемым зонам. - коэффициент развития для зоны с номером х
, где х
принимает множество значений, соответствующих всем рассматриваемым зонам.
Если через  обозначить прогнозируемое количество всех поездок между i-
той и j-
той зонами, то имеем обозначить прогнозируемое количество всех поездок между i-
той и j-
той зонами, то имеем
 . .
Поскольку величины, определяемые из двух приведенных выше соотношений, как правило, не удовлетворяют условию
 , ,
то для его выполнения необходимо использовать метод исследовательных приближений. Модель основана на предположении о том, что число людей, выезжающих из некоторого пункта, прямо пропорционально числу «возможностей», имеющихся на маршруте, и обратно пропорционально числу «реализованных возможностей». В качестве упомянутых «возможностей» можно рассматривать, например, места, в которых может быть предложена работа (для таких людей, ищущих работу), городские и загородные парки (для людей, совершающих поездку с целью отдыха или развлечений), наконец, торговые центры (для людей, выезжающих за покупками).
Модель конфликтующих возможностей математически может быть представлена с помощью выражения
 , ,
где  - количество поездок из i-
той зоны в j-
тую; - количество поездок из i-
той зоны в j-
тую;  - общее количество поездок, начинающихся в i-
той зоне; D– количество имеющихся (или отсутствующих) целей на маршрутах ведущих в j-
тую зону; - общее количество поездок, начинающихся в i-
той зоне; D– количество имеющихся (или отсутствующих) целей на маршрутах ведущих в j-
тую зону; 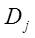 - количество поездок, заканчивающихся в j-
той зоне; L– некоторая оценка вероятности того, что в случайно выбранном пункте назначения может быть достигнута цель отдельной поездки (Lпредставляет собой величину, которую необходимо определить на основе исходных данных; она характеризует степень убывания величины - количество поездок, заканчивающихся в j-
той зоне; L– некоторая оценка вероятности того, что в случайно выбранном пункте назначения может быть достигнута цель отдельной поездки (Lпредставляет собой величину, которую необходимо определить на основе исходных данных; она характеризует степень убывания величины  с увеличением числа целей и длины маршрута), е
– основание натурального логарифма. с увеличением числа целей и длины маршрута), е
– основание натурального логарифма.
Основой модели равных возможностей является распределение поездок, характеризуемых одинаковыми временем, расстоянием и стоимостью, по группам однотипных поездок, т.е. поездок с одинаковыми целями. Выделенные таким способом поездки равновероятны в пределах каждой группы.
Модель предпочтения представляет собой модель распределения поездок несколько иного типа, чем рассмотренные выше. Основное предположение, используемое при построении этой модели, состоит в том, что для каждого пункта отправления можно оценить предпочтительность всех возможных пунктов назначения, а для каждого пункта назначения можно оценить предпочтительность всех возможных пунктов отправления. В данной модели сочетание двух определенных пунктов отправления и назначения может быть оптимальным только для одного из пунктов, причем такое сочетание должно удовлетворять некоторым условиям устойчивости.
В модели притяжения, являющейся наиболее широко распространенной моделью распределения поездок, делается оценка количества поездок из i-
той зоны в зонуj-
ю на основе предположения о том, что рассматриваемая величина прямо пропорциональна некоторому коэффициенту «привлекательности» j-
той зоны и обратно пропорциональна, характеризирующему удаленность i-
той и j-
той зон друг от друга ( в единицах времени или расстояния).
Модель притяжения можно представить математически с помощью следующего выражения:
 , ,
где  - количество поездок из i
-ой зоны, совершаемых благодаря «привлекательности» j-
той зоны; - количество поездок из i
-ой зоны, совершаемых благодаря «привлекательности» j-
той зоны;  - общее количество поездок, начинающихся в i-
той зоне; - общее количество поездок, начинающихся в i-
той зоне;  - общее количество поездок, «привлеченных» j-
той зоной; - общее количество поездок, «привлеченных» j-
той зоной;  - эмпирически определяемый коэффициент удаленности ( - эмпирически определяемый коэффициент удаленности ( представляется в виде представляется в виде  или, точнее, или, точнее, 
, где dij— расстояние между i-й и j-й зонами, abt
j— некоторый показатель степени, зависящий от величины d{
jи обычно определяемый с помощью линейной регрессии); Kij— коэффициент, с помощью которого учитываются эффекты социального и экономического характера (величина К13
определяется по исходным данным о распределении поездок). Таким образом, в модели притяжения должны быть предварительно определены (по исходным данным) два параметра —F
и К.
Успех этой модели объясняется, главным образом, ее просто той, а также тем, что на агрегированном уровне рассмотрения имеется небольшое число параметров, которые необходимо определять предварительно с требуемой для прогноза степенью точности. Однако вопрос о возможности использования модели притяжения при более низком уровне агрегации вызвал ожив ленную дискуссию.
Модели притяжения, конфликтующих и равных возможностей, а также метод Фратера были подвергнуты сравнительному анализу путем их одновременного использования для изучения распределения поездок в г. Вашингтоне в 1948 и 1955 гг. Оказалось, что прогноз на основе модели притяжения является не сколько более точным и полным, чем на основе модели конфликтующих возможностей. Однако исключение из первой модели коэффициента ,
учитывающего социально-экономические факторы, может привести к обратному результату. Это обстоятельство указывает, в частности, на то, что степень точности предварительного определения параметра ,
учитывающего социально-экономические факторы, может привести к обратному результату. Это обстоятельство указывает, в частности, на то, что степень точности предварительного определения параметра  влияет на точность прогноза, составленного с использованием этой модели. С точки зрения надежности и полезности модели притяжения и конфликтующих возможностей оказались примерно равноценными, хотя для последней, по-видимому, несколько проще проводить предварительное определение соответствующих параметров. В отличие от этих моделей эффективность метода Фратера проявилась лишь при анализе стабильных ситуаций. Если же за период прогноза происходили какие-либо изменения, например в характере использования городской территории, то метод Фратера оказывался совершенно непригодным. Что касается модели равных возможностей, то она по-настоящему не смогла конкурировать с тремя другими моделями, поскольку в рамках рассмотренной зональной структуры г. Вашингтона для нее невозможно было провести определение соответствующих параметров. Кроме того, значительное число небольших зон крайне затруднило установление оптимальных тарифов на проезд, что является серьезным недостатком модели равных возможностей, так как во многих исследованиях, связанных с использованием городской территории, необходимо рассматривать как раз весьма детальное разбиение на зоны.
влияет на точность прогноза, составленного с использованием этой модели. С точки зрения надежности и полезности модели притяжения и конфликтующих возможностей оказались примерно равноценными, хотя для последней, по-видимому, несколько проще проводить предварительное определение соответствующих параметров. В отличие от этих моделей эффективность метода Фратера проявилась лишь при анализе стабильных ситуаций. Если же за период прогноза происходили какие-либо изменения, например в характере использования городской территории, то метод Фратера оказывался совершенно непригодным. Что касается модели равных возможностей, то она по-настоящему не смогла конкурировать с тремя другими моделями, поскольку в рамках рассмотренной зональной структуры г. Вашингтона для нее невозможно было провести определение соответствующих параметров. Кроме того, значительное число небольших зон крайне затруднило установление оптимальных тарифов на проезд, что является серьезным недостатком модели равных возможностей, так как во многих исследованиях, связанных с использованием городской территории, необходимо рассматривать как раз весьма детальное разбиение на зоны.
Самое последнее достижение в области моделей распределения поездок представляет модификация модели притяжения, названная моделью максимизации энтропии [12].
1.4 Анализ распределения возможных видов транспортных средств
Данный этап исследования включает тщательный анализ состояния существующей транспортной сети. Основной целью такого анализа является сопоставление прогнозируемых потребностей в транспортном обслуживании с имеющимися в момент составления прогноза возможностями. По существу, на этом этапе решается вопрос, позволят ли изменения в организации сети и увеличение ее пропускной способности удовлетворить будущие потребности в перевозках людей и грузов.
Необходимо сразу же обратить внимание на то, что рассмотрение названных вопросов применительно к государственному и частному секторам проводится по-разному. Поскольку в част ном секторе выбором транспортных средств и маршрутов движения, а также выбором поставщиков занимается какое-то пред приятие, то распределение транспортных средств с целью удовлетворения будущих потребностей осуществляется в соответствии с решениями руководства данного предприятия. В государственном же секторе транспорта основные элементы транспортной системы связаны со случайными факторами, а удовлетворение потребностей является заботой самих людей, нуждающихся в транспортном обслуживании. Поэтому в государственном секторе распределение транспортных средств с целью удовлетворения будущих потребностей представляет собой проблему, которая может быть решена лишь методами прогнозирования.
С помощью методов исследования операций был разработан ряд моделей для обеспечения возможности наиболее эффективного распределения транспортных средств (в частном секторе) или для получения наиболее правильного варианта при прогнозировании распределения транспортных средств (в государственном секторе).
Применительно к частному сектору разработаны модели, пред назначенные для исследования вопросов управления запасами, составления производственных расписаний, выбора транспортных средств, составления расписаний их движения, локализации средств транспортного обслуживания и т. п., т. е. для рассмотрения практически всего комплекса вопросов, связанных с организацией системы распределения транспортных средств. Многие из этих вопросов рассматриваются в других главах данного тома. Важно отметить, что при применении упомянутых моделей необходимо делать определение предположения относительно всей транспортной системы, а решение, полученное па основе любой из моделей, является лишь частично оптимальным, так как позволяет оптимизировать только часть всей системы. Чтобы обойти эти трудности, были разработаны имитационные модели большой размерности, реализованные па ЭВМ, в которых удалось объединить все элементы системы распределения транспортных средств. Такие модели рассматриваются в одном из следующих разделов, который посвящен этапу «Оценка...» общей схемы исследования.
Особой областью приложения методов исследования операций в частном секторе транспорта является выбор конкретных транспортных средств. Модели выбора транспортных средств представляют собой описание некоторой процедуры выработки решения па основе подсчета полных затрат на реализацию проекта. В рамках этих моделей проводится сопоставление затрат с уровнем обслуживания, которое обеспечивается выбираемым транс портным средством. Затраты включают расходы па приобретение транспортного средства и эксплуатационные расходы. Уровень обслуживания характеризуется временем осуществления перевозки, грузоподъемностью и надежностью функционирования соответствующего транспортного средства [6].
На транспорте часто бывает очень сложно определить разницу в затратах, связанных с обеспечением различных уровней обслуживания. В качестве иллюстрации этого положения приведем следующий пример. Меньшее время перевозки грузов, например в случае их доставки по воздуху, а не по железной дороге, позволяет снизить уровень запасов при сохранении уровня надежности (под надежностью в данном случае можно понимать выраженное в процентах количество случаев, в которых заявка потреби теля не удовлетворяется за счет имеющихся запасов; при этом предполагается, что в рассматриваемой системе потребности формируются случайным образом). Выигрыш, связанный с более низким уровнем производственных запасов, определяется уменьшением потерь, обусловленных старением продукции и возможными перебоями в обслуживании. В таком случае конкретные значения потерь и сопоставление осуществляемых затрат часто определяются все же но на основе модельных представлений, а из соображений здравого смысла.
Как уже отмечалось, в государственном секторе транспорта модели распределения средств, удовлетворяющих будущие потребности в перевозках, являются, по существу, моделями для раз работки прогнозов. Некоторые из таких моделей, называемые транспортными моделями распределения маршрутов, позволяют определить, как в обеспечении перевозок могут использоваться существующие и проектируемые транспортные сети. Среди других моделей следует выделить модели кратчайшего пути (основанные на алгоритмах построения дерева решений и алгоритмах так называемого типа «все или ничего») и модели сетей минимальной стоимости (основанные на алгоритмах типа «беспорядок»). Другие модели распределения, известные под названием моделей разделения транспортных средств, предназначены для определения доли пассажиров, выбирающих то или иное конкретное транспортное средство.
При решении вопросов распределения транспортных средств используются два различных принципа. Первый принцип, который можно назвать «оптимизацией для потребителя», основан на предположении о том, что в системе возможно установление некоторого равновесного состояния. Последнее характеризуется том, что ни одно транспортное средство не имеет возможности сократить время пробега за счет изменения маршрута, так как маршрут выбран исходя из требования минимизации пути. Второй принцип, который можно назвать «оптимизацией для системы», основан на минимизации среднего времени пробега.
Использование алгоритмов определения наивыгоднейшего маршрута (или кратчайшего пути) предполагает, что люди, совершающие поездку, выбирают наивыгоднейший, с их точки зрения, или близкий к нему маршрут («оптимизация для потребителя»).
Алгоритмы построения дерева решения позволяют решать проблему поиска оптимальных маршрутов путем формирования дерева транспортных линий, соединяющих определенный пункт отправления с различными возможными пунктами назначения, причем одновременно может быть учтена и стоимость проезда по соответствующим маршрутам.
Проблема, относящаяся к определению стоимости проезда по транспортным линиям, состоит в том, что практически она должна учитывать степень интенсивности транспортного потока. Например, время проезда по главным транспортным линиям существенно увеличивается в часы пик, и тогда более приемлемым становится использование побочных транспортных линий. Проблема определения стоимости проезда в зависимости от степени интенсивности транспортного потока может быть решена с использованием метода ограниченной пропускной способности. Метод представляет собой повторяющийся (итеративный) процесс, в котором стоимость проезда по соответствующей транспортной линии увеличивается каждый раз, когда интенсивность транспортного потока превышает пропускную способность этой линии.
Среди методов распределения маршрутов, относящихся к методам определения наивыгоднейшего маршрута, наиболее распространенным является метод «все или ничего». Суть метода состоит в том, что весь транспорт, имеющий одни и те же пункты отправления и назначения, пропускается по наивыгоднейшему маршруту, а все другие транспортные средства этим маршрутом не пользуются. Данный метод обеспечивает «оптимизацию для системы».
Как уже отмечалось выше, «оптимизация для потребителя» основана на предположениях, выполняющихся далеко не во всех случаях. Однако надо иметь в виду, что имеются пакеты программ, которые позволяют осуществлять «рассредоточение маршрутов». В частности, весь транспорт, перемещающийся между двумя пунктами, может распределяться не по одному, а по двум наивыгоднейшим маршрутам, соединяющим эти пункты. Имеются возможности и для распределения транспорта по многим маршрутам.
«Оптимизация для системы» может осуществляться также с помощью алгоритмов построения сетей минимальной стоимости. Соответствующая проблема при условии задания пунктов отравления и назначения, а также в отсутствие ограничений на пропускную способность и ориентацию линий может быть сформулиpoвaнaкак задача линейного программирования, которая эффективно решается методами линейного программирования [12].
2. Параметры задачи и варианты решения
2.1 Определение параметров задачи и описание различных вариантов решения
К настоящему этапу исследования становится ясно, должно ли оно завершиться принятием решения. Если должно, то для рассматриваемой задачи необходимо задать значения параметров и определить входные переменные. Так как описать процесс выполнения этой работы в общем виде довольно сложно, ниже приводится лишь перечень наиболее типичных входных переменных, с которыми приходится иметь дело при решении задач, возникающих как в частном, так и в государственном секторе транспорта (табл. 2).
Табл. 2 Перечень типичных входных переменных при решении задач, возникающих в частном и государственном секторах транспорта.
| Частный сектор |
Государственный сектор |
| «Явные» переменные |
Пункты отправления и назначения
Местоположение центров рас распределения продукции, складов, предприятий и других
элементов транспортной системы
Транспортные средства
Частные, государственные или
арендованные ;автомобиль, железнодорожный состав или самолет и т.д.
Маршруты и расписания движения транспорта
|
Транспортные потоки
Ограничения на вместимость транспортных средств
|
| «Неявные» переменные |
Рекламы, цены
|
Государственный транспорт
Маршруты транспортных средств, пропускная способность линий, расписание движения, местоположение остановок городского транспорта
Законодательство
Законы образования государственных зон, принципы организации транспортных потоков
|
Следует отметить, что правильность выбора каких-то показателей в качестве входных переменных системы зависит от уровня рассмотрения задачи и имеющихся в ней ограничений. Напри мер, при рассмотрении вопросов планирования городского хозяйства постройка надземной скоростной транспортной магистрали (входная переменная) может оказаться совершенно неприемлемой из-за ограниченности фондов, выделяемых на соответствующие цели [5].
2.2 Оценка эффективности возможных вариантов решения
После того как сформировано множество возможных вариантов решений, должна быть осуществлена оценка каждого из этих вариантов. При рассмотрении вопросов, относящихся к частному сектору транспорта, для проведения указанной оценки используются такие же методы, что и на этапе «Анализ возможных видов распределения» общей схемы исследования. Среди них следует выделить методы составления расписания движения но заданным маршрутам, выбора транспортных средств, а также определения оптимального размещения складов, центров распределения продукции и других элементов транспортной системы. Что касается государственного сектора транспорта, то в этом случае при предсказании реакции общества на предполагаемые изменения в транспортной системе определенную роль должны сыграть модели распределения транспортных средств и возможных поездок.
1.
Критерии, используемые при оценке возможных вариантов решения
Поскольку многие элементы, учитываемые в каждом отдельной возможном решении, тесно связаны друг с другом, они должны оцениваться одновременно. Это требует проведения анализа типа, затраты - выгоды или затраты - полезность или, наконец, имитационного моделирования с использованием ЭВМ.
При оценке возможных вариантов решения для исследуемой транспортной системы обычно устанавливается соответствие между уровнем обслуживания и его стоимостью. В частном секторе транспорта разные уровни обслуживания характеризуются различием во времени доставки грузов и их состоянием, а также во времени удовлетворения специальных заявок. В государственном, секторе транспорта разные уровни обслуживания характеризуют ся различной степенью загрузки транспортных сетей, например, пропускной способностью воздушных линий, временем перевозок в городе на частном или па общественном транспорте, степенью доступности любого района города даже для небольшой части населения, уровнем травматизма, уровнем шума и другими показателями. Доступность рассматривается в основном с точки зрения времени проезда в тот или иной район города и равномерности; распределения маршрутов государственного транспорта.
Для транспортных проблем большого масштаба оценку возможных вариантов решения редко удается проводить с использованием только количественных методов. Масштабность проблемы, как правило, вызывает присутствие в ее описании неформализуемых качественных показателей. Поэтому используемые критерии оценки возможных вариантов решения в ряде случаев; могут выявлять лишь отдельные аспекты общей проблемы.
2.
Методы анализа возможных вариантов решения
Имитационное моделирование с использованием ЭВМ представляет собой один из наиболее важных методов анализа. Самаясущественная особенность такого моделирования состоит в том, что оно позволяет учесть многие качественные показатели транс портных систем. Иными словами, при некоторых предположениях относительно выявленных качественных показателей можно со поставить возможные варианты решения, определив для каждого уровня стоимости обслуживания набор соответствующих ему выходных переменных.
Одной из лучших имитационных моделей, предназначенных для анализа транспортных систем, является модель LREPS, которая носит название «Крупномасштабный имитатор планирования в различных внешних условиях». С помощью данной модели можно имитировать динамику процесса распределения упакованных грузов и на этой основе проводить сравнение сложившихся и возможных структур систем распределения продукции. Модель разработана в Университете шт. Мичиган [15].
Основными критериями, используемыми при анализе различных систем распределения продукции, являются пропускная способность линий обслуживания заказчиков (имеются в виду скорость и надежность) и соответствующая ей полная стоимость обслуживания. В общем случае с увеличением указанной пропуск ной способности повышается полная стоимость перевозок, что приводит к необходимости принятия компромиссного решения. Ниже приводятся некоторые особенности модели, позволяющие оценить степень ее эффективности.
a. Модель является динамической, так как позволяет осуществлять планирование во времени и учитывать последствия принимаемых решений.
b. Модель является стохастической, поскольку предоставляет исследователю возможность рассматривать объем потребностей, промежуток времени между поступлениями заказов, время пере дачи сообщений, длительность обработки заявок и время пере возки как случайные величины. Кроме того, имеется также возможность учитывать детерминированные связи элементов транс портной сети.
c. В рамках модели допускается комплексное рассмотрение проблем распределения производственных запасов и размещения предприятий, т. е. допускается одновременное исследование проблем временного и пространственного разделения элементов транспортной сети.
d. Модель является многоэтапной. На первом этапе осуществляется поочередный ввод данных о производственных предприятиях (их число может достигать 100), а также о складах, при надлежащих этим предприятиям. На втором этапе в модель вводятся сведения о центрах распределения разнообразной продукции (их число также может достигать 100). На третьем, послед нем, этане учитываются до 20 тыс. сведений, характеризующих потребности как отдельных заказчиков, так и групп заказчиков.
На каждом этапе и при переходе от этапа к этапу связь между отдельными элементами транспортной сети устанавливается с помощью величин потоков либо продукции, либо информации.
Модель была успешно использована при проектировании и анализе крупных систем распределения продукции для фирм различного профиля, производящих кожевенные, химические и агрохимические товары, замороженные продукты питания, оборудование для систем водо-и теплоснабжения.
Однако следует отметить, что эта модель имеет и некоторые недостатки. Так, для использования модели требуется обширная информация, на получение которой не каждая фирма может выделить необходимые средства и время. Кроме того, модель мало пригодна для исследования вопросов, не имеющих прямого отношения к транспорту [4].
Наряду с рассмотренной моделью существуют и другие имитационные модели для планирования и анализа систем распределения продукции. Наиболее полезной из них оказалась модель, имеющая название «Имитатор систем распределения» (DSS). Характерной особенностью этой модели является целенаправленная организация вопросов, заключающаяся в том, что переменные параметры имитационной модели определяются по ответам тина да — нет на 450 вопросов. Информация, получаемая с помощью такого вопросника, включает характеристики спроса и покупательной способности, стратегии формирования портфеля заказов и пополнения производственных запасов, размещения предприятий, их производственных возможностей, а также характеристики других важных элементов системы. Существенно, что все эти элементы в большинстве случаев могут быть легко проанализированы. В зависимости от ответов на поставленные вопросы могут быть сформированы 1012
различных вариантов рассматриваемой имитационной модели. При формировании этих вариантов используется специальная библиотека программ.
После того как определена структура имитационной модели, с помощью программы-редактора составляется специальный перечень информации, необходимой для проведения анализа. Благо даря такому перечню затраты на получение необходимой информации могут оказаться существенно меньше выгод от проведения данного исследования, поскольку для использования модели надо получать только ту информацию, которая действительно необходима.
Размерность модели может быть достаточно просто уменьшена путем соответствующей корректировки используемого вопросника. Такая возможность делает модель весьма ценной для средних, но величине и небольших фирм. Другой полезной для небольших фирм особенностью рассматриваемой модели является то, что для ее применения нет необходимости проводить большое число отладок программы. Однако, видимо, самым главным ее достоинством является возможность установления взаимосвязей между различными элементами системы. Необходимо также иметь в виду, что при использовании данной модели исследователь не только участвует в процессе моделирования, но и существенно влияет на него через вопросник. При этом исследователь лучше понимает модель и больше ей доверяет.
Хотя подобная программа может показаться излишне автоматизированной и потому не слишком полезной, однако благо даря ей обеспечивается адекватность модели для весьма сложных исследуемых систем. С помощью модели DSSможно анализировать сведения относительно трех групп элементов системы: сведения о потребностях, складах продукции и производственных ресурсах. Связи между этими элементами могут носить произвольный характер, каждый канал распределения продукции может характеризоваться двумя направлениями ее перевозок, все склады продукции могут быть связаны друг с другом, потребности могут возникать в любой точке системы, и, наконец, на каждом складе могут быть созданы запасы любого вида. При использовании этой модели оценки характеристик системы и основном определяются с помощью оценок подсистемы регионального распределения складов. К сожалению, в этой модели отсутствует возможность одновременного рассмотрения временных и пространственных параметров системы, а также возможность исследования ее динамических характеристик. Такие возможности, как уже указывалось, предоставляет рассмотренная модель [5].
В настоящее время многие фирмы хорошо знают, что правильное планирование систем распределения, проводимое на агрегированном уровне, может привести к весьма значительной экономии средств. Рассмотренные выше имитационные модели представляют собой как раз инструмент такого планирования. Они позволяют обеспечивать руководителей фирм информацией, на основе которой можно организовать или реорганизовать транспортную сеть таким образом, чтобы удовлетворить текущие или будущие потребности в перевозках грузов. Следует отметить, что для многих фирм создание совершенно новой системы распре деления продукции может быть неприемлемо. Поэтому очень важно, что такое ограничение, как и любое другое, может быть учтено в имитационных моделях рассмотренных типов.
Имитационные модели, основанные на использовании ЭВМ, применяются и при анализе систем государственного сектора транспорта, но реже, чем в случае частного сектора. Однако при всех достоинствах рассматриваемых имитационных моделей они все же обладают серьезным недостатком, связанным с невозможностью включения в модель таких переменных, которые не могут быть выражены количественно. К моделям, в которых делается попытка рассмотрения и количественных, и «неколичественных» переменных, относятся модели типа затраты - вы годы и затраты - эффективность. В моделях первого типа различным уровням общих затрат ставится в соответствие совокупность количественных и качественных оценок различных уровней обслуживания. Во многих случаях такое сопоставление осуществляется с использованием определенного типа показателей относительной стоимости. Однако при рассмотрении ряда важных показателей, таких, например, как загрязнение окружающей среды, влияние заторов на движение транспорта, уровень обслуживания небольших групп пассажиров, степень безопасности пользования транспортом, становится ясно, что сведение их к показателям стоимости является практически невозможным.
Данное обстоятельство привело к тому, что была разработана модель типа затраты - эффективность. Главная цель разработки этой модели состояла в том, чтобы для каждого возможного значения полных затрат представить оценки показателей уровня обслуживания в наиболее ясном и естественном для этих показателей виде. В качестве примеров показателей, о которых здесь могла бы идти речь, можно указать такие показатели, как время в пути, количество транспортных происшествий, уровень загряз нения окружающей среды, уровень комфортабельности. Возможные варианты решения для транспортной системы, представленные в естественном виде через качественные показатели рас смотренного выше типа, могут быть оценены в некоторой балльной шкале группой экспертов, аналогично тому как преподаватель оценивает школьные работы.
Модели типа затраты - выгоды и типа затраты - эффективность являются наиболее полными среди существующих моделей анализа транспортных систем. Эти модели, по существу, объединяют отдельные частные модели (главным образом основанные на использовании ЭВМ имитационные модели) с методами учета качественных переменных. При этом формируются возможные варианты решения, для которых проще, чем в других моделях, устанавливается связь ожидаемых результатов с общими затратами. Однако необходимо иметь в виду, что выбор окончательного варианта решения требует со стороны лиц, принимающих решения, боль шой работы для правильной оценки рассматриваемых вариантов [9].
2.3 Разработка макетов транспортной сети и оценка возможных вариантов решения
Действующие макеты довольно широко используются на практике для оценки проектируемых предприятий промышленности или производственных процессов. Аналогичные способы проверки различных вариантов решения используют и организации, контролирующие состояние шоссейных дорог. При этом применяются имитационные макеты, включающие в рассмотрение не только основные транспортные линии, но и тротуары, дорожки, проезды, а также систему сигнализации.
В последнее время все большее внимание уделяется макетам и имитационным моделям как средствам окончательной проверки возможных вариантов решения в области транспорта. Замечательные успехи в авиационной промышленности привели к широкому распространению хорошо зарекомендовавших себя имитационных моделей - макетов при проектировании транспортных сетей и управлении ими как в государственном, так и частном секторе.
Например, с использованием такого подхода для решения задач государственного сектора был разработан маршрут автобуса-экспресса, когда требовалось обеспечить проезд по 25 основным городским магистралям. Применение же имитационных моделей-макетов в частном секторе показало, что планирование прибыли от сдачи в аренду вагонеток для одноколейных дорог должно осуществляться Национальной компанией, предоставляю щей аренду грузового транспорта, не в масштабах всей страны, а в масштабах отдельных городов.
Наряду с существенным уменьшением затрат на перестройку исследуемой транспортной сети и уменьшением вероятности возникновения непредвиденных последствий принимаемых решений использование макетов имеет еще одно важное достоинство, заключающееся в возможности ведения «обратной связи». Эта обратная связь либо может быть организована в обычном для технических систем виде, либо может представлять реакцию общественного мнения на тот или иной вариант решения. Отметим, кстати, что в последнее время общественному мнению отводится все большая роль при выборе наилучшего варианта решения [14].
2.4 Реализация выбранного варианта решения
В данном разделе дается краткий обзор проблем реализации выбранных вариантов решений и причин, задерживающих эту реализацию. Такие проблемы и причины должны быть выявлены для того, чтобы исследователи могли оказывать непосредственное влияние па процесс принятия решения.
1. Особенности процесса принятия решения
К настоящему времени накоплено немало экспериментальных и теоретических данных, показывающих сходство процессов принятия решения в системах государственного и частного транс порта. В обоих случаях трудности, которые возникают в процессе принятия решения, приводят к задержкам в реализации рекомендаций, вырабатываемых с применением общих моделей.
Одна из проблем реализации таких рекомендаций связана с наличием разных интересов у различных предприятии. Существование разных интересов приводит к тому, что в процессе принятия решения определенную роль играют субъективный фактор и фактор «осторожности» (минимального риска). Выделенные факторы проявляются, например, в тех случаях, когда оптимальный вариант решения, предлагаемый для некоторого предприятия, является для него новым и не опробованным. Тогда фактор «осторожности» может привести даже к полному непринятию предложенного варианта. Таким образом, наличие целого ряда особых обстоятельств приводит к формированию либо положительного, либо отрицательного отношения к решениям определенного типа.
Другой проблемой, весьма близкой к только что рассмотрен ной, является проблема, связанная с наличием групп лиц, имеющих разные интересы. Каждая из таких групп поддерживает и отстаивает варианты решения определенного типа. Если учитывать динамику развития отдельных групп, характер поддерживаемых ими решений вполне можно предсказывать заранее. Аналитические транспортные модели строятся, как правило, без учета соображений об интересах различных групп. Поэтому вряд ли можно считать, что полученный с помощью модели тот или иной вариант решения будет удовлетворительным с точки зрения всех заинтересованных сторон. Принятое решение по организации транспортных сетей почти всегда вызывает оппозиционное отношение одних групп, поддержку других и равнодушное отношение со стороны остальных групп. Это обстоятельство приводит к тому, что принятое решение должно затем согласовываться аналогично процедурам политического характера (это справедливо как для государственного, так и для частного сектора транспорта).
2. Необходимость учета состояния окружающей среды и мнения людей в процессе принятия решений
Другие факторы, задерживающие практическое применение результатов анализа транспортных систем, связаны с необходимостью учета состояния окружающей среды и мнения людей при выборе наиболее желательного варианта решения. Эти факторы приходится учитывать при организации многих транспортных сетей государственного и частного секторов.
В последние годы в США, в отдельных штатах и округах, появились законы, требующие анализа всех предложений но организации транспортных сетей с точки зрения обеспечения условий, гарантирующих отсутствие отрицательного влияния транспорта на человека и окружающую среду. В связи с этим требованием моделирование транспортных систем должно включать дополни тельный этап тщательной доработки модели, на котором делается попытка максимально возможной компенсации отрицательных воз действий транспорта па человека и окружающую среду. С помощью соответствующих переменных, учитывающих указанные воздействия и включаемых в общие модели анализа, удалось сделать не которые оценки в рассматриваемой области, однако полученные данные оказались пока малоубедительными и дорогостоящими.
Таким образом, наличие воздействия транспорта на окружающую среду и человека требует некоторой модификации оптимальных решений, вырабатываемых без учета этих воздействий. Поэтому в будущих исследованиях нужно осуществлять такой учет и включать в количественном пли хотя бы в качественном виде в анализ все необходимые для этого параметры, переменные и ограничения [12].
Заключение
При анализе транспортной системы частного сектора главную роль играют методы прогнозирования (о нем свидетельствуют результаты приме нения многочисленных моделей распределения и целей поездок, специально предназначенных для предсказания потребностей населения в транспортных средствах). Это объясняется двумя причинами. Во-первых, в частном секторе контроль за удовлетворением большей части потребностей в транспортных средствах осуществляется централизованно соответствующими органами управления определенного предприятия; и государственном секторе аналогичным контроль, по существу, распределен но всей системе и осуществляется миллионами людей.
Во-вторых, целью планирования в частном секторе, как правило, является максимизация прибыли в то время как в государственном секторе цель планирования - это удовлетворение потребностей миллионов людей втранспортных средствах. Поэтому часто довольно трудно определить критерии оценки возможных вариантов решении при планировании городской транспортной сети, и возникает необходимость выработки стратегии, позволяющей устанавливать правильность и важность выбираемых целей.
Для иллюстрации различий и сходства в моделях, используемых в част ном и государственном секторах транспорта, рассмотрим модели, позволяющие сделать выбор транспортных средств. С помощью таких моделей проблема выбора транспортных средств как в частном, так и в государственном секторе решается путем определения соответствующих затрат и выгод. Однако к государственном секторе выбор транспортных средств осуществляется, по существу, населенном, и используемые моделираспределения предназначены для предсказания интенсивности потока пассажиров, выбирающих каждое из имеющихся транспортных средств. В частном секторе управление процессом выбора транспортных средств является функцией соответствующею планирующего органа, и поэтому модели для выбора транспортных средств нацелены па выявление одного или нескольких транспортных средств, наилучших в имеющемся парке. Следовательно, модели, используемые в частном секторе, являются оптимизационно-ориентированными, а модели, используемые в государственном секторе, прогностически-ориентированными. Ото положение справедливо для большинства моделей, применяемых на различных этапах общей схемы планирования транспортных сетей.
Что касается перспективы использования методов исследования операций для решения проблем транспортной сети, то, по-видимому, сложные и дорогостоящие имитационные модели должны уступить место менее сложным и менее общим моделям. Несомненно также, что более широкое применение найдут имитационные и операционные игры.
Список использованной литературы
1. Вентцель Е.С., Введение в исследование операций. М.; 1964
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М.; Наука, 2006г
3. Еремин И.И., Астафьев Н.Н. Введение в теорию линейного и выпуклого программирования М.; Наука, 1976г.
4. Ермаков В.И. “Общий курс высшей математики для экономистов”, Москва, Инфра-М, 2000г.
5. Иванов Ю.П., Лотов А.В. Математические модели в экономике. М.; Наука, 1979г.
6. Карманов В.Г. Математическое программирование: учебное пособие для студентов вузов. - М.: Физматлит, 2008. - 264с.
7. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом анализе: Учебник. 3-е изд., исп. М.: Дело, 2007. 688 с.
8. Кузнецов А.В. Математическое программирование: учебное пособие для вузов. - М.: Высшая школа, 1976. - 352с.
9. Кузнецов А.В., Сакович В.А., Холод Н.И. ”Высшая математика. Математическое программирование ”, Минск, Вышейшая школа, 2008г.
10. Моисеев Н.Н., Иванов Ю.П., Столярова Е.М. Методы оптимизации. М.; Наука, 1978г.
11. Мочалов И.А. Нечеткое линейное программирование. // Промышленные АСУ и контроллеры. - 2006. - № 10. - с.26-29.
12. Моудер Д., Элмаграби С., Исследование операций. М.; Мир, 1981г
13. Павлова Т.Н.. Линейное программирование. Учебное пособие. - Димитровград, 2007г.
14. Пашутин С.Оптимизация издержек и технология формирования оптимального ассортимента. // Управление персоналом. - 2005. - №5. - с.20-24.
15. Шимко П.Д., Оптимальное управление экономическими системами. М.; 2004г.
|