Кривые, заданные в полярных координатах
Р.Л. Ткачук
Вологда
Введение
Тема «Полярная система координат» позволяет познакомить учащихся с красивейшими результатами математической науки.
Полярная система координат на плоскости определяется заданием точки O(полюс), луча Ох (полярная ось) и единичного отрезка т. Кроме того, должен быть указан поворот луча Ох, называемый положительным. Пусть это будет поворот в направлении против движения часовой стрелки. Повороты луча, совершаемые в направлении, противоположном положительному, будем называть отрицательными.
Пусть М — произвольная точка плоскости, не совпадающая с полюсом. Обозначим через  длину отрезка ОМ, а через длину отрезка ОМ, а через  — величину угла, образованного лучами Ох и ОМ. Числа — величину угла, образованного лучами Ох и ОМ. Числа  и и  такие, что р>0 и 0 такие, что р>0 и 0  ф < 2π, именуют полярными координатами точки М. Число ф < 2π, именуют полярными координатами точки М. Число  называют первой полярной координатой, или полярным радиусом, число называют первой полярной координатой, или полярным радиусом, число  — второй полярной координатой, или полярным углом (рис. 1) Если точка М совпадает с полюсом, то — второй полярной координатой, или полярным углом (рис. 1) Если точка М совпадает с полюсом, то  = 0, а полярный утол = 0, а полярный утол  считаем равным нулю. Заметим, что при заданных нами условиях считаем равным нулю. Заметим, что при заданных нами условиях  > 0, 0 ≤ > 0, 0 ≤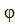 < 2π, полярные координаты любой точки определяются однозначно. < 2π, полярные координаты любой точки определяются однозначно.
Введение таких координат очень естественно, ведь местонахождение любой точки на земной поверхности для неподвижного наблюдателя удобно определять с помощью расстояния от наблюдателя до этой точки и направления к точке от наблюдателя (в этом случае точка, в которой находится наблюдатель, служит полюсом).
Школьникам можно напомнить, что в повести Р.Л.Стивенсона «Остров сокровищ» описано, как старый пират Флинт определил местоположение закопанного клада: «Десять футов к северу от высокого дерева на склоне Подзорной Трубы» (рис. 2).
Построение кривых, заданных полярными уравнениями, имеет некоторые специфические особенности, которые мы проиллюстрируем на примерах. Как известно, математики Древней Индии заменяли доказательства теорем геометрическим чертежом, сопровождая его короткой подписью: «Смотри!». Мы пользовались тем же принципом, заменив долгие разъяснения рисунками, из которых видны все свойства кривых.
В дальнейшем, при построении кривых мы позволим углу  принимать любые неотрицательные значения, выделяя на рисунках жирной линией фрагменты кривых, получающиеся при ограниче-нии 0 ≤ принимать любые неотрицательные значения, выделяя на рисунках жирной линией фрагменты кривых, получающиеся при ограниче-нии 0 ≤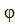 < 2π. < 2π.
Алгебраические спирали
Сначала рассмотрим так называемые алгебраические спирали, т.е. кривые, полярные уравнения которых являются алгебраическими относительно  и и  и имеют вид F( и имеют вид F( , ,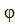 ) = 0, ) = 0,  ≥0, ≥0,  ≥ 0. Если перейти к прямоугольной системе координат, то эти уравнения уже не будут алгебраическими относительно х и у. Кривые, задаваемые такими уравнениями, принято называть трансцендентными. ≥ 0. Если перейти к прямоугольной системе координат, то эти уравнения уже не будут алгебраическими относительно х и у. Кривые, задаваемые такими уравнениями, принято называть трансцендентными.
Достаточно громоздкие декартовы уравнения упрощаются при переходе к полярной системе координат. Зависимость между полярными и декартовыми координатами весьма проста.
Пусть полюс Oсовпадает с началом декартовой системы координат, полярная ось совмещена с положительным направлением оси Ох; М(х; у) — произвольная точка декартовой плоскости. Легко убедиться, что

И обратно:
x=
Спираль Архимеда
 = =  . .
Поместим точку на секундную стрелку часов и будем перемешать точку вдоль секундной стрелки с постоянной скоростью, не обращая внимания на равномерное движение стрелки часов по кругу. Тогда точка опишет кривую, называемую спиралью Архимеда. Изобретение этой кривой приписывается Конону Самосскому, хотя ее основные свойства описал именно Архимед (ок. 287-212 гг. до н.э.). Архимеду, в частности, было известно, что расстояние между двумя последовательными витками спирали является постоянной величиной и равно 2π (рис. 3).
Кстати, в силу этой особенности в расположении витков реальный образ спирали Архимеда можно видеть, например, наблюдая туго завернутый рулон бумаги с его торцевой стороны.
На внеклассных занятиях полезно показать построение первого витка спирали Архимеда.
Начертим окружность. Разделим ее и радиус ОА на п равных частей.
Пусть n = 8. Проведем ко всем точкам деления лучи из центра О окружности и пронумеруем их (рис. 4). На луче 1 отметим точку на расстоянии = = ОА от центра окружности. На луче 2 отметим точку на расстоянии ОА от центра окружности. На луче 2 отметим точку на расстоянии  = = ОА, на луче 3 - точку на расстоянии ОА, на луче 3 - точку на расстоянии  = = ОА и т.д. На луче 8 поставим точку на расстоянии ОА и т.д. На луче 8 поставим точку на расстоянии 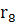 = = ОА. ОА.
Соединив последовательно плавной кривой полученные точки, мы увидим первый виток спирали Архимеда. Построение будет тем более точным, чем больше точек деления радиуса и окружности будет выбрано первоначально.
Спираль Архимеда используется в качестве линии, позволяющей разделить заданный угол на любое количество равных частей. В некоторых готовальнях в старину в состав рабочих инструментов входила металлическая пластинка с тщательно выгравированной на ней спиралью Архимеда. С помощью такого приспособления было нетрудно разделить угол на несколько равных частей. Например, для трисекции угла ВАС достаточно приложить пластину ее ровной частью к одному из лучей угла (рис. 5) и поделить получившийся отрезок АВ на 3 равные части. На дуге спирали следует сделать засечку радиусом АО = - АВ. Тогда угол САО будет равен одной трети угла ВАС.

В области техники спираль Архимеда находит применение в так называемых кулачковых механиз-мах, которые преобразуют вращательное движение шайбы в поступательное движение стержня. В некоторых механизмах (например, в часах) требуется, чтобы стержень двигался равномерно. Обеспечить это можно, очертив профиль шестеренки по спирали Архимеда.
В качестве второго объекта для применения спирали Архимеда в технике можно привести самоцентрирующийся патрон (рис. 6), направляющие канавки которого выполнены по спирали Архимеда. При одном повороте диска этого патрона кулачки перемещаются на величину радиального расстояния смежных канавок.
Кроме того, форму спирали Архимеда имеют звуковая дорожка на грампластинке и одна из деталей швейных машин - механизм для равномерного наматывания ниток на шпульку.
Логарифмическая спираль
lg = =  , ,  = =  . При . При  = 0 получаем = 0 получаем  = 1. При = 1. При  →+∞ видно, что →+∞ видно, что  →+∞ и спираль развертывается против хода часовой стрелки (рис. 7) →+∞ и спираль развертывается против хода часовой стрелки (рис. 7)

Логарифмическую спираль описывает точка, движущаяся по секундной стрелке не с постоянной скоростью (как в случае архимедовой спирали), а с возрастающей, причем это возрастание пропорционально расстоянию от центра часов.
Логарифмическую спираль можно построить с помощью так называемого золотого прямоугольника, т.е. такого, у которого отношение сторон равно золотому сечению:  . .
Если от золотого прямоугольника АВСDотрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник ЕFСD, но меньших размеров. Если продолжить этот процесс далее, а затем соединить плавной кривой вершины квадратов, как это сделано на рис. 8, то получим логарифмическую спираль.
Логарифмическая спираль обладает рядом интересных свойств:
• расстояния между последовательными витками образуют геометрическую прогрессию;
• последовательность длин радиусов, образующих одинаковые углы друг с другом, также составляет геометрическую прогрессию;
• образующиеся в процессе расширения секторы, отсекаемые такими радиусами, подобны другдругу.
Логарифмическая спираль часто встречается в природе и связана с определенными видами роста. У очень многих моллюсков последовательные витки раковины не одинаковы, а все более и более утолщаются. Во многих случаях приближенные значения толщины последовательных витков образуют геометрическую прогрессию. Хотя саму раковину моллюска нельзя назвать живой, она образуется растущим организмом. Один из простейших способов наращивания нового вещества автоматически приводит к образованию некоторой фигуры, очень близкой к логарифмической спирали. Во многих раковинах обнаруживается поразительно близкое совпадение между результатами измерений и теоретическими значениями, ожидаемыми для точной логарифмической спирали (рис. 9). В подсолнухе семечки расположены по характерным дугам, близким, как показывают соответствующие измерения, к дугам логарифмической спирали. В связи с подобными фактами некоторые ученые считают логарифмическую спираль кривой, являющейся одним из выражений законов органического роста.
Применения логарифмической спирали в технике основаны на свойстве этой кривой пересекать все свои радиус-векторы под одним и тем же углом2
. На этом свойстве основаны применения логарифмической спирали в технике. Так, вращающиеся ножи в различных режущих машинах (рис. 10) имеют профиль, очерченный по дуге спирали, благодаря чему угол резания (угол между лезвием ножа и направлением его скорости вращения) остается постоянным вдоль всей кромки подвижного ножа, что обеспечивает меньший его износ.
Труба, подводящая струю воды к лопастям турбинного колеса гидроэлектростанции, имеет профиль, очерченный по дуге логарифмической спирали. Это позволяет обеспечить минимальные потери энергии на изменение направления течения, и, следовательно, напор воды используется с максимальной производительностью.
В истории математики логарифмическая спираль упоминается впервые в 1638 г. Декартом, который определял новую спираль как линию, у которой отношение длины дуги к соответствующему радиус-вектору является постоянным.
Логарифмическая спираль - кривая с «твердым» характером. Она не изменяет своей природы при многих преобразованиях, к которым чувствительны другие кривые. Сжать или разжать эту спираль относительно ее полюса - то же самое, что повернуть ее на определенный угол. Это свойство логарифмической спирали было открыто Якобом Бернулли, называвшим ее spiramirablis— дивная спираль. Открытые Бернулли свойства логарифмической спирали оставаться неизменной при различных преобразованиях настолько поразили ученого, что он был склонен придать им мистический смысл. Якоб Бернулли завещал высечь логарифмическую спираль на своем надгробном камне, сопроводив изображение латинской фразой «Eademmutateresurgo» — «Измененная, возрождаюсь прежней».
Далее рассмотрим несколько примеров кривых, полярные уравнения которых содержат тригонометрические функции. Построение этих кривых можно выполнить по точкам, где 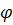 принимает значения от 0 до 2π. принимает значения от 0 до 2π.
Семейство роз Гранди
 =sink =sink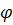 , ,
где k - положительная постоянная.
В XVIII в. итальянский геометр Гвидо Гранди (1671—1742) создал розы. Нет, вовсе не те прекрас-ные цветы, о которых вы, наверное, подумали. Розы Гранди радуют нас правильными и плавными линиями, но их очертания не каприз природы — они предопределены специально подобранными математическими зависимостями. Эти зависимости были подсказаны самой природой, ведь в большинстве случаев абрис листа или цветка представляет собой кривую, симметричную относительно оси.
Семейство роз Гранди имеет свойство, которое в природе не сразу и заметишь: так как
| sin(k | ≤1, | ≤1,
то вся кривая расположена внутри круга единичного радиуса. В силу периодичности тригонометрических функций роза состоит из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен 1.

Наиболее красивые «цветы» получаются при k = 2 (четырехлепестковая роза) и при k = 3 (трехлепестковая роза, хотя читателю, обратившему внимание на рис. 11,б, может показаться, что эта кривая больше напоминает пропеллер).
Покажем, как построить трёхлепестковую розу. Для построения этой кривой сначала заметим, что поскольку полярный радиус неотрицателен, то должно выполняться неравенство sin3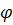 ≥0, решая которое находим область допустимых углов: 0≤ ≥0, решая которое находим область допустимых углов: 0≤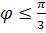 , , 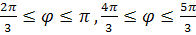
В силу периодичности функции sin3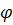 (ее период равен (ее период равен  ) достаточно построить график для углов ) достаточно построить график для углов 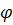 в промежутке 0 в промежутке 0  , а в остальных двух промежутках использовать периодичность. Итак, пусть0≤ , а в остальных двух промежутках использовать периодичность. Итак, пусть0≤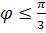 . Если угол . Если угол 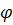 изменяется от 0 до 1 , sin3 изменяется от 0 до 1 , sin3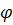 изменяется от 0 до 1, и, следовательно, изменяется от 0 до 1, и, следовательно,  изменяется от 0 до 1. Если угол изменяется от изменяется от 0 до 1. Если угол изменяется от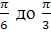 , то радиус изменяется от 1 до 0. Такимобразом, при изменении угла , то радиус изменяется от 1 до 0. Такимобразом, при изменении угла 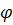 от 0 до от 0 до  , точкана плоскости описывает кривую, похожую на очертания лепестка и возвращается в начало координат. Такие же лепестки получаются, когда угол , точкана плоскости описывает кривую, похожую на очертания лепестка и возвращается в начало координат. Такие же лепестки получаются, когда угол 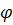 изменяется в пределах от изменяется в пределах от  до π и от до π и от  до до  . Рассмотрим теперь, как построить кривую, заданную в полярной системе координат уравнением . Рассмотрим теперь, как построить кривую, заданную в полярной системе координат уравнением  . .
Функция  — периодическая с периодом π, кроме того, — периодическая с периодом π, кроме того,
sin(2( , ,
поэтому достаточно построить кривую в первой четверти, потом зеркально отразить ее относительно оси Оу и использовать периодичность для построения кривой в третьей и четвертой четвертях.
Функция  = sin2 = sin2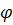 на отрезке [0; на отрезке [0; монотонновозрастает с 0 до 1 , а на отрезке [ монотонновозрастает с 0 до 1 , а на отрезке [ ; ; ] монотонно убывает от 1 до 0. Таким образом, мы получили лепесток розы, лежащий в первой четверти. Остальные три лепестка получатся, если построить кривую в оставшихся четвертях. ] монотонно убывает от 1 до 0. Таким образом, мы получили лепесток розы, лежащий в первой четверти. Остальные три лепестка получатся, если построить кривую в оставшихся четвертях.
Отметим следующие интересные свойства четырехлепестковой розы:
• четырехлепестковая роза есть геометрическое место оснований перпендикуляров, опущенных из начала координат на отрезок длиной 1, концы которого скользят по координатным осям;
• площадь, ограничиваемая четырехлепестковой розой, равна  . .
Розы Гранди нашли свое применение в технике, в частности, если некоторая точка совершает колебание вдоль прямой, вращающейся с постоянной скоростью вокруг неподвижной точки — центра колебаний, то траектория этой точки будет розой.
Вообще, если k — натуральное число, то роза состоит из 2kлепестков при четном kи из k: лепестков при k нечетном. Если k — рациональное число (k= , то роза состоит из т лепестков в случае, когда оба числа т и п нечетные, и из 2т лепестков, когда одно из этих чисел является четным; при этом лепестки частично перекрываются. Если k - иррациональное число, то роза состоит из бесконечного множества частично перекрывающихся лепестков. , то роза состоит из т лепестков в случае, когда оба числа т и п нечетные, и из 2т лепестков, когда одно из этих чисел является четным; при этом лепестки частично перекрываются. Если k - иррациональное число, то роза состоит из бесконечного множества частично перекрывающихся лепестков.
Лемниската Бернулли
р2
= 2соs2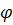 . .
Лемниската Бернулли — одна из самых замечательных алгебраических линий. Из вида уравнения кривой следует, что кривая состоит из двух симметричных лепестков (по внешнему виду эта кривая напоминает перевернутую восьмерку или бантик). Для точек лемнискаты должно выполняться нера-венство соs2 , поэтому она расположена между прямыми у=±х. Отметим также, что , поэтому она расположена между прямыми у=±х. Отметим также, что  = =  при при 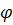 = 0. = 0.
Покажем, как построить лемнискату Бернулли. Но сначала отметим, что, поскольку квадрат полярного радиуса неотрицателен, должно выполняться неравенство соs2 . Решая это неравенство, находим область допустимых углов: . Решая это неравенство, находим область допустимых углов:
0≤ , , 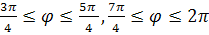
В силу периодичности функции соs2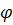 (ее период равен π) достаточно построить график для углов (ее период равен π) достаточно построить график для углов 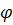 в промежутке в промежутке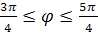 а в остальных случаях использовать периодичность а в остальных случаях использовать периодичность
Итак, пусть 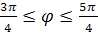 Если угол Если угол 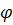 изменяется от изменяется от 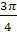 до π ,то cos2 до π ,то cos2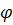 изменяется от 0 до 1 и, следовательно, изменяется от 0 до 1 и, следовательно,  изменяется от 0 до изменяется от 0 до
Если угол 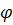 изменяется от π до изменяется от π до  , то , то  изменяется от изменяется от  до 0 .Таким образом при изменении угла от до 0 .Таким образом при изменении угла от точка на плоскости описывает кривую, напоминающую половинку от восьмерки, и возвращается в начало координат. Вторая половинка получится, когда угол точка на плоскости описывает кривую, напоминающую половинку от восьмерки, и возвращается в начало координат. Вторая половинка получится, когда угол изменяется в пределах от 0 до изменяется в пределах от 0 до  и от и от  до 2π. до 2π.
Лемниската Бернулли обладает рядом оригинальных геометрических и механических свойств:
• угол, составленный касательной к лемнискате в произвольной точке с радиус-вектором точки касания равен 2
• перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо ее точки, делит площадь соответствующего сектора пополам;
• эта кривая (в переводе с латинского lemniscatus— украшенный лентами) есть множество точек М, произведение расстояний которых r1
, и r2
до двух данных точек F1
, и F2
(фокусов) равно квадрату междуфокусного расстояния.
Впервые лемниската была рассмотрена Якобом Бернулли (1654—1705) в 1694 г. Впоследствии Бернулли много часов своих занятий уделял лемнискате и нашел несколько ее интересных свойств.
В технике лемниската используется, в частности, в качестве переходной кривой на закруглениях малого радиуса, как это имеет место на железнодорожных линиях в горной местности и на трамвай-ных путях. Таким образом она обеспечивает плавность закругления, без которой центробежная сила, действующая на поезд, возрастала бы резко, доставляя неудобство пассажирам.
В качестве примера применения лемнискаты в области физики можно указать, что линия поля, создаваемого двумя параллельными токами, текущими по бесконечно длинным проводникам в плоскости, к ним перпендикулярной, является лемнискатой.
Кардиоида
логарифмическая спираль полярный координата лемниската
 = 2(1 — соs = 2(1 — соs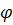 ). ).
Понаблюдаем за какой-нибудь точкой окружности, когда последняя катится по внешней стороне неподвижной окружности такого же радиуса. Траекторией точки будет кардиоида. По мнению математиков, придумавших название кривой, она отдаленно напоминает форму сердца (в переводе с греческого kardieidos— сердцеобразная).
Покажем способ построения кардиоиды.
Сначала выберем опорную окружность и ее радиус ОА примем за 1, а прямую ОА — за ось абсцисс, причем точка А произвольно выбирается на опорной окружности. Проведем другую окружность с центром в точке М, произвольно взятой на опорной окружности, и радиусом МА. Повторив затем такие построения для достаточно большого числа точек М, равномерно распределенных по опорной окружности, увидим, что огибающая всех окружностей радиуса МА и есть кардиоида (рис. 13).

Кардиоида используется как линия для вычерчивания профилей, если требуется, чтобы скользяший по профилю стержень совершал гармонические колебания. При этом скорость поступательного движения стержня будет изменяться без скачков. Этим свойством она выгодно отличается от спирали Архимеда, у которой, благодаря постоянности скорости стержня, в конце каждого хода стержня происходят удары (скорость скачком меняет значение скорости с vна —v), что вызывает быстрое изнашивание механизма.
Одна из составных частей в механизме для поднятия и опускания семафора очерчена по кардиоиде. При этом скорость поднятия' или опускания достигает максимального значения в середине хода семафора, что очень важно.
Кардиоида также хорошо знакома конструкторам и возникает при возвратно-поступательных движениях стержней в двигателях.
В заключение заметим, что полярные координаты широко применяются при определении длин кривых, площадей фигур, объемов и площадей поверхностей тел вращения, а также в задачах на определение центра масс и момента инерции тела. Кривые, рассмотренные в статье, нередко возникают при решении различных задач в электротехнике, акустике, гидростатике и механике.
Логарифмическая спираль в природе и технике
В технике часто применяют вращающиеся ножи. Сила, с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянства давления нуж-но, чтобы угол резания сохранял постоянное значению, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от обрабатываемого материала (рис. 64).
В гидротехнике по логарифмической спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря такой форме трубы потери энергии на изменение направления течения в трубе оказываются минимальными, и напор воды используется с максимальной производительностью.
Пропорциональность длины дуги спирали радиус-вектору используют при проектировании зубчатых колес с переменным передаточным числом. Для этого берут два квадрата, расположенных так, как показано на рисунке 65, и через середину и конец каждой стороны проводят дуги одинаковых логарифмических спиралей с полюсами в центрах квадратов, причем одна спираль закручивается по часовой стрелке, а другая — против часовой стрелки. Тогда при вращении этих квадратов дуги спиралей будут катиться одна по другой без скольжения. Передаточное же число, т. е. отношение угловых скоростей этих колес, будет непрерывно меняться, достигая в течение одного оборота колеса четыре раза максимального значения и четыре раза минимального.
Живые существа обычно растут, сохраняя общее начертание своей формы. При этом чаще всего они растут во всех направлениях — взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем рост совершается так, что сохраняется подобие раковины с ее первоначальной формой. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам (рис. 66). Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали. Можно сказать, что эта спираль является математическим символом соотношения формы и ;роста. Великий немецкий поэт Иоганн-Вольфганг Гёте считал ее даже математическим символом жизни и духовного развития.
По логарифмической спирали очерчены не только раковины — в подсолнухе семечки расположены по дугам,близким к логарифмической спирали и т. д. Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. По логарифмическим спиралям закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система.
|