Державна митна служба України
Академія митної служби України
Кафедра транспортних систем і технологій
КУРСОВА РОБОТА
З дисципліни «Основи теорії транспортних
процесів та систем»
На тему:
«ОПТИМІЗАЦІЯ ЗАВОЗУ-ВИВОЗУ ВАНТАЖІВ У ВУЗЛІ ВЗАЄМОДІЇ ЗАЛІЗНИЧНОГО, РІЧКОВОГО І АВТОМОБІЛЬНОГО ТРАНСПОРТУ»
Варіант №8
Виконав
курсант групи Т07
Джамілєв Є.О
Перевірив
доц. Лєснікова І.Ю
Дніпропетровськ 2010р.
ЗАВДАННЯ
Курсанта – Джамілєва Євгена Олеговича групи Т07-1 з дисципліни «Основи теорії транспортних процесів та систем»
На тему: «Оптимізація завозу – вивозу вантажів у вузлі взаємодії залізничного, річкового і автомобільного транспорту».
Частина 1. Визначення параметрів вхідного потоку поїздів, що прибувають на станцію:
Ø визначити параметри вхідного потоку поїздів, проаналізувавши інтервали прибуття поїздів або кількість поїздів, які прибувають на станцію за одну годину;
Ø побудувати гістограми і функції розподілення інтервалів прибуття;
Ø побудувати графіки статистичного розподілу величини поїздів і функції їх розподілу;
Ø визначити параметри розподілення кількості вагонів у поїзді;
Ø визначити параметри тривалості обробки складів поїздів у парку прийому;
Ø визначити тривалість обробки поїздів і її параметри при різній кількості груп у бригаді ПТО.
Частина 2. Оптимізація взаємодії залізничного і річкового транспорту при перевезенні мінерально - будівельних вантажів.
Потрібно розробити оптимальний план взаємодії залізничного і річкового транспорту під час перевезення мінерально-будівельних вантажів із трьох пунктів видобутку — Al
,, А2
, А3
— у 8 пунктів споживання — Бр, Мс, О, В3
, В5
, В7
, В8
, Л. Перевалка вантажу з залізниці на воду і назад може здійснюватися в п'ятьох портах – B1
, В2
, В3
, В5
, В6
при відомій перероблювальній спроможності портів по перевалці вантажів із залізничного транспорту на річковий і вартість перевалки 1 т у прямому і зворотному напрямках.
Частина 3. Розрахунок параметрів простою автомобілів та вагонів під вантажними операціями для доцільності введення нової системи регулювання методом імітаційного моделювання.
Визначити доцільність створення на вантажному дворі станції системи регулювання, що забезпечує збір і збереження інформації про місцезнаходження автомобілів на вантажних фронтах, стану вантажно-розвантажувальних механізмів і прийняття рішень про їхнє використання та передачу команд водіям автомобілів з метою підвищення ефективності взаємодії автомобільного та залізничного видів транспорту під час перевезення тарно-штучних вантажів. Відвантаження вантажів здійснюється двома бригадами з двох секцій ангарного складу. Автомобільний транспорт працює протягом 8 год. У процесі статистичного дослідження було встановлено, що прибуття автомобілів на вантажний двір носить випадковий характер і описується законом Пуассона з інтенсивністю  =2,8 авто/год.. Коливання тривалості обслуговування автомобіля в секції складу описується нормальним законом розподілу з параметрами: математичне очікування t0
= 28 хв., середнє квадратичне відхилення σ0
= 8 хв. =2,8 авто/год.. Коливання тривалості обслуговування автомобіля в секції складу описується нормальним законом розподілу з параметрами: математичне очікування t0
= 28 хв., середнє квадратичне відхилення σ0
= 8 хв.
Капітальні вкладення, необхідні для впровадження системи регулювання, 5000 у.г.о., додаткові річні експлуатаційні витрати, зв’язані з її експлуатацією, 4000 у.г.о.
ВХІДНІ ДАНІ
Частина 1. Визначення параметрів вхідного потоку поїздів, що прибувають на станцію.
Таблиця 1 – Розклад прибуття поїздів у розформування
| № потягу |
Момент прибуття |
Кількість вагонів |
№ потягу |
Момент прибуття |
Кількість вагонів |
№ потягу |
Момент прибуття |
Кількість вагонів |
| години |
хвилини |
години |
хвилини |
години |
хвилини |
| 1 |
0 |
44 |
47 |
35 |
15 |
15 |
53 |
69 |
5 |
14 |
45 |
| 2 |
1 |
15 |
47 |
36 |
15 |
28 |
53 |
70 |
5 |
19 |
46 |
| 3 |
1 |
19 |
48 |
37 |
16 |
12 |
51 |
71 |
7 |
18 |
45 |
| 4 |
1 |
28 |
54 |
38 |
16 |
24 |
52 |
72 |
7 |
45 |
46 |
| 5 |
1 |
48 |
53 |
39 |
17 |
35 |
51 |
73 |
9 |
22 |
47 |
| 6 |
2 |
29 |
54 |
40 |
17 |
48 |
51 |
74 |
9 |
28 |
47 |
| 7 |
2 |
38 |
52 |
41 |
18 |
16 |
50 |
75 |
9 |
49 |
47 |
| 8 |
3 |
10 |
54 |
42 |
18 |
55 |
49 |
76 |
10 |
11 |
48 |
| 9 |
3 |
36 |
52 |
43 |
18 |
59 |
50 |
77 |
11 |
35 |
51 |
| 10 |
4 |
25 |
53 |
44 |
19 |
08 |
49 |
78 |
12 |
18 |
48 |
| 11 |
6 |
09 |
53 |
45 |
19 |
19 |
45 |
79 |
12 |
22 |
52 |
| 12 |
6 |
33 |
51 |
46 |
19 |
23 |
46 |
80 |
13 |
29 |
55 |
| 13 |
7 |
44 |
52 |
47 |
19 |
29 |
45 |
81 |
13 |
32 |
55 |
| 14 |
7 |
49 |
51 |
48 |
19 |
33 |
46 |
82 |
13 |
39 |
54 |
| 15 |
7 |
55 |
51 |
49 |
19 |
58 |
47 |
83 |
13 |
42 |
53 |
| 16 |
8 |
22 |
50 |
50 |
20 |
24 |
48 |
84 |
14 |
35 |
54 |
| 17 |
10 |
42 |
49 |
51 |
20 |
56 |
55 |
85 |
15 |
13 |
52 |
| 18 |
10 |
48 |
50 |
52 |
21 |
49 |
55 |
86 |
15 |
16 |
54 |
| 19 |
10 |
52 |
49 |
53 |
22 |
36 |
54 |
87 |
15 |
22 |
52 |
| 20 |
11 |
16 |
45 |
54 |
22 |
45 |
53 |
88 |
15 |
42 |
53 |
| 21 |
11 |
44 |
46 |
55 |
22 |
48 |
54 |
89 |
16 |
18 |
53 |
| 22 |
12 |
10 |
45 |
56 |
23 |
23 |
52 |
90 |
16 |
42 |
51 |
| 23 |
12 |
15 |
46 |
57 |
0 |
14 |
54 |
91 |
17 |
22 |
52 |
| 24 |
12 |
28 |
47 |
58 |
0 |
16 |
52 |
92 |
17 |
29 |
51 |
| 25 |
12 |
33 |
47 |
59 |
0 |
26 |
53 |
93 |
17 |
34 |
51 |
| 26 |
12 |
47 |
48 |
60 |
1 |
29 |
53 |
94 |
18 |
18 |
50 |
| 27 |
12 |
55 |
47 |
61 |
2 |
24 |
51 |
95 |
18 |
37 |
49 |
| 28 |
12 |
59 |
47 |
62 |
2 |
44 |
52 |
96 |
18 |
48 |
50 |
| 29 |
13 |
06 |
48 |
63 |
3 |
15 |
51 |
97 |
19 |
17 |
49 |
| 30 |
13 |
09 |
53 |
64 |
3 |
25 |
51 |
98 |
19 |
24 |
45 |
| 31 |
14 |
08 |
54 |
65 |
4 |
08 |
50 |
99 |
19 |
30 |
46 |
| 32 |
14 |
10 |
52 |
66 |
4 |
17 |
49 |
100 |
19 |
44 |
45 |
| 33 |
14 |
47 |
54 |
67 |
4 |
26 |
50 |
101 |
19 |
55 |
46 |
| 34 |
15 |
10 |
52 |
68 |
4 |
39 |
49 |
Потрібно визначити параметри:
- вхідного потоку поїздів;
- розподілення кількості вагонів у поїзді;
- побудувати графіки щільності розподілення інтервалів прибуття.
Частина 2. Оптимізація взаємодії залізничного і річкового транспорту при перевезенні мінімально - будівельних вантажів
Таблиця 2.1
| Перероблювальна спроможність порту, тыс.т |
В1
|
В2
|
В3
|
В5
|
В6
|
В7
|
В8
|
| 180 |
106 |
155 |
100 |
160 |
- |
- |
| Вартість перевалки 1 т вантажу з річкового транспорту на залізничний, ум.гр.од. |
0,65 |
0,45 |
0,38 |
0,25 |
0, 3 |
0,8 |
0,65 |
Таблиця 2.2
| Потужність пунктів споживання |
| Пункти споживання |
Бр |
Мс |
О |
В3
|
В5
|
В7
|
В8
|
Л |
| Обсяг споживання, тис.т |
150 |
200 |
135 |
280 |
200 |
165 |
190 |
140 |
Таблиця 2.3
| Обсяг виробництва мінерально-будівельних вантажів, тис. т. |
Q1
|
780 |
| Q2
|
360 |
| Q3
|
190 |
| Вартість 1 т-км під час перевезення вантажів, у.о. |
по двоколійній лінії |
0,3 |
| по одноколійної |
0,5 |
| Базисні коефіцієнти |
аб
|
0,81 |
| ак
б
|
0,85 |
| атоп
|
1,1 |
| Базисні видаткові ставки, у.о./т.-км. |
Еб
ор
|
0,6 |
| Етоп
|
0,2 |
| Кб
ор
|
4,8 |
| Коефіцієнт завантаження судна |
ε |
0,89 |
| Нормований коефіцієнт ефективності капітальних вкладень |
Ен
|
0,11 |
Частина 3. Розрахунок параметрів простою автомобілів та вагонів під вантажними операціями для доцільності введення нової системи регулювання методом імітаційного моделювання.
Таблиця 3
| № варіанту |
λа
, авто/год. |
t0
, хв. |
σ0
, хв |
| 8 |
2,8 |
28 |
8 |
ВСТУП
Транспорт задовольняє одну з найважливіших потреб людини — потребу в переміщенні. Проте практично жоден вид транспорту (окрім, мабуть, автомобільного, і то не завжди) не може самостійно забезпечити повний цикл переміщення по схемі "від дверей до дверей". Таке переміщення можливо лише при чіткій взаємодії окремих частин транспортного комплексу. Організація роботи такого комплексу, як єдина транспортна система України, є одночасно і складним завданням, і нинішньою для економіки країни потребою, яка відповідає інтеграційним тенденціям соціально-економічного розвитку людства, досягненням науково-технічного прогресу і стратегічним інтересам країни. При цьому єдність транспортної системи України не повинна означати її відособленості від шляхів сполучення суміжних держав і територій, особливо країн СНД, розвиток і функціонування яких протягом сторіч здійснювався в єдиному комплексі.
Розподіл вантажних перевезень між видами транспорту відображає місце та роль кожного з них в економіці країни. Основними кількісними показниками, що характеризують цей розподіл, є об’єм перевезень вантажів (в тоннах) і вантажооберт (в тонно-кілометрах), що здійснюються тим чи іншим видом транспорту. Найбільш узагальнюючим з цих двох натуральних показників є вантажооберт, що враховує не лише об’єм перевезених вантажів, але і дальність перевезень. На вантажооберт всіх видів транспорту великий вплив має розміщення виробничих сил, освоєння природних багатств в нових районах, розвиток промислового і сільськогосподарського виробництва, капітального будівництва і товарооберту в країні.
РОЗРАХУНКИ
ЧАСТИНА 1. ВИЗНАЧЕННЯ ПАРАМЕТРІВ ВХІДНОГО ПОТОКУ ПОЇЗДІВ, ЯКІ ПРИБУВАЮТЬ НА ЗАЛІЗНИЧНУ СТАНЦІЮ
1.1 Визначення параметрів вхідного потоку
Визначити параметри вхідного потоку можна аналізуючи інтервали прибуття поїздів або кількість поїздів, прибуваючих на станцію за якийсь час t (t= 1год.).
Інтервали (І) прибуття поїздів мають різні значення, тому треба розглядати їх як випадкові величини.
Визначення інтервалів прибуття і кількості поїздів (а) за одну годину зручно представити у вигляді таблиці (табл. 1.1.).
Треба скласти статистичний ряд інтервалів прибуття поїздів. Для групування інтервалів треба визначити крок (інтервал) групування спостережень. Крок групування визначається за формулою
 (1.1) (1.1)
де Іmax
, Іmin
- відповідно максимальний і мінімальний інтервал прибуття поїздів;
n - кількість інтервалів (n = 100).
Для нашого випадку
Іmax
= 140 хв., Imin
= 2 хв.

Виконуємо групування інтервалів у статистичний ряд з кроком ΔI=18,65 хв. (табл. 1.2).
Таблиця 1.1 – Інтервали прибуття і кількість поїздів за 1 годину
| № потягу |
Момент прибуття |
Кількість вагонів |
інтервал (хв) |
№ потягу |
Момент прибуття |
Кількість вагонів |
інтервал (хв) |
| години |
хвилини |
години |
хвилини |
| 1 |
0 |
44 |
47 |
31 |
52 |
21 |
49 |
55 |
47 |
| 2 |
1 |
15 |
47 |
4 |
53 |
22 |
36 |
54 |
9 |
| 3 |
1 |
19 |
48 |
9 |
54 |
22 |
45 |
53 |
3 |
| 4 |
1 |
28 |
54 |
20 |
55 |
22 |
48 |
54 |
35 |
| 5 |
1 |
48 |
53 |
41 |
56 |
23 |
23 |
52 |
51 |
| 6 |
2 |
29 |
54 |
9 |
57 |
0 |
14 |
54 |
2 |
| 7 |
2 |
38 |
52 |
32 |
58 |
0 |
16 |
52 |
10 |
| 8 |
3 |
10 |
54 |
26 |
59 |
0 |
26 |
53 |
63 |
| 9 |
3 |
36 |
52 |
49 |
60 |
1 |
29 |
53 |
55 |
| 10 |
4 |
25 |
53 |
104 |
61 |
2 |
24 |
51 |
20 |
| 11 |
6 |
09 |
53 |
24 |
62 |
2 |
44 |
52 |
31 |
| 12 |
6 |
33 |
51 |
71 |
63 |
3 |
15 |
51 |
10 |
| 13 |
7 |
44 |
52 |
5 |
64 |
3 |
25 |
51 |
43 |
| 14 |
7 |
49 |
51 |
6 |
65 |
4 |
08 |
50 |
9 |
| 15 |
7 |
55 |
51 |
27 |
66 |
4 |
17 |
49 |
9 |
| 16 |
8 |
22 |
50 |
140 |
67 |
4 |
26 |
50 |
13 |
| 17 |
10 |
42 |
49 |
6 |
68 |
4 |
39 |
49 |
35 |
| 18 |
10 |
48 |
50 |
4 |
69 |
5 |
14 |
45 |
5 |
| 19 |
10 |
52 |
49 |
24 |
70 |
5 |
19 |
46 |
119 |
| 20 |
11 |
16 |
45 |
28 |
71 |
7 |
18 |
45 |
27 |
| 21 |
11 |
44 |
46 |
26 |
72 |
7 |
45 |
46 |
97 |
| 22 |
12 |
10 |
45 |
5 |
73 |
9 |
22 |
47 |
6 |
| 23 |
12 |
15 |
46 |
13 |
74 |
9 |
28 |
47 |
21 |
| 24 |
12 |
28 |
47 |
5 |
75 |
9 |
49 |
47 |
22 |
| 25 |
12 |
33 |
47 |
14 |
76 |
10 |
11 |
48 |
84 |
| 26 |
12 |
47 |
48 |
8 |
77 |
11 |
35 |
51 |
43 |
| 27 |
12 |
55 |
47 |
4 |
78 |
12 |
18 |
48 |
4 |
| 28 |
12 |
59 |
47 |
7 |
79 |
12 |
22 |
52 |
67 |
| 29 |
13 |
06 |
48 |
3 |
80 |
13 |
29 |
55 |
3 |
| 30 |
13 |
09 |
53 |
59 |
81 |
13 |
32 |
55 |
7 |
| 31 |
14 |
08 |
54 |
2 |
82 |
13 |
39 |
54 |
3 |
| 32 |
14 |
10 |
52 |
37 |
83 |
13 |
42 |
53 |
53 |
| 33 |
14 |
47 |
54 |
23 |
84 |
14 |
35 |
54 |
38 |
| 34 |
15 |
10 |
52 |
5 |
85 |
15 |
13 |
52 |
3 |
| 35 |
15 |
15 |
53 |
13 |
86 |
15 |
16 |
54 |
6 |
| 36 |
15 |
28 |
53 |
44 |
87 |
15 |
22 |
52 |
20 |
| 37 |
16 |
12 |
51 |
12 |
88 |
15 |
42 |
53 |
36 |
| 38 |
16 |
24 |
52 |
71 |
89 |
16 |
18 |
53 |
24 |
| 39 |
17 |
35 |
51 |
13 |
90 |
16 |
42 |
51 |
40 |
| 40 |
17 |
48 |
51 |
28 |
91 |
17 |
22 |
52 |
7 |
| 41 |
18 |
16 |
50 |
39 |
92 |
17 |
29 |
51 |
5 |
| 42 |
18 |
55 |
49 |
4 |
93 |
17 |
34 |
51 |
44 |
| 43 |
18 |
59 |
50 |
9 |
94 |
18 |
18 |
50 |
19 |
| 44 |
19 |
08 |
49 |
11 |
95 |
18 |
37 |
49 |
11 |
| 45 |
19 |
19 |
45 |
4 |
96 |
18 |
48 |
50 |
29 |
| 46 |
19 |
23 |
46 |
6 |
97 |
19 |
17 |
49 |
7 |
| 47 |
19 |
29 |
45 |
4 |
98 |
19 |
24 |
45 |
6 |
| 48 |
19 |
33 |
46 |
25 |
99 |
19 |
30 |
46 |
14 |
| 49 |
19 |
58 |
47 |
26 |
100 |
19 |
44 |
45 |
11 |
| 50 |
20 |
24 |
48 |
32 |
101 |
19 |
55 |
46 |
| 51 |
20 |
56 |
55 |
53 |
Таблиця 1.2 – Групування інтервалів у статистичний ряд
| № розряду |
Межі розряду |
Середнє значення інтервалів, І |
Кількість спостережень, ni
|
Pi
|
Ii
Pi
|
Ii
2
Pi
|
h(I) |
| 1 |
2,00 |
20,65 |
11,3243243 |
53 |
0,53 |
6,00 |
67,97 |
0,02842029 |
| 2 |
20,65 |
39,30 |
29,972973 |
25 |
0,25 |
7,49 |
224,59 |
0,0134058 |
| 3 |
39,30 |
57,95 |
48,6216216 |
12 |
0,12 |
5,83 |
283,69 |
0,00643478 |
| 4 |
57,95 |
76,59 |
67,2702703 |
5 |
0,05 |
3,36 |
226,26 |
0,00268116 |
| 5 |
76,59 |
95,24 |
85,9189189 |
1 |
0,01 |
0,86 |
73,82 |
0,00053623 |
| 6 |
95,24 |
113,89 |
104,567568 |
2 |
0,02 |
2,09 |
218,69 |
0,00107246 |
| 7 |
113,89 |
132,54 |
123,216216 |
1 |
0,01 |
1,23 |
151,82 |
0,00053623 |
| 8 |
132,54 |
151,19 |
141,864865 |
1 |
0,01 |
1,42 |
201,26 |
0,00053623 |
| 100 |
1 |
28,29 |
1448,10 |
Далі проведемо розрахунок параметрів розподілення інтервалів прибуття.
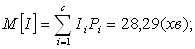
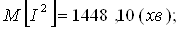
 (хв.) (хв.)

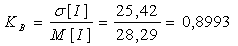
λ =  поїзд./хв. поїзд./хв.
На засаді розрахованих параметрів можна розрахувати параметр
Ерланга – K:
 (1.2) (1.2)

Приймаємо K = 1.
1.2 Побудова гістограми і функції розподілення інтервалів прибуття
Ордината гістограми визначається за формулою
hi
=Pi
/∆I (1.3)
Припустимо, що розподілення інтервалів прибуття підпорядковується закону Ерланга. Диференційна функція закону Ерланга має вигляд
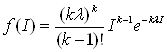 , (1.4) , (1.4)
Для К = 1 функція приймає вигляд:
 (1.5) (1.5)
Розрахунок f(I) і h(і) зручно представити у табличному вигляді (табл. 1.3)
Таблиця 1.3 – Ордината гістограми (hi) і диференційна функція (fi)

На засаді розрахунку будуємо гістограму і функцію розподілення інтервалів прибуття поїздів на сортувальну станцію (Рис.1.1).
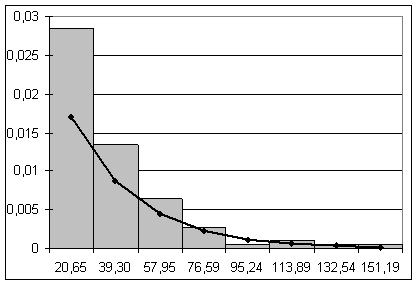
Рисунок 1.1 – Гістограма і функція розподілення інтервалів прибуття
1.3 Перевірка гіпотези про розподіл Ерланга інтервалів прибуття потягів по критерію згоди Пірсона
Для визначення міри розходження
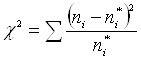
необхідно знати ймовірності Рі
*
попадання величини на кожний з інтервалів при обраному законі розподілу. Ймовірність попадання випадкової величини в інтервал визначається за формулою:
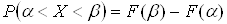
Теоретична ймовірність Рі
*
інтервалів визначеної величини в їх загальної сукупності дорівнює:

Але так як К=1, то

Обчислення приведенні в таблиці 1.4.
Таблиця 1.4

Складаємо таблицю 1.5 з якої знайдемо спостережне значення критерію . .
Таблиця 1.5
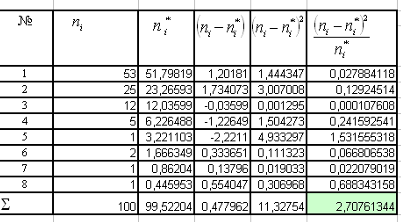
За таблицею критичних точок  рівню значущості a=0,05 і числу степінь волі r=s-3 (s – число розряду) знаходимо критичну точку правосторонню критичної області рівню значущості a=0,05 і числу степінь волі r=s-3 (s – число розряду) знаходимо критичну точку правосторонню критичної області  . . =11,1 , бо число ступенів свободи 5. =11,1 , бо число ступенів свободи 5.
Так як  =2,7 , то =2,7 , то  < < , бо 2,7 < 11,1. Отже, нема підстави відкидати гіпотезу про ерланговський закон розподілу вхідного потоку потягів на станцію. , бо 2,7 < 11,1. Отже, нема підстави відкидати гіпотезу про ерланговський закон розподілу вхідного потоку потягів на станцію.
1.4 Визначення параметрів вхідного потоку, аналізуючи кількість поїздів, які прибувають на станцію за годину
Складаємо статистичний ряд розподілення величини а - кількості поїздів за годину.
Величина а є випадковою до того ж дискретного типу.
М(а) = ∑ai
Pi
(1.6)
M(a2
) = ∑a2
i
Pi
(1.7)
D(а) = М(а2
) - (М(а))2
(1.8)
 (1.9) (1.9)
Розрахунок приведено у таблиці 1.6.
Таблиця 1.6 – Статистичний ряд розподілення кількості поїздів за годину
| № |
ai
|
ni
|
Pi
|
M(a) |
M(a2
) |
| 1 |
0 |
4 |
0,09091 |
0 |
0 |
| 2 |
1 |
9 |
0,20455 |
0,20454545 |
0,20455 |
| 3 |
2 |
14 |
0,31818 |
0,63636364 |
1,27273 |
| 4 |
3 |
10 |
0,22727 |
0,68181818 |
2,04545 |
| 5 |
4 |
4 |
0,09091 |
0,36363636 |
1,45455 |
| 6 |
5 |
1 |
0,02273 |
0,11363636 |
0,56818 |
| 7 |
6 |
1 |
0,02273 |
0,13636364 |
0,81818 |
| 8 |
7 |
1 |
0,02273 |
0,15909091 |
1,11364 |
| Σ |
44 |
1 |
2,29545455 |
7,47727273 |
Параметри розподілення величини a такі
М(а) = ∑ai
Pi
= 2,29 поїзда
M(a2
) = ∑a2
i
Pi
= 7,47 поїздів
D(а) = М(а2
) - (М(а))2
= 7,47 – 2,292
= 2,23 поїздів
 поїздів поїздів
1.5 Побудова графіку статистичного розподілу величини поїздів і функції їх розподілу
При аналізі багатьох випадкових дискретних процесів використовують розподіл Пуассона, і ми зробимо припущення, що потік поїздів підпорядкований Пауссонівському розподілу. Імовірність того, що в одиницю часу (t) відбудеться рівно а випадків визначається за формулою:
 , (1.10) , (1.10)
Оскільки t=1 година, маємо
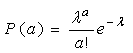 (1.11) (1.11)
де λ - середня кількість випадків за одиницю часу.
λ = М(а) = 2,29 поїзда/год.
Визначимо по закону Пуассона розподіл ймовірностей.
Розрахунок зведемо у табл. 1.7.
Таблиця 1.7 – Розподіл ймовірностей по закону Пуассона
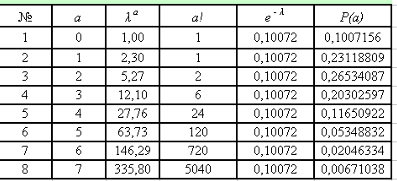
На засаді даних, розрахованих у табл.1.7 і табл.1.6 будуємо імовірнісну (Ра) і статистичну (Рi
) криві.
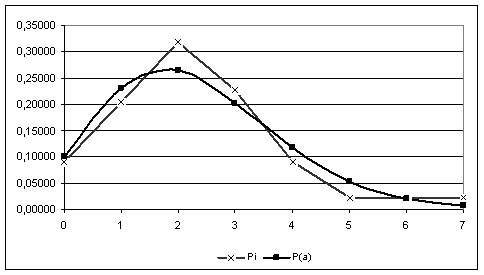
Рисунок 1.2 – Графік імовірнісної і статистичної кривої
Проаналізувавши графіки статистичної і імовірнісної кривих можна зробити висновок, що вхідний потік поїздів може бути описано законом Пуассона.
1.6 Визначення параметрів розподілення кількості вагонів у поїзді
Будемо розглядати кількість вагонів у поїзді як випадкову дискретну величину, яка змінюється в межах від 45 до 55 вагонів. Для визначення параметрів необхідно збудувати статистичний ряд розподілення кількості вагонів у потязі.
Таблиця 1.8 – Статистичний ряд розподілення кількості вагонів у потязі
| Кількість |
Частота спостережень, ki
|
Pi
= ki
/ Σki
|
mi
· Pi
|
mi
2
·Pi
|
| вагонів, mi
|
| 45 |
8 |
0,07921 |
3,56436 |
160,39604 |
| 46 |
8 |
0,07921 |
3,64356 |
167,60396 |
| 47 |
10 |
0,09901 |
4,65347 |
218,712871 |
| 48 |
6 |
0,05941 |
2,85149 |
136,871287 |
| 49 |
8 |
0,07921 |
3,88119 |
190,178218 |
| 50 |
8 |
0,07921 |
3,96040 |
198,019802 |
| 51 |
13 |
0,12871 |
6,56436 |
334,782178 |
| 52 |
13 |
0,12871 |
6,69307 |
348,039604 |
| 53 |
12 |
0,11881 |
6,29703 |
333,742574 |
| 54 |
11 |
0,10891 |
5,88119 |
317,584158 |
| 55 |
4 |
0,03960 |
2,17822 |
119,80198 |
| Σ |
101 |
1 |
50,16832 |
2525,73267 |
Проведемо розрахунок параметрів розподілення кількості вагонів у поїзді
M(m)= = 50,17 вагонів; = 50,17 вагонів;
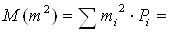 2525,73 вагонів 2525,73 вагонів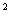 ; ;
 вагонів вагонів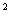 ; ;
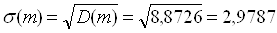 вагонів; вагонів;

1.7 Визначення параметрів тривалості обробки складів поїздів у парку прийому
Тривалість обробки визначається за формулою

де  - середній час обробки одного вагону, ( - середній час обробки одного вагону, ( =0,97хв); =0,97хв);
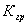 - кількість груп в бригаді ПТО, - кількість груп в бригаді ПТО, 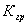 =4 =4
  , ,
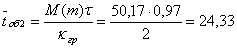  , ,
  , ,
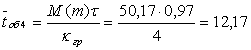  ; ;
Середньоквадратичне відхилення обслуговування одного вагона:
 (1.13) (1.13)
 - коефіцієнт варіації обробки одного вагона, ( - коефіцієнт варіації обробки одного вагона, ( =0,8 хв.) =0,8 хв.)
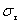 =0,8 ∙ 0,97=0,776 (хв/ваг). =0,8 ∙ 0,97=0,776 (хв/ваг).
Дисперсія обслуговування одного вагона:
D( ) = ) =  (1.14) (1.14)
D( ) = 0,7762
= 0,602 хв2
. ) = 0,7762
= 0,602 хв2
.
1.8 Визначення тривалості обробки поїздів і її параметри при різній кількості груп у бригаді ПТО
Оскільки тривалість обробки залежить від кількості вагонів і тривалості обробки одного вагона, а ці величини є випадкові, то тривалість обробки теж є випадковою величиною. Основними параметрами для розрахунку тривалості обробки є:
Математичне очікування тривалості обробки
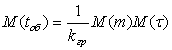 = = (1.15) (1.15)
Дисперсія тривалості обробки
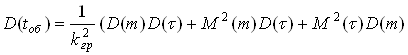 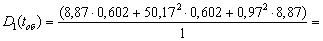 1529,28 1529,28
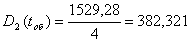


Середньоквадратичне відхилення тривалості обробки:
 (1.17) (1.17)
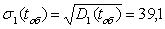



Коефіцієнт варіації тривалості обробки
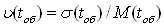 (1.18) (1.18)
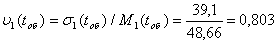



Інтенсивність обслуговування
 (1.19) (1.19)
 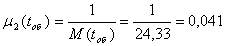
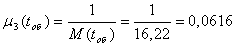 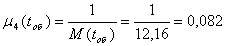
Коефіцієнт завантаження бригади ПТО:
 (1.20) (1.20)

 ; ;

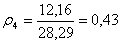
Параметри розподілення тривалості обробки будемо визначати для різної кількості груп у бригаді ПТО (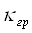 =1,2,3,4). Розрахунок зведемо у таблицю 1.9. =1,2,3,4). Розрахунок зведемо у таблицю 1.9.
Таблиця 1.9 – Параметри розподілення тривалості обробки
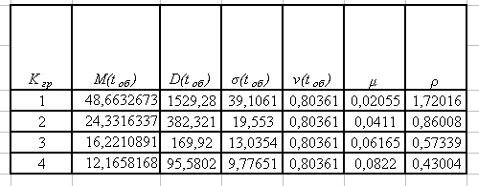
Аналізуючи коефіцієнт завантаження бригади ПТО можна зробити такий висновок, що чим більше кількість груп у бригаді ПТО, тим менше тривалість обробки поїздів. Оскільки при kгр
=1,ρ=1,72 бригада ПТО не зможе повністю виконати заданий об’єм роботи (оскільки ρ> 1). Використання 3 та 4 груп в бригаді не ефективне.
Найефективнішою бригадою являється друга (ρ=0,80), оскільки дане значення є близьким до оптимального коефіцієнта завантаження бригади ПТО, що становить від 0,82 до 1.
перевезення вантаж оптимальний транспорт
ЧАСТИНА 2. ОПТИМІЗАЦІЯ ВЗАЄМОДІЇ ЗАЛІЗНИЧНОГО І РІЧКОВОГО ТРАНСПОРТУ ПРИ ПЕРЕВЕЗЕННІ МІНІМАЛЬНО - БУДІВЕЛЬНИХ ВАНТАЖІВ
Потрібно розробити оптимальний план взаємодії залізничного і річкового транспорту під час перевезення мінерально-будівельних вантажів із трьох пунктів видобутку — Al
,, А 2
, А3
— у 8 пунктів споживання — Бр, Мс, О, В3
, В5
, В7
, В8
, Л. Перевалка вантажу з залізниці на воду і назад може здійснюватися в п'ятьох портах – B1
, В2
, В3
, В5
, В6
. Перероблювальна спроможність портів по перевалці вантажів із залізничного транспорту на річковий і вартість перевалки 1 т у прямому і зворотному напрямках приведені в табл. 2.1.
Таблиця 2.1
| Перероблювальна спроможність порту, тис.т |
В1
|
В2
|
В3
|
В5
|
В6
|
В7
|
В8
|
| 180 |
106 |
155 |
100 |
160 |
- |
- |
| Вартість перевалки 1 т вантажу з річкового транспорту на залізничний, ум.гр.од. |
0,65 |
0,45 |
0,38 |
0,25 |
0, 3 |
0,8 |
0,65 |
Обсяг виробництва мінерально-будівельних вантажів: Q1
= 780 тис.т, Q2
= 360 тис.т, Q3
= 190 тис.т. Дані про потужність пунктів споживання приведені в таблиці 2.2.
Таблиця 2.2
| Потужність пунктів споживання |
| Пункти споживання |
Бр |
Мс |
О |
В3
|
В5
|
В7
|
В8
|
Л |
Разом |
| Обсяг споживання, тис. т |
150 |
200 |
135 |
280 |
200 |
165 |
190 |
140 |
1460 |
Схема полігона транспортної мережі і відстані між вантажними пунктами показані на рис. 2.1.
Перевезення вантажів річковим транспортом здійснюються судами типу 10. Вартість 1 т-км під час перевезення вантажів по двоколійній лінії прийнята 0,3 ум.гр.од., а по одноколійної — 0,5 ум.гр.од.
2.1 Визначення середніх витрат на перевезення 1 т вантажу по ділянках транспортної мережі
На першому етапі визначають середні витрати на перевезення 1 т вантажу по ділянках транспортної мережі. Наприклад, для двоколійної ділянки Мс— О, використовуючи вихідні дані,
С = 0,3·209 = 62,7 (ум.гр.од.)
Аналогічно розраховані інші значення вартості перевезення 1 т вантажу по ділянках залізничної мережі.
Розрахунок питомих витрат на перевезення вантажу між портами річковим транспортом виконаний по формулі (2.1).
Питомі приведені витрати на перевезення вантажу річковим транспортом:
 (2.1) (2.1)
де 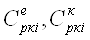 - відповідно експлуатаційні витрати і капітальні вкладення на - відповідно експлуатаційні витрати і капітальні вкладення на
перевезення 1 т вантажу річковим транспортом.
Експлуатаційні витрати:
 (2.2) (2.2)
де ε – коефіцієнт завантаження судна; Еор
– видаткова ставка по операції по організації руху; Епк
, Еоч
, Ешл
, Езм
– видаткові ставки на початково-кінцеві операції чекання відправлення судів, шлюзування, операції зміни тяги; Ен-в
, Ешг
, Епв
– відповідно видаткові ставки на операції при стоянці суден під навантаженням і вивантаженням, на витрати по колійному господарству і перевалка вантажу в шляху; ρik
– виправлення, що враховує вплив плавання навантажених або порожніх судів на швидкість руху. Якщо для перевезення вантажу використовуються спеціалізовані судна, що йдуть назад порожніми, то випливає просумувати ρik
lki
у навантаженому і зворотному напрямках.

Рисунок 2.1 – Полігон транспортної мережі
Капітальні витрати:
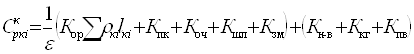 (2.3) (2.3)
Значення видаткових ставок у формулі (2.3) аналогічні відповідним величинам, використовуваним при розрахунку експлуатаційних витрат.
У розглянутому прикладі витрати на початково-кінцеві операції, чекання відправлення судів, на стоянку судів під навантаженням і вивантаженням, на перевалку вантажу в шляху, на колійне господарство не залежать від розподілу перевезень між причалами і тому в подальших розрахунках не враховуються.
Витрати на шлюзування судів, операції зміни тяги відсутні. Тому формула (2.2) спроститься:
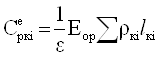
Видаткова ставка по операції організації руху:
 (2.5) (2.5)
де аб
, атоп
– базисні коефіцієнти ; Еб
ор
, Етоп
– базисні видаткові ставки.
Питомі експлуатаційні витрати на перевезення вантажу залізницею:
Сж
= Епк
+ Еор
lж
+ Епп
(2.6)
де Епк
, Еор
, Епп
– відповідно видаткова ставка по початково-кінцевих операціях, операції організації руху, змістові постійних пристроїв .
Питомі капітальні вкладення в рухомий склад і постійні пристрої:
Ск
ж
= Кпк
+ Кор
lж
+ Кпп
lж
, (2.7)
де– видаткові ставки по капітальних вкладеннях, аналогічні експлуатаційним.
Питома вартість вантажної маси:
Кгрi
= 100Ц· lj
/ 24·365υгр
(2.8)
де Ц – ціна 1 т вантажу; lj
– відстань перевезенню на j-м транспорті; υгр
середня швидкість доставки вантажу.
Розподіл обмеженого ресурсу між взаємодіючими видами транспорту виникає внаслідок різної ефективності використання капітальних вкладень або іншого виду ресурсів на j-му транспорті. Рішення такої задачі можливо методом динамічного програмування. Основною вимогою методу є сепарабельність показника ефективності функціонування складної транспортної системи.
Сутність динамічного програмування зводиться до розгляду багатокрокового процесу, у якому на кожнім кроці оптимізується функція тільки одного перемінного. Результати, отримані для одного кроку, запам'ятовуються і використовуються на наступних кроках.
Спростивши формулу (2.3) стосовно до умов розглянутого приклада одержимо:
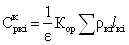
Видаткова ставка:
Кор
= ак
б
Кб
ор
(2.10)
де ак
б
– базисний коефіцієнт; Кб
ор
– базисна видаткова ставка,
Кор
= 0,85∙4,80 = 4,08 (ум.гр.од./10 т.-км.)
Використовуючи видаткові ставки, легко одержати загальні вирази для розрахунку
Се
р
, Ск
р
і Ср
.
Для умови задачі:
аб
= 0,81, атоп
= 1,1 , Еб
ор
= 0,6 , Етоп
= 0,2.
Підставимо чисельні значення:
Еор
= 0,81·0,6 + 1,1·0,2 = 0,706 (ум.гр.од./10 т-км).
Якщо перевезення виконується за течією, то:
Се
р
=0,706·10-1
· 1,16 l = 0,0818 l (ум.гр.од./т-км);
Ск
р
=4,08 ·10-1
· 1,16 l = 0,473 l (ум.гр.од./т-км);
Ср
= 0,0818l + 0,11 · 0,473 l = 0,133 l (ум.гр.од./т-км).
Якщо перевезення виконується проти течії, то:
Се
р
=0,706·10-1
· 1,47 l = 0,104 l (ум.гр.од./т-км);
Ск
р
=4,08 · 10-1
· 1,47 l = 0,599 l (ум.гр.од./т-км);
Ср
= 0,104 l + 0,11 · 0,599 l = 0,17 l (ум.гр.од./т-км).
Наприклад, при доставці 1 тис.т піску з пункту видобутку Д1 у порт А1
Се
р11
= 1/0,89·0,706(1,47·2 + 1,16·2) = 4,17 (ум.гр.од.);
Ск
р11
= 1/0,89·4,08(1,47·2 + 1,16·2) = 24,11 (ум.гр.од.).
У загальному вигляді
Cе
pki
= 1/0,89·0,706·2,63lik
= 2,086 lik
;
Ск
pik
= 1/0,89·4,08·2,63 lik
= 12,056 lik
;
Ср
кi
= 2,086lik
+ 0,11∙12,056 lik
= 3,41 lik
Наприклад, Ср11
= 3,41∙2 = 6,82 (ум.гр.од.).
За допомогою цих виражень визначені дільничні витрати під час перевезення 1 т вантажу річковим транспортом.
Наприклад, для ділянки В1
— В10
і перевезенню вантажу за течією
Ср
= 0,133·160 = 21,28 (ум.гр.од.)
У зворотному напрямку
Ср
= 0,17·160 = 27,2 (ум.гр.од.)
Результати розрахунків приведені на рис. 2.2.

Рисунок 2.2 – Розрахунковий полігон транспортної мережі
На другому етапі встановлюються найкоротші (по вартості) шляху доставки вантажу: з пунктів виробництва в пункти споживання безпосередньо залізничним транспортом, з пунктів виробництва в порти перевалки, з портів перевалки в пункти призначення і, нарешті, найкоротші шляхи між портами перевалки.
2.2 Визначення найкоротших (по вартості) шляхів доставки вантажу
Пошук найкоротших шляхів виконується по спеціальних алгоритмах. Послідовність обчислень наступна:
1. Усім вершинам транспортної мережі привласнюється потенціал, свідомо більший усіх відстаней на мережі иі
=∞.
2. Вершині, від якої визначається найкоротший шлях, привласнюється потенціал и0
= 0. Величина позначається спеціальною міткою (наприклад, «мінус»).
3. Перевіряється наявність на мережі вершин з мітками. Якщо їх немає рішення кінчене, якщо є — переходимо до наступного пункту.
4. Вибирається чергова вершина к з міткою. Вибирається перша з ще непереглянутих дуг, що виходять з вершини к. Перевіряється умова
uк
= СКj
< uj
,
де ик
, uj
— потенціали вершин k і j; Сkj
— «довжина» (вартість) дуги. Якщо умова виконується, переходимо до пункту 5,якщо немає — до пункту 6.
5. Величина ик
+ Ckj
привласнюється як новий потенціал вершині j, що міститься міткою. Надалі вершина до іменується «суміжної» для j , якщо існує дуга, що веде від однієї з них до інший, і потенціал uj
розрахований виходячи з потенціалу ик
.
6. Перевіряється, чи всі дуги, що виходять з вершини к, переглянуті. Якщо ні, переходимо до пункту 4, якщо так, знімається мітка з вершини к, і переходимо до пункту 3.
У табл. 2.3 приведені питомі витрати на перевезення вантажу залізничним транспортом у пункти перевалки (ум.гр.од. /т).
Таблиця 2.3 – Питомі витрати на перевезення вантажу залізничним транспортом у пункти перевалки (ум.гр.од. /т)
| Пункт видобутку |
Пункти перевалки |
| В1
|
В2
|
В3
|
В5
|
В6
|
A1
А2
А3
|
6/6,65
94,5/95,15
106,3/106,95
|
115/115,45
71,5/71,95
200,3/200,75
|
135/135,38
91,5/91,88
220,3/220,68
|
192,3/192,55
91,8/92,05
169/169,25
|
114,5/114,8
71/71,3
199,8/200,1
|
У чисельнику приведені витрати на доставку вантажу залізничним транспортом у порти перевалки, знаменнику зазначені витрати з урахуванням вартості перевалки.
Транспортні витрати на доставку 1 т вантажу залізничним транспортом з пунктів видобутку в пункти споживання по прямому варіанту приведені в табл. 2.4 (ум.гр.од. /т).
Таблиця 2.4 –Витрати на доставку 1 т вантажу залізничним транспортом з пунктів видобутку в пункти споживання по прямому варіанту (ум.гр.од. /т).
| Пункти видобутку |
Пункти споживання |
| Бр |
Мс |
О |
В3
|
В5
|
В7
|
В8
|
Л |
| А1
|
108,3 |
88,8 |
151,5 |
135 |
192,3 |
144,5 |
180 |
243 |
| А2
|
199 |
176 |
174,5 |
91,5 |
91,8 |
98 |
136,5 |
199,5 |
| А3
|
126 |
167,5 |
230,2 |
220,3 |
169 |
229,8 |
265,3 |
295,5 |
Аналогічні розрахунки виконані для визначення витрат на доставку вантажу з портів перевалки в пункти споживання залізничним транспортом.
При складанні матриці витрат Cкj, з метою спрощення подальших розрахунків для споживачів, доставка вантажу в які при використанні річкового транспорту вимагає великих витрат, чим доставка залізничним транспортом, умовно приймається, що величина Cкj
= М (свідомо велика вартість).
Наприклад, якщо вантаж доставляти в пункт споживання О після перевалки на річковий транспорт у порту В1
і перевезення його по річці до порту В8
з наступною перевалкою на залізницю, то приведені витрати:
С13
= Ср
18
+ Ср
8
+ Сп
+ Сж
(2.11)
де Ср
18
– витрати на перевезення вантажу річковим транспортом між портами В1
і B8
; Сп
— витрати на перевалку вантажу в порту B8
; Сж
— витрати на доставку вантажу з порту перевалки В8
у пункт О.
Використовуючи дані рис.2.2 і з огляду на, що Сп
=0,65 ум.гр.од./тону, одержимо
Ср13
= 21,28+29,26+14,45+13,6+6,8+45,5+28,9+0,65+38 = 198,44 (ум.гр.од.)
Якщо вантаж доставляти з пункту В1
без перевалки на річковий транспорт, то
Сж
13
=6+10,8+35,1+42,9+62,7=157,5 (ум.гр.од.)
Тому що Сж
13
< Ср
13
, то С13
= М.
Аналогічні розрахунки виконані для інших варіантів доставки вантажу з портів перевалки в пункти споживання. Питомі витрати на доставку вантажу з портів перевалки в пункти споживання (ум.гр.од. /т) приведені в табл.2.5.
Таблиця 2.5 – Питомі витрати на доставку вантажу з портів перевалки в пункти споживання (ум.гр.од. /т)
| Порт перевалки |
Пункти споживання |
| Бр |
Мс |
О |
В3
|
В5
|
В7
|
В8
|
Л |
| В1
|
М |
М |
М |
82,37 |
80,15 |
11,69 |
114,94 |
206,65 |
| В2
|
190,19 |
108,1 |
74,35 |
М |
51,65 |
33,1 |
51,65 |
М |
| В3
|
204,15 |
135 |
116,55 |
М |
54,21 |
60 |
78,55 |
М |
| В5
|
217,12 |
173,72 |
155,27 |
69,4 |
М |
98,72 |
117,27 |
М |
| В6
|
218,78 |
М |
67,55 |
45,31 |
68,84 |
М |
29,55 |
М |
2.3 Формування економіко-математичної моделі
Другий етап рішення задачі полягає у формуванні економіко-математичної моделі, що враховує технічні і технологічні обмеження. У випадку відсутності обмежень по пропускній здатності залізничних станцій, ліній і портів перевалки з річкового транспорту на залізничний оптимальний варіант взаємодії забезпечується, якщо будуть знайдені позитивні значення перемінних Xiк
, Xкj
, Xij
і при цьому досягається мінімум функції
 (2.12) (2.12)
де Cik
— вартість доставки 1 т вантажу i-го пункту видобутку в к-й порт перевалки з урахуванням витрат на перевалку; С'ij
— витрати на перевезення 1 т вантажу з i-го пункту видобутку в j-й пункт споживання по прямому варіанті; С"kj
— вартість перевезення 1т вантажу з к-ro пункту в j-й район з урахуванням витрат на перевалку з води на залізницю.
Крім того, перемінні повинні задовольняти наступним умовам:
 - вимога збалансованості обсягів виробництва обсягам споживання - вимога збалансованості обсягів виробництва обсягам споживання
 (2.13) (2.13)
Найважливішим обмеженням є облік перероблювальної спроможності річкових портів:
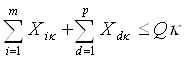 (2.14) (2.14)
де Qk
- перероблювальна спроможність к-го порту.
Для рішення задачі складають спеціальну таблицю, що складається з квадрантів (рис. 2.3).

Рисунок 2.3 – Приклад рішення задачі на ПК
У верхньому лівому квадранті відбивають зв'язки між пунктами видобутку і портами перевалки з залізничного транспорту на річковий, у нижньому правом — взаємозв'язку між портами перевалки і пунктами споживання вантажу. Нижній лівий квадрант представляє квадратну матрицю, у якій відбивають зв'язки між портами перевалки з залізничного транспорту на річковий. Ці зв'язки не мають змісту, тому постачання дозволені лише по головній діагоналі , де вартість перевалки приймається рівної нулеві. Інші клітки лівого нижнього квадранта заповнюються «забороненими» тарифами — коефіцієнтами М. На фіктивній діагоналі розмістяться значення перемінних, котрі відбивають недовикористану частину потужності портів перевалки, тобто їхній резерв. У верхньому правому квадранті відбивають прямі зв'язки пунктів видобутку зі споживачами.
З огляду на, що перероблювальна спроможність комунікацій, що проходять через порти перевалки з залізничного транспорту на річковий, є часто обмеженої, перевіряється спільність рівняння (2.7), а також двох додаткових:
 (2.15) (2.15)
Далі задача розв’язується в середовищі Excel за допомогою меню СервісÞПошук рішення.
2.4 Аналіз оптимального розв’язку
Аналіз оптимального розв’язку показує:
1) Пункт Мс потрібно забезпечувати залізничним транспортом з пункту А1
, Пункт В5
з пункту А2.
2) З пункту видобування А1
вантаж потрібно завозити в пункт Мс – 200 тис. тон вантажу та в В3
– 280 тис. тон. З пункту видобування А2
вантаж надходить у розмірі 149тис. тон на В5
, та 65 тис. тон на В7
.
3) У портах В3
, В5
не слід відкривати причали для перевантаження мінерально-будівельних вантажів із залізничного транспорту на річковий.
4) Реалізація такого плану зможе забезпечити оптимальний режим взаємодії залізничного і річкового транспорту при перевезенні мінерально-будівельних матеріалів у даному економічному районі. Витрати на перевезення вантажу складають:
Е=180*6,65+106*115,45+14*114,8+200*88,8+280*135+146*71,3+149*91
8+65*98+150*126+40*169+60*29,55=128492,90 (тис. т).
ЧАСТИНА 3. РОЗРАХУНОК ПАРАМЕТРІВ ПРОСТОЮ АВТОМОБІЛІВ ТА ВАГОНІВ ПІД ВАНТАЖНИМИ ОПЕРАЦІЯМИ МЕТОДОМ ІМІТАЦІЙНОГО МОДЕЛЮВАННЯ
Визначити доцільність створення на вантажному дворі станції системи регулювання, що забезпечує збір і збереження інформації про місцезнаходження автомобілів на вантажних фронтах, стану вантажно-розвантажувальних механізмів і прийняття рішень про їхнє використання та передачу команд водіям автомобілів з метою підвищення ефективності взаємодії автомобільного та залізничного видів транспорту під час перевезення тарно-штучних вантажів. Відвантаження вантажів здійснюється двома бригадами з двох секцій ангарного складу. Автомобільний транспорт працює протягом 8 год. У процесі статистичного дослідження було встановлено, що прибуття автомобілів на вантажний двір носить випадковий характер і описується законом Пуассона з інтенсивністю  =2,8 авто/год.. Коливання тривалості обслуговування автомобіля в секції складу описується нормальним законом розподілу з параметрами: математичне очікування t0
= 28 хв., середнє квадратичне відхилення σ0
= 8 хв. =2,8 авто/год.. Коливання тривалості обслуговування автомобіля в секції складу описується нормальним законом розподілу з параметрами: математичне очікування t0
= 28 хв., середнє квадратичне відхилення σ0
= 8 хв.
Капітальні вкладення, необхідні для впровадження системи регулювання, 5000у.г.о., додаткові річні експлуатаційні витрати, зв’язані з її експлуатацією, 4000у.г.о.
Традиційною технологією організації взаємодії автомобільного і залізничного транспорту на вантажних фронтах станцій не передбачається можливість оперативного регулювання підведення автомобілів до секцій складів. Зв'язано це з відсутністю системи, що забезпечує збір, збереження і передачу інформації про стан вантажного фронту, тривалості вивантаження (навантаження) автомобілів. У результаті створюються ситуації, коли виникають простои автомобілів в одних вантажних фронтів, коли інші в цей час вільні. Устаткування вантажних дворів залізничних станцій такою системою дозволяє скоротити непродуктивні простої автомобілів, підвищити перероблювальну спроможність вантажних фронтів, скоротити простої вагонів, зменшити потреба в складських приміщеннях. Однак упровадження такої системи вимагає додаткових витрат, і тому доцільність переходу до нової технології повинна визначатися техніко-економічними розрахунками.
Доцільність введення нової системи регулювання (рішення про адресування автомобіля до вантажного фронту передається диспетчером за інформацією про стан вантажного фронту)
Эа
+ Ен
Ка
≤ ΔЭ + Ен
ΔКа,
(3.1)
де Эа
, Ка — експлуатаційні витрати і капітальні вкладення, необхідні для впровадження системи регулювання підведення автомобілів до вантажних фронтів; ΔЭ — економія експлуатаційних витрат у системі «автомобільний транспорт — вантажний фронт — залізничний транспорт»:
ΔЭ = 365 еа-г
ΔТа
, (3.2)
еа-г
-вартість 1 автомобиле-ч; ΔТа
-скорочення простою автомобілів за добу в результаті регулювання підведення автомобілів; ΔКа
— капітальні вкладення в рухомий склад.
Для розрахунку параметрів, що входять у формулу (3.1), необхідно установити простої автомобілів і вагонів під вантажними операціями при традиційній технології і впровадженні системи регулювання. При ймовірнісному характері транспортних процесів виконати це найбільше повно можливо методом імітаційного моделювання.
Встановимо спочатку випадковий характер потоку автомобілів, що надходить на вантажні фронти.
Якщо інтенсивність потоку описується розподілом Пуассона, то інтервали між прибуваючими автомобілями описуються залежністю
 або або 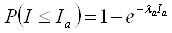 , , 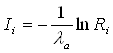 , (3.3) , (3.3)
де Ri
— випадкові числа з рівномірним їхнім розподілом в інтервалі від 0 до 1 ;
Ii
- інтервал між послідовно прибуваючими автомобілями.
3.1 Моделювання інтервалів між автомобілями
Моделювання інтервалів між автомобілями здійснимо в наступній послідовності:
1. Витягнемо довільно з додатка 1 рівномірно розподілених на інтервалі 0—1 випадкових чисел. Кількість імітацій інтервалів:
 (3.4) (3.4)
де х — величина, що береться з таблиці значень інтеграла імовірностей у залежності від значення Р: х =1,96 при Р= 0,95;
ε — допустима помилка.
2. Використовуючи вираз (3.3) і витягнуті випадкові числа, установимо інтервали між автомобілями. Наприклад, інтервал між першим і другим автомобілями
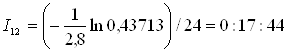
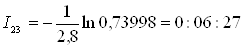
Результати інших розрахунків приведені в додатку 3.
Тривалість вантажної операції установимо, використовуючи довільно витягнуті з додатка 2 нормальні випадкові відхилення. Так, перший автомобіль буде обслуговуватися протягом
t1
= (28+0,077·8)/24/60 = 0:28:37
другий автомобіль
t2
= (28 +(- 1,365)·8)/24/60 = 0:17:05 і т.д. (див. додаток 3)
В умовах задачі відзначалося, що водій вибирає секцію складу випадково. Моделювання процесу вибору секції складу здійснюється за допомогою таблиці випадкових чисел (додаток 1). Якщо на складі дві секції і випадкове число попадає в інтервал від 0 до 0,5, то автомобіль направляється до першої секції, якщо в інтервал від 0,5 до 1,0, то — до другої.
Аналогічно моделюється і структура парку автомобілів, що здійснюють вивіз (завезення) вантажів зі станції.
При регульованому підведенні автомобілів кожен наступний автомобіль надходить до того вантажного фронту, що вільний від обслуговування, або до того, де обслуговування автомобіля закінчиться раніше інших.
При черговому підведенні автомобілів, перший стає в першу секцію, а другий в другу, третій стає в першу, четвертий – в другу. Аналогічно і інші автомобілі.
За даними приведеними в додатку 3, я побудувала епюру заняття вантажних фронтів після виконання імітацій і підрахувала простій автомобілів при різних дисциплінах вибору вантажного фронту. Епюри показані в додатках 4 – 9.
3.2 Визначення доцільності використання нової системи регулювання
При різній дисципліні вибору водієм складу і нормальному розподілі коливань тривалості вантажної операції за результатами моделювання отримала результати, що приведені в табл. 3.1.
Таблиця 3.1 – Результати моделювання
| Дисципліна вибору складу |
Число обслугованих автомобілів, шт. |
Тривалість чекання обслуговування |
Простій автомобілів у чеканні обслуговування, автомобілів |
Випадковий вибір
Почерговий вибір
Оптимальне регулювання
|
136
136
136
|
43,2
23,9
21,0
|
2810,4
1647,3
1491,4
|
Аналіз даних табл.3.1. дозволяє зробити наступні висновки:
1. Мінімальний простій автомобіля забезпечує оптимальне регулювання їхнього підведення до вантажних фронтів.
2. Друга по ефективності процедура регулювання – почергове проходження прибуваючих автомобілів до секцій складу.
Використовуючи дані табл.3.1 і прийнявши собівартість 1 автомобіле-години рівної 4,5 ум.гр.од., річна економія експлуатаційних витрат у системі «автомобільний транспорт — вантажний фронт -залізничний транспорт» при оптимальному регулюванні підведення автомобілів складе:

У результаті скорочення простою автомобілів у вантажних фронтів віддаляються капітальні вкладення на придбання автомобілів:
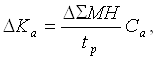
ΔΣМН— добова економія, автомобіле-година;
tp
— середня тривалість роботи автомобіля протягом доби, г;
Са
— вартість автомобіля, у.о. ; наприклад, для автомобіля ЗИЛ-130Са
= 3328 у.г.о.
Економія капітальних вкладень на придбання автомобілів:

Підставляючи розрахункові дані у формулу (3.1), знаходимо
4000+0,11·5000< 13613,04 + 0,11·2298,53 ,
4550<13865,8783.
Таким чином, організація оптимальної системи регулювання підведення автомобілів до вантажних фронтів дозволяє одержати річну економію в розмірі (13865,8783 — 4550) = 9315,8783 ум.гр.од. Досить ефективною є процедура почергового підведення автомобілів. На даному вантажному фронті її впровадження не вимагає додаткових капітальних і експлуатаційних витрат. Підхід автомобілів до секцій складу може регулювати диспетчер. Ефект диспетчеризації
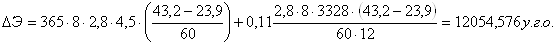
ВИСНОВОК
На основі даної курсової роботи я навчився розв’язувати на практиці деякі задачі, що дуже часто зустрічаються в реальному житті, і переконався, що використані методи є дієвими і досить ефективними для їх вирішення.
Висновки до першої частини:
Ø поїзди прибувають в середньому кожні 28,29 хв., тобто з інтенсивністю 0,0353 поїзд./хв.;
Ø побудувавши гістограму і функцію розподілення інтервалів прибуття, по якій видно, що найбільша кількість поїздів, що прибувають, припадає на інтервал від 2 до 20,65 хв., найменша – на інтервал від 76,59 до 151,19 хв.;
Ø в середньому за годину прибуває 2,29≈2 поїзди;
Ø проаналізувавши графіки статистичної та ймовірнісної кривих можна зробити висновок, що вхідний потік поїздів може бути описано законом Пуассона;
Ø аналізуючи коефіцієнт завантаження бригади ПТО, можна зробити такий висновок, що чим більше кількість груп у бригаді ПТО, тим менше тривалість обробки поїздів. Оскільки при kгр
=1 та ρ=1,76 бригада ПТО не зможе повністю виконати заданий об’єм роботи (оскільки ρ>1). Використання 3 та 4 груп в бригаді не ефективне. Найефективнішою бригадою являється друга ( ρ=0,86), оскільки оптимальний коефіцієнт завантаження бригади ПТО від 0,82 до 1.
Стосовно другої частини можна зробити такі висновки:
5) Пункт Мс потрібно забезпечувати залізничним транспортом з пункту А1
, Пункт В5
з пункту А2.
6) З пункту видобування А1
вантаж потрібно завозити в пункт Мс – 200 тис. тон вантажу та в В3
– 280 тис. тон. З пункту видобування А2
вантаж надходить у розмірі 149тис. тон на В5
, та 65 тис. тон на В7
.
7) У портах В3
, В5
не слід відкривати причали для перевантаження мінерально-будівельних вантажів із залізничного транспорту на річковий.
8) Реалізація такого плану зможе забезпечити оптимальний режим взаємодії залізничного і річкового транспорту при перевезенні мінерально-будівельних матеріалів у даному економічному районі. Витрати на перевезення вантажу складають
Е=180*6,65+106*115,45+14*114,8+200*88,8+280*135+146*71,3+149*918+65*98+150*126+40*169+60*29,55=128492,90 (тис. т).
Щодо третьої частини завдання можна зробити такі висновки:
В моєму випадку більш доцільно та економічно вигідно використовувати процедуру почергового підведення автомобілів, ніж наймати для цього диспетчера. На даному вантажному фронті впровадження даної процедури не вимагає додаткових капітальних і експлуатаційних витрат. Економія експлуатаційних річних витрат при застосування диспетчера складає 9315,8783 ум.гр.од., а при регульованому –  ум.гр.од. Тобто очевидно, що немає сенсу витрачати гроші на зарплатню диспетчеру, коли можна майже вдвічі зекономити, використавши почергове підведення автомобілів. ум.гр.од. Тобто очевидно, що немає сенсу витрачати гроші на зарплатню диспетчеру, коли можна майже вдвічі зекономити, використавши почергове підведення автомобілів.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ:
1. Единая транспортная система: Учеб. для вузов В.Г. Галабурда, В.А. Персианов, А.А. Тимошин и др.; Под ред. В.Г. Галабурды. 2-е изд. с измен. и дополн. – М.: Транспорт, 2001.- 303с.
2. Методичні вказівки до виконання курсової роботи “Оптимізація завозу вивозу вантажів в вузлі взаємодії залізничного, річкового і автомобільного транспорту” з дисципліни “Основи теорії транспортних процесів та систем”.
3. Правдин Н.В. «Взаимодействие различных видов транспорта».-
М. «Транспорт», 1989.-208с.
4. Теория транспортных процессов и систем: Учеб. для вузов / А.В. Вельможин, В.А. Гудков, Л.Б. Миротин. – М.: Транспорт, 1998.- 167с.
Додаток 1
Таблиця випадкових рівномірно розподілених чисел(гр. ТО7-1)
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
22719 |
92549 |
10907 |
35994 |
63461 |
83659 |
24494 |
53825 |
97047 |
76069 |
| 2 |
17618 |
88357 |
52487 |
79816 |
74600 |
50436 |
88823 |
19806 |
33960 |
30928 |
| 3 |
25267 |
35973 |
80231 |
60039 |
50253 |
63457 |
97444 |
13799 |
35853 |
03149 |
| 4 |
88594 |
69428 |
66934 |
27705 |
51262 |
63941 |
77660 |
66418 |
84755 |
29197 |
| 5 |
60482 |
33679 |
03078 |
08047 |
39891 |
34068 |
81957 |
82985 |
83113 |
36981 |
| 6 |
30753 |
19458 |
02849 |
30366 |
83892 |
80912 |
91335 |
41703 |
79401 |
97251 |
| 7 |
60551 |
24788 |
35764 |
57453 |
06341 |
10178 |
91896 |
70819 |
96440 |
98358 |
| 8 |
35612 |
09972 |
98891 |
92625 |
70599 |
95484 |
34858 |
13499 |
28966 |
88287 |
| 9 |
43713 |
18448 |
45922 |
55179 |
18442 |
31186 |
91047 |
37949 |
76542 |
79361 |
| 10 |
73998 |
97374 |
66685 |
06639 |
34590 |
17935 |
79544 |
15475 |
74765 |
11199 |
| 11 |
14971 |
68806 |
49122 |
16124 |
61905 |
22047 |
17229 |
46703 |
39727 |
16753 |
| 12 |
78976 |
48382 |
25242 |
97656 |
51686 |
15537 |
73857 |
35398 |
91783 |
92825 |
| 13 |
37868 |
82946 |
83732 |
63230 |
85306 |
56988 |
15570 |
98029 |
42208 |
00190 |
| 14 |
01666 |
48114 |
95183 |
02628 |
05355 |
97627 |
74554 |
91267 |
31240 |
34723 |
| 15 |
56638 |
70054 |
19427 |
24811 |
37164 |
71641 |
50515 |
88231 |
99539 |
75745 |
| 16 |
43973 |
07496 |
17405 |
08966 |
65989 |
68017 |
56975 |
94080 |
93689 |
98889 |
| 17 |
05141 |
07885 |
94399 |
41145 |
50210 |
92423 |
13308 |
09621 |
94153 |
25294 |
| 18 |
97905 |
05301 |
98496 |
20682 |
68082 |
68537 |
70220 |
78282 |
02396 |
10002 |
| 19 |
23458 |
57782 |
67537 |
38813 |
00377 |
93873 |
97813 |
10039 |
25457 |
28716 |
| 20 |
03954 |
14799 |
63187 |
46191 |
12805 |
50502 |
08810 |
19572 |
48024 |
58206 |
| 21 |
52251 |
06804 |
85959 |
20974 |
73104 |
15009 |
25486 |
09306 |
24721 |
04187 |
| 22 |
62361 |
59105 |
39338 |
59358 |
69193 |
15586 |
57695 |
89518 |
59788 |
04215 |
| 23 |
54954 |
90337 |
99340 |
60442 |
90933 |
58323 |
83183 |
90041 |
44236 |
90815 |
| 24 |
70773 |
03331 |
84228 |
01405 |
61494 |
72064 |
24713 |
39851 |
01431 |
60841 |
| 25 |
68702 |
08331 |
08923 |
83173 |
67081 |
87472 |
47980 |
08802 |
95495 |
78745 |
| 26 |
39599 |
33465 |
96705 |
41458 |
34670 |
55385 |
25484 |
71068 |
15155 |
85371 |
| 27 |
54958 |
34935 |
16858 |
16523 |
54262 |
63310 |
50348 |
53457 |
39440 |
80441 |
| 28 |
98124 |
08864 |
36485 |
78766 |
52802 |
56315 |
43523 |
06513 |
50899 |
86432 |
| 29 |
43099 |
88373 |
80091 |
35058 |
35755 |
47556 |
98602 |
71744 |
70442 |
92312 |
| 30 |
88667 |
44515 |
80435 |
17140 |
32588 |
98708 |
93010 |
98580 |
23656 |
85664 |
| 31 |
87009 |
95736 |
76930 |
71090 |
27143 |
95229 |
24799 |
02313 |
17436 |
20273 |
| 32 |
70581 |
40618 |
16631 |
54178 |
44737 |
02544 |
81368 |
08078 |
46740 |
52583 |
| 33 |
03723 |
25551 |
03816 |
97612 |
99833 |
06779 |
47619 |
12901 |
60179 |
23780 |
| 34 |
49943 |
30139 |
07932 |
29267 |
01934 |
19584 |
13356 |
35803 |
90284 |
97565 |
| 35 |
71559 |
30728 |
83499 |
65977 |
37442 |
72526 |
53123 |
99948 |
59762 |
19952 |
| 36 |
75500 |
16143 |
79028 |
81790 |
57747 |
87972 |
54981 |
10079 |
17490 |
15215 |
| 37 |
59894 |
59543 |
13668 |
27197 |
51979 |
38403 |
23989 |
38549 |
82968 |
53300 |
| 38 |
29757 |
26942 |
08736 |
15184 |
73650 |
51130 |
59160 |
89866 |
06030 |
88929 |
| 39 |
87650 |
08162 |
90596 |
70312 |
84462 |
07653 |
80962 |
96692 |
07030 |
62470 |
| 40 |
84094 |
70059 |
86833 |
23531 |
31749 |
23930 |
04763 |
89322 |
67576 |
38627 |
| 41 |
92101 |
17194 |
06003 |
99847 |
12781 |
38729 |
88072 |
92589 |
61828 |
36504 |
| 42 |
26641 |
99088 |
65294 |
37138 |
75881 |
12627 |
19461 |
69536 |
64419 |
82106 |
| 43 |
04920 |
91233 |
46959 |
14735 |
15153 |
28306 |
76351 |
28109 |
86078 |
46534 |
| 44 |
25417 |
97570 |
91045 |
09929 |
75140 |
23926 |
90282 |
99088 |
93605 |
03547 |
| 45 |
98874 |
96989 |
84371 |
87624 |
74090 |
71983 |
62424 |
62130 |
44470 |
74725 |
| 46 |
82127 |
82000 |
84618 |
58572 |
56716 |
79862 |
49862 |
50702 |
31938 |
18336 |
| 47 |
26311 |
59516 |
98602 |
47197 |
31139 |
27631 |
64619 |
01504 |
77617 |
30219 |
| 48 |
76176 |
03499 |
17999 |
84361 |
63898 |
97861 |
63620 |
23931 |
87903 |
91566 |
Додаток 2
Нормально розподіленні випадкові відхилення(гр. ТО7-1)
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
-0,202 |
-1,303 |
-0,671 |
-0,140 |
-0,018 |
1,565 |
-0,284 |
-0,622 |
2,073 |
0,481 |
| 2 |
0,420 |
-1,103 |
0,176 |
1,099 |
0,092 |
-0,482 |
0,543 |
-0,218 |
-1,683 |
2,836 |
| 3 |
2,417 |
1,181 |
-0,168 |
-0,238 |
0,560 |
-1,847 |
-0,061 |
0,578 |
0,513 |
2,014 |
| 4 |
0,260 |
0,580 |
0,539 |
0,955 |
-1,128 |
0,730 |
0,979 |
1,812 |
0,195 |
-1,322 |
| 5 |
-0,353 |
-0,151 |
-1,592 |
-1,213 |
0,189 |
-1,014 |
-0,678 |
-0,412 |
0,165 |
0,101 |
| 6 |
-2,555 |
-0,712 |
0,567 |
-0,085 |
1,792 |
0,116 |
0,252 |
-1,676 |
0,121 |
-0,346 |
| 7 |
0,666 |
-0,149 |
1,359 |
-0,760 |
0,214 |
0,446 |
0,682 |
0,584 |
- 0,126 |
0,662 |
| 8 |
0,077 |
0,526 |
-0,783 |
-1,960 |
0,854 |
0,084 |
0.552 |
-0,757 |
-1,108 |
0,578 |
| 9 |
-1,365 |
-0,027 |
-0,251 |
-0,273: |
0,494 |
-0,022 |
0,383 |
-253 |
-0,728 |
0,194 |
| 10 |
1,833 |
-0,154 |
1,804 |
-0,414 |
0,103 |
0,759 |
0,054 |
-0,504 |
0,066 |
1,647 |
| 11 |
0,308 |
2,537 |
1,220 |
-1,250 |
-0,371 |
-1,210 |
0,906 |
-0,604 |
-1,361 |
-0,519 |
| 12 |
0,768 |
0,132 |
1,464 |
-0,428 |
0,182 |
-1,792 |
0.864 |
0,483 |
-1,799 |
-0,349 |
| 13 |
-0,957 |
-0,265 |
0,724 |
0,055 |
0,885 |
-0,379 |
0,694 |
-1,448 |
-0,672 |
0,209 |
| 14 |
-0,148 |
-0,539 |
0,397 |
0,362 |
-0,245 |
1,194 |
-0,746 |
0,242 |
0,197 |
-0,109 |
| 15 |
-0,094 |
-0,957 |
-0,373 |
-0,792 |
0,086 |
-0,134 |
1,493 |
-0.210 |
1,830 |
1,375 |
| 16 |
-0,661 |
-0,654 |
-0,379 |
-0,759 |
0,804 |
0,282 |
-1,317 |
-0,219 |
-0,318 |
-0,580 |
| 17 |
1,231 |
-0,337 |
-0,125 |
-1,373 |
-0,535 |
0,119 |
0,776 |
-0,254 |
0,598 |
1,200 |
| 18 |
-1,117 |
-0,871 |
-0,187 |
-0,543 |
0,421 |
0,311 |
0,493 |
0,574 |
-0,145 |
-2,332 |
| 19 |
0,551 |
0,335 |
-1,746 |
0,235 |
1,455 |
0,251 |
1,024 |
0,062 |
0,009 |
0,676 |
| 20 |
0,743 |
1,076 |
0,766 |
-0,052 |
1,194 |
0,517 |
-0,401 |
1,292 |
-0.280 |
0,540 |
| 21 |
-0,329 |
0.277 |
1,736 |
0,175 |
-0,401 |
0,665 |
0,479 |
1,322 |
0,072 |
-4,867 |
| 22 |
-1,264 |
0,970 |
-0,639 |
-0,761 |
-0,502 |
-1,559 |
0,249 |
0,119 |
-0,065 |
-0,812 |
| 23 |
-2,092 |
1,610 |
-1,423 |
-1,071 |
0,642 |
-0,759 |
-2,276 |
0,133 |
-0,976 |
1,506 |
| 24 |
-1,447 |
-0,154 |
1,463 |
0,032 |
-0,107 |
0,327 |
-0,378 |
0,055 |
-0,521 |
-1,400 |
| 25 |
0,018 |
0,533 |
0,558 |
0,593 |
- 0,737 |
0,189 |
-1,876 |
-0,140 |
-1,380 |
-0,303 |
| 26 |
-1,445 |
1,357 |
-1,657 |
-0,887 |
-1,417 |
0,548 |
-0,423 |
0,398 |
0,167 |
0,147 |
| 27 |
0,002 |
1,537 |
0,113 |
-1,008 |
1,080 |
-0,772 |
-0,368 |
-0,290 |
2,146 |
-0,539 |
| 28 |
0,576 |
-1,201 |
-0,108 |
0,384 |
0,659 |
1,192 |
0,119 |
1,861 |
0,856 |
-0,018 |
| 29 |
0,108 |
-0,385 |
0,228 |
0,166 |
-1,169 |
1,099 |
-0,914 |
-0,462 |
1,132 |
-0,266 |
| 30 |
0,233 |
-1,043 |
0,852 |
-0,746 |
0,046 |
0,395 |
0,735 |
- 1,526 |
1,065 |
1,450 |
| 31 |
-1,239 |
-6,155 |
0,090 |
1,130 |
2,623 |
0,811 |
-1,372 |
0,647 |
0,858 |
-0,740 |
| 32 |
-0,928 |
0,802 |
-0,043 |
-0,463 |
0,985 |
-0,395 |
0,386 |
0,465 |
-0,372 |
-0,278 |
| 33 |
-0,670 |
-0,821 |
-1,092 |
1,062 |
0,601 |
2,509 |
-1,557 |
-0,814 |
-0,220 |
-0,019 |
| 34 |
0,643 |
1,339 |
1,287 |
0,446 |
-0,042 |
0,593 |
0,366 |
0,640 |
-0,850 |
0,847 |
| 35 |
2,503 |
-0, 162 |
1,125 |
-1,241 |
2,226 |
1,063 |
0,085 |
0,016 |
0,786 |
-0,766 |
| 36 |
0,895 |
-2,288 |
1,711 |
0,640 |
-0,067 |
-0,088 |
-0,031 |
1,184 |
1,550, |
0,417 |
| 37 |
-0,070 |
-1,367 |
-0,659 |
-1,025 |
0,475 |
0,059 |
-0,792 |
0,468 |
0,284 |
-0,184 |
| 38 |
0,891 |
-0,903 |
-0,213 |
1,847 |
0,223 |
-1,640 |
-0,772 |
0,324 |
-0,013 |
1,757 |
| 39 |
1,170 |
-0,340 |
-0,291 |
0,451 |
1,081 |
-1,073 |
0,073 |
-0,477 |
0,397 |
-1,282 |
| 40 |
0,130 |
-0,205 |
0,665 |
0,306 |
0,700 |
-0,851 |
0,935 |
- 0,502 |
0,650 |
0,254 |
| 41 |
0,591 |
-1,342 |
1,194 |
1,428 |
-1,470 |
-1,202 |
-0,450 |
-0,668 |
0,212 |
1,161 |
| 42 |
-0,487 |
-0,792 |
0,453 |
-1,465 |
0,390 |
0,796 |
-2, 186 |
0,461 |
0,848 |
-0,236 |
| 43 |
-1,048 |
-2,550 |
-0,241 |
-0,109 |
-1,385 |
-0,066 |
-2,523 |
1,270 |
0,914 |
-0,157 |
| 44 |
0,984 |
0,357 |
0,563 |
-1,177 |
0,371 |
-0,624 |
-0,614 |
0,566 |
1,292 |
0,776 |
| 45 |
1,217 |
6,976 |
-1,516 |
-0,737 |
0,018 |
-0,768 |
0,712 |
-1,001 |
0,012 |
-0,456 |
| 46 |
-1,008 |
-8,849 |
-1,272 |
0,903 |
-1,192 |
-2,081 |
0, 157 |
0,708 |
1,132 |
-0,297 |
| 47 |
-0,596 |
-0,219 |
-0,726 |
-0,417 |
-0,214 |
0,625 |
-0,699 |
0,276 |
1,505 |
0,672 |
| 48 |
-0,315 |
-0,999 |
1,788 |
0,592 |
0,640 |
0,677 |
-0,965 |
1,066 |
-1,189 |
0,657 |
| 49 |
-1,441 |
1,171 |
-0,192 |
-0,315 |
1,714 |
1,131 |
-0,001 |
-0,342 |
0,039 |
1,486 |
| 50 |
-0,413 |
0,269 |
0,602 |
0,085 |
-0,848 |
-0,207 |
0,396 |
-2,358 |
-0,045 |
-0,087 |
Додаток 3






|