| МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ВОДНОГО ГОСПОДАРСТВА ТА
ПРИРОДОКОРИСТУВАННЯ
СЛОВ’ЯНСЬКИЙ НКЦ
Курсова робота
З дисципліни: ВИЩА ГЕОДЕЗІЯ
РОЗВ'ЯЗУВАННЯ ЗАДАЧ СФЕРОЇДНОЇ ГЕОДЕЗІЇ
Виконав: студент
групи ЗВК – 42
Нікітін О.О.
Слов’янськ 2010 р.
ЗМІСТ
трикутник лежандр аддитамент геодезичний
Вступ
Завдання 1. Обчислення довжини дуги меридіану
Завдання 2. Обчислення довжини дуги паралелі
Завдання 3. Обчислення довжини сторін та площі знімальної трапеції
Завдання 4. Наближене розв’язування трикутників за теоремою Лежандра
Завдання 5. Наближене розв’язування трикутників способом аддитаментів
Завдання 6. Розв’язування прямої геодезичної задачі способом допоміжної точки (спосіб Шрейбера)
Завдання 7. Розв’язування прямої геодезичної задачі за формулами Гауса із середніми аргументами
Завдання 8. Розв’язування оберненої геодезичної задачі за формулами Гауса із середніми аргументами
Завдання 9. Пряма задача проекції Гауса-Крюгера (перехід з поверхні еліпсоїду на площину)
Завдання 10. Розрахунок геодезичних координат пункту за плоскими прямокутними координатами
Вступ
Визначення параметрів земного еліпсоїда і форми земної поверхні становить велику наукову зацікавленість та має важливе значення для практичної і інженерної геодезії, для топографії і картографії, а також для багатьох суміжних наук: астрономії, геофізики, геодинаміки тощо.
Вивчення геометрії земного еліпсоїда та методів розв’язування задач на його поверхні складає вагому частину змісту курсів "Основи вищої геодезії" та "Вища геодезія". Ці питання, а також питання зображення поверхні еліпсоїда на площині відносяться до частини вищої геодезії, яка історично отримала назву "сфероїдна геодезія".
Вища геодезія вивчає фігуру та зовнішнє гравітаційне поле Землі, методи створення систем геодезичних координат на всю поверхню Землі або на окремі її ділянки, а також способи визначення положення точок земної поверхні в тій чи іншій системі координат.
Завдання вивчення фігури та гравітаційного поля Землі, як основної задачі вищої геодезії, розв’язується за результатами вимірів на земній поверхні. Це геодезичні виміри в мережах тріангуляції, трилатерації, полігонометрії та нівелювання 1 класу, а також супутниково-навігаційні спостереження з метою визначення координат точок земної поверхні. Методи постановки та виконання вказаних вимірів складають предмет першої частини вищої геодезії.
Друга частина вищої геодезії – теоретична основа розв’язування основної задачі. В ній розглядаються і встановлюються аналітичні залежності між результатами вимірів і фігурою Землі та її гравітаційним полем.
Вища геодезія, в тому числі її частини - сфероїдна геодезія та теоретична геодезія, є однією із основних дисциплін, що забезпечує необхідну теоретичну і практичну спеціальну підготовку фахівців геодезичного профілю.
Завдання 1. Обчислення довжини дуги меридіану
А1
– точка на меридіанному еліпсі з широтою В1
. А2
– точка на меридіанному еліпсі з широтою В2
.

Загальна формула для дуги меридіану довільної довжини:
 (4) (4)
A,B,C,D – сталі коефіцієнти прийнятого референт-еліпсоїду; ρ – число кутових одиниць в одному радіані;  - середня широта дуги А1
А2
. - середня широта дуги А1
А2
.
Формула для довжини дуги меридіану при обчисленнях в тріангуляції на віддалі порядку сотень кілометрів:
 (6) (6)
Радіус кривизни меридіану перерізу Mm
обчислюється за середньою широтою Bm
.
За умови точності широти точки mB
= ±0.0001" всі зазначені формули забеспечують середню квадратичну помилку довжини дуги меридіану
mS
= ±0.001 м.
Вихідні дані
Номер варіанту №8
| В1
|
48º30′48.1111" - 8′
|
48º22′48.1111"
|
48,38003086
|
| В2
|
49º30′49.1111" + 8′
|
49º38′49.1111"
|
49,64700617
|
Сталі величини
| a
|
6378245 м
|
e2
|
0,00669342
|
ρº
|
57,29577951
|
| A
|
1,00506238
|
B
|
0,00506238
|
C
|
0,00001062
|
D
|
0,00000002
|
Обчислення довжини дуги меридіану за формулою (4):
| Позначення дій
|
Результати
|
| 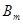
|
49,01351852
|
| 
|
6335552,727
|
| 
|
0,02222460
|
| 
|
- 0,00001563
|
| 
|
- 0,00000022
|
| 
|
0,00000000
|
| s (м)
|
140902,722
|
Обчислення довжини дуги меридіану за формулою (6):
| Позначення дій
|
Результати
|
| 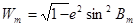
|
0,99809115
|
| 
|
6371972,436
|
| 
|
140902,730
|
| 
|
- 0,00000005
|
| s (м)
|
140902,723
|
Завдання 2. Обчислення довжини дуги паралелі
А1
та А2
– точка на паралелі з широтою В. L1
та L2
довготи точок А1
та А2
.

Паралель на земному еліпсоїді утворює коло. Радіус r паралелі з широтою В виражається формулою:
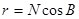

N – радіус кривизни перерізу першого вертикалу. Переріз першого вертикалу – це крива на поверхні еліпсоїду, утворена перетином поверхні еліпсоїду нормальною площиною, яка перпендикулярна до площини меридіанного перерізу у даній точці.

- перша функція геодезичної широти;
a – велика піввісь та e – перший ексцентриситет референт-еліпсоїду.
Дуга паралелі між точками А1
та А2
є дугою кола з центральним кутом, який дорівнює різниці довгот кінцевих точок дуги λ = L2
– L1
. Довжина s дуги паралелі з широтою В, яка відповідає різниці довгот λ = L2
– L1
, виражається формулою  . Остаточно: . Остаточно:
 (10) (10)
За умови точності широти і довгот точок mB
= mL
±0.0001" формула (5) забеспечує середню квадратичну помилку довжини дуги паралелі
mS
= ±0.001 м.
Вихідні дані
Номер варіанту №8
| B
|
48º30′48.1111" - 8′
|
48º22′48.1111"
|
48,38003086
|
| L1
|
25º30′25.1111" - 8′
|
25º22′25.1111"
|
25,37364197
|
| L2
|
27º30′27.2222" + 8′
|
27º38′27.2222"
|
27,64089506
|
Сталі величини
| a
|
6378245
|
e2
|
0,00669342
|
ρº
|
57,29577951
|
Обчислення довжини дуги паралелі за формулою (10):
| Позначення дій
|
Результати
|
| 
|
2,26725309
|
| 
|
0,99812791
|
| 
|
6390208,045
|
| s (м)
|
167951,005
|
Завдання 3. Обчислення довжини сторін та площі знімальної трапеції
Сторони знімальної трапеції чи листа карти заданого масштабу є лініями меридіанів та паралелей на поверхні земного еліпсоїду. Тому обчислення натуральних розмірів та площі знімальної трапеції – це визначення частини поверхні еліпсоїду в межах ліній меридіанів та паралелей, які окреслюють лист карти заданого масштабу.

Розміри знімальної трапеції на поверхні еліпсоїду описуються наступними параметрами:
- південна a1
та північна a2
сторони, які на поверхні еліпсоїду є дугами паралелей з широтами B1
і B2
, та окреслюються меридіанами з довготами L1
і L2
;
- західна та східна сторони с , які на поверхні еліпсоїду є дугами меридіанів, окреслених паралелями з широтами B1
і B2
, тому завжди рівні між собою;
- діагональ в трапеції:
 (11) (11)
Формули розрахунку довжин дуг a1
та a2
на широтах відповідно B1
і B2
:
 (12) (12)
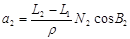 (13) (13)
Для вираження площі трапеції P маємо робочу формулу вигляду:
 , (15) , (15)
де b – мала піввісь і A’,B’,C’ – сталі коефіцієнти прийнятого референц-еліпсоїду. Формула забезпечує розрахунок площі трапеції із середньою квадратичною помилкою не більше mp
= ±0,0005 км2
.
Задано геодезичні координати точки А(BA
, LA
) на поверхні земного еліпсоїду. Визначити приналежність точки А знімальній трапеції масштабу 1:50000, номенклатуру та геодезичні координати рамки відповідного листа карти і розрахувати довжини сторін та площу цієї трапеції.
Вихідні дані
Номер варіанту №8
| BA
|
48º01′01.1111" + 7′*8
|
48,95030864
|
| LA
|
22º11′11.1111" + 30′*8
|
26,18641975
|
Сталі величини

Геодезичні координати сторін трапеції
| B1
|
48º50′
|
48,83333333
|
| B2
|
49º00′
|
49,0
|
| L1
|
26º00′
|
26,0
|
| L2
|
26º15′
|
26,25
|
Обчислення довжини сторін трапеції за формулами (11),(12),(13),(14).
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
0,99810160
|

|
0,99809194
|
| 
|
6390376,482
|

|
6390438,348
|
| 
|
18354,212
|

|
18293,253
|
|  (см карти) (см карти)
|
36,71
|
 (см карти) (см карти)
|
36,59
|
| 
|
48,91666667
|
| 
|
0,998096769
|
| 
|
6371864,921
|
| с (м)
|
18535,004
|
d (м)
|
26063,473
|
| с (см карти)
|
37,07
|
d (см карти)
|
52,13
|
Обчислення площі трапеції за формулою (15).
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
352641,2223
|

|
0,00095901
|
| 
|
-0,00000410
|

|
-0,00000001
|
| Р (км2
)
|
339,630
|
Р (га)
|
33963,07
|
Завдання 4. Наближене розв’язування трикутників за теоремою Лежандра
Після визначення кінцевих значень виміряних кутів або напрямів у тріангуляції на поверхні еліпсоїду розпочинають розв’язування трикутників, яке зводиться до послідовного обчислення довжин їх сторін за одним виміряним базисом і кутами трикутників. При довжинах сторін до 90 км розбіжностями між поверхнею еліпсоїду і сферою можна нехтувати, а трикутники вважати сферичними.
Теорема Лежандра: Малий сферичний трикутник АВС можна розв’язувати як плоский, якщо кожний з його кутів А, В, С зменшити на третину сферичного надлишку.
Розв’язати два малих сферичних трикутники, зображених на схемі, якщо:
- довжина вихідної сторони с1
= (60000 – 500*8) метрів;
- середня широта Bm
= 48º01′01.1111" + 7′*8.
Виміряні сферичні кути трикутників приведено в таблиці.

Вихідні дані
Номер варіанту №8
| Довжина вихідної сторони
|
с1
= (60000 – 500*8)
|
56000
|
| Середня широта
|
48º57′01.1111"
|
48,95030864
|
Сталі величини
| b
|
6356863,019
|
e2
|
0,00669342
|
ρº
|
57,29577951
|
Результати вимірів кутів
| № трикутника
|
Позначення кутів
|
Виміряні сферичні кути
|
| 1
|
A1
|
78º27′09.18"
|
| B1
|
51º33′02.51"
|
| C1
|
49º59′51.20"
|
| 2
|
A2
|
59º25′19.10"
|
| B2
|
51º46′48.52"
|
| C2
|
68º47′54.33"
|
Робочі формули:
Радіус сфери
 6381154,368 м. 6381154,368 м.
Трикутник №1:
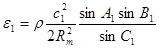 ; ;  ; ;
 ; ;  . .
Трикутник №2:
 ; ; 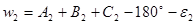 ; ;
 ; ;  . .
Відомість наближеного розв’язування трикутників
| Верш.
|
Виміряні
сферичні кути
|

|
Виправлені
сферичні кути
|
|
Виправлені
плоскі кути
|
Синуси
кутів
|
Довжини
сторін
|
| C
|
49º59′51.20"
|
1,689
|
49º59′52.888"
|
-2,652
|
49º59′50.237"
|
0,76601402
|
56000,000
|
| B
|
51º33′02.51"
|
1,689
|
51º33′04.198"
|
-2,652
|
51º33′01.547"
|
0,78315577
|
57253,160
|
| A
|
78º27′09.18"
|
1,689
|
78º27′10.868"
|
-2,652
|
78º27′08.217"
|
0,97975833
|
71625,930
|
| Σ1
|
180º00′02.89"
|
5,066
|
180º00′07.956"
|
-7,956
|
180º00′00"
|
| ε1
|
7,956
|
| w1
|
-5,066
|
| D
|
59º25′19.10"
|
3,035
|
59º25′22.134"
|
-3,685
|
59º25′18.450"
|
0,86093557
|
71625,930
|
| B
|
51º46′48.52"
|
3,035
|
51º46′51.554"
|
-3,685
|
51º46′48.870"
|
0,78564059
|
65361,729
|
| C
|
68º47′54.33"
|
3,035
|
68º47′57.364"
|
-3,685
|
68º47′53.680"
|
0,93231272
|
77564,185
|
| Σ2
|
180º00′01.95"
|
9,105
|
180º00′11.052"
|
-11,055
|
180º00′00"
|
| ε2
|
11,055
|
| w2
|
-9,105
|
Завдання 5. Наближене розв’язування трикутників способом аддитаментів
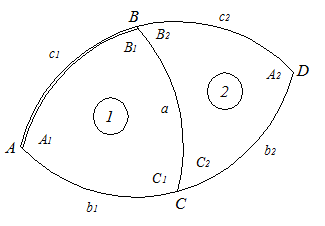
Аддитаменти – це поправки до сторін сферичного трикутника, з врахуванням яких його можна розв’язати за сферичними кутами на основі теореми синусів плоскої тригонометрії. Отже,
для сторони b   , ,
для сторони с 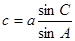 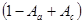 . .
Числові значення аддитаментів невідомих сторін можна розрахувати за приблизними значеннями їх довжин  та та  . .
Розв’язати два малих сферичних трикутники, зображених на схемі, якщо:
- довжина вихідної сторони с1
= (60000 – 500*8) метрів;
- середня широта Bm
= 48º01′01.1111" + 7′*8.
Виміряні сферичні кути трикутників приведено в таблиці.
Вихідні дані
Номер варіанту №8
| Довжина вихідної сторони
|
с1
= (60000 – 500*8)
|
56000
|
| Середня широта
|
48º57′01.1111"
|
48,95030864
|
Сталі величини
| b
|
6356863,019
|
e2
|
0,00669342
|
ρº
|
57,29577951
|
Результати вимірів кутів
| № трикутника
|
Позначення кутів
|
Виміряні сферичні кути
|
| 1
|
A1
|
78º27′09.18"
|
| B1
|
51º33′02.51"
|
| C1
|
49º59′51.20"
|
| 2
|
A2
|
59º25′19.10"
|
| B2
|
51º46′48.52"
|
| C2
|
68º47′54.33"
|
Робочі формули:

Трикутник №1:
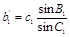 ; ; 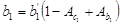 ; ;
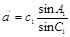 ; ;  . .
Трикутник №2:
 ; ;  ; ;
 ; ;  . .
Відомість наближеного розв’язування трикутників
| Верш.
|
Виміряні
сферичні кути
|

|
Виправлені
сферичні кути
|
Синуси
кутів
|
Приблизні
довжини
|
Аддита-
менти
|
Довжини
сторін
|
| C
|
49º59′51.20"
|
1,689
|
49º59′52.888"
|
0,76601402
|
-
|
0,00001284
|
56000,000
|
| B
|
51º33′02.51"
|
1,689
|
51º33′04.198"
|
0,78315577
|
57253,127
|
0,00001342
|
57253,160
|
| A
|
78º27′09.18"
|
1,689
|
78º27′10.868"
|
0,97975833
|
71625,345
|
0,00002100
|
71625,930
|
| Σ1
|
180º00′02.89"
|
5,066
|
180º00′07.956"
|
| ε1
|
7,956
|
| w1
|
-5,066
|
| D
|
59º25′19.10"
|
3,035
|
59º25′22.134"
|
0,86093557
|
-
|
0,00002100
|
71625,930
|
| B
|
51º46′48.52"
|
3,035
|
51º46′51.554"
|
0,78564059
|
65361,959
|
0,00001749
|
65361,729
|
| C
|
68º47′54.33"
|
3,035
|
68º47′57.364"
|
0,93231272
|
77563,903
|
0,00002462
|
77564,185
|
| Σ2
|
180º00′01.95"
|
9,105
|
180º00′11.052"
|
| ε2
|
11,055
|
| w2
|
-9,105
|
Завдання 6. Розв’язування прямої геодезичної задачі способом допоміжної точки (спосіб Шрейбера)
Розв’язування прямої геодезичної задачі способом допоміжної точки виконується посереднім шляхом – обраховують насамперед різниці координат пунктів, а за ними – абсолютні значення координат. За умови використання робочих формул приведеного нижче вигляду, спосіб забезпечує розрахунок геодезичних координат пунктів у тріангуляції 1 класу з точністю десятитисячних часток секунди, азимутів – з точністю тисячних часток секунди.

A і В – пункти на поверхні еліпсоїду з геодезичними координатами B1
,L1
і B2
,L2
. АР – меридіан т.А; ВР – меридіан т.В. А12
і А21
– прямий і зворотній азимут напряму АВ. s – довжина геодезичної лінії АВ. С – допоміжна точка поверхні еліпсоїду, розташована на меридіані т.A так, що геодезична лінія СВ має азимут АСВ
= 90º. Точка С має геодезичні координати B0
, L1
.
Черговість дій при розв’язуванні прямої геодезичної задачі способом допоміжної точки:
1. Обчислення широти точки С
 - перша функція геодезичної широти пункту А; - перша функція геодезичної широти пункту А;
 - радіус кривизни меридіанного перерізу в п. А; - радіус кривизни меридіанного перерізу в п. А;
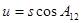 ; ;  - проміжні умовні позначення; b – різниця широт п.А і т.С. - проміжні умовні позначення; b – різниця широт п.А і т.С.
2. Обчислення широти пункту В
  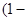  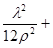 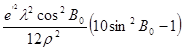 , ,
d – різниця широт п.В і т.С,
   , ,
с – різниця довгот пункту В і точки С,
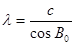 , , 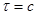  - проміжні величини. - проміжні величини.
3. Обчислення довготи пункту В
λ =  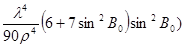 , ,
λ - різниця довгот пунктів А і В,
4. Обчислення зворотного азимуту А21
А21
=  , t – кут, утворений на поверхні еліпсоїду кривою ВР меридіанного перерізу в пункті В та кривою ВТ, яка паралельна меридіанному перерізові у пункті А, ε - сферичний надлишок трикутника АВС. , t – кут, утворений на поверхні еліпсоїду кривою ВР меридіанного перерізу в пункті В та кривою ВТ, яка паралельна меридіанному перерізові у пункті А, ε - сферичний надлишок трикутника АВС.
Вихідні дані
Номер варіанту №8
| B1
= 48º01′01.1111"+7′*8
|
48º57′01.1111"
|
48,95030864
|
| L1
= 22º11′11.1111"+30′*8
|
26º11′11.1111"
|
26,18641975
|
| A12
= 1º01′01.111"+3º*8
|
25º01′01.111"
|
25,01697528
|
| s = (60000 – 500*8)
|
56000 м
|
Сталі величини
| a
|
6378245 м
|
e2
|
0,00669342
|
e’2
|
0,00673853
|
ρº
|
57,29577951
|
Обчислення широти точки С
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
0,998094819
|

|
0,456307116
|
| 
|
6371902,273
|

|
0,00003975
|
| 
|
50746,22203
|
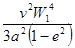
|
0,00000459
|
| 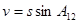
|
23681,65851
|

|
-0,00000003
|
| b
|
0,456291085
|
B0
|
49,40659972
|
| 0º27′22.65"
|
49º24′23.76"
|
Обчислення широти пункту В
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
0,99806840
|
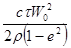
|
0,00046040
|
| 
|
0,21232144
|

|
0,00000312
|
| 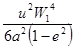
|
0,00001054
|

|
0,00000270
|
| с
|
0,21231920
|

|
0,00000004
|
| 
|
0,32630018
|
d
|
0,00046039
|
| 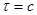 
|
0,24777482
|
B2
|
49,40613933
|
| 49º24′22.1"
|
Обчислення довготи пункту В
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 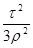
|
0,00000623
|
λ
|
0,32629814
|
| 
|
0,00000000
|
L2
|
26,51271789
|
| 26º30′45.78"
|
Обчислення зворотного азимуту
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
0,00084549
|
t
|
0,247772701
|
| 
|
0,00000541
|
A21
|
205,26390249
|
| 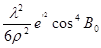
|
0,00000003
|
205º15′50"
|
Завдання 7. Розв’язування прямої геодезичної задачі за формулами Гауса із середніми аргументами
Вихідні дані та сталі величини наведено у завданні №6.
| Наближення (1)
|
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
6399698,916
|

|
1,001452017
|
| 
|
0,456307116
|

|
0,243826934
|
| 
|
0,32331773
|
| 
|
49,1784622
|

|
25,13888874
|
| Позначення дій
|
Результати в наближеннях
|
| (2)
|
(3)
|
(4)
|
(5)
|
| 
|
1,00143875
|
1,00143875
|
1,001438754
|
1,001438754
|
| 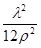
|
0,000002654
|
0,000002702
|
0,000002703
|
0,000002703
|
| 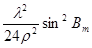
|
0,000000760
|
0,000000774
|
0,000000774
|
0,000000774
|
| 
|
0,00000264
|
0,00000264
|
0,00000264
|
0,00000264
|
| 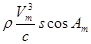
|
0,45583487
|
0,45582911
|
0,45582908
|
0,45582908
|
| 
|
0,32628147
|
0,32629866
|
0,32629871
|
0,32629871
|
| 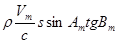
|
0,24691330
|
0,24692543
|
0,24692546
|
0,24692546
|
| b
|
0,455836428
|
0,45583069
|
0,45583067
|
0,45583067
|
| λ
|
0,326280859
|
0,32629805
|
0,32629811
|
0,32629811
|
| t
|
0,24691507
|
0,24692721
|
0,24692724
|
0,24692724
|
| 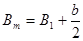
|
49,17822685
|
49,17822398
|
49,17822397
|
49,17822397
|
|  
|
25,14043282
|
25,14043888
|
25,14043890
|
25,14043890
|
Кінцеві результати
| Позначення дій
|
Результати
|
| 
|
49,40613931
|
49º24′22.1"
|
| 
|
26,51271786
|
26º30′45.78"
|
| 
|
205,26390252
|
205º15′50"
|
Завдання 8. Розв’язування оберненої геодезичної задачі за формулами Гауса із середніми аргументами
Для розв’язування оберненої геодезичної задачі, в якій за значенням геодезичних координат B1
, L1
та B2
, L2
пунктів А та В розраховують значення азимутів А12
, А21
та довжини s геодезичної лінії АВ, найбільш оптимально використовувати обернений алгоритм розв’язування за формулами Гауса із середніми аргументами.
У порівнянні з іншими способами розв’язування оберненої геодезичної задачі спосіб Гауса із середніми аргументами виділяється простотою робочих формул, тому розглядається як найбільш оптимальний.
Черговість дій при розв’язуванні оберненої геодезичної задачі за формулами Гауса із середніми аргументами:
1. Обчислення різниць координат  , , 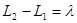 та середньої широти та середньої широти  . .
2. Обчислення середнього азимуту Аm
 , ,
за знаками P та Q визначають четверть, в якій розташований напрям Аm
.
3. Обчислення довжини геодезичної лінії
 або або  . .
4. Обчислення зближення меридіанів t
 . .
5. Обчислення азимутів
 та та 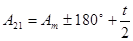 . .
Наведені формули за точністю результатів розрахунків дійсні для віддалей такого ж порядку, що й у прямій геодезичній задачі.
Вихідні дані
Номер варіанту №8
| B1
= 48º01′01.1111"+7′*8
|
48º57′01.1111"
|
48,95030864
|
| L1
= 22º11′11.1111"+30′*8
|
26º11′11.1111"
|
26,18641975
|
| B2
|
49º24′22.1"
|
49,40613931
|
| L2
|
26º30′45.78"
|
26,51271786
|
Геодезичні координати пункту В вибрано із завдання №7.
Сталі величини
| a
|
6378245 м
|
e’2
|
0,00673853
|
ρº
|
57,29577951
|
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 1. Обчислення різниць координат і середньої широти
|
| 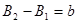
|
0,45583067
|

|
49,17822397
|
| 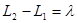
|
0,32629811
|
| 2. Обчислення сумм поправочних коефіцієнтів
|
| 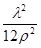
|
0,00000270
|
Δb
|
1,00000348
|
| 
|
0,00000264
|
| 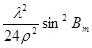
|
0,00000077
|
Δλ
|
0,99999814
|
| 3. Обчислення середнього азимуту Аm
|
| 
|
6399698,916
|

|
23790,954
|
| 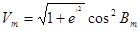
|
1,001438768
|

|
25,14043968
|
| 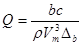
|
50695,072
|
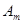
|
25º8′25.58"
|
| 4. Обчислення довжини геодезичної лінії s
|
| 
|
55999,998 м
|

|
55999,998 м
|
| 5. Обчислення зближення меридіанів t
|
| 
|
0,24692546
|

|
1,00000720
|
| 
|
0,24692724
|
| 6. Обчислення азимутів
|
| 
|
25,01697606
|
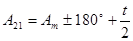
|
205,26390330
|
| 25º1′1.11"
|
205º15′50"
|
Завдання 9. Пряма задача проекції Гауса-Крюгера (перехід з поверхні еліпсоїду на площину)
Прямою задачею Гауса – Крюгера називають розв’язування завдання переходу з поверхні еліпсоїду на площину з метою визначення прямокутних координат пунктів, якщо вихідними даними є геодезичні координати B, L початкового пункту А, довжина геодезичної лінії s та азимуту ААВ
вихідної сторони АВ мережі геодезичних пунктів.
Хід дій при розв’язуванні прямої задачі Гауса – Крюгера:
1. Розрахунок номера зони n, довготи її осьового меридіану L0
та геодезичних координат ВА
, λ початкового пункту А, віднесених до зони його розташування.
2. Розрахунок прямокутних координат х,у початкового пункту А за його геодезичними координатами в зоні ВА
, λ:
  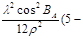 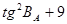 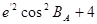 
   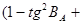  , ,
де  - радіус кривизни перерізу першого вертикалу; - радіус кривизни перерізу першого вертикалу;
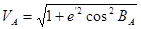 - друга функція геодезичної широти точки А; - друга функція геодезичної широти точки А;
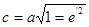 - радіус кривизни меридіанного перерізу при широті В = 90º; - радіус кривизни меридіанного перерізу при широті В = 90º;
X - довжина дуги осьового меридіану від екватора до паралелі з широтою ВА
.
3. Розрахунок зближення меридіанів γ на площині у пункті А за геодезичними координатами ВА
, λ:
  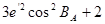  . .
4. Розрахунок масштабу зображення m в пункті А на площині за геодезичними координатами ВА
, λ:
 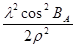 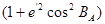
5. Розрахунок наближених довжин сторін геодезичної мережі на площині за виміряними сферичними кутами і довжиною геодезичної лінії s вихідної сторони мережі.
Наближені значення довжин на площині обчислюються з розв'язування трикутників за теоремою Лежандра чи способом аддитаментів (див. результати розрахунків завдань № 4,5).
6. Розрахунок наближених значень х',у' плоских прямокутних координат пунктів за координатами хА
,уА
початкового пункту А, наближеним значенням α'АВ
дирекційного кута вихідної сторони АВ, виправленими кутами та наближеними довжинами сторін трикутників на площині.
7. Редукція довжини геодезичної лінії s вихідної сторони АВ з еліпсоїду на площину.
S = s    . .
8. Редукція напрямів з еліпсоїду на площину.
Для редукції напряму з еліпсоїду на площину поправку δ завжди віднімають від виміряного напряму. Наприклад, остаточне значення дирекційного кута α'АВ
вихідної сторони АВ на площині
  . .
За поправками δ і виміряними сферичними кутами можна розрахувати виміряні кути у вершинах трикутників, редуковані на площину.
9. Зрівноважування мережі і розрахунок остаточних значень х, у плоских прямокутних координат пунктів за координатами хА
,уА
початкового пункту, дирекційиим кутом α'АВ
та довжиною S вихідної сторони і зрівноваженими кутами та довжинами сторін трикутників на площині.
Розв'язати пряму задачу проекції Гауса - Крюгера для мережі двох трикутників, зображених на схемі, геодезичні координати початкового пункту ВА
, LA
, азимут вихідної сторони ААВ
, довжина геодезичної лінії вихідної сторони АВ, надані у вихідних даних.

Вихідні дані
| № трикутника
|
Позначення кутів
|
Виміряні сферичні кути
|
| 1
|
A1
|
78º27′09.18"
|
| B1
|
51º33′02.51"
|
| C1
|
49º59′51.20"
|
| 2
|
A2
|
59º25′19.10"
|
| B2
|
51º46′48.52"
|
| C2
|
68º47′54.33"
|
Номер варіанту №8
| B1
= 48º01′01.1111"+7′*8
|
48º57′01.1111"
|
48,95030864
|
| L1
= 22º11′11.1111"+30′*8
|
26º11′11.1111"
|
26,18641975
|
| AАВ
= 1º01′01.111"+3º*8
|
25º01′01.111"
|
25,01697528
|
| s = (60000 – 500*8)
|
56000 м
|
Сталі величини
| a
|
6378245 м
|
b
|
6356863,019
|
e2
|
0.00669342
|
e’2
|
0,00673853
|
| A
|
1,00505177
|
B
|
0,00506238
|
C
|
0,00001062
|
D
|
0,00000002
|
| ρº
|
57,29577951
|
ρ"
|
206264,8062
|
1. Обчислення номера зони, довгот осевого меридіану та початкового пункту А в зоні.
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
4
|

|
5º11′11.11"
|
| 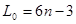
|
21
|
5,186419747
|
2. Обчислення прямокутних координат початкового пункту, масштабу зображень та зближення меридіанів за геодезичними координатами пункту в зоні і наближеного дирекційного кута вихідної сторони на площині:
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
6335552,727
|

|
379883,3465
|
| 
|
0,85866001
|
 
|
12966,34118
|
| 
|
0,00250716
|
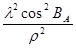
|
0,00353380
|
| 
|
-0,00000072
|

|
3,91128820
|
| 
|
0
|
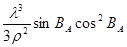 
|
0,00460723
|
| X
|
5424196,908
|
m
|
1,00177203
|
| 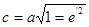
|
6399698,916
|
xA
|
5437177,406
|
| 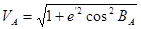
|
1,00145202
|
yA
|
4879812,687
|
| 
|
6390419,919
|
γ
|
3,91593568
|
| 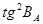
|
1,31872019
|
3º54′57.37"
|
| 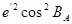
|
0,00290614
|

|
21,10103960
|
| 
|
0,00000845
|
21º06′3.74"
|
3. Обчислення наближених довжин сторін трикутників на площині (результати в завданнях 4, 5).
4. Відомість обчислення наближених прямокутних координат вершин трикутників.
| Вершини
|
Виправлені кути
|
Наближені дирекційні кути
|
Наближені довжини сторін
|
Наближені прямокутні
координати вершин
|
| 
|

|
| B
|
201º06′3.74"
|
| A
|
78º27′08.217"
|
5437177,406
|
4879812,687
|
| 99º33′11.96"
|
57253,160
|
| C
|
118º47′43.917"
|
5427675,361
|
4936271,835
|
| 38º20′55.88"
|
65361,729
|
| D
|
59º25′18.450"
|
5478935,142
|
4976825,387
|
| 277º46′14.3"
|
77564,185
|
| B
|
103º19′49.417"
|
5489422,438
|
4899973,456
|
| 201º06′3.74"
|
56000,000
|
| A
|
5437177,406
|
4879812,687
|
5. Редукція довжини вихідної сторони з еліпсоїду на площину.
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
6381154,376
|
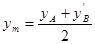
|
389893,0714
|

|
0,0000000
|
|  
|
20160,769
|

|
0,001866648
|
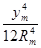
|
0,0000000
|
| Довжина вихідної сторони на площині S (м)
|
56104,620
|
6. Редукція напрямів з еліпсоїду на площину.
Відомість обчислення поправок до напрямів за кривизну зображення геодезичних ліній на площині.
| Напрями
Дії
|
1: А
2: В
|
1: А
2: С
|
1: С
2: В
|
1: С
2: D
|
1: B
2: D
|
| 
|
6381154,376
|
6381154,376
|
6381154,376
|
6381154,376
|
6381154,376
|
| 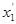
|
5437177,406
|
5437177,406
|
5427675,361
|
5427675,361
|
5489422,438
|
| 
|
5489422,438
|
5427675,361
|
5489422,438
|
5478935,142
|
5478935,142
|
| 
|
379812,687
|
379812,687
|
436271,835
|
436271,835
|
399973,456
|
| 
|
399973,456
|
436271,835
|
399973,456
|
476825,387
|
476825,387
|
| 
|
389893,071
|
408042,261
|
418122,646
|
456548,611
|
438399,422
|
| 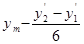
|
386532,943
|
398632,403
|
424172,376
|
449789,686
|
425590,766
|
| 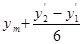
|
393253,200
|
417452,119
|
412072,916
|
463307,537
|
451208,077
|
| 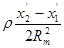
|
0,00013232
|
-0,00002407
|
0,00015639
|
0,00012983
|
-0,00002656
|
| 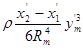
|
0,064
|
-0,013
|
0,094
|
0,101
|
-0,018
|
| 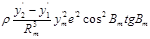
|
0,008
|
0,025
|
-0,017
|
0,022
|
0,039
|
| 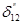
|
51,092"
|
-9,555"
|
66,226"
|
58,317"
|
-11,247"
|
| 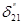
|
-51,981"
|
10,008"
|
-64,334"
|
-60,072"
|
11,927"
|
Дирекційний кут вихідної сторони на площині  21º5′13.2" 21º5′13.2"
7. Відомість обчислення поправок до виміряних сферичних кутів за кривизну зображення геодезичних ліній їх сторін на площині.
| №
тр
|
Вершини
|
Поправки до напрямів сторін у вершинах кутів
|
Поправки до виміряних сферичних кутів
|
№
тр
|
Вершини
|
Поправки до напрямів сторін у вершинах кутів
|
Поправки до виміряних сферичних кутів
|
| 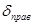
|

|
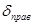
|

|
| 1
|
A
|
-9,555"
|
51,092"
|
-60,647"
|
2
|
C
|
58,317"
|
66,226"
|
-7,909"
|
| B
|
-51,981"
|
-64,334"
|
12,353"
|
D
|
11,927"
|
-60,072"
|
72,000"
|
| C
|
66,226"
|
10,008"
|
56,218"
|
B
|
-64,334"
|
-11,247"
|
-53,087"
|
| Контроль:  7,956" 7,956"
|
7,924"
|
Контроль:  11,055" 11,055"
|
11,003"
|
8. Відомість зрівноважування трикутників та обчислення довжин сторін на площині.
| №
тр.
|
Верш.
|
Виміряні
сферичні кути
|
- δ
|
Виміряні
плоскі кути
|
- w/3
|
Зрівноважені
плоскі кути
|
Синуси
кутів
|
Довжини сторін
|
| 1
|
C
|
49º59′51.20"
|
-56,218
|
49º58′54.98"
|
1,678
|
49º58′56.66"
|
0,76584702
|
56104,621
|
| B
|
51º33′02.51"
|
-12,353
|
51º32′50.16"
|
1,678
|
51º32′51.83"
|
0,78312649
|
57370,485
|
| A
|
78º27′09.18"
|
60,647
|
78º28′09.83"
|
1,678
|
78º28′11.51"
|
0,97981970
|
71779,887
|
| Σ1
|
180º00′02.89"
|
-7,924
|
179º59′54.9"
|
5,034
|
180º00′00"
|
| ε1
|
7,956"
|
| w1
|
-5,034"
|
| 2
|
D
|
59º25′19.10"
|
-72,000
|
59º24′7.1"
|
3,018
|
59º24′10.12"
|
0,86076700
|
71779,887
|
| B
|
51º46′48.52"
|
53,087
|
51º47′41.61"
|
3,018
|
51º47′44.63"
|
0,78581079
|
65529,244
|
| C
|
68º47′54.33"
|
7,909
|
68º48′2.24"
|
3,018
|
68º48′5.26"
|
0,93233302
|
77747,822
|
| Σ2
|
180º00′01.95"
|
-11,003
|
179º59′50.9"
|
9,053
|
180º00′00"
|
| ε2
|
11,055"
|
| w2
|
-9,053"
|
9. Відомість обчислення остаточних прямокутних координат вершин трикутників.
| Вершини
|
Зрівноважені
плоскі кути
|
Дирекційні кути
сторін
|
Довжини
сторін
|
Прямокутні координати вершин
|
| xi
|
yi
|
| B
|
201º05′12.65"
|
|
|
| A
|
78º28′11.51"
|
5437177,406
|
4879812,687
|
| 99º33′24.16"
|
57370,485
|
| C
|
118º47′1.92"
|
5427652,544
|
4936386,970
|
| 38º20′26.07"
|
65529,244
|
| D
|
59º24′10.12"
|
5479049,572
|
4977037,030
|
| 277º44′36.3"
|
77747,822
|
| B
|
103º20′36.4"
|
5489525,045
|
4899998,155
|
| 201º05′12.65"
|
56104,621
|
| A
|
5437177,406
|
4879812,687
|
Завдання 10. Розрахунок геодезичних координат пункту за плоскими прямокутними координатами
За своїм змістом поставлене завдання є частиною оберненої задачі проекції Гауса - Крюгера, яка має на меті здійснення переходу з площини на поверхню еліпсоїду з обчисленням геодезичних координат B,L, якщо вихідними даними є прямокутні координати х,у геодезичних пунктів.
Абсциса x точки а на площині виражається відрізком, який відповідає довжині дуги осьового меридіану від екватора до точки а1
з широтою В1
.
Широту В1
можна обчислити за довжиною дуги меридіану, що відповідає х. Тут можна скористатись формулою обчислення довжини дуги меридіану вигляду (5) і виразити з неї потрібну широту В1
, прийнявши s = x. Отже, В1
- широта основи ординати точки у = 0:
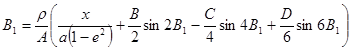
По мірі віддалення від осьового меридіану на величину ординати у для широти В точки А має місце нерівність В < В1
. Широті В відповідає довжина дуги Х осьового меридіану від екватора до паралелі точки А. Тому остаточно потрібна широта точки А залежатиме від В1
та ординати у точки в зоні проекції Гауса — Крюгера:
       , ,
де  - радіус кривизни меридіанного перерізу; - радіус кривизни меридіанного перерізу;  - радіус кривизни перерізу першого вертикалу; - радіус кривизни перерізу першого вертикалу;  - радіус кривизни меридіанного перерізу в полюсі; - радіус кривизни меридіанного перерізу в полюсі;  - друга функція широти B1
. - друга функція широти B1
.
Довгота λ точки А в зоні проекції Гауса – Крюгера:
    
Довгота точки на поверхні еліпсоїду: L = L0
+ λ.
Вихідні дані
| Плоскі прямокутні координати
пункту B
|
xB
(м)
|
5489525,045
|
| yB
(м)
|
4899998,155
|
Сталі величини
| a
|
6378245 м
|
e’2
|
0,00673853
|
ρ"
|
206264,8062
|
Відомість обчислення широти В1
| Позначення дій
|
Результати в наближеннях
|
| (1)
|
(2)
|
(3)
|
(4)
|
(5)
|
| 0.0007114572
|
-0,0006
|
-0,0006
|
-0,0006
|
-0,0006
|
| 0.5451113292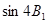
|
-0,1646
|
-0,1698
|
-0,1698
|
-0,1698
|
| 519.4709177
|
513,3693
|
512,9677
|
512,9680
|
512,9680
|
| 0.032930760 x
|
177822,6020
|
177822,6020
|
177822,6020
|
177822,6020
|
177822,6020
|
| 
|
177822,6020
|
178336,1353
|
178335,7388
|
178335,7391
|
178335,7391
|
| Широта В1
= 49º32′15.7"
|
Відомість обчислення геодезичних координат пункту В.
| Позначення дій
|
Результати
|
Позначення дій
|
Результати
|
| 
|
6399698,916
|
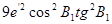
|
0,035106423
|
| 
|
1,001417903
|

|
475,04343609
|
| 
|
6390637,612
|
B
|
177862,1057
|
| 
|
6372553,476
|
49º24′22.1"
|
| 
|
19894,332286
|
λ
|
19845,5951
|
| 
|
0,00391767
|
5º30′45.6"
|
| 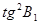
|
1,374547573
|
L = L0
+ λ
|
95445,5951
|
| 
|
0,002837816
|
26º30′45.7"
|
|