Курсовая работа: Цифровая система передачи информации с импульсно-кодовой модуляцией

ВВЕДЕНИЕ

На сегодняшний день в России наиболее интенсивно развиваются сети связи. В условиях современного общества для успешного ведения бизнеса своевременный быстрый и качественный обмен различного рода информацией занимает доминирующую позицию. Каждодневно растет объем передаваемой информации, повышаются требования к качеству ее передачи. За последние 6-7 лет в России с нуля было построено огромное количество сетей мобильной связи, охвативших почти всю территорию страны. Если несколько лет назад мобильный телефон являлся скорее предметом роскоши, то сегодня нельзя представить себе современного делового человека, не обладающего качественной мобильной связью.

Наряду с сетями мобильной связи интенсивно развиваются и модернизируются сети ТФОП. Прокладываются новые кабельные магистрали, устаревшая аналоговая аппаратура заменяется современной и технически более совершенной цифровой аппаратурой, расширяются емкости сетей связи, скорость передачи и помехозащищенность информации. В последние годы все шире внедряются цифровые системы связи (ЦСС) для передачи речи и данных. В данный момент на рынке присутствует большое количество предприятий, выпускающих цифровую аппаратуру для сетей связи. ЦСС позволяют достичь высоких скоростей передачи, высокой производительности узлов коммутации, высокой помехоустойчивости. Были впервые использованы для цифровой передачи речи. Наиболее известны системы цифровой передачи телефонных сигналов с помощью импульсно-кодовой модуляции (ИКМ).

Широкое применение получили цифровые сети интегрального обслуживания - ISDN. В них, используя указанный подход, организуются цифровые каналы, которые объединяются в уплотненный тракт. Эти сети позволяют одновременную передачу различных видов информации: данные, речь, видеоизображение.

Импульсно-кодовая модуляция ИКМ (Pulse-Code Modulation - PCM-модуляция) используется для оцифровки аналоговых сигналов перед их передачей. Практически все виды аналоговых данных (видео, голос, музыка, данные телеметрии, виртуальные миры) допускают применение PCM-модуляции.

Чтобы получить на входе канала связи (передающий конец) PCM-модулированный сигнал из аналогового, амплитуда аналогового сигнала измеряется через равные промежутки времени. Количество оцифрованных значений в секунду (или скорость оцифровки) кратна максимальной частоте (Гц) в спектре аналогового сигнала. Мгновенное измеренное значение аналогового сигнала округляется до ближайшего уровня из нескольких заранее определенных значений. Этот процесс называется квантованием, а количество уровней всегда берется кратным степени двойки, например, 8, 16, 32 или 64. Номер уровня может быть соответственно представлен 3, 4, 5 или 6 битами. Таким образом, на выходе модулятора получается набор битов (0 или 1).

На приемном конце канала связи демодулятор преобразует последовательность битов в импульсы с тем же уровнем квантования, который использовал модулятор. Далее эти импульсы используются для восстановления аналогового сигнала.

Для преобразования в цифровую форму каждый речевой сигнал (fречи = 4 КГц) должен быть подвергнут дискретизации с частотой 2fp = 8 КГц, т.е. период квантования Тк = 1/2fp = 125 мкс. Дискретные отсчеты амплитуды речевого сигнала обычно квантуются по уровню и представляются 8-разрядными двоичными числами.

В результате типичный цифровой канал с ИКМ требует скорость передачи 64 Кбит/с. Отдельные цифровые каналы в свою очередь объединяются в общий поток. Широкое применение получили 2 формата объединения:

Североамериканский стандарт, разработанный компанией AT&T (T1) и принятый также в Канаде и Японии, предусматривает объединение 24 8-разрядных речевых каналов в поток со скоростью передачи 24 * 64 Кбод = 1.544 Мбит/с. В начале каждого цикла добавляется 1 разряд для цикловой синхронизации. Поэтому за время Ту = 125 мксек передается 24 * 8 + 1 = 193 разряда. Такая система получила название Т1.

Каждое 8-разрядное слово в цифровом потоке с временным разделением называется также временным отсчетом или канальным интервалом ( другое название: time-slot – тайм слот).

Хотя формат Т1 сначала был разработан для цифровой передачи речи, он сейчас успешно применяется для передачи данных. Например, в этот формат естественно вписывается передача данных со скоростью 56 Кбит/с: здесь младший 8-й разряд через каждые 5 циклов на 6-ой используется для сигнализации. Возможны также и более высокие скорости передачи объединенных цифровых потоков (трактов). Например, в системе коммутации ESS-4 компании AT&T 5 цифровых потоков Т1 объединяются в поток, содержащий 120 8-разрядных каналов. К ним добавляется еще 8 канальных интервалов, в результате чего уплотненный канал - ТПД содержит 128 каналов, в которых скорость передачи обеспечивается V = 128 * 64 Кбит/с = 8.192 Мбит/с. Это стандарт Т2.

В Европе используется другой стандарт, который предусматривает объединение 30 речевых каналов со скоростью 64 Кбит/с и 2-х каналов управления и сигнализации с той же скоростью. В результате обеспечивается скорость передачи 2,048 Мбит/с. Это обеспечивает аппаратура первичного временного группообразования. Из 30 каналов ТЧ формируется первичный цифровой поток Е1. Потоки Е1 могут объединяться в потоки более высоких уровней Е2, Е3 и Е4 по принципу: 4 потока более низкого уровня объединяются в поток на одну ступень выше.

Иерархия систем передачи с ИКМ представлена на рис. 1

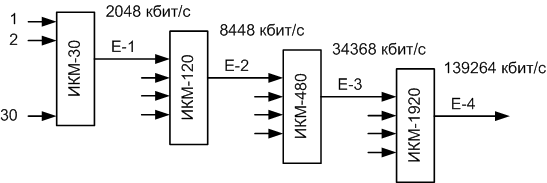
Рис.1

Цифра в названии аппаратуры ИКМ указывает количество каналов ТЧ, уплотняемых и передаваемых данной аппаратурой. (ИКМ-30 - 30 каналов ТЧ и т. д.)

В состав аппаратуры ИКМ входят следующие основные узлы и блоки:

Аппаратура аналого-цифрового преобразования. Обеспечивает преобразование аналоговых сигналов приходящих от абонентов связи в цифровые сигналы для их последующего уплотнения и передачи по линии связи. На приемной стороне обеспечивает преобразование из цифрового сигнала в аналоговый для отправки к абоненту.

Мультиплексоры временного группообразования. Уплотняют цифровые сигналы от разных каналов (потоков) в общий цифровой поток.

Оконечная аппаратура линейного тракта (ОАЛТ) выполняет задачу перекодировки сигнала цифрового группового тракта в линейный цифровой сигнал, а также задачу согласования электрических характеристик станционного оборудования с линией.

Переход к цифровой передаче аналоговых сообщений и использование ИКМ имеет ряд достоинств:

системы с временным разделением каналов ИКМ обладают более высокой помехозащищенностью, чем системы с частотным уплотнением и с однополосной модуляцией, что позволяет использовать их в линиях с большим уровнем шумов и значительным уровнем нелинейных искажений. Таким образом, качество передачи информации почти не зависит от расстояния и топологии сети;

в системах с ИКМ отсутствует накопление шумов при ретрансляции благодаря возможности регенерации сигнала и применению корректирующих кодов;

позволяют упростить коммутацию сигналов, так как цифровая аппаратура сравнительно просто контролируется и требует минимума регулировочных операций;

системы с ИКМ легко сопрягаются с электронными АТС, что позволяет более простыми методами создавать интегральные сети связи;

кроме всего прочего системы с ИКМ экономически выгодны как при разработке, так и при производстве.

При всех вышеперечисленных достоинствах у цифровых систем есть недостатки, основным из которых является значительное расширение полосы частот. При одном и том же числе каналов для передачи группового сигнала системе с ИКМ потребуется полоса частот примерно в 15 раз больше, чем системе с частотным уплотнением. При организации линии связи с использованием металлического кабеля уменьшается длина регенерационного участка, т. к. передача ведется на более высокой частоте, а при повышении частоты передачи растет километрическое затухание в кабеле связи. Однако эти недостатки компенсируется перечисленными выше достоинствами.

цифровая модуляция связь декодер

1. СТРУКТУРНАЯ СХЕМА И ИСХОДНЫЕ ДАННЫЕ

Объектом расчета является цифровая система передачи непрерывных сообщений с импульсно-кодовой модуляцией по каналу с шумом. Структурная схема системы приведена на рис. 2.

Рис. 2

ИС - источник сообщений,

Д - дискретизатор,

КОД - кодирующее устройство,

МОД - модулятор,

ЛС - линия связи,

ДЕМ - демодулятор,

ДЕК – декодер,

ФВ - фильтр-восстановитель.

Исходные данные:

Интервал уровня передаваемого сообщения – [-12,8 ÷ +12,8] В

Закон распределения – равномерный

Полоса частот сообщения - 5∙104 Гц

Номер передаваемой кодовой комбинации – 126

Вид модуляции – ФМ

Спектральная плотность мощности шума – 2,2∙10-5 В2 / Гц

Способ приема - когерентный

Число каналов - 4

2. ИСТОЧНИК СООБЩЕНИЙ

Непрерывное сообщение, поступающее от ИС и представленное первичным электрическим сигналом в форме напряжения a(t), является случайным стационарным процессом, мгновенные значения которого равномерно распределены в интервале [amin, amax], где amin = -12,8 и amax = +12,8.

2.1 Одномерная плотность вероятности

Равномерная одномерная плотность вероятности для мгновенных значений ИС описывается формулой ([3], с.20-21):

(2.1)

А ее график имеет вид:

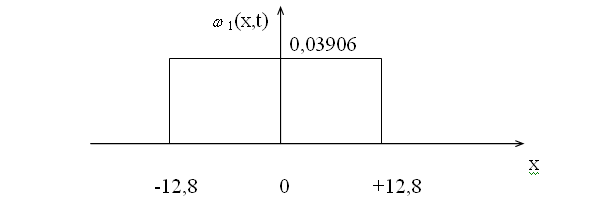
Рис.2.1. График одномерной плотности вероятности мгновенных значений ИС

2.2 Интегральная функция распределения

Одномерные дифференциальная и интегральная функции распределения связаны соотношением ([3],c.20, ф.(1.3)):

(2.2)

Интегральная функция распределения для равномерного закона имеет вид ([3], с.20-21):

(2.3)

График этой функции распределения имеет вид :

Рис.2.2. График для функции распределения мгновенных значений ИС

2.3 Числовые характеристики сигнала

Значительную роль при исследовании случайных процессов играют их числовые характеристики:

1. Математическое ожидание сообщения a(t) вычисляется по формуле ([5], с.32, ф.(2,14)):

(2.4)

2. Дисперсия сообщения вычисляется по формуле ([5], с.32, ф.(2.15)):

(2.5)

цифровая модуляция связь декодер

3. РАСЧЕТ ДИСКРЕТИЗАТОРА

Выбор частоты дискретизации. Осуществляется в соответствии с теоремой Котельникова, которая гласит, что любой непрерывный сигнал ограниченный по спектру верхней частотой Fв, полностью определяется последовательностью своих дискретных отсчетов, взятых через промежуток времени Тд .

Таким образом, если требуется передать непрерывный сигнал с ограниченным спектром, то не обязательно передавать весь сигнал, а достаточно передать лишь его мгновенные значения, отсчитанные через определенные интервалы времени. В соответствии с этим частота следования дискретных отсчетов сигнала т.е частота дискретизации Fд.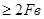

Определим интервал дискретизации по формуле:

Расчет уровней квантования. Число уровней квантования L рассчитывается как число шагов длиной Δa, которое может поместиться в заданном интервале значений передаваемого сообщения.

Число уровней квантования, необходимых для представления данного сообщения:

Т.е каждый отсчет данного сообщения можно представить в виде 8-разрядной двоичной комбинации.

Расчет шума квантования. В цифровых системах связи определяющим является шум квантования. Шум квантования обусловлен конечностью числа уровней отсчетов и, как следствие, неточностью представления мгновенного уровня сигнала. Разность между исходным и квантованным сигналом называется шумом квантования. Конечность числа уровней квантования определяет максимальную амплитуду входного сигнала. Превышение максимальной амплитуды входного сигнала приводит к ограничению уровня квантованного сигнала (перегрузка дискретизатора). При равномерном шаге квантования шум квантования не зависит от уровня сигнала, поэтому для получения приемлемого соотношения сигнал/шум при малом уровне сигнала необходимо уменьшать шаг, что ведет либо к увеличению числа уровней, либо к ограничению максимальной амплитуды сигнала. При заданном равномерном законе распределения сообщения a(t), все его значения, попадающие в интервал между двумя соседними уровнями квантования, равновероятны и не зависят от номера уровня (т.к. шаг квантования равномерный). Поэтому и шум квантования e(t), вычисляемый в каждый момент времени как отклонение значения исходного сообщения от ближайшего к нему уровню квантования, распределен равномерно в интервале ().

Для равномерно распределенного случайного процесса средняя мощность шума квантования определяется по формуле:

Отношение мощностей сигнал/шум. Рассчитаем отношение средних мощностей сигнала и шума – это отношение дисперсии сигнала к средней мощности шума. Рассчитывается по формуле:

Расчет энтропии источника. Для того чтобы получить исчерпывающую информационную характеристику источника сообщений, который может выдавать последовательности неограниченной длины, нужно вычислить предел среднего количества информации, отнесенный к одному символу последовательности. Эта величина была названа энтропией источника. Вычисляется по формуле:

Расчет производительности источника. Производительность источника – это количество бит информации, которое можно передать за один интервал дискретизации сообщения с определенной скоростью, называемой производительностью источника. Интервал дискретизации рассчитан по теореме Котельникова и составляет 0,01мс. Таким образом, скорость передачи составит:

4. РАСЧЕТ КОДЕРА

Кодер обеспечивает представление квантованных по уровню отсчетов сообщения помехоустойчивым двоичным кодом. Эта операция осуществляется в два этапа:

примитивное кодирование: каждый уровень квантованного сообщения a(t) представляется комбинацией равномерного k-разрядного двоичного кода

формирование комбинации помехоустойчивого кода.

Примитивное кодирование. Определим число разрядов примитивного кода к, необходимое для кодирования всех L= 256 уровней квантованного сообщения. Оно равно:

Теперь представим передаваемое число 126 в виде примитивного двоичного кода. Для этого просто переведем число 126 в двоичную систему исчисления.

В примитивном коде передаваемой комбинации содержится 7 информационных символов.

Помехоустойчивое кодирование. Для помехоустойчивого кодирования передаваемого сообщения применим широко распространенный код Хэмминга. Этот вид кодирования является систематическим: т.е. он содержит информационные символы, а также избыточные или проверочные символы. Код Хэмминга хорош тем, что он позволяет обнаружить все одиночные и двойные ошибки и исправлять все одиночные ошибки в схеме декодирования с исправлением. Код Хэмминга является совершенным т.к. вся его избыточность расходуется на исправление ошибок заданной кратности, и он не может исправить ни одной ошибки более высокого порядка. Комбинации, принадлежащие данному коду, содержат 4 информационных символа и 3 проверочных – итого 7 символов в каждой разрешенной комбинации. Чтобы обеспечить возможность передачи всего диапазона возможных сообщений, требующих для примитивного кодирование 5- разрядный код, добавим нулевые символы в старшие разряды кодовой комбинации. Заданное число 14 в двоичной системе исчисления представлено 4-мя разрядами, но с учетом нулей в старших разрядах следует перед передачей кода числа 14 передать нулевую последовательность.

Проверочные символы кодовой комбинации формируются по следующему принципу:

1-й символ равен сумме 1-го, 2-го и 3-го информационных символов

2-й проверочный символ равен сумме 1-го, 3-го и 4-го информационных символов

3-й – сумме 2-го, 3-го и 4-го символов сообщения.

При формировании проверочных символов суммирование производится по модулю 2. Это значит, что при сложении по модулю 2:

1 и 0 в сумме дадут 1,

два нуля или две единицы в сумме дают 0.

Для нахождения всех разрешенных комбинаций кода Хэмминга составим порождающую матрицу размера (k x n), здесь n – общее число символов в одной кодовой комбинации, k – число информационных символов. Эта матрица строится по принципу: строками служат разрешенные ненулевые комбинации, информационные символы которых образуют единичную матрицу 4x4, а проверочные символы определяются по правилу, описанному выше. При построении матрицы надо помнить, что кодовые комбинации, определяющие строки порождающей матрицы, записываются слева направо.

Все разрешенные кодовые комбинации можно найти с помощью порождающей матрицы. Для этого нужно сложить по модулю 2 две или более строк порождающей матрицы. А чтобы получить нулевую комбинацию, нужно сложить по модулю 2 любую строку саму с собой.

Порождающая матрица для кода Хэмминга типа (7,4,3) имеет следующий вид:

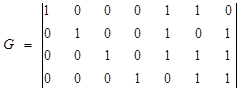
С помощью порождающей матрицы найдем все разрешенные кодовые комбинации, сведем их в таблицу.

Таблица разрешенных кодовых комбинаций

Из таблицы находим необходимую комбинацию. Числу 126 соответствует семизначная последовательность 0. Все сообщение состоит из двух частей: заданная комбинация и дополнительная нулевая последовательность. Передаваемый код имеет окончательный вид 01110011110100.

5. РАСЧЕТ МОДУЛЯТОРА

Модулятор осуществляет модуляцию несущего гармонического колебания U(t) = Um0cos(2pf0t) сигналом, представляющим передаваемую кодовую последовательность. Согласно заданию на курсовую работу применяется фазовая модуляция.

Временные диаграммы передаваемых сигналов. Отсчеты дискретного сигнала поступают на вход кодера с некоторой периодичностью. За время одного периода необходимо передать 14 бит информации, поэтому тактовый интервал, приходящийся на один символ кода равен:

`=(- з)/4=(0,00001-0,000006)/4=0,000001

При фазовой модуляции сигналам «0» и «1» соответствуют противофазные элементы сигнала длительностью Т вида:

Канальная скорость Vk определяется как:

а частота несущего колебания:

Диаграмма исходного и промодулированного сигналов представлена на рис. 5 (На диаграмме модулированного сигнала несущая частота не совпадает с рассчитанной)

Рис. 5

Аналитическое выражение модулированного сигнала b(t) при ФМ записывается следующим образом:

Где - разность фаз для двух позиций кода. Девиация фазы при этом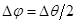

При вычислении корреляционной функции первичного сигнала воспользуемся формулой для модели стохастического дискретного источника синхронного двоичного сигнала:

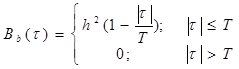
График корреляционной функции первичного сигнала представлен на рис. 6

Рис. 6

Энергетический спектр модулирующего сигнала рассчитывается по теореме Винера-Хинчина как преобразование Фурье от корреляционной функции.

График энергетического спектра модулирующего сигнала представлен на рис.7

Рис. 7

Найдем энергетический спектр радиосигнала с ФМ Спектры сигналов двоичной ФМ легко найти, представив этот сигнал в виде суммы двух сигналов AM с разными фазами. При этом складываются и их энергетические спектры. Общая формула для вычисления ФМ радиосигнала:

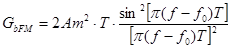
График энергетического спектра ФМ радиосигнала изображен на рис. 8

Рис. 8

6. РАСЧЕТ КАНАЛА СВЯЗИ

Для того чтобы дать математическое описание канала, необходимо и достаточно указать пространство входных и выходных сигналов, а также некоторый оператор, характеризующий поведение сигнала в этом канале. Точное математическое описание любого канала обычно достаточно сложное, поэтому используют упрощенные модели. В данной работе используется канал с аддитивным гауссовским шумом.

Полученный в результате модуляции высокочастотный сигнал u(t) передается по каналу связи с постоянными параметрами и аддитивной помехой. Предполагается, что частотные характеристики канала выбраны таким образом, что сигнал в нем только затухает без искажений формы и временного рассеяния. С выхода такого канала на вход приемного устройства поступает смесь сигнала и шума.

где s(t)— полезный сигнал на выходе канала, связанный с переданным сигналом u(t) известными соотношениями, n(t)- аддитивная помеха, приведенная к выходу канала.

Аддитивная помеха n(t) представляет собой флуктуационный гауссовский шум с равномерным энергетическим спектром N0/2 (белый шум)

s(t) – полезный сигнал на выходе канала;

n(t) – аддитивный гауссовский шум (помеха) c энергетическим спектром N0/2, - белый шум s(t)= Кu(t - τ)= Кu(t)

гдеК - коэффициент передачи равный (l+1), (где l - последняя цифра номера студенческого билета), К=3+8=11;

τ – коэффициент запаздывания.

Часто τ можно не учитывать, что соответствует изменению начала отсчета времени на выходе канала. Сигнал на выходе канала:

Z(t)= Кu(t)+n(t),

Найдем мощность шума на выходе канала связи. Шум в канале связи является белым, поэтому его спектральная плотность мощности на всех частотах одинаковая. Поэтому найдем мощность шума в полосе пропускания канала. Рассчитаем полосу частот отводимую на канал связи. Примем ее равной ширине спектра модулированного сигнала. Ширина спектра ФМ сигнала зависит от индекса модуляции, который рассчитывается по формуле:

m=∆ω/Ω,

Δω- девиация фазы. (при модуляции противоположными по знаку сигналами равна π), для нашего случая равна π/2.

Ω – частота модулирующего колебания, равная 1/Т (2π*420 кГц)

Рассчитанное значение m<<1, поэтому ширину спектра ФМ сигнала примем равной

Рассчитаем мощность шума на нагрузке в 1 Ом:

Рассчитаем мощность сигнала на выходе канала связи. Под «мощностью сигнала» в теории связи условно принято понимать мощность, выделяемую на резисторе с сопротивлением 1 Ом. В соответствии с этим определением средняя мощность сигнала S(t) на интервале времени Т рассчитывается по известной формуле как квадрат нормы сигнала. Для синусоидальных сигналов, которые используются в рассматриваемой системе, в результате интегрирования получается известное выражение

Pci = Usi2/2 , где i= 0; 1.

Здесь Usi есть амплитуда элемента сигнала si в приемнике, связанная с амплитудой переданного сигнала ui(t) коэффициентом передачи К. (Usi=KUm0)

Вычислим мощность сигнала: Среднюю мощность следует рассматривать в расчете на элемент сигнала:

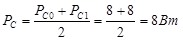
Отношение сигнал-шум в канале связи рассчитывается как

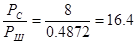
Пропускная способность канала связи – это количество бит информации, которое канал способен передать за 1 секунду. Определим пропускную способность канала при помощи формулы Шеннона.

7. РАСЧЕТ ДЕМОДУЛЯТОРА

В демодуляторе осуществляется оптимальная когерентная обработка принимаемой смеси сигнала с шумом z(t), целью которой является решение о том, какой символ был передан. Но в данном случае не требуется восстанавливать форму исходного сигнала.

Критерии оптимальности - это условие максимума или минимума основного показателя качества приема, представляющего интерес для пользователя системы связи. Таковым при приеме дискретных сообщений является средняя вероятность ошибки (коэффициент ошибок). Критерий ее минимума (или, что то же самое, максимума вероятности правильного приема) называют критерием «идеального наблюдателя».

Алгоритм приема - это уже совокупность конкретных операций над принятой смесью, имеющая целью установить, какой именно из двух (0 или 1) возможных символов был передан.

Критерий максимального правдоподобия может быть выражен следующей функцией:

-отношение правдоподобия гипотезы о передаче 1 к гипотезе о передаче 0

-отношение правдоподобия гипотезы о передаче 0 к гипотезе о передаче 1

Алгоритм приема двоичных сигналов с фазовой модуляцией при когерентном приеме сводится к выражению:

Структура оптимального приемника для сигналов с ФМ показана на рис 9.

Рис. 9

При реализации демодулятора для когерентного приема возникают проблемы. В частности – проблема поддержания равенства фаз опорного генератора и приходящего напряжения. В практических схемах опорный сигнал формируется из принимаемого колебания. Для этого по принимаемому сигналу необходимо восстановить немодулированную гармоническую несущую. Однако на практике все схемы формирования опорного сигнала таковы, что возможно случайное изменение знака опорного сигнала. Это значит, что все «1» будут записаны как «0», а «0» как «1». Это будет продолжаться до тех пор, пока не произойдет процесс изменения фазы. Данное явление получило название обратной работы. Из-за него практическое внедрение систем с двоичной фазовой манипуляцией оказалось затруднительным. Возможность избавления от обратной работы – это переход к относительной фазовой манипуляции (ОФМ). В этом случае сообщение содержится не в абсолютном значении фазы элемента сигнала, а в разности фаз двух соседних символов.

При этом, например «1» передается повторением той реализации сигнала, которая имела место в предыдущем элементе, а «0» - реализацией с обратной фазой.

Структурная схема оптимального приемника с ОФМ (Рис. 10):

Рис. 10

Ячейка памяти задерживает сигнал на длительность посылки. В этой схеме обязательно должна быть предусмотрена ФАПЧ. При таком методе приема перескок фазы опорного генератора вызывает ошибку в только в одном символе. Последующие символы регистрируются верно, и обратной работы не возникает.

Средняя вероятность ошибки приема сигнала вычисляется по формуле:

Q(h) – дополнительная функция ошибок, зависит от функции Крампа

Ф(h) – функция Крампа, определяемая формулой

Вероятность ошибки зависит от отношения сигнал/шум на выходе канала связи.

В MathCad’е посчитаем значение вероятности ошибки

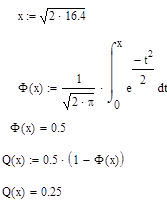
Таким образом, получается, что вероятность ошибки для данного канала связи 0.25

Рассчитаем, как нужно изменить энергию сигнала, чтобы в системах передачи с другими видами модуляции сохранялось такое же значение вероятности ошибки при когерентном приеме.

Для АМ системы с пассивной паузой вероятность ошибки рассчитывается по формуле:

Для ЧМ систем с ортогональными сигналами:

Для ФМ систем с противоположными сигналами:

Исходя из анализа значений вероятности ошибки для различных видов модуляции следует, что при переходе от системы с АМ к системе с ЧМ энергетический выигрыш по максимальной мощности равен 2, а при переходе к системе с ФМ – 4. Если же сравнение вести по средней мощности, то переход от АМ к ЧМ выигрыша не дает. Таким образом, максимальную потенциальную помехоустойчивость обеспечивает система с ФМ.

8. РАСЧЕТ ДЕКОДЕРА

Задачей декодера является исправление ошибок, которые могут возникать при передаче сигнала по каналу связи.

Построение проверочной матрицы Н: проверочная матрица может быть получена из порождающей матрицы кода. Матрица Н имеет n столбцов и n-k строк. Она связана с порождающей матрицей уравнениями:

где Т – символ транспонирования.

Для кода (7,4,3) проверочная матрица имеет вид:

Если принятую кодовую комбинацию С умножить на порождающую матрицу Н, то в результате мы получим вектор синдрома (локатор ошибки) S,который однозначно связан с номером ошибочного символа: S = H*C. C есть вектор- столбец, содержащий n элементов, где n =7. Для синдромов, определяющих ошибку в конкретном разряде кода, составим таблицу.

В принимаемой комбинации определяются проверочные символы по четырем информационным с помощью порождающей матрицы. Затем они складываются по модулю 2 с принимаемыми из канала связи проверочными символами, тем самым определяя вектор – синдром.

Если в принимаемой комбинации символов ошибка содержится в информационных символах, то вычисленные проверочные символы не будут совпадать с принимаемыми, и при сложении с принятыми проверочными символами дадут ненулевой синдром. Также при ошибке в проверочных символах и верных информационных вычисленные символы не совпадут с принятыми и синдром получится отличным от нуля. По виду синдрома определяется, в каком разряде принятой кодовой комбинации содержится ошибка, для исправления которой надо проинвертировать этот символ.

Пусть рассчитанная ранее комбинация символов принята из канала связи верно (ошибок нет). Декодер производит ее проверку. Принимаемые комбинации S1=0000000 и S2=1110100

Для последовательности S1:

Принимаемые проверочные символы: a1=0, a2=0, a3=0.

Вычисляемые проверочные символы: b1=0, b2=0, b3=0.

Для последовательности S2:

Принимаемые проверочные символы: a1=1, a2=0, a3=0.

Вычисляемые проверочные символы: b1=1, b2=0, b3=0.

Векторы – синдромы имеют нулевое значение, значит прием произведен безошибочно.

Теперь введем в принимаемые комбинации одиночную ошибку. Пусть в четвертом разряде комбинаций принимаются 1 вместо 0.

Для последовательности S1:

Принимаемые проверочные символы: a1=0, a2=0, a3=0.

Вычисляемые проверочные символы: b1=0, b2=1, b3=1.

Для последовательности S2:

1. Принимаемые проверочные символы: a1=1, a2=0, a3=0.

Вычисляемые проверочные символы: b1=1, b2=1, b3=1.

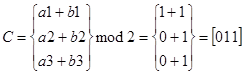
Синдром указывает, что ошибочно принят 4 информационный символ, следовательно, для исправления ошибки необходимо инвертировать 4 разряд каждого кодового слова.

Введем двукратную ошибку. Т. е. Два символа в каждом слове приняты неверно.

Пусть в слове S1 неверно приняты символы 1-й и 4-й т.е принята комбинация 1001000

1. Принимаемые проверочные символы: a1=0, a2=0, a3=0.

Вычисляемые проверочные символы: b1=1, b2=0, b3=1.

В слове S2 ошибочно принимаются символы 2-й и 7-й. Комбинация 1010101

1. Принимаемые проверочные символы: a1=1, a2=0, a3=1.

Вычисляемые проверочные символы: b1=0, b2=0, b3=1.

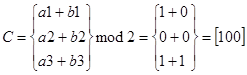
Как видно, синдромы получились ненулевые, значит, в коде зафиксирована ошибка. Но исправить эту ошибку код уже не может. Т. к. инвертирование символа, на который указывает синдром, не приводит к исходной комбинации. Таким образом, код Хэмминга позволяет регистрировать одиночные и двойные ошибки, но исправить может только одиночные.

9. РАСЧЕТ ФИЛЬТРА-ВОССТАНОВИТЕЛЯ

Фильтр-восстановитель выполняет функцию восстановления непрерывного сигнала из дискретных отсчетов. Этот элемент представляет собой идеальный ФНЧ с прямоугольной АЧХ и частотой среза, рассчитываемой из условия формирования дискретного сигнала по теореме Котельникова.

Частота среза фильтра определяется по формуле:

Частотные характеристики идеального ФНЧ определяются формулами

АЧХ: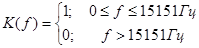

ФЧХ: ,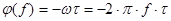

где β- целое положительное число от 1 до 3 (возьмем равным 1).

Частотные характеристики фильтра представлены на рис.11

Рис.11

Найдем импульсную характеристику фильтра-восстановителя. Импульсная характеристика – это отклик системы на δ-функцию.Импульсная характеристика идеального ФНЧ рассчитывается по формуле:

В связи с нереализуемостью идеального ФНЧ используют модель, в которой импульсная характеристика содержит фазовый множитель, линейно зависящий от частоты и тогда формула приобретает вид:

График импульсной характеристики представлен на рис. 12

Рис.12

Оценим погрешность реализуемой характеристики по отношению к идеальной. Это можно сделать, рассчитав отношение:

Посчитаем это отношение в MathCad’е

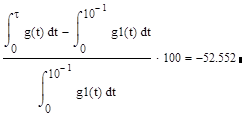
Погрешность реальной характеристики по сравнению с идеальной составляет приблизительно 52%.

Так как отклик системы не может появиться раньше входного воздействия, то для физической реализуемости импульсной характеристики необходимо и достаточно, чтобы:

- условие физической реализуемости импульсной характеристики.

ВЫВОДЫ

В ходе данной работы были исследованы основные принципы передачи информации с импульсно-кодовой модуляцией по каналу связи. Были изучены все необходимые приемы и процессы происходящие с сообщением от момента его выработки в источнике до прихода его к абоненту.

Источник сообщений представляет собой генератор случайного электрического сигнала с равномерным законом распределения и нулевым средним значением. Спектр сигнала сосредоточен в полосе частот от 0 до 15кГц.

Далее исходный непрерывный сигнал преобразуется в дискретный с частотой отсчетов 0,033мс (определяется в соответствии с теоремой Котельникова) и квантуется по уровням с дискретностью 0.1В на каждый уровень. Данный сигнал квантуется по 32 уровням, это значит, что для каждый отсчет может быть представлен числом от 0 до 31. При квантовании обычно производится «округление» амплитуды отсчета до целого числа уровней, поэтому происходит некоторое искажение исходного значения амплитуды сигнала – это явление носит название шума квантования. Мощность этого шума 0.83мВт. Источник сигнала работает с производительностью 75кбит/с, его энтропия равна 5бит на уровень.

Далее квантованный дискретный сигнал кодируется. Для обеспечения более высокой помехозащищенности сигнал кодируется избыточным кодом Хэмминга. Так как сигнал квантуется по 32 уровням, для его представления примитивным двоичным кодом требуется 5-разрядное число. Выбирается код Хэмминга: в нем информация представлена 7-разрядным кодовым словом, в котором 4 первых разряда являются носителями информации, а остальные 3 обеспечивают защиту от ошибок. Принимая это во внимание, разобьем передаваемое 5-значное двоичное число на два слова по 4 знака (добавляем нули в старшие разряды). После кодирования полученная комбинация выглядит так: 00000001110100.

Для эффективной передачи сигнала по каналу связи необходимо его спектр перенести в высокочастотную область - промодулировать сигнал. В качестве модуляции используется фазовая манипуляция с частотой несущего колебания 42МГц и разностью фаз для сигналов 0 и 1 равной π/2.

Модулированный сигнал поступает в канал связи, в котором присутствует аддитивный белый гауссовский шум со спектральной плотностью мощности 5,8∙10-7 В2 / Гц. Коэффициент передачи канала связи равен 4. Ширина полосы пропускания канала определяется шириной спектра ФМ сигнала и равна 840 кГц. Мощность шума в канале равна 0,4872 Вт. Отношение сигнал/шум в канале равно16,4. Пропускная способность канала связи 1,020Мбит/с.

Из канала связи на приемной стороне сигнал попадает на демодулятор – по сути устройство, которое решает, какой символ был передан 0 или 1. Демодулятор собран по схеме оптимального приемника для ФМ сигнала. Средняя вероятность ошибки 25%. Это связано с малым отношением сигнал/шум в канале связи.

Далее сигнал попадает на декодирующее устройство, которое преобразует закодированный сигнал в дискретные отсчеты. Если сигнал был принят с ошибкой, то в декодере может произойти ее исправление. С помощью анализа вектора-синдрома можно точно определить в каком разряде слова появилась ошибка и исправить ее, проинвертировав символ в этом разряде. Если в одном кодовом слове было две ошибки – то произойдет только их обнаружение. Исправить более одной ошибки код Хэмминга не в состоянии.

После декодирования дискретный сигнал поступает на фильтр-восстановитель. Это идеальный ФНЧ с полосой пропускания 15151Гц. С помощью этого ФНЧ можно восстановить исходный непрерывный сигнал из дискретных отсчетов. Частотные характеристики физически реализуемых фильтров отличаются от идеальных. В ходе работы была рассчитана импульсная характеристика реального ФНЧ. Она отличается от идеальной с погрешностью 52%.

СПИСОК ЛИТЕРАТУРЫ

Теория электрической связи /под ред. Д.Д. Кловского. - Москва, «Радио и связь», 1998.

Баскаков С.И. Радиотехнические цепи и сигналы. – Москва, «Высшая школа» , 1983.

Кловский Д.Д. Теория передачи сигналов. – Москва, «Связь», 1973.

Васильев К.К., Новосельцев Л.Я., Смирнов В.Н. Основы теории помехоустойчивых кодов – учебное пособие, УлГТУ, 2000.

Романов Б.Н. Теория электрической связи. Методические указания к курсовой работе. – Ульяновск, 2002.

Васильев К.К. Методы обработки сигналов – учебное пособие, УлГТУ, 2001.

Лекции по ТЭС.