Курсовая работа: Аналогія: теорема Піфагора на площині і в просторі
|
Название: Аналогія: теорема Піфагора на площині і в просторі Раздел: Рефераты по математике Тип: курсовая работа | ||||||||||||||||||||||||||||||||||||||||||||||||
Зміст Вступ Розділ 1. Теорема Піфагора на площині 1.1Різні доведення теореми Піфагора 1.2Теорема Піфагора та цілочислові прямокутні трикутники 1.3 Історичні відомості 1.4 Розв’язування задач Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Розділ 2. Теорема Піфагора у просторі або стереометричний аналог теореми Піфагора 2.1 Теорема(стереометричний аналог теореми Піфагора) Доведення 1 Доведення 2 Доведення 3 Доведення 4 Доведення 5 Доведення 6 Доведення 7 Доведення 8 Доведення 9 Висновок Література Вступ Математик – це той , хто вміє знаходити аналогії між твердженнями; кращий математик той, хто встановлює аналогії доведень; більш сильний математик той, хто помічає аналогії теорій; але можна уявити собі й такого, хто між аналогіями бачить аналогії. (Стефан Банах) Аналогія є таким умовидом, при якому, встановивши схожість будови об’єктів у деяких властивостях, припускають , що вони, можливо, схожі і в інших властивостях. Відомо, що в процесі розвитку науки висновки за аналогією відіграють велику роль. Аналогія, як важлива форма мислення завжди привертала до себе увагу і була предметом дослідження видатних вчених, мислителів. Чудові зразки міркувань за аналогією дали такі відомі природодослідники, як Леонардо да Вінчі, Й. Кеплер, Г. Галілей, М.В. Ломоносов, Ч. Дарвін, Д.І. Менделєєв, К. Максвелл, А. Ейнштейн та інші. За допомогою аналогії вони обґрунтували ряд найважливіших наукових відкриттів. Серед цінностей інтелекту «вищого порядку», що являють собою найважливішу частину математичної освіти, одне з пріоритетних місць, ймовірно, займає вміння знаходити і застосовувати аналогії. Про цей метод поетично і захоплено говорив Стефан Банах: «Математик – це той, хто вміє знаходити аналогії між твердженнями; кращий математик той, хто встановлює аналогії доведень; більш сильний математик той, хто помічає аналогії теорій; але можна уявити собі й такого, хто між аналогіями бачить аналогії. » Але більш багатогранно аналогія виявляється у творчій діяльності людини. Велике значення має аналогія для творчого мислення. Аналогія застосовується в учнівському пізнанні П.М. Єрднієв вважає, що володіння ум овидом за аналогією «сприяє як творчості вченого – математика, так і успішному навчанню цієї науки або самостійному вивченню її». Роль аналогії значно зростає в сучасних умовах навчання, коли перед школою стоїть завдання озброювати учнів не лише знаннями, а й методами самостійного здобуття знань. Звернемо увагу на основні дидактичні функції аналогії. По-перше, аналогія сприяє більш глибокому осмисленню матеріалу, що вивчається. При цьому застосовується ті види аналогії, які конкретизують образи і уявлення. По-друге, аналогія при вивченні нового матеріалу допомагає підводити учнів до визначення нових для них понять, самостійних пошуків способу розв’язання задачі, ефективної організації повторення, узагальнення і систематизації матеріалу. Вбачаючи в аналогії великі дидактичні можливості, вчені радять користуватись нею і вчителю, і учням. Проте слід пам’ятати, що висновки в умовиводах за аналогією не дає відповіді на питання про правильність припущення, ця правильність повинна перевірятись іншими засобами. Та аналогія важлива вже тим,що вона наводить на здогади, подає думку про те чи інше припущення. Це дуже важливо як у розвитку науки, так і в вивченні математики. Звідси випливає актуальність вибраної теми. Об'єкт дослідження – теорема Піфагора на площині і в просторі; Предмет дослідження – аналогія між теоремою Піфагора на площині і в просторі; Мета дослідження – розглянути в чому полягає аналогія міжтеоремою Піфагора на площині і в просторі. Для реалізації поставленої мети необхідно розв'язати наступні завдання: - підібрати, опрацювати та систематизувати літературні джерела з обраної теми; - підібрати, класифікувати та зібрати задачі про теорему Піфагора на площині і в просторі (на доведення та обчислення). Курсова робота складається зі вступу, двох розділів,висновку,списку використаної літератури, що містить 3 найменування. У вступі визначається об'єкт, предмет,мета та завдання дослідження,обґрунтовується актуальність обраної теми,описана структура курсової роботи. В наступних розділах йде огляд і доведення аналогії між трикутником та тетраедром.У висновку підведено підсумок про виконану роботу. Розділ 1. Теорема Піфагора на площині Теорема Піфагора . У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжини катетів. Дано:
ΔАВС, Довести
: с2
= а2
+ b2
1.1 Різні доведення теореми Піфагора Доведення 1
. На гіпотенузі і катетах побудуємо квадрати і виконаємо додаткові побудови, які видно на рисунку 1. Тоді
Таким чином, за першою ознакою рівності трикутників маємо: ΔNAB = ΔCAE. Але SΔNAB
= SANKC + SBCQF = SAEHR + SHRBD, але SAEHR + SHRBD = SAEDB. Таким чином, SANKC+ SAEDBабо b2 + a2 = c2
Рис. 1
Рис. 2 Доведення 2 Побудуємо ΔBDE = ΔACB так, щоб B Тоді чотирикутник ACDE – трапеція, бо AC || DE як два перпендикуляри до CD. Маємо: SACDE
= Крім того, SACDE
= SΔABE
+ 2SΔABC
. Трикутник ABE рівнобедрений і прямокутний. Дійсно, якщо позначимо Тоді SACDE
= Порівнюючи рівності ( 1 ) і ( 2 ), дістанемо:
Доведення 3.
Побудуємо CD Нехай SΔABC
= Аналогічно: SΔACD
= SΔBCD
= За побудовою SΔABC = SΔACD + SΔBCD . ( 4 ) З рівностей ( 1 ), ( 2 ), ( 3 ), ( 4 ) випливає:
тобто
Доведення 4. Впишемо в трикутник АВС коло ( О, r ) ( Рис.4 ). Тоді: SΔABC
= SΔOAC
+ SΔOAB
= Чотирикутник OKCL – квадрат з стороною r. За властивістю дотичних, проведених з точок А та В до кола, маємо: AH = AK = Тоді AB = AH + HB =
З іншого боку SΔABC
= Таким чином,
Доведення 5 Виконуємо побудови, які показано на рисунку 5 а), 5 б).
Рис.5,а
Рис.5,б CDMN, TQRE – квадрати зі стороною За побудовою маємо: SCDMN = SABLK + 4SΔABC , STQRE = SPQBC + SACFE + 4SΔABC . Порівнюючи ці рівності, дістанемо: SABLK + 4SΔABC = SPQBC + SACFE + 4SΔABC , або SABLK
= SPQBC
+ SACFE
, тобто Доведення 6 Побудуємо квадрат CDMN з стороною a+b( Рис.6)
Рис. 6 Тоді ΔАСВ = ΔBDK = ΔKLM = ΔLNA ( за двома катетами ) , звідки AB = BK = KL = LA = c. Отже, чотирикутник ABKL – ромб. Оскільки
Порівнюючи останні рівності, дістанемо:
Доведення 7 На сторонах прямокутного трикутника АВС побудуємо квадрати АВКМ, АDЕС, ВСFR. (Pис. 7). Трикутники ЕСF, КLМ і АСВ рівні між собою. АDRВ = EDRF як симетричні відносно прямої DR фігури; ACLM = КLСВ як центрально-симетричні фігури відносно центра квадрата АВКМ; АDRB=АСLМ як відповідні фігури при повороті навколо центра А на кут 90°. Враховуючи одержані три рівності, маємо: ADEFRB = ACBKLM, але SADEFRB = SADEC + 2SΔABC + SBCFR , SACBKLM = SABKM + 2SΔABC . Отже, SADEC
+ SBCFR
= SABKM
, тобто
Рис.8 Доведення 8 Прямокутний трикутник АСВ з прямим кутом С повернемо навколо точки С на 90° так, щоб він зайняв положення А´СВ´ ( Рис. 8 ).Продовжимо гіпотенузу А´В´ до перетину з АВ у точці D. Відрізок В´D буде висотою трикутника В´АВ. Розглянемо тепер чотирикутник А´АВ´В. Його можна розкласти на два рівнобедрені трикутники СА´А і СВ´В. Маємо: ЫΔ
СФ
´
Ф
= Таким чином ЫФ
´
ФИ
´
И
= ЫΔ
СФ
´
Ф
+ ЫΔ
СИ
´
И
= Трикутники АА´В´ і ВА´В´ мають спільну основу В´А´ і висоти AD і BD відповідно. Тому ЫФ
´
ФИ
´
И
= ЫΔ
А
Ф
´В´
+ ЫΔ
ВА´
И
= Порівнявши два вирази для площі чотирикутника А´АВ´В, одержимо:
1.2 Теорема Піфагора та цілочислові прямокутні трикутники Співвідношення між сторонами прямокутного трикутника, яке подається в підручниках математики та інших джерелах під назвою теореми Піфагора, було відоме з давніх часів. Так, клинописі пам'ятки Вавілона свідчать про те, що за 2-2,5 тисячі років до нашої ери там уже користувалися названим співвідношенням для обчислень. Було відоме воно і стародавнім єгиптянам (за 2300 років до н.е.) ,про що свідчить папірус Берлінського музею. Чому ж ця закономірність названа ім'ям Піфагора, який жив у VIcт. до н.е., тобто значно пізніше? Піфагор, про життя якого є лише відомості, переписані легендами, народився на о. Самос. У молоді роки він багато подорожував і цілком імовірно, що, відвідавши країни Стародавнього Сходу, познайомився з відомою вже там закономірністю про співвідношення між сторонами прямокутного трикутника. Повернувшись на батьківщину (в Грецію) та оселившись у м. Кротоні, Піфагор заснував філософську школу і серйозно зайнявся систематизацією та узагальненням математичних знань. Піфагор систематизував здобуті фрагментарні відомості про прямокутний трикутник, дав їм логічне обґрунтування, зробивши їх надбанням своїх співвітчизників. Першопрохідці помітили, що рівність a2 +b2 =c2 (1) справджується при натуральних значеннях довжин катетів а і b та гіпотенузи с, бо інших чисел вони не знали. З’ясуємо насамперед, чи є такі три послідовності натуральних чисел, що задовольняють рівність (1). Якщо є, то скільки таких трійок чисел? Нехай a=n -1; b=n ; c=n+1. Тоді (n -1)2 +n2 =(n+1)2 , звідки n2 -4n=0; n1 =0; n2 =4. Умову задачі задовольняє n=4. Отже, маємо трійку чисел 3,4,5, для яких 32 +42 =5 2 .Оскільки інших розв’язків рівняння не має, то існує лише одна така трійка чисел. Прямокутний трикутник зі сторонами 3, 4 і 5 був відомий стародавнім єгиптянам. Ним вони користувалися, будуючи прямі кути під час землевимірювальних робіт. Поділивши вірьовку на 12 рівних частин, закріплювали її кілками в поділках, які від одного кінця відділяли 3 відрізки, а від другого – 5. Натягуючи вільні кінці вірьовки та суміщаючи їх, діставали прямокутний трикутник з прямим кутом між відрізками 3 і 4 одиниці. Людей, які займалися цією справою, називали гарпедонаптами (натягувачі вірьовок), а прямокутний трикутник зі сторонами 3, 4, і 5 дістав назву єгипетського. Назвемо прямокутні трикутники довжини сторін яких виражаються цілими числами, цілочисловими. Зрозуміло, що трикутники зі сторонами 3k, 4ki 5k прямокутні цілочислові, бо (3k)2 +(4k)2 =(5k)2 ↔ 32 +42 =5 2 . Таких трикутників безліч. Чи існують цілочислові прямокутні трикутники, крім єгипетського, довжини сторін яких – три числа, що мають найбільшим спільним дільником число 1? Шукатимемо такі трикутники, тобто такі трійки натуральних чисел, які задовольнятимуть зазначену вище умову. Виходячи з умови, вони не можуть бути всі парними, але не можуть бути й не парними,бо , якщо a і b непарні, то с парне. (Зазначимо тут, що коли, наприклад, a парне, то a2 кратне 4, бо якщо a=2п ,то a2 =4п2. Якщо a непарне, тобто a=2п+1, то a2 =4п2 +4п+1=4п1 +1 – непарне). Взагалі, якщо будь-які два числа з трійки натуральних чисел a, b і c ,що задовольняють a2 +b2 =c2 (такі числа називають піфагоровими), мають спільний дільник відмінний від 1, то він буде також дільником і третього числа. Отже, будь-яка пара чисел з шуканих трійок є взаємно-простими числами. Нехай aнепарне і bпарне, тоді c також непарне. Маємо : a2 +b2 =c2 ↔b2 =c2 - a2 ↔ b2 =(c-a)(c+a).(2) Числа (c-a) і (c+a) парні, тому тому
Числа
Отже С = и (р1 +р2 ) і а = и (р1 -р2 ), тобто числа с і а матимуть спільний дільник и, що суперечить умові. Добуток двох взаємно простих чисел є точним квадратом (рівність 3) лише в тому випадку, коли кожне з цих чисел є точним квадратом. Нехай
Маємо тотожність (х2 -у2 )2 +(2ху)2 =(х2 +у2 )2 . Формули а=х2 -у2 ; b=2ху і с=х2 +у2 дають можливість обчислювати a, b і c за значеннями х і у. Якщо числа х і у взаємно прості й до того ж одне з них парне, а друге непарне, то трійки (a,b,c) будуть саме такі, як у вихідній задачі(найбільший спільний дільник a, b, c дорівнює 1) . Такі трійки піфагорових чисел називаються основними. Основні трійки піфагорових чисел модна дістати, склавши таку таблицю.
Її можна продовжити як завгодно довго. Отже, таких трійок чисел безліч. Єгипетський трикутник, як видно з таблиці, дістанемо, якщо х=2, у=1. Помічаємо також, що коли х-у=1, гіпотенуза більша від більшого катета на 1. Це природно, бо коли х=у+1, b=2xy=2у(у+1)=2у2 +2у; с=(у+1)2 +у2 =2у2 +2у+1 і тому с-b=1. При цьому менший катет а=х2 -у2 =2у+1, а різниця довжин катетів b-а=2у2 -1.Цей вираз дорівнює 1 тільки тоді, коли у=1. Знову приходимо до висновку, що існує лише один прямокутний трикутник, довжини сторін якого виражаються трьома послідовними натуральними числами. Сума довжин гіпотенузи й катета b є точний квадрат, бо с+b=х2 +у2 +2ху=(х+у)2 . Точним квадратом є також і їх різниця, тобто с-b=х2 +у2 -2ху=(х-у)2 . Якщо х-у=п, то с-b=п2 . Наприклад, якщо х=5 і у=2, маємо b=20 і с=29; х+у=7; b+с=20+29=49=72 ; с-b=29-20=9=32 . Зрозуміло,що з кожної основної трійки піфагорових чисел модна дістати безліч похідних, бо a2 +b2 =c2 ↔(3а)2 +(4b)2 =(5с)2 Наприклад, маючи трійку (3;4;5), дістанемо трійки (6;8;10), (9;12;15), (12;16;20) та ін. До речі, усі трійки піфагорових чисел, які походять від основної трійки (3;4;5), і основна трійка є арифметичними прогресіями. Інших трійок піфагорових чисел, які б були арифметичними прогресіями немає. Неважко показати, що серед основних трійок(а отже, і похідних) немає жодної, яка була б геометричною прогресією. Припустимо, то така трійка (а;b;с) існує. Тоді b2 =ас і значить а2 +ас=с2 . Звідси ас=с2 -а2 , або ас=(с+а)(с-а). Числа а і с непарні, тоді як (с+а) і (с-а) парні. Отже рівність, хибна, а це означає, що зроблене неправильне припущення. Похідні трійки можна дістати також, надаючи х і у цілих значень(крім тих, при яких дістанемо основні трійки) або коли Якщо, наприклад, х=1000 і у=999, то дістанемо основну трійку а=х+у=1999, b=1998000 і с=b+1=1998001. 1.3 Історичні відомості Піфагор Самосський (бл. 580–500 р.р. до н. е.) – давньогрецький математик і філософ. Народився на острові Самос в багатій купецькій сім’ї, здобув ґрунтовану освіту. За переказами, Піфагор для ознайомлення з мудрістю східних учених виїхав до Єгипту і, нібито, прожив там 22 роки, після чого провів 12 років у Вавілоні, де вивчив наукові праці вавілонських жерців. Близько 530 р. до н. е. повернувся на батьківщину і оселився в місті Кротоні. Тут йому вдалося організувати власну школу, яка діяла майже 30 років і здобула велику популярність. Школа Піфагора багато зробила для перетворення геометрії в науку. Характерною рисою методу Піфагора було поєднання геометрії з арифметикою: відрізки відігравали роль, аналогічну тому, як букви в сучасній алгебрі. Піфагор багато займався пропорціями та прогресіями. Вчення Піфагора та його учнів стосувалося гармонії, геометрії, теорії чисел, астрономії тощо. Піфагорійці понад усе цінували результати, здобуті в теорії гармонії, бо саме тут підтверджувалась їхня ідея, що числа визначають все. Піфагор один з перших вважав, що Земля має форму кулі є центром Всесвіту, що сонце, Місяць і планети мають власний рух, відмінний від добового руху нерухомих зірок. Ці погляди передували геліоцентричному вченню Коперніка. Піфагору приписують доведення теореми, яка має його ім’я. Її історія оповита легендами. Виявляється, що вона ще до Піфагора була відома єгиптянам, вавілонянам, китайцям та індійцям.
Рис.1 Німецький історик мате математики Кантор вважає, що рівність 32 + 42 = 52 була відома єгиптянам ще близько 2300 р. до н. е. в часи царя Аменетхета Ι. На думку Кантора, гарпедонапти, або "натягувачі вірьовок", будували прямі кути за допомогою прямокутних трикутників зі сторонами 3, 4, 5. Можна легко відновити їх спосіб побудови. Візьмемо вірьовку довжиною 12м і прив’яжемо до неї кольорові стрічки на відстані 3м від одного кінця і 4м від другого (рис.1). Потім натягнемо вірьовку так, як це вказано на рисунку. Прямий кут буде між сторонами довжиною в 3 і 4 метри. Близько 2000 р. до н. е. вавілоняни вміли робити окремі обчислення з прямокутними трикутниками. Геометрія в індусів, як і в єгиптян, була тісно пов’язана з культом. Цілком ймовірно, що теорема про квадрат гіпотенузи була відома в Індії близько 8 ст. до н.е. Властивості трикутника з сторонами 3, 4, 5 були відомі в Китаї за 1100 р. до н. е., про що засвідчує математична книга Чупей. Теорема Піфагора має різні формулювання. В "Початках" Евкліда вона формулюється так: У прямокутному трикутнику квадрат сторони, натягнутої над кутом, дорівнює квадратам на сторонах, що утворюють прямий кут. Латинський переклад арабського тексту: У всякому прямокутному трикутнику квадрат, утворений на стороні, натягнутій над прямим кутом, дорівнює сумі двох квадратів, утворених на двох сторонах, що замикають прямий кут. У перекладі з німецького читається так: Площа квадрата, виміряна довгою стороною трикутника, настільки ж велика, як у двох квадратів, які виміряні двома сторонами його, що прилягають до прямого кута. У першому російському перекладі евклідових "Початків", зроблено з грецької Ф.І. Петрушевським у 1819 році, теорема Піфагора викладена так: У прямокутних трикутниках квадрат із сторони, протилежної прямому куту, дорівнює сумі квадратів із сторін, що містять прямий кут. У Франції і деяких областях Німеччини теорему Піфагора називали "мостом ослів". Вважають, що вона формулювалась так: Квадрат, побудований на гіпотенузі прямокутного трикутника, рівновеликий сумі квадратів, побудованих на його катетах. В епоху середньовіччя теорема Піфагора визначала границі математичних знань. Характерне креслення теореми Піфагора використовувалось як символ математики, перетворювалось школярами в карикатури. Нині всі погоджуються з тим, що ця теорема не була відкрита Піфагором. Однак, одні вважають, що Піфагор першим дав її повноцінне доведення, інші відомляють йому в цій заслузі. Дехто приписує йому доведення, яке Евклід (жив близько 300 р. до н.е. в Олександрії) наводить у першій книзі своїх "Початків". Проте Прокл, який жив у 410 – 485 р. р. у Візантії і Афінах, стверджує, що доведення в "Початках" належать самому Евкліду. Відомий голандський математик Ван-дер-Варден прийшов до висновку: "Заслугою перших грецьких математиків, таких, як Фалес, Піфагор і піфагорійці, є не відкриття математики, а її систематизація і обґрунтування. В їх руках обчислювальні рецепти перетворились в точну науку". 1.4 Розв’язування задач Задача 1 Основа трикутника дорівнює 40 см. До неї проведені висота довжиною 12 см і медіана довжиною Розв’язання Нехай у трикутнику АВС, АВ=40см, висота СН=12 см, медіана СМ= З трикутника МНС(Н=90о ): МН= Крім того, точка Н лежить між точками М і В. Оскільки МВ= НВ=МВ-МН=5(см) і АН=АВ-НВ=35(см). З З Отже Р=АВ+ВС+АС=40+13+37=90(см.)
Рис. 1
Рис. 2 Задача2 Периметр ромба дорівнює 100 см, а діагоналі відносяться як 3:4. Обчислити площу ромба. Розв’язання Нехай АВСD – ромб, у якому ВD:АС=3:4 і Р=100(см) (рис.2) Оскільки Р=4*АD, то АD=25 см. Враховуючи, що ВD=2*ОD, АС=2*АО, Одержимо
звідки ОD=3k, AO=4k(k>0). З Тоді OD=3*5=15 (см), АО=4*5=20(см), SABCD
=
4*SAOD
=4* Задача3 (задача Леонардо Фібоначчі) Дві башти висотою 30 і 40 футів розташовані одна проти другої на відстані 50 футів одна від одної. Між ними знаходиться фонтан, до якого з обох башт злітають два птахи, і , пролітаючи з однаковою швидкістю, прилітають до фонтану в один і той же час. Яка відстань по горизонталі відділяє фонтан від обох башт(рис.3)? Розв’язання Позначимо АЕ=х, тоді DЕ=50-х. З прямокутних трикутників ВАЕ і СDЕ за теоремою Піфагора маємо : ВЕ2 =АЕ2 +АВ2 , СЕ2 =DЕ2 +DС2 .За умовою ВЕ=ЕС, тоді маємо АЕ2 +АВ2 = DЕ2 +DС2 , х2 +402 =(50-х)2 +302 , х2 +1600=2500-100х+х2 +900, 100х=1800, х=18, DЕ=50-18=32. Отже, АЕ=18 футів, DЕ=32 фути.
Рис. 3
Рис.4.1 Задача 4 Обчислити довжину висоти трикутника, якщо відомо довжини його сторін. Розв'язання Нехай ΔАВС, АВ = с, АС =
Дістанемо рівняння
Розв’язуючи його, одержимо:
Тоді
У другому випадку відповідь буде та сама
Рис. 4.2
Рис. 5 Задача 5 На сторонах рівнобедреного прямокутного трикутника з катетом Розв'язання Нехай ΔАВС, ABMN,ACDF, BCKL- квадрати
Неважко переконатись в тому, що ΔO1 O2 O3 – рівнобедрений, O1 C – висота(рис.5). Тоді За теоремою Піфагора
Таким чином,
Розділ 2. Теорема Піфагора у просторі або стереометричний аналог теореми Піфагора Метод аналогії є одним з ефективних і розповсюджених методів математики. Його застосування приводить до плідних і часто до неочікуваних результатів. Деякі властивості трикутника і тетраедра схожі, а деякі геометричні поняття, пов’язані з трикутником , мають просторові аналоги: наприклад, сторона трикутника – грань тетраедра, довжина сторони – площа грані, вписане коло – вписана сфера, площа – об’єм,бісектриса кута – бісектор двогранного кута тощо. Багато теорем про трикутники, якщо замінити в їх формулюванні планіметричні терміни відповідними стереометричними і конкретно сформулювати, то вони перетворюються в теореми про тетраедри. Однією з таких є аналог теореми Піфагора в стереометрії. Означення. Якщо три ребра, які виходять з однієї вершини тетраедра, попарно ортогональні, то тригранний кут, що визначається ними, називається прямим, а тетраедр – прямокутним. Теорема (стереометричний аналог теореми Піфагора).У прямокутному тетраедрі квадрат площі грані, що лежить проти прямого тригранного кута, дорівнює сумі квадратів площ решти граней. Доведення 1 . Нехай у прямокутному тетраедрі OABC
Доведемо, що
Маємо:
У Δ АВС:
Площу трикутника АВС обчислимо за формою Герона
Виконаємо перетворення:
Використовуючи (2), (3), одержимо:
тобто Враховуючи (1), (4), одержимо
Розглянемо доведення, в якому використовується метод проекцій Доведення 2 Нехай у прямокутному тетраедрі ОАВС грані ОВС, ОАС, ОАВ утворюють з основою АВС кути У прямокутному паралелепіпеді з діагоналлюОН і ребрами ОА1 , ОВ1 , ОС1 справджується рівність
або звідки Оскільки Маємо:
звідси Враховуючи (1) і (2), одержимо:
Пропонуємо інші доведення теореми Піфагора для прямокутного тетраедра. Доведення 3 Нехай у прямокутному тетраедрі ОАВС
Побудуємо висоту СН трикутника АВС і сполучимо точки О і Н. Маємо: СН – похила, ОН – її проекція, СН
З ΔСОН ( Знайдемо ОН, для цього виразимо площу трикутника АОВ через катети, тобто
теорема піфагор площина простір і через гіпотенузу АВ та висоту ОН, опущену на неї, тобто
або З рівностей (3), (4)
звідки Враховуючи ( 2 ), ( 5 ), одержимо:
Спосіб 1 . Враховуючи ( 1 ), ( 6 ) одержимо:
Тоді
Спосіб 2 . Можна використати формулу проекцій
Оскільки
то звідки або Доведення 4
. Нехай у тетраедрі ОАВС
Оскільки ΔАОВ – ортогональна проекція ΔАВС, то
Враховуючи рівності (1) і (2), одержимо:
З ΔАОВ ( тоді звідки
Крім цього,
Формула (3) набуває вигляду
тобто Останній вираз є вірною рівністю, одержаною з рівності ( 1 ) за допомогою тотожних перетворень, тому можна зробити висновок: початкове припущення вірне і справедлива теорема: У прямокутному тетраедрі квадрат площі грані, що лежить проти прямого тригранного кута дорівнює сумі квадратів площ решти граней.
Доведення 5 . Нехай ОН – висота прямокутного тетраедра ОАВС з прямим тригранним кутом при вершині О, тоді АН1 – висота ΔАВС (Рис.2.6). З ΔАОН1
Помноживши цю рівність на
або або Аналогічно одержимо:
Додамо почленно рівності (1), (2), (3), одержимо
Таким чином,
Доведення 6
. Нехай у тетраедрі ОАВС Позначимо
Оскільки ΔАОС – ортогональна проекція ΔАВС, то
З (1), (2) слідує
звідки Аналогічно одержимо
Додамо почленно (3), (4), (5), одержимо:
Таким чином,
Доведення 7
. Нехай у прямокутному тетраедрі ОАВС Оскільки
Отже,
Обчислимо
Враховуючи (1), (2), (3), одержимо
звідки З ΔАСН Маємо Тоді
Оскільки
то звідси Доведення 8 . Для обчислення площі трикутника АВС (Рис.2.7) використаємо геометричне тлумачення векторного добутку двох векторів, а саме:
Оскільки
то одержимо:
Тоді Таким чином,
звідки Враховуючи, що
остаточно одержимо
Доведення 9
.У вибраній системі координат Об’єм тетраедра можна обчислити за формулою:
де Застосуємо цю формулу
З іншого боку
де ОН – висота тетраедра (Рис. 2.6). Висоту ОН знайдемо як відстань від точки О до площини трикутника АВС. Для цього складемо рівняння площини (АВС) "у відрізках на осях":
або Тоді
З (1), (2), (3) слідує
звідки або
Доведення 10 . Використаємо (рис.2.8) і позначення на ньому. Висоту ОО1 обчислимо як відстань між точками О і О1 , для цього складемо рівняння прямої ОО1 . Рівняння площини (АВС) має вигляд
(див. розв’язання 9), де Оскільки Таким чином, вектор
звідси одержимо параметричні рівняння ОО1 :
Обчислимо координати точки О1 , розв'язавши систему рівнянь:
Тоді Обчислимо об’єм тетраедра ОАВС за формулою
Враховуючи, що
одержимо:
звідки або Доведення 11 . Теорему Піфагора для прямокутного тетраедра можна розглядати як наслідок теореми косинусів для довільного тетраедра [3], яка формулюється так: квадрат площі будь-якої грані тетраедра дорівнює сумі квадратів площ інших граней без подвоєних добутків площ цих граней, взятих попарно, на косинус двогранних кутів між ними, тобто
У прямокутному тетраедрі двогранні кути
площі граней - катетів, а Таким чином, стереометричний аналог теореми Піфагора можна сформулювати так: У прямокутному тетраедрі квадрат площі грані гіпотенузи дорівнює сумі квадратів площ граней - катетів. Зауваження. Має місце наслідок з цієї теореми: площі граней - катетів є середніми геометричними між площею грані — гіпотенузи і площами їх проекцій на грань - гіпотенузу (див. доведення 5). Висновок Мабуть, найпопулярнішою з усіх теорем є теорема Піфагора. Причинами такої популярності є простота, краса, значення. Справді, теорема Піфагора проста, але не очевидна. Це поєднання двох суперечностей і надає їй особливої привабливості.Теорема Піфагора - важливий інструмент геометричних обчислень. Використовуючи її, можна обчислити у планіметрії діагональ квадрата і прямокутника, висоту, медіану, бісектрису рівностороннього або рівнобедреного трикутника, висоту рівностороннього трикутника, радіуси вписаного і описаного кіл правильного трикутника, рівнобедреного трикутника тощо. Теорема Піфагора використовується при розв’язанні трикутників, у теорії площ. У стереометрії теорема Піфагора застосовується при обчисленні висоти, ребра або апофеми правильної піраміди, при вивченні многогранників, тіл обертання та їх комбінацій. Взагалі, перелічити з достатньою повнотою всі випадки, де використовується теорема Піфагора в геометрії неможливо. Вона має не лише теоретичний характер, а й широко використовується на практиці при розрахунках покрівель дахів, верхніх частин вікон у будинках готичного і романського стилю, паркетуванні підлоги тощо. З теореми Піфагора випливає чимало наслідків, які є її вінцем, зокрема: - у прямокутному трикутнику будь – який катет менший від гіпотенузи; - косинус кута а менше одиниці для будь – якого гострого кута а; - якщо до прямої з однієї точки провести перпендикуляр і похилі ,то похилі більші перпендикуляра; рівні похилі мають рівні проекції; з двох похилих більша та, у якої проекція більша. Сама теорема Піфагора є наслідком теореми : косинус кута залежить лише від градусної міри кута. Тому, якщо теорему Піфагора «вплести» у вінок її наслідків, то отримаємо вінок наслідків теореми про косинус кута. Із означень sinα, cosα, tgαвипливають такі властивості: - катет, протилежний куту α , дорівнює добутку гіпотенузи на sinα; - катет, прилеглий до кута α , дорівнює добутку гіпотенузи на cosα; - катет, протилежний куту α , дорівнює добутку другого катета наtgα; - катет прямокутного трикутника є середнє пропорційне між гіпотенузою і його проекцією на гіпотенузу; - висота прямокутного трикутника, опущена з вершини прямого кута, є середнє пропорційне між проекціями катетів на гіпотенузу. Вся геометрія складеться з таких прекрасних віночків, слід лише придивитись до них, звертати на них увагу, порівнювати, запам’ятовувати і вміло використовувати їх при розв’язанні задач. Література 1. Боровик В.Н., Зайченко І.В., Кобко Л.М. «Гармонія і естетика трикутника». Навчальний посібник для студентів вищих навчальних закладів – 2-е вид., виправл. і доп.. Рекомендовано МОН України – К.: Освіта України, 2007. – 180с. 2. Кобко Л.М. «Аналогія: планіметрія–стереометрія в таблицях». Навчальний посібник для студентів педагогічних вищих навчальних закладів. – Чернігів, 2008.- 64с. 3. Кобко Л.М. «У світі геометрії». Навчально–методичний посібник для студентів педагогічних вищих навчальних закладів. – Чернігів, 2009.- 209с. |
||||||||||||||||||||||||||||||||||||||||||||||||


 Рис.3
Рис.3  Рис.4
Рис.4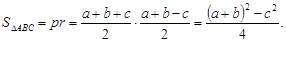













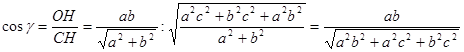 ,
, 
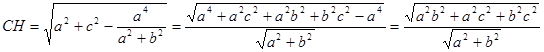
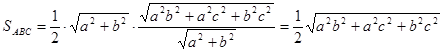 ,
, 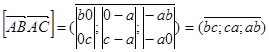
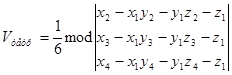 ,
, 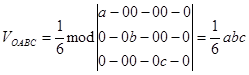 . (1)
. (1)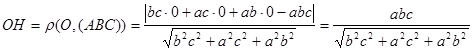 . (3)
. (3)
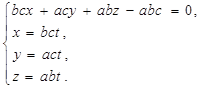
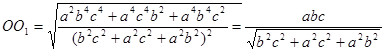 (1)
(1)