|
Данная работа посвящена теоретическим и практическим аспектам внедрения в начальный школьный курс математики логических задач.
«Главная задача обучения математике, причём с самого начала, с первого класса, – учить рассуждать, учить мыслить», – писал ведущий отечественный методист А.А. Столяр.
Такая тема как «Использование логических задач на уроке математики в начальной школе» очень актуальна сегодня. Актуальность данной темы заключается в том, что учитель из-за отсутствия системы работы над этими задачами не всегда знает, как сформировать у учащихся способность мыслить последовательно, по законам логики.
Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в методической литературе, в объяснительных записках к учебным программам. Однако, как это делать, учитель не всегда знает. Нередко это приводит к тому, что развитие логического мышления в значительной мере идёт стихийно, поэтому большинство учащихся, даже старшеклассников, не овладевает начальными приёмами логического мышления (анализ, сравнение, синтез, абстрагирование и др.)
Роль математики в развитии логического мышления исключительно велика. Причина столь исключительной роли математики в том, что это самая теоретическая наука из всех изучаемых в школе. В ней высокий уровень абстракции и в ней наиболее естественным способом изложения знаний является способ восхождения от абстрактного к конкретному. Как показывает опыт, в младшем школьном возрасте одним из эффективных способов развития мышления является решение школьниками нестандартных логических задач.
Кроме того, решение нестандартных логических задач способно привить интерес ребёнку к изучению «классической» математики. В этом отношении весьма характерен следующий пример. Крупнейший математик современности, создатель московской математической школы, академик Николай Николаевич Лузин, будучи гимназистом, получал по математике сплошные двойки. Учитель прямо сказал родителям Н.Н. Лузина, что их сын в математике безнадёжен, что он туп и что вряд ли он сможет учиться в гимназии. Родители наняли репетитора, с помощью которого мальчик еле-еле перешёл в следующий класс.
Однако репетитор этот оказался человеком умным и проницательным. Он заметил невероятную вещь: мальчик не умел решать простые, примитивные задачи, но у него иногда вдруг получались задачи нестандартные, гораздо более сложные и трудные. Он воспользовался этим и сумел заинтересовать математикой этого, казалось бы, бездарного мальчика. Благодаря такому творческому подходу педагога из мальчика впоследствии вышел учёный с мировым именем, не только много сделавший для математики, но и создавший крупнейшую советскую математическую школу.
Значительное место вопросу обучения младших школьников логическим задачам уделял в своих работах известнейший отечественный педагог В.А. Сухомлинский. Суть его размышлений сводится к изучению и анализу процесса решения детьми логических задач, при этом он опытным путём выявлял особенности мышления детей.
Логика – это наука о законах правильного мышления, о требованиях, предъявляемых к последовательному и доказательному рассуждению (немецкий философ И. Кант). Отсюда следует, что мы должны научить учащихся анализировать, сравнивать, выделять главное, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия, ставить и разрешать проблемы. Овладение этими методами и означает умение мыслить. Нельзя сформировать логическое мышление, не изучая логику, нельзя надеяться, что логическое мышление развивается в полной мере спонтанно на уроках математики, литературы и др. Во многих ситуациях учащиеся поступают интуитивно, полагаясь на сообразительность и смекалку, а иногда жизненный опыт или подсказку старших. Но логическая интуиция нуждается в прояснении.
Проблемой внедрения в школьный курс математики логических задач занимаются не только исследователи в области математики, но и педагогики и психологии. Поэтому, при написании работы использовалась специализированная литература, как первого, так и второго направления.
Изложенные выше факты определили выбранную тему: «Использование логических задач на уроке математики в начальной школе».
В связи с этим выделим объект исследования – развитие логического мышления младших школьников на уроках математики.
Предмет исследования – использование нестандартных задач на уроках математики в начальной школе как средство развития логического мышления детей.
Цель исследования: выявить значение и особенности развития логического мышления у учащихся начальных классов.
Задачи:
1) проанализировать психолого-педагогическую и методическую литературу по проблеме исследования;
2) раскрыть сущность нестандартных задач и их роль в развитии логического мышления младших школьников;
3) выработать систему мер по совершенствованию логического мышления младших школьников на уроках математики.
Можно предположить, что развитие логичности мышления младших школьников в процессе решения нестандартных задач способствует формированию умственных приёмов деятельности, творческих способностей учащихся, развитию интеллекта, повышению успеваемости.
Для решения поставленных задач и проверки исходных предположений автором применялись различные методы исследования: анализ психолого-педагогической и методико-математической литературы, наблюдение и анализ продуктов творческой деятельности учащихся, изучение опыта школьных учителей, беседа, теоретический анализ и синтез, сравнение, обобщение, классификация и др.
ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ ЛОГИЧЕСКИХ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ В НАЧАЛЬНОЙ ШКОЛЕ
1.1 Психологические предпосылки использования нестандартных логических задач на уроке математики в начальной школе
Среди первоклассников в среднем 15 – 20% детей сталкиваются с трудностями при принятии новой для них социальной позиции школьника, иначе говоря, вхождение в школьную жизнь для них затруднено. Школьная жизнь воспринимается ими, прежде всего, с формальной стороны, а содержательные стороны учебной деятельности – ориентация на самоизменение и присвоение научного знания – не выступают для них в качестве актуальных.
Исходя из вышесказанного, важно на начальном этапе обучения создавать для детей условия, органично сочетающие игровой и учебный типы жизнедеятельности: необходимо организовать своеобразную комплементарную деятельность детей, являющуюся игровой по форме, знакомой и привлекательной для ребёнка, но учебной по своей направленности. Такая деятельность должна предполагать достижение целей, связанных с занятием ребёнком позиции субъекта по присвоению нового учебно-игрового опыта.
Развитие мышления происходит при условии овладения тремя формами мышления: наглядно-действенным, наглядно-образным и логическим.
Сначала, в 3 – 4 года, формируется наглядно-действенное мышление. Это мышление в действии. Ребёнок пытается последовательно собрать пирамидку, а потом сам переходит к сравниванию, сопоставлению и т.д.
В 5 – 6 лет формируется наглядно-образное мышление, которое позволяет выделять самое существенное в предметах, а также видеть соотношение этих предметов друг с другом и соотношение их частей (ребёнок играет в «школу», «магазин», с большим интересом рассматривает картинки, лепит, рисует).
Психолог Л.С. Выготский отмечал интенсивное развитие интеллекта в младшем школьном возрасте. Чтобы развитие было успешным, нужна помощь со стороны учителя. Для этого требуется знание особенностей психического развития младших школьников, а также понимание конечных целей.
Ребёнок лет 7 – 8 обычно мыслит конкретными категориями, часто подменяет аргументацию и доказательство простым указанием на реальный факт или опирается на аналогию, далеко не всегда правомерную. Необходимо показать ребёнку дифференцированный подход к признакам предмета (существенным и несущественным), научить его давать обоснованное доказательство, понимать причинно-следственные связи.
В связи с преобладанием деятельности первой сигнальной системы у младших школьников более развита наглядно-образная память. Они склонны к механическому запоминанию, без осознания смысловых связей. К переходу в среднее звено у учащегося должна сформироваться способность к запоминанию и воспроизведению смысла материала, аргументации, логических схем рассуждений.
В начальной школе необходимо не только закладывать основу знаний учащихся, но следует учить самостоятельно мыслить и творчески работать.
В дальнейшем развитое образное мышление подводит к воротам логики. Ребёнок учится рассуждать, анализировать, устанавливать простые закономерности, делать умозаключения в соответствии с законами логики.
Логические и психологические исследования последних лет (в особенности работы Ж. Пиаже) вскрыли связь некоторых "механизмов" детского мышления с общематематическими и общелогическими понятиями.
На первый взгляд понятия "отношение", "структура", "законы композиции" и др., имеющие сложные математические определения, не могут быть связаны с формированием математических представлений у маленьких детей. Конечно, весь подлинный и отвлечённый смысл этих понятий и их место в аксиоматическом построении математики как науки есть объект усвоения уже хорошо развитой и "натренированной" в математике головы. Однако некоторые свойства вещей, фиксируемые этими понятиями, так или иначе, проступают для ребёнка уже сравнительно рано: на это имеются конкретные психологические данные.
Прежде всего, следует иметь в виду, что от момента рождения до 7 – 10 лет у ребёнка возникают и формируются сложнейшие системы общих представлений об окружающем мире и закладывается фундамент содержательно-предметного мышления. Причём на сравнительно узком эмпирическом материале дети выделяют общие схемы ориентации в пространственно-временных и причинно-следственных зависимостях вещей. Эти схемы служат своеобразным каркасом той "системы координат", внутри которой ребёнок начинает всё глубже овладевать разными свойствами многообразного мира. Конечно, эти общие схемы мало осознаны и в малой степени могут быть выражены самим ребёнком в форме отвлечённого суждения. Они, говоря образно, являются интуитивной формой организации поведения ребёнка (хотя, конечно, всё более и более отображаются и в суждениях).
В последние десятилетия особенно интенсивно рассматривались вопросы формирования интеллекта детей и возникновения у них общих представлений о действительности, времени и пространстве известным швейцарским психологом Ж. Пиаже и его сотрудниками. Некоторые его работы имеют прямое отношение к проблемам развития математического мышления ребёнка.
В одной из своих последних книг, написанной совместно с Б. Инельдер, Ж. Пиаже приводит экспериментальные данные о генезисе и формировании у детей (до 12 – 14 лет) таких элементарных логических структур, как классификация и сериация. Классификация предполагает выполнение операции включения (например, А + А' = В) и операции, ей обратной (В – А' = А). Сериация – это упорядочение предметов в систематические ряды (так, палочки разной длины можно расположить в ряд, каждый член которого больше всех предыдущих и меньше всех последующих).
Анализируя становление классификации, Ж. Пиаже и Б. Инельдер показывают, как от её исходной формы, от создания "фигурной совокупности", основанной лишь на пространственной близости объектов, дети переходят к классификации, основанной уже на отношении сходства ("нефигурные совокупности"), а затем к самой сложной форме – включению классов, обусловленному связью между объёмом и содержанием понятия. Авторы специально рассматривают вопрос о формировании классификации не только по одному, но и по двум-трём признакам, о формировании у детей умения изменять основание классификации при добавлении новых элементов.
Эти исследования преследовали вполне определённую цель – выявить закономерности формирования операторных структур ума и прежде всего такого их конституирующего свойства как обратимость, т.е. способности ума двигаться в прямом и обратном направлении. Обратимость имеет место тогда, когда "операции и действия могут развёртываться в двух направлениях, и понимание одного из этих направлений вызывает ipso facto (в силу самого факта) понимание другого".
Ж. Пиаже считает, что психологическое исследование развития арифметических и геометрических операций в сознании ребёнка (особенно тех логических операций, которые осуществляют в них предварительные условия) позволяет точно соотнести операторные структуры мышления со структурами алгебраическими, структурами порядка и топологическими.
В период от 7 до 11 лет система отношений, основанная на принципе взаимности, приводит к образованию в сознании ребёнка структуры порядка. Рассмотрим основные положения, сформулированные Ж. Пиаже, применительно к вопросам построения учебной программы. Прежде всего, исследования Ж. Пиаже показывают, что в период дошкольного и школьного детства у ребёнка формируются такие операторные структуры мышления, которые позволяют ему оценивать фундаментальные характеристики классов объектов и их отношений. Причём уже на стадии конкретных операций (с 7 – 8 лет) интеллект ребёнка приобретает свойство обратимости, что исключительно важно для понимания теоретического содержания учебных предметов, в частности математики.
Эти данные говорят о том, что традиционная психология и педагогика не учитывали в достаточной мере сложного и ёмкого характера тех стадий умственного развития ребёнка, которые связаны с периодом от 7 до 11 лет. Сам Ж. Пиаже эти операторные структуры прямо соотносит с основными математическими структурами. Он утверждает, что математическое мышление возможно лишь на основе уже сложившихся операторных структур (и при этом остаётся в тени объект этих операций). Это обстоятельство можно выразить и в такой форме: не "знакомство" с математическими объектами и усвоение способов действия с ними определяют формирование у ребёнка операторных структур ума, а предварительное образование этих структур (как "координации действий") является началом математического мышления, "выделения" математических структур.
Рассмотрение результатов, полученных Ж. Пиаже, позволяет сделать ряд существенных выводов применительно к конструированию учебной программы по математике. Прежде всего, фактические данные о формировании интеллекта ребёнка с 7 до 11 лет говорят о том, что ему в это время не только не "чужды" свойства объектов, описываемые посредством математических понятий "отношение – структура", но последние сами органически входят в мышление ребёнка.
Традиционные задачи начальной школьной программы по математике не учитывают этого обстоятельства. Поэтому они не реализуют многих возможностей, таящихся в процессе интеллектуального развития ребёнка. В этой связи практика внедрения в начальный школьный курс математики логических задач должна стать нормальным явлением.
Материалы, имеющиеся в современной детской психологии, позволяют положительно оценивать общую идею внедрения в учебные программы таких задач, в основе которых лежали бы понятия об исходных математических структурах. Конечно, на этом пути возникают большие трудности, так как ещё нет опыта построения такого учебного предмета. В частности, одна из них связана с определением возрастного "порога", с которого осуществимо обучение по новой программе. Если следовать логике Ж. Пиаже, то, видимо, по этим программам можно учить лишь тогда, когда у детей уже полностью сформировались операторные структуры (с 14 – 15 лет). Но если предположить, что реальное математическое мышление ребёнка формируется как раз внутри того процесса, который обозначается Ж. Пиаже как процесс складывания операторных структур, то эти программы можно вводить гораздо раньше (например, с 7 – 8 лет), когда у детей начинают формироваться конкретные операции с высшим уровнем обратимости. В "естественных" условиях, при обучении по традиционным программам, формальные операции, возможно, только и складываются к 13 – 15 годам. Но нельзя ли "ускорить" их формирование путём более раннего введения такого учебного материала, усвоение которого требует прямого анализа математических структур?
Представляется, что такие возможности есть. К 7 – 8 годам у детей уже в достаточной мере развит план мыслительных действий. Путём обучения по соответствующей программе, в которой свойства математических структур даны "явно" и детям даются средства их анализа, можно быстрее подвести детей к уровню "формальных" операций, чем в те сроки, в которые это осуществляется при "самостоятельном" открытии этих свойств. При этом важно учитывать следующее обстоятельство. Есть основания полагать, что особенности мышления на уровне конкретных операций, приуроченном Ж. Пиаже к 7 – 11 годам, сами неразрывно связаны с формами организации обучения, свойственными традиционной начальной школе.
Таким образом, в настоящее время имеются фактические данные, показывающие тесную связь операторных структур детского мышления и общематематических и общелогических структур, хотя "механизм" этой связи далеко не ясен и почти не исследован. Наличие этой связи открывает принципиальные возможности для построения учебного предмета, развертывающегося по схеме "от простых структур – к их сложным сочетаниям".
Можно сделать вывод, что логические мышление необходимо развивать в раннем детстве, так как от момента рождения до 7 – 10 лет у ребёнка возникают и формируются сложнейшие системы общих представлений об окружающем мире и закладывается фундамент содержательно-предметного мышления. Отсюда следует, что значительное место должно принадлежать широкому применению в процессе обучения младших школьников нестандартных логических задач.
1.2 Роль логических задач в формировании умственных способностей у младших школьников
В отличие от естественнонаучных дисциплин математика отражает объективную реальность лишь опосредованно. Предмет её изучения – мысленные идеальные обобщённые образы, являющиеся результатом многоуровневой абстракции. Поэтому изучение математики связано с необходимостью создавать образы и оперировать ими, что требует значительно большего интеллектуального напряжения, чем оперирование предметно данными объектами.
Другая особенность математики в том, что она исследует абстрактные сущности независимо от той реальности, отражением которой они являются. Этим определяется преимущественно дедуктивный её характер, в силу чего изучение математики требует умения правильно рассуждать. Но умение правильно, последовательно рассуждать в незнакомой обстановке даётся с трудом. Как всякое умение, оно может быть усвоено только при целенаправленном обучении. В школьной практике учащиеся овладевают такими умениями, как правило, стихийно в процессе решения задач, требующих специальных математических знаний, но математика имеет неограниченные возможности в развитии интеллекта школьника. Математические задачи, накопленные и проверенные в ходе многолетней педагогической практики, позволяют эффективно развивать различные стороны психической деятельности человека: внимание, воображение, фантазию, образное и понятийное мышление, зрительную, слуховую и смысловую память. В методической литературе за развивающими задачами закрепились специальные названия: задачи на соображение, задачи с «изюминкой», задачи на смекалку и др. (логические задачи).
Во всём этом многообразии можно выделить в особый класс такие задачи, которые называют задачами-ловушками, «обманными» задачами, провоцирующими задачами. В условиях таких задач содержатся различного рода упоминания, указания, намёки, подсказки, подталкивающие к выбору ошибочного пути решения или неверного ответа.
Логические задачи обладают высоким потенциалом. Они способствуют воспитанию одного из важнейших качеств мышления – критичности, приучают к анализу воспринимаемой информации, её разносторонней оценке, повышают интерес к занятиям математикой.
Дидактическая ценность таких задач неоспорима. Попадая в заранее приготовленную ловушку, ученик испытывает досаду, сожаление от того, что не придал особого значения тем нюансам, из-за которых он попал в неловкое положение. Простое сообщение детям о том, что учащиеся, как правило, допускают в заданиях такого рода ошибки, малодейственное. Ибо оно, несмотря на общность и адресность, не является для конкретно взятого ученика личностно значимым. Во-первых, событие, о котором сообщается, происходило когда-то давно, в прошлом, а во-вторых, каждый из учеников наивно полагает, что в число неудачников сам Он не попадает.
Чтобы получить целостное представление обо всём многообразии логических задач, их возможностях в развитии критичности мышления младших школьников, приведём одну из имеющихся типологий этих задач.
I тип.Задачи, условия которых в той или иной мере навязывают неверный ответ. (Сколько прямоугольников можно насчитать в изображении окна?
II тип. Задачи, условия которых тем или иным способом подсказывают неверный путь решения. (Тройка лошадей проскакала 15 километров. Сколько километров проскакала каждая лошадь?)
Хочется выполнить деление 15 : 3 и тогда ответ: 5 км. На самом деле деление выполнять вовсе не нужно, поскольку каждая лошадь проскакала столько же, сколько и вся тройка, т.е. 15 км.)
IIIтип.Задачи, вынуждающие придумывать, составлять, строить такие математические объекты, которые при заданных условиях не могут иметь места. (Используя цифры 1 и 4 запишите трёхзначное число, дающее при делении на 3 остаток, равный 2. Придумать такое число невозможно, поскольку любое число, удовлетворяющее условию задачи, делится на 3 без остатка.)
IV тип. Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов, словесных оборотов, буквенных или числовых выражений. (На листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить это число в полтора раза? Здесь имеется в виду не математическое действие, а просто игра с листком бумаги. Если перевернуть лист, на котором написано число 606, то увидим запись 909, т.е. число, которое в полтора раза больше числа 606.)
Vтип. Задачи, которые допускают возможность «опровержения» семантически верного решения синтаксическим или иным нематематическим способом. (Крестьянин продал на рынке трёх коз за 3 рубля. Спрашивается: «По чему каждая коза пошла?». Очевидный ответ: «по одному рублю» – опровергается: козы по деньгам не ходят, а ходят по земле.)
Описанные разновидности задач не исчерпывают всего их многообразия, но дают представление о способах их составления и использования в обучении математике.
Логические задачи способствуют формированию умения рассуждать, овладению приёмами правильных рассуждений. Так как их решение не опирается на специальные знания, объектом усвоения в процессе решения являются приёмы рассуждений. Информация, из которой необходимо сделать выводы, задаётся текстом, описывающим вполне обычные ситуации. Решение таких задач учит до конца придумывать незнакомые ситуации, не отступать перед трудностями, вселяет уверенность в свои силы.
2.1 Организация форм работы с логическими задачами
Выше неоднократно утверждалось, что развитие у детей логического мышления – это одна из важных задач начального обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определённым правилам – необходимое условие успешного усвоения учебного материала.
Основная работа для развития логического мышления должна вестись с текстовой задачей. Ведь в любой задаче заложены большие возможности для развития логического мышления. Нестандартные логические задачи – отличный инструмент для такого развития. Существует значительное множество такого рода задач; особенно много подобной специализированной литературы было выпущено в последние годы. Конкретные примеры логических задач приведены в приложениях 2 и 3.
Однако что зачастую наблюдается на практике? Учащимся предлагается задача, они знакомятся с нею и вместе с учителем анализируют условие и решают её. Но извлекается ли из такой работы максимум пользы? Нет. Если дать эту задачу через день-два, то часть учащихся может вновь испытывать затруднения при решении.
Наибольший эффект при этом может быть достигнут в результате применения различных форм работы над задачей. Это:
1. Работа над решённой задачей. Многие учащиеся только после повторного анализа осознают план решения задачи. Это путь к выработке твёрдых знаний по математике. Конечно, повторение анализа требует времени, но оно окупается.
2. Решение задач различными способами. Мало уделяется внимания решению задач разными способами в основном из-за нехватки времени. А ведь это умение свидетельствует о достаточно высоком математическом развитии. Кроме того, привычка нахождения другого способа решения сыграет большую роль в будущем, хотя это доступно не всем учащимся, а лишь тем, кто любит математику, имеет особые математические способности.
3. Правильно организованный способ анализа задачи – с вопроса или от данных к вопросу.
4. Представление ситуации, описанной в задаче (нарисовать "картинку"). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
5. Самостоятельное составление задач учащимися.
Составить задачу: 1) используя слова: больше на; столько, сколько; меньше в, на столько больше, на столько меньше; 2) решаемую в 1, 2, 3 действия; 3) по данному её плану решения, действиям и ответу; 4) по выражению и т.д.
6. Решение задач с недостающими или лишними данными.
7. Изменение вопроса задачи.
8. Составление различных выражений по данным задачам и объяснение, что обозначает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.
9. Объяснение готового решения задачи.
10. Использование приёма сравнения задач и их решений.
11. Запись и сравнение двух решений на доске – одного верного и другого неверного.
12. Изменение условия задачи так, чтобы задача решалась другим действием.
13. Закончить решение задачи.
14. Какой вопрос и какое действие лишние в решении задачи (или, наоборот, восстановить пропущенный вопрос и действие в задаче).
15. Составление аналогичной задачи с измененными данными.
16. Решение обратных задач.
Систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на развитие логического мышления, организованных согласно приведённой выше схеме, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
логический задача урок математика
2.2 Методики, направленные на определение степени овладения логическими операциями мышления
Способность выделять существенное
Учитель предлагает школьникам ряд слов, в каждом из которых пять даётся в скобках, а одно – перед ними. Ученики должны за 20 секунд исключить из скобок, то есть выделить, два слова, наиболее существенные для слова перед скобками.
Сад (растение, садовник, собака, забор, земля) растение, земля
Река (берег, рыба, тина, рыболов, вода) берег, вода
Куб (углы, чертёж, сторона, камень, дерево) углы, сторона
Чтение (глаза, книга, картина, печать, слово) глаза, печать
Игра (шахматы, игроки, штрафы, правила, наказания) игроки, правила
Лес (лист, яблоня, охотник, дерево, кустарник) дерево, кустарник
Город (автомобиль, здание, толпа, улица, велосипед) здание, улица
Кольцо (диаметр, проба, круглость, печать, алмаз) диаметр, круглость
Пение (звон, голос, искусство, мелодия, аплодисменты) голос, мелодия
Больница (сад, врач, помещение, радио, больные) помещение, больные
Любовь (розы, чувство, человек, город, природа) чувство, человек
Война (аэроплан, пушки, сражения, солдаты, ружья) сражения, солдаты
Спорт (медаль, оркестр, состязание, победа, стадион) стадион, состязание
Обработка полученных данных: ученики, которые правильно выполнили задание, очевидно, обладают умением выделять существенное, т.е. способны к абстрагированию. Те, кто допустил ошибки, не умеют выделять существенные и несущественные признаки.
Учащимся достаточно предложить из данного перечня по 5 заданий.
Сравнение
Цель: установить уровень развития у учащихся умения сравнивать предметы, понятия.
Учащимся предъявляются или называются какие-либо 2 предмета либо понятия. Например: озеро – река
книга – тетрадьсолнце – луна
лошадь – коровасани – телега
линейка – треугольникдождь – снег
Каждый ученик на листе бумаги должен написать черты сходства – слева, а справа – черты различия названных предметов, понятий.
На выполнение задания по одной паре слов даётся 4 минуты. После этого листки собираются.
Обработка полученных результатов: составляется общий список черт сходства и различия названных предметов, затем устанавливается, какую часть из этого списка сумел написать ученик. Доля названных учеником черт сходства и различия из общего числа черт в % – это уровень развития у учащегося умения сравнивать.
Обобщение
Предлагается два слова. Учащемуся нужно определить, что между ними общего:
дождь – граджидкость – газ
нос – глазапредательство – трусость
сумма – произведениеводохранилище – канал
сказка – былинашкола – учитель
Учащемуся можно предложить 5 пар слов. Время: 3 – 4 минуты.
Классификация
Эта методика также выявляет умение обобщать, строить обобщение на отвлечённом материале.
Инструкция: даны пять слов. Четыре из них объединены общим признаком. Пятое слово к ним не подходит. Найдите это слово.
1) приставка, предлог, суффикс, окончание, корень;
2) треугольник, отрезок, длина, квадрат, круг;
3) дождь, снег, осадки, иней, град;
4) запятая, точка, двоеточие, тире, союз;
5) сложение, умножение, деление, слагаемое, вычитание;
6) дуб, дерево, ольха, тополь, ясень;
7) Василий, Фёдор, Иван, Петров, Семён;
8) молоко, сыр, сметана, мясо, простокваша;
9) секунда, час, год, вечер, неделя;
10) горький, горячий, кислый, солёный, сладкий;
11) футбол, волейбол, хоккей, плавание, баскетбол;
12) тёмный, светлый, голубой, яркий, тусклый;
13) самолёт, пароход, техника, поезд, дирижабль;
14) круг, квадрат, треугольник, трапеция, прямоугольник;
15) смелый, храбрый, решительный, злой, отважный.
Учащимся можно предложить 5 заданий. Время – 3 минуты.
Анаграмма
Цель:выявить наличие или отсутствие у школьников теоретического анализа.
Ход эксперимента:учащимся предлагаются анаграммы (слова, преобразованные путём перестановки входящих в них букв).
Учащиеся должны по данным анаграммам найти исходные слова:
1) лбко, 2) раяи, 3) упкс, 4) еравшн, 5) ркдети, 6) ашнрри.
Учащиеся в результате выполнения задания разделяются на 2 группы.
1 группа – решают каждую задачу, как новую. У них отсутствует теоретический анализ (способность мысленно выделять свойства предметов, в данном случае структуру слова).
2 группа – учащиеся быстро находят ответы, обнаружив общее правило.
Анализ отношений понятий (аналогия)
Даны 3 слова, первые два находятся в определённой связи. Между третьим и одним из предложенных пяти слов существуют такие же отношения, найдите это четвёртое слово.
Например:
Песня : композитор = самолёт : ?
а) аэродром, б) горючее, в) конструктор, г) лётчик, д) истребитель
Функциональные отношения: песню сочинил композитор.
Ответ – конструктор (конструктор сделал самолёт).
Задания:
1) школа : обучение = больница : ?
а) доктор, б) ученик, в) лечение, г) учреждение, д) больной
2) песня : глухой = картина : ?
а) слепой, б) художник, в) рисунок, г) больной, д) хромой
3) нож : сталь = стол : ?
а) вилка, б) дерево, в) стул, г) пища, д) скатерть
4) паровоз : вагоны = конь : ?
а) поезд, б) лошадь, в) овёс, г) телега, д) конюшня
5) лес : деревья = библиотека : ?
а) город, б) здание, в) книги, г) библиотекарь, д) театр
6) бежать : стоять = кричать : ?
а) ползать, б) молчать, в) шуметь, г) звать, д) плакать
7) утро : ночь = зима : ?
а) мороз, б) день, в) январь, г) осень, д) сани
8) волк : пасть = птица : ?
а) воздух, б) клюв, в) соловей, г) яйцо, д) пение
9) холодно : горячо = движение : ?
а) покой, б) взаимодействие, в) инерция, г) молекула, д) бежать
10) слагаемое : сумма = множители : ?
а) разность, б) делитель, в) произведение, г) умножение, д) деление
11) круг : окружность = шар : ?
а) пространство, б) сфера, в) радиус, г) диаметр, д) половина
12) светло : темно = притяжение : ?
а) металл, б) магнит, в) отталкивание, г) движение, д) взаимодействие
Эта методика направлена на выявление у учащихся умения определять отношения между понятиями или связи между понятиями:
а) причина – следствие;
б) противоположность;
в) род – вид;
г) часть – целое;
д) функциональные отношения.
Для изучения скорости протекания мыслительных процессов учащихся можно использовать метод, суть которого состоит в заполнении пропущенных букв в предложенных словах.
п – роз – р – оз – о – ок
к – сад – р – вот – а – а
р – как – м – ньк – н – а
г – ках – л – дк – ы – а
п – лек – в – рп – е – а
Учитель обращает внимание на то, сколько потребовалось школьнику времени на обдумывание каждого отдельного слова и заполнение пропущенных букв в каждом из столбцов в целом.
По предложенной методике было проведено обследование учащихся четвёртых классов одной из средних школ. В исследование были включены методики по выше приведённой программе:
1-й час: внимание – работоспособность, «Слова», исследование памяти, исследование саморегуляции;
2-й час: методики на исследование мышления (анаграмма, определение существенного, обобщение, классификация, аналогия, сравнение).
Получены следующие результаты:
Тест «Школа – учительница – мама» выявил сравнительно низкие речевые способности учащихся. К слову «школа» подобрано в среднем – 3,65 слова, к слову «учительница» подобрано – 3,6 слова, к слову «мама» – 3,7 слова. Слово «мама» является для учащихся более эмоционально значимым, важным по сравнению со словами «школа» и «учительница»
Результаты проведения теста «Саморегуляция»:
1 группа – учащиеся, которые успешно справились с заданием, составила 49 %;
2 группа – учащиеся начали выполнять задание хорошо, потом сбились – 43,5 %;
3 группа – учащиеся сбились в последовательности – 6,6 %;
4 группа – смогли сделать не более 2 строк – 1 %.
Эти результаты позволили сделать вывод о том, что у большинства учащихся саморегуляция сформирована для дальнейшей работы в среднем звене.
Тест «Внимание – работоспособность» показал, что только 35 % учащихся 4-х классов к концу обучения в начальном звене имеют среднюю и высокую работоспособность, произвольное внимание. Следует подчеркнуть, что это довольно низкий показатель.
Уровень памяти низкий у единиц (по 1 человеку в каждом классе параллели).
Тесты на развитие мышления показали, что логические операции мышления в недостаточной мере сформированы у учащихся четвёртых классов. Несколько лучше учащиеся выделяют существенное, обобщают, хуже выявляют отношения между понятиями (особенно такие, как причина – следствие, противоположность).
На развитие этих мыслительных операций и придётся прежде всего обратить внимание преподавателям в среднем звене школы.
В целом можно сделать вывод о том, что обследованные учащиеся в недостаточной мере готовы к обучению в среднем звене. И у учащихся возможны трудности при обучении в среднем звене, и у преподавателей тоже.
Методические указания по проведению эксперимента приведены в приложении 1.
Предложенные в данном исследовании материалы позволят родителям, преподавателям начальной школы, среднего звена, психологам подготовить учащихся к обучению в среднем звене, а также выявить те слабые стороны, которые могут быть развиты при обучении в среднем звене школы.
ЗАКЛЮЧЕНИЕ
Важнейшей задачей математического образования является вооружение учащихся общими приёмами мышления, пространственного воображения, развитие способности понимать смысл поставленной задачи, умение логично рассуждать, усвоение навыков алгоритмического мышления. Каждому важно научиться анализировать, отличать гипотезу от факта, отчётливо выражать свои мысли, а с другой стороны – развить воображение и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения).
Именно математика предоставляет благоприятные возможности для воспитания воли, трудолюбия, настойчивости в преодолении трудностей, упорства в достижении целей. Сегодня математика как живая наука с многосторонними связями, оказывающая существенное влияние на развитие других наук и практики, является базой научно-технического прогресса и важной компонентой развития личности. Одной из основных целей изучения математики является формирование и развитие мышления человека, прежде всего, абстрактного мышления, способности к абстрагированию и умения "работать" с абстрактными, "неосязаемыми" объектами. В процессе изучения математики в наиболее чистом виде может быть сформировано логическое (дедуктивное) мышление, алгоритмическое мышление, многие качества мышления – такие, как сила и гибкость, конструктивность и критичность и т.д.
Поэтому в качестве одного из основополагающих принципов новойконцепции в "математике для всех" на первый план выдвинута идея приоритетаразвивающей функции обучения математике. В соответствии с этим принципомцентром методической системы обучения математике становится не изучениеоснов математической науки как таковой, а познание окружающего человекамира средствами математики и, как следствие, к динамичной адаптациичеловека к этому миру, к социализации личности. Основной целью математического образования должно быть развитие умения математически, а значит, логически и осознанно исследовать явления реального мира.
Реализации этой цели может и должно способствовать решение на уроках математики различного рода нестандартных логических задач. Поэтому использование учителем начальной школы этих задач на уроках математики является не только желательным, но даже необходимым элементом обучения математике.
Гипотеза данного исследования подтверждена. Мы доказали, что развитие логичности мышления младших школьников в процессе решения нестандартных задач способствует формированию умственных приёмов деятельности, творческих способностей учащихся, развитию интеллекта, повышению успеваемости.
Наработанный материал можно использовать в повседневной жизни, так как логические задачи – это своеобразная "гимнастика для ума", средство для утоления естественной для каждого мыслящего человека потребности испытывать и упражнять силу собственного разума, а так же можно его использовать при обучении детей младшего школьного возраста.
СПИСОК ЛИТЕРАТУРЫ
1. Баракина Т.В. Возможности изучения элементов логики на уроках математики и информатики в начальной школе // Начальная школа плюс до и после. – 2009. – №4. – С. 33 – 37.
2. Белошистая А.В. Развитие математических способностей школьника как методическая проблема // Начальная школа. – 2003. – №1. – С.44 – 45.
3. Гороховская Г.Г. Диагностика уровня сформированности компонентов логического мышления у младших школьников // Начальная школа. – 2008. – №6. – С. 40 – 43.
4. Григорьева Г.И. Логика. Занимательные материалы для развития логического мышления. 2 класс. – Учитель – АСТ, 2004. – 112с.
5. Еланская З.А. Активизация познавательной деятельности // Начальная школа. – 2001. – №6. – С.52 – 54.
6. Житомирский В., Шеврин Л. Математическая азбука. 3-е издание. М.: Педагогика, 1988. – 199с.
7. Зайкин М.И., Колосова В.А.. Провоцирующие задачи как средство развития критичности мышления школьников // Начальная школа. – 2002. – №9. – С. 73 – 77.
8. Зак А.З. 600 игровых задач для развития логического мышления детей. – Ярославль: Академия развития, 1998. – 192с.
9. Иванова Е.В. Развитие логического мышления на уроках математики // Начальная школа плюс до и после. – 2006. – №6. – С.59 – 60.
10. Керова Г.В. Нестандартные задачи по математике 1 – 4 классы. Москва: ВАКО, 2008. – 237с.
11. Конева С.А. Как развивать познавательные способности детей на уроках математики // Начальная школа плюс до и после. – 2006. – №10. – С.36 – 40.
12. Липина И. Развитие логического мышления на уроках математики // Начальная школа. – 1999. – № 8. – С. 37 – 39.
13. Логика. 1 класс. Занимательные материалы для развития логического мышления / Сост. О.Ю. Нежинская. – Волгоград: Учитель – АСТ, 2004. – 96 с.
14. Максимова Т.Н. Интеллектуальный марафон: 1 – 4 классы. – М.: ВАКО, 2009. – 208с.
15. Методика обучения математике учащихся начальной школы. Курс лекций для студентов, обучающихся по специальности Преподавание в начальных классах. Часть 2. – Издание 4-е, перераб. / Сост. Т.А. Бартенева. – Бутурлиновка, 2009. – 149 с.
16. Останина Е.Е. Обучение младших школьников решению нестандартных задач // Начальная школа. – 2004. – №7. – С. 36 – 37.
17. Пиаже Ж. Избранные психологические труды. – СПб: Питер, 1999.
18. Тихомирова Л.Ф., Басов А.В. Развитие логического мышления детей. – Ярославль: ТОО Академия развития, 1996. – 240с.
19. Тонких А.П., Кравцова Т.П., Лысенко Е.А., Стогова Д.А., Голощапова С.В. Логические игры и задачи на уроках математики. – Ярославль: Академия развития, 1997. – 240 с.
20. Царева С.Е. Нестандартные виды работы с задачами на уроке как средство реализации современных педагогических концепций и технологий // Начальная школа. – 2004. – №4. – С. 49 – 51.
ПРИЛОЖЕНИЕ 1
Методические указания по проведению эксперимента
Предлагаемые методики были апробированы. Перечень предложенных третьеклассникам заданий выглядит следующим образом:
1-й час (урок 45 минут):
Методика «Счёт»(на переключение внимания и работоспособность) с объяснением занимает 15 мин, на выполнение даётся 5 минут.
Диагностика кратковременной и смысловой памяти – 15 минут.
«Саморегуляция» – на выполнение задания даётся 15 минут, объяснение занимает ещё 4 минуты.
«Слова» – даётся 6 минут (по 2 минуты на слово). Предлагались слова: школа – учительница – мама.
2-й час (45 минут)
Учащимся раздаются задания по вариантам (на исследование мышления).
Варианты задания приведены ниже.
На выполнение 1-го задания необходимо дать 5 минут;
на 2-е – 5 минут;
на 3-е – 5 минут;
на 4-е – 5 минут;
на 5-е – 5 минут;
на 6-е – 15 минут.
ВАРИАНТ 1
Задание 1. В приведённых словах буквы переставлены местами. Запишите эти слова.
1) лбко; 2) раяи; 3)еравшн; 4) ркдети; 5) рбкадоле
Задание 2. Перед скобками слово, а в скобках ещё 5 слов. Найдите 2 слова из написанных в скобках, которые наиболее существенны для слова перед скобками. Запишите эти слова.
1) Чтение (слово, глаза, книга, печать, очки)
2) Сад (растение, садовник, земля, вода, забор)
3) Река (берег, тина, вода, рыболов, рыба)
4) Игра (шахматы, игроки, правила, футбол, штраф)
5) Куб (углы, дерево, камень, чертёж, сторона)
Задание 3. Сравните понятия: книга – тетрадь. Общие и отличительные черты выпишите на листке в 2 столбика.
Задание 4. Какое понятие в каждом из перечней является лишним? Выпишите его.
1) дуб, дерево, ольха, ясень
2) горький, горячий, кислый, солёный, сладкий
3) дождь, снег, осадки, иней, град
4) запятая, точка, двоеточие, союз, тире
5) сложение, умножение, деление, слагаемое, вычитание
Задание 5. Вам предлагается 5 пар слов. Надо определить, что между ними общего (очень коротко, предложение должно содержать не более 3 – 4 слов).
1) дождь – град;
2) нос – глаз;
3) сумма – произведение;
4) водохранилище – канал;
5) предательство – трусость
Задание 6. Даны 3 слова. Два первых находятся в определённой связи. Третье и одно из 5 слов приведённых ниже находятся в такой же связи. Найдите и запишите на листе это четвёртое слово.
1) волк : пасть = птица : ?
а) воздух; б) клюв; в) соловей; г) яйцо; д) пение
2) библиотека : книга = лес : ?
а) берёза; б) дерево; в) ветка; г) бревно; д) клён
3) птица : гнездо = человек : ?
а) люди; б) рабочий; в) птенец; г) дом; д) разумный
4) слагаемое : сумма = множители : ?
а) разность; б) делитель; в) произведение; г) умножение; д) вычитание
5) холодно : горячо = движение : ?
а) взаимодействие; б) покой; в) мяч; г) трамвай; д) идти
6) Запад : Восток = обмеление : ?
а) засуха; б) юг; в) наводнение; г) река; д) дождь
7) война : смерть = тепло : ?
а) дыхание; б) жизнедеятельность; в) вещество; г) температура; д) гибель
8) молния : свет = жара : ?
а) солнце; б) трава; в) жажда; г) дождь; д) река
9) роза : цветок = газ : ?
а) кислород; б) дыхание; в) горение; г) состояние вещества; д) прозрачный
10) берёза : дерево = стихотворение : ?
а) сказка; б) богатырь; в) поэзия; г) лирика; д) драма
ВАРИАНТ 2
Задание 1. В приведённых словах буквы переставлены местами. Напишите эти слова.
1) упск; 2) ашнрри; 3) вцтеко; 4) окамднри; 5) лкбуинак
Задание 2. Перед скобками слово, а в скобках ещё 5 слов. Найдите 2 из них, которые являются наиболее существенными для слова перед скобками.
1) деление (класс, делимое, карандаш, делитель, бумага);
2) озеро (берег, рыба, вода, рыболов, тина);
3) огород (забор, земля, растение, собака, лопата);
4) чтение (глаза, очки, книга, печать, картинка);
5) игра (шахматы, теннис, игроки, штраф, правила)
Задание 3. Сравните понятия: озеро – река. На листе общие и отличительные черты выпишите в 2 столбика.
Задание 4. Какое понятие в каждом из перечней является лишним? Выпишите его.
1) холодный, горячий, тёплый, кислый, ледяной;
2) роза, тюльпан, нарцисс, цветок, гладиолус;
3) справедливость, доброта, искренность, зависть, честность;
4) треугольник, отрезок, квадрат, круг, прямоугольник;
5) пословица, поговорка, басня, сказка, былина
Задание 5. Предлагается 5 пар слов. Надо определить, что между ними общего (очень коротко, фраза должна содержать до 3-х слов).
1) русский язык – математика;
2) разность – частное;
3) землетрясение – смерч;
4) газ – жидкость;
5) зависть – трусость
Задание 6. Даны 3 слова. Два первых находятся в определённой связи. Третье и одно из 4-х приведённых ниже находятся в такой же связи. Найдите и запишите на вашем листе это четвёртое слово.
1) песня : композитор = самолёт : ?
а) горючее; б) лётчик; в) конструктор; г) аэродром
2) прямоугольник : плоскость = куб : ?
а) пространство; б) ребро; в) высота; г) треугольник
3) школа : обучение = больница : ?
а) доктор; б) больной; в) лечение; г) учреждение
4) ухо : слышать = зубы : ?
а) видеть; б) лечить; в) жевать; г) рот
5) глагол : спрягать = существительное : ?
а) понятие; б) склонять; в) название; г) образовывать
6) светло : темно = притяжение : ?
а) металл; б) молекула; в) отталкивание; г) движение
7) жара : засуха = дожди : ?
а) паводок; б) наводнение; в) осень; г) лето
8) берёза : дерево = стихотворение : ?
а) сказка; б) богатырь; в) поэзия; г) драма
ПРИЛОЖЕНИЕ 2
Избранные страницы из книги И.Г. Сухина "800 новых логических и математических головоломок"
СЮЖЕТНЫЕ ЗАДАЧИ
1. Гном Путалка идёт к клетке с тигром. Каждый раз, когда он делает два шага вперёд, тигр рычит, и гном отступает на шаг назад. За какое время он дойдёт до клетки, если до неё 5 шагов, а 1 шаг Путалка делает за 1 секунду?
2. Гном Забывалка учился писать цифры заострённой палочкой на песке. Только он успел нарисовать 5 цифр: 12345, как увидел большую собаку, испугался и убежал. Вскоре в это место пришёл другой гном Путалка. Он тоже взял палочку и начертил вот что: 12345 = 60.
Вставь между цифрами плюсы таким образом, что получившийся пример был решён правильно.
3. Какую отметку впервые в жизни получил по математике Фома, если известно, что она является числом не простым, а составным?
4. Сколько лет сиднем просидел на печи Илья Муромец? Известно, что если бы он просидел ещё 2 раза по столько, то его возраст составил бы наибольшее двузначное число.
5. Барон Мюнхгаузен пересчитал число волшебных волос в бороде старика Хоттабыча. Оно оказалось равным сумме наименьшего трёхзначного числа и наибольшего двузначного. Что это за число?
6. Раздели самое маленькое четырёхзначное число на наименьшее простое и узнаешь, сколько лет не умывалась и не чистила зубы злая волшебница Гингема из повести-сказки А. Волкова "Волшебник Изумрудного города".
ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ, ОТГАДЫВАНИЕ ЧИСЕЛ
7. Угадай число от 1 до 28, если в его написание не входят цифры 1, 5 и 7; кроме того, оно нечётное и не делится на 3.
8. Отгадай число от 1 до 58, если в его написание не входят цифры 1, 2 и 3; кроме того, оно нечётное и не делится на 3, 5 и 7.
9. Преврати в числе 123 одну цифру в пятёрку так, чтобы получившееся число делилось на 9. Каково оно?
10. Вычти из произвольного двузначного числа сумму его цифр. Всегда ли разность разделится на 3? А на 9?
МАТЕМАТИЧЕСКИЕ ФОКУСЫ
11. Напиши такое трёхзначное число, чтобы первая цифра была по крайней мере на 2 больше, чем третья. Например: 311. Запиши его цифрами в обратном порядке: 113. Из первого вычти второе: получится 198. Это число снова напиши наоборот: 891. И два последние числа сложи.
891 + 198 = 1089
Удивительное дело: какие бы числа мы ни брали, в ответе всегда будет 1089!
Теперь предложи провести все эти действия с числами кому-то из друзей. Представляешь, как он удивится, когда ты, не спрашивая у него, сколько получилось в результате (как это бывает в других математических фокусах), сам назовёшь ответ! Для эффекта можешь сообщить его не сразу, а через несколько секунд, как бы что-то подсчитывая в уме.
Почему так происходит?
12. Попроси товарища задумать какое-нибудь двузначное число, вычесть из него сумму его цифр, зачеркнуть в полученном результате одну цифру и сообщить, какое число осталось. После этого ты тотчас скажешь, какая цифра зачёркнута! Для этого ты всего-навсего из 9 вычтешь оставшееся однозначное число.
Пример: 97 – 16 = 81, 8 зачёркивается, и друг говорит, что осталось 1. Ты выполняешь в уме вычитание и получаешь в результате зачёркнутую цифру: 9 – 1 = 8.
Почему так происходит?
ПРИЛОЖЕНИЕ 3
Примерные задания для детей, мотивированных к интеллектуальной деятельности от 6 до 10 лет
Эти задания были использованы на занятиях по комплексной развивающей программе в группе "ШСМ-чик" в Зеленоградском Психолого-медико-социальном Центре в 1999/2001 учебном году Мельченко И.В.
1. Сидели на скамеечке 4 девушки: Ольга, Наталья, Людмила и Оксана. Оксана сидела рядом с Ольгой, а Наталья была в синем платье. Людмила была в зелёном. Оксана была не последней. Красное платье Ольги хорошо сочеталось с синим платьем одной из подруг. Платья у девушек были красного, жёлтого, синего и зелёного цветов. Нарисуйте, в каком порядке сидели девушки, и какого цвета у них были платья. Если можно, дайте несколько вариантов правильных ответов.
2. На столе лежало 5 синих и 7 красных карандашей. Девочка взяла 6 карандашей. Взяла ли она хоть 1 красный карандаш? Докажите (Нарисуйте и объясните).
3. Посмотрите на схему (рис. 1):
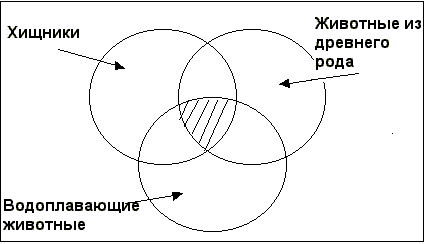
Рис. 1
Догадайтесь, каких животных мы можем поместить в заштрихованную область нашей схемы. Докажите. Перечислите животных и напишите объяснение.
4. Есть 5 квадратов, выложенных с помощью спичек. Переложите три спички так, чтобы получилось три прямоугольника, и не осталось лишних спичек.
5. У Кати был день рожденья. Вечером должны были прийти гости. Катя с мамой испекли торт и решили заранее порезать его на части, чтобы всем хватило по кусочку, включая Катю и маму. Мама разрезала торт пополам. Катя каждую половину разрезала ещё раз пополам. Дальше резать было сложно – торт сыпался, крошился, и она отдала нож маме. Мама каждый кусочек торта разрезала ещё на 3 одинаковые части.
Сколько гостей должно было прийти к Кате? Объясните.
6. Найди закономерность в расстановке чисел в квадрате (6 ´ 6) и заполни пустые клетки.
| 1 |
7 |
13 |
16 |
| 19 |
22 |
28 |
31 |
34 |
| 40 |
43 |
49 |
| 55 |
67 |
70 |
Ответ: число + 3 = следующее число
| 1 |
4 |
7 |
10 |
13 |
16 |
| 19 |
22 |
25 |
28 |
31 |
34 |
| 37 |
40 |
43 |
46 |
49 |
52 |
| 55 |
58 |
61 |
64 |
67 |
70 |
|