Практичне використання законів розподілу розмірівдля аналізу точності обробки
На використанні цих законів базується ймовірнісно-статистичний метод дослідження та розрахунку точності технологічних процесів.
Суть цього методу полягає в тому, що в результаті обробки даних експерименту визначають точність обробки. Він може бути застосований за умови обробки значної кількості заготовок (50 і більше) як методом пробних робочих ходів, так і методом автоматичного отримання розмірів. Після обробки в певних умовах партії заготовок проводять вимірювання зацікавленого параметра інструментом за шкалою і на основі методів математичної статистики виявляють точність обробки досліджуваного процесу.
Простота визначення характеристик розсіяння і побудови кривих розподілу за даними вимірювання звичайних виробничих заготовок в нормальних умовах роботи цеху, дає можливість за допомогою цього методу:
· вибрати метод обробки;
· визначити показники точності та стабільності технологічної операції (коефіцієнт розсіяння, коефіцієнт надійності операції, точність налагодження тощо);
· визначити кількість ймовірного браку при обробці;
· визначити кількість оброблюваних заготовок, що потребують додаткової обробки;
· розрахувати економічну доцільністьвикористання високопродуктивних верстатів зниженої точності;
· розрахувати настройки верстатів;
· порівняти точність обробки заготовок при різному стані обладнання, інструменту, мастильно-охолоджуючої рідини;
· порівняти точність обробки на різних верстатах;
· оцінити якість ремонту верстатів (шляхом порівняння кривих розсіювання розмірів заготовок, оброблених до і після ремонту верстатів);
· порівняти точність обробки одних і тих же заготовок у денні та нічні зміни.
До особливих переваг методу відноситься можливість проведення різноманітних досліджень точності та стійкості технологічних процесів без зупинки нормального виробничого процесу і без виготовлення спеціальних експериментальних зразків.
До недоліків методу можна віднести:
· метод потребує великого обсягу спостережень, тому економічно доцільний у великосерійному та масовому виробництвах;
· не враховується послідовність обробки;
· не визначається вплив на точність окремих факторів і не вказуються шляхи підвищення точності.
1. Вибір методу обробки
Метод обробки чи набір технологічних переходів для виконання будь-якої операції вибирають на основі порівняння допуску за кресленням на оброблюваний розмір з полем розсіювання методу Δм. При цьому повинна виконуватись умова:
T > Δм.
Величину Δм беруть з довідника технолога. Конкретний верстат вибирає технолог цеху за статистичними даними про його технічний стан (за величиною емпіричного середнього квадратичного відхилення S).
Тоді теоретичне середнє квадратичне відхилення дорівнює:
σ = γS.
Допуск розміру за кресленням має задовольняти умові:
T > 6σабоT > Δp.
У протилежному випадку неминучим буде брак при обробці.
2. Умови обробки без браку для закону нормального розподілу
Для обробки без браку повинні виконуватися дві наступні умови:
– перша:
 , (1) , (1)
де Тп – коефіцієнт точності процесу; якщо Тп > 1,12 процес вважається надійним, при Тп = 1…1,12 – процес точний, але ненадійний;
T– поле допуску на розмір, що аналізується;
– друга:
eфакт ≤ едоп, (2)
де eфакт – фактичний коефіцієнт точності настроювання;
eдоп – допустимий коефіцієнт точності настроювання.
Для визначення цих коефіцієнтів розглянемо рис. 1.
На рис. 1:
спд– середина поля допуску
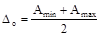 (3) (3)
Δо – координата середини поля допуску:
спр – середина поля розсіяння розмірів;
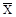 – фактичний настроювальний розмір; – фактичний настроювальний розмір;
Eфакт, Eдоп– фактичне і допустиме зміщення центра групування відхилень розмірів відΔо:
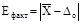 ; (4) ; (4)
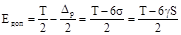 . (5) . (5)

Рис. 1. Схема визначення коефіцієнтів точності настроювання
Коефіцієнти точності настроювання представляють собою відношення Е до допуску Т. Тоді:
 ;(6) ;(6)
 . (7) . (7)
Порушення будь-якої з цих умов призводить до неминучої появи браку.
3. Визначення кількості ймовірного браку заготовок
У тих випадках, коли для закону нормального розподілу розміру не виконуються умови, зазначені в п. 1.2 можливий брак заготовок.
Ймовірний відсоток браку від всієї партії оброблюваних заготовок обчислюється наступним чином. При розсіюванні розмірів за законом нормального розподілу (Гаусса) приймається з похибкою не більше 0,27 %, що всі заготовки партії мають дійсні розміри в межах поля розсіювання.
При цьому очевидно, що площа, яка обмежена кривою нормального розподілу і віссю абсцис (рис. 2), дорівнює одиниці і визначає 100 % заготовок партії. Площа заштрихованих ділянок представляє собою кількість (в частках одиниці або у відсотках) заготовок, що виходять своїми розмірами за межі допуску.
Для визначення кількості придатних заготовок необхідно знайти площу, яка обмежена кривою та віссю абсцис на довжині, рівній допуску:
 . .
При симетричному розташуванні поля розсіювання відносно поля допуску (рис.2, а) потрібно знайти подвоєне значення інтегралу, що визначає половину площі, обмеженої кривою Гаусса та абсцисоюx0:
 . (8) . (8)
Вираз (8) можна записати в нормованому вигляді у формі відомої функції Лапласа:
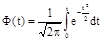 . (9) . (9)
Значення цієї функції табульоване в залежності від величини t та наведене у додатку 3.

Рис. 2. Кількість ймовірного браку при симетричному (а) і несиметричному (б) розташуванні поля розсіювання відносно поля допуску
У формулі (9) величина t представляє собою нормований параметр розподілу або коефіцієнта ризику і визначається виразом:
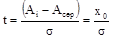 . (10) . (10)
Якщо заданий допуск на розмір і граничні відхилення деталі за кресленням хв і хн, то формулу (10) можна записати у вигляді:
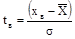 , ,  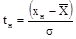 , (11) , (11)
а ймовірний відсоток браку складе:
– по верхній границі поля допуску:
Рб.в = [0,5 – Ф(tв)] ∙ 100 %;(12)
– по нижній границі поля допуску:
Рб.н = [0,5 – Ф(tн)] ∙ 100 %. (13)
Таким чином, розрахунок кількості бракованих заготовок зводиться до встановлення за формулами (11) величин t по верхній і нижній границях допуску та визначення Ф(tв) і Ф(tн) за таблицею додатку 2 з наступним перерахунком отриманих величин у відсотках в кількість штук заготовок.
4. Приклад обробки статистичних даних і визначення характеристик емпиричного розподілу
Завдання
Визначити точність та стабільність операції токарної обробки вала  мм при випадковій вибірці деталей, що оброблені на верстаті при декількох налагодженнях. мм при випадковій вибірці деталей, що оброблені на верстаті при декількох налагодженнях.
Розв’язання
1. З метою забезпечення випадковості вибірки деталі, що складають генеральну сукупність, ретельно переміщуємо в тарі і відбираємо з різних місць тари вибірку для досліджень з кількості 88 шт.
2. Вимірюємо деталі інструментом за шкалою (індикаторною скобою) з ціною поділки с = 0,002 мм. Результати вимірювань заносимо в табл. 1.
Таблиця 1
Початкові дані
| 80,247 |
80,246 |
80,235 |
80,252 |
80,245 |
80,257 |
80,244 |
80,246 |
| 80,250 |
80,241 |
80,250 |
80,240 |
80,251 |
80,239 |
80,249 |
80,228 |
| 80,259 |
80,253 |
80,238 |
80,246 |
80,264 |
80,248 |
80,243 |
80,253 |
| 80,233 |
80,262 |
80,247 |
80,244 |
80,258 |
80,255 |
80,245 |
80,234 |
| 80,242 |
80,251 |
80,236 |
80,249 |
80,243 |
80,241 |
80,256 |
80,247 |
| 80,260 |
80,245 |
80,255 |
80,248 |
80,247 |
80,250 |
80,242 |
80,252 |
| 80,252 |
80,248 |
80,231 |
80,242 |
80,254 |
80,236 |
80,243 |
80,241 |
| 80,239 |
80,237 |
80,251 |
80,256 |
80,243 |
80,248 |
80,254 |
80,248 |
| 80,254 |
80,242 |
80,234 |
80,238 |
80,253 |
80,235 |
80,239 |
80,244 |
| 80,240 |
80,249 |
80,244 |
80,245 |
80,237 |
80,249 |
80,246 |
80,250 |
| 80,251 |
80,257 |
80,247 |
80,252 |
80,255 |
80,241 |
80,258 |
80,240 |
За результатами вимірювань визначаємо різницю між найбільшим і найменшим розмірами:
W = xmax – xmin= 80,264 – 80,228 = 0,036 мм.
3. Отримані значення розбиваємо на 7 інтервалів (d=0,006 мм)
4. Для кожного інтервалу визначаємо частоту, тобто підраховуємо кількість деталей, що ввійшли в кожен з інтервалів, причому в кожен інтервал включаються деталі з розмірами, які лежать в межах від найменшого значення інтервалу включно до найбільшого значення інтервалу, виключаючи його. Отримані дані заносимо в табл. 2.
5. Побудова гістограми та емпіричної кривої розподілу похибок
Для побудови гістограми розподілу на осі абсцис відкладаємо інтервали розмірів і на кожному з цих інтервалів, як на основі, будуємо прямокутник, висота якого пропорційна частоті емпіричного розподілу. З’єднуючи середини верхніх сторін прямокутників відрізками прямих, отримуємо графік, який називається емпіричною кривою або полігоном розподілу (рис. 3).
Таблиця 2
Підрахунок частот емпіричного розподілу
| Інтервали розмірів |
Середина
інтервалу xi
|
Підрахунок
частот
|
Частота
ni
|
| від |
до |
| 80,225 |
80,231 |
80,228 |
1 |
1 |
| 80,231 |
80,237 |
80,234 |
11111111 |
8 |
| 80,237 |
80,243 |
80,240 |
111111111111111111 |
18 |
| 80,243 |
80,249 |
80,246 |
11111111111111111111111111 |
26 |
| 80,249 |
80,255 |
80,252 |
1111111111111111111111 |
22 |
| 80,255 |
80,261 |
80,258 |
11111111111 |
11 |
| 80,261 |
80,267 |
80,264 |
11 |
2 |
| Всього |
88 |

Рис. 3. Гістограма (1), емпірична крива (2) та теоретична крива нормальногорозподілу (3) розмірів деталей
На основі полігону розподілу похибок за гіпотезу теоретичного розподілу частот досліджуваного параметра приймаємо закон нормального розподілу.
Визначення основних параметрів прийнятого закону розподілу.
За оцінку основних параметрів закону нормального розподілу використовують вибіркове середнє арифметичне значення досліджуваного параметра 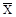 і вибіркове середнє квадратичне відхилення S, які обчислюються за формулами (2.3) та (2.2): і вибіркове середнє квадратичне відхилення S, які обчислюються за формулами (2.3) та (2.2):
 ; ;
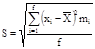 . .
Для полегшення підрахунків використовуємо табл. 3.
Таблиця 3
Допоміжна таблиця для обчислення 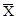 і S вибірки і S вибірки
Інтервали
розмірів
|
Середина
інтервалу
xi
|
Частота
mi
|
ximi |
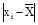 |
 |
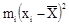 |
| від |
до |
| 80,225 |
80,231 |
80,228 |
1 |
80,228 |
0,019 |
0,000361 |
0,000361 |
| 80,231 |
80,237 |
80,234 |
8 |
641,872 |
0,013 |
0,000169 |
0,001352 |
| 80,237 |
80,243 |
80,240 |
18 |
1444,32 |
0,007 |
0,000049 |
0,000882 |
| 80,243 |
80,249 |
80,246 |
26 |
2086,396 |
0,001 |
0,000001 |
0,000026 |
| 80,249 |
80,255 |
80,252 |
22 |
1765,544 |
0,005 |
0,000025 |
0,00055 |
| 80,255 |
80,261 |
80,258 |
11 |
882,838 |
0,011 |
0,000121 |
0,001331 |
| 80,261 |
80,267 |
80,264 |
2 |
160,528 |
0,017 |
0,000289 |
0,000578 |
| Всього |
88 |
7061,726 |
0,00508 |
Вибіркове середнє арифметичне значення 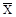 дорівнює: дорівнює:
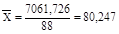 мм, мм,
а вибіркове середнє квадратичне відхилення S:
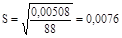 мм. мм.
7.Порівняння емпіричного розподілу з теоретичним та побудова теоретичної кривої
За зовнішнім виглядом емпіричної кривої можна приблизно встановити закон розподілу похибок в генеральній сукупності. Для більш точного висновку необхідно співставити емпіричну криву з кривою, що передбачається теоретично. З цією метою для кожного інтервалу значень необхідно обчислити теоретичні частоти або частості і по них побудувати теоретичну криву розподілу.
При побудові теоретичної кривої нормального розподілу приймається, що  і σ = S. і σ = S.
Теоретичну частоту обраховуємо за формулою:
 . .
Величина Zt обчислена для різних значень t і наведена в додатку 1. Значення t для кожного інтервалу розмірів знаходяться за формулою:
 . .
Отже, для підрахунку теоретичних частот необхідно для кожного інтервалу розмірів за формулою визначити значення t, за таблицею додатку 1 знайти Zt i потім скористатися формулою. При підрахунку теоретичних частот доцільно використовувати допоміжну табл. 4.
Таблиця 4
Обчислення теоретичних частот нормального розподілу
| Інтервали розмірів |
Середина
інтервалу
xi
|
Частота
mi
|
 |
t |
Zt |
Теоретична
частота
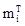
|
Теоретична
частота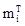
(зокругленням)
|
| від |
до |
| 80,225 |
80,231 |
80,228 |
1 |
0,019 |
2,5 |
0,0175 |
1,2 |
1 |
| 80,231 |
80,237 |
80,234 |
8 |
0,013 |
1,71 |
0,0925 |
6,4 |
7 |
| 80,237 |
80,243 |
80,240 |
18 |
0,007 |
0,92 |
0,2613 |
18,2 |
18 |
| 80,243 |
80,249 |
80,246 |
26 |
0,001 |
0,13 |
0,3956 |
27,5 |
28 |
| 80,249 |
80,255 |
80,252 |
22 |
0,005 |
0,66 |
0,3209 |
22,3 |
22 |
| 80,255 |
80,261 |
80,258 |
11 |
0,011 |
1,45 |
0,1394 |
9,7 |
10 |
| 80,261 |
80,267 |
80,264 |
2 |
0,017 |
2,24 |
0,0325 |
2,3 |
2 |
| Всього |
88 |
88 |
Для точної побудови теоретичної кривої нормального розподілу обчислюють координати характерних точок кривої нормального розподілу за формулами, які наведені в табл. 2.3 і будується табл. 5
Таблиця 5
Координати характерних точок кривої нормального розподілу
Характерні
точки
|
Абсциса |
Ордината |
Вершина
кривої
|
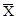 |
80,247 |
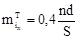 |
28 |
Точка
перегину
|
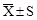 |
80,2546 |
 |
17 |
| 80,2394 |
Точка
перегину
|
 |
80,2622 |
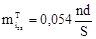 |
4 |
| 80,2318 |
Точка
перегину
|
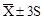 |
80,2698 |
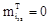 |
0 |
| 80,2242 |
Графік теоретичної кривої нормального розподілу поєднується з гістограмою та емпіричною кривою, тобто зображається на рис. 3.
8. Перевірка гіпотези про розподіл випадкової величини
Для перевірки відповідності емпіричного розподілу теоретичному існує ряд критеріїв. В даному прикладі з цією метою використовується критерій Персона χ2:
 . .
Для зручності обчислення доцільно використовувати табл. 6
Таблиця 6
Допоміжна таблиця для обчислення критерію χ2
| Інтервали розмірів |
Середина
інтервалу
хi
|
Частота
mi
|
Теоретична
частота 
|
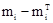
|

|
 |
| від |
до |
| 80,225 |
80,231 |
80,228 |
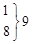 |
 |
1 |
1 |
0,125 |
| 80,231 |
80,237 |
80,234 |
| 80,237 |
80,243 |
80,240 |
18 |
18 |
0 |
0 |
0 |
| 80,243 |
80,249 |
80,246 |
26 |
28 |
-2 |
4 |
0,143 |
| 80,249 |
80,255 |
80,252 |
22 |
22 |
0 |
0 |
0 |
| 80,255 |
80,261 |
80,258 |
 |
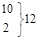 |
1 |
1 |
0,083 |
| 80,261 |
80,267 |
80,264 |
| Всього |
88 |
88 |
0,351 |
При визначенні критерію необхідно, щоб частота була не менше п’яти. Якщо в будь-якому інтервалі частота буде менше п’яти, то її необхідно об’єднати з сусіднім значенням.
Потім необхідно знайти число k за формулою:
k = m – p – 1,
де p – число параметрів теоретичного розподілe. Для нормального розподілe p=2.
За таблицею додатку Б за знайденими значеннями χ2 і k визначається ймовірність P(x2). Якщо буде виконуватися нерівність Р(χ2) > 0.05, то можна вважати, що емпіричній розподіл відповідає теоретичному (нормальному) і можна використовувати його закономірності для аналізу точності обробки.
Якщо вказана нерівність виконуватися не буде, то як теоретичний розподіл потрібно використовувати інший закон розподілу.
В наведеному прикладі:
χ2 = 0,351;
k=5 – 2 – 1=2;
Р(χ2) =0,8 > 0,05.
Відповідно можна вважати, що розподіл розмірів відповідає нормальному закону.
9. Визначення ймовірності відсотка браку при виконанні операції, що досліджується.
Для нормального розподілу поле розсіювання похибок (в генеральній сукупності) визначається за формулою:
Δp = 6σ. (14)
Вибіркове середнє квадратичне відхилення S є наближеною оцінкою середньоквадратичного відхилення випадкової величини σ. Похибка оцінки σ по S залежить від обсягу вибірки.
Враховуючи цю обставину, необхідно при використанні формули (14) значення σ визначати із співвідношення (2.6):
σ = γS,
де γ – коефіцієнт, який приймається в залежності від обсягу вибірки.
Необхідною умовою обробки деталі без браку є виконання двох умов (1) та (2):
а) перевірка першої умови за (1):
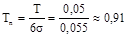 ;Tn < 1; ;Tn < 1;
б) перевірка другої умови за (2)
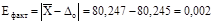 мм, мм,
де  мм; мм;
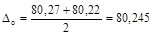 мм; мм;
 мм; мм;
 ; ;
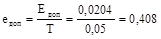 ; ;
eфакт ≤ едоп.
Одна з умов (перша) не виконується. Отже уникнути браку неможливо, необхідно розрахувати величину ймовірного браку.
Якщо задані допуск на розмір і граничні розміри деталі за кресленням xв і хн, то ймовірний відсоток браку буде рівним:
– по верхній границі поля допуску:
Рб.в = [0,5 – Ф(tв)] ∙ 100 %;(15)
– по нижній границі поля допуску:
Рб.н = [0,5 – Ф(tн)] ∙ 100 %. (16)
У формулах (15) і (16):
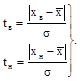 (17) (17)
У наведеному прикладі:
σ = 1,21 ∙ 0,0076 = 0,0092 мм;
Δp = 6 ∙ 0,0092 = 0,055 мм;
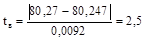 ; Ф(tв) = 0,4940; ; Ф(tв) = 0,4940;
 ;Ф(tн) = 0,4980; ;Ф(tн) = 0,4980;
– по верхній границі поля допуску (виправний брак):
Рб.в = [0,5 – 0,4940] ∙ 100 % = 0,6 %;
– по нижній границі поля допуску (невиправний брак):
Рб.н = [0,5 – 0,4980] ∙ 100 % = 0,2 %.
Отже, можливий брак складає:
Рб = Рб.в + Рб.н = 0,6 + 0,2 =0,8 %,
що дорівнює 1 деталі при розмірі вибірки N = 88.
Отже, точність технологічної операції недостатня і ймовірний відсоток браку складає 0,8%, процес обробки ненадійний, хоча точність налагоджування виконана правильно.
Технологічний допуск, який можна витримати на даній операції, при обробці деталі без браку згідно з першою умовою п. 1.2 складає:
Т = 1,12Δр = 1,12×0,055 = 0,062 мм.
Визначення ймовірної кількості браку при розподілі розмірів за функцією a(t)
У випадку, коли розсіювання розмірів заготовок викликається не тільки випадковими, але й змінними систематичними похибками і розподіл розмірів підкоряється функції a(t) з параметрами σa і λa, порядок обчислення ймовірної кількості браку при Δp > T принципово нічим не відрізняється від розрахунку при розподілі розмірів за законом Гаусса.
Також, як і при нормальному розподілі, ймовірна кількість бракованих заготовок визначається сумою заштрихованих ділянок площі, обмеженої кривою функції a(t), при симетричному розташуванні кривої розподілу по відношенню до поля допуску (рис. 4, а) або величиною заштрихованої ділянки цієї площі при однобічному виході бракованих заготовок за межі поля допуску (рис. 4, б).

Рис. 4. Кількість ймовірного браку при симетричному (а) та несиметричному (б) розташуванні поля розсіювання, обмеженого кривою функції a(t), відносно середини поля допуску
Аналогічно закону Гаусса функцію a(t) можна виразити в нормованому вигляді за допомогою нормованого параметра розподілу, який у даному випадку визначається за формулою:
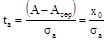 , (18) , (18)
де σa – середнє квадратичне відхилення функції.
Після відповідних перетворень функція
a(t) = Ф(ta, λa) (19)
табулюється.
При симетричному розташуванні кривої розподілу функції a(t) відносно середини поля допуску (рис. 4, а) розміри заштрихованих ділянок площі (а, отже і частку браку) визначають послідовним розрахунком величин:
 ; ; 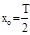 ; ;  і ta за формулою (18). і ta за формулою (18).
За встановленими значенням λa і ta (по таблиці додаток 4 ) знаходять Ф(λa,ta), що виражає у частках одиниці половину загальної кількості придатних заготовок (незаштрихована ділянка площі на рис. 4, а, розташована по один бік середини поля допуску), і розраховують загальну кількість бракованих заготовок у відсотках за формулою:
Qбр = 100 % ∙ [1 – 2Ф(ta, λa)]. (20)
Приклад
На револьверному верстаті обробляють 300 шт. валиків зі сталі 45. Розміри заготовок Æ25х40 мм. Допуск на обробку – 0,1 мм. Матеріал різця – Т30К4. Режим різання: V = 150 м/хв; подача S = 0,08 мм/об; t = 0,5 мм.
При обробці пробної партії заготовок експериментально встановлено і підраховано, що розсіювання розмірів заготовок при обробці на даному верстаті характеризується середнім квадратичним відхиленням σ = 0,025 мм.
Визначити кількість придатних і бракованих заготовок при умові, що настроювання верстата забезпечує симетричне розташування кривої розсіювання відносно середини поля допуску.
Розв’язання
У зв’язку з тим, що за рахунок зношування різця при обробці 300 шт. заготовок відбувається безперервне зміщення вершини кривої розсіювання Гаусса вправо (в бік збільшення розмірів), вважаємо, що фактичний розподіл розмірів підкоряється функції a(t) і за умовами задачі відповідає схемі, зображеній на рис. 4, а.
1. Зміщення центра групування 2l кривої визначається збільшенням діаметра оброблюваних заготовок, зношуванням різця під час обробки заготовок, тобто 2l= 2i, де у відповідності з формулою (2.5) [3, табл. 2.1]: n = 300 шт.
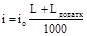 ; io = 6,5 мкм. ; io = 6,5 мкм.
Шлях різання 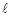 при обробці n = 300 шт. заготовок дорівнює при обробці n = 300 шт. заготовок дорівнює
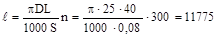 мм; мм;
зношування
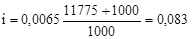 мм; мм;
l = i = 0,083 мм.
Зміщення центра групування 2l =0,166 мм.
2. За формулою:
 . .
3. Середнє квадратичне відхилення функції a(t) за формулою:
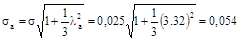 мм. мм.
4. Поле розсіювання для a(t) при λa= 3:
Δp = 4,74σa = 4,74 ∙ 0,054 = 0,256 мм
значно перевищує поле допуску Т = 0,1 мм, тому при обробці всієї партії заготовок без підналагодження верстата брак є технічно неминучим (рис. 4, а).
5. Для визначення кількості ймовірного браку обчислюється значення ta за формулою (18):
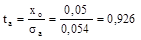 . .
Кількість придатних деталей при λa = 3,0 і ta = 0,926 (див. додаток 4):
Q = 2Ф(ta, λa) = 2 ∙ 0,2969 = 0,5938,
тобто 59,38 % від всієї партії, або 178 шт. Брак заготовок – 40,62 % або 122 шт.
Як бачимо, брак великий (40,62 %).
Для зменшення браку доцільно замінити різець з твердого сплаву Т30К4 більш стійким різцем з ельбору, який має відносне зношування io = 3,0 мкм при V= 550 м/хв і S = 0,06 мм/об (див.[3, табл. 2.1]).
В цьому випадку шлях різання при обробці однієї заготовки зростає:
 м, м,
проте зношування різця при обробці партії знижується до
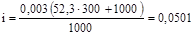 мм мм
і l= 0,0501 мм.
Відповідно зменшується:

 мм мм
і поле розсіювання
Δp = 4,74σa = 4,74 ∙ 0,038 = 0,181 мм.
При цьому збільшуються
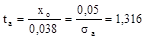 ; ;
Q = 2Ф(ta, λa) = 2 ∙ 0,3984,
тобто 79,7 % партії заготовок чи 239 шт. є придатними. Брак у цьому випадку складає 20,3 %, чи 61 шт., тобто стає у два рази меншим, ніж при обробці різцем з твердого сплаву.
Великі переваги застосування ельбору у порівнянні з твердим сплавом пов’язані не тільки зі значним підвищенням точності обробки, але й з одночасним зростанням її продуктивності за рахунок збільшення швидкості різання із 150 до 550 м/хв.
Досить часто при обробці заготовок в умовах одночасної дії випадкових і змінних систематичних похибок настроювання верстата проводять за першими пробними заготовками без врахування наступного зношування різця та зміщення центра групування. При цьому крива розподілу розмірів оброблених заготовок розташовується так, що її початок збігається з однією з границь поля допуску (рис. 4, б). В цьому випадку кількість бракованих заготовок у відсотках визначається площею заштрихованої ділянки, розташованої з одного боку за межами поля допуску, тобто:
Qбр = [0,5 – 2Ф(ta, λa)] ∙ 100 %,(21)
а кількість придатних заготовок Q – сумою площ А = 0,5 і В = Ф(λa,ta), тобто:
Q = [0,5 + Ф(ta, λa)] ∙ 100 %. (22)
Приклад
Для умов, аналогічних прикладу при обробці заготовок різцем з ельбору, визначити кількість придатних і бракованих заготовок, якщо настроювання верстата забезпечує збігання початку кривої розподілу з нижньою границею поля допуску (рис. 4, б).
Розв’язання
За результатами розрахунку попереднього прикладу λa= 2,0, σa= 0,038 мм і поле фактичного розсіювання розмірів Δp = 0,181 мм.
З рис. 4, б видно, що
обробка заготовка брак точність
 мм; мм;
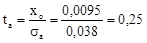 . .
З додатку 4 маємо Ф(λa,ta) = 0,083. За формулою (21) отримуємо:
Qбр = (0,5 – 0,083) ∙ 100 % = 41,7 % чи 125 шт.
З розрахунку випливає, що при однобічному розташуванні бракованих заготовок (рис. 4, б) загальна кількість браку значно більша, ніж при симетричному розташуванні (рис. 4, а), однак у першому випадку є можливість виправити отриманий брак шляхом додаткової обробки. Наприклад, валики з надто великими діаметрами (рис. 4, б) можна піддати додатковому шліфуванню.
Для зменшення браку при одночаснійдії випадкових та систематичних похибок можуть бути здійснені такі заходи:
· підбір більш точного обладнання та методів обробки, що дасть зниження міри розсіювання (σ);
· застосовування інструменту більш зносостійкого, що зменшить зміщення вершини кривої розсіювання;
· введення періодичного піднастроювання верстата (краще, якщо це буде автоматичне піднастроювання).
Визначення ймовірної кількості браку при розподілірозмірів за законом ексцентриситету (Релея)
У випадку визначення ймовірного відсотка браку при розподілі додатних величин, які підкоряються закону Релея (закону ексцентриситету), методика розрахунку повністю збігається з розглянутими вище методиками розрахунку при розподілі за законом Гаусса і функцією a(t).
При розподілі Релея, коли фактичне поле розсіювання перевищує поле допуску, тобто Δp > T, можлива поява бракованих заготовок (рис. 5).

Рис. 5. Кількість ймовірного браку (заштрихована площа)при розподілі розміру за законом Релея
Загальну площу F, обмежену кривою розподілу, знаходять за інтегральним законом розподілу ексцентриситету (див. (2.18)):
 , (23) , (23)
який після звичайної підстановки величин:
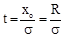 ; (24) ; (24)
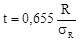 (25) (25)
набуває нормованого виду:
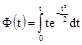 (26) (26)
і табулюється аналогічно функції Лапласа.
Розрахунок кількості придатних і бракованих заготовок у відсотках зводиться до визначення t і Ф(t) аналогічно розглянутим вище прикладам.
Приклад
Розрахувати ймовірний відсоток браку за ексцентриситетом R між двома шийками ступінчастого вала, якщо допуск на биття дорівнює 0,08 мм. В результаті безперервних вимірювань перших 25 заготовок партії встановлене середнє квадратичне відхилення ексцентриситету SR = 0,09 мм.
Розв’язання
Розрахункове значення середнього квадратичного відхилення ексцентриситету за формулою (2.6) і табл. 2.1:
σR = γSR = 1,4 ∙ 0,09 = 0,0126 мм.
Фактичне поле розсіювання значень ексцентриситету за формулою дорівнює:
Δp = 5,252σR = 5,252 ∙ 0,0126 = 0,0662 мм.
Допуск на ексцентриситет, що дорівнює половині поля допуску на биття (TR=0,04 мм), значно менший фактичного поля розсіюванняTR < Δp, тому ймовірне виникнення браку.
При xo = TRмм і

і у відповідності з додатком 5 Ф(t)=0,8851, тобто кількість придатних заготовок складає 88,51 % і кількість браку 11,49 %.
Визначення кількості заготовок, що потребують додаткової обробки
З цією ситуацією доводиться зустрічатись, коли на заводі немає обладнання необхідної точності та обробку доводиться виконувати на верстаті менш точному, але, як правило, більш продуктивному, наприклад, замість револьверної обробки виконується робота на токарному автоматі. При цьому з економічних міркувань не допускається отримання браку.
В таких випадках настроювання верстата проводять зі свідомим зміщенням m вершини кривої розподілу по відношенню до середини поля допуску з таким розрахунком, щоб весь брак заготовок, який отримується на даній операції, можна було виправити шляхом додаткової обробки заготовок.
В цьому випадку необхідно при обробці валів вершину кривої розподілу змістити на деяку величину m вправо від середини поля допуску (рис. 6, а), щоб всі вали, що виходять за межі допуску, мали розмір більший за визначений за кресленням і після додаткової операції шліфування могли стати придатними. Аналогічно цьому отвори, що виходять за межі допуску, повинні мати діаметр менший за мінімальний, для чого при настроюванні верстата криву розподілу розмірів отвору потрібно змістити на величину mвліво по відношенню до середини поля допуску (рис. 6, б).
Величина зміщення визначається за формулою:
 . .
Щоб повністю виключити можливість появи невиправного браку, розмір зміщення m вершини кривої розподілу збільшують на величину похибки Δн настроювання. При цьому однак загальна кількість заготовок, що потребують додаткової обробки, помітно зростає.
Кількість заготовок, що потребують доробки (на рис. 6 заштрихована площа), визначають аналогічно попередньому за значеннями xв (для валів) і xА (для отворів). Згідно з рис. 6:
хА = хв = Т – 3σ – Δн. (27)

Рис. Налагодження верстату для обробки валів (а) та отворів (б) з виправним браком
За величиною хА(хв) і формулою (10) знаходять tA(tB) і за таблицею додатку В розраховують відповідні значення Ф(tA) або Ф(tB), що визначають розміри площ А і В.
Кількість заготовок Qдод у відсотках, що потребують доробки, визначається за формулою:
Qдод = [0,5 – Ф(t)] ∙ 100 %.
Приклад
Визначити кількість заготовок, що потребують додаткової обробки при Т = 0,1 мм, σ = 0,025 мм, Δн =0,02 мм.
Розв’язання
За формулою (27):
хв = 0,1 – 3·0,025 – 0,02 = 0,005.
У відповідності з формулою (10):
tв = 0,005/0,25 = 0,2.
Отже, Ф(tв) =0,0793 (див. додаток 3). Кількість заготовок, що потребують додаткової обробки, дорівнює:
Qдод = [0,5 – 0,0793] ∙ 100 = 42,07 % чи 127 штук.
Визначення економічної доцільності застосування високопродуктивних верстатів зниженої точності
Практика показує, що при симетричному розташуванні кривої розподілу розмірів оброблюваних заготовок, кількість бракованих заготовок, що характеризуються площею заштрихованих ділянок, порівняно невелика (рис. 2).
Наприклад, при обробці валиків з допуском Т = 0,1 мм при σ = 0,025 мм і 6σ=0,15 мм, тобто у випадку, коли поле розсіювання у 1,5 раза перевищує поле допуску і запас точності 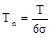 = 0,67 < 1,0, кількість бракованих заготовок складає всього 4,56 %. = 0,67 < 1,0, кількість бракованих заготовок складає всього 4,56 %.
Отже, в ряді випадків можна і доцільно використовувати для обробки точних заготовок високопродуктивні верстати навіть тоді, коли їх точність за розрахунками є недостатньою. При цьому ціною порівняно малих затрат на неминучий брак заготовок можна добитись значного збільшення випуску виробів та зниження собівартості.
При розрахунку економічної доцільності обробки заготовок на більш продуктивному обладнанні зі свідомим допущенням деякої кількості браку заготовок визначають:
· кількість очікуваного браку чи кількість заготовок, що потребують додаткової обробки;
· збитки від браку (внаслідок непродуктивного витрачання металу та втрати часу на попередню обробку і обробку бракованих заготовок на даній операції) або вартість додаткової обробки заготовок, розміри яких виходять за межі допуску;
· зниження собівартості та відповідну економію при обробці заготовок на більш продуктивному обладнанні.
Порівняння збитків від браку або вартості додаткової обробки заготовок з економією від переведення обробки на більш продуктивні верстати дозволяють виявити економічну доцільність застосування високопродуктивних верстатів зниженої точності при виробництві точних заготовок.
Порівняння точності обробки заготовок при різному стані технологічної системи на різних системах, в різних змінах, а також після проведення ремонтів верстатів проводиться за допомогою параметрів законів статичного розподілу  . .
Список використаної літератури
1. Балакшин Б.С. Основы технологии машиностроения. – М., 1969. – 559 с.
2. Бондаренко С.Г. Розмірні розрахунки механоскладального виробництва. – К. 1993. – 544 с.
3. Корсаков В.С. Основы технологии машинобудування. – М., 1977. – 415 с.
4. Косилова А.Г., Мещеняков Р.К. Справочник технолога-машиностроителя. Т. 1. – М., 1985. – 655 с.; Т. 2. – М., 198 – 496 с.
5. Маталин А.А. Технология машиностроения. – Л. – М., 1985 – 496 с.
Руденко П.А. Теоретические основы технологии машиностроения:Конспект лекций. – Чернигов, 198 – 258 с.
7. Сборник задач и упражнений по технологии машиностроения / В.А. Аверников, О.А. Горленко, В.Б. Ильецкий и др. / Под общ. ред. О.А. Горленко – М., 1988.– 192 с.
8. Справочник технолога машиностроителя / Под ред. А.Н. Малова. Т. 2. – М., 198 – 446 с.
|