Курсовая работа: Проектирование привода к ленточному конвейеру
|
Название: Проектирование привода к ленточному конвейеру Раздел: Промышленность, производство Тип: курсовая работа | ||||||||||||||||||||||||
1. Подбор электродвигателя и кинематический расчет привода1.1 Требуемую мощность электродвигателя Ртр, кВт, определяем согласно [5,c.4] по формуле
где Р5 - требуемая мощность на ведомом валу, Р5 = 6 кВт
По ГОСТ 19523-81 выбираем электродвигатель 4А112М2У3 с синхронной частотой вращения n = 3000 мин-1, с параметрами Рдв = 7,5 кВт и скольжением s = 2,5%. 1.2 Номинальную частоту вращения электродвигателя n, мин-1, определяем согласно [5,c.6] по формуле
1.3 Угловую скорость на валу электродвигателя 1, с-1, определяем по формуле
1.4 Общее передаточное отношение привода u определяем согласно [5,c.8] по формуле
где n5 - частота вращения ведомого вала, n5 = 50 мин-1
Принимаем передаточное число зубчатой прямозубой передачи согласно [5,с.7, с.36] u2 = 4 Принимаем передаточное число зубчатой косозубой передачи согласно [5,с.7, с.36] u3 = 4 Передаточное число клиноременной передачи u1 определяем по формуле
Частота вращения вала электродвигателя n1 = 2925 мин-1 Частоту вращения валов редуктора ni, мин-1, определяем по формуле
где i - порядковый номер вала Частоту вращения ведущего вала n2, мин-1, определяем по формуле (1.7)
Частоту вращения промежуточного вала n3, мин-1, определяем по формуле (1.7)
Частоту вращения ведомого вала n4, мин-1, определяем по формуле (1.7)
Частота вращения вала привода n5 = n4 = 50 мин-1 Угловая скорость вала электродвигателя 306,31 с-1 Угловую скорость валов редуктора с-1, определяем по формуле
Угловую скорость ведущего вала с-1, определяем по формуле (1.8)
Угловую скорость промежуточного вала с-1, определяем по формуле (1.8)
Угловую скорость ведомого вала с-1, определяем по формуле (1.8)
Угловая скорость вала привода 5,23 с-1 Вращающий момент на валу электродвигателя Т1, Нм, определяем согласно [5,c.4] по формуле
где Р1 - мощность на валу электродвигателя, Р1 = 6,98 103 Вт
Вращающий момент на ведущем валу редуктора Т2, Нм, определяем по формуле Т2 = Т1u1 4 (1.10) Т2 = 22,79 3,66 0,97 0,9980,1НЧм Вращающий момент на промежуточном валу редуктора Т3, Нм, определяем по формуле Т3 = Т2u24 (1.11) Т3 = 80,140,970,99 = 307,68НЧм Вращающий момент на ведомом валу редуктора Т4, Нм, определяем по формуле Т4 = Т3u34 (1.12) Т4 = 307,684 0,97 0,99 = 1181,9НЧм Вращающий момент валу привода, Т5, Нм, определяем по формуле Т5 = Т44 (1.13) Т5 = 1181,9 0,99 = 1146,7НЧм 2. Расчет плоскоременной передачи2.1 Диаметр меньшего шкива плоскоременной передачи d1, мм, определяем согласно [5, c.120] по формуле
Подбираем диаметр шкива из стандартного ряда по ГОСТ 17383-73 d1 = 180 мм 2.2 Диаметр ведомого шкива d2, мм, определяем согласно [5, c.120] по формуле d2 = d1 u1, (2.2) d2 = 180 3,66 = 658,8 мм 2.3 Межосевое расстояние а, мм, определяем согласно [5, c.121] по формуле a= 2 (d1 + d2), (2.3) a= 2 (180 + 658,8) = 1677,6 мм 2.4 Угол обхвата меньшего шкива a1, град, определяем согласно [5, c.121] по формуле
2.5 Длину ремня L, мм, (без учета припуска на соединение концов) определяем согласно [5, c.121] по формуле
2.6 Скорость ремня v, м/с, определяем согласно [5, c.121] по формуле v= 0,5 w1 d1, (2.6) v= 0,5 306,31 180 10-3 = 27,57 м/с 2.7 Окружную силу Ftр, Н, определяем согласно [5, c.121] по формуле
2.8 По табл. 7.1. [5,с.119] выбираем ремень БКНЛ имеющий число прокладок z= 3; расчетную толщину прокладки с резиновой прослойкой d=1,2 мм; наибольшую допускаемую нагрузку на прокладку Po= 3 Н/мм ширины ремня Проверяем выполнение условия согласно [5,c.123] по формуле d< 0,025 d1 (2.8) где d= do z= 1,2 3 = 3,6 d= 0,025 180 = 4,5 условие выполнено т. к. 3,6 < 4,5 2.9 Допускаемую рабочую нагрузку [ p], МПа на 1мм ширины прокладки определяем согласно [5, c.122] по формуле [p] = Po Ca Cv Cp Cq (2.9) где Ca- коэффициент угла обхвата определяем согласно [5,c.122] по формуле Ca= 1 - 0,003 (180 - 1), (2.10) Ca= 1 - 0,003 (180 - 162,88) = 0,95 Cv- коэффициент, учитывающий влияние скорости ремня определяем согласно [5,c.122] по формуле Cv= 1,04 - 0,0004 v2, (2.11) Cv= 1,04 - 0,0004 27,572 = 0,74 Cp- коэффициент режима работы, Cp= 1 [5,c.122]; Cq- коэффициент, учитывающий угол наклона линии центров пере дачи Cq= 1 [5,c.122] [p] = 3 0,95 0,74 1 1 = 1,89 МПа 2.10 Ширину ремня b, мм , определяем согласно [5,c.121] по формуле
принимаем b= 50 мм 2.11 Предварительное натяжение ветви ремня Fo, Н, определяем согласно [5, c. 121] по формуле Fo= o b d, (2.13) где o-напряжение от предварительного натяжения ремня, o= 1,8 МПа [5,с.121] Fo= 1,8 50 3,6 = 324 Н 2.12 Натяжение ведущей ветви F1, Н, определяем согласно [5, c.121] по формуле F1 = Fo+ 0,5 Ftр, (2.14) F1 = 324 + 0,5 253,2 = 450,6 Н 2.13 Натяжение ведомой ветви F1, Н, определяем согласно [5, c.121] по формуле F2 = Fo- 0,5 Ftр, (2.15) F2 = 324 - 0,5 253,2 = 197,4 Н 2.14 Напряжение от растяжения ремня s1, МПа, определяем согласно [5, c.123] по формуле
2.15 Напряжение от изгиба ремня sи, МПа, определяем согласно [5, c.123] по формуле
где Eи = 100 МПа [5,с.123]
2.16 Напряжение ремня от центробежной силы v, МПа, определяем согласно [5, c.123] по формуле v= r v2 10-6,(2.18) где r- плотность ремня, r=1100 кг/м3 [5,c.123] v= 1100 27,572 10-6 = 0,84 МПа 2.17 Максимальное напряжение в сечении ремня max, МПа, определяем согласно [5, c.123] по формуле max= 1 + и + v, (2.19) max= 2,5 + 2 + 0,84 = 5,34 МПа Максимальное напряжение не должно превышать предела выносливости max£7 МПа [5,с.123)] 2.18 Число пробегов ремня с секунду lопределяем согласно [5, c.124] по формуле
2.19 Долговечность ремня Но, ч, определяем согласно [5, c.124] по формуле
где s - предел выносливости ремня, s = 7 МПа [5,c.123]; Сi- коэффициент, учитывающий влияние передаточного отношения определяем согласно [5,c.124] по формуле
Сн - коэффициент, зависящий от изменения нагрузки, Сн = 1 [5,c.124]
Рекомендуемая долговечность ремня Но не менее 2000 час [5,с.124] 2.2 Нагрузку на валы ременной передачи Fв, Н, определяем согласно [5, c.124] по формуле
3. Расчет цилиндрической прямозубой передачиВыбираем материалы: для шестерни сталь 45, термическая обработка - улучшение, 230 HВ1, для зубчатого колеса сталь 45, термическая обработка - улучшение, 200HВ2. 3.1 Определяем предел контактной выносливости Hlimbi, МПа, согласно [5, с.34] по формуле Hlimbi = 2 HВi + 70,(3.1) Определяем предел контактной выносливости шестерни Hlimb1, МПа, по формуле [3.1] Hlimb1 = 2 230 + 70 = 530 МПа Определяем предел контактной выносливости для зубчатого колеса Hlimb2, МПа, по формуле [3.1] Hlimb2 = 2 200 + 70 = 470 МПа 3.2 Определяем допускаемые контактные напряжения
где KHL - коэффициент долговечности, KHL =1 [5, с.33]; [SН] - коэффициент безопасности, [SН] = 1,1 [5, с.33]. Коэффициент долговечности KHLопределяем согласно [5, c.33] по формуле
где NHO- число циклов напряжений, соответствующее пределу вынос- ливости, NHO= 15 106 [3, c.130]; N- число циклов перемены напряжений зубьев за весь срок службы согласно [3, c.130] определяем по формуле
где Lh- ресурс передачи. Ресурс передачи Lh, ч, определяем по формуле Lh= Т 365 24 Кгод Ксут, (3.5) Lh= 5 365 24 0,6 0,3 = 7884 ч Число циклов перемены напряжений зубьев шестерни N1 за весь срок службы определяем согласно [3, c.145] по формуле
Число циклов перемены напряжений зубьев зубчатого колеса за весь срок службы N2 определяем по формуле [3.4]
при N> NHO, KHL= 1 [5, c.33]. Коэффициент долговечности для шестерни KHL1 при соблюдении условия N1 > NHO, 379 106 > 15 106 равняется KHL1 = 1. Коэффициент долговечности для зубчатого колеса KHL2 при соблюдении условия N2 > NHO, 94,5 106 > 15 106 равняется KHL2 = 1. Определяем допускаемые контактные напряжения для шестерни
Определяем допускаемые контактные напряжения для зубчатого колеса
Для дальнейших расчетов принимаем меньшее значение. 3.3 Определяем межосевое расстояние aw, мм, из условия контактной выносливости зубьев согласно [5, c.32] по формуле
где KH-коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, KH= 1 [5, с.32]; ba - коэффициент ширины венца колеса, ba = 0,2 [5, с.32].
Ближайшее значение межосевого расстояния по ГОСТ 2185-66 aw=200 мм 3.4 Определяем нормальный модуль зацепления m, мм, согласно [5, c.36] по формуле m = (0,010,02) aw (3.7) m = (0,010,02) 200 = 2,0 ё 4,0 мм принимаем модуль по ГОСТ 9563-60 m = 2 мм. 3.5 Определяем число зубьев шестерни z1 согласно [5, c.37] по формуле
3.6 Определяем число зубьев зубчатого колеса z2 по формуле z2 = z1 u2,(3.9) z2 = 40 4 = 160 3.7 Определяем делительные диаметры зубчатой передачи di, мм, согласно [5, c.37] по формуле di = m zi,(3.10) Определяем делительный диаметр шестерни d1, мм, по формуле [3.10] d1 = 2 40 = 80 мм Определяем делительный диаметр зубчатого колеса d2, мм, по формуле [3.10] d1 = 2 160 = 320 мм 3.8 Уточняем межосевое расстояние aw, мм, согласно [5, c.37] по формуле
3.9 Определяем диаметры вершин зубчатых колес dai, мм, согласно [5, c.293] по формуле dai = di + 2m, (3.12) Определяем диаметр вершин шестерни da1, мм, по формуле [3.12] da1 = 80 + 2 2 = 84 мм Определяем диаметр вершин зубчатого колеса da2, мм, по формуле [3.12] da2 = 320 + 2 2 = 324 мм 3.10 Определяем ширину колеса b2, мм, согласно [5, c.294] по формуле b2 =aw(3.13) b2 = 0,2 200 = 40 мм 3.11 Определяем ширину шестерни b1, мм, согласно [5,c.294] по формуле b1 = b2 + 5, (3.14) b1 = 40 + 5 = 45 мм 3.12 Определяем коэффициент ширины шестерни по диаметру bd согласно [5, c.33] по формуле
3.13 Определяем окружную скорость колес v, м/с, согласно [5, c.294] по формуле
При такой скорости для прямозубых колес по ГОСТ 1643-81 принимаем 8-ю степень точности. 3.14 Определяем коэффициент нагрузки KH согласно [5, c.39] по формуле KH = KH KHv KH (3.17) где KH- коэффициент, KH 1,06 [5, с.39]; KHv - коэффициент, KHv = 1,05 [5, с.40]; KH- коэффициент, KH= 1 [5, с.39]. KH = 1,06 1,05 1 1,11 3.15 Проверяем контактные напряжения Н, МПа, согласно [5, c.31] по формуле
недогруз составляет 3.16 Определяем окружную силу, действующую в зацеплении, Ft1, Н, согласно [5, c.41] по формуле
3.17 Определяем радиальную силу, действующую в зацеплении, Fr, Н, согласно [5, c.294] по формуле Ft1 = Ft1 tg, (3.20) где 20 - угол зацепления Fr1 = 2003 tg20 = 729 Н 3.18 Определяем допускаемые напряжения согласно [5, c.43] по формуле
где Flimb1 - значение предела выносливости при отнулевом цикле изгиба Значение предела выносливости при отнулевом цикле изгиба для шестерни
Значение предела выносливости при отнулевом цикле изгиба для колеса
формуле
где
Определяем допускаемые напряжения для шестерни
Определяем допускаемые напряжения для зубчатого колеса
3.19 Находим отношения согласно [5,c.295] по формуле
где YF1 - коэффициент, учитывающий форму зуба шестерни, YF1 = 3,7 [5, с.42]; YF2 - коэффициент, учитывающий форму зуба зубчатого колеса, YF2 = 3,6 [5, с.42]. Находим отношения для шестерни по формуле [3.23]
Находим отношения для зубчатого колеса по формуле [3.23]
Дальнейший расчет ведем для зубьев колеса, для которого найденное отношение меньше. 3.20 Проверяем зубья на выносливость по напряжениям изгиба F, МПа, согласно ГОСТ 21354-75 по формуле
где KF - коэффициент нагрузки определяем согласно [5, c.42] по формуле KF = KFKFv, (3.25) где KF - коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба, KF = 1,04 [5, c.43]; KFv - коэффициент, учитывающий динамическое действие нагрузки, KFv = 1,45 [5,с.43]. KF = 1,041,45 =1,51
условие F < [F ]2 выполнено. 4. Расчет цилиндрической шевронной передачиВыбираем материалы: для шестерни сталь 40Х, термическая обработка - улучшение 250 HВ1 , для зубчатого колеса сталь 40Х, термическая обработка - улучшение 220 HВ2 4.1 Предел контактной выносливости Hlimbi, МПа, определяем согласно [5, с.34] по формуле Hlimbi= 2 HВi + 70,(3.1) Предел контактной выносливости шестерни Hlimb3, МПа, определяем по формуле [3.1] Hlimb3 = 2 250 + 70 = 570 МПа Предел контактной выносливости для зубчатого колеса Hlimb4, МПа, определяем по формуле [3.1] Hlimb4 = 2 220 + 70 = 510 МПа 4.2 Допускаемые контактные напряжения
где KHL- коэффициент долговечности определяем согласно [5, c.33] по формуле, KHL1 = 1 [SН] - коэффициент безопасности, [SН] = 1,2 [5, с.33] Допускаемые контактные напряжения для шестерни
Допускаемые контактные напряжения для зубчатого колеса
Расчетное допускаемое контактное напряжение [sн], МПа, определяем согласно [5, c.35] по формуле
Проверяем выполнение условия согласно [5, c.35] по формуле
405 < 525,55 МПа - условие выполнено 4.3 Межосевое расстояние aw, мм, из условия контактной выносливости зубьев определяем согласно [5, c.32] по формуле
где KH-коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, KH= 1,25 [5, с.32]; ba- коэффициент, ba= 0,8 [5, с.32]
Ближайшее значение межосевого расстояния по ГОСТ 2185-66 aw= 200 мм 4.4 Нормальный модуль зацепления mn,, мм, определяем согласно [5, c.36] по формуле mn= (0,010,02) aw (3.9) mn= (0,010,02) 200 = 2,0 ¸ 4,0 мм принимаем модуль по ГОСТ 9563-60 mn= 2,0мм 4.5 Число зубьев шестерни z3 определяем согласно [5, c.37] по формуле
где b - угол наклона зуба, предварительно принимаем b =35°
принимаем z3 = 33 4.6 Число зубьев зубчатого колеса z4 определяем по формуле z4 = z3 u3, (3.11) z4 = 33 4 = 132 Уточняем значение угла наклона b согласно [5, c.37] по формуле
откуда находим значение b = 34°25¢ 4.7 Делительные диаметры зубчатой передачи di, мм, определяем согласно [5, c.37] по формуле
Делительный диаметр шестерни d3, мм, определяем по формуле [3.13]
Делительный диаметр зубчатого колеса d4, мм, определяем по формуле [3.13]
4.8 Межосевое расстояние aw, мм, уточняем согласно [5, c.37] по формуле
4.9 Диаметры вершин зубчатых колес dai, мм, определяем согласно [5, c.293] по формуле dai = di + 2mn,(3.15) Диаметр вершин шестерни da3, мм, определяем по формуле [3.15] da3 = 80 + 2 = 84 мм Диаметр вершин зубчатого колеса da4, мм, определяем по формуле [3.15] da4 = 320 + 2 2 = 324 мм 4.10 Ширину колеса b4, мм, определяем согласно [5, c.294] по формуле b4 =aw(3.16) b4 = 0,8 200 = 160 мм 4.11 Ширину шестерни b3, мм, определяем согласно [5, c.294] по формуле b2 = b4 + 5, (3.17) b1 = 160 + 5 = 165 мм 4.12 Коэффициент ширины шестерни по диаметру y bdопределяем согласно [5, c.33] по формуле
4.13 Окружную скорость колес v, м/с, определяем согласно [5, c.294] по формуле
При такой скорости для косозубых колес по ГОСТ 1643-81 принимаем 8-ю степень точности. 4.14 Определяем коэффициент нагрузки KHсогласно [5, c.39] по формуле KH= KH KHv KH (3.20) где KH- коэффициент, KH1,3 [5, с.39]; KHv- коэффициент, KHv= 1 [5, с.40]; KH- коэффициент, KH= 1,06 [5, с.39] KH= 1,3 1 1,06 1,38 4.15 Проверку контактных напряжений sН, МПа, определяем согласно [5, c.31] по формуле
условие H< [H] выполнено 4.16 Окружную силу, действующую в зацеплении, Ft2, Н, определяем согласно [5, c.41] по формуле
4.17 Радиальную силу, действующую в зацеплении, Fr2, Н, определяем согласно [3, c.152] по формуле
где 20 - угол зацепления
4.18 Допускаемые напряжения определяем согласно [5, c.43] по формуле
где Flimbi- значение предела выносливости при отнулевом цикле изгиба, МПа, определяем согласно [5, c.44] по формуле Flimbi= 1,8 НВi, (3.25) Значение предела выносливости при отнулевом цикле изгиба для шестерни, Flimb3, МПа, определяем по формуле [3.25] Flimb3 = 1,8 250 = 450 МПа Значение предела выносливости при отнулевом цикле изгиба для зубчатого колеса, Flimb4, МПа, определяем по формуле [3.25 Flimb4 = 1,8 220 = 396 МПа
формуле
где
зубчатого колеса,
Допускаемые напряжения для шестерни
Допускаемые напряжения для зубчатого колеса
4.19 Находим отношения согласно [5, c.295] по формуле
где YFi- коэффициент, учитывающий форму зуба , который следует выбирать по эквивалентному числу зубьев Эквивалентное число зубьев определяем согласно [5, c.46] по формуле
Эквивалентное число зубьев шестерни zv3 определяем по формуле [3.28]
Эквивалентное число зубьев зубчатого колеса zv4 определяем по формуле [3.28]
Коэффициент, учитывающий форму зуба шестерни, YF1 = 3,63 [5, с.42] Коэффициент, учитывающий форму зуба зубчатого колеса, YF2 = 3,6 [5, с.42] Находим отношения для шестерни по формуле (3.28)
Находим отношения для зубчатого колеса по формуле [3.28]
Дальнейший расчет ведем для зубьев колеса, для которого найденное отношение меньше. 4.20 Зубья на выносливость по напряжениям изгиба s F, МПа, согласно ГОСТ 21354-75 проверяем по формуле
где KF- коэффициент нагрузки определяем согласно [5, c.42] по формуле KF= KFKFv, (3.30) где KF- коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба, KF= 1,07 [5, c.43]; KFv- коэффициент, учитывающий динамическое действие нагрузки, KFv= 1,1 [5, с.43] KF= 1,071,1 =1,18 Yb- коэффициент для компенсации погрешностей определяем со- гласно [5, c.46] по формуле
KF- коэффициент, KF= 0,92 [5, c.47]
условие F< [F]4 выполнено 5. Расчет валов5.1 Диаметр выходного конца вала редуктора dкi, мм, по расчету на кручение определяем согласно [1.c.161] по формуле
где [t]к - допускаемое напряжение на кручение, МПа Диаметр выходного конца ведущего вала dв1, мм, при []к = 25 МПа определяем по формуле (5.1)
принимаем: dв1 = 25 мм Диаметр подшипниковых шеек dп1 = 30 мм Диаметр подшипниковых шеек промежуточного вала dп2, мм, при []к = 35 МПа определяем по формуле (5.1)
Диаметр подшипниковых шеек dп2 = 35 мм Диаметр вала под зубчатым колесом dк2 = 40 мм Диаметр выходного конца ведомого вала dв3, мм, при []к = 35 МПа определяем по формуле (5.1)
принимаем: dв2 = 55 мм Диаметр подшипниковых шеек dп2 = 60 мм Диаметр вала под зубчатым колесом dк2 = 65 мм 6. Конструктивные размеры передач 6.1 Диаметр ступицы dстi, мм, определяем согласно [1.c.233] по формуле dстi = 1,6 dвi, (6.1) Диаметр ступицы зубчатого колеса промежуточного вала dст1, мм, определяем по формуле (6.1) dст1 = 1,6 40 = 64 мм Диаметр ступицы зубчатого колеса ведомого вала dст2, мм, определяем по формуле (6.1) dст2 = 1,6 65 = 104 мм 6.2 Длину ступицы Lстi, мм, определяем согласно [1.c.233] по формуле Lстi = (1,2 1,5) dвi, (6.2) Длину ступицы зубчатого колеса промежуточного вала Lст1, мм, определяем по формуле (6.2) Lст1 = (1,2 1,5) 40 = 48 ¸ 60 мм принимаем Lст1 = 60 мм Длину ступицы зубчатого колеса ведомого вала Lст2, мм, определяем по формуле (6.2) Lст2 = (1,2 1,5) 65 = 78 ¸ 97,5 мм принимаем Lст2 = 160 мм по ширине венца зубчатого колеса. 6.3 Толщину обода зубчатого колеса промежуточного вала o1, мм, определяем согласно [1.c.233] по формуле o1 = (2,5 4) m, (6.3) o1 = (2,5 4) 2 = 5 ¸ 8 мм принимаем o1 = 8 мм 6.3 Толщину обода зубчатого колеса ведомого вала o2, мм, определяем согласно [1.c.233] по формуле o2 = (2,5 4) mn, (6.4) o2 = (2,5 4) 2 = 5 ¸ 8 мм приняли o = 8 мм 6.4 Толщину диска зубчатого колеса промежуточного вала C1, мм, определяем согласно [1.c.233] по формуле C1 = 0,3 b2, (6.5) C1 = 0,3 b2 = 0,3 40 = 12 мм 6.4 Толщину диска зубчатого колеса ведомого вала C2, мм, определяем согласно [1.c.233] по формуле C2 = 0,3 b4, (6.6) C2 = 0,3 b4 = 0,3 16 = 48 мм 7. Конструктивные размеры корпуса редуктора7.1 Толщину стенок корпуса редуктора , мм, определяем согласно [1.c.241] по формуле = 0,025 aw+ 3, (7.1) = 0,025 200 + 3 = 8 мм принимаем = 8 мм 7.2 Толщина стенок крышки редуктора 1, мм, определяем согласно [1.c.241] по формуле 1 = 0,02 aw+ 3, (7.2) 1 = 0,02 200 + 3 = 7 мм принимаем = 8 мм 7.3 Толщину фланцев верхнего пояса корпуса редуктора b, мм, определяем согласно [1.c.241] по формуле b = 1,5 , (7.3) b = 1,5 = 12 мм 7.4 Толщину фланцев нижнего пояса крышки редуктора b1, мм, определяем согласно [1.c.241] по формуле b1 = 1,5 1, (7.4) b1 = 1,5 = 12 мм 7.5 Толщину фланцев нижнего пояса корпуса редуктора p, мм, определяли согласно [1.c.241] по формуле p = 2,35 , (7.5) p = 2,35 = 19 мм 7.6 Диаметр фундаментных болтов d1, мм, определяем согласно [1.c.241] по формуле d1 = (0,03 0,036) aw+ 12, (7.6) d1 = (0,03 0,036) 200 + 12 = 18 ¸ 19,2 мм принимаем болты с резьбой M20 7.7 Диаметр болтов, крепящих крышку к корпусу редуктора у подшипников d2, мм, определяем согласно [1.c.241] по формуле d2 = (0,7 0,75) d1; (7.7) d2 = (0,7 0,75) 20 = 14 ¸15 мм принимаем болты с резьбой M16 7.8 Диаметр соединяющих крышку с корпусом d3, мм, определяем согласно [1.c.241] по формуле d3 = (0,5 0,6) d1, (7.8) d3 = (0,5 0,6) 20 = 10 ¸12 мм принимаем болты с резьбой M12 8. Проверка прочности шпоночных соединенийВыбираем шпонки призматические со скругленными торцами. Размеры сечений по ГОСТ 23369-78. Материал шпонок: сталь 45, нормализованная. 8.1 Ведущий вал При диаметре шейки вала в = 25 мм выбираем шпонку сечением b = 8 мм, h = 7 мм, глубина паза t1 = 4 мм, принимаем длину шпонки L = 40 мм Проверяем выбранную шпонку на смятие, при допускаемом напряжении []см = 110...190 МПа [3,с.77] по формуле
Условие см []см выполнено 8.2 Промежуточный вал При диаметре шейки вала в = 40 мм, выбираем шпонку сечением b=12мм, h = 8 мм, глубина паза t1 = 5 мм, приняли длину шпонки L = 50 мм Проверяем выбранную шпонку на смятие, при допускаемом напряжении []см = 110...190 МПа [3,с.77] по формуле
Условие см []см выполнено 8.3 Ведомый вал При диаметре шейки вала в = 55 мм, выбираем шпонку сечением b = 16 мм, h = 10 мм, глубина паза t1 = 6 мм, приняли длину шпонки L = 80 мм Проверяем выбранную шпонку на смятие, при допускаемом напряжении []см = 110...190 МПа [3,с.77] по формуле
Условие см []см выполнено При диаметре шейки вала в = 65 мм, выбираем шпонку сечением b = 18 мм, h = 11 мм, глубина паза t1 = 7 мм, приняли длину шпонки L = 80 мм Проверяли выбранную шпонку на смятие, при допускаемом напряжении []см = 110...190 МПа [3.с.77] по формуле
Условие см []см выполнено 9. Первыйэтапкомпоновкиредуктора Компоновочный чертеж выполняем в одной проекции - разрез по осям валов при снятой крышке редуктора в масштабе 1:1. Проводим горизонтальную линию - ось ведущего вала, наметим положение оси промежуточного вала, при этом ось промежуточного вала проводим параллельно оси ведущего вала на расстоянии aw = 200 мм. Намечаем положение оси ведомого вала, при этом ось ведомого вала проводим параллельно оси промежуточного вала на расстоянии aw = 200 мм. Конструктивно упрощенно оформляем по найденным выше размерам шестерни и зубчатого колеса. Ступицы выполняем симметрично относительно зубчатого венца. Предварительно намечаем подшипники: - ведущий вал - dп1 = 30 мм, шариковые радиальные однорядные; - промежуточный вал - dп2 = 35 мм, шариковые радиальные однорядные; - ведомый вал - dп2 = 60 мм, шариковые радиальные однорядные. Данные о подшипниках выписываем из каталога ГОСТ 8338-75 и заносим в таблицу 9.1 Таблица 9.1 - Данные подшипников
Очерчиваем внутреннюю стенку корпуса: а) принимаем зазор от окружностей вершин зубьев шестерни и зубчатого колеса 8 мм, равной толщине стенки редуктора; б) принимаем зазор между торцом ступицы зубчатого колеса и внутренней стенкой корпуса 1,2d; в) глубину гнезда подшипника принимаем равной 40 мм, для размещения болта, соединяющего крышку редуктора с корпусом, принятого выше М16; г) толщину фланца крышки подшипника принимаем равной 8 мм, болты для крепления крышки подшипника принимаем равными М8; д) высота головки болта, крепящего крышку подшипника равна 5,5 мм, принимаем зазор между торцом крышки подшипника и ступицей звездочки цепной передачи равным 5 мм. Измерением устанавливаем расстояние l1 = 80мм, l2 = 240мм; l3 = 50 мм, l4 = 116мм, l5 = 125 мм; l6 = 55 мм, l7 = 120 мм; l8 = 180 мм; l9 = 145 мм 10 Расчет подшипниковВедущий вал Реакции опор в плоскости xz
проверка: Ft1 - Rx1 - Rx2 = 2003 - 345 - 1658 = 0 Реакции опор в плоскости yz
проверка: Fr1 + Fв - Ry1 - Ry2 = 729 + 961 - 1352 - 338 = 0 Суммарные реакции
Эквивалентную динамическую радиальную нагрузку наиболее нагруженной опоры Pэ1, Н, определяем согласно [1.c.212] по формуле Pэi= V Pri Kб KТ , (10.1) где V - коэффициент, учитывающий вращение колец подшипников, V = 1 [1.c.212] Kб - коэффициент нагрузки, Kб = 1 [1.с.214] KТ - температурный коэффициент, KТ = 1 [1.с.214] Pэ1 = 1 1691,8 1 1 = 1691,8 Н Расчетную долговечность выбранного подшипника L1, млн.об., определяем согласно [1.c.211] по формуле
Рис
Расчетную долговечность выбранного подшипника Lh1, ч, определяем согласно [1.c.211] по формуле
Условие Lh1 > Lh выполнено, подшипник пригоден. 10.2 Промежуточный вал Реакции опор в плоскости xz
проверка: Ft1 + Ft2 - Rx3 - Rx4 = 2003 + 7692 - 5050 - 4645 = 0 Реакции опор в плоскости yz
проверка: Fr2 -Fr1 - Ry3 - Ry4 = 3394 - 729 – 1928,5 – 736,5 = 0 Суммарные реакции
Эквивалентную динамическую радиальную нагрузку наиболее нагруженной опоры Pэ3, Н, определяем согласно по формуле [10.1] Pэ3 = 1 5405,5 1 1 = 5405,5 Н Расчетную долговечность выбранного подшипника L2, млн.об., определяем согласно [1.c.211] по формуле
Рисунок 3.2 Расчетная схема промежуточного вала Расчетную долговечность выбранного подшипника Lh2, ч, определяли согласно [1.c.211] по формуле
Условие Lh2 > Lh выполнено, подшипник пригоден. 10.3 Ведомый вал Реакции опор в плоскости xz
где Fм - радиальная сила, вызванная радиальным смещением муфты. Радиальную силу Fм, Н, зубчатой муфты определяем согласно [3, с.352 ] по формуле
где dм – делительный диаметр зубчатого зацепления муфты, dм = 75 мм
принимаем Fм = 6000 Н.
проверка: Ft2 + Fм - Rx5 - Rx6 = 7692 + 6000 – 1715 - 11977 = 0 Реакции опор в плоскости yz
проверка: Fr2 - Ry5 - Ry6 = 3394 - 2036 - 1358 = 0 Суммарные реакции
Рисунок 3.3 Расчетная схема ведомого вала Эквивалентную динамическую радиальную нагрузку наиболее нагруженной опоры Pэ6, Н, определяем по формуле [10.1] Pэ6 = 1 12053 1,3 1 = 15670 Н Расчетную долговечность выбранного подшипника L3, млн.об., определяем согласно [1.c.211] по формуле
Расчетную долговечность выбранного подшипника Lh1, ч, определяем по формуле [10.2]
Условие Lh3 > Lh выполнено, подшипник пригоден. 11 Уточненный расчет валовПринимаем, что нормальные напряжения изгиба изменяются по симметричному циклу, а касательные от кручения - по отнулевому (пульсирующему). 11.1 Ведущий вал Принимаем материал вала сталь 45, термообработка - нормализация, В = 570МПа Предел выносливости стали при симметричном цикле изгиба , МПа, определяем согласно [5,c.162] по формуле = 0,43 В, (11.1) = 0,43 570 = 245,1 МПа Предел выносливости стали при симметричном цикле касательных напряжений -1, МПа, определяем согласно [5,c.164] по формуле -1 = 0,58 (11.2) -1 = 0,58 245,1 = 142,16 МПа Сечение А - А. Концентрация напряжений обусловлена наличием шпоночной канавки. так как в этом сечении изгибающего момента нет, то рассчитываем только на кручение. Момент сопротивления кручению нетто сечения вала
где в - диаметр вала, мм; b - ширина шпоночной канавки, мм; t1 - глубина шпоночной канавки, мм
Амплитуду отнулевого цикла касательных напряжений при кручении вала v, МПа, определяем согласно [5,c.166] по формуле
Определяем коэффициент запаса прочности по касательным напряжениям
где k - эффективный коэффициент концентрации касательных напряже- ний, k = 1,9 [5,c.165]; масштабный фактор для касательных напряжений, = 0,8 [5,c.166]; - коэффициент, = 0,1 [5,c.166]
Сечение Б - Б. В этом сечении действуют максимальные крутящий и изгибающий моменты. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом. Находим значения коэффициентов:
Определяем изгибающий момент M, Нмм, в сечении M = Fв l1 = 961 80 = 76,88 103 Нмм Осевой момент сопротивления W, мм3, определяем согласно [5,c.165] по формуле
Амплитуду нормальных напр яжений
Полярный момент сопротивления
Амплитуду касательных напряжений
Определяем коэффициент запаса прочности по нормальным напряжениям
Коэффициент запаса прочности по касательным напряжениям
Результирующий коэффициент запаса прочности sопределяем согласно [5,c.162] по формуле
11.2 Промежуточный вал Принимаем материал вала сталь 45, термообработка - улучшение, В = 780МПа Предел выносливости стали при симметричном цикле изгиба , МПа, определяем по формуле (11.1) = 0,43 780 = 335,4 МПа Предел выносливости стали при симметричном цикле касательных напряжений -1, МПа, определяем по формуле (11.2) -1 = 0,58 335,4 = 194,53 МПа Сечение А - А. Концентрация напряжений обусловлена наличием шпоночной канавки. Определяем изгибающие моменты в сечении Mx = Rx3 L4 = 5050 116 = 585,77 103 Нмм Mу = Rу3 L4 = 1928,5 116 = 223,7 103 Нмм Суммарный изгибающий момент в сечении М, Нмм, определяем согласно [5,c.298] по формуле
Момент сопротивления кручению нетто сечения вала
Момент сопротивления изгибу нетто сечения вала
Амплитуду отнулевого цикла касательных напряжений при кручении вала
Амплитуду симметричного цикла нормальных напряжений при изгибе вала
Находим значения коэффициентов: k = 1,7; k = 1,8; = 0,73 [5,c.166]; = 0,85 [5,c.166]. Определяем коэффициент запаса прочности по касательным напряжениям по формуле (11.5)
Определяем коэффициент запаса прочности по нормальным напряжениям по формуле (11.10)
Результирующий коэффициент запаса прочности определяем по формуле (11.11)
11.3 Ведомый вал Принимаем материал вала сталь 45, термообработка - нормализация, В = 610 МПа Предел выносливости стали при симметричном цикле изгиба , МПа, определяем по формуле (11.1) = 0,43 610 = 262,3 МПа Предел выносливости стали при симметричном цикле касательных напряжений -1, МПа, определяем по формуле (11.2) -1 = 0,58 262,3 = 152,13 МПа Сечение А - А. Концентрация напряжений обусловлена наличием шпоночной канавки. так как в этом сечении изгибающего момента нет, то рассчитываем только на кручение. Момент сопротивления кручению нетто сечения вала определяем по формуле (11.3)
Амплитуду отнулевого цикла касательных напряжений при кручении вала определяем по формуле (11.4)
Находим значения коэффициентов: = 0,68 [5,c.166]; k = 1,5 [5,c.166]; Определяем коэффициент запаса прочности по касательным напряжениям по формуле (11.5)
Сечение Б - Б. В этом сечении действуют максимальные крутящий и изгибающий моменты. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом. Находим значения коэффициентов:
Определяем изгибающий момент M, Нмм, в сечении M = Fм l9 = 6000 145 = 870 103 Нмм Осевой момент сопротивления W, мм3, определяем по формуле [11.6]
Амплитуду нормальных напряжений
Полярный момент сопротивления
Амплитуду касательных напряжений
Определяем коэффициент запаса прочности по нормальным напряжениям
Коэффициент запаса прочности по касательным напряжениям
Результирующий коэффициент запаса прочности sопределяем по формуле [11.11]
Сечение В - В. Концентрация напряжений обусловлена наличием шпоночной канавки. Определяем изгибающие моменты в сечении Mx = Rx5 L7 = 1715 120 = 205,82 103 Нмм My = Ry5 L7 = 2036 120 = 244,37 103 Нмм Суммарный изгибающий момент в сечении определяем согласно по формуле (11.12)
Момент сопротивления кручению нетто сечения вала определяем по формуле (11.3)
Момент сопротивления изгибу нетто сечения вала определяем по формуле (11.13)
Амплитуду отнулевого цикла касательных напряжений при кручении вала определяем по формуле (11.4)
Амплитуду симметричного цикла нормальных напряжений при изгибе вала определяем по формуле (11.7)
Находим значения коэффициентов: k = 1.6 [5,c.166]; = 0,68 [5,c.166]; = 0,78 [5,c.166] Определяем коэффициент запаса прочности по касательным напряжениям по формуле (11.5)
Определяем коэффициент запаса прочности по нормальным напряжениям по формуле (11.10)
Результирующий коэффициент запаса прочности определяем по формуле (11.11)
12 Подбор и расчёт муфтыпривод редуктор передача шевронная Расчетный вращающий момент Tp, Н мм, определяем согласно [7,c.20] по формуле
где К1 - коэффициент, учитывающий степень ответственности передачи, К1 = 1 [7,с.20]; К2 - коэффициент, учитывающий условия работы, К2 = 1 [7,с.20]; К3 - коэффициент, углового смещения, К3 = 1 [7,с.21]
Подбираем муфту зубчатую с посадочным отверстием ∅55 типа 1 и номинальным крутящим моментом 1600 Н м. Муфта 1-1600-55 ГОСТ Р 50895-96. 13 Подбор смазки редуктораСмазывание зубчатого зацепления производится окунанием зубчатого колеса в масло, заливаемого внутрь корпуса до уровня, обеспечивающего погружение колеса примерно на высоту зуба. Объем масляной ванны V, л, определяем из расчета 0,5 0,8л на 1 кВт передаваемой мощности согласно [5,c.251] по формуле V = 0,5 Pтр, (13.1) V = 0,5 6,98 = 3,49 л По табл. 10.8. [5,с.253] устанавливаем вязкость 60 106 м2/с. По табл. 10.10. [5,с.253] принимаем масло индустриальное марки И-30А по ГОСТ 20799-75 Камеры подшипников заполняем пластичным смазочным материалом УТ-1 [5,с.203]. Литература1 Анурьев В.И. Справочник конструктора-машиностроителя: -4-е изд. Перераб. и доп. М., Машиностроение. 1974 - Т.2 -576с.: ил. 2 ГОСТ Подшипники качения: М., Издательство стандартов. 1989 - Ч.1 440с. ил. 3 Куклин Н.Г., Куклина Г.С. Детали машин: Учеб. для машиностроит. Спец. Техникумов. -4-е изд. Перераб. и доп. - М.: Высш. шк., 1987г. - 363с.: ил. 4 Решетов Д.Н. Детали машин. Учебник для вузов. Изд. 3-е, испр. и перераб. М., Машиностроение. 1975 - 656с.: ил. 5 Чернавский С.А., Боков К.Н., Чернин И.М. и др. Курсовое проектирование деталей машин: Учеб. Пособие для учащихся машиностроительных специальностей техникумов - 2-е изд. перераб. и доп. -М.; Машиностроение, - 1988г. - 416с.; ил. 6 Шейнблит А.Е. Курсовое проектирование деталей машин. Учеб. Пособие для техникумов. - М.: Высш. Шк., 1991. - 432с.: ил. 7. ГОСТ Р 50895-96. |
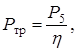 (1.2)
(1.2)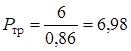 кВт
кВт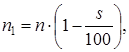 (1.3)
(1.3)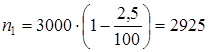 мин-1
мин-1 (1.5)
(1.5)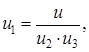 (1.6)
(1.6)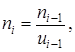 (1.7)
(1.7)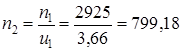 мин-1
мин-1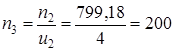 мин-1
мин-1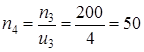 мин-1
мин-1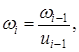 (1.8)
(1.8)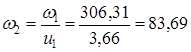 с-1
с-1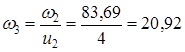 с-1
с-1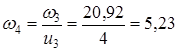 с-1
с-1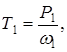 (1.9)
(1.9)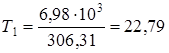 НЧм
НЧм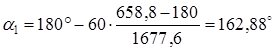
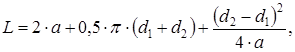 (2.5)
(2.5)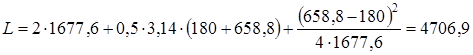 мм
мм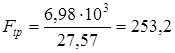 Н
Н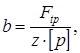 (2.12)
(2.12)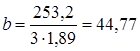 мм
мм МПа
МПа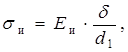 (2.17)
(2.17)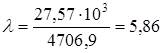
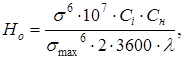 (2.21)
(2.21)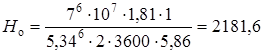
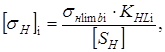 (3.2)
(3.2)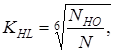 (3.3)
(3.3)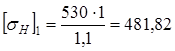 МПа
МПа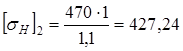 МПа
МПа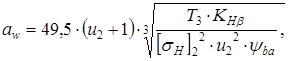 (3.6)
(3.6) мм
мм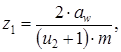 (3.8)
(3.8)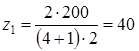
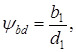 (3.15)
(3.15)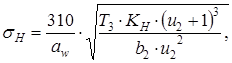 (3.18)
(3.18)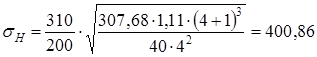 МПа
МПа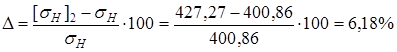
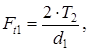 (3.19)
(3.19)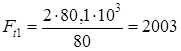 Н
Н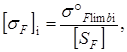 (3.21)
(3.21)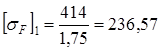 МПа
МПа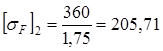 МПа
МПа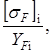 (3.23)
(3.23)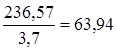
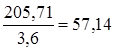
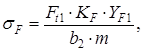 (3.24)
(3.24)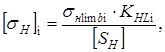 (3.2)
(3.2)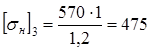 МПа
МПа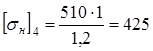 МПа
МПа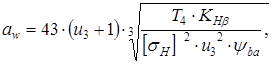 (3.8)
(3.8) мм
мм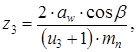 (3.10)
(3.10)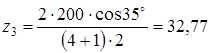
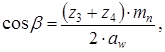 (3.12)
(3.12)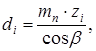 (3.13)
(3.13)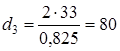 мм
мм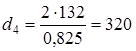 мм
мм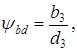 (3.18)
(3.18)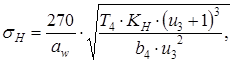 (3.21)
(3.21) МПа
МПа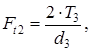 (3.22)
(3.22)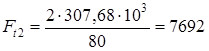 Н
Н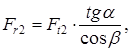 (3.23)
(3.23)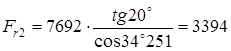 Н
Н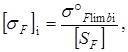 (3.24)
(3.24)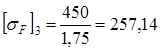 МПа
МПа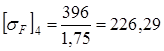 МПа
МПа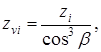 (3.28)
(3.28)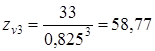
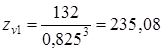
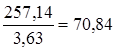
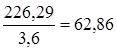
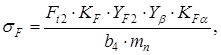 (3.29)
(3.29)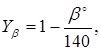 (3.32)
(3.32)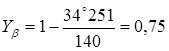
 (5.1)
(5.1)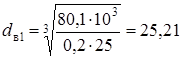 мм
мм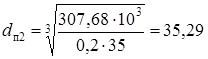 мм
мм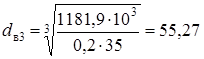 мм
мм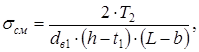 (8.1)
(8.1) МПа
МПа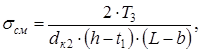 (8.2)
(8.2) МПа
МПа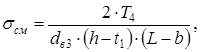 (8.3)
(8.3)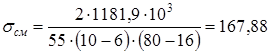 МПа
МПа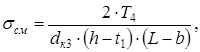 (8.4)
(8.4)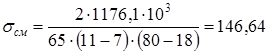 МПа
МПа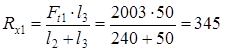 Н
Н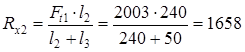 Н
Н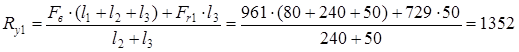 Н
Н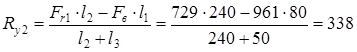 Н
Н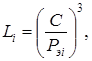 (10.2)
(10.2)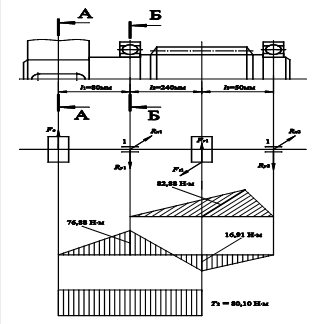
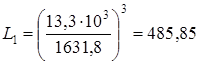 млн.об.
млн.об.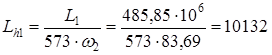 ч
ч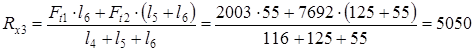 Н
Н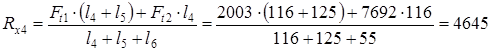 Н
Н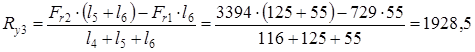 Н
Н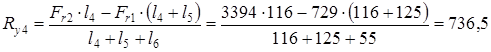 Н
Н млн.об.
млн.об.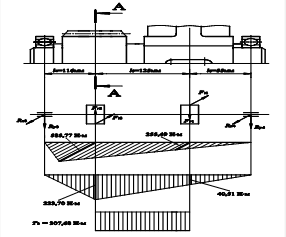
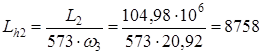 ч
ч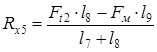 ,
,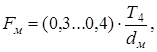 (10.3)
(10.3)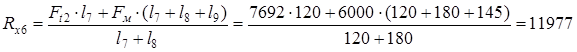 Н
Н Н
Н Н
Н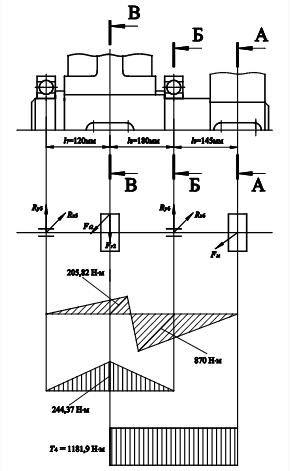
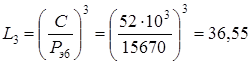 млн.об.
млн.об. ч
ч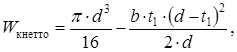 (11.3)
(11.3) мм3
мм3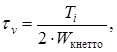 (11.4)
(11.4)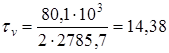 МПа
МПа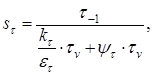 (11.5)
(11.5)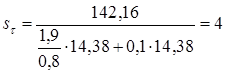
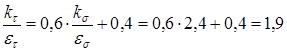 [5,c.166]
[5,c.166] (11.6)
(11.6)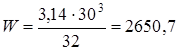 мм3
мм3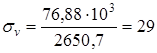 МПа
МПа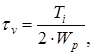 (11.9)
(11.9)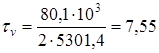 МПа
МПа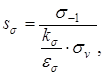 (11.10)
(11.10)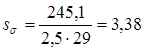
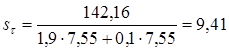
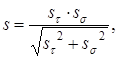 (11.11)
(11.11)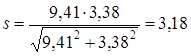
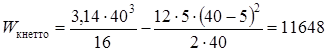 мм3
мм3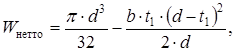 (11.13)
(11.13)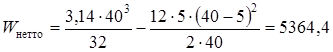 мм3
мм3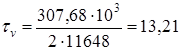 МПа
МПа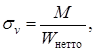 (11.14)
(11.14)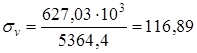 МПа
МПа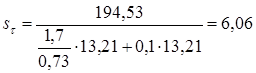
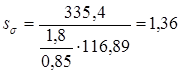
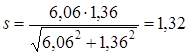
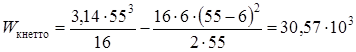 мм3
мм3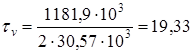 МПа
МПа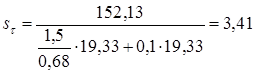
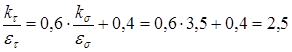 [5,c.166].
[5,c.166].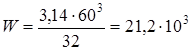 мм3
мм3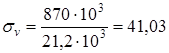 МПа
МПа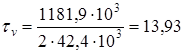 МПа
МПа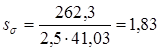
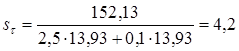
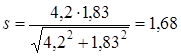
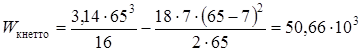 мм3
мм3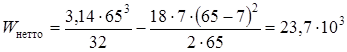 мм3
мм3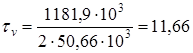 МПа
МПа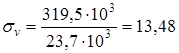 МПа
МПа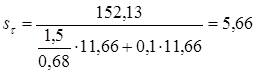
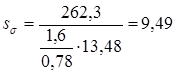
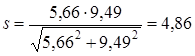
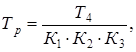 (12.1)
(12.1)