Курсовая работа: Проектирование и исследование механизмов компрессора
|
Название: Проектирование и исследование механизмов компрессора Раздел: Промышленность, производство Тип: курсовая работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Тульский Государственный университет Кафедра «Проектирование механизмов и деталей машин» ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту по ТММ: «Проектирование и исследование механизмов компрессора» Выполнил: студент гр. 620832 Решилин А.В. Консультировал: профессор Крюков В.А. Тула 2005 Содержание Введение 1 Структурный анализ и синтез стержневого механизма 1.1 Структурный анализ стержневого механизма 1.2 Структурныйсинтез рационального механизма 2 Кинематический анализ стержневого механизма 2.1 Построение планов положений механизма 2.2 Построение планов скоростей 2.3 Построение планов ускорений 3 Динамический анализ и синтез машинного агрегата 3.1 Динамическая модель машинного агрегата 3.2 Построение графика приведенных моментов сил сопротивления 3.3 Построение графика работ сил сопротивления 3.4 Построение графика движущих сил и определение движущего момента 3.5 Построение графика приращения кинетической энергии 3.6 Построение графика приведенного момента инерции 3.7 Построение диаграммы Виттенбауэра 3.8 Подбор маховика 3.9 Построение графика угловой скорости входного звена стержневого механизма 4 Кинематический расчет передаточного механизма 5 Геометрический синтез эвольвентной цилиндрической зубчатой передачи 5.1 Условия и ограничения синтеза 5.2 Выбор оптимального варианта передачи 5.3 Расчет геометрических параметров, качественных характеристик и контрольных размеров передачи 5.4 Построение картины зацепления 6 Синтез планетарной передачи 6.1 Условия синтеза 6.2 Синтез планетарной передачи 6.3 Построение плана скоростей и диаграммы угловых скоростей Список используемой литературы Введение Механизм компрессора состоит из стержневого механизма, передаточного механизма и исполнительного органа. Функциональная схема механизма показана на рисунке В.1. Передаточный механизм выполнен в виде последовательного соединения планетарной передачи и рядной зубчатой передачи. Стержневой механизм предназначен для преобразования вращательного движения кривошипа во возвратно–поступательного движения ползуна. Передаточный механизм предназначен для уменьшения угловой скорости и увеличения крутящего момента.
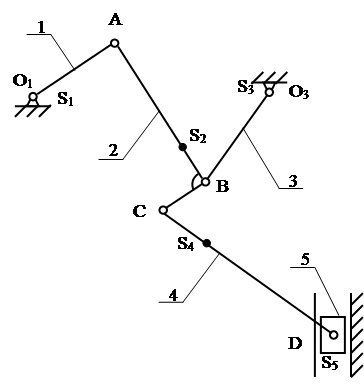
Рис. В.1. Функциональная схема машинного агрегата ЭД – электродвигатель ПМ – передаточный механизм СМ – стержневой механизм ИО – исполнительный орган 1. Структурный анализ и синтез стержневого механизма 1.1 Структурный анализ стержневого механизма проектирование механизм компрессор Стержневой механизм предназначен для преобразования вращательного движения в возвратно-поступательное. Стержневой механизм является плоским и состоит из пяти подвижных звеньев и семи кинематических пар. Структурная схема механизма приведена на рисунке 1.1, характеристики звеньев в таблице 1.1., характеристики кинематических пар в таблице 1.2
Рис.1.1 Структурная схема стержневого механизма В состав механизма входят 5 подвижных звеньев, одно неподвижное звено (стойка) и 7 КП. Характеристики звеньев приведены в таблице 1.1, а характеристики КП в таблице 1.2. Таблица 1.1 Характеристика звеньев
Таблица 1.2 Характеристика кинематических пар
Определим число степеней свободы механизма по формуле Чебышева:
где n – число подвижных звеньев; pн – число низших кинематических пар; pв – число высших кинематических пар.
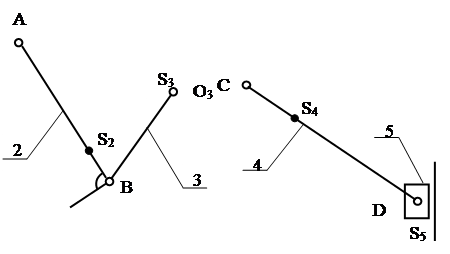
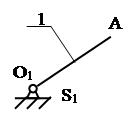
Разбиваем механизм на группы Ассура. Структурные схемы группы приведены на рисунке1.2.
Рис.1.2. Структурные группы Ассура Т.к. в механизм входят группы только второго класса, то весь механизм относится ко второму классу. 1.2 Структурный синтез рационального механизма Определим число избыточных связей стержневого механизма по формуле Сомова-Малышева:
где р5 – число кинематических пар 5 класса; р4 – число кинематических пар 4 класса; р3 – число кинематических пар 3 класса; р2 – число кинематических пар 2 класса; р1 – число кинематических пар 1 класса;
Для устранения избыточных связей понижаем класс кинематических пар. Характеристика кинематических пар рационального механизма приведена в таблице 1.3. Таблица 1.3 Характеристика кинематических пар рационального механизма
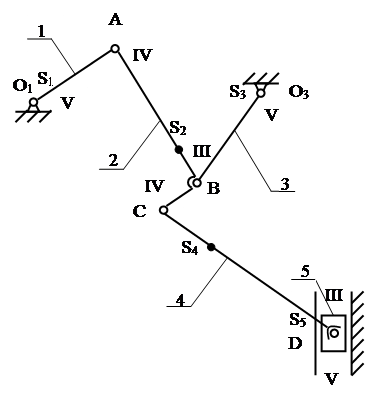
Структурная схема синтезированного рационального механизма приведена на рисунке 1.3.
Рис. 1.3. Структурная схема рационального механизма Для проверки определяем число степеней свободы синтезированного механизма.
2. Кинематический анализ стержневого механизма 2.1 Построение планов положения механизма Рассчитываем длины отрезков, изображающих звенья механизма на чертеже.
Для построения планов положений выбираем масштабный коэффициент Строим план положений механизма: 1. Наносим на чертеже точки, соответствующие неподвижным КП и линию по которой движется ползун. 2. Проводим окружность с центром O1 и радиусом O1A. 3. Разбиваем окружность на 12 равных частей с интервалом 30о и пронумеровываем их в направлении угловой скорости, так чтобы крайнему положению поршня соответствовала точка „0”. 4. Методом засечек рисуем планы положений звеньев для всех 12 положений на окружности. 2.2 Построение плана скоростей Метод планов скоростей относится к графическому методу кинематики и позволяет определить скорости точек и угловых ускорений звеньев. Рассчитываем угловую скорость кривошипа:
Определяем скорость точки А кривошипа 1, совершающего вращательное движение
Принимаем длину масштабного отрезка, изображающего скорость точки А ра= 60 мм и рассчитываем масштабный коэффициент плана скоростей
Принимаем Пересчитываем значение масштабного отрезка
Находим скорость точки B: VB=VA+VBAгде, VBA – относительная скорость точки В, направленная перпендикулярно АВ; VB– абсолютная скорость точки В, направленная перпендикулярно ВО3. Решаем это уравнение графически. Положение точки C на плане скоростей находим из условия подобия одноименных фигур планов скоростей и планов механизма. Находим скорость точки D: VD=VC+VDCгде, VDC – относительная скорость точки D, направленная перпендикулярно CD VD – абсолютная скорость точки D, направленная вертикально. Решаем это уравнение графически. Рассчитываем абсолютные скорости точек:
Относительные скорости:
Угловые скорости звеньев:
Результаты расчетов скоростей заносим в таблицу 2.1. Таблица 2.1 Скорости точек и угловые скорости звеньев
2.3 Построение планов ускорений Определяем ускорение точки а кривошипа 1, совершающего вращательное движение:
Принимаем длину масштабного отрезка, изображающего ускорение точки А
Принимаем Пересчитываем значение масштабного отрезка:
Ускорение точки В считается по формулам:
Решаем это уравнение графически. Используя условие подобия одноименных фигур плана ускорений и плана механизма находим положение точки C на плане ускорений. Ускорение точки в считается по формуле:
Решаем это уравнение графически. Рассчитываем ускорения:
Рассчитываем угловые ускорения звеньев:
Полученные данные заносим в таблицу 2.2. Таблица 2.2 Ускорения точек и угловые ускорения звеньев
3 . Динамический анализ и синтез машинного агрегата 3.1 Динамическая модель машинного агрегата Основным условием синтеза машинного агрегата является обеспечение заданной неравномерности движения Конструктивно эта задача решается с помощью установки маховика. В результате решения задачи синтеза определяется: 1- необходимый момент инерции маховика; 2- размеры маховика; 3- место установки маховика. Для упрощения решения задач синтеза механизм заменяется его расчетной динамической моделью (рис.3.1.). Эта модель представляет собой твердое тело, обладающее некоторым моментом инерции
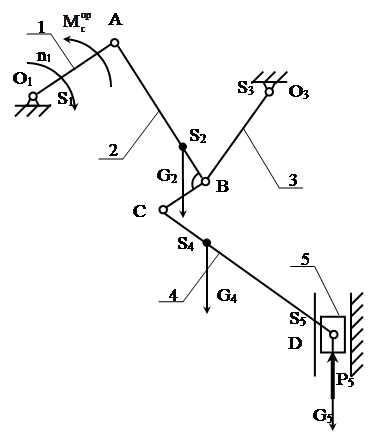
Рис. 3.1. Динамическая модель машинного агрегата 3.2 Построение графика приведенного момента сил сопротивления Схема механизма с приложенными к ней силами показана на рисунке 3.2.
Рис.3.2 Схема механизма с приложенными силами На звенья механизма действуют следующие силы: 1. Силы тяжести звеньев
2. Момент сил сопротивления. Приведенный момент сил сопротивления рассчитываем по формуле:
углы Индикаторная диаграмма, показывающая давление газов в цилиндре изображена на рисунке 3.3.
Рис. 3.3 Индикаторная диаграмма Исходные данные для расчета и значения приведенного момента сил сопротивления заносим в таблицу 3.1. Таблица 3.1 Расчет приведенного момента сил сопротивления
По таблице строим график зависимости принимаем Ординаты графика рассчитываем по формуле:
3.3 Построение графика работ сил сопротивления. Работа сил сопротивления определяется как интеграл от момента сил сопротивления:
Интегрирование выполняется графически: 1. Разбиваем график функции на равные участки; 2. Находим значение функции в середине каждого участка; 3. Проецируем полученные точки на ось ординат; 4. Выбираем полюс интегрирования р и соединяем его с точками на оси ординат; 5. Из нулевой точки графика работ луч 1, из его конца луч 2 и т.д. Масштабный коэффициент работ:
h – полюсное расстояние интегрирования h=45,8 мм. 3.4 Построение графика движущих сил и определение движущего момента При построении графика движущих сил принимаем следующие допущения: 1. Момент движущих сил постоянный Мдв=const; 2. Машина работает в режиме установившегося двигателя, следовательно за цикл Адв=Ас. График Адв строим, соединяя начало и конец графика Ас. Момент сил сопротивления определяем с помощью графика, дифференцируя график Ас( Мощность двигателя рассчитывается по формуле:
3.5 Построение графика приращения кинетической энергии Приращение кинетической энергии вычисляется по формуле:
Вычитание производим графически.
3.6 Построение графика приведенного момента инерции
Исходные данные для расчета и результаты расчетазаносим в таблицу 3.2. Таблица 3.2 Расчет приведенного момента инерции
Выбираем масштабный коэффициент:
Рассчитываем ординаты графика:
и строим график 3.7 Построение диаграммы Виттенбауэра Для построения диаграммы Виттенбауэра Рассчитываем углы наклона касательных в диаграмме Виттенбауэра.
Проводим под углами Рассчитываем начальную кинетическую энергию и приведенный момент инерции:
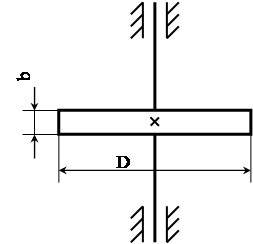
3.8 Подбор маховика Согласно заданию маховик установлен на валу кривошипа. Маховик выполняем в виде стального диска.
Рис. 3.4 Эскиз маховика Ширину маховика принимаем равной b=0,12 м. Диаметр маховика рассчитываем по формуле:
3.9 Построение графика угловой скорости входного звена стержневого механизма Угловая скорость:
Расчет угловых скоростей заносим в таблицу 3.3. Таблица 3.3 Расчет угловых скоростей
Определив значения угловых скоростей, строим график в масштабе.
Средняя угловая скорость:
Расчетное значение коэффициента неравномерности:
Погрешность:
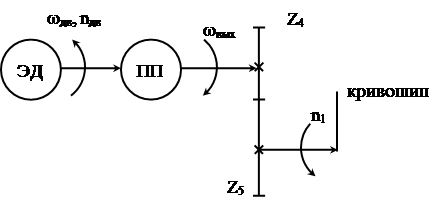
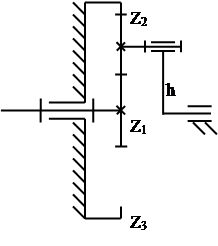
Ошибка не превышает предельно допустимое значение – 10%. 4. Кинематический расчет передаточного механизма Передаточный механизм предназначен для уменьшения угловой скорости и увеличения крутящего момента. Передаточный механизм состоит из соединенных последовательно планетарной зубчатой передачи Z1, Z2, Z3, h и рядовой зубчатой передачи Z4, Z5. Структурная схема передаточного механизма приведена на рисунке 4.1.
Рис.4.1. Структурная схема передаточного механизма Определяем общее передаточное отношение:
С другой стороны общее передаточное отношение равно:
Тогда передаточное отношение планетарной передачи:
Угловая скорость на входе планетарного механизма:
Угловая скорость на выходе планетарного механизма:
5. Геометрический синтез эвольвентной зубчатой передачи 5.1 Условия и ограничения синтеза Задачей геометрического синтеза зубчатой передачи является создание передачи, удовлетворяющей всем основным и дополнительным условиям синтеза и имеющей заданного значения качественных показателей. Основные параметры зубчатой передачи: 1. Числа зубьев зубчатых колес 2. Угол наклона линии зуба 3. коэффициент высоты головки зуба 4. коэффициент радиального зазора 5. Угол профиля нормального исходного контура 6. Коэффициенты смещения шестерни и зубчатого колеса Основные условия синтеза: 1. Получения заданного передаточного отношения:
2. Получение постоянного передаточного отношения
Дополнительные условия синтеза: 1. Отсутствие подрезания зубьев; 2. Отсутствие интерференции зубьев; 3. Обеспечение непрерывности зацепления 4. Отсутствие заострения зубьев
Качественные показатели зацепления: 1. Коэффициент перекрытия 2. Угол зацепления 3. Коэффициент удельного давления 4. Коэффициенты удельного скольжения 5.2 Выбор оптимального варианта передачи Принимаем Проверяем с помощью программы GEAR выполнение дополнительных условий синтеза и рассчитываем значения качественных показателей. Результаты расчетов заносим в таблицу 5.1. По результатам расчетов строим области дополнительных значений коэффициента смещения Выбираем вариант передачи 5.3 Расчет геометрических параметров, качественных характеристик и контрольных размеров передачи Расчет выбранного варианта зубчатой передачи выполняем с помощью компьютера. Результаты расчетов заносим в таблицу 5.2. Диаметры основных окружностей:
5.4 Построение картины зацепления Для построения картины зацепления выбираем масштабный коэффициент Таблица 5.3 Размеры для построения зубчатых колес
Порядок построения картины зацепления: 1. Проводим межосевую линию и отмечаем центры зубчатых колес. 2. Строим окружности впадин, основную, делительную, начальную, вспомогательную и вершин. 3. По точкам строим профиль зубьев. 4. Рассчитываем радиус переходной кривой и строим её:
5. Строим 5–7 зубьев для каждого зубчатого колеса. 6. Строим линию зацепления и измеряем угол зацепления. 7. Выделяем активный участок зацепления. 8. Строим контрольные размеры, измеряем их и результаты измерения заносим в таблицу. Вывод о точности изготовления зубчатых колес:
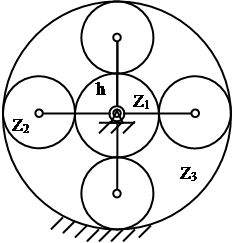
6. Синтез планетарной передачи 6.1 Условие синтеза Структурная схема планетарной передачи приведена на рисунке 6.1.
Рис. 6.1 Структурная схема планетарной передачи Основным условием синтеза планетарной передачи является обеспечение заданного передаточного отношения
Дополнительное условие синтеза: 1. Условие соосности 2. Условие соседства 3. Условие сборки 6.2 Синтез планетарной передачи Принимаем z1=19. Из основного условия синтеза находим z3:
Принимаем z3=45. Рассчитываем фактическое передаточное отношение:
Ошибка воспроизведения передаточного отношения:
Из условия соосности определяем z2:
Принимаем число сателлитов k=4. Проверяем выполнение условия соседства:
Проверяем выполнение условия сборки:
6.3 Построение плана скоростей и диаграммы угловых скоростей Рассчитываем делительные диаметры зубчатых колес:
Выбираем масштабный коэффициент Скорость точки А колеса z1:
Выбираем масштабный коэффициент скорости
соответствующий скорости точки А. Соединяя точи a и О1 получаем линию распределения скоростей колеса z1. Соединяя точки р и a получаем линию распределения скоростей точек сателлита. Строим отрезок О2о2, изображающий скорость точки О2. Соединяя точки о2 и О1 получаем линию распределения скоростей водила. Пользуясь углами По диаграмме угловых скоростей рассчитываем передаточное отношение.
Ошибка составляет 2,08%. Список используемой литературы 1. Синтез механизмов с низшими КП. Методические указания по выполнению курсового проекта для студентов машиностроительных специальностей дневного обучения. Тула, 1990.–38с. 2. Синтез механизмов с высшими КП. Методические указания по выполнению курсового проекта для студентов машиностроительных специальностей дневного обучения. Тула, 1991.–68с. 3. Кореняко А.С. и др. Курсовое проектирование по теории механизмов и машин. – Киев: Выща школа, 1970. – 332с. 4. Попов С.А. и др. Курсовое проектирование по теории механизмов и машин. – М.: Высш. шк., 1998. – 351с. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

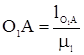 ;
; 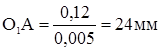 ;
;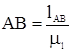 ;
;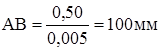 ;
; ;
; 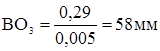 ;
;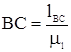 ;
;  ;
;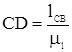 ;
; 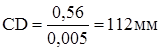 ;
;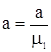 ;
; 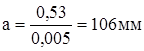 ;
;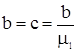 ;
; 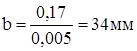 .
.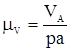 =
=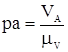 =
=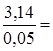 62,8мм.
62,8мм.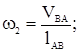 ;
; ;
;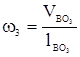 .
.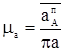
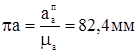 .
. ,
,  ;
;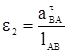 ;
;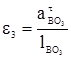 ;
;

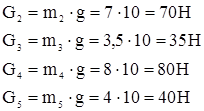
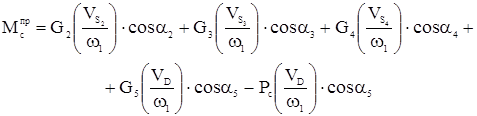
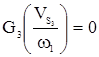 , т.к.
, т.к. 
 ;
;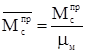 ;
; ;
;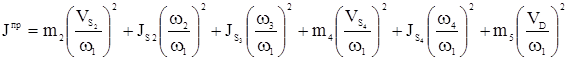 ;
;
 ;
;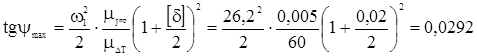 ;
;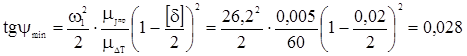 ;
;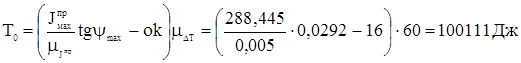 ;
;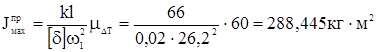
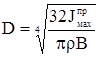 где,
где,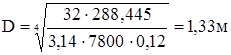
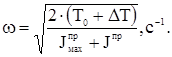
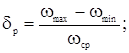
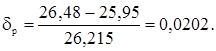
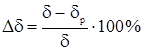
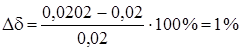
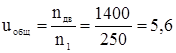

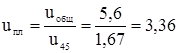
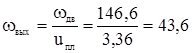
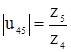 ;
; ;
; 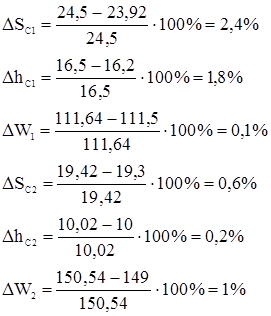
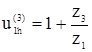 ;
;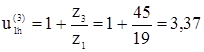

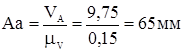 ;
;