КОНТРОЛЬНАЯ РАБОТА
«ПРЕОБРАЗОВАНИЕ ЭНЕРГИИ В ЭЛЕКТРИЧЕСКИХ МАШИНАХ ПОСТОЯННОГО ТОКА»
Задача 1.
По следующим параметрам обмотки якоря машины постоянного тока: число пар полюсов р
, число эффективных проводников N
, число витков секции wc
, число секций в катушке ис
, вычертить развернутую схему неперекрещивающейся простой петлевой обмотки, показать полюсы, расставить щетки.
Таблица 1.
Решение
Произведем расчет параметров схемы обмотки якоря.
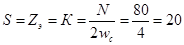 , ,
где  – число секций в обмотке якоря, – число секций в обмотке якоря,
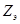 – число элементарных пазов, – число элементарных пазов,
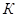 – число коллекторных пластин. – число коллекторных пластин.
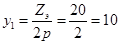 – первый частичный шаг обмотки по якорю (измеряется в элементарных пазах).
– первый частичный шаг обмотки по якорю (измеряется в элементарных пазах).
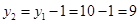 - второй частичный шаг обмотки по якорю (измеряется в элементарных пазах). - второй частичный шаг обмотки по якорю (измеряется в элементарных пазах).
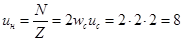 – число эффективных проводников в пазу, – число эффективных проводников в пазу,
где 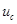 – число секций в катушке. – число секций в катушке.
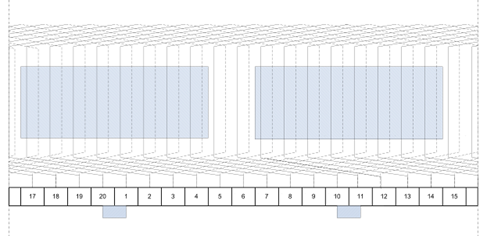
Рис. 1. Развернутая схема неперекрещивающейся петлевой обмотки
Задача 2
.
Генератор постоянного тока мощностью Рн
имеет кпд h
, активное сопротивление цепи якоря Ra
, сумма механических, магнитных и добавочных потерь составляет D
Р0
, %
от номинальной мощности, потери в цепи параллельного возбуждения D
Рв
. Определить ток обмотки якоря.
Таблица 2.
| №
|
Рн
,
кВт
|
h
,
%
|
Ra
,
Ом
|
D
Р0
, %
|
D
Рв
,
Вт
|
| 7 |
30 |
85,6 |
0,12 |
4,2 |
480 |
Решение
КПД двигателя постоянного тока определяется соотношением полезной мощности на валу 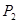 к мощности к мощности 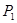 , потребляемой из сети: , потребляемой из сети:
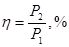 , ,
где 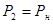 - механическая мощность на валу двигателя, - механическая мощность на валу двигателя,
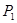 – мощность потребляемой двигателем из питающей сети энергии. – мощность потребляемой двигателем из питающей сети энергии.
Мощность 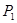 можно представить в виде суммы мощностей: можно представить в виде суммы мощностей:
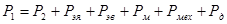 , Вт, , Вт,
где 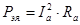 – электрические потери мощности в цепи якоря, – электрические потери мощности в цепи якоря,
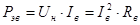 – электрические потери мощности в цепи возбуждения, – электрические потери мощности в цепи возбуждения,
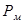 – потери мощности на гистерезис и вихревые токи в магнитопроводе (магнитные потери), – потери мощности на гистерезис и вихревые токи в магнитопроводе (магнитные потери),
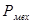 – механические потери, – механические потери,
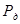 – добавочные потери. – добавочные потери.
По условию задачи сумма магнитных, механических и добавочных потерь известна:
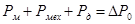 , %. , %.
По условию задачи потери в цепи параллельного возбуждения нам известны: 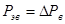 . .
Учитывая это, формулу КПД можно записать в следующем виде:
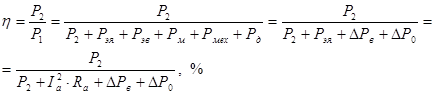
Следовательно, окончательно формула КПД имеет вид:
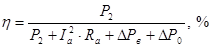 . .
Выразим из этой формулы 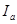 : :
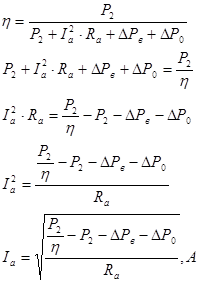
Следовательно, окончательно формула тока обмотки якоря 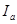 имеет вид: имеет вид:
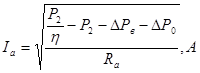
Вычислим значение 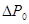 : :
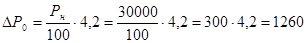 (Вт). (Вт).
Подставляем в числовые значения и вычисляем 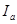 : :

Задача 3
Генератор постоянного тока с параллельным возбуждением имеет следующие данные: номинальную мощность Рн
, номинальное напряжение U
н
, сопротивление цепи якоря Ra
, сопротивление цепи возбуждения R
в
. Определить КПД генератора, если сумма механических, магнитных и добавочных потерь составляет D
Р0
, %
от номинальной мощности.
Таблица 3.
| №
|
Рн
,
кВт
|
U
н
,
В
|
Ra
,
Ом
|
R
в
,
Ом
|
D
Р0
,
%
|
| 7 |
22 |
320 |
0,4 |
210 |
4 |
Решение
КПД двигателя постоянного тока определяется соотношением полезной мощности на валу 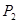 к мощности к мощности 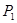 , потребляемой из сети: , потребляемой из сети:
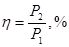 , ,
где 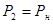 - механическая мощность на валу двигателя, - механическая мощность на валу двигателя,
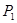 – мощность потребляемой двигателем из питающей сети энергии. – мощность потребляемой двигателем из питающей сети энергии.
Мощность 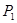 можно представить в виде суммы мощностей: можно представить в виде суммы мощностей:
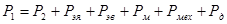 , Вт, , Вт,
где 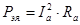 – электрические потери мощности в цепи якоря, – электрические потери мощности в цепи якоря,
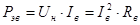 – электрические потери мощности в цепи возбуждения, – электрические потери мощности в цепи возбуждения,
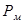 – потери мощности на гистерезис и вихревые токи в магнитопроводе (магнитные потери), – потери мощности на гистерезис и вихревые токи в магнитопроводе (магнитные потери),
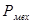 – механические потери, – механические потери,
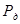 – добавочные потери. – добавочные потери.
По условию задачи сумма магнитных, механических и добавочных потерь известна:
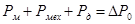 , %. , %.
Учитывая это, формулу КПД можно записать в следующем виде:
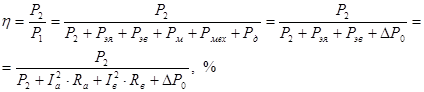
Известно, что 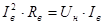 . Выразим из этого равенства . Выразим из этого равенства 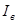 : :
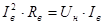
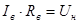
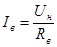 , А. , А.
Из равенства 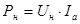 выразим выразим 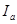 : :
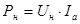
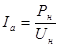 , А. , А.
Подставляем полученные выражения в формулу КПД двигателя:

Следовательно, окончательно формула КПД имеет вид:
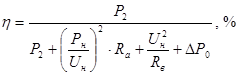 . .
Вычислим значение 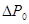 : :
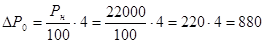 (Вт). (Вт).
Подставляем в числовые значения и вычисляем КПД генератора постоянного тока:
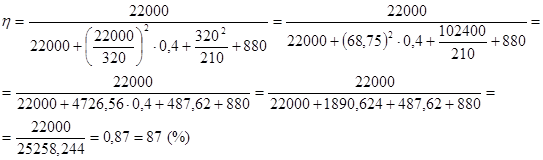
Задача 4
Полезная механическая мощность двигателя постоянного тока Рн
, номинальное напряжение U
н
, номинальный ток I
н
. Определить КПД, номинальный вращающий момент и сумму потерь двигателя, если номинальная частота вращения n
н
.
Таблица 4.
| №
|
Рн
, кВт
|
U
н
, В
|
I
н
, А
|
n
н
, об/мин
|
| 7 |
2,5 |
220 |
12,3 |
1100 |
Решение
1. КПД двигателя постоянного тока
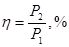
где 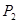 - механическая мощность на валу двигателя, - механическая мощность на валу двигателя,
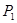 – мощность потребляемой двигателем из питающей сети энергии: – мощность потребляемой двигателем из питающей сети энергии:
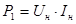 , Вт. , Вт.
При работе двигателя в номинальном режиме 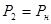 , Вт. , Вт.
Учитывая это, формулу для расчета КПД двигателя можно записать в следующем виде:
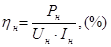 . .
Подставим числовые значения и рассчитаем 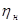 : :
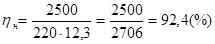 . .
2. Номинальный вращающий момент
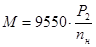 , Н М , Н М
где 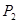 - механическая мощность на валу двигателя, - механическая мощность на валу двигателя,
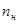 - номинальная частота вращения. - номинальная частота вращения.
В номинальном режиме работы 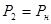 , Вт. Учитывая это, запишем формулу номинального вращающего момента в следующем виде: , Вт. Учитывая это, запишем формулу номинального вращающего момента в следующем виде:
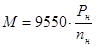 , Н М. , Н М.
Подставляем числовые значения:
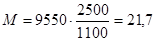 , кН М. , кН М.
3. Сумма потерь двигателя
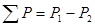 , Вт. , Вт.
где 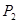 - механическая мощность на валу двигателя, - механическая мощность на валу двигателя,
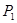 – мощность потребляемой двигателем из питающей сети энергии: – мощность потребляемой двигателем из питающей сети энергии:
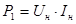 , Вт. , Вт.
При работе двигателя в номинальном режиме 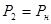 , Вт. , Вт.
С учетом этого, формула для расчета суммы потерь двигателя запишется в следующем виде:
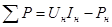 , Вт. , Вт.
Подставляем числовые значения:
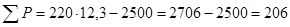 (Вт). (Вт).
схема обмотка генератор двигатель
Задача 5
Двигатель постоянного тока смешанного возбуждения при номинальном напряжении U
н
потребляет из сети ток I
а
и ток возбуждения I
в
. Сопротивление обмотки якоря Ra
, сопротивление сериесной обмотки R
с
, сопротивление дополнительных полюсов R
д
, падение напряжения на щетках D
U
щ
, кпд h
. Определить сумму механических, магнитных и добавочных потерь, потребляемую и номинальную полезную мощность двигателя.
Таблица 5.
| №
|
U
н
, В
|
I
а
, А
|
I
в
, А
|
Ra
, Ом
|
R
с
, Ом
|
R
д
, Ом
|
D
U
щ
, В
|
h
, %
|
| 7 |
220 |
468 |
4,62 |
0,00875 |
0,0007 |
0,0042 |
1,8 |
87,5 |
Решение
1. Номинальная полезная мощность двигателя
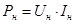 , Вт, , Вт,
где 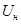 – номинальное напряжение, – номинальное напряжение,
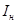 – номинальный ток. – номинальный ток.
Номинальный ток можно найти по формуле:
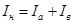 , А, , А,
где 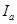 – потребляемый из сети ток, – потребляемый из сети ток,
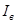 – ток возбуждения. – ток возбуждения.
Следовательно, формулу полезной мощности можно записать в следующем виде:
 , А. , А.
Подставляем числовые значения:
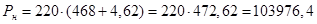 (Вт) (Вт)
2. Потребляемая мощность двигателя
Потребляемую мощность двигателя можно найти с помощью формулы КПД двигателя:
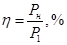
где 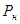 - механическая мощность на валу двигателя, - механическая мощность на валу двигателя,
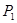 – мощность потребляемой двигателем из питающей сети энергии. – мощность потребляемой двигателем из питающей сети энергии.
Тогда формула для вычисления потребляемой мощности запишется следующем виде:
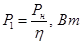
Подставляем числовые значения и вычисляем значение потребляемой мощности:
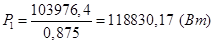
3.
Сумма механических, магнитных и добавочных потерь
Сумму механических, магнитных и добавочных потерь можно найти с помощью формулы потребляемой мощности:
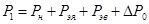 , Вт, , Вт,
где 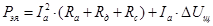 – электрические потери мощности в цепи якоря, – электрические потери мощности в цепи якоря,
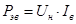 – электрические потери мощности в цепи возбуждения, – электрические потери мощности в цепи возбуждения,
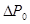 – сумма механических, магнитных и добавочных потерь. – сумма механических, магнитных и добавочных потерь.
Выражаем сумму механических, магнитных и добавочных потерь из формулы потребляемой мощности:
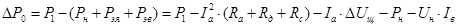 , Вт. , Вт.
Подставляем числовые значения:
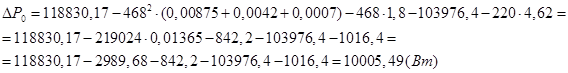
Задача 6.
Генератор независимого возбуждения при номинальной частоте вращения 1460 об/мин имеет характеристику холостого хода, приведенную в табл. 6. Сопротивление цепи возбуждения R
в
. Определить ЭДС генератора при номинальной частоте вращения и частоту вращения для получения ЭДС Е1
. Обмотка возбуждения включена на зажимы якоря. Определить величину сопротивления цепи возбуждения R
в1
, при котором ЭДС генератора равна Е1
при номинальной частоте вращения. При каком предельном значении R
в. кр.
генератор возбуждается?
Таблица 6.
| I
в
, А
|
0,6 |
0,94 |
1,71 |
4,05 |
| Е, В
|
115 |
172,5 |
230 |
287,5 |
Таблица 7.
| №
|
R
в1
, Ом
|
Е1
,
В
|
| 7 |
135 |
250 |
Решение
На рис. 2 приведена характеристика холостого хода генератора независимого возбуждения, построенная по данным, представленным в таблице 6.

Рис. 2. Характеристики генератора
Ток в цепи возбуждения находится по формуле:
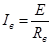 , А. , А.
Уравнение 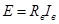 представляет собой характеристику цепи возбуждения, которое представлено на рис. 2 прямой 1, которая построенная по значениям, приведенным в таблице 8 при представляет собой характеристику цепи возбуждения, которое представлено на рис. 2 прямой 1, которая построенная по значениям, приведенным в таблице 8 при 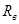 =135 Ом. =135 Ом.
Таблица 8.
| I в, А |
E, В |
| 0 |
0 |
| 0,6 |
81 |
| 0,94 |
126,9 |
| 1,71 |
230,85 |
| 4,05 |
546,75 |
ЭДС генератора при номинальной частоте вращения соответствует значению ЭДС в точке пересечения характеристики холостого хода и характеристики цепи возбуждения (рис. 2.):
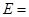 235 (В). 235 (В).
ЭДС генератора также можно найти по формуле:
 , В, , В,
где n – номинальная частота вращения.
Из этой формулы выражаем значение  , с помощью которого находим частоту вращения, которая необходима для получения ЭДС , с помощью которого находим частоту вращения, которая необходима для получения ЭДС 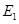 : :
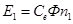 , В. , В.
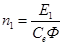 , об/мин. , об/мин.
Подставляем числовые значения:
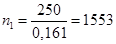 (об/мин). (об/мин).
Сопротивление 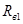 , при котором ЭДС генератора равна , при котором ЭДС генератора равна 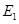 находим с помощью уравнения, представляющего собой характеристику цепи возбуждения и прямой 1 на рис. 2: находим с помощью уравнения, представляющего собой характеристику цепи возбуждения и прямой 1 на рис. 2:
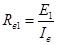 , Ом. , Ом.
Подставляем числовые значения:
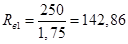 (Ом). (Ом).
Для нахождения 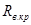 необходимо построить касательную к характеристике холостого хода генератора и определить тангенс угла касательной (рис. 2): необходимо построить касательную к характеристике холостого хода генератора и определить тангенс угла касательной (рис. 2):
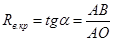 , Ом. , Ом.
Подставляем числовые значения:
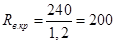 (Ом). (Ом).
Задача 7.
Какое сопротивление необходимо включить в цепь якоря двигателя параллельного возбуждения номинальной мощности Рн
с номинальным напряжением U
н
, чтобы при неизменных значениях номинального момента на валу и тока возбуждения частота вращения двигателя уменьшилась вдвое? Сопротивление цепи якоря Ra
, сопротивление цепи возбуждения R
в
, кпд двигателя h
.
Таблица 9.
| №
|
Рн
,
кВт
|
U
н
,
В
|
Ra
,
Ом
|
R
в
,
Ом
|
h
,
%
|
| 7 |
5,3 |
220 |
0,242 |
96,3 |
80 |
Решение
Формула для вычисления частоты вращения:
 , об/мин. , об/мин.
Для изменения частоты вращения в цепь якоря включают добавочное сопротивление, которое можно выразить из формулы:
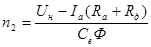 , об/мин. , об/мин.
Очевидно, что частота вращения зависит от тока якоря 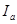 , который, в свою очередь, зависит от номинального момента на валу двигателя , который, в свою очередь, зависит от номинального момента на валу двигателя 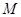 . Ток якоря можно выразить через номинальный момент следующим образом: . Ток якоря можно выразить через номинальный момент следующим образом:
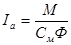 , А. , А.
Таким образом, формула для вычисления частоты вращения запишется в следующем виде:
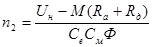 , об/мин. , об/мин.
По условию задачи 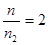 , тогда , тогда
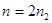
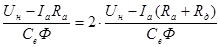
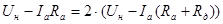
Выразим из последнего равенства значение 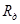 : :
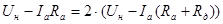
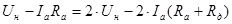
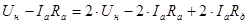
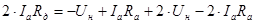
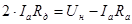
 , Ом. , Ом.
Значение 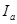 можно выразить из формулы КПД двигателя: можно выразить из формулы КПД двигателя:
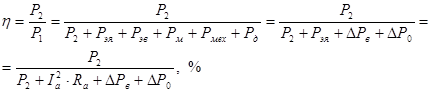
Сумму механических, магнитных и добавочных потерь 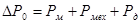 можно найти седеющим образом: можно найти седеющим образом:
· Согласно ГОСТу в двигателях без компенсационной обмотки значение мощности добавочных потерь 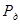 принимают равным 1% от полезной мощности: принимают равным 1% от полезной мощности:
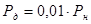 , Вт. , Вт.
· Сумма механических и магнитных потерь 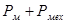 вычисляется следующим образом: вычисляется следующим образом:
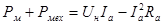 , Вт. , Вт.
Мощность потерь обмотки возбуждения находится по формуле:
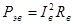 , Вт. , Вт.
Значение тока возбуждения можно выразить как отношение номинального напряжения 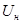 к сопротивлению обмотки возбуждения к сопротивлению обмотки возбуждения 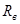 : :
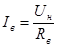 , А. , А.
Тогда формула мощности потерь обмотки возбуждения запишется в следующем виде:
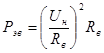

Подставляем полученные выражения в формулу КПД:
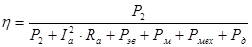
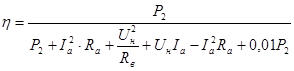
 , %. , %.
Выразим из полученного равенства ток якоря 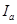 : :
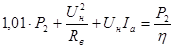
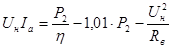
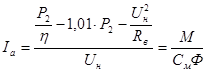 , А. , А.
Последняя формула показывает, что при неизменном номинальном моменте ток якоря не изменяется. Подставляем полученное выражение силы тока якоря в формулу добавочного сопротивления:

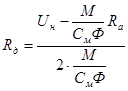
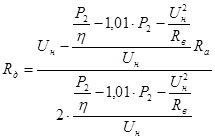
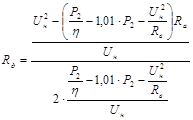
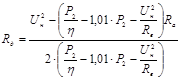 , Ом. , Ом.
схема обмотка генератор двигатель
Подставляем числовые значения:
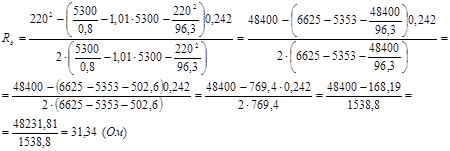
|