Задание
| номер интервала |
границы интервалов t |
частота m |
| свыше |
до(включительно) |
| 1 |
57,997 |
57,999 |
2 |
| 2 |
57,999 |
58,001 |
2 |
| 3 |
58,001 |
58,003 |
8 |
| 4 |
58,003 |
58,005 |
25 |
| 5 |
58,005 |
58,007 |
33 |
| 6 |
58,007 |
58,009 |
50 |
| 7 |
58,009 |
58,011 |
65 |
| 8 |
58,011 |
58,013 |
71 |
| 9 |
58,013 |
58,015 |
32 |
| 10 |
58,015 |
58,017 |
37 |
| 11 |
58,017 |
58,019 |
26 |
| 12 |
58,019 |
58,021 |
6 |
| 13 |
58,021 |
58,023 |
3 |
1.
Определение теоретической функции плотности распределения. Графическое изображение эмпирического и теоретического распределений
плотность распределение доверительный математический ожидание
При построении гистограмм и полигонов по оси абсцисс откладывают значения результатов измерений (середины интервалов xi
), по оси ординат – частности появления результатов измерения в каждом i-м интервале.
Из-за ограниченности числа результатов измерений при обработке вместо математического ожидания и дисперсии получают их приближенные оценки– соответственно эмпирическое среднее 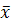 и эмпирическую дисперсию S2
, характеризующие средний результат измерений и степень разброса измерений. и эмпирическую дисперсию S2
, характеризующие средний результат измерений и степень разброса измерений.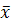 и S2
определяются из выражений: и S2
определяются из выражений:

Значения вероятности попадания результата измерения в конкретный интервал можно определить, используя значения функции:
 , ,
где 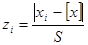 . .
Тогда вероятность попадания результата в i-й интервал величиной h
 . .
Внесем все вычисления в таблицу и на основании полученных результатов построим кривую теоретического распределения, а так же гистограмму и полигон эмпирического распределения:
| Середина интервала xi
|
Эмпирич. частости P’i
|
mi
xi
|
xi
-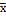 |
zi
|
mi
xi
2
|
φi
(z) |
Pi
|
| 57,998 |
0,006 |
115,996 |
-0,01285 |
2,874965 |
6727,536 |
0,006399 |
0,002863 |
| 58 |
0,006 |
116 |
-0,01085 |
2,4275 |
6728 |
0,020956 |
0,009377 |
| 58,002 |
0,022 |
464,016 |
-0,00885 |
1,980034 |
26913,86 |
0,056179 |
0,025138 |
| 58,004 |
0,069 |
1450,1 |
-0,00685 |
1,532569 |
84111,6 |
0,123277 |
0,055162 |
| 58,006 |
0,092 |
1914,198 |
-0,00485 |
1,085103 |
111035 |
0,221427 |
0,099081 |
| 58,008 |
0,139 |
2900,4 |
-0,00285 |
0,637638 |
168246,4 |
0,325553 |
0,145674 |
| 58,01 |
0,181 |
3770,65 |
-0,00085 |
0,190173 |
218735,4 |
0,391793 |
0,175314 |
| 58,012 |
0,197 |
4118,852 |
0,00115 |
0,257293 |
238942,8 |
0,385954 |
0,172701 |
| 58,014 |
0,089 |
1856,448 |
0,00315 |
0,704758 |
107700 |
0,311212 |
0,139257 |
| 58,016 |
0,103 |
2146,592 |
0,00515 |
1,152223 |
124536,7 |
0,20541 |
0,091914 |
| 58,018 |
0,072 |
1508,468 |
0,00715 |
1,599689 |
87518,3 |
0,110976 |
0,049658 |
| 58,02 |
0,017 |
348,12 |
0,00915 |
2,047154 |
20197,92 |
0,049077 |
0,02196 |
| 58,022 |
0,008 |
174,066 |
0,01115 |
2,494619 |
10099,66 |
0,017765 |
0,007949 |
| Сумма |
20883,91 |
1211493 |
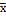 = = |
58,01085 |
| S2
= |
1,99775E-05 |
| S= |
0,00446962 |

2.
Критерий согласия эмпирического и теоретического распределений
Считают, что эмпирическое распределение хорошо согласуется с теоретическим, если (1 - g) больше 0,1. Согласно критерию Колмогорова, сравнивают эмпирические и теоретические значения, но уже не плотности распределения, а интегральной функции. Значение максимальной (по абсолютной величине) разности между ними DN
подставляют в выражение:
 , ,
где N – объем выборки.
Вычисление эмпирических F’i
и теоретических Fi
значений интегральной функции производим путем последовательного суммирования соответственно значений P’i
и Pi
. Результаты вычислений сведены в таблицу:
| Номер интервала |
Pi
|
P’i
|
Fi
|
F’i
|
Fi-Fi' |
| 1 |
0,002863 |
0,005556 |
0,002863 |
0,005556 |
0,002692 |
| 2 |
0,009377 |
0,005556 |
0,01224 |
0,011111 |
-0,00113 |
| 3 |
0,025138 |
0,022222 |
0,037379 |
0,033333 |
-0,00405 |
| 4 |
0,055162 |
0,069444 |
0,092541 |
0,102778 |
0,010237 |
| 5 |
0,099081 |
0,091667 |
0,191622 |
0,194444 |
0,002823 |
| 6 |
0,145674 |
0,138889 |
0,337295 |
0,333333 |
-0,00396 |
| 7 |
0,175314 |
0,180556 |
0,512609 |
0,513889 |
0,00128 |
| 8 |
0,172701 |
0,197222 |
0,68531 |
0,711111 |
0,025801 |
| 9 |
0,139257 |
0,088889 |
0,824566 |
0,8 |
-0,02457 |
| 10 |
0,091914 |
0,102778 |
0,91648 |
0,902778 |
-0,0137 |
| 11 |
0,049658 |
0,072222 |
0,966138 |
0,975 |
0,008862 |
| 12 |
0,02196 |
0,016667 |
0,988098 |
0,991667 |
0,003568 |
| 13 |
0,007949 |
0,008333 |
0,996048 |
1 |
0,003952 |
DN
= F'8
– F8
=0,025801,
N=åmi
=360,
Тогда получаем:
λ= 0,48953
Для lN
=0,52 g» 0,05 Þ (1 – 0,05)=0,95 >0,1.
Отсюда можно сделать вывод: согласие эмпирического распределения с нормальным теоретическим можно считать хорошим.
3.
Определение доверительных интервалов
В ряде задач, особенно при малом числе измерений, требуется не только найти эмпирическую оценку для того или иного параметра, но и определить доверительный интервал, в котором с доверительной вероятностью будет находиться теоретическое значение параметра.
Доверительный интервал для математического ожидания определяем из выражения:
интегральный доверительный интервал математический ожидание

Значения tγ
табулированы и равняется tγ
= 2,18 для N=13 и γ*=0,95.
58,00814756<M<58,01355244
Доверительный интервал для среднего квадратического отклонения определяем из выражения:

Значения χ1
2
, χ2
2
табулированы и определяется в зависимости от числа измерений N и односторонних вероятностей γ1
, γ2
:

Значение χ1
2
определяем при вероятности (1- γ1
), χ2
2
– при γ2
.
χ1
2
=24,1 χ2
2
=4,18
И тогда
| 0,003024897 |
<σ< |
0,008194587 |
4. Определение диапазона рассеивания значений
Определение границ диапазона рассеивания значений по результатам измерений, при вероятности риска 0,0027
.
М
»
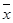 =
58,01085 =
58,01085
 »
S
=
0,00446962
»
S
=
0,00446962
М-3 »
57.997442
»
57.997442
М+3 »
58.024258
»
58.024258
Определение границ диапазона рассеивания значений по результатам измерений, при допускаемом значении вероятности риска 2β=0,001
М± σ σ
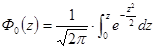
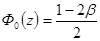
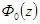 =0,4995
при этом =0,4995
при этом =3,29
(по справочнику) =3,29
(по справочнику)
М-3,29 =57,996146 =57,996146
М+3,29 =58,025554 =58,025554
Список использованной литературы
1. Зябрева Н.Н. и др. Пособие к решению задач по курсу "Взаимозаменяемость, стандартизация и технические измерения". Учеб. Пособие для вузов. М., "Высш. школа", 1977.
|