Содержание
Введение
Краткая характеристика берилла
Построение гистограмм каждого элемента
Расчет среднего состава каждой однородной совокупности, получение статистических характеристик
Проверка зависимости второстепенных элементов от главных
Заключение
Список используемой литературы
Введение
Главная цель курсовой работы – освоить методы статистической обработки больших массивов данных с помощью программ кафедры.
Частная задача – определить степень однородности материала, выделить однородные группы и дать их среднюю характеристику.
Для исследований предлагаются химические анализы распространенных минералов. В данной курсовой работе представлены химические анализы блеклой руды. Так же можно обрабатывать анализы горных пород и руд.
Краткая характеристика берилла
Берилл
Кристаллы - шестигранные призмы. Разновидности: изумруд, аквамарин, гелиодор, воробьевит (драгоценные камни), ростерит.
Встречается в пневматолито-гидротермальных месторождениях, в пегматитах, грейзенах, кварцевых жилах и др. Руда бериллия.
Химический состав—содержание (в %): ВеО— 14,1, Аl2
О3
— 19; Si02 — 66,9; отмечаются примеси натрия, калия, лития, цезия, рубидия, железа, ванадия, иногда хрома.
Цвет
прозрачный густо-зеленый хромсодержащий — изумруд,
голубой (зеленовато-голубой) — аквамарин
золотисто-желтый — гелиодор
розовый цезийсодержащий — воробьевит (морганит)
очень редко встречающиеся красный — биксбиит
бесцветный — ростерит
(гошенит)темно-синий максис-берилл.
Сингония —
гексагональная, дигексагонально-дипирамидальный вид симметрии. Спайность —
отсутствует; иногда отмечается отдельность по пинакоиду (0001).
Агрегаты.
Плотные, вкрапленность.
Химическая формула
Al2
Be3
[Si6
O18
]
Изумруд
Изумруд — разновидность минерала берилла
Зеленый цвет изумруда обусловлен наличием в нем примеси хрома Cr. Типичные изумруды содержат 0,14% хрома Cr, 0,12% железа Fe и 0,05% ванадия V.
Аквамарин
разновидность минерала берилла
Название аквамарина произошло от латинского aqua marina – «морская вода», поскольку цвет камня напоминает теплые тропические моря. Когда-то аквамаринами украшали царские короны, кроме того их использовали в качестве линз для очков (первые линзы датируются 1300 годом).
Великолепнейшие месторождения аквамаринов находятся в Бразилии, на одном из южноамериканских месторождений добыт кристалл аквамарина весом 110,5 кг. Самый крупный из известных ограненных камней весит 2594 каратов.
Считается, что аквамарин способен укрощать бушующее море. Это талисман верной любви, оберегающий дружбу и сохраняющий справедливость. Когда-то считалось, что он укрепляет сердце, помогает при заболеваниях легких, кожи и нервной системы.
Астрологи рекомендуют украшения с аквамарином родившимся под знаком Водолея и Весов
Гелиодор
Гелиодор (Heliodor) – минерал, прозрачная разновидность берилла
Для предварительной обработки материалов был использован редактор Лексикон. В ходе работы исходный файл данных был разделен на несколько частей. Выделяется файл главных компонентов минерала, сумму, плотность минерала и список литературных источников. Данный файл скопирован и помещен в приложение №2. Далее выделятся файлы для каждого компонента – примеси, чтобы получить по ним статистику и характер зависимости от главных компонентов. В данной работе были выделены следующие примеси: Cs, Li, Rb
Построение гистограмм каждого элемента
Первый шаг в исследованиях – построение гистограммы по каждому компоненту, чтобы установить степень однородности или неоднородности исходного материала (программа stanp.exe). Работа ведется в пакете VC(Волков-командер). Если по каким-то компонентам анализы неоднородные, то имеет смысл разделить данные на однородные совокупности с помощью редактора Лексикон.
В работе представлены все построенные гистограммы, т.к. по ним можно выделить неоднородные совокупности.
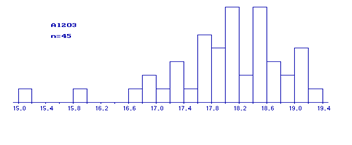
Рис
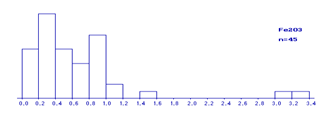
Рис
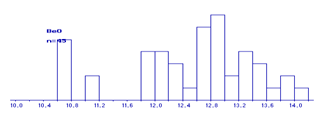
Рис
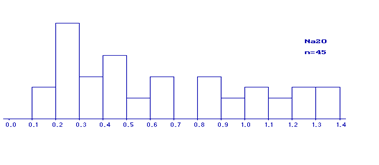
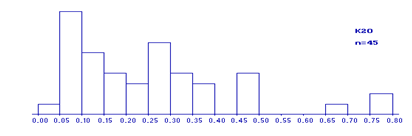
Рис
По построенным гистограммам были выделены области нормальных и аномальных компонентов. Аномальные значения были исключены из исходных данных и сохранены в отдельных файлах.
Расчет среднего состава каждой однородной совокупности, получение статистических характеристик
Следующее изучение заключается в расчете среднего состава каждой однородной совокупности, в получении статистических характеристик, в расчете коэффициентов корреляции между компонентами (программа stxp.exeили mregp.exe).
Расчет статистических характеристик
Таблица. Статистические характеристики
| SiO2 |
Al2O3 |
Fe2O3 |
BeO |
Na2O |
K2O |
| Cреднее значение |
64,848 |
18,267 |
0,587 |
12,85 |
0,516 |
0,223 |
36 |
| Cреднее значение |
64,459 |
17,481 |
0,254 |
10,794 |
1,137 |
0,324 |
7 |
| Mr |
60 |
102 |
160 |
25 |
62 |
94 |
56 |
| SiO2 |
Al2O3 |
Fe2O3 |
BeO |
Na2O |
K2O |
| Cреднее значение |
64,848 |
18,267 |
0,587 |
12,85 |
0,516 |
0,223 |
| Mr |
60 |
102 |
160 |
25 |
62 |
94 |
| атомы |
10808 |
3582 |
73 |
5140 |
166 |
47 |
| формула |
6 |
1,98 |
2,91 |
| SiO2 |
Al2O3 |
Fe2O3 |
BeO |
Na2O |
K2O |
| Cреднее значение |
64,459 |
17,481 |
0,254 |
10,794 |
1,137 |
0,324 |
| Mr |
60 |
102 |
160 |
25 |
62 |
94 |
| атомы |
10743 |
3428 |
32 |
4318 |
367 |
69 |
Результат: Отсюда можно сделать вывод, что бериллы схожи по составу и могут образовывать однородную группу.
Проверка зависимости второстепенных компонентов от главных
В данном разделе курсовой работы были изучены множественные корреляционные зависимости второстепенных компонентов от главных компонентов с помощью программы mregr.exe
Примусные элементы
Литий
Количество столбцов 7
Наберите номер столбца 7
Уравнение регрессии
Li2O= - 0.042*SiO2
- 0.087*Al2
O3
- 0.201*Fe2
O3
- 0.199*BeO+ 0.458*Na2
O
- 0.280*K2
O+ 7.060
Погрешность уравнения при t=1 0.039414
Коэффициент множественной корреляции 0.951273
Дисперсия отклонений без учета степеней свободы 0.016338
Дисперсия отклонений cучетом степеней свободы 0.019515
Цезий
Количество столбцов 7
Наберите номер столбца 7
Уравнение регрессии
Cs2O = - 0.511*SiO2
- 0.268*Al2
O3
- 0.867*Fe2
O3
- 0.371*BeO - 0.050*Na2
O
+ 0.537*K2
O + 43.525
Погрешность уравнения при t=1 0.274752
Коэффициент множественной корреляции 0.845169
Дисперсия отклонений без учета степеней свободы 0.264234
Дисперсия отклонений c учетом степеней свободы 0.315612
Рубидий
Количество столбцов 7
Наберите номер столбца 7
Уравнение регрессии
Rb2O = - 0.006*SiO2
- 0.007*Al2
O3
- 0.003*Fe2
O3
+ 0.000*BeO + 0.009*Na2
O
- 0.030*K2
O + 0.551
Погрешность уравнения при t=1 0.013837
Коэффициент множественной корреляции 0.526225
Дисперсия отклонений без учета степеней свободы 0.000265
Дисперсия отклонений c учетом степеней свободы 0.000316
Вывод:
С помощью программы mregr.exeможно изучить множественные корреляционные зависимости второстепенных компонентов от главных компонентов, по которым возможно прогнозирование, что и было продемонстрировано в данном разделе курсовой работы.
Заключение
химический берилл кристалл корреляционный
Главной целью данной курсовой работы было освоение методов статистической обработки больших массивов данных с помощью программ кафедры. А в свою очередь, частная задача – определить степень однородности материала, выделить однородные группы и дать их среднюю характеристику.
В ходе работы были произведены исследования при обработке исходных данных. Исследование проводилось с помощью редактора Лексикон, программ stanp.exe, stxp.exe, mregr.exe- пакет VC(Волков-командер).
Благодаря перечисленным программам мы познакомились с возможностью современных методов обработки данных химического анализа того или иного минерала, а также получили навык работы в пакетеVC(Волков-командер).
Данный пакет программ позволяет без особых проблем исследовать минерал, проанализировав его химический состав, выделить примеси, главные компоненты, а также оценить влияние главных компонентов на второстепенные, рассчитать статистические характеристики, коэффициент корреляции и получить формулу минерала.
Полученная формула, показывает, что все 45 проб однородны. И примесные элементы, не оказывают влияния на разновидность.
45 берилл1
------------------------------------------
N SiO2 Al2O3 Fe2O3 BeO Na2O K2O
------------------------------------------
1 62.02 17.22 0.49 10.71 1.32 0.27
2 66.03 19.11 0.24 12.70 0.17 0.06
3 66.49 18.08 0.40 13.04 0.22 0.07
4 64.98 17.40 0.12 11.10 1.23 0.26
5 62.75 17.74 0.10 13.50 0.99 0.27
6 64.90 17.80 0.25 12.70 0.40 0.23
7 65.10 18.80 0.67 13.20 0.33 0.15
8 64.58 16.84 0.73 12.08 1.24 0.47
9 63.20 17.20 0.19 12.00 1.14 0.22
10 65.80 17.40 0.23 10.70 1.28 0.31
11 65.42 17.50 0.26 10.60 1.35 0.39
12 63.78 18.74 0.86 11.95 0.32 0.25
13 64.74 19.39 0.36 12.66 0.41 0.26
14 64.40 19.19 0.86 12.80 0.62 0.13
15 65.56 17.66 0.38 13.96 0.16 0.48
16 65.61 17.88 0.98 12.29 0.27 0.77
17 65.72 18.18 0.91 12.89 0.32 0.00
18 64.86 19.04 0.72 13.46 0.24 0.21
19 65.78 17.85 0.49 13.66 0.35 0.17
20 65.71 17.88 0.98 12.29 0.27 0.77
21 66.80 17.76 0.59 12.91 0.15 0.40
22 65.30 18.53 0.20 13.20 0.42 0.10
23 65.83 18.77 0.47 13.02 0.26 0.30
24 66.30 19.01 0.21 13.37 0.25 0.18
25 64.17 18.21 0.66 12.61 0.70 0.48
26 64.98 18.60 1.03 12.91 0.63 0.26
27 63.42 18.84 0.96 12.82 0.46 0.31
28 63.84 18.55 1.12 12.78 0.51 0.26
29 64.70 16.82 1.51 12.81 0.63 0.40
30 63.89 18.88 0.97 12.70 0.56 0.06
31 66.10 16.60 0.41 10.69 0.85 0.31
32 64.88 18.12 0.82 12.89 0.82 0.05
33 65.00 18.16 0.95 12.47 0.40 0.09
34 64.75 18.26 0.50 12.37 0.82 0.05
35 63.35 18.51 0.63 12.12 0.97 0.07
36 64.76 18.10 0.20 11.83 1.14 0.06
37 64.12 17.88 0.11 11.89 1.33 0.05
38 63.82 17.70 0.12 11.04 1.09 0.07
39 63.07 18.55 0.15 10.72 0.84 0.66
40 65.29 15.00 3.01 12.02 1.08 0.50
41 61.93 15.91 3.39 11.80 1.03 0.15
42 64.66 18.43 0.19 13.84 0.20 0.10
43 64.61 18.11 0.24 14.18 0.20 0.10
44 64.65 18.16 0.32 13.49 0.27 0.10
45 65.30 18.53 0.22 13.20 0.42 0.10
Список использованной литературы
1. Поротов Г.С. Краткие методические указания по курсовой работе “Математические методы в геологии” в электронном виде.
2. Бетехтин А.Г. Минералогия. М: Недра, 1956.
|