2
3
4
4
4
4
4
6
6
6
7
8
9
12
12
13
14
15
16
17
17
17
18
21
22
22
23
24
25
|
|
СодержаниеВведение
1. Анализ рычажного механизма
1.1 Структурный анализ механизма
Анализ строения механизма на уровне звеньев и кинематических пар
Определение степени подвижности механизма
Анализ строения механизма на уровне структурных групп
1.2 Кинематический анализ механизма
Подготовка данных к расчету на ЭВМ по программе KDSARM
1.3 Анализ динамики установившегося движения
Расчет параметров динамики установившегося движения
Определение движущего момента при условии, что этот момент постоянный
Определение закона движения входного звена
Определение момента инерции маховика
Закон движения входного звена после установки маховика
1.4 Кинетостатический анализ
Выбор расчетного положения
Определение ускорений и сил инерции
Кинетостатический анализ групп Ассура и первичного механизма
Подсчет погрешности вычислений
2. Синтез зубчатого механизма
2.1 Выбор коэффициентов смещения исходного производящего контура
2.2 Геометрический расчет эвольвентного зубчатого зацепления
2.3 Расчет показателей качества зубчатого зацепления
Заключение
Список используемой литературы
Курсовой проект включает в себя исследование рычажного, зубчатого механизма.
Целью исследования рычажного механизма является подготовка данных к прочностному расчету механизма - отыскание реакций кинетостатическом расчете.
а) проектирование структурной и кинематической схемы механизма по данным условиям;
б) анализ установившегося движения механизма при действии заданных сил;
в) силовой анализ механизма с учетом геометрии масс звеньев, сил инерции;
Целью синтеза зубчатого механизма является получение оптимальной геометрии зубчатого зацепления, удовлетворяющей заданным условиям.
Примечание: расчеты пункта 1,1 выполнены в среде
Math
Cad
Professional
2001.
Основные задачи: анализ строения механизма на уровне звеньев и кинематических пар и подсчет степени подвижности, строения механизма на уровне структурных групп.
Допущение 1: независимо от особенностей конструктивного выполнения, все шарнирные соединения считаем вращательными кинематическими парами, а все соединения допускаемые прямолинейное относительное движение звеньев - поступательными парами, поэтому все пары рычажного механизма относим к пятому классу.
Таблица звеньев и кинематических пар
| № |
Обозначения |
Тип |
Соединение звеньев |
| 1 |
O |
Вращательная |
0 - стойка
1 - кривошип
|
| 2 |
А1 |
Вращательная |
1 - кривошип
2 - кулисный камень
|
| 3 |
В |
Вращательная |
0 - стойка
3 - кулиса
|
| 4 |
А2 |
Поступательная |
2 - кулисный камень
3 - кулиса
|
| 5 |
D′ |
Вращательная |
3 - кулиса
4 - шатун
|
| 6 |
Е2 |
Поступательная |
0 - стойка
5 - ползун
|
| 7 |
Е1 |
Вращательная |
4 - кривошип
5 - кривошип
|
Степень подвижности механизма определяется по формуле Чебышева
W=3n - 2p5 - p4,
где n - число подвижных звеньев;
p5 - вращательных и поступательных пар пятого класса;
W=3∙5 - 2·7=15 - 14=1
Степень подвижности исследуемого механизма равна 1
Вывод: В данном механизме можно задать движение одному звену.
Исходный механизм Ι (0,1) (рис.1)
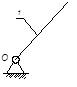
Рис.1. Группы Ассура
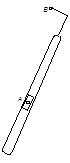
Рис. 2. Группа Асура II класс (3,2) 3 вид 2 порядок
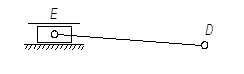
Рис. 3. Группа Асура II класс (4,5) 2 вид 3 порядок
Механизм является механизмом второго класса, так как в его составе нет групп старше второго класса. Формула механизма 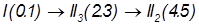
1.2
Кинематический анализ механизма
Задача: составление векторных контуров для определения неизвестных параметров механизма таких, как неизвестные длинны, углы положения звеньев механизма, а также определение аналогов скоростей и ускорений.
Рассмотрим механизм при 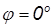
Для удобства, все расчеты выполнены в среде MATCAD. 2001 Professional
Входное звено (Рис.4)
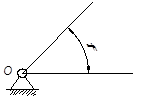
Рис.4
Дано: 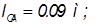
Задача о положениях
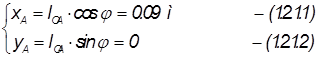
Задача о скоростях
Возьмем производные от уравнений (1.2.1.1) и (1.2.1.2)
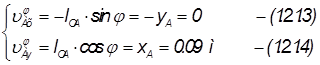
Задача об ускорениях
Возьмем производные от уравнений (1.2.1.3) и (1.2.1.4)
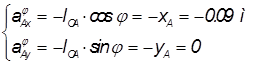
Рассмотрим векторный контур ОАВС
(Рис.5)

Рис.5
Дано: 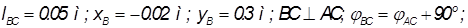
Векторное уравнение контура 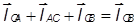
Задача о положениях
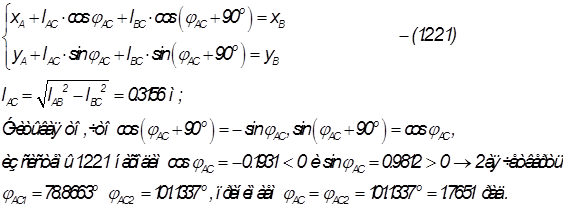
Задача о скоростях
Продифференцируем первое уравнение системы 1.2.2.1.
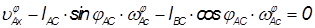 ,
,
получаем выражение для аналога угловой скорости 3его звена:
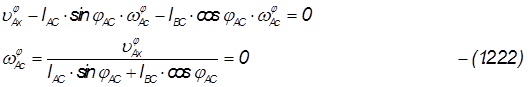
Задача об ускорениях
Продифференцируем уравнение 1.2.2.2:
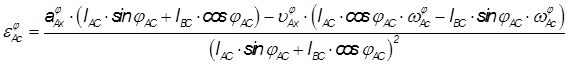
так как аналог линейной скорости по х равен 0, то мы получаем 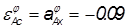
Рассмотрим векторный контур ОА
D (
Рис.6)

Рис.6
Дано: 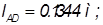
Векторное уравнение контура 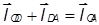
Задача о положениях

Задача о скоростях
Продифференцируем систему уравнений 1.2.3.1., получим:
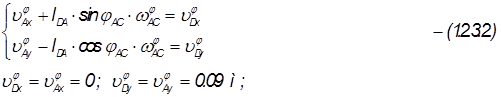 :
:
Задача об ускорениях
Продифференцируем систему уравнений 1.2.3.2:
рычажный механизм зубчатый
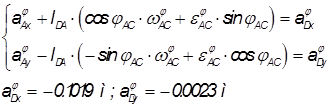
Рассмотрим векторный контур О
DE (
Рис.7)
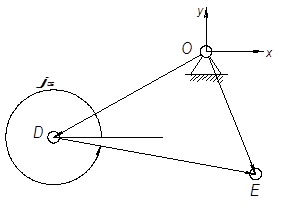
Рис.7
Дано: 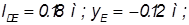
Векторное уравнение контура 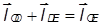
Задача о положениях
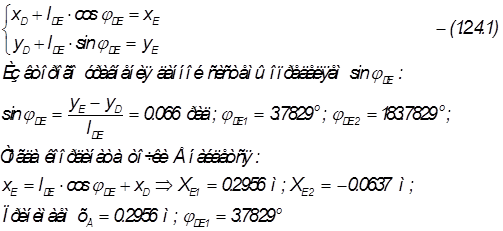
Задача о скоростях
Продифференцируем систему уравнений 1.2.4.1., получим:
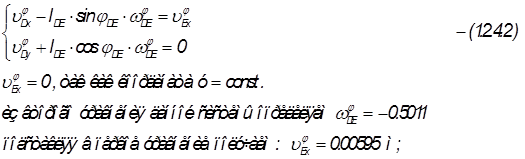 :
:
Задача об ускорениях
Продифференцируем систему уравнений 1.2.4.2:
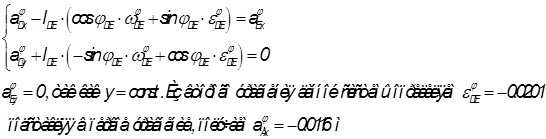
Программа KDSARM предназначена для решения задач кинематических плоских механизмов. Она позволяет рассчитать координаты, аналоги скоростей и ускорений точек, аналоги угловых скоростей и ускорений точек и звеньев. Для описания геометрических размеров звеньев механизма используются подвижные системы координат, которые связываются с каждым звеном механизма. Подвижные системы координат движутся вместе со своими звеньями. Кинематические пары, в которые входят звенья механизма, любые точки звена, занимают всегда одно и тоже положение в подвижной системе координат звена.
Для расчета на ЭВМ нужно ввести в нее три таблицы:
1. Таблицу кинематических пар;
2. Таблицу координат кинематических пар и характерных точек звеньев;
3. Таблицу начальных приближений;

Рис.8
Таблица кинематических пар:
| Обозначения |
Тип |
Соединения |
| O |
Vr |
0 1 |
| A1 |
Vr |
1 2 |
| A2 |
Po |
2 3 |
| D |
Vr |
3 4 |
| E1 |
Vr |
4 5 |
| E2 |
Po |
5 0 |
| B |
Vr |
3 0 |
Таблица координат и смещений кинематических пар:
| № звена |
Обозначение пары |
Xί (Rί), м |
Yί (αί), м |
| 0 |
O |
0.0 |
0.00 |
| 0 |
B |
-0.02 |
0.3 |
| 0 |
E2 |
-0.12 |
1.570796 |
| 1 |
O |
0.00 |
0.0 |
| 1 |
A1 |
0.09 |
0.0 |
| 2 |
A1 |
0.0 |
0.0 |
| 2 |
A2 |
0.0 |
1.571796 |
| 3 |
A2 |
-0.05 |
1.570796 |
| 3 |
B |
0.0 |
0.00 |
| 3 |
D |
-0.45 |
-0.05 |
| 4 |
D |
0.0 |
0.0 |
| 4 |
E1 |
0.18 |
0.0 |
| 5 |
E1 |
0.0 |
0.0 |
| 5 |
E2 |
0.0 |
1.570796 |
| Номер звена |
Обозначение
центра масс
|
Координата Xί |
Координата Yί |
| 3 |
S3 |
-0.139 |
0.08 |
| 4 |
S4 |
0.06 |
0.0 |
Таблица координат характерных точек звеньев механизма:
Для ввода значений в таблицу начальных приближений необходимо определить координаты точек звеньев в главных осях при произвольном угле φ графическим либо аналитическим методом.
Таблица начальных приближений при угле 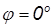 :
:
Таблица 4
| № звена |
Xί |
Yί |
φί |
| 1 |
0.0 |
0.0 |
0.0 |
| 2 |
0.09 |
0.0 |
1.7651 |
| 3 |
-0.02 |
0.3 |
1.7651 |
| 4 |
0.1160 |
-0.1319 |
0.0660 |
| 5 |
0.2956 |
-0.1200 |
0.0 |
После ввода данных в ЭВМ, получаем распечатку зависимостей аналогов скоростей, аналогов ускорений и перемещения выходного звена от угла поворота входного звена (приложение Б).
Силы, возникающие при работе машины, можно разделить на следующие группы: движущие силы F
или их моменты М
(работа этих сил за цикл положительна); силы полезного сопротивления F
или их моменты М
(полезные сопротивления - это силы, для преодоления которых предназначен данный механизм или машина); силы трения F
или их моменты М
(они могут быть как силами сопротивления, тормозящими движение звеньев механизма, так и движущими, например силы трения); силы тяжести G
- бывают движущими (при опускании центров масс звеньев) силы инерции F
или их моменты сил инерции М
, возникающие при движении звеньев с ускорениями. Внутренними являются силы взаимодействия между звеньями, образующими кинематические пары, в том числе и силы трения.
Целью динамического анализа является определение закона движения машины по заданным действующим на нее силам.
Основные задачи динамического анализа:
1. Построение динамической модели машины.
2. Численный анализ параметров динамической модели, угловой скорости и углового ускорения главного вала машины (без маховика).
3. Определение работы сопротивлений, величины момента и мощности двигателя.
4. Оценка неравномерности хода машины, определение момента инерции маховика и значения угловой скорости главного вала в начале цикла.
5. Численный анализ угловой скорости и углового ускорения главного вала машины с маховиком.
Допущение 4: пренебрегаем трением в кинематических парах и вредным сопротивлением среды.
Допущение 5: момент, развиваемый двигателем, считаем
постоянным на всем периоде установившегося движения.
Допущение 6: полезное сопротивление зависит лишь от положения механизма.
Допущение 7: пренебрегаем весом и инертностью кулисных камней.
Характерными режимами движения машин являются установившийся и переходный режимы. Установившийся режим характерен для машин, выполняющих циклически повторяющийся рабочий процесс. При этом скорость звена приведения является периодической функцией времени, период которой равен одному циклу. За цикл установившегося движения работа движущих сил полностью затрачивается на преодоление сил полезного и вредного сопротивлений.
После определения закона движения звена приведения (начального звена) законы движения остальных звеньев механизма могут быть получены методами кинематического анализа.
В состав исследуемой машины входят: 1 - двигатель, 2 - редуктор, 3 - рычажный механизм, выполняющий роль технологической машины.
Примечание: все расчеты были проведены с помощью
Microsoft
Excel.
График сил полезного сопротивления: строится из условия:
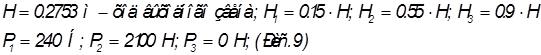

Рис.9
При решении задач динамики используют динамическую модель.
Динамической моделью механизма является модель, основанная на допущениях.
Математическое описание динамической модели машины осуществляется путём составления соответствующих уравнений.
Нахождение обобщённой силы называют приведением сил к звену приведения.
Приведённый моментМПР
- это пара сил, приложенная к звену приведения и определяемая из равенства элементарной работы этой пары сил сумме элементарных работ сил и моментов, действующих на звенья механизма.
В результате приведения сил и масс механизм заменяется эквивалентной динамической моделью (расчётной схемой), состоящей из одного вращающегося звена - звена приведения, которое имеет момент инерции IПР
(приведённый момент инерции механизма) и находится под действием приведённого момента МПР
.
В качестве звена приведения принимается начальное звено.
Приведённый момент инерции вычисляем из условия равенства кинетической энергии звена приведения и кинетической энергии механизма.
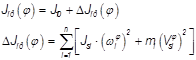
Таким образом получаем следующую формулу, для расчета приведенного момента инерции:
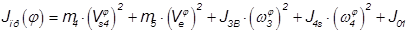
Производная от приведенного момента инерции:
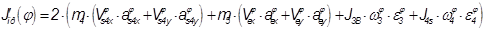
Таблица результатов
| φ |
Jпр |
J`пр |
| 0 |
2,8000 |
0,0000 |
| 1 |
2,9038 |
0,2915 |
| 2 |
3,0446 |
0,2177 |
| 3 |
3,1168 |
0,0545 |
| 4 |
3,1045 |
-0,0951 |
| 5 |
3,0251 |
-0, 2006 |
| 6 |
2,9047 |
-0,2438 |
| 7 |
2,8039 |
-0,0801 |
| 8 |
2,9277 |
0,6862 |
| 9 |
3,5678 |
1,5208 |
| 10 |
3,8589 |
-0,9176 |
| 11 |
3,0804 |
-1,2396 |
| 12 |
2,8000 |
0,0000 |
По формуле рассчитывается момент сил сопротивления для двенадцати положений механизма
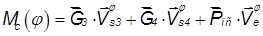
или
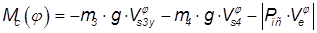
Таблица результатов
| φ |
Pпс |
Mc |
| 0 |
0,00 |
0,000 |
| 1 |
266,57 |
-13,849 |
| 2 |
862,81 |
-77,024 |
| 3 |
1558,86 |
-161,518 |
| 4 |
1790,85 |
-181,979 |
| 5 |
694,59 |
-59,900 |
| 6 |
0,00 |
0,299 |
| 7 |
0,00 |
0,024 |
| 8 |
0,00 |
-0,262 |
| 9 |
0,00 |
-2,044 |
| 10 |
0,00 |
-4,770 |
| 11 |
0,00 |
-3,416 |
| 12 |
0,00 |
0,000 |
По значениям момента сил сопротивления строится диаграмма моментов сил сопротивления, затем графическим методом определяется работа сил сопротивления.
Исходя из условия, что сумма работ за один цикл равна нулю, получаем
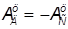 .
.
Для вычисления движущего момента используется формула
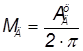 ,
,
результат вычислений  . Далее рассчитывается сумма работ внешних сил для каждого положения механизма:
. Далее рассчитывается сумма работ внешних сил для каждого положения механизма:
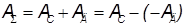 ,
,
Таблица результатов
| φ |
Ac |
Ad |
AΣ |
| 0 |
0,0000 |
0,0000 |
0,0000 |
| 1 |
7,2508 |
21,9971 |
14,7463 |
| 2 |
47,5776 |
43,9942 |
-3,5834 |
| 3 |
132,0879 |
65,9842 |
-66,1037 |
| 4 |
227,3530 |
87,9863 |
-139,3667 |
| 5 |
258,7404 |
110,0192 |
-148,7212 |
| 6 |
258,7405 |
132,0804 |
-126,6601 |
| 7 |
258,7282 |
153,9798 |
-104,7484 |
| 8 |
258,8651 |
175,9769 |
-82,8882 |
| 9 |
259,9355 |
197,9740 |
-61,9614 |
| 10 |
262,4326 |
219,9711 |
-42,4615 |
| 11 |
263,9654 |
241,9683 |
-21,9971 |
| 12 |
263,9654 |
263,9654 |
0,0000 |
Определение угловой скорости из уравнения движения машины в интегральной форме:
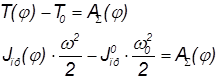 ,
,
исходя из условия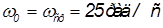 , получим
, получим
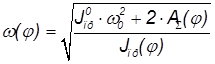 .
.
Угловое ускорение определяется из уравнения движения машины в дифференциальной форме:
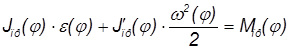 ,
,
исходя из условия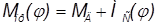 , получится:
, получится:
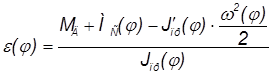 .
.
Далее определяется разность между угловыми скоростями для каждого положения механизма и средней угловой скоростью: 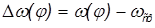 .
.
Результаты вычислений записываются в таблицу:
| φ |
ω (φ) |
ε (φ) |
Δω |
| 0 |
25,0000 |
15,0043 |
0,0000 |
| 1 |
24,7553 |
-21,0616 |
-0,2447 |
| 2 |
23,9254 |
-31,9603 |
-1,0746 |
| 3 |
22,7827 |
-42,8808 |
-2,2173 |
| 4 |
21,7695 |
-37,8244 |
-3,2305 |
| 5 |
21,9129 |
10,0051 |
-3,0871 |
| 6 |
22,6996 |
36, 1901 |
-2,3004 |
| 7 |
23,4394 |
22,8357 |
-1,5606 |
| 8 |
23,2619 |
-49,1503 |
-1,7381 |
| 9 |
21,3488 |
-85,9351 |
-3,6512 |
| 10 |
20,7723 |
60,9526 |
-4,2277 |
| 11 |
23,5335 |
123,9596 |
-1,4665 |
| 12 |
25,0000 |
15,0043 |
0,0000 |
Определяются экстремальные значения угловой скорости:
 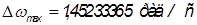 ,
,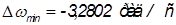 .
.
По формуле вычисляется коэффициент неравномерности движения:
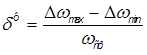 ,
, .
.
Так как δф > δ (δ = 0.1), то его значение уменьшают с помощью маховика.
Для определения момента инерции маховика используется формула
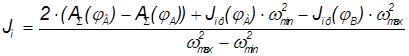
Так как,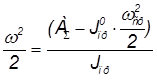
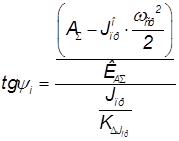 или
или 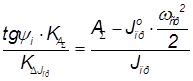 ,
,
то. 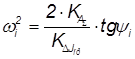
То есть 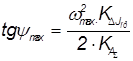 ,
, 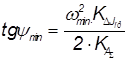 ,
,
где KA∑ = 1 Н м/мм, KΔJпр = 0,005 кг м2/с2 мм, ωmax = 26.452 рад/с, ωmin = 21.720 рад/с.
Отсюда получается, что tgψmax =1.749315, tgψmin =1.17937, то есть ψmax = 60.24545 град, ψmin = 49.715 град. Под полученными углами проводятся касательные к кривой на “Диаграмме ΔJпр - A∑” и определяются для точек А и В величины Jпр, A∑:
Jпр (φА) = 3.853677 кг м2/с2
Jпр (φВ) = 2.80939 кг м2/с2,A∑ (φА) = - 44.17 Н м,
A∑ (φВ) = 4.9977 Н м.
По формулам определяются максимальная и минимальная угловые скорости для движения машины с маховиком:
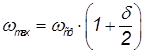 и
и 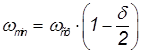 ,
,
ωmax = 26,25 рад/с, ωmin = 23,75 рад/с. Используя рассчитанные параметры, вычисляется момент инерции маховика: Jм = 2.68955 кг м2/с2.
Рассчитывается начальная угловая скорость при движении механизма с маховиком по формуле
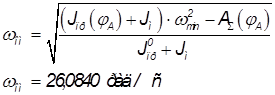 ,
,
Вычисляется значение угловой скорости для двенадцати положений механизма по формуле:
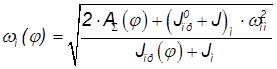
Для расчета углового ускорения используется формула:
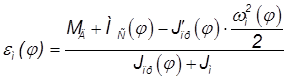 .
.
Результаты вычислений записываются в таблицу:
| φ |
ωм (φ) |
εм (φ) |
| 0 |
26,084 |
7,653087 |
| 1 |
25,94276 |
-12,5029 |
| 2 |
25,49701 |
-18,4438 |
| 3 |
24,90948 |
-23,4941 |
| 4 |
24,42358 |
-19,2602 |
| 5 |
24,52613 |
7,425869 |
| 6 |
24,94724 |
21,12433 |
| 7 |
25,33282 |
12,32854 |
| 8 |
25, 20709 |
-31,3752 |
| 9 |
24,02271 |
-63,7408 |
| 10 |
23,60903 |
44,73941 |
| 11 |
25,29202 |
75,40104 |
| 12 |
26,084 |
7,653087 |
Целью кинетостатического анализа является определение исходных данных для прочностного расчёта.
Основные задачи динамического анализа:
1. Определение реакций в кинематических парах механизма и внешней уравновешивающей силы (уравновешивающего момента), при которой обеспечивается приятный закон движения начального звена.
2. Расчёт входного звена и построение плана сил.
Чтобы выполнить расчёт, необходимо определить внешние силы и моменты сил, действующие на звенья механизма (движущие силы, силы полезного сопротивления, силы тяжести и сопротивления среды).
Возникновение реакций в кинематических парах обусловлено не только воздействием внешних сил, но и движением звеньев с ускорениями. Дополнительные динамические составляющие реакций учитывают путём введения в расчёт сил инерции звеньев.
В основе кинетостатического метода расчёта лежит принцип ДАламбера.
Силовой анализ ведется от последней группы Ассура к начальному звену, для которого определятся кроме реакций стойки еще и уравновешивающая сила (или уравновешивающий момент).
Исходные данные для силового анализа кривошипно-ползунного механизма кроме данных для кинематического анализа включают следующие параметры: масса кривошипа m2, масса шатуна m3, масса ползуна m5, момент инерции массы кривошипа I2S, момент инерции массы шатуна I3C и силы полезного сопротивления Pп. с.
Силовой анализ производится в обратном порядке кинематическому анализу, то есть от группы Ассура к начальному звену.
За расчетное принимается положение механизма, для которого значение силы полезного сопротивления является наибольшим.
Выбранное положение - 4, для которого характерно:
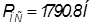 ,
,  ,
,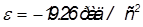
 .
.
Ускорение звеньев находятся по формулам:
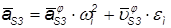 или
или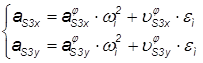 ,
,
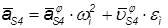 или
или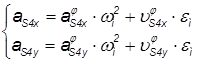 ,
,
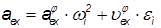 .
.
По расчетам получается:
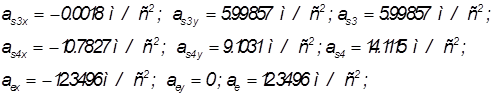 .
.
Угловые ускорения звеньев находятся по формулам:
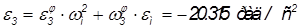 ,
,
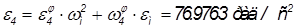 .
.
Силы инерции и моменты сил инерции находятся по формулам:
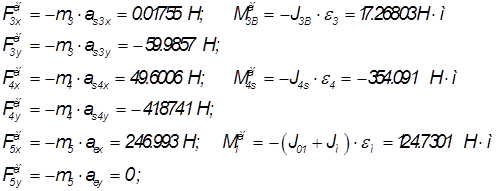
Анализ группы Ассура 4-5
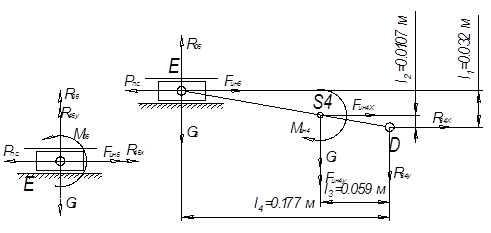
рис.10
Уравнения равновесия:
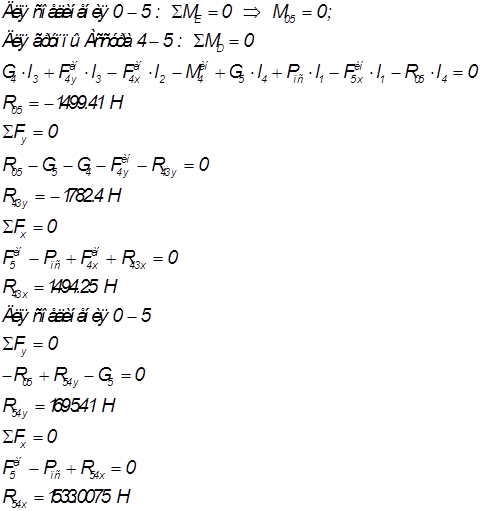
Анализ группы Ассура 2-3

Рис.11
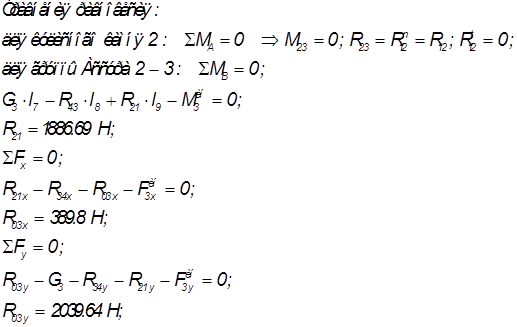
Анализ первичного механизма
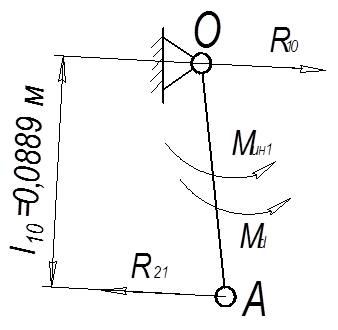
Рис.12
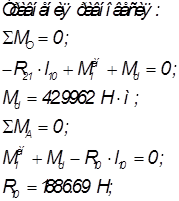
Причины погрешности: измерения плеч сил выполнялись при помощи измерительных средств в графическом режиме; погрешности округлений и вычислений. Подсчет погрешности выполняется по формуле
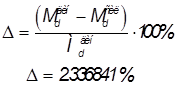
Задача: спроектировать эвольвентную зубчатую передачу по заданному межосевому расстоянию, исключить подрезание ножки зуба меньшего колеса.
Примечание: все расчеты выполнены в программе MATCAD. (Приложение В)
Модульm = 10 мм
Межосевое расстояниеaw = 115 мм
Числа зубьевz1 = 8
z2 = 14
Постоянные параметрыh*a = 1
c* = 0.25
α = 20°
Выражается из формулы межосевого расстояния
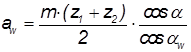 ,
,
где угол зацепления - αw (необходимо определить)
 ;
;
 .
.
Инвалюта угла определяется по формуле
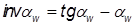 ;
;
 ,
,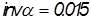 .
.
Вычисляются коэффициенты смещения (суммарный, для первого и второго зубчатого колеса)
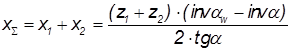 , ,
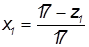 , , ; ;
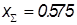 , , , ,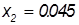 . .
Делительный диаметр:
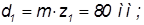 ,
,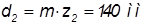 ;
;
Диаметр:
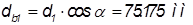 ,
,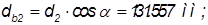 ;
;
Диаметр впадин:
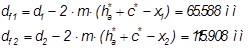 ,
,
Диаметр вершин:
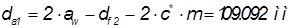 ,
,
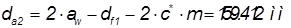 ; ;
Делительный окружной шаг:
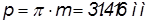 ;
;
Делительная окружная толщина зуба:
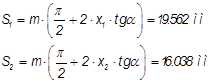 , ,
Делительная окружная ширина впадины:
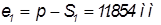 , , ; ;

где инвалюта рассчитывается по формуле:
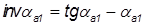 ,
,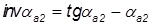 ,
,
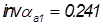 ,
,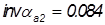 .
.
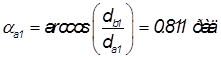 
Рассчитывается окружная толщина зуба по формуле
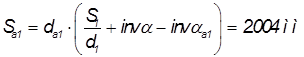 ,
,
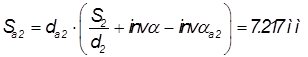 ,
,
Так как 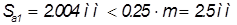 , то первое зубчатое колесо выполнено с заострением зубьев,
, то первое зубчатое колесо выполнено с заострением зубьев, 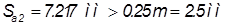 - на втором колесе нет заострений.
- на втором колесе нет заострений.
Коэффициент торцевого перекрытия рассчитывается по формуле
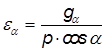 ,
,
где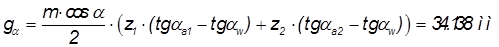 ;
;
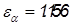
Так как 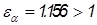 , то зацепление нормальное.
, то зацепление нормальное.
15,6% времени двухконтактное зацепление, а 84,4% времени одноконтактное зацепление.
Коэффициенты удельного давления вычисляются по формулам
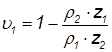 ,
,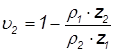 ,
,
где ρ1 и ρ2 - радиусы кривизны зуба первого и второго колеса (соответственно) в точке контакта.
Значения радиусов кривизны и вычисленные коэффициенты удельного давления записываются в таблицу:
| B1 |
H2 |
P |
H1 |
B2 |
| ρ1
|
0 |
10.95 |
18.35 |
34.85 |
50.4 |
| ρ2
|
50.4 |
39.45 |
32.05 |
15.55 |
0 |
| υ1
|
1,00000 |
-1.059 |
0 |
0.745 |
-∞ |
| υ2
|
-∞ |
0.514 |
0 |
-2.922 |
1,00000 |
В связи с тем, что коэффициенты удельного давления для второго зубчатого колеса больше, чем для первого, то износу будет подвержено больше второе колесо.
Цели курсового проекта были выполнены:
а) проектирование структурной и кинематической схемы механизма по данным условиям;
б) анализ установившегося движения механизма при действии заданных сил;
в) силовой анализ механизма с учетом геометрии масс звеньев, сил инерции;
А также выполнен синтез зубчатого механизма с целью получения оптимальной геометрии зубчатого зацепления, удовлетворяющей заданным условиям.
1. Флусов Н.И. Кинематический анализ рычажных механизмов с использованием программы KDSARM.
2. Гуляев К.И. Расчет эвольвентной цилиндрической зубчатой передачи внешнего зацепления.
3. Артоболевский И.И. Теория механизмов и машин. - 4-е изд. - М.: Наука. Гл. ред. физ. - мат. лит., 1988.
|