|
Оглавление. 1
1. Постановка задачи. 2
2. Краткие теоретические сведения. 3
3. Реализация программного средства.7
3.1 Проектирование. 7
3.2 Алгоритм поиска парето-оптимальных решений. 7
3.3 Листингпрограммногокода. 10
4. Пример работы программы.. 24
4.1 Многокритериальная задача. 24
4.2 Двухкритериальная задача. 25
3. Аналитическое задание критериев. 27
Выводы.. 28
Используемая литература. 29
Используемые программные средства. 29
математическая модель парето оптимальность
Необходимо разработать программное средство для поиска парето-оптимальных решений для следующих видов задач:
1) многокритериальная задача
входные данные: количество критериев и решений; весовые значения, заданные напрямую, либо в параметрическом виде.
выходные данные: решения, входящие в множество Парето; номера парето-оптимальных решений из множества исходных решений
2) двухкритериальная задача
входные данные: количество критериев и решений; весовые значения, заданные напрямую, либо в параметрическом виде.
выходные данные: решения, входящие в множество Парето; номера парето-оптимальных решений из множества исходных решений; графическое представление парето-оптимальных решений.
Пусть задан набор числовых функций 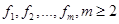 , определенных на множестве возможных решений X. В зависимости от содержания задачи выбора эти функции именуют критериями оптимальности, критериями эффективности или целевыми функциями. , определенных на множестве возможных решений X. В зависимости от содержания задачи выбора эти функции именуют критериями оптимальности, критериями эффективности или целевыми функциями.
Указанные выше числовые функции образуют векторный критерий 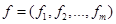 , который принимает значения в пространстве m-мерных векторов , который принимает значения в пространстве m-мерных векторов 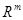 . Это пространство называют критериальным пространством или пространством оценок, а всякое значение . Это пространство называют критериальным пространством или пространством оценок, а всякое значение  именуют векторной оценкой возможного решения x. Все возможные векторные оценки образуют множество возможных оценок (возможных или допустимых векторов) именуют векторной оценкой возможного решения x. Все возможные векторные оценки образуют множество возможных оценок (возможных или допустимых векторов) 
Как правило, между множествами возможных решений X и соответствующим множеством векторов Y можно установить взаимно однозначное соответствие, т.е. каждому возможному решению поставить в соответствие определенный возможный вектор, и обратно – каждому возможному вектору сопоставить определенное возможное решение. В таких случаях выбор во множестве решений с математической точки зрения равносилен выбору во множестве векторов и все определения и результаты можно формулировать как в терминах решений, так и в терминах векторов, причем при желании всегда можно без труда осуществить переход от одной формы изложения к другой.
Задачу выбора, которая включает множество допустимых решений X и векторный критерий f, обычно называют многокритериальной задачей или задачей многокритериальной оптимизации.
Необходимо отметить, что формирование математической модели принятия решений (т.е. построение множества X
и векторного критерия f
) нередко представляет собой сложный процесс, в котором тесно взаимодействуют специалисты двух сторон. А именно, представители конкретной области знаний, к которой относится исследуемая проблема, и специалисты по принятию решений (математики). С одной стороны, следует учесть все важнейшие черты и детали реальной задачи, а с другой, – построенная модель не должна оказаться чрезмерно сложной с тем, чтобы для ее исследования и решения можно было успешно применить разработанный к настоящему времени соответствующий математический аппарат. Именно поэтому этап построения математической модели в значительной степени зависит от опыта, интуиции и искусства исследователей обеих сторон. Его невозможно отождествить с простым формальным применением уже известных, хорошо описанных алгоритмов.
Здесь следует еще добавить, что любая задача выбора (в том числе и многокритериальная) тесно связана с конкретным ЛПР
(лицо, принимающее решение). Уже на стадии формирования математической модели при построении множества возможных решений и векторного критерия дело не обходится без советов, рекомендаций и указаний ЛПР, тем более что векторный критерий как раз и служит. Принятие решения при многих критериях для выражения целей ЛПР. При этом ясно, что построить модель в точности соответствующую всем реальным обстоятельствам невозможно. Модель всегда является упрощением действительности. Важно добиться, чтобы она содержала те черты и детали, которые в наибольшей степени влияют на окончательный выбор наилучшего решения.
Рассмотрим два произвольных возможных решения 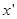 и и  . Для них имеет место один и только один из следующих трех случаев: . Для них имеет место один и только один из следующих трех случаев:
1) справедливо соотношение  (ЛПР первое решение предпочитает второму), (ЛПР первое решение предпочитает второму),
2) справедливо соотношение  (ЛПР второе решение предпочитает первому), (ЛПР второе решение предпочитает первому),
3) не выполняется ни соотношение  , ни соотношение , ни соотношение  (ЛПР не может отдать предпочтение ни одному из указанных двух решений). (ЛПР не может отдать предпочтение ни одному из указанных двух решений).
Заметим, что четвертый случай, когда оба участвующих здесь соотношения  и и  выполняются, невозможен благодаря асимметричности отношения предпочтения выполняются, невозможен благодаря асимметричности отношения предпочтения 
В первом из указанных выше случаев, т.е. при выполнении соотношения  , говорят, что решение , говорят, что решение 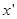 доминирует решение доминирует решение  . .
Если же реализуется третий случай, то говорят, что решения 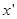 и и  не сравнимы по отношению предпочтения. не сравнимы по отношению предпочтения.
Аксиома Парето.
Для всех пар допустимых решений  , для которых имеет место неравенство , для которых имеет место неравенство  , выполняется соотношение , выполняется соотношение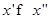
Решение  называется оптимальным по Парето (парето-оптимальным), если не существует такого возможного решения называется оптимальным по Парето (парето-оптимальным), если не существует такого возможного решения  , для которого имеет место неравенство , для которого имеет место неравенство 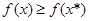 . Все парето-оптимальные решения образуют множество Парето, обозначаемое . Все парето-оптимальные решения образуют множество Парето, обозначаемое 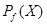
Парето-оптимальное решение – это такое допустимое решение, которое не может быть улучшено (увеличено) ни по одному из имеющихся критериев без ухудшения (уменьшения) по какому-то хотя бы одному другому критерию.
Иначе говоря, предпочитая одному парето-оптимальному решению другое парето-оптимальное решение, ЛПР(лицо, принимающее решение) вынуждено идти на определенный компромисс, соглашаясь на некоторую потерю хотя бы по одному критерию (получая, разумеется, определенный выигрыш, по крайней мере, по какому-то другому критерию). По этой причине множество Парето нередко называют множеством компромиссов.
Понятие оптимальности по Парето играет важную роль в математической экономике. Именно в этой области часто вместо парето-оптимальности используют наименования эффективное решение и множество эффективных решений. Тем самым, парето-оптимальность и эффективность в математической экономике нередко оказываются синонимами.
Среда разработки: VisualStudio 2010
Язык программирования: C#
При проектировании программного средства будем использовать объектно-ориентированный подход.
Список классов с кратким описанием:
1) MainView.cs – это главное окно, служит для ввода данных и запуска работы алгоритма поиска парето-оптимальных решений.
2) SolutionsView.cs – это окно, которое содержит найденные парето-оптимальные решения, представленные в табличной форме
3) GraphView.cs– окно, на котором будет отображаться графическое представление множества Парето для двухкритериальных задач
4) Pareto.cs – это основной класс. Содержит 2 алгоритма поиска множества Парето.
5) Graph.cs – класс, содержащий методы для построения графиков (в данном случае будем использовать стороннюю библиотеку ZedGgraph.dll)
6) File.cs –методы для сохранения и загрузки данных в/из файл(а).
Шаг 1. Положить P(Y) =Y , i =1, j = 2 . Тем самым образуется так называемое текущее множество парето-оптимальных векторов, которое в начале работы алгоритма совпадает с множеством Y , а в конце составит искомое множество парето-оптимальных векторов. Алгоритм устроен таким образом, что искомое множество парето-оптимальных векторов получается из Y последовательным удалением заведомо неоптимальных векторов.
Шаг 2. Проверить выполнение неравенства 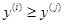 . Если оно оказалось истинным, то перейти к Шагу 3. В противном случае перейти к Шагу 5. . Если оно оказалось истинным, то перейти к Шагу 3. В противном случае перейти к Шагу 5.
Шаг 3. Удалить из текущего множества векторов P(Y) вектор 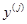 , так как он не является парето-оптимальным. Затем перейти к Шагу 4. , так как он не является парето-оптимальным. Затем перейти к Шагу 4.
Шаг 4. Проверить выполнение неравенства j < N . Если оно имеет место, то положить j = j +1 и вернуться к Шагу 2. В противном случае – перейти к Шагу 7.
Шаг 5. Проверить справедливость неравенства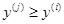 . В том случае, когда оно является истинным, перейти к Шагу 6. В противном случае – вернуться к Шагу 4. . В том случае, когда оно является истинным, перейти к Шагу 6. В противном случае – вернуться к Шагу 4.
Шаг 6. Удалить из текущего множества векторов P(Y) вектор  и перейти к Шагу 7. и перейти к Шагу 7.
Шаг 7. Проверить выполнение неравенства i < N -1. В случае истинности этого неравенства следует последовательно положить i = i +1 , а затем j = i +1. После этого необходимо вернуться к Шагу 2. В противном случае (т.е. когда ) вычисления закончить. К этому моменту множество парето-оптимальных векторов построено полностью. ) вычисления закончить. К этому моменту множество парето-оптимальных векторов построено полностью.
Вначале реализуем вспомогательные методы:
// поэлементное сравнение вектора v1 с вектором v2
private void Compare(List<int> v1, List<int> v2)
{
more = 0;
less = 0;
equal = 0;
for (int i = 0; i < v1.Count; i++)
{
if (v1[i] > v2[i])
more++;
else if (v1[i] < v2[i]) less++;
else equal++;
}
}
// возвращает истину если v1 >= v2
private bool MoreOrEqual()
{
if (more >= 0 && less == 0)
return true;
else return false;
}
Далее напишем рекурсивную процедуру удаления доминируемых решений, опираясь на алгоритм, описанный выше:
// y – списокрешений
public void DeleteDominated(List<List<int>> y)
{
foreach (List<int> yi in y)
{
foreach (List<int> gj in y)
{
if (!Equals(gj, yi))
{
Compare(gj, yi);
if (MoreOrEqual())
{
y.Remove(yi);
DeleteDominated(y);
return;
}
Compare(yi, gj);
if (MoreOrEqual())
{
y.Remove(gj);
DeleteDominated(y);
return;
}
}
}
}
}
И наконец получаем метод, возвращающий список парето-оптимальных решений:
public List<List<int>> GetParetoList(List<List<int>> y)
{
DeleteDominated(y);
return y;
}
3.3
Листингпрограммногокода
public class Graph
{
public ZedGraphControl DisplayGrahpics(Panel panel, int[] x, int[] y, int[] pareto_x, int[] pareto_y)
{
var control = new ZedGraphControl();
control.Width = panel.Width;
control.Height = panel.Height;
GraphPane myPane = control.GraphPane;
// Set the title and axis labels
myPane.Title.IsVisible = false;
//myPane.Title.Text = title;
myPane.XAxis.Title.IsVisible = false;
myPane.YAxis.Title.IsVisible = false;
myPane.YAxis.Scale.MaxAuto = true;
myPane.Legend.IsVisible = false;
PointPairList list1 = new PointPairList();
for (int i = 0; i < x.Length; i++)
list1.Add(x[i], y[i]);
LineItem curve1 = myPane.AddCurve("label", list1, Color.Black, SymbolType.Circle);
curve1.Symbol.Fill = new Fill(Color.Black);
curve1.Symbol.Size = 7;
curve1.Line.IsVisible = false;
PointPairList list2 = new PointPairList();
for (int i = 0; i < pareto_x.Length; i++)
list2.Add(pareto_x[i], pareto_y[i]);
LineItem curve2 = myPane.AddCurve("label", list2, Color.Red, SymbolType.Circle);
curve2.Symbol.Fill = new Fill(Color.Red);
curve2.Symbol.Size = 7;
curve2.Line.IsVisible = false;
// Fill the axis background with a color gradient
myPane.Chart.Fill = new Fill(Color.White, Color.FromArgb(255, 255, 166), 45.0F);
control.AxisChange();
// expand the range of the Y axis slightly to accommodate the labels
myPane.YAxis.Scale.Max += myPane.YAxis.Scale.MajorStep;
return control;
}
}
public class File
{
private StreamWriter writer;
private StreamReader reader;
public void WriteData(List<List<int>> y, string fileName)
{
writer = new StreamWriter(new FileStream(fileName, FileMode.Create, FileAccess.Write));
writer.WriteLine(y.Count.ToString()+ " " + y[0].Count.ToString());
for (int i = 0; i < y.Count; i++)
{
for (int j = 0; j < y[i].Count; j++)
{
writer.Write(y[i][j].ToString() + " ");
}
writer.WriteLine();
}
writer.Close();
}
public List<List<int>> ReadData(string fileName)
{
List<List<int>> y = new List<List<int>>();
int n,m;
reader = new StreamReader(new FileStream(fileName, FileMode.Open, FileAccess.Read));
while (!reader.EndOfStream)
{
char[] separator = { ' ' };
string[] vals = reader.ReadLine().Split(separator, StringSplitOptions.RemoveEmptyEntries);
n = Convert.ToInt32(vals[0]);
m = Convert.ToInt32(vals[1]);
for (int i = 0; i < n; i++)
{
List<int> list = new List<int>();
vals = reader.ReadLine().Split(separator, StringSplitOptions.RemoveEmptyEntries);
for (int j = 0; j < m; j++)
{
list.Add(Convert.ToInt32(vals[j]));
}
y.Add(list);
}
}
reader.Close();
return y;
}
}
public partial class SolutionsView : Form
{
public SolutionsView(List<List<int>> list)
{
InitializeComponent();
int n = list[0].Count;
int m = list.Count;
dataGridView2.ColumnCount = n;
dataGridView2.RowCount = m;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
dataGridView2[j, i].Value = list[i][j];
}
}
}
public partial class GraphView : Form
{
public GraphView()
{
InitializeComponent();
}
public Panel GetPanel()
{
return panel1;
}
}
public partial class MainView : Form
{
private int n, m, krit, comp, var;
private List<List<int>> y;
private List<int> paretoSet;
private List<int> paretoSet2;
private Pareto pareto;
public MainView()
{
InitializeComponent();
InitComboboxes(2, 20, 1);
y = new List<List<int>>();
paretoSet = new List<int>();
dataGridView1.AllowUserToAddRows = false;
dgA.AllowUserToAddRows = false;
dgK.AllowUserToAddRows = false;
dgX.AllowUserToAddRows = false;
}
private void InitComboboxes(int minimum, int maximum, int step)
{
for (int i = minimum; i < maximum; i+=step)
{
comboBox1.Items.Add(i);
comboBox2.Items.Add(i);
comboBox3.Items.Add(i);
comboBox4.Items.Add(i);
comboBox5.Items.Add(i);
}
}
private void button1_Click(object sender, EventArgs e)
{
n = Convert.ToInt32(comboBox1.Text);
m = Convert.ToInt32(comboBox2.Text);
dataGridView1.ColumnCount = n;
dataGridView1.RowCount = m;
for (int i = 0; i < n; i++)
dataGridView1.Columns[i].Name = "k" + (i+1).ToString();
}
private void GetValuesFromGrid()
{
y = new List<List<int>>();
if (tabControl1.SelectedIndex == 0)
{
for (int i = 0; i < m; i++)
{
var list = new List<int>();
for (int j = 0; j < n; j++)
list.Add(Convert.ToInt32(dataGridView1[j, i].Value.ToString()));
y.Add(list);
}
}
else if (tabControl1.SelectedIndex == 1)
{
for (int i = 0; i < var; i++)
{
var list = new List<int>();
for (int j = 0; j < krit; j++)
{
int sum = 0;
for (int k = 0; k < comp; k++)
{
int ai = Convert.ToInt32(dgA[k, j].Value.ToString());
int ki = Convert.ToInt32(dgK[k, j].Value.ToString());
int xi = Convert.ToInt32(dgX[k, i].Value.ToString());
sum += ai * Convert.ToInt32(Math.Pow((double)xi, (double)k));
}
list.Add(sum);
}
y.Add(list);
}
}
}
private void button2_Click(object sender, EventArgs e)
{
textBox1.Text = "";
paretoSet = new List<int>();
if (y.Count == 0)
GetValuesFromGrid();
pareto = new Pareto();
paretoSet = pareto.GetPareto(y);
paretoSet2 = pareto.GetPareto2(y);
WriteList("метод1: ",paretoSet);
WriteList(" метод2: ", paretoSet2);
SolutionsView solView = new SolutionsView(pareto.GetParetoList(y));
solView.Show();
if (krit == 2 || n==2)
DrawGraph();
}
private void WriteList(string text, List<int> set)
{
textBox1.Text += text;
foreach (int val in set)
textBox1.Text += (val+1).ToString() + "; ";
}
private void InitGrid()
{
krit = Convert.ToInt32(comboBox3.Text);
var = Convert.ToInt32(comboBox4.Text);
comp = Convert.ToInt32(comboBox5.Text);
dgA.ColumnCount = comp;
dgK.ColumnCount = comp;
dgX.ColumnCount = comp;
dgA.RowCount = krit;
dgK.RowCount = krit;
dgX.RowCount = var;
}
private void button3_Click(object sender, EventArgs e)
{
InitGrid();
for (int q = 0; q < comp; q++)
{
dgK.Columns[q].Name = (q + 1).ToString();
dgA.Columns[q].Name = (q + 1).ToString();
dgX.Columns[q].Name = (q + 1).ToString();
}
}
private void dataGridView1_CellFormatting(object sender, DataGridViewCellFormattingEventArgs e)
{
}
// Двумерный случай/ графическое представление
private void DrawGraph()
{
GraphView form2 = new GraphView();
form2.Show();
GetValuesFromGrid();
int cnt;
if (m == 0)
cnt = var;
else cnt = m;
int[] x_ = new int[cnt - paretoSet.Count];
int[] y_ = new int[cnt - paretoSet.Count];
for (int i = 0; i < cnt - paretoSet.Count; i++)
{
x_[i] = y[pareto.deleted[i]][0];
y_[i] = y[pareto.deleted[i]][1];
}
cnt = paretoSet.Count;
int[] pareto_x = new int[cnt];
int[] pareto_y = new int[cnt];
for (int i = 0; i < cnt; i++)
{
pareto_x[i] = y[paretoSet[i]][0];
pareto_y[i] = y[paretoSet[i]][1];
}
panel1 = form2.GetPanel();
var control = new Graph().DisplayGrahpics(panel1, x_,y_, pareto_x, pareto_y);
panel1.Controls.Clear();
panel1.Controls.Add(control);
panel1.Invalidate();
}
// Random values
private void button2_Click_1(object sender, EventArgs e)
{
Random random = new Random();
if (tabControl1.SelectedIndex == 0)
{
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
dataGridView1[j, i].Value = random.Next(20);
}
}
}
else if (tabControl1.SelectedIndex == 1)
{
for (int i = 0; i < comp; i++)
{
for (int j = 0; j < krit; j++)
{
dgA[i, j].Value = random.Next(5);
dgK[i, j].Value = random.Next(5);
}
for (int q = 0; q < var; q++)
{
dgX[i, q].Value = random.Next(5);
}
}
}
}
private void сохранитьКакToolStripMenuItem_Click(object sender, EventArgs e)
{
if (this.saveFileDialog1.ShowDialog() == DialogResult.OK)
{
if (y.Count == 0)
GetValuesFromGrid();
new File().WriteData(y, this.saveFileDialog1.FileName);
}
}
private void открытьToolStripMenuItem_Click(object sender, EventArgs e)
{
if (this.openFileDialog1.ShowDialog() == DialogResult.OK)
{
y = new File().ReadData(this.openFileDialog1.FileName);
FillGridFromList(y);
}
}
private void FillGridFromList(List<List<int>> list)
{
n = list[0].Count;
m = list.Count;
dataGridView1.ColumnCount = n;
dataGridView1.RowCount = m;
comboBox1.Text = n.ToString();
comboBox2.Text = m.ToString();
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
dataGridView1[j, i].Value = list[i][j];
}
}
}
}
1) Реализуем пример, описанный в пособии №1 из списка использованной литературы. Для этого воспользуемся уже заготовленным файлом пример1.txt:

2) Найдем парето-оптимальные решения:

1) Продемонстрируем работу программы для двухкритериальной задачи. Пусть количество решений будет равно 11.

2) Результат работы программы:

Красным цветом выделены парето-оптимальные решения. Черным – доминируемые решения.
Пусть количество критериев 6
Количество решений 16
Весовые значения будут находиться по формуле:
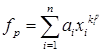 , где p – число критериев, n – количество компонент решения, a, k, x – задаются в таблице: , где p – число критериев, n – количество компонент решения, a, k, x – задаются в таблице:

В результате получаем список парето-оптимальных решений, состоящих из трех векторов:
В результате проделанной работы было разработано программное средство для поиска парето-оптимальных решений для многокритериальных задач.
Данное приложение может использоваться лишь как демонстрационно-обучающее по теме «Многокритериальные задачи. Множество Парето» дисциплины «Теория принятия решений». Это связано с тем, что практически невозможно формализовать математическую модель векторных оценок. Каждая задача поиска оптимальных решений требует собственного подхода.
1. В.Д. Ногин. Принятие решений при многих критериях. Учебнометодическое
пособие.– СПб. Издательство «ЮТАС», 2007. – 104 с.
2. Парето-оптимальные решения многокритериальных задач. Подинвоский В.В., Ногин В.Д. –М. Главная редакция физико-математической литературы, 1982. – 256с.
MicrosoftVisualStudio 2010
|