Задание 1
Осуществить интерполяцию с помощью полинома Ньютона исходных данных из табл. 1 вычислить значение интерполяционного полинома в точке 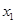 . .
Таблица 1
| Порядковый номер исходных данных |
| № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Х |
1,415 |
1,420 |
1,425 |
1,430 |
1,435 |
1,440 |
1,445 |
1,450 |
1,455 |
1,460 |
| У |
0,888 |
0,889 |
0,89 |
0,891 |
0,892 |
0,893 |
0,894 |
0,895 |
0,896 |
0,897 |
интерполяция погрешность производная
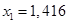
Решение
Интерполяционный многочлен Ньютона для равноотстоящих узлов записывается в виде

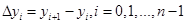 - конечная разность первого порядка - конечная разность первого порядка
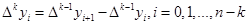 - конечная разность К-го порядка. - конечная разность К-го порядка.
Таблица конечных разностей для экспериментальных данных:
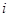 |
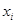 |
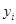 |
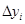 |
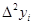 |
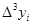 |
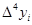 |
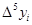 |
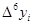 |
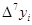 |
 |
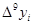 |
| 1 |
1,415 |
0,888 |
0,001 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
1,420 |
0,889 |
0,001 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
1,425 |
0,89 |
0,001 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
1,430 |
0,891 |
0,001 |
0 |
0 |
0 |
0 |
0 |
| 5 |
1,435 |
0,892 |
0,001 |
0 |
0 |
0 |
0 |
| 6 |
1,440 |
0,893 |
0,001 |
0 |
0 |
0 |
| 7 |
1,445 |
0,894 |
0,001 |
0 |
0 |
| 8 |
1,450 |
0,895 |
0,001 |
0 |
| 9 |
1,455 |
0,896 |
0,001 |
| 10 |
1,460 |
0,897 |
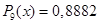 . .
Задание 2
Уточнить значение корня на заданном интервале тремя итерациями и найти погрешность вычисления.
 , [0,4]. , [0,4].
Решение
Вычислим первую и вторую производную функции
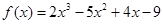 . Получим . Получим 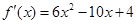 и и 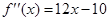 . .
Итерационное уравнение запишется так:
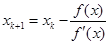 . .
В качестве начального приближения возьмем правый конец отрезка 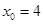 . .
Проверяем условие сходимости:
 . .
Условие сходимости метода Ньютона выполнено.
Таблица значений корня уравнения:
| i |
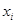 |
| 1 |
3,083 |
| 2 |
2,606 |
| 3 |
2,453 |
Уточненное значение корня 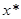 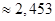 . .
В качестве оценки абсолютной погрешности полученного результата можно использовать величину
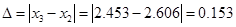 . .
Задание 3
Методами треугольников, трапеций и Симпсона вычислить определенный интеграл.

Решение
Метод прямоугольников
Значение интеграла на интервале определяется следующей формулой:
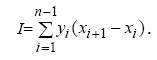
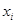 |
 слева слева |
 справа справа |
| 1 |
0,25 |
0,2 |
| 2 |
0,2 |
0,1667 |
| 3 |
0,1667 |
0,1429 |
| 4 |
0,1429 |
0,125 |
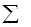 |
0,7595 |
0,6345 |
Значение интеграла:  . .
Метод трапеций
Площадь трапеции равняется полусумме оснований, умноженной на высоту, которая равна расстоянию между точками по оси х. интеграл равен сумме площадей всех трапеций.

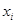 |
 |
| 1 |
0,25 |
| 2 |
0,2 |
| 3 |
0,1667 |
| 4 |
0,1429 |
| 5 |
0,125 |
Значение интеграла:  . .
Метод Симпсона
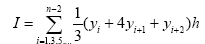
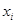 |
 |
| 1 |
0,25 |
| 2 |
0,2 |
| 3 |
0,1667 |
| 4 |
0,1429 |
Значение интеграла: 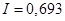 . .
Задание 4
Проинтегрировать уравнение методом Эйлера на интервале [0.2, 1.2] . Начальное условие у(0,2)=0,25.
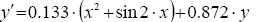
Решение
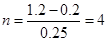
Все вычисления удобно представить в виде таблицы:
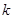 |
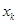 |
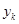 |
 |
 |
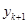 |
| 0 |
0,2 |
0,2500 |
0,2751 |
0,0688 |
0,3188 |
| 1 |
0,45 |
0,3188 |
0,4091 |
0,1023 |
0,4211 |
| 2 |
0,7 |
0,4211 |
0,5634 |
0,1408 |
0,5619 |
| 3 |
0,95 |
0,5619 |
0,7359 |
0,1840 |
0,7459 |
| 4 |
1,2 |
0,7459 |
0,9318 |
0,2329 |
Таким образом, задача решена.
Задание 5
Задача 1. Вычислить сумму и разность комплексных чисел, заданных в показательной форме. Переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.
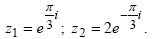
Задача 2. Вычислить произведение и частное комплексных чисел. Операнды и результаты изобразить на комплексной плоскости.
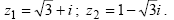
Решение
Задача 1.
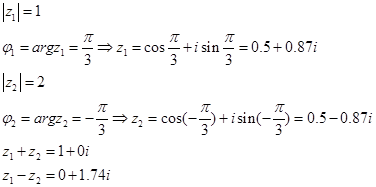

Задача 2.


Задание 6
Вычислить производную функции f(z) в точке 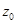 . .


Решение
Так как для аналитических функций справедливы все формулы и правила дифференцирования действительного аргумента, то

Задание 7
Вычислить интеграл по замкнутым контурам а) и б), считая обход контура в положительном направлении. Нарисовать область интегрирования, указать на рисунке особые точки.

Решение
а)

Подынтегральная функция имеет особые точки: 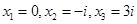 . Тогда интеграл вычистится по следующей формуле: . Тогда интеграл вычистится по следующей формуле:
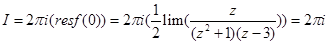 . .
б)

Подынтегральная функция имеет особые точки: 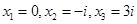 . Тогда интеграл вычистится по следующей формуле: . Тогда интеграл вычистится по следующей формуле:
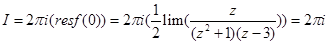 . .
|