Министерство образования и науки Российской Федерации
Волгоградский государственный технический университет
(ВолгГТУ)
Кафедра Технология машиностроения
Семестровая работа
по метрологии
Обработка результатов прямых многократных измерений
Выполнил: ст. гр. АУ – 323 Добриньков А. В.
Проверил: Карабань В. Г.
Волгоград 2010
Задание
1. Построить полигон, гистограмму и теоретическое распределение измеренных величин.
2. Проверить согласие теоретического и эмпирического распределений.
3. Определить доверительные интервалы.
4. Определить границы диапазона рассеивания значений и погрешностей.
Исходные данные
| Номер интервала |
Границы интервалов  |
Частотаmi
|
| свыше |
до |
| 1 |
19,97 |
19,99 |
2 |
| 2 |
19,99 |
20,01 |
2 |
| 3 |
20,01 |
20,03 |
12 |
| 4 |
20,03 |
20,05 |
25 |
| 5 |
20,05 |
20,07 |
35 |
| 6 |
20,07 |
20,09 |
62 |
| 7 |
20,09 |
20,11 |
66 |
| 8 |
20,11 |
20,13 |
77 |
| 9 |
20,13 |
20,15 |
39 |
| 10 |
20,15 |
20,17 |
29 |
| 11 |
20,17 |
20,19 |
20 |
| 12 |
20,19 |
20,21 |
7 |
| 13 |
20,21 |
20,23 |
2 |
1. Построение эмпирического и теоретического распределений
При построении гистограмм и полигонов по оси абсцисс откладывают значения результатов измерений (середины интервалов xi
), а по оси ординат – вероятность попадания в каждый i – тый интервал:
 . .
Вычислим  на каждом участке: (Σmi
= 378) на каждом участке: (Σmi
= 378)
| Номер интервала |
Эмпирические частности  |
Середина интервала  , мм , мм |
| 1 |
0,005291 |
19,98 |
| 2 |
0,005291 |
20,00 |
| 3 |
0,031746 |
20,02 |
| 4 |
0,066138 |
20,04 |
| 5 |
0,092593 |
20,06 |
| 6 |
0,164021 |
20,08 |
| 7 |
0,174603 |
20,10 |
| 8 |
0,203704 |
20,12 |
| 9 |
0,103175 |
20,14 |
| 10 |
0,07672 |
20,16 |
| 11 |
0,05291 |
20,18 |
| 12 |
0,018519 |
20,20 |
| 13 |
0,005291 |
20,22 |
Построим гистограмму и полигон по полученным значениям:
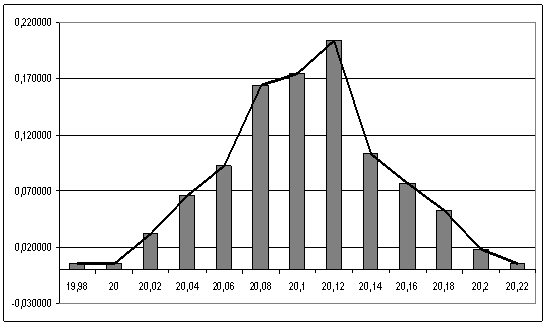
Для построения теоретического распределения необходимо определить приближённые значения математического ожидания 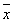 и среднеквадратического отклонения S. и среднеквадратического отклонения S.
| Номер интервала |
Частота  |
Середина интервала  |
mi
xi
|
mi
xi
2
|
S |
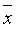 |
| 1 |
2 |
19,98 |
39,96 |
798,4008 |
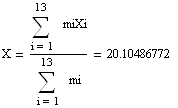
0,043395663 |
20,10486772 |
| 2 |
2 |
20 |
40 |
800 |
| 3 |
12 |
20,02 |
240,24 |
4809,6048 |
| 4 |
25 |
20,04 |
501 |
10040,04 |
| 5 |
35 |
20,06 |
702,1 |
14084,126 |
| 6 |
62 |
20,08 |
1244,96 |
24998,7968 |
| 7 |
66 |
20,1 |
1326,6 |
26664,66 |
| 8 |
77 |
20,12 |
1549,24 |
31170,7088 |
| 9 |
39 |
20,14 |
785,46 |
15819,1644 |
| 10 |
29 |
20,16 |
584,64 |
11786,3424 |
| 11 |
20 |
20,18 |
403,6 |
8144,648 |
| 12 |
7 |
20,2 |
141,4 |
2856,28 |
| 13 |
2 |
20,22 |
40,44 |
817,6968 |
| Σ |
378 |
7599,64 |
152790,47 |

По виду гистограммы и полигона предполагаем нормальный закон распределения с функцией плотности
рассеивание погрешность гистограмма плотность
 , ,
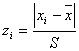 , ,
а вероятность попадания результата измерений в i-тый интервал величиной h = 0.02:
 . .
| Номер интервала |
Середина интервала  |
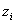 |
 |
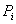 |
 |
| 1 |
19,98 |
2,877424 |
0,006354 |
0,002928 |
0,005291 |
| 2 |
20,00 |
2,416549 |
0,02152 |
0,009918 |
0,005291 |
| 3 |
20,02 |
1,955673 |
0,058938 |
0,027163 |
0,031746 |
| 4 |
20,04 |
1,494797 |
0,13053 |
0,060158 |
0,066138 |
| 5 |
20,06 |
1,033922 |
0,233766 |
0,107737 |
0,092593 |
| 6 |
20,08 |
0,573046 |
0,338534 |
0,156022 |
0,164021 |
| 7 |
20,10 |
0,112171 |
0,39644 |
0,18271 |
0,174603 |
| 8 |
20,12 |
0,348705 |
0,37541 |
0,173017 |
0,203704 |
| 9 |
20,14 |
0,80958 |
0,287466 |
0,132486 |
0,103175 |
| 10 |
20,16 |
1,270456 |
0,178001 |
0,082036 |
0,07672 |
| 11 |
20,18 |
1,731331 |
0,089127 |
0,041076 |
0,05291 |
| 12 |
20,20 |
2,192207 |
0,036087 |
0,016632 |
0,018519 |
| 13 |
20,22 |
2,653083 |
0,011815 |
0,005445 |
0,005291 |
Построим теоретическое распределение результатов измерений
 : :

2. Проверка согласия эмпирического и теоретического распределений
Согласно критерию Колмогорова, сравнивают эмпирические и теоретические значения, но уже не плотности распределения, а интегральной функции F(xi
). Значение максимальной (по абсолютной величине) разности между ними DN
подставляют в выражение:
 , ,
где  – объём выборки. Считают, что эмпирическое распределение хорошо согласуется с теоретическим, если – объём выборки. Считают, что эмпирическое распределение хорошо согласуется с теоретическим, если 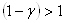 . .
Таблица
| Номер интервала |
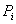 |
 |
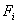 |
 |
 |
| 1 |
0,002928 |
0,005291 |
0,002928 |
0,005291 |
0,002363 |
| 2 |
0,009918 |
0,005291 |
0,012846 |
0,010582 |
0,002264 |
| 3 |
0,027163 |
0,031746 |
0,040009 |
0,042328 |
0,002319 |
| 4 |
0,060158 |
0,066138 |
0,100168 |
0,108466 |
0,008298 |
| 5 |
0,107737 |
0,092593 |
0,207904 |
0,201058 |
0,006846 |
| 6 |
0,156022 |
0,164021 |
0,363927 |
0,365079 |
0,001153 |
| 7 |
0,182710 |
0,174603 |
0,546636 |
0,539683 |
0,006954 |
| 8 |
0,173017 |
0,203704 |
0,719653 |
0,743386 |
0,023733 |
| 9 |
0,132486 |
0,103175 |
0,852140 |
0,846561 |
0,005579 |
| 10 |
0,082036 |
0,076720 |
0,934176 |
0,923280 |
0,010895 |
| 11 |
0,041076 |
0,052910 |
0,975252 |
0,976190 |
0,000938 |
| 12 |
0,016632 |
0,018519 |
0,991884 |
0,994709 |
0,002825 |
| 13 |
0,005445 |
0,005291 |
0,997329 |
1,000000 |
0,002671 |
В нашем случае максимальное значение разности:
DN
= F’8
– F8
= 0,023733, N = ∑mi
= 378
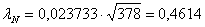
Для lN
=0,4614 по таблице находим g = 0,01 Þ (1 – 0,01) = 0,99 > 0,1. Т. о. эмпирическое распределение хорошо согласуется с теоретическим.
3. Определение доверительных интервалов
Доверительный интервал для математического ожидания M определяется из выражения:
 , ,
значение tg
возьмём из справочника, для g » 0,01 и N = 13: tg
= 3,06,
тогда 20,06804 мм < M < 20,14170 мм
Доверительный интервал для среднего квадратического отклонения  определим из выражения: определим из выражения:
 , ,
значения c1
2
и c2
2
определяем по справочнику, для g1
» 0,01 , g2
» 0,99 и N=13: c1
2
=26,2; c2
2
=3,57,
тогда 0,02937 мм <
 <0,07956 мм <0,07956 мм
4. Определение диапазона рассеивания значений
Определение границ диапазона рассеивания значений по результатам измерений, при вероятности риска 0,027.
М » 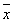 = 20,10486772 мм = 20,10486772 мм
S »  = 0,043395663 мм = 0,043395663 мм
М-3 » 19.9747 мм » 19.9747 мм
М+3 » 20.2351 мм » 20.2351 мм
Определение границ диапазона рассеивания значений по результатам измерений, при допускаемом значении вероятности риска 2β=0,001.
М± σ σ


 = 0,4995, Þ = 0,4995, Þ  = 3,29 = 3,29
М-3,29 = 19,9621 мм = 19,9621 мм
М+3,29 = 20,2476 мм = 20,2476 мм
Для партии деталей проведены измерения координат X,Y двух отверстий 1 и 2. Определить средний размер и среднее квадратическое отклонение размера межцентрового расстояния.
| Номер измерения |
Значения параметра |
| X1 |
X2 |
Y1 |
Y2 |
| 1 |
26,792 |
28,394 |
29,9 |
31,911 |
| 2 |
26,787 |
28,487 |
29,901 |
31,922 |
| 3 |
26,79 |
28,39 |
29,913 |
31,914 |
| 4 |
26,792 |
28,592 |
29,902 |
31,899 |
| 5 |
26,791 |
28,494 |
29,903 |
31,898 |
| 6 |
26,782 |
28,485 |
29,912 |
31,91 |
| 7 |
26,792 |
28,591 |
29,901 |
31,891 |
| 8 |
26,792 |
28,791 |
29,903 |
31,902 |
| 9 |
26,787 |
28,584 |
29,912 |
31,898 |
| 10 |
26,793 |
28,572 |
29,906 |
31,907 |
| 11 |
26,79 |
28,493 |
29,9 |
31,899 |
| 12 |
26,794 |
28,493 |
29,912 |
31,898 |
| 13 |
26,786 |
28,576 |
29,903 |
31,889 |
Для определения среднего размера 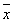 и среднего квадратического отклонения S воспользуемся следующими формулами: и среднего квадратического отклонения S воспользуемся следующими формулами:


где N=13
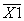 = 26,7898 мм = 26,7898 мм  = 0,003411895 мм = 0,003411895 мм
 = 28,534 мм = 28,534 мм  = 0,10339165 мм = 0,10339165 мм
 = 29,9052 мм = 29,9052 мм  = 0,005117842 мм = 0,005117842 мм
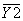 = 31,9029 мм = 31,9029 мм  = 0,009393806 мм = 0,009393806 мм
Определим средний размер межцентрового расстояния:
 = 2,1318 мм = 2,1318 мм
Определим среднее квадратическое отклонение размера межцентрового расстояния по формуле:
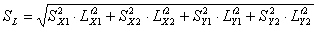 , ,
где  – частная производная по – частная производная по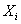 от от  и и  – частная производная по – частная производная по  от от  : :
 = -0,3491 = -0,3491
 = 0,3491 = 0,3491
 = -0,9371 = -0,9371
 = 0,9371 = 0,9371
Т. о. SL
= 0,0375 мм.
|