Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
Бийский Педагогический Государственный Университет имени В.М. Шукшина
Физико-математический факультет
Кафедра математики
Курсовая работа
Уравнение Дирака в квантовой теории
Выполнил: студент 4курса ФМФ
Губин А.А.
Научный руководитель:
Царегородцев Л.И.
Бийск, 2011
Содержание
Введение
1. Уравнение Дирака
2. Матрица Дирака. Свойства матриц Дирака
3. Спиноры
4. Общее решение уравнения Дирака
Заключение
Список литературы
Введение
Курсовая работа состоит из введения, четырех параграфов, заключения и списка с литературой.
В первом параграфе раскрывается понятие об уравнение Дирака и вводится обозначение матриц Дирака  , записывается вид уравнения Дирака. Во втором параграфе рассматриваются основные свойства матриц Дирака. В третьем – определяется понятие о спиноре. А в четвертом параграфе выводится решение уравнения Дирака в виде плоских волн. , записывается вид уравнения Дирака. Во втором параграфе рассматриваются основные свойства матриц Дирака. В третьем – определяется понятие о спиноре. А в четвертом параграфе выводится решение уравнения Дирака в виде плоских волн.
Кратко остановимся на релятивистских обозначениях, которые будут нами использоваться.
Пространственно-временные координаты будут обозначаться 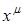 , причем , причем  , ,  , ,  и и  ; ; 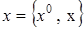 . Мы будем использовать метрический тензор . Мы будем использовать метрический тензор  с компонентами с компонентами

 при при 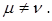
уравнение дирак матрица спинор
В связи с этим нужно различать ковариантные и контравариантные векторы. Контравариантный вектор (преобразующийся как координатный вектор 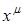 ) будет обозначаться ) будет обозначаться  , а ковариантный (преобразующийся как градиент) будет обозначаться , а ковариантный (преобразующийся как градиент) будет обозначаться 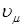 . Аналогичные обозначения будут приняты и для тензоров. Греческие индексы будут применяться для обозначения компонент (0, 1, 2, 3) пространственно-временного тензора, а латинские индексы – только для обозначения пространственных компонент (1, 2, 3). Операции опускания и поднимания индексов с помощью метрического тензора определяются следующим образом: . Аналогичные обозначения будут приняты и для тензоров. Греческие индексы будут применяться для обозначения компонент (0, 1, 2, 3) пространственно-временного тензора, а латинские индексы – только для обозначения пространственных компонент (1, 2, 3). Операции опускания и поднимания индексов с помощью метрического тензора определяются следующим образом:

где предполагается суммирование от 0 до 3 по повторяющимся греческим индексам, т.е

Тензор 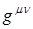 определяется уравнением определяется уравнением 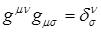 , где , где 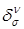 – символ Кронекера: – символ Кронекера:  , если , если  , и , и 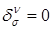 в противном случае. в противном случае.
Введем в рассмотрение еще несколько понятий.
Транспонированным к 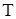 называют тензор называют тензор 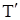 , который имеет в каком-либо базисе , который имеет в каком-либо базисе  "перевернутые" компоненты: "перевернутые" компоненты:

Транспонированный тензор обозначают как  . .
Симметричным называют такой тензор, транспонированный к которому совпадает с исходным:

Тензор 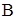 называют обратным к называют обратным к 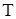 , если его скалярное произведение на , если его скалярное произведение на 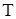 дает единичный тензор. Такой тензор дает единичный тензор. Такой тензор 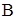 обозначают как обозначают как 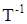 : :

Ортогональным называют тензор 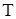 , обратный к которому тензор , обратный к которому тензор 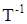 совпадает с транспонированным совпадает с транспонированным  . .
1. Уравнение Дирака
В начале XX века, пытаясь преодолеть трудности с отрицательными плотностями вероятности в уравнении Клейна-Гордона, которое выглядит следующим образом:
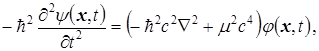 (1.1) (1.1)
Дирак открыл релятивистское уравнение, которое теперь называют в его честь. Долгое время после открытия уравнения Дирака считали, что для частиц с массой это единственное правильное релятивистское волновое уравнение. И только после того, как Паули и Вайскопф дали новую интерпретацию уравнения Клейна-Гордона как уравнения для поля, это широко распространившееся мнение было опровергнуто. Но даже и теперь уравнение Дирака имеет особое значение, так как оно описывает частицы со спином 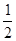 , а спин , а спин 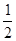 имеют электроны и протоны (с понятием "спинор" познакомимся ниже). Многие другие "элементарные частицы" также обладают спином имеют электроны и протоны (с понятием "спинор" познакомимся ниже). Многие другие "элементарные частицы" также обладают спином 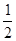 . .
Соображения, которые привели Дирака к его уравнению, следующие. Для того, чтобы предотвратить появление отрицательных вероятностей, нужно, чтобы в выражении для плотности
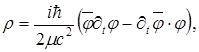 (1.2) (1.2)
не было производных по времени. Поэтому волновое уравнение должно содержать производные по времени не выше первого порядка. Но релятивистская ковариантность требует полной симметрии по всем пространственным и временным координатам. Поэтому нужно, чтобы в волновое уравнение входили производные только первого порядка и по пространственным переменным. Таким образом, волновая функция Дирака должна удовлетворять линейному дифференциальному уравнению первого порядка по всем четырем координатам. Линейность уравнения нужна, чтобы удовлетворить принципу суперпозиции квантовой механики. Если мы хотим, чтобы волновая функция  описывала свободную частицу с массой m, то нужно потребовать, чтобы она подчинялась уравнению описывала свободную частицу с массой m, то нужно потребовать, чтобы она подчинялась уравнению
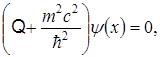 (1.3) (1.3)
Где

оператор Даламбера, так как уравнение означает, что между энергией и импульсом свободной частицы выполняется соотношение 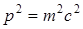 и что в согласии с принципом соответствия имеется предельный переход к случаю классической теории относительности. и что в согласии с принципом соответствия имеется предельный переход к случаю классической теории относительности.
Аналогичная ситуация встречается и электродинамике, где уравнения Максвелла являются уравнениями первого порядка, связывающими компоненты напряженностей поля. В то же время каждая компонента электрической и магнитной напряженностей подчиняется волновому уравнению. Волновое уравнение в электродинамике является уравнением второго порядка, не содержащим массового члена, что свидетельствует о нулевой массе покоя фотона.
Предположим, что  имеет N компонент имеет N компонент  , причем мы заранее не фиксируем значение N. Наиболее общим линейным уравнением первого порядка является уравнение, выражающее временную производную одной компоненты в виде линейной комбинации всех компонент и их пространственных производных. Если подставить соответствующие размерные множители, то наиболее общее уравнение можно записать в виде , причем мы заранее не фиксируем значение N. Наиболее общим линейным уравнением первого порядка является уравнение, выражающее временную производную одной компоненты в виде линейной комбинации всех компонент и их пространственных производных. Если подставить соответствующие размерные множители, то наиболее общее уравнение можно записать в виде
 (1.4) (1.4)
На основе предположения об однородности пространства-времени 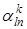 и и 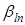 являются безразмерными константами, не зависящими от пространственно-временных координат являются безразмерными константами, не зависящими от пространственно-временных координат 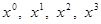 . Естественный способ упрощения вида этих уравнений состоит в использовании матричной записи, которая позволяет представить систему уравнений (1.4) в виде . Естественный способ упрощения вида этих уравнений состоит в использовании матричной записи, которая позволяет представить систему уравнений (1.4) в виде
 (1.5) (1.5)
В этом уравнении  есть матрица-столбец с N строками, а есть матрица-столбец с N строками, а  и и  – матрицы, имеющие по N строк и столбцов. Уравнение (1.5) и известно как уравнение Дирака. – матрицы, имеющие по N строк и столбцов. Уравнение (1.5) и известно как уравнение Дирака.
Теперь найдем выражения для плотности и тока, которые соответствуют уравнению (1.5). Так как мы хотим сохранить для  привычное определение, то полагаем привычное определение, то полагаем
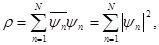 (1.6а) (1.6а)
или в матричной записи
 (1.6б) (1.6б)
где  – величина, эрмитово сопряженная – величина, эрмитово сопряженная  , а следовательно, являющаяся матрицей-строкой, содержащей одну строку и N столбцов. Выражения (1.6) для плотности явно положительны определены и, таким образом, отвечают основным требованиям Дирака. Далее потребуем, чтобы , а следовательно, являющаяся матрицей-строкой, содержащей одну строку и N столбцов. Выражения (1.6) для плотности явно положительны определены и, таким образом, отвечают основным требованиям Дирака. Далее потребуем, чтобы  удовлетворяла уравнению неразрывности удовлетворяла уравнению неразрывности
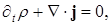 (1.7) (1.7)
где ток j еще должен быть определен. Можно надеяться, что тогда будет применима обычная вероятностная интерпретация. Величина  удовлетворяет уравнению удовлетворяет уравнению
 (1.8) (1.8)
которое получается эрмитовым сопряжением уравнением (1.5). Как и выше, " " является знаком эрмитова сопряжения, при котором матрицы " является знаком эрмитова сопряжения, при котором матрицы 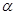 и и  транспонируются и комплексно сопрягаются, например транспонируются и комплексно сопрягаются, например
 (1.9) (1.9)
Перестановка  с с  в (1.8) необходима потому, что в (1.8) необходима потому, что  – строка, и, следовательно, – строка, и, следовательно, 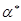 и и  должны стоять после нее (а не перед ней). должны стоять после нее (а не перед ней).
Уравнение неразрывности типа (1.7) можно теперь вывести из уравнений (1.5) и (1.8), если первое умножить на  слева, а второе – на слева, а второе – на  справа и сложить получившиеся результаты. Это приводит к уравнению справа и сложить получившиеся результаты. Это приводит к уравнению
 (1.10) (1.10)
Последний член не содержит производных. Поэтому, если мы хотим отождествить уравнение (1.10) с уравнением (1.7), нужно добиться, чтобы этот член был равен нулю. Это можно достигнуть, если потребовать, чтобы
 (1.11) (1.11)
то есть чтобы матрица  была эрмитовой. Для отождествления второй группы членов в уравнении (1.10) с дивергенцией мы потребуем далее, чтобы была эрмитовой. Для отождествления второй группы членов в уравнении (1.10) с дивергенцией мы потребуем далее, чтобы
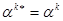 (1.12) (1.12)
Другими словами, и 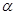 и и  должны быть эрмитовыми матрицами. Другой путь, ведущий к тому же результату,— переписать уравнение (1.5) в гамильтоновой форме: должны быть эрмитовыми матрицами. Другой путь, ведущий к тому же результату,— переписать уравнение (1.5) в гамильтоновой форме:
 (1.13) (1.13)
Ясно, что для эрмитовости H матрицы 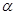 и и  должны быть эрмитовыми. Сравнивая (1.7) с (1.10), заключаем должны быть эрмитовыми. Сравнивая (1.7) с (1.10), заключаем
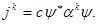 (1.14) (1.14)
Для вывода дальнейших свойств матриц 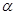 и и  нужно исследовать условия, которое накладывает требование, чтобы функция нужно исследовать условия, которое накладывает требование, чтобы функция  удовлетворяла уравнению удовлетворяла уравнению
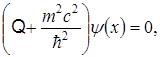 (1.3) (1.3)
Где

С этой целью умножим уравнение (1.5) на оператор

Который приведет к появлению вторых производных. Члены с  и со смешанными пространственно-временными производными сокращаются, и мы получаем и со смешанными пространственно-временными производными сокращаются, и мы получаем
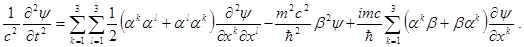 (1.15) (1.15)
Мы симметризовали здесь член 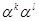 , что можно зделать вследствие коммутации , что можно зделать вследствие коммутации  и и  . Чтобы уравнение (1.15) согласовалось с уравнением Клейна-Гордона, необходимо его правую часть свести к . Чтобы уравнение (1.15) согласовалось с уравнением Клейна-Гордона, необходимо его правую часть свести к

Это накладывает следующие условия:
 (1.16) (1.16)
 (1.17) (1.17)
 (1.18) (1.18)
то есть матрицы 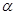 должны антикоммутировать между собой и с матрицей должны антикоммутировать между собой и с матрицей  , а квадрат каждой из четырех матриц должен быть равен единице. , а квадрат каждой из четырех матриц должен быть равен единице.
В уравнении (1.16) символ  – контравариантный символ Кронекера, значение которого совпадает с – контравариантный символ Кронекера, значение которого совпадает с  , где , где  – смешанный символ Кронекера, причем – смешанный символ Кронекера, причем

В практических приложениях нет необходимости использовать явное представление для 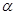 и и  ; достаточно знать, что они эрмитовы и обладают свойствами (1.16) – (1.18). Более того, при решении задач удобнее обходиться без явного вида матриц. Однако их явное представление легко можно получить. Прежде всего замечаем, что размерность N должна быть четной. ; достаточно знать, что они эрмитовы и обладают свойствами (1.16) – (1.18). Более того, при решении задач удобнее обходиться без явного вида матриц. Однако их явное представление легко можно получить. Прежде всего замечаем, что размерность N должна быть четной.
На самом деле. Перепишем соотношение (1.17) в виде
 (1.19) (1.19)
где I – единичная матрица. Взяв детерминант от обеих частей равенства (1.19), получим
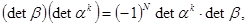 (1.20) (1.20)
где учтено, что  . Отсюда . Отсюда  , и число N должно быть четным. , и число N должно быть четным.
Придадим уравнению Дирака ковариантный вид. В записи
 (1.5) (1.5)
для уравнения Дирака пространственные производные умножены на матрицы, а временные нет. Чтобы устранить это неравноправие, умножим уравнение (1.5) слева на матрицу  : :
 (1.21) (1.21)
Уравнение примет более симметричный вид, если ввести матрицы
 (1.22) (1.22)
 (1.23) (1.23)
Отметим, что при таком определении матрица 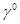 эрмитова и эрмитова и  ,а матрицы ,а матрицы  – антиэрмитовы, то есть – антиэрмитовы, то есть 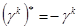 , и , и 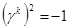 . Отсюда следует, что матрицы . Отсюда следует, что матрицы  удовлетворяют перестановочным соотношениям удовлетворяют перестановочным соотношениям
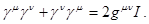 (1.24) (1.24)
С помощью  -матриц уравнение (1.21) записывается в виде -матриц уравнение (1.21) записывается в виде
 (1.25) (1.25)
где снова использовано соглашение о суммировании. Уравнение (1.25) и является ковариантной формой уравнения Дирака, в которой пространственные и временные производные входят равноправно.
Для упрощения полученного уравнения введем обозначения. Обозначим при помощи 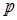 величину величину
 (1.26) (1.26)
где матрицы 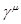 определяются согласно определяются согласно
 (1.27) (1.27)
С помощью этого обозначения и в естественной системе единиц уравнение Дирака записывается в виде
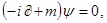 (1.28) (1.28)
Где
 (1.29) (1.29)
Ток и плотность можно записать с помощью матриц  следующим образом. Умножая равенство (1.23) на матрицу следующим образом. Умножая равенство (1.23) на матрицу  слева, находим слева, находим  , а поэтому ток , а поэтому ток
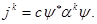 (1.14) (1.14)
примет следующий вид
 (1.30) (1.30)
С помощью "сопряженной" волновой функции 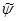 , определенно согласно , определенно согласно
 (1.31) (1.31)
выражение для тока записывается в виде
 (1.32) (1.32)
Аналогично через матрицы  записывается и плотность записывается и плотность
 (1.33) (1.33)
Уравнение для сопряженной функции 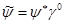 получают из уравнения (1.8), вставляя в каждом члене справа от получают из уравнения (1.8), вставляя в каждом члене справа от  множитель множитель  и используя затем соотношения (1.11), (1.12) и (1.23). В естественной системе единиц это уравнение запишется так: и используя затем соотношения (1.11), (1.12) и (1.23). В естественной системе единиц это уравнение запишется так:
 (1.34) (1.34)
2. Матрица Дирака. Свойства матриц Дирака
Матрицы  образуют совокупность гиперкомплексных чисел, удовлетворяющих перестановочным соотношениям образуют совокупность гиперкомплексных чисел, удовлетворяющих перестановочным соотношениям 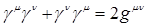 . .
Рассмотрим 16 элементов:


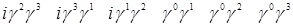
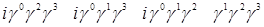
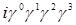
Все другие произведения матриц  с помощью перестановочных соотношений могут быть сведены к одной из шестнадцати. Множитель i вставлен для того, чтобы квадрат каждого элемента был равен +1. Обозначим элементы в выписанном порядке при помощи с помощью перестановочных соотношений могут быть сведены к одной из шестнадцати. Множитель i вставлен для того, чтобы квадрат каждого элемента был равен +1. Обозначим элементы в выписанном порядке при помощи 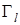 (l=1, 2, …,16). Замечаем, что с точностью до множителей (l=1, 2, …,16). Замечаем, что с точностью до множителей 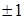 или или  произведение любых двух элементов всегда равно третьему. Для каждого элемента произведение любых двух элементов всегда равно третьему. Для каждого элемента 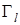 , за исключением , за исключением  , всегда можно найти такой элемент , всегда можно найти такой элемент  , что , что  . Это утверждение мы докажем, но для этого укажем элемент . Это утверждение мы докажем, но для этого укажем элемент  для каждого для каждого 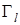 . Так, для l=2, …,5, т.е. для элементов второй строки списка, . Так, для l=2, …,5, т.е. для элементов второй строки списка,  ; в случае третьей строки, например, элементу ; в случае третьей строки, например, элементу  соответствует соответствует 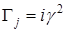 , так как , так как 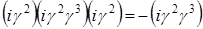 ; для всей четвертой строки ; для всей четвертой строки  , а для пятой в качестве , а для пятой в качестве  можно выбрать, например, можно выбрать, например,  . Отсюда следует, что след любой матрицы . Отсюда следует, что след любой матрицы  с с 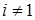 равен нулю, так как равен нулю, так как
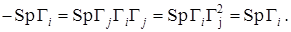
Шестнадцать элементов  линейно независимы, другими словами, равенство линейно независимы, другими словами, равенство  справедливо только тогда, когда все справедливо только тогда, когда все 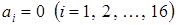 . .
Докажем. Вычисляя след от  , получим , получим 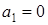 . Аналогично, последовательно умножая уравнение на каждую из . Аналогично, последовательно умножая уравнение на каждую из  и вычисляя след, получаем, что и вычисляя след, получаем, что 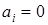 , что и требовалось доказать. Отсюда следует, что гиперкомплексные числа нельзя представить матрицами размерности, меньшей , что и требовалось доказать. Отсюда следует, что гиперкомплексные числа нельзя представить матрицами размерности, меньшей  , так как при меньшей размерности не существует 16 линейно независимых матриц. Обратно, , так как при меньшей размерности не существует 16 линейно независимых матриц. Обратно,  можно представить матрицами, размерностью можно представить матрицами, размерностью  , потому что среди этих матриц имеется ровно 16 линейно независимых (так как число элементов , потому что среди этих матриц имеется ровно 16 линейно независимых (так как число элементов  матрицы равно 16). Это представление (как и все ему эквивалентные) оказывается неприводимым. Любое другое представление может быть приведено к виду матрицы равно 16). Это представление (как и все ему эквивалентные) оказывается неприводимым. Любое другое представление может быть приведено к виду
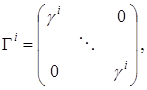
где  – матрицы размерности – матрицы размерности  . .
Из линейной независимости  следует, что всякая следует, что всякая  матрица X может быть записана в виде матрица X может быть записана в виде
 (2.1) (2.1)
Где
 (2.2) (2.2)
Так как  -матрицы неприводимы, то по лемме Шура следует, что любая -матрицы неприводимы, то по лемме Шура следует, что любая  матрица, коммутирующая со всеми матрицами матрица, коммутирующая со всеми матрицами 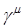 , кратна единичной матрице. , кратна единичной матрице.
На самом деле. Пусть X будет матрицей, коммутирующей со всеми матрицами 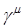 , а следовательно, и со всеми , а следовательно, и со всеми 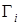 . Представим X в виде . Представим X в виде
 (2.3) (2.3)
Пусть 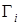 такая матрица, что такая матрица, что  . По предположению, . По предположению,  , а потом, умножая (2.3) слева и справа на , а потом, умножая (2.3) слева и справа на 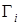 , получаем , получаем
 (2.4) (2.4)
где множители  возникают в зависимости от того, коммутируют или антикоммутируют возникают в зависимости от того, коммутируют или антикоммутируют 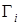 и и 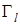 друг с другом. Умножая (2.3) и (2.4) на друг с другом. Умножая (2.3) и (2.4) на  и вычисляя след, получаем, что и вычисляя след, получаем, что  . Так как в качестве . Так как в качестве  бралась любая из матриц Г, за исключением единичной, то единственный отличный от нуля коэффициент разложения (2.3) есть бралась любая из матриц Г, за исключением единичной, то единственный отличный от нуля коэффициент разложения (2.3) есть 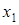 , что и требовалось доказать. , что и требовалось доказать.
Основная теорема о матрицах  гласит: если даны две системы гласит: если даны две системы  матриц матриц 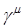 и и  , удовлетворяющих перестановочным соотношениям , удовлетворяющих перестановочным соотношениям
 (2.5а) (2.5а)
 (2.5б) (2.5б)
то существует такая несобственная матрица S, что
 (2.6) (2.6)
Явный вид S дается выражением
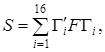 (2.7) (2.7)
где F – произвольная  матрица, которая может быть выбрана таким образом, чтобы матрица S была несобственной. Совокупность 16 линейно независимых матрица, которая может быть выбрана таким образом, чтобы матрица S была несобственной. Совокупность 16 линейно независимых  построена из матриц построена из матриц  точно так же, как были построены точно так же, как были построены 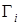 из из 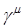 . Для доказательства теоремы заметим, что если . Для доказательства теоремы заметим, что если  , где , где , то тогда , то тогда 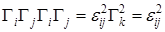 , так что , так что  . Отметим, что в штрихованной системе число . Отметим, что в штрихованной системе число  будет тем же самым, т.е будет тем же самым, т.е  , так как его значение определяется только перестановочными соотношениями, а они одинаковы для обеих совокупностей матриц. Так как , так как его значение определяется только перестановочными соотношениями, а они одинаковы для обеих совокупностей матриц. Так как  равно либо равно либо  , либо , либо  , то , то  . Воспользовавшись для S представлением (2.7), получаем . Воспользовавшись для S представлением (2.7), получаем
 (2.8) (2.8)
с учетом того, что при фиксированном  матрица матрица 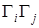 , находящаяся под знаком суммы по , находящаяся под знаком суммы по  , пробегает все значения 16 элементов алгебры. Это позволило заменить сумму по , пробегает все значения 16 элементов алгебры. Это позволило заменить сумму по  суммой по суммой по  . Таким образом, получаем . Таким образом, получаем
 (2.9) (2.9)
Так как матрицы  неприводимы, то по лемме Шура матрица S является несобственной. Кроме того, с точностью до множителя матрица S определяется однозначно. В самом деле, предположим, что таких матриц S имеется две, скажем неприводимы, то по лемме Шура матрица S является несобственной. Кроме того, с точностью до множителя матрица S определяется однозначно. В самом деле, предположим, что таких матриц S имеется две, скажем 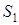 и и  , так что , так что  и и  . Тогда исключая . Тогда исключая  , получаем , получаем  , т.е. что матрица , т.е. что матрица коммутирует со всеми матрицами коммутирует со всеми матрицами  и, следовательно, кратен единичной матрице. Отсюда и, следовательно, кратен единичной матрице. Отсюда  . Часто бывает удобным наложить условие нормировки . Часто бывает удобным наложить условие нормировки  , которая определяет матрицу S уже с точностью до множителя , которая определяет матрицу S уже с точностью до множителя 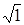 , равного , равного  , или , или  . .
Интересен частный случай соотношения (2.7), когда  . В этом случае . В этом случае 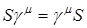 , и S есть матрица, кратная единичной: , и S есть матрица, кратная единичной: 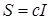 . Тогда матричный элемент соотношения (2.7) с индексами . Тогда матричный элемент соотношения (2.7) с индексами  равен равен
 (2.10) (2.10)
Так как это тождество верно при любом выборе матрицы F, то из него следует
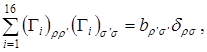 (2.11) (2.11)
где 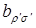 – некоторая постоянная. Для определения этой постоянной свернем индексы – некоторая постоянная. Для определения этой постоянной свернем индексы  и и  : :
 (2.12) (2.12)
откуда  , и, таким образом, приходим к тождеству , и, таким образом, приходим к тождеству
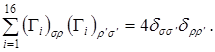 (2.13) (2.13)
3. Спиноры
Связь между координатами точек трехмерного пространства для двух наблюдателей, системы координат которых повернуты друг относительно друга вокруг общего начала, имеет вид
 (3.1а) (3.1а)
или
 (3.1б) (3.1б)
Длина вектора и угол между векторами остаются неизменными при вращениях, т.е.
 (3.2) (3.2)
Следовательно,
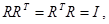 (3.3) (3.3)
т. е. вращения представляются ортогональными матрицами. Из (3.3) следует
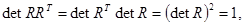
так что для матриц, удовлетворяющих (3.3), 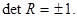 Преобразования, для которых Преобразования, для которых 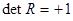 , называют собственными преобразованиями или вращениями, а те, для которых , называют собственными преобразованиями или вращениями, а те, для которых 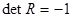 , несобственными ортогональными преобразованиями. Примером несобственного преобразования является отражение в начале координат, которое представляется матрицей , несобственными ортогональными преобразованиями. Примером несобственного преобразования является отражение в начале координат, которое представляется матрицей
 (3.4) (3.4)
причем  . Преобразование . Преобразование  соответствует переходу от правой системы координат к левой. Каждое несобственное преобразование соответствует переходу от правой системы координат к левой. Каждое несобственное преобразование 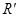 с с  может быть записано в виде может быть записано в виде  , т. е. как отражение , т. е. как отражение  , вслед за которым уже выполняется вращение; в самом деле, , вслед за которым уже выполняется вращение; в самом деле,

Совокупность всех вращений в евклидовом трехмерном пространстве образует группу – группу вращений. Группа всех вращений вместе с отражениями называется ортогональной группой. Так как каждый элемент группы может быть охарактеризован заданием трех непрерывно изменяющихся параметров (например, направляющих косинусов оси, вокруг которых совершается вращение, и угла поворота), то группа вращений является непрерывной трехпараметрической группой. Число параметров группы называется размерностью группы.
Вообще представление какой-либо группы G есть отображение (соответствие), сопоставляющее каждому элементу g из G линейный оператор Tg
, действующий в некотором векторном пространстве V, и притом такое, что сохраняется таблица умножения для группы, а единица e группы G отображается тождественным преобразованием I в V.
Подпространство V1
пространства V называют инвариантным подпространством относительно представления Tg
, если все векторы 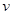 в V1
преобразуются по Tg
в векторы в V1
преобразуются по Tg
в векторы 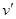 , снова принадлежащие V1
, и это справедливо при всех преобразованиях Tg
. , снова принадлежащие V1
, и это справедливо при всех преобразованиях Tg
.
Каждое вращение является вращением вокруг некоторой оси, так что она может быть характеризовано заданием оси вращения, т.е. оси, вокруг которой осуществляется поворот и величины угла поворота. Таким образом, вращение может быть задано вектором  , направленным вдоль оси вращения и равным по величине углу поворота. Так, вращение вокруг оси 1 задается вектором , направленным вдоль оси вращения и равным по величине углу поворота. Так, вращение вокруг оси 1 задается вектором  , вокруг оси 2 – вектором , вокруг оси 2 – вектором  и т.д. Элемент группы может рассматриваться как функция и т.д. Элемент группы может рассматриваться как функция  , т.е. , т.е.  , и тоже относится к представлению: , и тоже относится к представлению:  . Вектор . Вектор  соответствует тождественному преобразованию соответствует тождественному преобразованию
 (3.5) (3.5)
Рассмотрим бесконечно малые вращения вокруг той или иной оси. Их важность связана с тем, что они порождают однопараметрические подгруппы и что любое конечное вращение может быть построено как последовательность бесконечно малых. Бесконечно малые вращения коммутируют друг с другом, тогда как конечные вращения в общем случае не коммутируют.
Пусть  будет матрицей поворота на угол будет матрицей поворота на угол 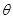 вокруг оси 3, и пусть определена матрица вокруг оси 3, и пусть определена матрица
 (3.6) (3.6)
Оператор  называют генератором вращения вокруг оси 3. При бесконечно малом называют генератором вращения вокруг оси 3. При бесконечно малом  можно записать можно записать
 (3.7) (3.7)
Теперь вращения  на угол на угол 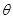 вокруг оси 3 может рассматриваться как результат n поворотов на угол вокруг оси 3 может рассматриваться как результат n поворотов на угол  . Поэтому мы можем записать . Поэтому мы можем записать
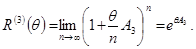 (3.8) (3.8)
Аналогичным образом можно определить генераторы вращений вокруг осей 1 и 2. Так как
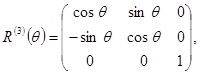 (3.9) (3.9)
то явным видом для  будет будет
 (3.10а) (3.10а)
и аналогично
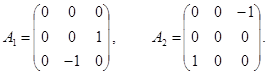 (3.10б) (3.10б)
Можно проверить, что генераторы 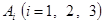 удовлетворяют следующим перестановочным соотношениям: удовлетворяют следующим перестановочным соотношениям:
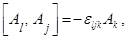 (3.11) (3.11)
где  – полностью антисимметричный тензор 3-го ранга с компонентами, равными +1, если ljk есть четная перестановка 1 2 3, равными –1, если перестановка нечетная, и равными нулю в остальных случаях. Отметим, что оператор отражения – полностью антисимметричный тензор 3-го ранга с компонентами, равными +1, если ljk есть четная перестановка 1 2 3, равными –1, если перестановка нечетная, и равными нулю в остальных случаях. Отметим, что оператор отражения 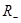 коммутирует со всеми вращениями коммутирует со всеми вращениями
 (3.12) (3.12)
Бесконечно малый поворот вокруг  на угол на угол  может быть записан в виде может быть записан в виде
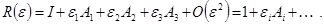 (3.13) (3.13)
Соответствующий оператор представления запишем
 (3.14) (3.14)
где  образуют представление генераторов и удовлетворяют перестановочным соотношениям образуют представление генераторов и удовлетворяют перестановочным соотношениям
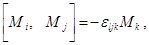 (3.15) (3.15)
Пусть операторы  . Эти операторы будут эрмитовыми и удовлетворяют перестановочным соотношениям для операторов момента количества движения . Эти операторы будут эрмитовыми и удовлетворяют перестановочным соотношениям для операторов момента количества движения
 (3.16) (3.16)
В случае группы вращений со всеми генераторами коммутирует оператор 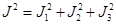 , и поэтому он является инвариантом группы. Его собственные значения, как известно из теории оператора момента количества движения, равны , и поэтому он является инвариантом группы. Его собственные значения, как известно из теории оператора момента количества движения, равны   , где , где  .Таким образом, каждое неприводимое представление характеризуется положительным целым или полуцелым j, включая 0. Размерность неприводимого представления равна .Таким образом, каждое неприводимое представление характеризуется положительным целым или полуцелым j, включая 0. Размерность неприводимого представления равна  при любом весе j, целым или полуцелым. Переходя к классификации неприводимых представлений ортогональной группы, заметим, что линейный оператор при любом весе j, целым или полуцелым. Переходя к классификации неприводимых представлений ортогональной группы, заметим, что линейный оператор 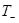 , соответствующий операции отражения , соответствующий операции отражения 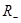 , коммутирует со всеми вращениями. , коммутирует со всеми вращениями.
В теории представления групп, осуществляемых комплексными матрицами, фундаментальное значение имеет лемма Шура, в которой доказывается, что необходимое и достаточное условие для неприводимости представления состоит в том, чтобы единственными матрицами, коммутирующими со всеми матрицами представления, были матрицы, кратные единичной.
По лемме Шура в каждом неприводимом представлении он должен быть кратен единичному оператору. Таким образом, неприводимые представления ортогональной группы классифицируются парой индексов  , где второй индекс является собственным значением , где второй индекс является собственным значением 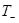 , соответствующий данному представлению. При целых j имеем , соответствующий данному представлению. При целых j имеем  (ибо (ибо 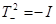 ), так что существуют два различных неприводимых представления ортогональной группы. В одном из них ), так что существуют два различных неприводимых представления ортогональной группы. В одном из них  , в другом , в другом 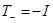 . .
При  представление одномерно, каждый элемент группы отображается единичным элементом, а генераторы тождественно равны нулю. Представление, в котором представление одномерно, каждый элемент группы отображается единичным элементом, а генераторы тождественно равны нулю. Представление, в котором  , назовем скалярным, а то, в котором , назовем скалярным, а то, в котором 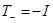 , – псевдоскалярным. , – псевдоскалярным.
При 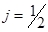 представление группы вращений двумерно, и генераторы представление группы вращений двумерно, и генераторы 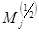 могут быть реализованы эрмитовыми матрицами Паули могут быть реализованы эрмитовыми матрицами Паули  , умноженными на , умноженными на 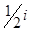 : :
 (3.17) (3.17)
Они удовлетворяют соотношению
 (3.18) (3.18)
Таким образом, в представлении веса 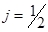 оператор поворота на угол оператор поворота на угол  вокруг оси 3 записывается в виде вокруг оси 3 записывается в виде
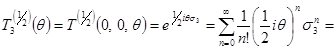

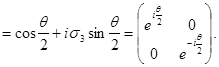 (3.19а) (3.19а)
Аналогично, в представлении 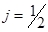 записываются и операторы поворота на угол записываются и операторы поворота на угол  вокруг осей 1 и 2: вокруг осей 1 и 2:
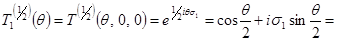
 (3.19б) (3.19б)

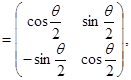 (3.19в) (3.19в)
Отметим, что матрицы 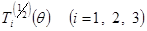 унитарны и имеют детерминант, равный единице. Отметим также, что поворот на угол унитарны и имеют детерминант, равный единице. Отметим также, что поворот на угол  вокруг любой оси дает вокруг любой оси дает
 (3.20) (3.20)
Таким образом, представление двузначно, и соответствие между элементами группы и операторами можно выразить  . .
При 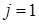 представление трехмерно, и в качестве матричного представления генераторов представление трехмерно, и в качестве матричного представления генераторов  можно взять матрицы можно взять матрицы  , определенные выше в виде (3.10а) и (3.10б). Обычное же квантово-механическое представление для , определенные выше в виде (3.10а) и (3.10б). Обычное же квантово-механическое представление для  при при 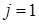 имеет вид имеет вид
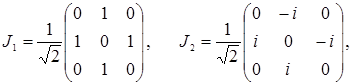
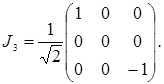 (3.21) (3.21)
Оно унитарно эквивалентно представлению, полученному для 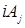 : :  соответствует базису соответствует базису 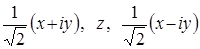 , вместо обычного декартова базиса , вместо обычного декартова базиса 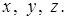
Величины 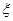 , которые при вращении системы координат , которые при вращении системы координат
 (3.22) (3.22)
преобразуются по закону
 (3.23) (3.23)
называют скалярами при  , спинорами 1-го ранга при , спинорами 1-го ранга при 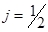 , векторами при , векторами при 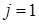 и т.д. При бесконечно малых поворотах на угол и т.д. При бесконечно малых поворотах на угол 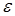 вокруг l-ой оси закон преобразования (3.23) принимает вид вокруг l-ой оси закон преобразования (3.23) принимает вид
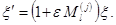 (3.24) (3.24)
Таким образом, скаляр есть однокомпонентная величина, которая при вращениях  преобразуется по закону преобразуется по закону 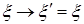 . Спинор 1-го ранга является двухкомпонентной величиной . Спинор 1-го ранга является двухкомпонентной величиной
 (3.25) (3.25)
которая при бесконечно малых поворотах на угол  вокруг l-ой оси вокруг l-ой оси
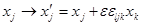 (3.26) (3.26)
преобразуется по закону
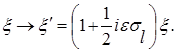 (3.27) (3.27)
Как было отмечено выше, при вращениях на любой конечный угол спинор 1-го ранга преобразуется при помощи унитарной матрицы размерностью 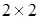 и с детерминантом, равным единице. Наконец, вектор является трехкомпонентной величиной и с детерминантом, равным единице. Наконец, вектор является трехкомпонентной величиной
 (3.28) (3.28)
компоненты которой  при вращении (3.22) преобразуются так же, как сами координаты. при вращении (3.22) преобразуются так же, как сами координаты.
Сопряжение спинора 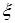 выполняется обычным образом путем транспонирования и комплексного сопряжения. Таким образом, при выполняется обычным образом путем транспонирования и комплексного сопряжения. Таким образом, при  спинор спинор  , сопряженный к , сопряженный к 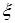 , имеет вид , имеет вид
 (3.29) (3.29)
При бесконечно малом повороте вокруг l-ой оси он преобразуется по закону
 (3.30) (3.30)
4. Общее решение уравнения Дирака
Уравнение Дирака имеет решение в виде плоских волн:
 (4.1) (4.1)
где  – 4-компонентный спинор, удовлетворяющий уравнению – 4-компонентный спинор, удовлетворяющий уравнению
 (4.2) (4.2)
Скалярное произведение двух спиноров  и и 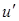 записывается в виде записывается в виде
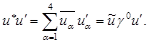 (4.3) (4.3)
Если I – единичная  матрица, а матрица, а 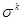 – Матрицы Паули, то тогда – Матрицы Паули, то тогда  матрицы матрицы
 (4.4) (4.4)
эрмитовы и антикоммутируют друг с другом.
При таком определении скалярного произведения гамильтониан  эрмитов: эрмитов:
 (4.5) (4.5)
(здесь учтено, что  и и 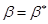 ), и поэтому его собственные значения действительны. Уравнение (4.2) является системой четырех линейных однородных уравнений для компонент ), и поэтому его собственные значения действительны. Уравнение (4.2) является системой четырех линейных однородных уравнений для компонент  . Нетривиальные решения существуют только, если . Нетривиальные решения существуют только, если  . Итак, уравнение имеет решение только тогда, когда . Итак, уравнение имеет решение только тогда, когда  , т.е. , т.е. 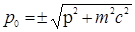 . Пусть . Пусть 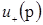 будет решением, соответствующим будет решением, соответствующим  и, следовательно, удовлетворяющим уравнению и, следовательно, удовлетворяющим уравнению
 (4.6) (4.6)
Если представить решение 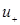 в виде в виде 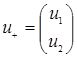 , где , где  и и  имеют по две компоненты, и если принять для матриц имеют по две компоненты, и если принять для матриц  и и  представление (4.4), то получим уравнение для представление (4.4), то получим уравнение для  и и  : :
 (4.7а) (4.7а)
 (4.7б) (4.7б)
С учетом того, что  , находим из (4.7б) , находим из (4.7б)
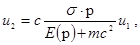 (4.8) (4.8)
а подставляя это выражение обратно в (4.7а), получаем уравнение
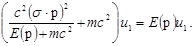 (4.9) (4.9)
Однако, поскольку  и и
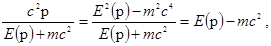 (4.10) (4.10)
то мы приходим к заключению, что уравнение (4.7а) удовлетворяется тождественно. Таким образом, при каждом значении импульса p имеются два линейно независимых решения с положительной энергией, которые соответствуют, например, выбору 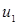 в виде в виде 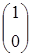 и и  . Это же можно выяснить и несколько другим путем. Оператор Гамильтона . Это же можно выяснить и несколько другим путем. Оператор Гамильтона  коммутирует с эрмитовым оператором коммутирует с эрмитовым оператором
 (4.11) (4.11)
Где
 (4.12) (4.12)
Оператор 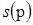 называется оператором спиральности, или, просто, спиральностью частицы. С физической стороны он соответствует проекции спина частицы на направление движения. Так как коммутации H и называется оператором спиральности, или, просто, спиральностью частицы. С физической стороны он соответствует проекции спина частицы на направление движения. Так как коммутации H и 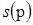 в качестве решений, то можно выбрать общие собственные функции этих операторов. Но, т.к. в качестве решений, то можно выбрать общие собственные функции этих операторов. Но, т.к.  , то собственные значения операторов , то собственные значения операторов 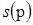 равны равны 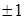 . Решение с заданным импульсом и фиксированном знаком энергии можно классифицировать и решения с отрицательной энергией, когда . Решение с заданным импульсом и фиксированном знаком энергии можно классифицировать и решения с отрицательной энергией, когда  . В этом случае снова имеются два линейно независимых решения, соответствующих собственным значениям +1 и – 1 оператора . В этом случае снова имеются два линейно независимых решения, соответствующих собственным значениям +1 и – 1 оператора 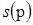 . Итак, при фиксированном импульсе p уравнение Дирака имеет четыре линейно независимых решения, характеризующихся решениями . Итак, при фиксированном импульсе p уравнение Дирака имеет четыре линейно независимых решения, характеризующихся решениями 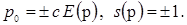
Явный вид двух линейно независимых решения уравнения Дирака с импульсом p и положительной энергией следующий:
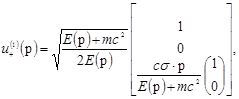 (4.13а) (4.13а)
 (4.13б) (4.13б)
Нормировочные множители здесь определены из условия  . Отметим, что эти два решения ортогональны друг другу: . Отметим, что эти два решения ортогональны друг другу:
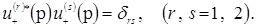 (4.14) (4.14)
Выписанные решения не являются собственными функциями оператора 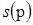 . Решения с положительной энергией и с определенной спиральностью можно получить, если принять во внимание, что уравнение . Решения с положительной энергией и с определенной спиральностью можно получить, если принять во внимание, что уравнение  записывается в виде записывается в виде
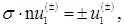 (4.15а) (4.15а)
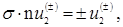 (4.15а) (4.15а)
где  и и  – верхние и нижние пары компонент спинора – верхние и нижние пары компонент спинора  , а n – единичный вектор, направленный по p, , а n – единичный вектор, направленный по p,  . Отсюда для нормированных величин . Отсюда для нормированных величин  получаем выражение получаем выражение
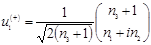 (4.16а) (4.16а)
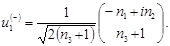 (4.16б) (4.16б)
Таким образом, нормированная собственная функция со спиральностью +1 и с положительной энергией записывается в виде
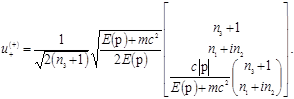 (4.17) (4.17)
Заключение
Итак, мы рассмотрели небольшую тему из раздела квантовой теории поля – уравнение Дирака. Узнали вид уравнения Дирака, матрицы Дирака и общее решение этого уравнения.
Без знаний тензорного анализа трудно было бы понять суть нашей темы.
В тензорном анализе понятие тензора вводится следующим образом. Пусть нам задан какой-нибудь вектор  и будем его рассматривать в различных системах координат. Тогда в каждой системе координат с какими-нибудь базисными векторами у нас будет задана своя система чисел, причем при переходе от одной какой-нибудь системы координат к любой другой эти числа преобразуются по какому-нибудь закону, то говорят в таких случаях, что нам задан тензор. и будем его рассматривать в различных системах координат. Тогда в каждой системе координат с какими-нибудь базисными векторами у нас будет задана своя система чисел, причем при переходе от одной какой-нибудь системы координат к любой другой эти числа преобразуются по какому-нибудь закону, то говорят в таких случаях, что нам задан тензор.
С помощью некоторых операций над тензорами мы и пришли к решению уравнения Дирака.
Список литературы
1. Швебер С. Введение в релятивистскую квантовую теорию поля. М.: Изд-во ин. лит-ры, 1963, 844 с.
2. Рашевский П.К. Введение в риманову геометрию и тензорный анализ. М.-Л.: ОНТИ, 1936, 200 с.
3. Димитриенко Ю.И. Тензорное исчисление. М.: Высш. шк., 2001, 575 с.
4. Мак-Конел А.Дж. Введение в тензорный анализ. М.: Физматгиз, 1963, 412 с.
|

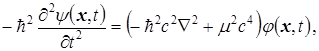 (1.1)
(1.1)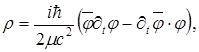 (1.2)
(1.2)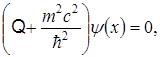 (1.3)
(1.3)
 (1.10)
(1.10) справедливо только тогда, когда все
справедливо только тогда, когда все 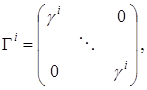
 (2.1)
(2.1)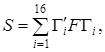 (2.7)
(2.7) (2.10)
(2.10)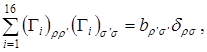 (2.11)
(2.11) (2.12)
(2.12)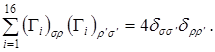 (2.13)
(2.13) (3.4)
(3.4)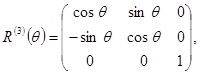 (3.9)
(3.9) (3.10а)
(3.10а)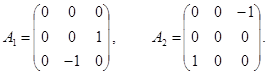 (3.10б)
(3.10б)
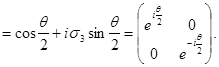 (3.19а)
(3.19а) (3.19б)
(3.19б)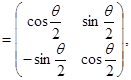 (3.19в)
(3.19в)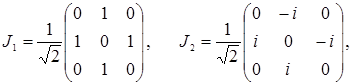
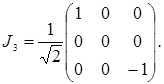 (3.21)
(3.21) (3.25)
(3.25)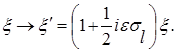 (3.27)
(3.27) (3.28)
(3.28) (4.4)
(4.4)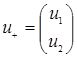 , где
, где 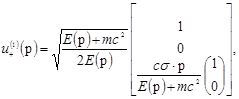 (4.13а)
(4.13а) (4.13б)
(4.13б) . Отсюда для нормированных величин
. Отсюда для нормированных величин 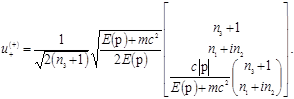 (4.17)
(4.17)