КУРСОВАЯ РАБОТА
Электромагнитные переходные процессы в электроэнергетических системах
Красноярск 2011
Задание
1 Для заданной простейшей схемы электропередачи определить запас статической устойчивости по идеальному пределу мощности при передаче от эквивалентного генератора G
1
в систему GS
мощности S
0
.
1.1 Генераторы не снабжены автоматическими регуляторами возбуждения (АРВ), явнополюсность гидрогенераторов не учитывается.
1.2 Генераторы не имеют АРВ (с учетом явнополюсности гидрогенераторов).
1.3 Генераторы снабжены АРВ пропорционального типа (с учетом явнополюсности гидрогенераторов).
1.4 Генераторы имеют АРВ сильного действия (с учетом явнополюсности гидрогенераторов).
2 Определить запас статической устойчивости по действительному пределу передаваемой мощности с учетом нагрузки и без АРВ на генераторах (с учетом явнополюсности гидрогенераторов).
3 Выполнить расчет динамической устойчивости при трехфазном КЗ и двухфазном КЗ на землю на заданной линии при наличии АРВ пропорционального типа на генераторах.
3.1 Рассчитать и построить угловые характеристики мощности нормального, аварийного и послеаварийного режимов в простейшей схеме электро-передачи.
3.2 Определить предельные углы отключения при коротких замыканиях графически и аналитически.
3.3 Произвести численные расчеты динамических переходов и построить зависимости изменения угла 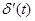 для обоих видов короткого замыкания (КЗ). для обоих видов короткого замыкания (КЗ).
3.4 Вычислить предельное время отключения КЗ.
статический генератор электропередача мощность
Исходные данные

Рисунок 1 – Электрическая схема системы
Таблица 1 – Параметры станции 1 (ГЭС)
Количество
генераторов n
1
|
Номинальная мощность генератораS
ном
, МВ·А |
Коэффициент мощности  |
Номинальное напряжение U
ном
, кВ |
Сопротивление в относительных единицах |
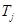 , с , с |
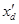 , о. е. , о. е. |
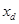 , о. е. , о. е. |
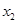 , о. е. , о. е. |
| 3 |
68,75 |
0,85 |
13,8 |
0,32 |
0,77 |
0,3 |
7 |
Таблица 2 – Параметры станции 2 (ТЭС)
Количество
генераторов n
2
|
Номинальная мощность генератораS
ном
,
МВ·А
|
Коэффициент мощности  |
Номинальное напряжение
U
ном
, кВ
|
Сопротивление в относительных единицах |
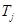 , с , с |
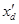 , о. е. , о. е. |
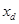 , о. е. , о. е. |
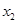 , о. е. , о. е. |
| 6 |
353 |
0,85 |
20 |
0,3 |
2,22 |
0,238 |
6,3 |
Таблица 3 – Параметры подстанции 1 (ПС1)
| Количество трансформаторов n
1
|
Номинальная мощность одного, S
ном
, МВ·А |
Номинальное напряжение 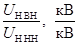 |
Напряжение короткого замыкания u
К
, % |
| 3 |
80 |
242/13,8 |
11 |
Таблица 4 – Параметры подстанции 2 (ПС2)
| Количество трансформаторов n
2
|
Номинальная мощность одного, S
ном
, МВ·А |
Номинальное напряжение 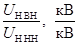 |
Напряжение короткого замыкания
u
К
, %
|
| 6 |
400 |
235/20 |
10,7 |
Таблица 5 – Параметры линии электропередачи (W
)
| Передаваемая мощность Р
0
, МВт |
Коэффициент мощности  |
Номинальное напряжение
U
ном
, кВ
|
Длина, км |
Удельное сопротивление  , Ом/км , Ом/км |
| 145 |
0,96 |
220 |
250 |
0,39 |
Таблица 6 – Параметры нагрузки
| Активная мощность Р
н
, МВт |
Коэффициент мощности 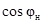 |
| 1700 |
0,91 |
Введение
Одним из важнейших показателей качества электроснабжения потребителей является его надежность как в установившихся режимах работы ЭЭС, так и в переходных процессах.
Необходимость выполнения условий, обеспечивающих устойчивую параллельную работу генераторов ЭС, диктуется требованиями надежного, бесперебойного электроснабжения.
Если учесть, что мощности современных ЭЭС и объединений достигают десятков и сотен МВт, а нарушение устойчивой работы приводит к потере значительной части генерирующих мощностей электростанций, то важность расчета и оценки статической и динамической устойчивости, обоснованного выбора мероприятий по устранению возможных неустойчивых режимов очевидна.
В процессе выполнения работы приобретаются навыки определения устойчивости электропередачи со станциями как без АРВ, так и с АРВ различных типов. Рассматриваются основные виды устойчивости электрической системы и причины, которые могут привести к ее нарушению.
1. Составление схемы замещения и определение ее параметров
Расчет начинается с составления схемы замещения электроэнергетической системы и проводится в относительных единицах при базисных условиях и точном приведении параметров схемы к выбранной ступени напряжения, т.е. с учетом действительных коэффициентов трансформации. Активными сопротивлениями пренебрегаем.
За базисное напряжение примем напряжение на шинах эквивалентной системы GS
бесконечной мощности (обладающей бесконечным регулирующим эффектом нагрузки, что приводит к неизменности напряжения на шинах эквивалентной системы) U
б1
=220 кВ. Базисную мощность примем равной S
б
=1000 МВ∙А.
Определим базисные напряжения других ступеней, кВ,
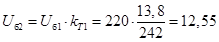 ; ;
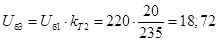
Определим сопротивления элементов:
– G
1:
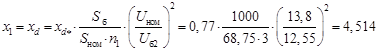 , ,
где 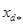 – синхронная реактивность генератора по продольной оси, о. е.; – синхронная реактивность генератора по продольной оси, о. е.;
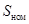 – номинальная мощность генератора, МВ·А; – номинальная мощность генератора, МВ·А;
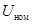 – номинальное напряжение генератора, кВ; – номинальное напряжение генератора, кВ;
n
1
– количество генераторов;
– G
2:
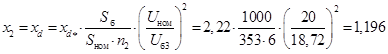 ; ;
– Т
1:
 , ,
где 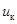 – напряжение короткого замыкания, %; – напряжение короткого замыкания, %;
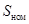 – номинальная мощность трансформатора, МВ·А; – номинальная мощность трансформатора, МВ·А;
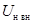 – номинальное напряжение трансформатора, кВ; – номинальное напряжение трансформатора, кВ;
n
1
– количество трансформаторов;
– Т
2:
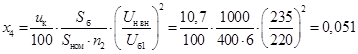 ; ;
– W
:
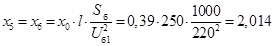 , ,
где  – удельное сопротивление линии, Ом/км; – удельное сопротивление линии, Ом/км;
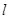 – длина линии, км. – длина линии, км.
Представим номинальную полную мощность нагрузки и мощность, подтекающую к шинам неизменного напряжения, в виде суммы активной и реактивной составляющих, о. е.,


Пересчитаем напряжение основной ступени в относительные единицы:
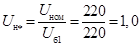
Представим схему замещения на рисунке 2.

Рисунок 2 – Исходная схема замещения
2. Определение запаса статической устойчивости
В этом разделе выключатели в линии Q
1 и Q
2 и выключатель системы бесконечной мощности Q
3 включены. Системы GS
обладает бесконечным регулирующим эффектом нагрузки, что приводит к неизменности напряжения на шинах эквивалентной системы, а поэтому при изменениях режима напряжение U
н
=1,0 будет постоянным.
2.1 Определение запаса статической устойчивости простейшей системы с генераторами без АРВ
Так как в данной задаче речь идет о неявнополюсном эквивалентном генераторе, то есть о синхронной машине с симметричным ротором, то имеет место равенство синхронных индуктивных сопротивлений по продольной и поперечной осям xd
= xq
,а также постоянство синхронной ЭДС Е
q
=const, которая пропорциональна току возбуждения if
.
Определим сопротивление системы (суммарное сопротивление электрической сети между шинами эквивалентного генератора G
1 и шинами неизменного напряжения)

Суммарная реактивность

Определяем синхронную ЭДС (холостого хода) генерирующей станции
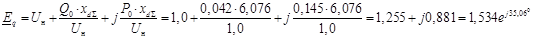
Для проверки исходного режима воспользуемся выражением, определяющим передаваемую мощность

Определим предел (идеальный) передаваемой мощности
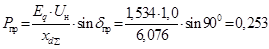
Строим угловую характеристику мощности (рисунок 3)
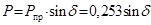
Рассчитываем коэффициент запаса статической устойчивости по идеальному пределу передаваемой мощности и по углу, %,
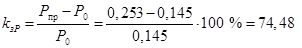 , ,
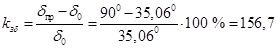
Анализируя значения полученных коэффициентов запаса статической устойчивости по мощности и углу, можно сделать вывод о том, что система является слабо загруженной, работающей с большим запасом по статической устойчивости.
Таблица 7 – Результаты расчетов для построения угловой характеристики мощности неявнополюсного генератора без АРВ
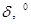 |
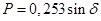 |
| 0 |
0 |
| 10 |
0,0439 |
| 20 |
0,0865 |
| 30 |
0,126 |
| 40 |
0,163 |
| 50 |
0,194 |
| 60 |
0,219 |
| 70 |
0,238 |
| 80 |
0,249 |
| 90 |
0,253 |
| 100 |
0,249 |
| 110 |
0,238 |
| 120 |
0,219 |
| 130 |
0,194 |
| 140 |
0,163 |
| 150 |
0,126 |
| 160 |
0,0865 |
| 170 |
0,0439 |
| 180 |
0 |

Рисунок 3 – Угловая характеристика мощности неявнополюсного генератора без АРВ
2.2 Определение запаса статической устойчивости простейшей системы с генераторами без АРВ с учетом явнополюсности гидрогенераторов
Гидрогенератор с учетом явнополюсности представляем в расчетах синхронной реактивностью по поперечной оси x
q
и фиктивной расчетной ЭДС 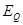 , которая зависит от режима и рассчитывается по формуле: , которая зависит от режима и рассчитывается по формуле:
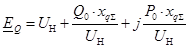
Сопротивление гидрогенератора G
1 с учетом явнополюсности

Суммарная реактивность

Далее определим расчетную ЭДС Е
Q
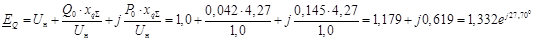
Из векторной диаграммы для явнополюсной синхронной машины следует

После подстановки вместо продольной составляющей тока его значения
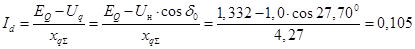
Определим значение синхронной ЭДС
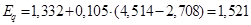
При определении мощности явнополюсного генератора приходится рассматривать более сложную зависимость мощности от угла d
вследствие не – симметрии ротораxd
¹xq
.
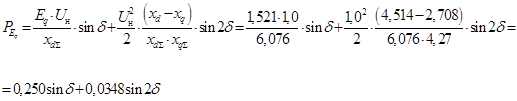
Для определения предельной величины активной мощности в этом случае нужно найти угол, обеспечивающий максимальное значение последнего выражения. Как известно, экстремум функции определяется при равенстве нулю ее производной. Приравниваем производную активной мощности по углу к 0, получим квадратное уравнении и решаем его относительно cosd
.
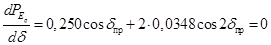 ; ;
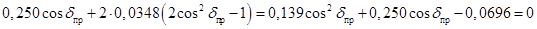 ; ;
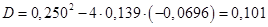 ; ;
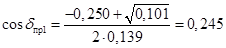 , , 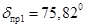 ; ;
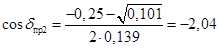 , , 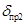 не существует. не существует.
Определим предел передаваемой мощности

Рассчитываем коэффициент запаса по мощности и по углу, %,
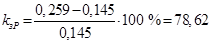 ; ;
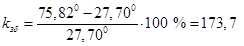
Характеристика мощности явнополюсного генератора кроме основной синусоидальной составляющей содержит вторую составляющую – синусоиду двойной частоты, амплитуда которой пропорциональна разности индуктивных сопротивлений xd
и xq
. Составляющая двойной частоты смещает максимум характеристики мощности в сторону меньших углов. Амплитуда характеристики мощности возрастет по сравнению с характеристикой, не учитывающей явнополюсности машины.
Проверка:
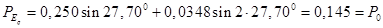
Таблица 8 – Результаты расчетов для построения угловой характеристики мощности явнополюсного генератора без АРВ
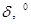 |
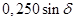 |
 |
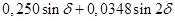 |
| 0 |
0 |
0 |
0 |
| 10 |
0,043 |
0,012 |
0,055 |
| 20 |
0,086 |
0,022 |
0,108 |
| 30 |
0,125 |
0,030 |
0,155 |
| 40 |
0,161 |
0,034 |
0,195 |
| 50 |
0,192 |
0,034 |
0,226 |
| 60 |
0,217 |
0,030 |
0,247 |
| 70 |
0,235 |
0,022 |
0,257 |
| 80 |
0,246 |
0,012 |
0,258 |
| 90 |
0,250 |
0 |
0,250 |
| 100 |
0,246 |
-0,012 |
0,234 |
| 110 |
0,235 |
-0,022 |
0,213 |

Рисунок 4 – Угловая характеристика мощности явнополюсного генератора без АРВ
2.3 Определение запаса статической устойчивости системы при установке на генераторах АРВ пропорционального типа
При установке на генераторах АРВ пропорционального действия в качестве самой простой математической модели генератора G
1 принимается неизменной поперечная составляющая переходной ЭДС ( ) за переходным сопротивлением ) за переходным сопротивлением 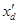 : :
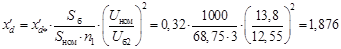
Суммарная реактивность

Определим переходную ЭДС
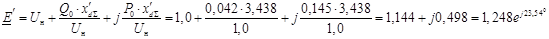
Определим поперечную составляющую переходной ЭДС
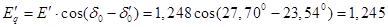
Определим передаваемую мощность
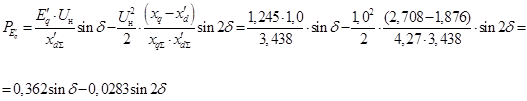
Определим предельную величину активной мощности.
 ; ;
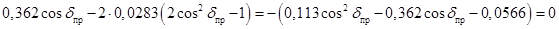 ; ;
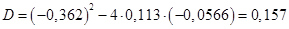 ; ;
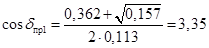 , , 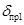 не существует; не существует;
 , , 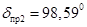
Определим предел передаваемой мощности

Рассчитываем коэффициент запаса по мощности и по углу, %,
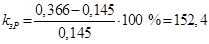 ; ;

У генераторов, снабженных АРВ пропорционального типа, увеличивается предел передаваемой мощности. Это происходит из-за регулирования тока возбуждения.
Проверка: 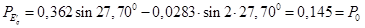 . .
Таблица 9 – Результаты расчетов для построения угловой характеристики мощности явнополюсного генератора с АРВ пропорционального типа
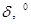 |
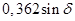 |
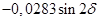 |
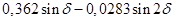 |
| 0 |
0 |
0 |
0 |
| 10 |
0,063 |
-0,010 |
0,052 |
| 20 |
0,124 |
-0,018 |
0,106 |
| 30 |
0,181 |
-0,024 |
0,157 |
| 40 |
0,233 |
-0,028 |
0,205 |
| 50 |
0,277 |
-0,028 |
0,249 |
| 60 |
0,314 |
-0,024 |
0,290 |
| 70 |
0,340 |
-0,018 |
0,322 |
| 80 |
0,356 |
-0,010 |
0,346 |
| 90 |
0,362 |
0 |
0,362 |
| 100 |
0,356 |
0,010 |
0,366 |
| 110 |
0,340 |
0,018 |
0,358 |
| 120 |
0,314 |
0,024 |
0,338 |
| 130 |
0,277 |
0,028 |
0,305 |
| 140 |
0,233 |
0,028 |
0,261 |
| 150 |
0,181 |
0,024 |
0,205 |
| 160 |
0,124 |
0,018 |
0,142 |
| 170 |
0,063 |
0,010 |
0,073 |
| 180 |
0 |
0 |
0 |

Рисунок 5 – Угловая характеристика мощности генератора с АРВ пропорционального типа
2.4 Определение запаса статической устойчивости системы при установке на генераторах АРВ сильного действия
При установке на генераторах АРВ сильного действия в качестве простой математической модели генератора принимается неизменной поперечная составляющая напряжения генератора, т.е. реактивность самого генератора принимается равной нулю.
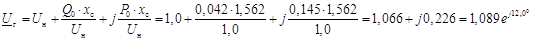
Определим поперечную составляющую напряжения генератора
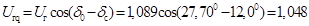
Определим передаваемую мощность

Определим предельную величину активной мощности.
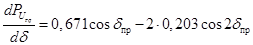 ; ;
 ; ;
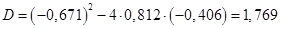 ; ;
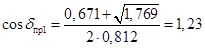 , , 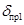 не существует; не существует;
 , , 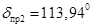
Определим предел передаваемой мощности
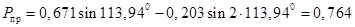
Рассчитываем коэффициент запаса по мощности и по углу, %,
 ; ;
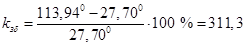
Проверка: 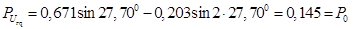 . .
Таблица 10 – Результаты расчетов для построения угловой характеристики мощности явнополюсного генератора с АРВ сильного действия
 |
 |
 |
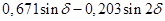 |
| 0 |
0 |
0 |
0 |
| 10 |
0,117 |
-0,069 |
0,048 |
| 20 |
0,229 |
-0,130 |
0,099 |
| 30 |
0,336 |
-0,176 |
0,160 |
| 40 |
0,431 |
-0,2 |
0,231 |
| 50 |
0,514 |
-0,2 |
0,314 |
| 60 |
0,581 |
-0,176 |
0,405 |
| 70 |
0,631 |
-0,130 |
0,501 |
| 80 |
0,661 |
-0,069 |
0,592 |
| 90 |
0,671 |
0 |
0,671 |

Рисунок 6 – Угловая характеристика мощности генератора с АРВ сильного действия
Анализируя угловые характеристики мощности генераторов с АРВ и без АРВ, можно сделать вывод, что применение устройств АРВ значительно увеличивает предел передаваемой мощности за счет регулирования тока возбуждения синхронной машины. Увеличение запаса по мощности увеличивает способность электрической системы сохранить устойчивость при малых возмущениях.
3. Определение запаса статической устойчивости системы с учетом регулирующего эффекта нагрузки (с учетом явнополюсности гидрогенераторов)
Предел (действительный) передаваемой активной мощности определим, представляя генераторы обеих станций неизменными синхронными ЭДС и сопротивлениями, при учете регулирующего эффекта нагрузки. В этом разделе выключатель системы бесконечной мощности Q
3 отключен и связи с системой нет, а поэтому при изменениях режима напряжение U
н
не будет постоянным, так как комплексная нагрузка на шинах приемной системы, соизмеримая по мощности с эквивалентным генератором, не обладает бесконечным регулирующим эффектом. Следовательно, устойчивость передачи изменится.
Определим параметры схемы замещения.
Для первой станции c гидрогенератором G
1 (см. подраздел 2.2)
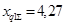 , , 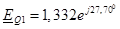
Для второй станции с турбогенератором G
2 (см. рисунок 2)

Определим значение передаваемой мощности от второй станции
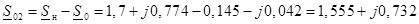
Вычислим значение ЭДС

Определим сопротивление суммарной нагрузки по формуле
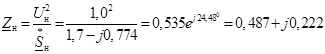
Представим полученную схему замещения на рисунке 14.

Рисунок 7 – Расчетная схема замещения
Определим собственные и взаимные сопротивления.
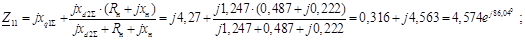
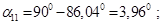
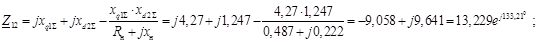
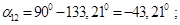
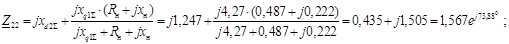
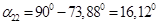
Взаимный угол между роторами генераторов двух станций:

Активная мощность, выдаваемая первой и второй станцией:
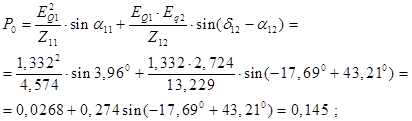
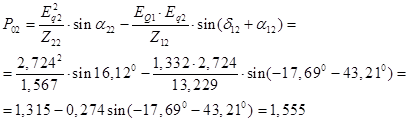
Определим величины максимума характеристик активных мощностей:
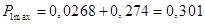 при при
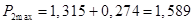 при при
Выражения для построения угловых характеристик мощности:
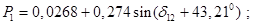
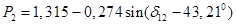
Рассчитываем коэффициенты запаса по мощности для первой и второй станций, %,


Таблица 11 – Результаты расчетов для построения угловых характеристик мощности с учетом нагрузки
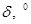 |
 |
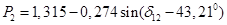 |
| -180 |
-0,161 |
1,127 |
| -160 |
-0,218 |
1,207 |
| -140 |
-0,245 |
1,300 |
| -120 |
-0,240 |
1,394 |
| -100 |
-0,202 |
1,479 |
| -80 |
-0,137 |
1,544 |
| -60 |
-0,052 |
1,582 |
| -40 |
0,042 |
1,587 |
| -20 |
0,135 |
1,560 |
| 0 |
0,214 |
1,503 |
| 20 |
0,271 |
1,423 |
| 40 |
0,299 |
1,330 |
| 60 |
0,294 |
1,236 |
| 80 |
0,256 |
1,151 |
| 100 |
0,191 |
1,086 |
| 120 |
0,106 |
1,048 |
| 140 |
0,011 |
1,043 |
| 160 |
-0,081 |
1,070 |
| 180 |
-0,161 |
1,127 |
Таким образом, при учете нагрузки и подключении второй станции, предел передаваемой мощности увеличивается. График смещается как по оси абсцисс, так и по оси ординат.

Рисунок 8 – Угловая характеристика мощности с учетом нагрузки
4. Анализ динамической устойчивости электроэнергетической системы
Исследуем динамическую устойчивость ЭЭС, рассмотрев ее как систему консервативную, не имеющую потерь энергии, зависящих от скорости. При включенном выключателе системы бесконечной мощности Q
3 схема замещения в нормальном режиме будет аналогична схеме замещения простейшей системы (рисунок 2).
Все расчеты выполняются для трехфазного и двухфазного КЗ на землю. КЗ происходит в начале цепи линии W
. Качественный анализ устойчивости ЭЭС проведем при наличии на эквивалентном генераторе регуляторов возбуждения пропорционального действия, принимая изменяющуюся в момент коммутации ЭДС Е
¢
за постоянную величину Е
¢
=const. Работа устройств АПВ здесь не рассматривается.
4.1 Расчет и построение угловых характеристик мощности нормального, аварийного и послеаварийного режимов
4.1.1 Нормальный режим
Для нормального режима работы все параметры берем из пункта 2.3. Характеристика мощности имеет следующий вид
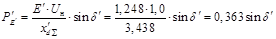 ; ;
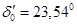
4.1.2
Послеаварийный режим
В послеаварийном режиме (режим II) происходит отключение цепи линии W
, на которой произошло короткое замыкание. Тогда сопротивление системы составит 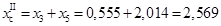 . .
Находим взаимное сопротивление
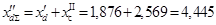
Характеристика мощности в послеаварийном режиме примет следующий вид:
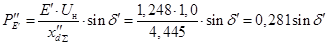
4.1.3 Аварийный режим
В аварийном режиме рассматривается 2 вида КЗ: трехфазное и двухфазное на землю. В месте аварии вводится шунт с сопротивлением x
D
. Для трехфазного режима x
D
=0, для двухфазного на землю x
D
=x
2
S
//x
0
S
.
Определим результирующие сопротивления схем обратной и нулевой последовательностей. В схеме замещения обратной последовательности сопротивления трансформатора Т
1 и линии W
остаются неизменными (см. раздел 1), а сопротивление генератора G
1 пересчитывается. ЭДС источников равны нулю.
Сопротивления генератора G
1 обратной последовательности:
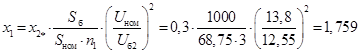 , ,
где 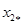 – сопротивление генератора токам обратной последовательности, о. е. – сопротивление генератора токам обратной последовательности, о. е.
Преобразуем схему замещения обратной последовательности.
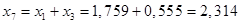 ; ;
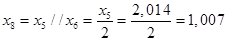 ; ;

Рисунок 9 – Схема замещения обратной последовательности
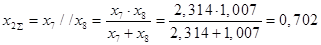
В схеме замещения нулевой последовательности сопротивления двухцепной линии W
увеличивается в 5 раз.
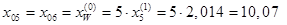
Сопротивление трансформатора Т
1 не изменяется и равно 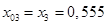 . .
Генератор G
1 в схеме замещения нулевой последовательности участвовать не будет, так как находится за обмоткой трансформатора Т
1, соединенной в треугольник.

Рисунок 10 – Схема замещения нулевой последовательности
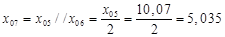 ; ;
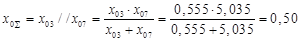
Определим сопротивление шунта при двухфазном КЗ на землю

Преобразуем схему к расчетному виду.
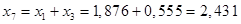 ; ;

Рисунок 11 – Схема замещения аварийного режима
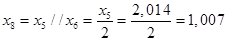

Рисунок 12 – Преобразованная схема замещения
– трехфазное КЗ
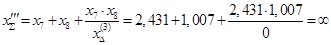 ; ;
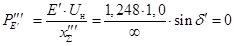
При трехфазном КЗ передача мощности в приемную систему невозможна.
– двухфазное КЗ на землю
 ; ;

4.2 Определение предельного угла отключения КЗ в простейшей ЭЭС. Построение зависимости изменения угла
d
¢
(
t
) и определение предельного времени отключения
Для определения предельного угла отключения пользуются критерием динамической устойчивости. Площадка ускорения должна быть равна площадке возможного торможения. Предельный угол и определяет равенство этих площадок.
Выражение для определения предельного угла отключения:
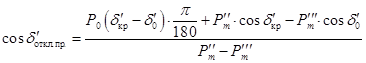 , ,
где 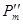 –
максимальная мощность генератора в послеаварийном режиме; –
максимальная мощность генератора в послеаварийном режиме;
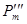 – максимальная мощность генератора в аварийном режиме; – максимальная мощность генератора в аварийном режиме;
 – максимальная мощность генератора в нормальном режиме; – максимальная мощность генератора в нормальном режиме;
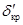 – критический угол, равный – критический угол, равный

– трехфазное КЗ
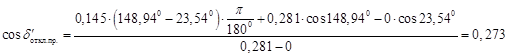 ; ;
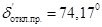
– двухфазное КЗ на землю
 ; ;
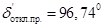
Из полученных результатов видно, что система неустойчива при обоих видах КЗ и требует отключения по условию сохранения динамической устойчивости.
Характер изменения угла δ
/
(t
), по которому можно найти предельное время отключения КЗ t
откл.пр.
или время tmax
достижения углом величины δ/
max
при возникших качаниях ротора эквивалентного генератора, определится решением дифференциального уравнения относительно движения ротора эквивалентного генератора
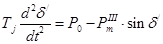 , ,
где Т
j
– постоянная инерции генератора.
Постоянная инерции эквивалентного генератора G
1 равна
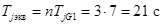
Решим дифференциальное уравнение методом последовательных интервалов. Принимаем шаг интегрирования Δt
=0,05 с. При этом коэффициент k
(в электрических градусах) будет равен
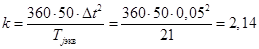
Приращение угла на первом интервале составит

где избыток мощности в начале интервала равен
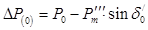
Величина угла к концу первого интервала
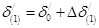
Приращение угла за любой последующий i
-
ый интервал времени определим по выражению
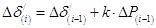
Прибавив к значению угла на предыдущем интервале его приращение на данном интервале, определим угол к концу i
-го интервала:
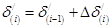
При трехфазном КЗ и двухфазном КЗ на землю расчет ведем до предельного угла отключения КЗ. Расчет проводим в табличной форме для трехфазного (таблица 12) и двухфазного КЗ на землю (таблица 13).
Таблица 12 – Изменение угла δ
/
(t
) при трехфазном КЗ
| t, c |
d/
|
 |
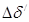 |
| 0 |
23,54 |
0,145 |
0 |
| 0,05 |
23,54 |
0,145 |
0,31 |
| 0,10 |
23,85 |
0,145 |
0,62 |
| 0,15 |
24,47 |
0,145 |
0,93 |
| 0,20 |
25,40 |
0,145 |
1,24 |
| 0,25 |
26,64 |
0,145 |
1,55 |
| 0,30 |
28,16 |
0,145 |
1,86 |
| 0,35 |
30,02 |
0,145 |
2,17 |
| 0,40 |
32,19 |
0,145 |
2,48 |
| 0,45 |
34,67 |
0,145 |
2,79 |
| 0,50 |
37,46 |
0,145 |
3,10 |
| 0,55 |
40,56 |
0,145 |
3,41 |
| 0,60 |
43,97 |
0,145 |
3,72 |
| 0,65 |
47,69 |
0,145 |
4,03 |
| 0,70 |
51,72 |
0,145 |
4,34 |
| 0,75 |
56,06 |
0,145 |
4,65 |
| 0,80 |
60,71 |
0,145 |
4,96 |
| 0,85 |
65,67 |
0,145 |
5,27 |
| 0,90 |
70,94 |
0,145 |
5,58 |
| 0,95 |
76,52 |
Таблица 13 – Изменение угла δ
/
(t
) при двухфазном КЗ на землю
| t, c |
d/
|
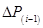 |
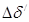 |
| 0 |
23,54 |
0,103 |
0,11 |
| 0,05 |
23,65 |
0,102 |
0,33 |
| 0,10 |
23,98 |
0,102 |
0,55 |
| 0,15 |
24,53 |
0,101 |
0,77 |
| 0,20 |
25,30 |
0,100 |
0,98 |
| 0,25 |
26,28 |
0,098 |
1,19 |
| 0,30 |
27,47 |
0,096 |
1,40 |
| 0,35 |
28,87 |
0,094 |
1,60 |
| 0,40 |
30,47 |
0,091 |
1,80 |
| 0,45 |
32,27 |
0,088 |
1,99 |
| 0,50 |
34,26 |
0,085 |
2,17 |
| 0,55 |
36,43 |
0,082 |
2,35 |
| 0,60 |
38,78 |
0,079 |
2,52 |
| 0,65 |
41,30 |
0,075 |
2,68 |
| 0,70 |
43,98 |
0,071 |
2,83 |
| 0,75 |
46,81 |
0,068 |
2,98 |
| 0,80 |
49,79 |
0,064 |
3,12 |
| 0,85 |
52,91 |
0,060 |
3,25 |
| 0,90 |
56,16 |
0,057 |
3,37 |
| 0,95 |
59,53 |
0,054 |
3,48 |
| 1,00 |
63,01 |
0,050 |
3,59 |
| 1,05 |
66,60 |
0,048 |
3,69 |
| 1,10 |
70,29 |
0,045 |
3,79 |
| 1,15 |
74,08 |
0,043 |
3,88 |
| 1,20 |
77,96 |
0,041 |
3,97 |

Рисунок 13 – Зависимость δ
/
(t
): а)
I– зависимость d
¢
(t
) для трехфазного КЗ; б)
II – зависимость d
¢
(t
) для двухфазного КЗ на землю
По рисунку 13 определим графически предельное время отключения З для обеспечения устойчивости системы. Предельное время отключения трехфазного КЗ составляет 0,93 с, двухфазного КЗ на землю – 1,43 с.
По полученным зависимостям мощности построим угловые характеристики мощности соответствующих режимов.
Таблица 14 – Результаты расчетов для построения угловых характеристик мощности при анализе динамической устойчивости
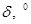 |
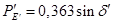 |
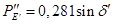 |
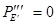 |
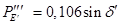 |
| 0 |
0 |
0 |
0
|
0 |
| 10 |
0,063 |
0,049 |
0,018 |
| 20 |
0,124 |
0,096 |
0,036 |
| 30 |
0,182 |
0,141 |
0,053 |
| 40 |
0,233 |
0,181 |
0,068 |
| 50 |
0,278 |
0,215 |
0,081 |
| 60 |
0,314 |
0,243 |
0,092 |

Рисунок 28 – Угловые характеристики мощности при отключении трехфазного КЗ

Рисунок 29 – Угловые характеристики мощности при отключении двухфазного КЗ на землю
Список источников
1 Электромеханические переходные процессы в электроэнергетических системах: метод. Указания по курсовой работе для студентов укрупненной группы направления подготовки специалистов 140000 – «Энергетика, энергетическое машиностроение и электротехника» (спец. 140203.65, 140204.65, 140205.65) всех форм обучения / сост.: А.Э. Бобров, А.М. Дяков, В.Б. Зорин, Л.И. Пилюшенко. – Красноярск: ИПЦ КГТУ, 2006. – 48 с.
2 Герасименко, А.А. Передача и распределение электрической энергии: учеб. пособие / А.А. Герасименко, В.Т. Федин. – Красноярск: ИПЦ КГТУ; Минск: БНТУ, 2006. – 808 с.
3 Веников, В.А. Переходные электромеханические процессы в электрических системах / В.А. Веников. – М. Высш. школа 1978. – 415 с.
4 Сильченко, Т.В. Стандарт организации. Система менеджмента качества. Общие требования к построению, изложению и оформлению документов учебной и научной деятельности / Т.В. Сильченко, В.К. Младенцева, Л.В. Белошапко. – Красноярск: ЦМСМК СФУ, 2010. – 57 с.
|