МЕТОДИ ПЕРЕТВОРЕННЯ БІОСИГНАЛІВ ТА АНАЛІЗ
МЕДИКО-БІОЛОГІЧНОЇ ІНФОРМАЦІЇ
Сигнал – процес зміни у часі фізичного стану певного об'єкта, який можна зареєструвати, відобразити та передати.
Детерміновані сигнали – сигнали, значення яких у будь-який момент часу повністю відомі, тобто передбачувані з імовірністю, що дорівнює одиниці.
Випадкові сигнали – сигнали, значення яких у будь-який момент часу неможливо передбачити з імовірністю, що дорівнює одиниці.
Періодичним називається будь-який сигнал, для якого виконується умова
 , ,
де період Т є кінцевим відрізком, а k – будь-яке ціле число.
Сигнали, що існують в усі моменти часу, називають аналоговими.
Послідовність чисел, що подає сигнал при цифровій обробці, називається дискретним сигналом. Числа, що складають послідовність, є значеннями сигналу в окремі (дискретні) моменти часу й називаються відліками. Переважно відліки беруть через рівні проміжки часу Тд
, що мають назву період дискретизації (або крок дискретизації). Величина, зворотна періоду дискретизації, називається частотою дискретизації
 , ,
відповідна їй кругова частота
 . .
Процес перетворення відліків сигналу в числа називається квантуванням за рівнем.
Сигнал, дискретний у часі та квантований за рівнем, називають цифровим сигналом.
Динамічним поданням називається спосіб подання сигналів, при якому реальний сигнал приблизно подається сумою деяких елементарних сигналів, що виникають у послідовні моменти часу. Якщо спрямувати до нуля тривалість окремих елементарних сигналів, то границя суми дасть точне подання вихідного сигналу.
Два сигнали u і v називають ортогональними, якщо їх скалярний добуток, а отже, і взаємна енергія дорівнюють нулю:
 . .
Якщо в просторі сигналів задана нескінченна система ортогональних функцій {a1
, a2
, …, an
} з одиничними нормами

це означає, що в просторі сигналів заданий ортонормований базис.
Розкладання сигналу:
 , ,
де сk
– «проекції» сигналу на координатні вісі, напрямок яких задається функціями hk
(t), називається узагальненим рядом Фур'є сигналу s(t) в обраному базисі.
Сукупність коефіцієнтів ряду Фур'є {ck
} – спектр сигналу s(t).
Тригонометричний ряд Фур'є:
 , ,
де t0
– довільна величина;
 – період базисних функцій; – період базисних функцій;
 – кругова частота, що відповідає періоду повторення сигналу Т; частоти, кратні w0
, що входять у формулу, називаються гармоніками; – кругова частота, що відповідає періоду повторення сигналу Т; частоти, кратні w0
, що входять у формулу, називаються гармоніками;
 ; ;
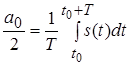 ; ;
 . .
Дійсна форма тригонометричного ряду Фур'є:
 , ,
де
 ; ;
 ; ;
 . .
Експоненційний ряд Фур'є:
 ; ;  , ,
де
 . .
Сукупність амплітуд гармонік ряду Фур'є називають амплітудним спектром.
Сукупність фаз гармонік ряду Фур'є називають фазовим спектром.
Коефіцієнти ряду залежать тільки від форми одиночного імпульсу s(t) і характеризуються інтегралом:
 , ,
який називається спектральна щільність одиночного імпульсу s(t).
Періодичне коливання має дискретний або лінійчатий спектр.
Відношення періоду послідовності прямокутних імпульсів до тривалості імпульсів називають щілинністю.
Амплітудний спектр послідовності прямокутних імпульсів має вигляд функції  , графік якої носить пелюстковий характер. , графік якої носить пелюстковий характер.
Важливою властивістю спектра послідовності прямокутних імпульсів є те, що у ньому відсутні (мають нульові амплітуди) гармоніки з номерами, кратними щілинності.
Відстань за частотою між сусідніми гармоніками спектра періодичного сигналу дорівнює частоті імпульсів 2p/Т.
Ширина пелюсток спектра послідовності прямокутних імпульсів, виміряна в одиницях частоти, дорівнює 2p/t, тобто зворотно пропорційна тривалості імпульсів.
Часове й частотне подання неперіодичного сигналу, що заданий на інтервалі (-¥, ¥), складає пару перетворень Фур'є:
 – зворотне перетворення Фур'є, – зворотне перетворення Фур'є,
 – пряме перетворення Фур'є. – пряме перетворення Фур'є.
Неперіодичні сигнали мають безперервний (суцільний) спектр.
Властивість спектра: чим коротше сигнал, тим ширше його спектр.
Добуток ефективних значень тривалості сигналу й ширини його спектра називається базою сигналу.
Дуальність перетворення Фур'є: якщо парній функції часу f(t) відповідає спектральна функція g(w) (вона буде також парною), то функції часу g(t) відповідатиме спектральна функція 2pf(w).
Прямокутному імпульсу відповідає спектральна функція, що має вигляд sin(w)/w. Отже, спектральна функція сигналу sin(t)/t буде прямокутною.
Перетворення Фур'є є лінійним інтегральним перетворенням, тобто спектр суми дорівнює сумі спектрів або, математичною мовою, лінійна комбінація сигналів має спектр у вигляді такої самої (з тими ж коефіцієнтами) лінійної комбінації їх спектральних функцій.
При затримці сигналу в часі амплітудний спектр цього сигналу не змінюється, фазовий спектр здобуває додатковий доданок, що лінійно залежить від частоти.
Зміна тривалості сигналу приводить до зміни ширини спектра зворотним чином в поєднанні зі збільшенням (при розтяганні, a<1) або зменшенням (при стиску, a>1) рівня спектральних складових.
Спектр похідної отримують шляхом множення спектра вихідного сигналу на jw. Отже, при диференціюванні низькі частоти послаблюються, а високі підсилюються. Фазовий спектр зсувається на 90° для позитивних частот і на – 90° для негативних. Множник jw називають оператором диференціювання сигналу в частотній зоні.
При інтегруванні вихідного сигналу його спектр множиться на 1/(jw). Високі частоти послаблюються, а низькі підсилюються. Фазовий спектр сигналу зсувається на ‑90° для позитивних частот і на 90° для негативних. Множник 1/(jw) називають оператором інтегрування в частотній зоні.
Спектр згортки сигналів дорівнює добутку спектрів.
Спектр добутку дорівнює згортці спектрів. Єдиною додатковою особливістю є множник 1/(2p) перед інтегралом згортки.
При множенні сигналу на гармонічну функцію спектр «роздвоюється» – розпадається на дві складові вдвічі меншого рівня, зсунутих на w0
праворуч (w-w0
) та ліворуч (w+w0
) за віссю частот. При кожному доданку є множник, що враховує початкову фазу гармонічного коливання.
Спектр дельта-функції є константа, тобто є рівномірним у нескінченній смузі частот.
Спектром константи є дельта-функція частоти.
Крок квантування:
 , ,
де Umax
– максимальне значення аналогового сигналу на вході АЦП, що не викликає переповнення арифметичного пристрою,
m – кількість двійкових розрядів.
Теорема Котельникова: будь-який сигнал s(t), спектр якого не містить складових із частотами вище wВ
=2pfВ
, може бути без втрат інформації поданий своїми дискретними відліками {s(k)}, узятими з інтервалом Т, що задовольняє наступній нерівності:
 ( ( або або  ). ).
Частота Найквіста –
 . .
Спектр дискретного сигналу є нескінченним рядом зсунутих на величину частоти дискретизації wд
копій спектра вихідного безперервного сигналу s(t), тобто спектр дискретного сигналу періодичний з періодом, що дорівнює частоті дискретизації.
сигнал аналоговий перетворення фур'є
Дискретне перетворення Фур'є (ДПФ):
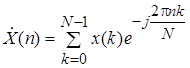 , ,
де x(k) – відліки дискретного сигналу;
N – кількість відліків дискретного сигналу;
n – номер коефіцієнта ДПФ.
Перехід від дискретного спектра до часових відліків сигналу здійснюється за допомогою зворотного дискретного перетворення Фур'є (ЗДПФ):
 . .
ДПФ є лінійним перетворенням, тобто якщо послідовностям {x(k)} і {y(k)} з періодом N відповідають набори гармонік  і і 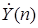 , то послідовності {ax(k)+by(k)} відповідатиме спектр , то послідовності {ax(k)+by(k)} відповідатиме спектр  . .
Кількість різних коефіцієнтів ДПФ  , ,  , ,  , …, , …,  дорівнює кількості відліків N за період; при n = N коефіцієнт дорівнює кількості відліків N за період; при n = N коефіцієнт  . .
Нульовий коефіцієнт ДПФ  (постійна складова) дорівнює сумі всіх відліків сигналу. (постійна складова) дорівнює сумі всіх відліків сигналу.
Властивість симетричності ДПФ: коефіцієнти ДПФ, номери яких розташовуються симетрично відносно  , утворюють спряжені пари. , утворюють спряжені пари.
Якщо кількість відліків дискретного сигналу N не є простим числом і її можна розкласти на множники, процес обчислень коефіцієнтів ДПФ можна прискорити, розділивши набір відліків на частини, обчисливши їх ДПФ та об'єднавши результати. Такі способи обчислення ДПФ називаються швидким перетворенням Фур'є (ШПФ).
Залежно від способу розподілу послідовності відліків на частини при реалізації ШПФ можливо кілька варіантів організації обчислень: проріджування за часом; проріджування за частотою. Можливі різні варіанти також залежно від того, на скільки фрагментів розбивають послідовності на кожному кроці (основа ШПФ).
Вибір кінцевого інтервалу тривалістю n секунд (Т – інтервал дискретизації, n – кількість відліків) для заданого сигналу визначає таку особливість спектрального розкладання: крім основних спектральних складових з'являються «фальшиві» – «розмивання» спектра. Причина «розмивання» спектра – наявність розривів на межах інтервалу спостережуваного сигналу і його періодичного продовження.
Вікна – це вагові функції, що використовують для зменшення розмивання спектральних компонентів, обумовленого скінченністю інтервалу спостереження.
Аналогові фільтри обробляють сигнали x(t), які є безперервною величиною.
Цифрові фільтри перетворюють відлікові значення сигналу x(n) у дискретні моменти часу n, де Т – інтервал дискретизації.
Реакція системи на подану на вхід дельта-функцію називається імпульсною характеристикою системи й позначається h(t).
Вихідний сигнал лінійної системи з постійними параметрами дорівнює згортці вхідного сигналу й імпульсної характеристики системи:
 . .
Перехідною характеристикою називають реакцію системи на подану на вхід функцію одиничного стрибка. Позначається перехідна характеристика як g(t).
У частотній зоні проходження сигналу через лінійну систему має вигляд:
 , ,
де  – перетворення Фур'є імпульсної характеристики системи – перетворення Фур'є імпульсної характеристики системи
(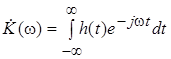 ) )
Ця функція називається комплексним коефіцієнтом передачі системи, а її модуль і фаза – амплітудно-частотною (АЧХ) і фазочастотною (ФЧХ) характеристиками системи.
Фільтри нижніх частот (ФНЧ) пропускають частоти, менші деякої частоти зрізу w0
.
Фільтри верхніх частот (ФВЧ) пропускають частоти, більші деякої частоти зрізу w0
.
Смугові фільтри (СФ) пропускають частоти в деякому діапазоні w1
…w2
(вони можуть також характеризуватися середньою частотою w0
=(w1
+w2
)/2 і шириною смуги пропускання Dw=w2
-w1
).
Режекторні фільтри (фільтр-пробка) пропускають на вихід всі частоти, крім частот з деякого діапазону w1
…w2
(вони можуть також характеризуватися середньою частотою
w0
=(w1
+w2
)/2
і шириною смуги затримування
Dw=w2
-w1
).
Дискретний фільтр – це довільна система обробки дискретного сигналу, що має властивості лінійності та стаціонарності.
У загальному вигляді цифровий фільтр підсумовує (з ваговими коефіцієнтами) деяку кількість вхідних відліків і деяку кількість вихідних відліків. Дана формула називається алгоритмом цифрової фільтрації:
 , ,
де aj
і bi
– дійсні коефіцієнти.
Якщо по-іншому згрупувати доданки, одержимо форму запису, що називається різницевим рівнянням:
 . .
Сутність z-перетворення полягає в тому, що послідовності чисел {x(k)} ставиться у відповідність функція комплексної змінної z, яка визначається так:
 . .
Зв'язок z-перетворення X(z) з перетворенням Фур'є  : :
 , ,
 . .
Z-перетворення є лінійною комбінацією відліків, тому воно підлягає принципу суперпозиції: якщо
 й й
 , ,
то
 . .
Якщо z-перетворення послідовності {x(k)} дорівнює X(z), то z-перетворення послідовності, затриманої на k0
тактів
(y(k)=x(k-k0
)),
матиме вигляд
 , ,
тобто при затримці послідовності на k0
тактів необхідно помножити її z-перетворення на  (оператор затримки дискретної послідовності на k0
тактів). (оператор затримки дискретної послідовності на k0
тактів).
Згортці дискретних послідовностей відповідає добуток їх z-перетворень.
Вихідна реакція на одиничний імпульс x0
(k) називається імпульсною характеристикою дискретної системи й позначається h(k).
Вихідний сигнал є лінійною комбінацією імпульсних характеристик, що випливає з лінійності та стаціонарності розглянутої системи. Цей вираз називається дискретною згорткою:
 . .
Для системи, що фізично реалізується, формула дискретної згортки має вигляд:
 . .
Функція H(z), що дорівнює відношенню z‑перетворень вихідного та вхідного сигналів і є z‑перетворенням імпульсної характеристики системи, називається функцією передачі або системною функцією дискретної системи:
 . .
Щоб одержати комплексний коефіцієнт передачі (частотну характеристику) дискретної системи, скористаємося формулою, що описує зв'язок z‑перетворення й перетворення Фур'є:
 . .
Частотна характеристика дискретної системи є періодичною функцією частоти з періодом, що дорівнює частоті дискретизації.
Функція K(jw) є перетворенням Фур'є імпульсної характеристики ЦФ.
Модуль комплексної частотної характеристики A(w)=|K(jw)| називається амплітудно-частотною характеристикою фільтра (АЧХ).
Аргумент комплексної частотної характеристики j(w)=arg[K(jw)] називається фазо-частотною характеристикою фільтра (ФЧХ).
Цифрові фільтри, які при обчисленнях не використовують попередні відліки вихідного сигналу, називаються нерекурсивними (трансверсальні фільтри) (НЦФ):
 . .
Кількість попередніх відліків m, що використовуються у розрахунках, називається порядком фільтра.
Цифрові фільтри, які при обчисленнях використовують попередні відліки вихідного сигналу, називаються рекурсивними (РЦФ):
 . .
Кількість попередніх вхідних та вихідних відліків, що використовуються для обчислень, може не збігатися. У такому випадку порядком фільтра вважається максимальне із чисел m і n.
Рекурсія – математичний прийом, що становить циклічне звертання до даних, які отримані на попередніх етапах.
Характеристики випадкових сигналів є статистичними.
Імовірність події оцінюють частотою сприятливих результатів.
Якщо проведено N незалежних випробувань, причому в n із них спостерігалася подія А, то емпірична (вибіркова) оцінка ймовірності Р(А):
 . .
Функція розподілу випадкової величини дорівнює ймовірності того, що випадкове число з Х прийме значення, рівне або менше певного х:
 ; ;
 ; ;
 ; ; 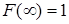 , ,
де Х – випадкова величина, тобто сукупність дійсних чисел х, що приймають випадкові значення.
Щільність імовірності випадкової величини – імовірність влучення випадкової величини Х у півінтервал (х, х + dx], тобто похідна від функції розподілу:
 ; ;
 ; ;
 ; ;  . .
Математичне очікування (момент першого порядку) є теоретичною оцінкою середнього значення випадкової величини:
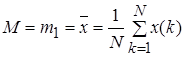 . .
Дисперсія (центральний момент):
 . .
Середньоквадратичне відхилення, необхідне для кількісного опису міри розкиду результатів окремих випадкових випробувань щодо математичного очікування:
 . .
Випадковий процес X(t) – функція, що характеризується тим, що в будь-який момент часу t прийняті нею значення є випадковими величинами.
Фіксуючи на певному проміжку часу миттєві значення випадкового сигналу, одержуємо реалізацію випадкового процесу.
Випадковий процес є нескінченною сукупністю реалізацій, що утворюють статистичний ансамбль.
Випадкові процеси, статистичні характеристики яких однакові у всіх часових перетинах, називають стаціонарними випадковими процесами.
Стаціонарний випадковий процес називається ергодичним, якщо при визначенні будь-яких його статистичних характеристик усереднення за ансамблем реалізацій еквівалентно усередненню за часом однієї, теоретично довгої, реалізації.
Кореляційний аналіз полягає у кількісному вимірі ступеня подібності різних сигналів.
Автокореляціна функція (АКФ) дозволяє судити про ступінь зв'язку (кореляції) сигналу s(t) з його зсунутою за часом копією:
 , ,
де t – величина часового зсуву сигналу.
Взаємна кореляційна функція (ВКФ) дозволяє оцінити ступінь подібності двох сигналів s1
(t) і s2
(t):
 . .
ВКФ зв'язана перетворенням Фур'є із взаємним спектром сигналів. Взаємний спектр  для сигналів – це s1
(t) і s2
(t) є добутком їх спектральних функцій, одна з яких піддана комплексному спряженню: для сигналів – це s1
(t) і s2
(t) є добутком їх спектральних функцій, одна з яких піддана комплексному спряженню: 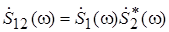 . Якщо спектри сигналів не перекриваються, то їх взаємний спектр дорівнює нулю на всіх частотах, отже, дорівнює нулю і їх ВКФ при будь-яких часових зсувах t. Отже, сигнали зі спектрами, що не перекриваються, є некорельованими. . Якщо спектри сигналів не перекриваються, то їх взаємний спектр дорівнює нулю на всіх частотах, отже, дорівнює нулю і їх ВКФ при будь-яких часових зсувах t. Отже, сигнали зі спектрами, що не перекриваються, є некорельованими.
АКФ сигналу зв'язана перетворенням Фур'є із квадратом модуля спектральної функції, або з енергетичним спектром сигналу.
Коваріаційна функція – це статистично усереднений добуток значень випадкової функції X(t) у моменти часу t1
і t2
:
 . .
Кореляційна функція є статистично усередненим добутком значень центрованої випадкової функції X(t)-mx
(t) у моменти часу t1
і t2
:
 . .
Мірою лінійного статистичного зв'язку між випадковими величинами є коефіцієнт кореляції:
 , ,
 , граничні значення ±1 досягаються, якщо реалізації випадкових величин жорстко зв'язані лінійним співвідношенням x2
=ax1
+b, де a і b – деякі константи. Знак коефіцієнта кореляції збігається зі знаком множника a. Рівність коефіцієнта кореляції нулю свідчить про відсутність лінійного статистичного зв'язку між випадковими величинами (тобто вони некорельовані). , граничні значення ±1 досягаються, якщо реалізації випадкових величин жорстко зв'язані лінійним співвідношенням x2
=ax1
+b, де a і b – деякі константи. Знак коефіцієнта кореляції збігається зі знаком множника a. Рівність коефіцієнта кореляції нулю свідчить про відсутність лінійного статистичного зв'язку між випадковими величинами (тобто вони некорельовані).
Для стаціонарного випадкового процесу кореляційна функція залежить не від самих моментів часу, а тільки від інтервалу між ними t=t2
-t1
:
 . .
Абсолютні значення кореляційної функції при будь-яких t не перевищують її значення при t=0 (це значення дорівнює дисперсії випадкового процесу):
 . .
Використовують коефіцієнт кореляції (його також називають нормованою кореляційною функцією):
 ; ;
rx
(0) =1, |rx
(t)|£1 і rx
(-t)=rx
(t).
Функції Rx
(t) і rx
(t) характеризують зв'язок (кореляцію) між значеннями X(t), розділеними проміжком t. Чим повільніше убувають ці функції з ростом абсолютного значення t, тим більше проміжок, протягом якого спостерігається статистичний зв'язок між миттєвими значеннями випадкового процесу, і тим повільніше, плавніше змінюються в часі його реалізації. Усереднена спектральна щільність випадкового процесу є спектром його детермінованої складової (математичного очікування). Для центрованих випадкових процесів:
 та та  . .
Усереднене значення спектральної щільності не несе ніякої інформації про флуктуаційну, тобто випадкову, складову випадкового процесу.
Обчислення спектра випадкового процесу виконується на основі його кореляційної функції за допомогою теореми Вінера-Хінчина – кореляційна функція випадкового процесу і його спектральна щільність потужності зв'язані перетворенням Фур'є:
 , ,
де 
– спектральна щільність середньої потужності реалізації («спектральна щільність потужності» або «спектр потужності»);
 – спектральна щільність реалізації на інтервалі часу Т, обчислена за допомогою прямого перетворення Фур'є. – спектральна щільність реалізації на інтервалі часу Т, обчислена за допомогою прямого перетворення Фур'є.
Дискретний аналог теореми Вінера-Хінчина – спектр дискретного випадкового процесу є перетворенням Фур'є від його кореляційної функції:

|