Вопросы поля комплексных чисел, описывается построение поля комплексных чисел, приводятся алгебраическая форма записи комплексных чисел, определение комплексного числа, действия над комплексными числами.
п.1. Построение поля комплексных чисел.
Рассмотрим множество 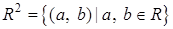 . Определим на . Определим на  бинарные операции сложения бинарные операции сложения  , умножения , умножения  , унарную операцию , унарную операцию 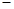 и определим элементы и определим элементы 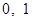 . .
Для 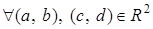 : :
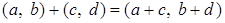 ; ;
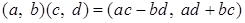 ; ;
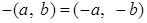 . .
Обозначим: 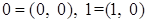 . .
Теорема 1. Алгебра 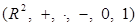 является полем. является полем.
Доказательство. Проверим, что алгебра 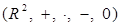 есть абелева группа. есть абелева группа.
Для 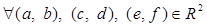
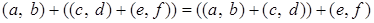 . .
Для 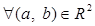
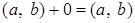 . .
Для 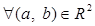
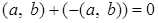 . .
Для 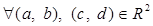
( . .
Проверим, что операция 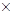 - ассоциативна, то есть - ассоциативна, то есть 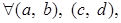 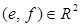
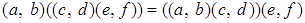 . .
Действительно,
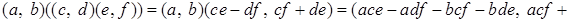 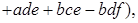
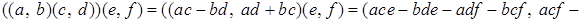 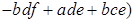 . .
Проверим левый закон дистрибутивности, то есть для 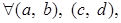 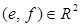
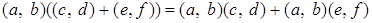 . .
Действительно,
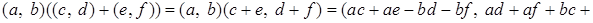 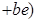 , ,
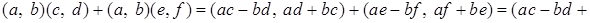 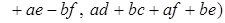 . .
Аналогично проверяется справедливость правого закона дистрибутивности.
Из выше доказанного следует, что алгебра 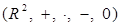 есть кольцо. есть кольцо.
Проверим, что кольцо 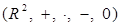 коммутативно, то есть для коммутативно, то есть для 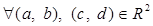 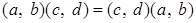 . .
Действительно,
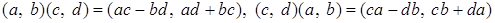 . .
Проверим, что 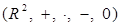 - кольцо с единицей 1, то есть - кольцо с единицей 1, то есть 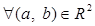
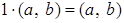 . .
Действительно,
 . .
Так как 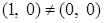 , то , то 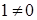 . .
Докажем, что каждый ненулевой элемент кольца 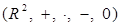 обратим. Пусть обратим. Пусть 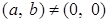 , что равносильно , что равносильно 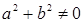 . Рассмотрим пару . Рассмотрим пару 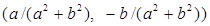 и проверим, что эта пара является обратной к паре и проверим, что эта пара является обратной к паре 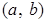 . Действительно, . Действительно,
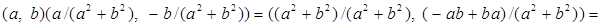 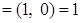 . .
Из выше доказанного следует, что алгебра 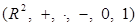 - поле. - поле.
Определение. Поле 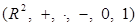 называется полем комплексных чисел, а его элементы - комплексными числами. называется полем комплексных чисел, а его элементы - комплексными числами.
п.2. Алгебраическая форма записи комплексных чисел.
Обозначение. Множество комплексных чисел принято обозначать 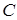 , то есть , то есть 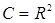 . Приняты также следующие обозначения: . Приняты также следующие обозначения:
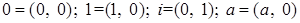 для для 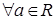 . .
Теорема 2. Каждое комплексное число  может быть, и притом единственным образом, записано в виде: может быть, и притом единственным образом, записано в виде:
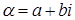 , где , где 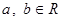 . (Такая запись называется алгебраической формой записи комплексного числа . (Такая запись называется алгебраической формой записи комплексного числа  ). ).
Доказательство. Существуют 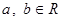 такие, что такие, что  . Имеем . Имеем
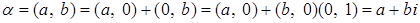 . .
Теорема 3. Число 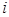 обладает свойством: обладает свойством: 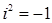 . .
Доказательство. 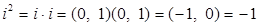 . .
Из равенства 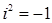 следует, что следует, что  . .
Определение. Пусть 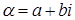 , где , где 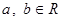 . Число . Число 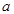 называется действительной частью, называется действительной частью, 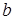 - мнимой частью комплексного числа - мнимой частью комплексного числа  . Пишем . Пишем  . .
Пусть 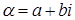 - алгебраическая форма записи комплексного числа - алгебраическая форма записи комплексного числа  . Тогда: . Тогда:
если 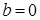 , то , то 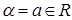 ; ;
если 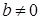 , то , то 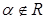 . .
Определение. Если 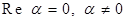 , то комплексное число , то комплексное число  называют чисто мнимым числом. называют чисто мнимым числом.
Действия над комплексными числами
в алгебраической форме
1) Для 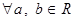
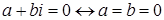 . .
Другими словами: комплексное число равно нулю тогда и только тогда, когда у него действительная и мнимая части равны нулю.
Доказательство. 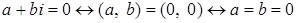 . .
2) Для 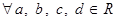
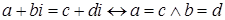 . .
Другими словами: два комплексных числа равны тогда и только тогда, когда у них, соответственно, равны действительная и мнимая части.
Доказательство. 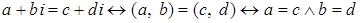 . .
3) Для 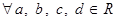
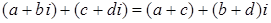 . .
Другими словами: чтобы сложить два комплексных числа, нужно, соответственно, сложить их действительные и мнимые части.
Доказательство. 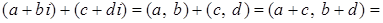
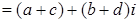 . .
4) Для 
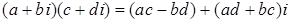 . .
Доказательство. 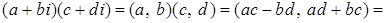
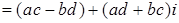 . .
5) Для 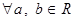
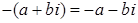 . .
Доказательство. 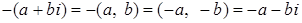 . .
6) Для 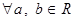 , если , если 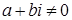 , то , то
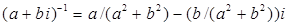 . .
Доказательство. 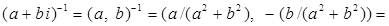
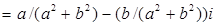 . .
п.3. Операция сопряжения.
Определение. Пусть комплексное число 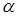 записано в алгебраической форме записано в алгебраической форме 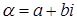 . Числом сопряжённым с . Числом сопряжённым с 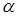 называется число называется число 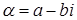 . .
Свойства операции сопряжения
Для 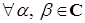 , где , где 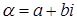 , , 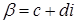 , , 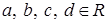 . .
1).
Доказательство.
.
2) .
Доказательство. .
3) .
Доказательство.
.
.
4) Если a¹ 0, то 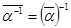 . .
Доказательство. 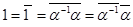 . .
5) 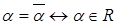 . .
Доказательство.  . .
6) 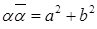 . .
Доказательство. 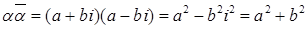 . .
С помощью операции сопряжения удобно производить деление комплексных чисел. Чтобы записать в алгебраической форме дробь с комплексными числителем и знаменателем нужно умножить числитель и знаменатель дроби на число, сопряжённое со знаменателем, и вычислить произведения в числителе и знаменателе.
п.4. Модуль комплексного числа.
Пусть  записано в алгебраической форме записано в алгебраической форме 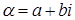 . .
Определение. Модулем комплексного числа  называется неотрицательное действительное число называется неотрицательное действительное число 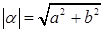 . .
Свойства модуля.
Для 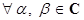 , где , где 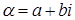 , , 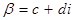 , , 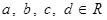 . .
1) 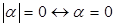 . .
Доказательство. 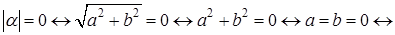
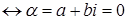 . .
2) 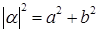 . .
3) 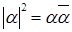 . .
Доказательство. Свойство следует из свойства 6 операции сопряжения.
4) 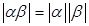 . .
Доказательство. 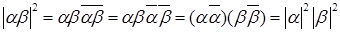 . .
Отсюда следует нужное утверждение.
5) Если 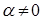 , то , то 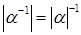 . .
Доказательство. 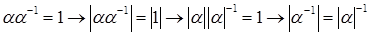 . .
6) Неравенство треугольника:  . .
Доказательство. Докажем сначала неравенство
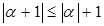 . .
Имеем
(2) 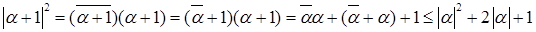 , ,
так как
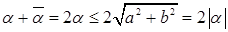 . .
Из (2) следует, что
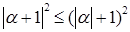 . .
Из последнего неравенства следует неравенство (1).
Докажем теперь неравенство треугольника. Неравенство треугольника, очевидно, выполнено для 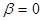 . Докажем неравенство треугольника для . Докажем неравенство треугольника для 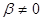 . Имеем . Имеем
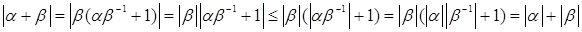 . .
7) 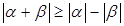 . .
Доказательство. 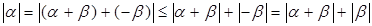 . Отсюда следует нужное неравенство. . Отсюда следует нужное неравенство.
8) 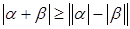 . .
Доказательство. Справедливы неравенства
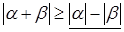 , , 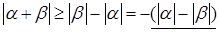 . .
Одно из подчёркнутых чисел совпадает с 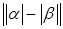 . .
п.5. Геометрическая интерпретация комплексных чисел.
Пусть  записано в алгебраической форме записано в алгебраической форме 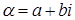 . Поставим в соответствие числу . Поставим в соответствие числу  точку плоскости с координатами точку плоскости с координатами 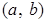 . Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью. . Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
Числа  и и 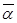 расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел. расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
Геометрический смысл модуля
Из Рис.1 видно, что расстояние от начала координат до числа  равно равно 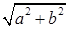 . Поэтому геометрический смысл . Поэтому геометрический смысл 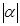 - расстояние от - расстояние от  до начала координат. до начала координат.
y
   bi a bi a
i
 -1+i 1+i -1+i 1+i
 - 1 0 1 a - 1 0 1 a
x
- 1-i 1-i
- i
Рис.1.
 - bi `a - bi `a
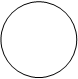
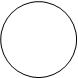
Пример. Изобразим на комплексной плоскости, на Рис.2, множества, заданные, соответственно, следующими условиями: 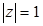 ; ; 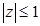 ; ; 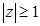 . .
   y | z | =1 y | z |£1 y | z |³1 y | z | =1 y | z |£1 y | z |³1
                 i i i i i i
       - 1 1 - 1 1 - 1 1 - 1 1 - 1 1 - 1 1
          0 0 0 0 0 0
           
- i - i - i
Рис.2.
Пусть 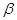 записано в алгебраической форме записано в алгебраической форме 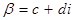 . Имеем . Имеем
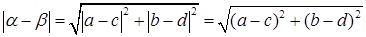 . .
Из Рис.3 видно, что геометрический смысл модуля разности комплексных чисел - расстояние между этими числами.
 y y
  b a b a

d |b-d|
    b|a-c| b|a-c|
Рис.3.
0 c a x
Пример. Изобразим на комплексной плоскости, на Рис.4, множества, заданные, соответственно, следующими условиями: 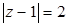 ; ; 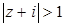 . .
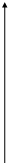 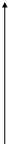 y y y y
 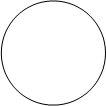 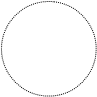  | z-1| =2 0 | z-1| =2 0
x
- i
- 1 0 1 3 x |z+i |> 1
- 2i
Рис.4.
Геометрическая интерпретация комплексных чисел
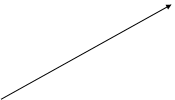
векторами плоскости
Поставим в соответствие числу  связаный вектор плоскости с началом в начале координат и с концом в точке связаный вектор плоскости с началом в начале координат и с концом в точке  . Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5. . Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
 y y
   a+b a+b
 b b
  a a
0 Рис.5
x
Геометрический смысл модуля комплексного числа  , при интерпретации чисел векторами, - длина вектора , при интерпретации чисел векторами, - длина вектора  . Сумма комплексных чисел находится как сумма векторов. . Сумма комплексных чисел находится как сумма векторов.
п.6. Тригонометрическая форма записи
комплексного числа.
Определение. Аргументом комплексного числа  называется число называется число 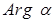 , равное величине угла между положительным направлением оси абсцисс и вектором , равное величине угла между положительным направлением оси абсцисс и вектором  , , 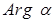 определяется с точность до углов, кратных определяется с точность до углов, кратных 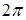 . Главным значением аргумента комплексного числа . Главным значением аргумента комплексного числа  называется то значение называется то значение 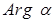 , которое принадлежит промежутку , которое принадлежит промежутку 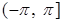 , оно обозначается , оно обозначается  и и 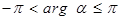 . .
Пусть  записано в алгебраической форме записано в алгебраической форме 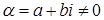 . Тогда из геометрической интерпретации . Тогда из геометрической интерпретации  следует, что: следует, что:
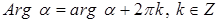 ; ;
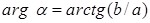 , если , если 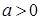 ; ;
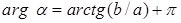 , если , если 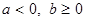 ; ;
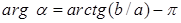 , если , если 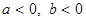 . .
Заметим, что  выражается только в радианах, выражается только в радианах, 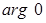 не определён. не определён.
Теорема 4. Каждое комплексное число 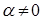 может быть записано в виде может быть записано в виде
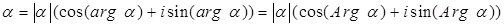 . .
Доказательство. Изобразим  вектором комплексной плоскости, вектором комплексной плоскости,
см. Рис.6.
  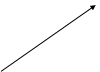  
y
b a
Рис.6.
0 a x
Угол, образованный вектором  и положительным направлением оси абсцисс, равен и положительным направлением оси абсцисс, равен  , следовательно, , следовательно, 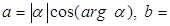 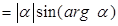 . Поэтому . Поэтому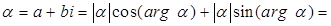 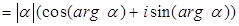 . .
Определение. Если комплексное число  записано в виде записано в виде 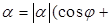 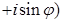 , то говорят, что , то говорят, что  записано в тригонометрической форме. записано в тригонометрической форме.
Правила действий с комплексными числами,
записанными в тригонометрической форме.
Пусть комплексные числа 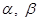 записаны в тригонометрической форме записаны в тригонометрической форме
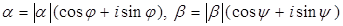 . .
1) 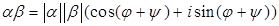 , ,
то есть при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
Доказательство.
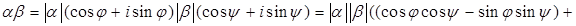
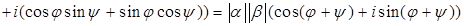 . .
2) Если 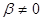 , то , то
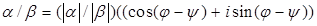 , ,
то есть при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Доказательство. Обозначим 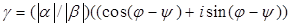 . Так как . Так как 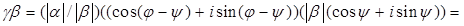 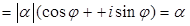 , то нужное утверждение доказано. , то нужное утверждение доказано.
3) Если 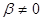 , то , то
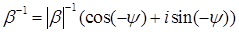 . .
4) Формула Муавра. Для 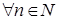 , ,
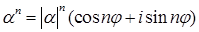 . .
Доказательство. Формула Муавра является следствием правила 1.
5) Обобщённая формула Муавра. Для 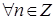 , ,
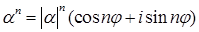 . .
Доказательство. Обобщённая формула Муавра является следствием формулы Муавра и свойства 3).
п.7. Показательная форма записи комплексного числа.
Обозначение. Для 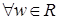 обозначим обозначим
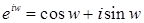 . (1) . (1)
Равенство (1) называют формулой Эйлера. При этом обозначении, запись комплексного числа 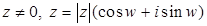 в показательной форме принимает вид в показательной форме принимает вид
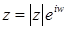 . (2) . (2)
Из равенства (1) и правил действия с комплексными числами, записанными в тригонометрической форме, следует справедливость следующей теоремы .
Теорема 5. Для 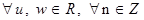 справедливы равенства: справедливы равенства:
1) 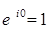 ; ;
2) 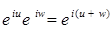 ; ;
3) 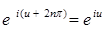 ; ;
4) 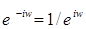 ; ;
5) 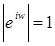 ; ;
6) 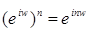 ; ;
7) 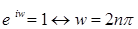
п.8. Связь между тригонометрическими и гиперболическими функциями.
Из формул Эйлера следует, что для 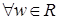
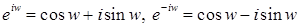 . .
Складывая и вычитая эти равенства находим, что для 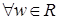 : :
(1) 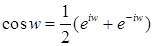 ; ;
(2) 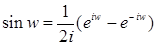 . .
Как известно, из курса математического анализа, гиперболические косинус, синус, тангенс, котангенс, соответственно, 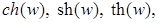  , для , для 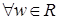 , определяются равенствами: , определяются равенствами:
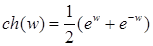 ; ; 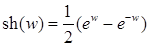 ; ;
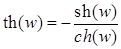 ; ; 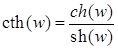 . .
Если в формулах (1), (2), заменить 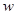 на на 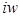 , то мы получим формулы для определения значений , то мы получим формулы для определения значений 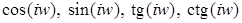 . Эти формулы выражают гиперболические формулы через тригонометрические. Для . Эти формулы выражают гиперболические формулы через тригонометрические. Для 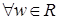 : :
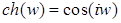 ; ; 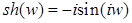 ; ;
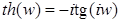 ; ; 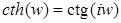 . .
п.9. Корни из комплексных чисел.
Определение. Пусть 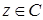 , , 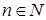 . Комплексное число . Комплексное число 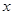 называется корнем степени называется корнем степени 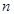 из из 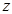 , если , если 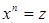 . .
Теорема 6. Пусть 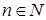 , , 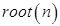 - множество всех корней степени - множество всех корней степени 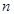 из 1. Тогда алгебра из 1. Тогда алгебра 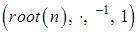 - группа, (которая называется группой корней степени - группа, (которая называется группой корней степени 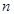 из 1). из 1).
Доказательство. Пусть 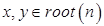 . .
Проверим, что умножение – бинарная операция. Имеем 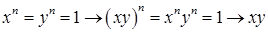 - корень степени - корень степени 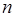 из 1. из 1.
Проверим, что 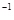 - унарная операция. Имеем - унарная операция. Имеем 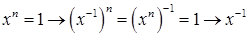 - корень степени - корень степени 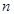 из 1. из 1.
Очевидно, что 1 – корень степени 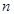 из 1. из 1.
Доказано, что 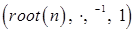 - алгебра. - алгебра.
То, что алгебра 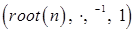 - группа, следует из свойств комплексных чисел. - группа, следует из свойств комплексных чисел.
Теорема 7. Для 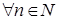 существует точно существует точно 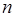 различных корней различных корней 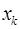 степени степени 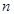 из 1, из 1, 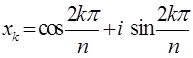 , , 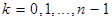 . (1) . (1)
Все корни расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0).
Доказательство. Проверим сначала, что числа 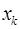 , заданные равенством (1), являются корнями степени , заданные равенством (1), являются корнями степени 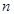 из 1. Действительно, из 1. Действительно, 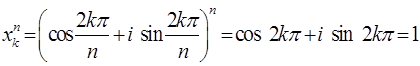 . .
Докажем, что любой корень 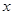 степени степени 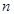 из 1 может быть вычислен по формуле (1). Т.к. из 1 может быть вычислен по формуле (1). Т.к. 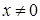 , то , то 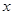 можно записать в показательой форме можно записать в показательой форме  . .
Имеем 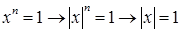 . Поэтому . Поэтому 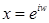 , , 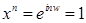 , , 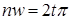 , где , где 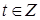 . По теореме о делении с остатком, существуют такие . По теореме о делении с остатком, существуют такие 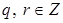 , что , что 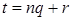 , где , где 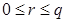 . .
Значит, 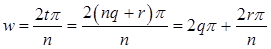 , , 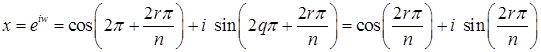 , т.е. вычисляется по формуле (1). , т.е. вычисляется по формуле (1).
Изобразив числа, заданные формулой (1), на комплексной плоскости, мы увидим, что они расположены в вершинах правильного n-угольника, вписанного в окружность единичного радиуса, одна из которых расположена в точке с координатами (1, 0). В частности, числа, заданные формулой (1), попарно различны.
Теорема 8. Пусть 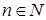 , , 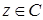 , , 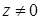 , , 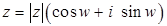 . Тогда существует точно . Тогда существует точно 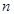 различных корней различных корней 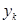 степени степени 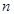 из из 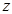 , , 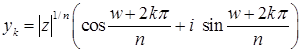 , , 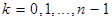 . (2) . (2)
Доказательство. Проверим сначала, что числа 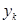 , заданные равенством (2), являются корнями степени , заданные равенством (2), являются корнями степени 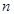 из из 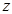 . Действительно, . Действительно, 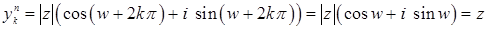 . .
Пусть 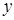 - корень степени - корень степени 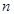 из из 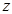 . Докажем, что он вычисляется по формуле (2). Рассмотрим число . Докажем, что он вычисляется по формуле (2). Рассмотрим число 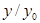 , где , где 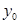 определено формулой (2). Имеем определено формулой (2). Имеем 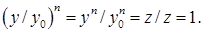
Следовательно 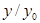 - корень степени - корень степени 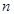 из 1, т.е. из 1, т.е. 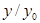 совпадает с одним из чисел совпадает с одним из чисел 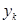 . Имеем . Имеем 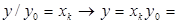 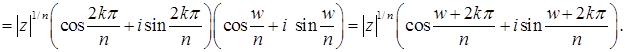
Из вышедоказанного следует, что числа 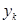 попарно различны. попарно различны.
п.10. Мультисекция.
Теорема 1. (о мультисекции многочлена) Пусть
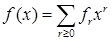 - многочлен с числовыми коэффициентами, - многочлен с числовыми коэффициентами, 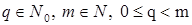 . Тогда . Тогда
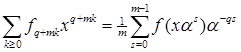 , (1) , (1)
где 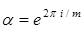 . .
Доказательство. Для 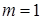 равенство (1) очевидно выполнено. Докажем (1) для равенство (1) очевидно выполнено. Докажем (1) для 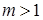 . Имеем . Имеем
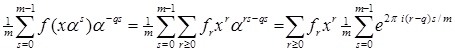 (2) (2)
Если - целое, то 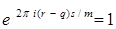 и и 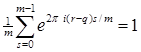 . .
Если - не целое, то 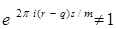 и по формуле суммы членов геометрической прогрессии и по формуле суммы членов геометрической прогрессии
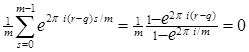 . .
Поэтому в (2) суммирование нужно вести только по тем 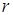 , для которых , для которых 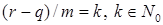 . Отсюда следует (1). . Отсюда следует (1).
Заметим, что равенство (1) справедливо не только для многочленов, но и для рядов.
Следствие 1. Пусть 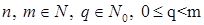 . Тогда . Тогда
. (3)
Доказательство. Рассмотрим многочлен
.
Применяя мультисекцию к многочлену , получим, что
,
где . Полагая 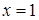 в последнем равенстве получим, что в последнем равенстве получим, что
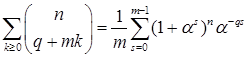 . (4) . (4)
Имеем
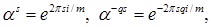
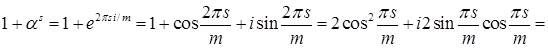
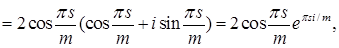
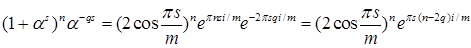
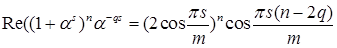 . .
Приравнивая действительные части обеих частей равенства (4), получаем равенство (3).
п.11. Упорядоченные поля
.
Определение. Упорядоченным полем называется алгебраическая система
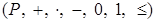 такая, что: такая, что:
1) алгебра 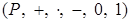 - поле; - поле;
2) 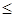 - линейный порядок на - линейный порядок на 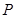 ; ;
3) для 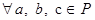
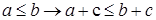 ; ;
4) для 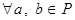
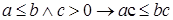 . .
Другими словами, упорядоченное поле - это поле, на множестве элементов которого определён линейный порядок 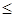 , согласованный условиями 3), 4), с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел. , согласованный условиями 3), 4), с операциями сложения и умножения. Нетрудно проверить, что для упорядоченного поля выполнены обычные свойства неравенств, известные для действительных чисел.
Примерами упорядоченных полей являются поле рациональных и поле действительных чисел.
Теорема 9. Если 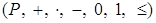 - упорядоченное поле, то для - упорядоченное поле, то для 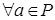 из условия из условия 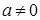 , следует, что , следует, что 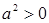 . .
Доказательство. Так как 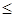 - линейный порядок, то - линейный порядок, то 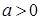 или или 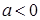 . Если . Если 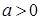 , то по условию 4) , то по условию 4) 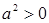 . Если . Если 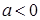 , то , то 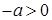 и по условию 4), и по условию 4), 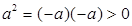 . .
Теорема 10. Если 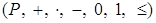 - упорядоченное поле, то для - упорядоченное поле, то для 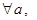 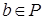 из условия из условия 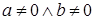 следует, что следует, что 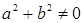 . .
Доказательство. Из теоремы 9 следует, что 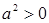 и и 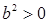 . Из условия 3 следует, что . Из условия 3 следует, что 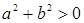 . .
Теорема 11. Поле комплексных чисел 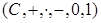 нельзя упорядочить. нельзя упорядочить.
Доказательство. Предположим противное - поле комплексных чисел 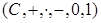 упорядоченно. Так как упорядоченно. Так как 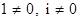 , то по теореме 10 , то по теореме 10 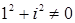 - противоречие. - противоречие.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
|