Министерство образования и науки Республики Казахстана
Павлодарский государственный университет им. С. Торайгырова
Кафедра «Радиотехника и телекоммуникации»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным занятиям
по дисциплине «Электротехника»
для студентов неэлектрических специальностей
Павлодар
Предисловие
Значение электротехники для всех областей знаний все более возрастает. Современные производственные процессы в большом масштабе обслуживаются электроприводами, электрическими системами измерений, регулирования и управления. Инженеры неэлектрических специальностей должны иметь понятия об электрических процессах, протекающих в электрических цепях, а также об электрических приборах и установках.
Настоящий лабораторный практикум составлен в соответствии с учебной типовой программой для выполнения лабораторных работ фронтальным методом в лаборатории «Электротехника» на универсальных стендах «Уралочка».
Лабораторные работы преследуют следующие цели:
1) закрепление теоретических знаний, полученных студентами в лекционной части курса;
2) ознакомление со схемами включения;
3) получение студентами практических навыков проведения эксперимента и обработки его результатов.
Описания лабораторных работ содержат теоретическую часть, что облегчает самостоятельную работу студентов в части подготовки их к выполнению работ, а также содержат список литературы, рекомендуемой для более глубокого изучения курса электротехники.
Лабораторная работа №1 Методика выполнения лабораторного практикума в лаборатории электротехники
Цель работы: знакомство с общей структурой лаборатории, устройством лабораторных стендов, правилами выполнения лабораторных работ, техникой безопасности при работе с электроустановками.
Правила выполнения лабораторных работ
Лабораторная работа по электротехнике является исследовательской работой, в результате выполнения которой подтверждаются теоретические положения, полнее осмысливаются физические явления и установленные теорией закономерности.
Студенты, работающие в лаборатории, разделяются на бригады по три-четыре человека. В начале каждого занятия проверяется подготовленность студента к выполнению лабораторной работы. При этом студенту задаются вопросы:
- какую лабораторную работу собираетесь выполнять?
- что в данной работе должно быть установлено?
- какие данные будут определены из опыта? Что должно быть рассчитано аналитически?
- какие графики, кривые, векторные диаграммы необходимо получить из опыта?
- какие схемы и таблицы для записи опытных данных заготовлены студентом?
- какие электроизмерительные приборы, аппараты и проводники будут использованы при опыте?
Студент, получивший допуск к лабораторной работе, приступает к сборке электрической цепи опыта. Рекомендуется сначала выполнить сборку последовательной части цепи, а затем параллельной; сборку схемы следует начинать от одного зажима источника питания и, пройдя по схеме последовательную цепь, закончить ее на другом зажиме. Включать стенд под напряжение не разрешается до проверки преподавателем правильности соединения приборов, аппаратов и прочего оборудования. В случае каких-либо пересоединений в собранной цепи последняя перед включением должна быть еще раз проверена преподавателем.
Закончив испытание, каждый студент обязан до разборки схемы предъявить преподавателю для подписи бланк с результатами наблюдений. Если результаты опыта будут признаны неудовлетворительными, то необходимо повторить опыт. По окончании работы все соединения должны быть разобраны, все проводники аккуратно возвращены на место.
Подготовка к лабораторной работе
Очередность и даты выполнения лабораторных работ объясняются преподавателем на вводном занятии. Студент должен заблаговременно подготовиться в читальном зале к предстоящему занятию в лаборатории. В подготовку входит6 изучение соответствующих разделов теоретического курса по лекционным записям и учебной литературе, указанной в описании каждой работы; подробном изучении содержания работы; в аккуратном вычерчивании электрических схем экспериментов и таблиц наблюдений в отчет для выполнения лабораторной работы.
До начала лабораторных занятий надо познакомиться с правилами выполнения лабораторных работ, методикой оценки погрешностей, способами приближенных вычислений, приемами построения графиков и векторных диаграмм.
Каждый студент обязан усвоить правила техники безопасности, уметь оказать первую помощь при поражении электрическим током и механических травмах.
Студенты, явившиеся на занятие неподготовленными, не допускаются к работе в течение времени, отведенном для выполнения лабораторной работы, изучают в читальном зале или лаборатории не освоенный ими материал по учебной литературе.
Отчет по лабораторной работе
Отчет должен содержать: титульный лист, схемы экспериментов, таблицы с данными измерений, графики, векторные диаграммы, результаты вычислений, расчетные формулы, перечень использованного оборудования и выводы.
Полученные данные наблюдений студент частично обрабатывает в лаборатории, а окончательно – дома. Электрические схемы, векторные диаграммы и графики следует вычерчивать аккуратно карандашом, применяя чертежные принадлежности. Векторные диаграммы строятся с соблюдением масштаба: выбранный масштаб указывается рядом с начерченной диаграммой. При вычерчивании электрических схем следует использовать условные обозначения в соответствии с ГОСТами (табл. 1.1 ÷ 1.4). При построении графиков необходимо на осях координат написать обозначения откладываемых величин, единицы их измерений. Вдоль осей координат наносят деления и представляют в масштабе числовые значения.
Отчет выполняется рукописно на стандартных листах формата А4 (размеры 210х297 мм) и скрепляется скрепкой. Нумерация страниц отчета – сквозная (первой страницей является титульный лист). Отчет с проставленной датой выполнения работы и подписанный студентом представляется преподавателю на следующее лабораторное занятие. При защите работы студент обязан объяснить любой выполненный опыт или расчет и ответить на дополнительные вопросы преподавателя по данной теме.Студенты не представившие отчет и не получившие зачет по предыдущей работе, к выполнению последующих работ не допускаются.
Обработка пропущенных лабораторных работ производится в дополнительное время по согласованию с преподавателем.
Правила техники безопасности в лаборатории
1 Нельзя касаться руками клемм, открытых токоведущих частей и находящихся под напряжением элементов цепей.
2 Прежде чем производить какие-либо изменения в схеме, ее нужно отключить от источника электрической энергии.
3 Все переключения в электрических схемах необходимо производить только при снятом напряжении, то есть при отключенном автомате.
4 Прежде чем приступить к соединению элементов схемы, расположенных на стенде, необходимо убедиться, что контакты автоматов сети отключены.
5 Нельзя проверять пальцами наличие напряжения между выводами источника питания или линейных проводов сети.
6 Не прикасайтесь к зажимам отключенных конденсаторов. Помните, что в нем может сохраняться опасный остаточный заряд.
7 Сборка электрических схем должна производиться соединительными проводами с исправной изоляцией. Нельзя пользоваться проводами без наконечников или штырей.
8 Прежде чем разбирать цепь, убедитесь, что контакты автоматов сети разомкнуты, источники питания отключены.
9 Нельзя самостоятельно исправлять вышедшее из строя электрооборудование.
10 Во время выполнения лабораторной работы категорически запрещается хождение по лаборатории.
Устройство лабораторного стенда «Уралочка»
Стенд представляет собой сборную конструкцию каркаса стола и встроенного в него поворотного барабана с приборами для проведения лабораторных работ. В закрытом и открытом состоянии барабан фиксируется фиксатором, расположенным на правой боковой стенке стола. Стенд можно использовать для проведения практических занятий, при этом барабан должен быть повернут в нерабочее состояние.
На передней панели стенда размещены 6 блоков, состоящих из приемников электроэнергии, измерительной и коммутационной аппаратуры (слева направо): 1 – блок линейных элементов; 2 – блок сопротивлений; 3 – блок постоянного тока; 4 – блок переменного тока; 5 – блок емкостей; 6 – блок магнитных цепей.
На первом левом блоке стола установлено : перекидной ключ (тумблер); 4 резистора R1
= 100 Ом; R2
= 100 Ом; R3
= 200 Ом; R4
= 50 Ом; 2 резистора  R = 100 Ом. R = 100 Ом.
На втором блоке размещены три магазина сопротивлений.
На третьем блоке установлено : автомат постоянного тока U = 30 В (выход – средние клеммы); два источника электрической энергии с э.д.с. Е = 4,5 В; катушка на стальном сердечнике.
На четвертом блоке установлен автомат переменного трехфазного тока UФ
= 30 В , UЛ
= 52 В.
На пятом блоке установлено: магазин емкостей с СМ
= 121 мкФ и ключ (тумблер).
На шестом блоке установлено: перекидной ключ (тумблер), катушка индуктивности.
Каждый блок содержит многопредельный вольтамперметр (рисунок 1.2).

Рисунок 1.2 – Многопредельный вольтамперметр
С левой стороны прибора размещены гнезда переменного, а с правой – постоянного тока и напряжения.
Для использования прибора микроамперметром штекеры вставляют в гнезда, отмеченные 0,3 А (т.е. общее гнездо вольтметра и гнездо амперметра с пределом ),1 Ф) постоянного тока.
Для определения цены деления прибора следует исходить из установленного предела измерения. Установленный предел измерения следует разделить на 50 (вся шкала имеет 50 делений). Например, для амперметра: установленный предел измерения 2А, тогда цена одного деления ( n ) равна n =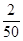 = 0,04А. = 0,04А.
Лаборатория обеспечивает: одновременное проведение одной лабораторной работы на всех стендах 9 столах; отключение стола при аварийных режимах; приведение в рабочее состояние в течение 1 минуты.
По ходу выполнения работы преподаватель может подать на столы переменное или постоянное напряжение. После сборки соответствующей электрической схемы и проверки ее преподавателем, студенты подают питание в схему самостоятельно включением соответствующего автомата, расположенного на столе.
Таблица 1.1 – Единицы измерения электрических величин
| Наименование электрической величины
|
Буквенное обозначение
|
Единица измерения
|
Наименование единицы измерения
|
Производные
единицы измерения
|
| 1
|
2
|
3
|
4
|
5
|
| Ток
|
I
|
А
|
ампер
|
1мА=10-3
А;
1мкА=10-6
А;
1кА=103
А.
|
| Напряжение
|
U
|
В
|
вольт
|
1мВ=10-3
В;
1мкВ=10-6
В;
1кВ=103
В.
|
| ЭДС
|
E
|
В
|
вольт
|
1мВ, 1мкВ, 1кВ.
|
| Мощность:
-активная
|
P
|
Вт
|
ватт
|
1кВт=103
Вт;
1МВт=106
Вт.
|
| -реактивная
|
Q
|
ВАр
|
вольт-ампер реактивный
|
1кВАр=103
ВАр;
1МВАр=106
ВАр.
|
| -полная
|
S
|
ВА
|
вольт-ампер
|
1кВА=103
ВА;
1МВА=106
ВА.
|
| Сопротивление:
-активное
|
r
|
Ом
|
ом
|
1кОм=103
Ом;
1МОм=106
Ом.
|
| -реактивное
|
x
|
Ом
|
ом
|
| -полное
|
z
|
Ом
|
ом
|
| Проводимость:
-активная
|
g
|
См
|
симменс
|
-
|
| -реактивная
|
b
|
См
|
симменс
|
-
|
| -полная
|
y
|
См
|
симменс
|
-
|
| 1
|
2
|
3
|
4
|
5
|
| Емкость
|
C
|
Ф
|
фарада
|
1мкФ=10-6
Ф;
1nФ=10-12
Ф.
|
| Индуктивность
|
L
|
Гн
|
генри
|
1мГн=10-3
Гн
|
Таблица 1.2 – Обозначения условные графические в схемах
| ГОСТ
|
Наименование
|
Обозначение
|
| буквенное
|
графическое
|
| 1
|
2
|
3
|
4
|
| 2.728-74
|
Резистор постоянный
|
r, R
|
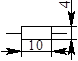
|
| 2.728-74
|
Резистор переменный
|
r, R
|
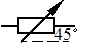
|
| 2.728-74
|
Конденсатор постоянной емкости
|
C
|

|
| 2.728-74
|
Конденсатор переменной емкости
|
C
|
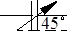
|
| 2.728-68
|
Катушка индуктивности без сердечника
|
L
|
 |
| 2.728-68
|
Катушка индуктивности с ферромагнитным сердечником
|
L
|

|
| 2.723-68
|
Источник э.д.с.
|
e
|
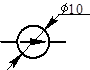
|
| 2.729-68
|
Прибор электроизмерительный
|
A
V
W
|
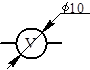
|
| 2.755-74
|
Выключатель однополосный
|
B
|

|
| 2.755-74
|
Выключатель трехполосный
|
B
|
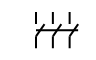
|
| 2.755-74
|
Заземление
|
З
|
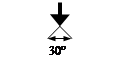
|
| 2.75
5.74
|
Корпус (машины,
аппарата, прибора)
|
К
|

|
| 2.730-73
|
Диод
|
Д
|
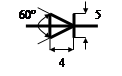
|
Таблица 1.3 – Ряд тока и напряжения (ГОСТ 2.750-68)
| Наименование
|
Обозначение
|
| Ток постоянный
|
-
|
| Ток переменный
|
~
|
| Ток постоянный и переменный
|
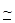
|
| Ток переменный с числом фаз m и частотой f
|
m~f
|
| Например, ток трехфазный 50 Гц
|
3~50Гц
|
| Ток переменный с числом фаз m, частотой f и напряжением U
|
m~f,U
|
| Полярность отрицательная
|
-
|
| Полярность положительная
|
+
|
Таблица 1.4 – Электроизмерительные приборы (ГОСТ 2.729-68)
| Наименование
|
Обозначение
|
| 1
|
2
|
| амперметр
|
A
|
| вольтметр
|
V
|
| вольтамперметр
|
VA
|
| ваттметр
|
W
|
| варметр
|
var
|
| микроамперметр
|
μA
|
| милливольтметр
|
mV
|
| омметр
|
Ω
|
| мегаомметр
|
M Ω
|
| частотометр
|
Mz
|
| фазометр, измеряющий сдвиг фаз
|
j
|
| фазометр, измеряющий коэффициент мощности
|
cosj
|
| счетчик ампер-часов
|
Ah
|
| счетчик ватт-часов
|
Wh
|
| счетчик вольт-ампер-часов переменный
|
varh
|
Лабораторная работа № 2 Исследование неразветвленной и разветвленной электрических цепей постоянного тока
Цель работы: опытная проверка законов Кирхгофа и баланса мощностей в цепях постоянного тока с последовательным и параллельным соединением сопротивлений, построение потенциальной диаграммы.
Теоретические сведения
Электрической цепью называют совокупность устройств, соединенных между собой определенным образом, и образующих путь для электрического тока. В состав цепи могут входить источники электрической энергии, токоприемники, соединительные провода, аппараты управления, защиты и сигнализации, электроизмерительные приборы и т.п. В цепи постоянного тока получение электрической энергии в источниках, ее передача и преобразование в приемниках происходит при неизменных (постоянных) во времени токах и напряжениях.
Любой реальной электрической цепи соответствует эквивалентная схема. Схемой цепи является графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающее их соединение. Геометрическая конфигурация схемы характеризуется понятиями ветвь, узел и контур. Ветвь – это участок электрической цепи, вдоль которого протекает один и тот же ток. Узел – это точка соединения трех и более ветвей. Контур – это любой замкнутый путь, образованный ветвями и узлами. Независимым называется контур, который отличается от других контуров схемы одной или несколькими ветвями. Электрическая схема рисунок 2.1 содержит три ветви, два узла и три контура, из которых два любых контура – независимые, а третий – зависимый.
Для анализа и расчета электрических цепей используют законы Ома и Кирхгофа. К узлам схемы применим 1 закон Кирхгофа, согласно которому алгебраическая сумма токов в любом узле электрической цепи равна нулю
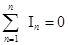 (2.1) (2.1)
При этом токи, текущие к узлу цепи, следует брать с одним знаком, а токи, текущие от узла – с другим знаком, например, для узла-а (см. рис. 2.1) с учетом принятых условно положительных направлений токов в ветвях цепи
I1
– I2
+ I3
= 0
К контурам схемы применим 2 закон Кирхгофа, согласно которому алгебраическая сумма э.д.с. в любом замкнутом контуре равна алгебраической сумме падений напряжений на элементах этого контура
  EК
= EК
=  IК
RК
, (2.2) IК
RК
, (2.2)
где Rк
– сопротивление контура.
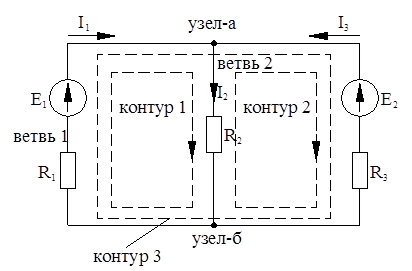
Рисунок 2.1 – Пример схемы электрической цепи
Так для контура 1 (рисунок 2.1)
Е1
= I1
R1
+ I2
R2
,
для контура 3
E1
– E3
= I1
R1
+ I3
R3
При обходе контура э.д.с. и токи, направления которых совпадают с принятым направлением обхода, следует считать положительными, а э.д.с. и токи, направленные встречно обходу – отрицательными. Элементы электрической цепи могут быть соединены между собой последовательно, параллельно, в треугольник, в звезду или более сложные схемы. Последовательным соединением сопротивлений называется такая неразветвленная цепь, когда к концу одного сопротивления присоединяется начало второго, к концу второго – начало третьего сопротивления и т.д. В результате, ток протекает последовательно по всем элементам замкнутого контура (рисунок 2.2), не изменяя своей величины.
В цепи с последовательным соединением сопротивлений (рисунок 2.2) по 2 закону Кирхгофа
E = U1
+ U2
+ U3
,
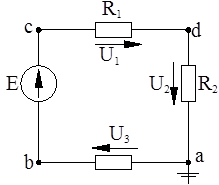
Рисунок 2.2 – Последовательное соединение
Ток в неразветвленной цепи определяют по закону Ома
I = 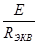 , (2.3) , (2.3)
где RЭКВ
– эквивалентное сопротивление цепи
RЭКВ
= 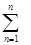 RК
(2.4) RК
(2.4)
Мощности, выделяющиеся на отдельных участках цепи
P1
= I2
R1
P2
= I2
R2
P2
= I2
R2
P3
= I2
R3
Выработанная источником электрическая энергия преобразуется в приемниках в другие виды энергии: тепловую, световую, механическую и т.п. Поэтому справедливо уравнение баланса мощностей, которое для неразветвленной электрической цепи (рисунок 2.2) имеет вид
PE
= P1
+ P2
+ P3
,
где PE
= EI – мощность источника;
P1
, P2
, P3
– мощности приемников (сопротивлений).
Параллельным соединением сопротивлений называется такая разветвленная цепь, когда начала всех сопротивлений соединены в один узел, а концы всех сопротивлений – в другой узел (рисунок 2.3). В результате ток, подходящий к узлу, разветвляется, затем, пройдя по элементам ветвей, суммируется, приобретая первоначальную величину. Для параллельного соединения характерно одинаковое падение напряжения на всех параллельных ветвях.
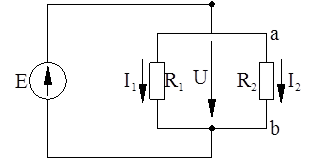
Рисунок 2.3 – Параллельное соединение
Токи в параллельных ветвях пропорциональны проводимостям
I1
= g1
U, I2
= g2
U,
где g1
, g2
– проводимости ветвей
 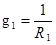 , , 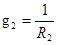
Эквивалентная проводимость цепи при параллельном соединении
gЭКВ
= 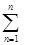 gК
(2.5) gК
(2.5)
Эквивалентное сопротивление цепи
RЭКВ
= 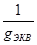 (2.6) (2.6)
Мощности, выделяющиеся на отдельных участках цепи
 P1
= U2
g1
, P2
= U2
g2 P1
= U2
g1
, P2
= U2
g2
Уравнение баланса мощностей для разветвленной электрической цепи (рисунок 2.3) имеет вид
PE
= P1
+ P2
.
График распределения потенциала вдоль замкнутой электрической цепи называется потенциальной диаграммой (рисунок 2.4) по оси абсцисс диаграммы откладывают в масштабе величины сопротивлений участков цепи, а по оси ординат – соответствующие величины электрических потенциалов. При построении диаграммы одну из точек схемы (любую, например, рисунок 2.2, точка – «а») мысленно соединяют с землей. Тогда ее потенциал будет равен нулю (ja
= 0). Потенциалы остальных точек цепи могут быть определены опытным путем, либо путем расчетов. Каждой точке цепи соответствует своя точка на потенциальной диаграмме.
На участке цепи с сопротивлением потенциал изменяется линейно, на участке цепи с источником э.д.с. потенциал изменяется скачком. Пользуясь диаграммой, можно определить напряжение между точками цепи.
Объект и средства исследования
Объектом исследования является неразветвленная и разветвленная электрические цепи постоянного тока (рисунок 2.5, 2.6).
Для проведения исследования используют:
1) источник электрической энергии постоянного тока на третьем блоке (автомат постоянного тока U = 30 В, выход – средние клеммы);
2) реостат 9делитель напряжения) на третьем блоке (0 ÷ 200, I ≤ 0,4 А);
3) магазин сопротивлений на втором блоке (R1
, R2
, R3
);
4) вольтметр (V), пределы измерения 0 ÷ 30 В;
5) амперметры (А1
÷ А4
), пределы измерения 0 ÷ 2 А;
6) провода соединительные.
Напряжения на участках цепи (рисунок 2.5) измеряют вольтметром со свободными концами. При измерении потенциалов точек один зажим вольтметра следует соединить с точкой – «а», потенциал которой принять равным нулю, а другой зажим попеременно подключать к остальным точкам цепи ( b, c, в ).
Рисунок 2.4 – Потенциальная диаграмма для схемы (рисунок 2.2)

Рисунок 2.5 – Схема неразветвленной электрической цепи
Рабочее задание
1 Собрать неразветвленную, а затем разветвленную электрические цепи (рисунок 2.5, 2.6). Произвести измерения токов, напряжений. Данные измерений занести в таблицу 2.1, 2.2.
2 Построить по опытным данным потенциальную диаграмму для неразветвленной электрической цепи.
3 Расчетным путем произвести проверку законов Кирхгофа для разветвленной и неразветвленной цепей.
4 Проверить баланс мощности в неразветвленной и разветвленной цепях.
5 Полученные результаты вычислений и опытов сравнить и сделать письменные выводы.
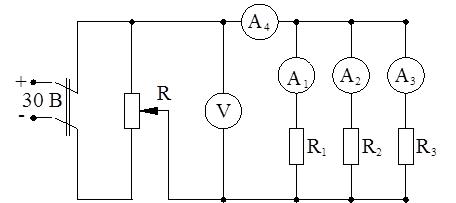
Рисунок 2.6 – Схема разветвленной электрической цепи
Таблица 2.1
| Участок цепи
|
Результаты измерений
|
Результаты вычислений
|
| U,B
|
I,A
|
j
a,В
|
j
b,В
|
j
c,В
|
j
d,В
|
P,Вт
|
R,Ом
|
| Сопротивление R1
|
0
|
-
|
-
|
-
|
| Сопротивление R2
|
-
|
-
|
-
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| Сопротивление R3
|
-
|
-
|
-
|
| Вся цепь
|
-
|
-
|
-
|
Таблица 2.2
| Участок цепи
|
Результат измерений
|
Результаты вычислений
|
| U,B
|
I,A
|
P,Вт
|
R,Ом
|
g, См
|
| Сопротивление R1
|
| Сопротивление R2
|
| Сопротивление R3
|
| Вся цепь
|
Контрольные вопросы
1. Из каких элементов состоит электрическая цепь и каково их значение?
2. Что называется ветвью, узлом и контуром электрической цепи?
3. В чем заключается смысл I закона Кирхгофа? II закона Кирхгофа?
4. Какое соединение сопротивлений называют последовательным и какое параллельным?
5. Как определить эквивалентное сопротивление неразветвленной цепи?
6. Как определить эквивалентную проводимость разветвленной цепи?
7. Что понимают под балансом мощностей цепи?
8. Каково назначение потенциальной диаграммы?
9. Как изменяется потенциал на участке цепи с сопротивлением?
10. Как изменяется потенциал на участке цепи с источником э.д.с.?
Рекомендуемая литература
1 Герасимов В.Г. Электротехника. – М. : Высшая школа, 1985, с.17-25.
2 Касаткин А.С., Немцов М.В. Электротехника. – М. : Энергоатомиздат, 1983. – с.19 -23.
3 Иванов И.И., Равдоник В.С. Электротехника. – М. : Высшая школа, 1984, с.13-15, 19-21.
Лабораторная работа № 3 Исследование
нелинейных цепей постоянного тока
Цель работы: Снять вольтамперные характеристики нелинейных элементов при различных способах соединения. Выполнить графический расчет неразветвленной и разветвленной нелинейной цепи и проверить его опытом.
Теоретические сведения
Расчет линейных электрических цепей, сопротивления которых не зависят ни от тока, ни от напряжения выполняются на основании закона Ома
I =   (3.1) (3.1)
Вольтамперная характеристика (в.а.х.) – это зависимость тока, протекающего через сопротивление, от напряжения на нем. Для линейного сопротивления представляет собой прямую линию.
Под нелинейными электрическими цепями принято понимать электрические цепи, содержащие нелинейные сопротивления (НС) вольтамперные характеристики которых в отличии от линейных сопротивлений носят нелинейный характер. Нелинейные сопротивления могут быть подразделены на две большие группы: неуправляемые и управляемые НС. В управляемых НС в отличии от неуправляемых, кроме основной цепи, как правило, есть еще по крайней мере одна вспомогательная, или управляющая цепь, воздействуя на ток или напряжение которой можно деформировать в.а.х. основной цепи. В неуправляемых НС в.а.х. изображаются одной кривой, а в управляемых – семейством кривых. В группу управляемых НС входят лампы накаливания, электрическая дуга, бареттер, газотрон, стабиловольт, полупроводниковые выпрямители (диоды) и другие НС.
В группу управляемых НС входят трех ( и более) электродные лампы, полупроводниковые триоды (транзисторы), тиристоры и другие элементы.
НС входят в электрические цепи, применяемые в автоматике, телемеханике, измерительной и вычислительной технике.
Статическое сопротивление характеризует поведение нелинейного элемента в режиме неизменного тока, а дифференциальное при малых отклонениях тока от установившегося значения.
Расчеты нелинейных электрических цепей ведутся большей частью графическим методом, в основу которого положены законы Кирхгофа и в.а.х. отдельных элементов, входящих в электрическую цепь.
Для расчета неразветвленной цепи (рисунок 3.3) с двумя нелинейными элементами, имеющими в.а.х. I = F1
(U1
) и I = F2
(U2
) строят в выбранном масштабе вспомогательную кривую I = F2
(U1
+ U2
) представленную на рисунке 3.4. Наличие этой кривой позволяет найти графическим путем значение тока I и напряжения на отдельных участках цепи (U1
и U2
) для любого значения U.
Из сравнения кривых, приведенных на рисунке 3.1б и рисунке 3.1в следует, что величина сопротивления нелинейных элементов зависит не только от величины протекающего тока или приложенного напряжения, но и от направления их действия.
На рисунке 3.1 представлены в.а.х. линейного (а), нелинейного (б) и нелинейного несимметричного (в) элементов.
Для каждого нелинейного элемента различают статическое сопротивление rст
, соответствующее данной точке в.а.х., например, точке А (рисунок 3.2)
rСТ
= 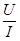 = = 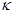 tgα , (3.2) tgα , (3.2)
и дифференциальное сопротивление rД
, которое для той же точки А определяется по формуле
rД
=  = =  tg tg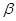 , (3.3) , (3.3)
где 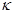 – масштаб сопротивлений. – масштаб сопротивлений.
Расчет цепи с параллельно включенными НС (рисунок 3.5) при заданном напряжении на зажимах разветвления заключается в нахождении токов в ветвях по их в.а.х. (рисунок 3.6). поскольку напряжение на ветвях одинаково, то отложив его на оси абцисс, найдем токи I1
и I2
. результирующий ток равен сумме токов в ветвях I = I1
+ I2
.В случае смешанного соединения сопротивлений сначала определяются характеристики параллельных участков, затем строятся характеристики цепи по характеристикам участков, соединенных последовательно.
аб
Рисунок 3.1
Рисунок 3.2 – Вольтамперная характеристика полупроводникового выпрямителя

Рисунок 3.3 – Последовательное включение цепи HC
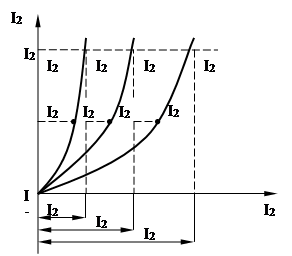
Рисунок 3.4 – В.А.Х. неразветвленной цепи
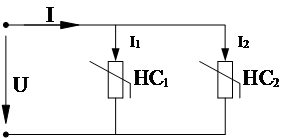
Рисунок 3.5 – Параллельное соединение двух НС
Объект и средства исследования
Объектом исследования служит электрическая цепь постоянного тока, состоящая из линейных и нелинейных элементов (рисунок 3.7)
Для проведения исследования используют:
1) источник постоянного тока – 30 В;
2) реостат Rper
;
3) амперметры А, А1
, А2
– (0-2)А;
4) вольтметр V – (0-30)В;
5) магазин сопротивлений R;
6) лампа накаливания.
Рисунок 3.6 – В.А.Х. параллельной цепи двух НС
Рабочее задание
1 Собрать электрическую схему (рисунок 3.7)
2 Снять вольтамперную характеристику резистора, для этого установить ключ S1
в нейтральное положение, ключ S2
в положение (I). Изменяя регулировочным сопротивлением (Rper
) напряжение от 0 до 27 В. Результаты измерения записать в таблицу 3.1.
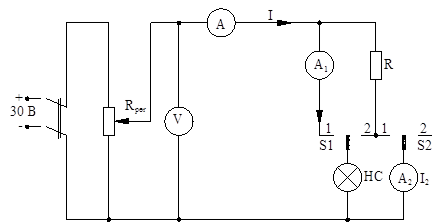
Рисунок 3.7 – Электрическая схема
3 Снять вольтамперную характеристику лампы, для этого установить ключ S1
в положение (I), а ключ S2
в нейтральное положение. Изменяя Rper
напряжение от 0 до 27 В определить силу тока. Результаты измерения записать в таблицу 3.1.
Таблица 3.1
| Резистор
|
Лампа
|
| U,B
|
I,A
|
U,B
|
I,A
|
| 1
|
| 2
|
| 3
|
| 4
|
| 5
|
4 При 2-х значениях приложенного U измерить напряжение на лампе UЛ
и на резисторе UR
, ток цепи I (ключ S1
установить в положение (2), а ключ S2
в нейтральное положение. Результаты измерения записать в таблицу 3.2.
Таблица 3.2 – Последовательное соединение
| Из опыта
|
Из графика
|
| U,B
|
UR
,B
|
U
л
,B
|
I,A
|
U,B
|
UR
,B
|
U
л
,B
|
I,A
|
| 1
|
| 2
|
5 При 2-х значениях напряжения U измерить токи: I, I1
, I2
(ключи S1
и S2
установить в положение I). Результаты измерения записать в таблицу 3.3.
Таблица 3.3 – Параллельное соединение
| Из опыта
|
Из графика
|
| U,B
|
I,A
|
I1
,A
|
I2
,A
|
U,B
|
I,A
|
I1
,A
|
I2
,A
|
| 1
|
| 2
|
6 Построить в общей системе координат в.а.х. резистора и лампы, графически определить их общую в.а.х. для последовательного соединения.
7 Выполнить пункт 6 для параллельного соединения.
8 Построить нагрузочную характеристику резистора в отрезках на осях координат по выражению для двух значений напряжения
U = I R + UЛ
; IХХ
= 0 ; IКЗ
= 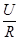 ; ;
UR
= I R ; U = UЛ
; UЛ
= 0.
9 Для этих же значений напряжения U определить графически UR
, UЛ
, I и записать данные в таблицу 3.2 (из графика).
10 На графике построенном в пункте 7 для двух значений напряжения определить токи I, I1
, I2
и записать в таблицу 3.3 (из графика).
11 Сравнить данные полученные опытным и графическим путем (см. таблицу 3.2 и 3.3).
12 Сделать выводы по работе.
Контрольные вопросы
1. Какой элемент электрической цепи называют нелинейным?
2. Что называется в.а.х. нелинейного элемента?
3. Где проходит (на графике) общая в.а.х. при параллельном и последовательном соединении НС?
4. Какие элементы обладают нелинейными в.а.х.?
5. Как графически построить вольтамперную характеристику последовательной цепи?
6. Как графически построить вольтамперную характеристику параллельной цепи?
7. В чем заключается суть графического метода расчета нелинейной электрической цепи со сменным соединением ее элементов?
8. Справедливы ли законы Кирхгофа для нелинейных электрических цепей постоянного тока?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника : Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова. – 3-е изд., перераб. и доп. – М. : Высшая школа, 1985, с.137-146.
2 Касаткин А.С., Немцов М.В. Электротехника : Учебное пособие для вузов. – 4-е изд., перераб. – М. : Энергоатомиздат, 1983, с.40-46.
3 Иванов И.И., Равдоник В.С. Электротехника : Учебное пособие для неэлектрических специальностей вузов. – М. : Высшая школа, 1984, с.22-32.
Лабораторная работа № 4 Исследование работы линии электропередачи постоянного тока
Цель работы: изучить модель линии электропередачи электрической энергии постоянным током. Определить потерю напряжения, потерю мощности и КПД электрической линии от величины тока нагрузки. Познакомиться с выбором сечения проводов по таблицам. Определить сопротивление проводов электрической линии при различных режимах работы.
Теоретические сведения
Одним из наиболее важных преимуществ электрической энергии, перед другими видами, является возможность передачи ее на большие расстояния при высоком коэффициенте полезного действия.
При передаче энергии по проводам (рисунок 4.1) часть ее теряется на нагревание проводов,
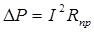 ,
(4.1) ,
(4.1)
где Rпр
–сопротивление проводов линии.
Из формулы 4.1 следует, что для уменьшения потерь в линии необходимо выполнить следующее условие:
1) уменьшить ток в линии. Это можно достичь, увеличив соответственно передаваемое напряжение, при этом мощность на нагрузке не изменится, т.к.
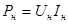 (4.2) (4.2)
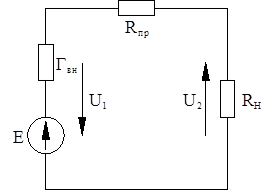
Рисунок 4.1 – Схема передачи электрической энергии постоянным током с нагрузкой в конце линии
2) уменьшить сопротивление проводов линии
 (4.3) (4.3)
Это можно достичь следующим образом:
выбрать материал проводов с меньшим удельным электрическим сопротивлением;
уменьшить длину линии  (если это возможно); (если это возможно);
увеличить сечение проводника линии  . .
Обычно значение сечения проводов 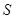 определяется выражением определяется выражением
 , (4.4) , (4.4)
где 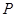 –передаваемая мощность (мощность в нагрузке); –передаваемая мощность (мощность в нагрузке);
 – длинна линии; – длинна линии;
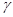 –удельная проводимость проводов; –удельная проводимость проводов;
 –напряжение в конце линии; –напряжение в конце линии;
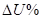 –допустимое относительное падение напряжение в линии. –допустимое относительное падение напряжение в линии.
Провода, сечение которых рассчитано по допустимому падению напряжения, нужно проверить на нагрев. Это делается по таблицам допустимых нагрузок на провода. Из двух сечений – рассчитанного по допустимому значению падению напряжения и выбранного по таблице допустимых нагрузок – окончательно берётся большее. Провода выпускаются стандартных сечений.
Допустимые нагрузки на голые провода, проложенные открыто, приводятся в таблице 4.1. Наибольший ток в линии передачи имеет место при коротком замыкании в нагрузке. Величина его ограничивается только внутренним сопротивлением генератора и сопротивлением проводов линии
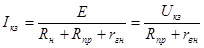 , (4.5) , (4.5)
где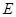 – э.д.с. генератора; – э.д.с. генератора;
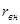 – сопротивление генератора. – сопротивление генератора.
При коротком замыкании генератор развивает наибольшую мощность, но вся она теряется на нагревание его обмоток и проводов линии. Обмотки генератора и провода линии на такой большой ток не рассчитаны. Для защиты генератора и линии от токов короткого замыкания ставятся плавкие предохранители.
Таблица 4.1 – Допустимые нагрузки на голые провода, проложенные открыто
| Медные
|
Алюминиевые
|
| Сечение
S
, мм2
|
Допустимый ток
I
, А
|
Сечение
S,
мм2
|
Допустимый ток
I
, А
|
| М-4
|
50
|
| М-6
|
70
|
| М-10
|
95
|
А-10
|
75
|
| М-16
|
130
|
А-16
|
105
|
| М-25
|
180
|
А-25
|
135
|
| М-35
|
220
|
А-35
|
170
|
| М-50
|
270
|
А-50
|
215
|
Полезная мощность при коротком замыкании отсутствует, поэтому КПД короткого замыкания
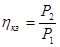 (4.6) (4.6)
Режим, когда линия на концах разомкнута, т.е. к ней не подключены потребители, называется режимом холостого хода (х.х.). Полезная мощность в этом случае тоже равна нулю, но генератор не развивает никакой мощности. При х.х. в линии тока нет
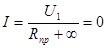 (4.7) (4.7)
Величина потери напряжения 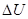 может быть определена как разность показаний вольтметров, один из которых включен в начале электрической линии, а другой в конце ее т.е. может быть определена как разность показаний вольтметров, один из которых включен в начале электрической линии, а другой в конце ее т.е.
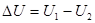 (4.8) (4.8)
При холостом ходе потери напряжения в проводах отсутствуют, напряжение на конце линии равно э.д.с. генератора,
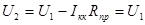 , (4.9) , (4.9)
где 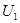 – напряжение в начале линии. – напряжение в начале линии.
Величина сопротивления проводов электрической линии, положенной от источника электрической энергии к электроприемникам, определяется опытно, по результатам измерения, на основании закона Ома т.е.
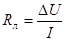 (4.10) (4.10)
Мощность источника электрической энергии 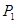 в основном подводится к электроприемникам, приключенным в конце линии и составляет в основном подводится к электроприемникам, приключенным в конце линии и составляет 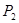 , а частично идет на покрытие потерь в проводах линии , а частично идет на покрытие потерь в проводах линии  , т.е. , т.е.
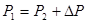 (4.11) (4.11)
Режим, при котором сопротивление нагрузки равно сумме сопротивлений проводов линии и внутреннего источника, называется согласованным режимом
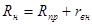 ,(4.12) ,(4.12)
где 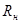 – сопротивление нагрузки. – сопротивление нагрузки.
При этом может быть получена максимальная мощность
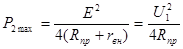 (4.13) (4.13)
В таком режиме напряжение на нагрузке
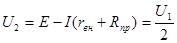 ,(4.14) ,(4.14)
а к.п.д. равен 50%. Такой режим работы допустим лишь в линиях связи, где важно получать наибольшую мощность сигнала в цепи нагрузки, а вопросы, связанные с потерями 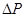 , отодвигаются на второй план. Электрические сети промышленных предприятий нормально работают с потерей не выше 10% от передаваемой мощности, и экономичность их работы характеризуется величиной коэффициента полезного действия , отодвигаются на второй план. Электрические сети промышленных предприятий нормально работают с потерей не выше 10% от передаваемой мощности, и экономичность их работы характеризуется величиной коэффициента полезного действия
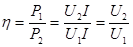 (4.15) (4.15)
Электрические сети работают в режиме, более близком к режиму холостого хода. Это обеспечивает более высокий КПД и меньшие колебания напряжения на нагрузке при изменении её величины. Такой режим называется номинальным и рассчитан на длительную работу линии.
Объект и средства исследования
Объектом исследования служит модель линии электропередачи постоянного тока. В качестве модели линии электропередачи применяется реостат с сопротивлением 2R1
, а потребителями являются сопротивления одного из магазина сопротивлений с эквивалентным сопротивлением R2
, (рисунок 4.3)
Для проведения исследования используют:
1) Источник электрической энергии переменного тока на третьем блоке (автомат переменного тока подключается к фазному напряжению) от трехфазного источника напряжения;
2) реостат на третьем блоке (R= 0+200; I≤0,4 А);
3) магазин сопротивлений (R1
, R2
, R3
, R4
,);
4) вольтметры (V1
, V2
), пределы измерения от 0 до 100 В;
5) амперметр (А), пределы измерения от 0 до 1 А;
6) ваттметры (W1
, W2
), пределы измерения по току от 0 до 0,4 А, по напряжению 100 В;
7) провода соединительные со штекерами одно-, двух-, трех- и четырехлучевые;
8) двухполюсный выключатель В1
;
9) однополюсный выключатель В2
.

Рисунок 4.2– Зависимость величин U2
, ΔU, P1
, P2
, и η от тока I нагрузки, включенной в конце линии, при U1
=const в начале линии

Рисунок 4.3 – Схема линии электропередачи постоянного тока
Рабочее задание
1 Исследование режима холостого хода линии электропередач постоянного тока.
Режим холостого хода – потребители отключены, т.е. цепь нагрузки разомкнута с помощью тумблера В2
.
Измерить напряжение на выходных зажимах схемы (напряжение в начале линии – U1
) и напряжение в конце линии – U2
, ток в цепи I, мощность P1
в начале линии, а мощность P2
в конце линии. Данные занести в таблицу 4.2.
2 Режимы нагрузки.
Включить тумблер В2
(2R1
=max). Произвести измерение тока I, напряжения U1
и U2
, мощности Р1
и Р2
при одном, двух и трех включенных сопротивлениях. Данные занести в таблицу 4.2.
3 Согласованный режим.
Согласованный режим работы линии передачи и потребителей имеет место, когда сопротивление потребителей равно сопротивлению линии передачи
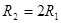 , ,
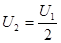 , ,
где 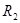 – эквивалентное сопротивление потребителей; – эквивалентное сопротивление потребителей;
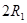 – сопротивление 2-х проводной линии. – сопротивление 2-х проводной линии.
Изменяя сопротивление нагрузки 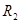 с помощью тумблеров, добиться того, чтобы с помощью тумблеров, добиться того, чтобы
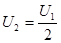
Произвести измерения I, U1
, U2
, P1
и P2
. Данные занести в таблицу 4.2.
4 Режим короткого замыкания.
В этом режиме сопротивление нагрузки должно быть равно нулю (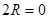 ), закорочены все перемычки на цепочке последовательно соединенных резисторов, а ), закорочены все перемычки на цепочке последовательно соединенных резисторов, а  стоит в положении max). Произвести измерения I, U1
, U2
, P1
и P2
. Данные измерений занести в таблицу 4.2. При коротком замыкании (к.з.) стоит в положении max). Произвести измерения I, U1
, U2
, P1
и P2
. Данные измерений занести в таблицу 4.2. При коротком замыкании (к.з.) 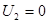 , следовательно, , следовательно,
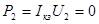
5 По данным измерений и результатам вычислений построить график в одной системе координат для следующих зависимостей: 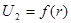 , , 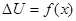 , , 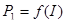 , ,  , , 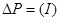 , , 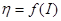 . .
Таблица 4.2
| Данные измерений
|
Результаты вычислений
|
| Режим
работы
линии эл. энергии
|
I,
A
|
U1
,
B
|
U2
,
B
|
P1
,
Bт
|
Р2
,
Вт
|
ΔU,
В
|
ΔР1
,
Вт
|
2R1
,
Ом
|
R2,
Ом
|
Rэ,
Ом
|
η,
%
|
| Режим х.х.
|
| Режим нагрузки
1
2
3
|
| Согласован-
ный режим
|
| Режим к. з.
|
Контрольные вопросы
1. Каково назначение линии электропередачи?
2. Что понимают под номинальным режимом работы линии электропередачи?
3. Что понимают под режимом короткого замыкания линии электропередачи?
4. Что понимают под согласованным режимом работы линии электропередачи?
5. Что понимают под режимом холостого хода линии электропередачи?
6. От чего зависят потери напряжения в линии и величина напряжения на зажимах электроприемников?
7. В чем заключается опасность короткого замыкания в линии, и какие способы прекращения короткого замыкания применяются?
8. Перечислить факторы, влияющие на величину к.п.д. линии электропередачи.
9. Перечислить факторы, определяющие нагрев проводов линии электропередачи.
10.Как экспериментально найти сопротивление проводов линии передачи?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника : Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова. – 3-е изд., перераб. и доп. – М. : Высшая школа, 1985, с.137-146.
2 Касаткин А.С., Немцов М.В. Электротехника : Учебное пособие для вузов. – 4-е изд., перераб. – М. : Энергоатомиздат, 1983, с.40-46.
3 Иванов И.И., Равдоник В.С. Электротехника : Учебное пособие для неэлектрических специальностей вузов. – М. : Высшая школа, 1984, с.22-32.
Лабораторная работа № 5 Цепь переменного тока с последовательным соединением сопротивлений
Цель работы: экспериментальное и аналитическое исследование цепи переменного тока с последовательным соединением сопротивлений.
Теоретические сведения
К пассивным элементам электрической цепи относятся резистивные элементы, катушки индуктивности и конденсаторы. Любой элемент имеет активное сопротивление r , индуктивность L и емкость C. Однако при анализе и расчетах электрических цепей учитывают лишь тот параметр, который оказывает заметное влияние на режим работы элемента или цепи в целом. В расчетных электрических схемах резистивный элемент представляют активным сопротивлением, катушку индуктивности последовательным соединением активного сопротивления и индуктивности , конденсатор – емкостью.
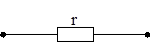 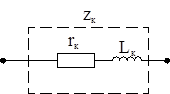 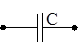
а б в
Рисунок 5.1 – Схемы замещения резистивного элемента, катушки индуктивности и конденсатора
Резистивный элемент характеризует наличие в замещаемом элементе необратимых процессов преобразования электрической энергии в другие виды энергии.
Индуктивный элемент схемы замещения реальной цепи с изменяющимся током характеризует наличие изменяющегося магнитного поля, созданного этим током.
Емкостной элемент вводится в схему замещения реальной цепи с изменяющимся током, когда хотят учесть влияние изменяющегося электрического поля элементов цепи.
В простейшей цепи с резистивным элементом (рисунок 5.2,а) синусоидальное напряжение
U = Um
sinω t (5.1)
вызывает синусоидальный ток
i =  = = 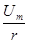 sinω t = Im
sinω t , (5.2)
sinω t = Im
sinω t , (5.2)
где Um
, Im
– амплитудные значения и тока, В, А;
r – активное сопротивление элемента, Ом.
В случае резистивного элемента согласно (5.2) синусоида тока имеет ту же частоту, что и синусоида напряжения и совпадает с ней по фазе (рисунок 5.2, б) j=0. j - угол сдвига фаз между напряжением и током.
На практике для оценки величины тока и напряжения в цепях переменного тока используют действующие значения тока и напряжения, связанные с амплитудными значениями Um
и Im
следующими соотношениями
I = 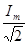 , A; U = , A; U =  , B. (5.3) , B. (5.3)
По закону Ома ток в цепи с резистивным элементом определяется
I = 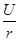 (5.4) (5.4)
Применение комплексных чисел позволяет представить не только соотношение между действующими значениями тока и напряжения, но и учесть угол сдвига фаз между ними. Закон Ома в комплексной форме для цепи с резистором имеет вид
I
=  , (5.5) , (5.5)
где I
, U
– комплекс действующего значения тока и напряжения.
Наиболее удобной формой представления угла сдвига фаз между синусоидальными величинами является векторная диаграмма, которую строят на комплексной плоскости для действующих значений тока и напряжения (рисунок 5.2,в).
  
 аб аб
Рисунок 5.2 – Схема, временная диаграмма тока и напряжения, векторная диаграмма цепи с резистором
Мощность, выделяющаяся в резисторе, оценивается ее средним за период T значением и называется активной мощностью
P = 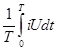 = I U = I2
r , Вт (5.6) = I U = I2
r , Вт (5.6)
В цепи с идеальной катушкой индуктивности, то есть не имеющей активного сопротивления (рисунок 5.3, а), напряжение численно равно э.д.с. самоиндукции с обратным знаком и при синусоидальном токе i = Im
sin ω t синусоидально
U = - e = L 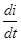 = ω l Im
cosω t = xL
Im
sin(ω t + = ω l Im
cosω t = xL
Im
sin(ω t + 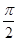 ) = Um
sin(ω t + ) = Um
sin(ω t + 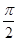 ), (5.7) ), (5.7)
где L – индуктивность катушки, Гн;
xL
= ωL =2πfL – индуктивное сопротивление, Ом;
Um
= xL
Im
– амплитудное значение напряжения, В.
Как видно из выражения (5.7) синусоида тока отстает от синусоиды напряжения на угол j = 90° 9см. рисунок 5.3, б)
Закон Ома для действующих значений напряжения и тока в катушке имеет вид
I =  , (5.8) , (5.8)
 
Рисунок 5.3 – Цепь с идеальной катушкой индуктивности
в комплексной форме
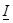 = =  . (5.9) . (5.9)
где j = 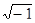 – мнимый коэффициент, умножение на который соответствует повороту вектора на 90º против часовой стрелки. – мнимый коэффициент, умножение на который соответствует повороту вектора на 90º против часовой стрелки.
Реальная катушка (рисунок 5.4, а) имеет некоторое активное сопротивление, это приводит к уменьшению угла сдвига фаз между напряжением на ее зажимах и током, то есть j < 90°. В реальной катушке происходит преобразование электрической энергии в тепловую.
Векторная диаграмма показана на рисунке 5.4, в. Приложенное напряжение U может быть выражено в виде суммы двух составляющих: падений напряжения на активном и индуктивном сопротивлениях.

а
бв
Рисунок 5.4 – Схема замещения, векторная диаграмма и треугольник сопротивлений реальной катушки индуктивности
Путем геометрического сложения векторов падений напряжений с учетом угла сдвига фаз получают прямоугольный треугольник (рисунок 5.4, б), называемый треугольником напряжений, для которого
U =  I = zK
I , (5.10) I = zK
I , (5.10)
где Ua
= Ur
= I r – активная составляющая напряжения, В;
Up
= UL
= I x2
– реактивная составляющая напряжения, В;
zK
= 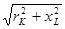 – полное сопротивление катушки, Ом. – полное сопротивление катушки, Ом.
Закон Ома для действующих значений тока и напряжения
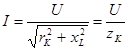 (5.11) (5.11)
Из треугольника сопротивлений (рисунок 5.4, в) можно определить угол сдвига фаз между током и напряжением
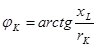 (5.12) (5.12)
Активная мощность, потребляемая реальной катушкой индуктивности, расходуется на ее нагрев и может быть определена по выражению
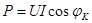 , (5.13) , (5.13)
где 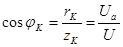 - коэффициент мощности цепи.(5.14) - коэффициент мощности цепи.(5.14)
В цепи с конденсатором (рисунок 5.5, а) при синусоидальном напряжении ток тоже синусоидальный, мгновенное его значение
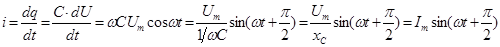 , (5.15) , (5.15)
где q – заряд конденсатора, Кл;
С – емкость конденсатора, Ф;
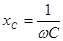 - емкостное сопротивление конденсатора, Ом. - емкостное сопротивление конденсатора, Ом.
Из выражения (5.15) следует, что ток опережает напряжение на четверть периода, то есть j = - 90° (рисунок 5.5, б). Векторная диаграмма показана на рисунке 5.5, в.
Закон Ома для действующих значений тока и напряжения
I = 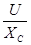 , (5.16) , (5.16)
в комплексной форме
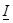 = = 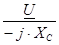 . (5.17) . (5.17)
При последовательном соединении резистора и конденсатора (рисунок 5.6, б)
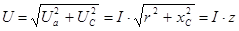 , (5.18) , (5.18)
где Ua
– напряжение на активном сопротивлении, В;
UC
– напряжение на емкости, В;
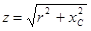 – полное сопротивление цепи, Ом. – полное сопротивление цепи, Ом.
Закон Ома для действующих значений тока и напряжения
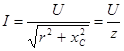 , (5.19) , (5.19)
в комплексной форме
I
= 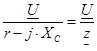 , (5.20) , (5.20)
где 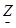 – комплекс полного сопротивления. – комплекс полного сопротивления.
 
аб

в
Рисунок 5.5 – Цепь с конденсатором
Угол сдвига фаз
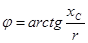 (5.21) (5.21)
При последовательном соединении реальной катушки и конденсатора (рисунок 5.7, а) напряжение на зажимах цепи определяется из треугольника напряжений (рисунок 5.7, б)
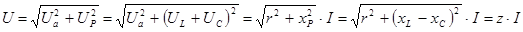 , (5.22) , (5.22)
где 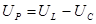 – суммарное реактивное напряжение, В; – суммарное реактивное напряжение, В;
 – суммарное реактивное сопротивление, Ом; – суммарное реактивное сопротивление, Ом;
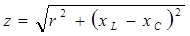 – полное сопротивление цепи, Ом. – полное сопротивление цепи, Ом.
 
аб в
Рисунок 5.6 – Последовательное соединение резистора и конденсатора
Закон Ома для действующих значений тока и напряжения
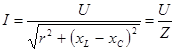 , (5.23) , (5.23)
в комплексной форме
I = 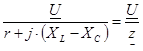 , (5.24) , (5.24)
где  – комплекс полного сопротивления. – комплекс полного сопротивления.
Угол сдвига фаз определяется из треугольника сопротивления (рисунок 5.7, в)
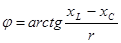 (5.25) (5.25)
Активная мощность, потребляемая цепью
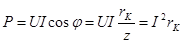 (5.26) (5.26)
Сдвиг между током и напряжением зависит от соотношения реактивных сопротивлений, так если xL
> xC
, нагрузка носит активно-индуктивный характер (0 < j < 90°). В случае равенства индуктивного и емкостного сопротивлений цепи xL
= xC
угол j = 0, напряжение и ток совпадают по фазе. Такой режим называется резонансным
 (5.27) (5.27)
Из выражения (5.27) следует, что резонанс напряжений можно получить, изменяя частоту напряжения сети 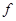 , индуктивность L или емкость С. , индуктивность L или емкость С.


Рисунок 5.7 – Последовательное соединение реальной катушки и конденсатора
При резонансе входное сопротивление цепи чисто активное и минимальное по величине 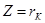 . .
Ток имеет максимальную величину, так как ограничен минимальным сопротивлением
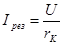 (5.28) (5.28)
Напряжение на индуктивности UL
и на емкости UC
равны по величине и могут значительно превышать входное напряжение. Резонанс в рассматриваемой цепи называется резонансом напряжений.
Описание лабораторного стенда
Объектом исследования служит электрическая цепь, состоящая из последовательно соединенных резистивных элементов, катушки индуктивности и емкости (рисунок 5.8)
 
Рисунок 5.8
Для проведения исследования используют:
1) источник электрической энергии переменного тока – 30 В;
2) магазин сопротивлений;
3) магазин емкостей;
4) катушка индуктивности;
5) амперметр (А), пределы измерения 0 ÷ 2 А;
6) вольтметры (V), пределы измерения 0 ÷ 1200 Вт.
Рабочее задание
1 Собрать электрическую цепь (рисунок 5.8), состоящую из последовательно соединенных двух резисторов. Произвести измерения тока, напряжения и мощности. Данные измерений занести в таблицу 5.1.
2 Заменить в схеме (рисунок 5.8) один из резисторов катушкой индуктивности. Произвести измерения тока, напряжения и мощности. Данные измерений занести в таблицу 5.2
Таблица 5.1
| Данные измерений
|
Данные вычислений
|
| I,A
|
U,B
|
U1
,B
|
U2
,B
|
P,
Вт
|
Р1
,Вт
|
Р2
,Вт
|
R
,Ом
|
R1
,
Ом
|
R2
,
Ом
|
Таблица 5.2
| Данные измерений
|
Результаты вычислений
|
| Параметры катушки
|
Параметры цепи
|
| I
|
U
|
U1
|
U2
|
P
|
Р1
|
Р2
|
zK
|
rK
|
xL
|
cos
j
K
|
z
|
r
|
xL
|
cos
j
|
3 Заменить в схеме (рисунок 5.8) катушку индуктивности емкостью. Исследовать цепь при последовательном соединении резистора и конденсатора. Произвести измерения тока, напряжения, мощности. Данные измерений занести в таблицу 5.3.
Таблица 5.3
| Данные измерений
|
Результаты вычислений
|
| I
|
U
|
U1
|
U2
|
P
|
Р1
|
Р2
|
z
|
r
|
xL
|
cos
j
|
4
5
6 В схему (рисунок 5.8) последовательно включить катушку индуктивности и конденсатор. Исследовать явление резонанса напряжений. Изменяя емкость, добиться максимального тока в цепи, этому значению тока соответствует резонансная емкость (С0
). Произвести измерения тока, напряжения и мощности. Изменить емкость, взяв (С < C0
) и (C > C0
). Измерить ток, напряжение и мощность. Данные измерений занести в таблицу 5.4.
7 По данным таблиц 5.1; 5.2; 5.3 построить в масштабе (МU
– В/см; МI
– А/см) векторные диаграммы напряжений относительно вектора тока.
По данным таблицы 5.4 построить векторные диаграммы для трех режимов:
1 до резонанса С < С0
;
2 при резонансе С = С0
;
3 после резонанса С > C0
.
построить кривые 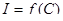 и и 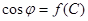 по данным таблицы 5.4. по данным таблицы 5.4.
8 По данным таблиц 5.1; 5.2; 5.3 построить в масштабе (МU
– В/см; МI
– А/см) векторные диаграммы напряжений относительно вектора тока.
Таблица 5.4
| Емкость
|
Данные измерений
|
Результаты вычислений
|
| I,A
|
U,B
|
U1
,B
|
U2
,B
|
Р1
,Вт
|
С,мкФ
|
cos
j
|
| С=С0
|
| С<C0
|
| C>C0
|
Контрольные вопросы
1. Что такое активное сопротивление и как оно измеряется?
2. Что такое индуктивное и емкостное сопротивление и от чего они зависят?
3. Как определить активное, индуктивное и полное сопротивление катушки индуктивности?
4. Как определить емкость конденсатора?
5. Какой режим называется резонансом напряжений?
6. В какой электрической цепи и при каком условии может иметь место резонанс напряжения?
7. Чему равно напряжение на зажимах цепи, настроенной на режим резонанса напряжений?
8. Чему равно полное сопротивление цепи, настроенной на режим резонанса напряжений?
9. каковы отрицательные последствия резонанса напряжений?
10. Почему при резонансе напряжений возникают перенапряжения на катушке и конденсаторе?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника: Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова. – 3-е изд., перераб. и доп. – М. : Высшая школа, 1985, с.69-73.
2 Касаткин А.С., Немцов М.В. Электротехника: Учебное пособие для вузов. – 4-е изд., перераб. – М. : Энергоатомиздат, 1983, с.73-77, 94-97.
3 Иванов И.И., Равдоник В.С. Электротехника: Учебное пособие для неэлектрических специальностей вузов. – М. : Высшая школа, 1984, с. 53-68.
Лабораторная работа № 6 Цепь переменного тока с параллельным соединением сопротивлений.
Цель работы: экспериментальное и аналитическое исследование цепи переменного тока с параллельными соединениями сопротивлений.
Теоретические сведения
Любой элемент электрической цепи переменного тока обладает сопротивлением R, индуктивностью L, и емкостью С. В расчетных электрических схемах резистивный элемент представляют активным сопротивлением, катушку индуктивности – последовательным соединением активного сопротивления и индуктивности, конденсатор – емкостью. На рисунке 6.1 показаны схемы замещения резистивного элемента, катушки индуктивности и конденсатора.
С  
а б в
Рисунок 6.1
Резистивный элемент является пассивным элементом схемы замещения, характеризует наличие в замкнутом элементе необратимых процессов преобразования электрической энергии в другие виды энергии. Индуктивный элемент схемы замещения реальной цепи с изменяющимся током характеризует наличие изменяющегося магнитного поля, созданного этим током. Емкостной элемент вводится в схему замещения реальной цепи с изменяющимся током, когда хотят учесть влияния изменяющегося электрического поля элементов цепи.
Элетроприемники переменного тока, как правило, включаются параллельно на общее напряжение сети (рисунок 6.2).
Общий ток i в неразветвленной части цепи в любой момент равен алгебраической сумме мгновенных значений токов в отдельных ветвях (первый закон Кирхгофа).
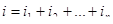 . (6.1) . (6.1)

Рисунок 6.2
Для действующих значений этих токов можно записать
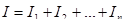 . (6.2) . (6.2)
Токи в отдельных ветвях определяются по формулам (закон Ома)
 (6.3) (6.3)
Коэффициенты мощности отдельных ветвей будут равны
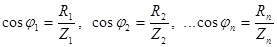 . (6.4) . (6.4)
где Z1
, Z2
, . . . Zn
– полные сопротивления ветвей;
R1
, R2
, . . . Rn
– активные составляющие, этих сопротивлений.
Для аналитического определения общего тока удобно ток каждого электроприемника, т.е. ток в каждой параллельной ветви, рассматривать состоящим из двух слагающих:
активного тока, совпадающего по фазе с напряжением
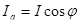 ,(6.5) ,(6.5)
и реактивного тока, сдвинутого по фазе относительно напряжения на 1/4 периода (90º)
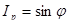 .(6.6) .(6.6)
Активная слагающая тока Ia
определяет величину активности, потребляемой данным электроприемником,
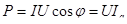 ,(6.7) ,(6.7)
Ia
реактивная составляющая Ip
определяет величину реактивной мощности
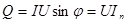 . (6.8) . (6.8)
Есть отдельные электроприемники (например, лампы накаливания), которые потребляют только активный ток; другие электроприемники (конденсаторы) – только реактивный ток.
Примером разветвленной цепи переменного тока является параллельное соединение катушки индуктивности и активного сопротивления (рисунок 6.3).
Синусоидальное напряжение
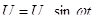 . (6.9) . (6.9)
на зажимах цепи вызывает синусоидальные токи в каждой из ветвей и во всей цепи
 . (6.10) . (6.10)

Рисунок 6.3
Ток в цепи с резистором совпадает по фазе с напряжением (рисунок 6.4).
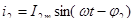 . (6.11) . (6.11)
Ток в цепи с катушкой индуктивности отстает по фазе от напряжения на угол φк
(рисунок 6.5).
Ток в неразветвленной части цепи отстает по фазе от напряжения на угол φ (рисунок 6.6).
Действующее значение токов в ветвях определяются по закону Ома:
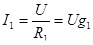 , (6.13) , (6.13)
где 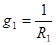 – активная проводимость ветви с резистором, Ом. – активная проводимость ветви с резистором, Ом.
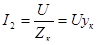 (6.14) (6.14)
где 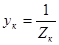 – общая проводимость ветви с катушкой индуктивности, Ом. Ток в неразветвленной части цепи может быть рассчитан по первому закону Кирхгофа с использованием векторной диаграммы (рисунок 6.7) или комплексных чисел. – общая проводимость ветви с катушкой индуктивности, Ом. Ток в неразветвленной части цепи может быть рассчитан по первому закону Кирхгофа с использованием векторной диаграммы (рисунок 6.7) или комплексных чисел.
Примечание: для параллельного соединения приемников строится векторная диаграмма токов относительно общего вектора напряжения. Выбирается масштаб для напряжения 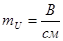 и масштаб для тока и масштаб для тока 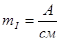 . В масштабе откладываются векторы тока и вектор напряжения. . В масштабе откладываются векторы тока и вектор напряжения.

Рисунок 6.4

Рисунок 6.5

Рисунок 6.6
Действующее значение тока всей цепи определяется
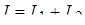 (6.15) (6.15)
Из векторной диаграммы (рисунок 6.7) видно, что ток в цепи с катушкой I2
можно разложить на активную Ia
и реактивную Ip
2
составляющие токов
 ,(6.16) ,(6.16)
где 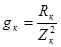 – активная проводимость катушки. – активная проводимость катушки.

Рисунок 6.7
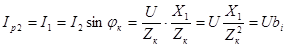 ,(6.17) ,(6.17)
где 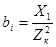 – индуктивная (реактивная) проводимость катушки. – индуктивная (реактивная) проводимость катушки.
Полный ток цепи можно определить (рисунок 6.7)
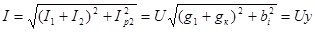 ,(6.18) ,(6.18)
где 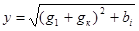 – полная проводимость всей цепи; – полная проводимость всей цепи;
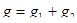 – активная проводимость всей цепи. – активная проводимость всей цепи.
Реактивную составляющую тока катушки Ip
2
называют индуктивной составляющей и обозначают I1
.
из треугольника проводимостей катушки и всей цепи (рисунок 6.8) можно определить
 ; (6.19) ; (6.19)
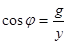 ; (6.20) ; (6.20)
 (6.21) (6.21)
Активная мощность, потребляемая резистором:
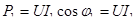 , (6.22) , (6.22)
где 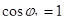 . .
Активная мощность, потребляемая катушкой индуктивности
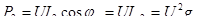 , (6.23) , (6.23)
Рисунок 6.8
Активная мощность, потребляемая всей цепью
 , (6.24) , (6.24)
При параллельном соединении резистора и конденсатора (рисунок 6.9) синусоидальное напряжение 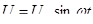 на зажимах цепи вызывает синусоидальные токи в ветвях с резистором, конденсатором и в неразветвленной части цепи. на зажимах цепи вызывает синусоидальные токи в ветвях с резистором, конденсатором и в неразветвленной части цепи.

Рисунок 6.9
Ток в цепи с резистором совпадает по фазе с напряжением φ1
=0, (рисунок 6.10).
 . (6.25) . (6.25)
Ток в цепи с емкостью опережает напряжение на угол 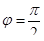 (рисунок 6.11). (рисунок 6.11).
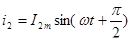 .(6.26) .(6.26)

Рисунок 6.10

Рисунок 6.11
Ток в неразветвленной части цепи опережает по фазе напряжение на угол φ (рисунок 6.12).
 . (6.27) . (6.27)
Действующее значение в ветвях с резистором и конденсатором можно определить по закону Ома:
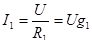 . (6.28) . (6.28)
Ток I1
по характеру активный, его обозначают – Iа
 , (6.29) , (6.29)
где 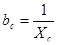 – емкостная проводимость; – емкостная проводимость;
ток I2
– емкостной ток, его обозначают – Ic
.

Рисунок 6.12
Полный ток в неразветвленной части цепи можно определить из векторной диаграммы (рисунок 6.13)
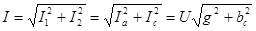 , (6.30) , (6.30)
где  – полная проводимость цепи. – полная проводимость цепи.
Цепь, содержащая индуктивность и емкость, может являться колебательным контуром, т.е. системой, в которой может происходить колебательный разряд емкости на индуктивность. При параллельном соединении катушки индуктивности и конденсатора (рисунок 6.15) синусоидальное напряжение на зажимах цепи  вызывает синусоидальные токи в параллельных ветвях и в неразветвленной части цепи. вызывает синусоидальные токи в параллельных ветвях и в неразветвленной части цепи.

Рисунок 6.13
Угол φ можно определить из треугольника проводимостей (рисунок 6.14)
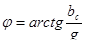 . (6.31) . (6.31)

Рисунок 6.14
Действующее значение тока в цепи с катушкой
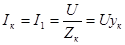 , (6.32) , (6.32)
в цепи с конденсатором
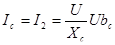 . (6.33) . (6.33)
Ток в неразветвленной цепи можно определить из векторной диаграммы (рисунок 6.16).
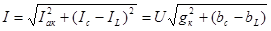 ,(6.34) ,(6.34)
где 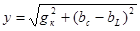 – полная проводимость всей цепи. – полная проводимость всей цепи.
Реактивная проводимость цепи при параллельном соединении катушки и конденсатора уменьшается, и это приводит к уменьшению тока в неразветвленной части цепи. Этот ток может быть значительно меньше токов в параллельных ветвях.
Коэффициент мощности цепи можно определить из треугольника проводимостей (рисунок 6.17.)
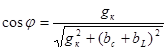 .(6.35) .(6.35)

Рисунок 6.15

Рисунок 6.16

Рисунок 6.17
Ток в общей цепи может по фазе как отставать (рисунок 6.18), так и опережать его (рисунок 6.18), в зависимости от соотношения реактивных проводимостей катушки и конденсатора.
Если индуктивная и емкостная проводимости будут равны, то в этой цепи наступит резонанс токов
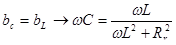 .(6.36) .(6.36)

Рисунок 6.18
Полная проводимость цепи становится наименьшей и равной активной проводимости катушки.
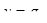
Сдвиг фаз между током и напряжением в общей цепи отсутствует 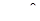 , а коэффициент мощности , а коэффициент мощности 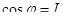 . Ток в неразветвленной части цепи минимален и носит активный характер (рисунок 6.19). . Ток в неразветвленной части цепи минимален и носит активный характер (рисунок 6.19).

Рисунок 6.19
Частотные характеристики будут иметь вид (рисунок 6.20)
Резонанс токов не сопровождается перенапряжением, как это имеет место при резонансе напряжений. Резонанс токов, а также режимы, близкие к резонансу токов, используются для повышения 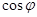 электроустановок. Для этого параллельно к индуктивным приемникам электроэнергии (асинхронные двигатели, трансформаторы) включают конденсаторы. Сеть и источник электроэнергии разгружается от реактивных токов, и это позволяет присоединить к ним дополнительно приемники электроэнергии. электроустановок. Для этого параллельно к индуктивным приемникам электроэнергии (асинхронные двигатели, трансформаторы) включают конденсаторы. Сеть и источник электроэнергии разгружается от реактивных токов, и это позволяет присоединить к ним дополнительно приемники электроэнергии.
При резонансе токов полная мощность, потребляемая приемниками, будет активной.

Рисунок 6.20
где wp
– резонансная частота
Объект и средства исследования
Объектом исследования является цепь переменного тока с параллельными соединениями сопротивлений (рисунок 6.21)
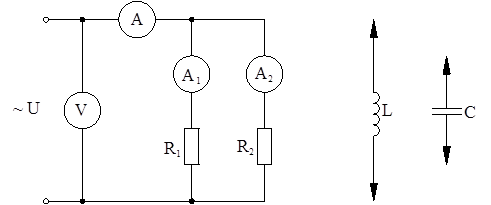
Рисунок 6.21
Для проведения исследования используют:
1) источник электрической энергии переменного тока – 30 В;
2) магазин сопротивлений (R1
, R2
);
3) магазин емкостей (С = 121 мкФ);
4) катушка индуктивности (L);
5) амперметры (А, А1
, А2
,) пределы измерения от 0 до 1 А;
6) вольтметр (V) пределы измерения от 0 до 100 В;
7) ваттметр (W) предел измерения от 0 до 1200 Вт;
8) провода со штекерами.
Рабочее задание
1 Собрать электрическую цепь (рисунок 6.2), состоящую из параллельно соединенных двух резисторов. Произвести измерение напряжения, токов. Данные занести в таблицу 6.1.
Таблица 6.1
| Данные измерений
|
Результаты вычислений
|
| U
,В
|
I
,А
|
I1
,А
|
I2
,А
|
g1
,См
|
g2
,См
|
g
,См
|
cosφ
|
2 Собрать электрическую цепь (рисунок 6.22), состоящую из параллельно соединенных резисторов и катушки индуктивности.
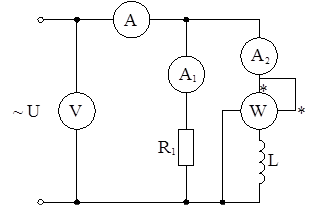
Рисунок 6.22
Произвести измерения напряжения, токов, мощности. Данные занести в таблицу 6.2.
Таблица 6.2
| Данные измерений
|
Результаты вычислений
|
| U
|
I
|
I1
|
I2
|
Р
|
параметры катушки
|
параметры цепи
|
| g
к
|
b
к
|
y
к
|
I
а
|
I
р
|
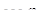
|
g
ц
|
b
ц
|
y
ц
|
I
а
|
I
р
|
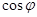
|
3 Заменить в схеме (рисунок 6.22) катушку индуктивности емкостью. Произвести измерения токов, напряжения, мощности. Данные измерений занести в таблицу 6.3.
4 Исследование режима резонанса токов. Собрать электрическую цепь (рисунок 6.23).
Изменяя емкость, добиться минимального значения тока в общей цепи (фиксируется по амперметру). Емкость, соответствующая резонансу, называется резонансной и обозначается С0
. Произвести измерения величин, указанных в таблице 6.4 при резонансной емкости.
Изменяя емкость (С < С0
, С > С0
), исследовать цепь до и после резонанса. Произвести измерения напряжения, токов, мощности. Данные измерений занести в таблицу 6.4.
Таблица 6.3
| Данные измерений
|
Результаты вычислений
|
| С
|
U
|
I
|
I
1
|
I
2
|
P
с
|
параметры конденсатора и резистора
|
Параметры цепи
|
| bc
|
g
|
g
ц
|
b
ц
|
y
ц
|
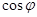
|
Ia
|
Ip
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|

Рисунок 6.23
Таблица 6.4
| Данные измерений
|
Результаты вычислений
|
| С, мкФ
|
U, B
|
I, A
|
I1
, A
|
I2
, A
|
P,
Вт
|
cosφ
|
По данным измерений и вычислений п.1, п.2, п.3 построить, в масштабе, векторные диаграммы токов (рисунок 6.7 и 6.13). Построить в масштабе аналогичные векторные диаграммы по п.4 для трех режимов: до резонанса С < С0
; при резонансе С = С0
; после резонанса С > C0
(см. рисунки 6.16, 6.18 и 6.19).
По данным таблицы 6.4 построить кривые:   . .
Обработка результатов измерений
1 Используя данные измерений таблицы 6.1 рассчитаем проводимости и коэффициент мощности электрической цепи:

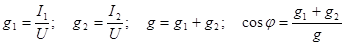 . .
2 Используя данные измерений, таблицы 6.2 рассчитаем параметры катушки:
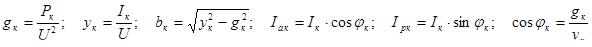
параметры цепи:
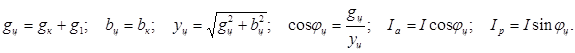
3 Используя данные измерений таблицы 6.3 расчитаем параметры конденсатора и резистора:
 , ,
параметры цепи:
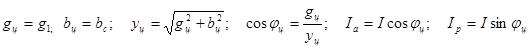
4 Используя данные измерений таблицы 6.4 определим
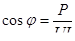
Контрольные вопросы
1. Как определить общий ток разветвленной цепи графическим (векторным) и аналитическим методом?
2. Как определить проводимость катушки и конденсатора, если известны их сопротивления?
3. Как строится векторная диаграмма для разветвленной цепи?
4. В какой электрической цепи и при каком условии может иметь место резонанс токов?
5. Где на практике используют явление резонанса токов?
6. Чему равны активная, индуктивная, емкостная и полная проводимости разветвленной цепи?
7. С помощью, каких измерительных приборов можно определить наступление резонанса токов в разветвленной цепи?
8. Чему равна полная проводимость параллельной цепи с катушкой и конденсатором, настроенной на режим резонанса токов?
9. Каким образом на практике повышается коэффициент мощности?
10.Какими явлениями сопровождается резонанс токов?
Рекомендуемая литература
1 Зайдель Э.Х. и др. Электротехника: учебник для неэлектрических специальностей вузов. – М. : Высшая школа, 1985. – с. 73-77, 86-89.
2 Иванов И.И., Равдоник Н.С. Электротехника: учебник для неэлектрических специальностей вузов. – М. : Высшая школа, 1984. - с. 68-70, 73-77.
3 Касаткин А.С., Немцов М.А. Электротехника: учебное пособие для вузов. – Энергоатомиздат.-1983. - с.68-70, 73-77.
Лабораторная работа № 7. Трехфазные цепи с соединением нагрузки в звезду
Генерирование, передачи и потребление электрической энергии осуществляется, главным образом, посредством переменного трехфазного тока. Энергосистемы состоят из генераторов, ЛЭП, трансформаторов, электродвигателей и других потребителей. Упрощенная схема энергосистемы (рисунок 7.1) содержит генератор, фазные обмотки которого соединены в звезду. Нейтральную точку генератора N заземляют. При этом линия имеет четвертый, нейтральный провод.
Фазы трехфазной нагрузки могут быть соединены в звезду или в треугольник. При соединении нагрузки звездой возможно подключение ее к трехфазной сети с использованием нейтрального провода или без него. Если нейтральная точка приемника подключена к нейтральному проводу, то такая система называется четырехпроводной (рисунок 7.2). При подключении нагрузки только к линейным проводам получаем трехпроводную систему (рисунок 7.2б).
Электродвижущие силы ЕА
, ЕВ
, ЕС
наводимые в фазных обмотках генератора, напряжения на фазах приемника UА
, UВ
, UС
, сопротивление фаз приемника ZА
, ZВ
, ZС
, а также токи в них IА
, IВ
, IС
называют фазными (EФ
, UФ
, ZФ
, IФ
). Напряжение между линейными проводниками UАВ
, UВС
, UСА
и токи в них IА
, IВ
, IС
называют линейными (U^
, I^
). При соединении фаз нагрузки звездой линейные токи равны фазным 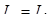 . (7.1) . (7.1)

а)
а
А
В
б)
С
N
Рисунок 7.1 – Схема соединения обмотки генератора звездой (а);схема трехфазной цепи (б)
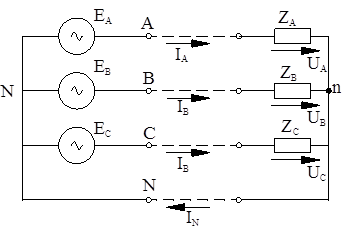
Рисунок 7.2 а – Четырехпроводная цепь;
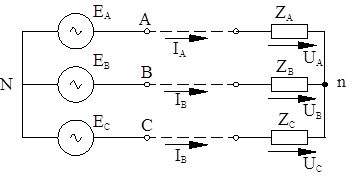
Рисунок 7.2 б – Трехпроводная цепь
Трехфазный генератор обеспечивает симметрическую систему фазных э.д.с. и напряжений. Здесь э.д.с. и напряжения: имеющие одинаковые действующие значения, сдвинуты по фазе относительно друг друга на 1/3 периода (120°) (рисунок 7.3а)
В векторной диаграмме (рисунок 7.3б) использованы соотношения между линейными и фазными напряжениями.
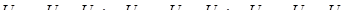 (7.2) (7.2)
На практике чаще используют диаграмму (рисунок 7.3в). В симметричной системе напряжений, для которой
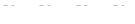 ; ;  , ,
и линейные и напряжения связаны с фазными соотношениями, которое следует, например, из треугольника ANB
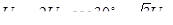 . (7.3) . (7.3)
В практических задачах обычно используют напряжения питающей сети, а не самого генератора. При этом для упрощения считают, что напряжение сети, также как и генератора не зависят от нагрузки и симметричны, за номинальное напряжение трехфазной сети принимают линейное UЛ
.
Фазные напряжения нагрузки, соединенной звездой, симметричны только в случае четырехпроводной системы при очень малом сопротивлении нейтрального провода, либо в случае равенства фазных комплексных сопротивлений нагрузки (ZA
= ZB
= ZC
) в трехпроводной системе.
В четырехпроводной системе токи фаз нагрузки в комплексной форме
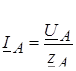 ; ; 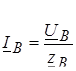 ; ; 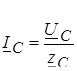 , (7.4) , (7.4)
где 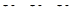 – комплексные действующие значения фазных напряжений нагрузки. – комплексные действующие значения фазных напряжений нагрузки.
а б

в
Рисунок 7.3
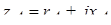 ; ; 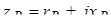 ; ; 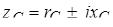 , (7.5) , (7.5)
где 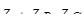 – комплексные сопротивления фаз нагрузки. – комплексные сопротивления фаз нагрузки.
Ток в нейтральном проводе
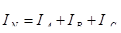 (7.6) (7.6)
Векторная диаграмма напряжений и токов (рисунок 7.4а) соответствует чисто активной нагрузке в фазе А, В, С. Диаграмма приведенная на рисунке 7.4б для случая, когда в фазе А активно-индуктивная нагрузка, в фазе В – чисто активная нагрузка, в фазе С – активно-емкостная нагрузка.

а б
Рисунок 7.4 – Векторная диаграмма напряжения и токов четырехпроводной системы: симметричный режим (а), несимметричный режим (б)
При симметричной нагрузке токи фаз равны по величине (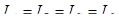 ) и сдвинуты относительно соответствующих фазных напряжений на один и тот же угол ( ) и сдвинуты относительно соответствующих фазных напряжений на один и тот же угол (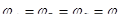 ), то есть составляют симметричную систему векторов (рисунок 7.7, а). при этом ток в нейтральном проводе отсутствует (IN
= 0) и необходимость в нем отпадает. Поэтому симметричные приемники включают в трехфазную сеть посредством трехпроводной линии, а расчет проводят для одной фазы. ), то есть составляют симметричную систему векторов (рисунок 7.7, а). при этом ток в нейтральном проводе отсутствует (IN
= 0) и необходимость в нем отпадает. Поэтому симметричные приемники включают в трехфазную сеть посредством трехпроводной линии, а расчет проводят для одной фазы.
Активную мощность трехфазной нагрузки в общем случае определяют суммированием активных мощностей отдельных фаз
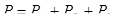 , (7.7) , (7.7)
где 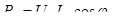 ; ;
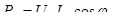 ; ;
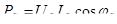 . (7.8) . (7.8)
Для симметричной нагрузки
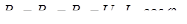 , ,
Следовательно
 . (7.9) . (7.9)
Активная мощность трехфазного приемника может быть измерена однофазным ваттметром (схемы одного рисунок 7.5, двух или трех ваттметров) или одним трехфазным.

Рисунок 7.5 – Схема измерения активной мощности одним ваттметром
Объект и средства исследования
Объектом исследования служит трехфазная четырехпроводная цепь при соединении приемника по схеме «звезда» (рисунок 7.6)
В процессе исследования используют:
1) источник трехфазного переменного тока;
2) магазин сопротивлений (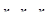 ); );
3) магазин емкостей;
4) катушка индуктивности;
5) амперметр (А1
, А2
, А3
, А4
) пределы измерения от 0 до 2 А;
6) вольтметр (V), пределы измерения от 0 до 100 В;
7) ваттметр (W), пределы измерения от 0 1200 Вт;
Вольтметр переносной, используется для измерения фазных и линейных напряжений.
Рабочее задание
Исследовать трехфазную четырехпроводную цепь при симметричном и несимметричном приемнике, соединенном по схеме «звезда».
Симметричный приемник.
1 Собрать цепь (рисунок 7.6). в каждую фазу включить активные сопротивления (магазин сопротивлений).
2 Включить автомат источника трехфазного переменного тока.
3 Измерить ток в линейных проводах и в нейтральном проводе.

Рисунок 7.6
4 Измерить фазные и линейные напряжения.
5 Измерить мощность одной фазы, для этого снять штекеры с амперметра одной из фаз и соединить их с токовой катушкой ваттметра, а катушку напряжения включить на фазное напряжение. ВНИМАНИЕ: Включать ваттметр при отключенном автомате источника.
6 Данные измерения занести в таблицу 7.1.
Таблица 7.1
| Данные измерений
|
Результаты вычислений
|
| UA
|
UB
|
UC
|
UAB
|
UBC
|
UCA
|
IA
|
IB
|
IC
|
IN
|
P
Ф
|
Р
|
cos
j
|
j
|
| |
|
Несимметричный приемник.
1 Собрать цепь (рисунок 7.6), включив в одну фазу активное сопротивление (магазин сопротивлений), в другую – катушку индуктивности, в третью – емкость.
2 Включить автомат источника трехфазного переменного тока.
3 Измерить токи, фазные и линейные напряжения.
4 измерить мощность каждой фазы. Для этого снять штекеры с амперметра фазы А и соединить их с токовой катушкой ваттметра, катушку напряжения поставить под фазное напряжение Uj
. После измерения мощности в фазе А штекеры вернуть на амперметр. Мощность фазы В и С измерить аналогично измерению мощности фазы А.
5 Данные измерения занести в таблицу 7.2 а, б.
Таблица 7.2 а
| Результаты измерений
|
| UA
|
UB
|
UC
|
UAB
|
UBC
|
UCA
|
IA
|
IB
|
IC
|
РА
|
РВ
|
РС
|
IN
|
Таблица 7.2 б
| Результаты вычислений
|
| P
|
cosjА
|
cosjВ
|
cosjС
|
| |
|
|
Контрольные вопросы
1. Как соединить фазы нагрузки в звезду?
2. Для чего предназначен нейтральный провод между генератором и приемником в четырехпроводной цепи?
3. Что понимают под нейтральной точкой трехфазного генератора или приемника?
4. Каковы соотношения между линейными и фазным токами и напряжениями для симметричной нагрузки соединенной по схеме «звезда»?
5. В чем заключается преимущество четырехпроводной трехфазной цепи по сравнению с трехпроводной цепью?
6. Как определить ток в нейтральном проводе, если известны токи в фазах?
7. В каком случае ток в нейтральном проводе четырехпроводной цепи равняется нулю?
8. Каков вид уравнений мощности трехфазного тока для симметричного и несимметричного приемника?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника : Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова. – 3-е изд., перераб. и доп. – М. : Высшая школа, 1985. - с.151-155.
Лабораторная работа № 8 Трехфазные цепи с соединением нагрузки в треугольник
Цель работы: исследование трехфазной системы при соединении нагрузки в треугольник. Определение опытным путем линейных и фазных токов. Проверка соотношений между ними. Построение векторных диаграмм для различных режимов работы.

Рисунок 8.1
Теоретические сведения
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывают несимметричными (zAB
=zBC
=zCA
), очень важно на практике (в частности, в схемах с осветительными приборами) обеспечить независимость режима работы отдельных фаз. Кроме четырехпроводной цепи подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника треугольником.
Трехфазная цепь состоит из трех основных частей: трехфазного генератора, линии электропередачи и электроприемников (рисунок 8.1).
Фазные обмотки генератора соединены в звезду (рисунок 8.2), нагрузка соединена в треугольник (рисунок 8.3). Соединить нагрузку в треугольник – это значит начало одной фазы соединить с концом следующей фазы. Начало фаз нагрузки соединяют с началом фаз генератора с помощью линейных проводов. В них имеют место линейные токи: İАВ
, İВС
, İСА
. при соединении нагрузки в треугольник каждая фаза оказывается включенной на линейное напряжение, то есть
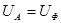 (8.1) (8.1)
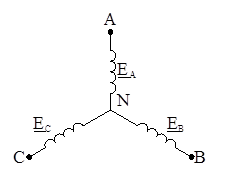
Рисунок 8.2
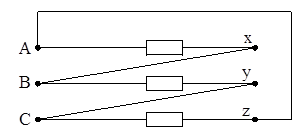
Рисунок 8.3
В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Зависимость между линейными и фазными токами можно определить из уравнений, составленных по первому закону Кирхгофа для каждого из узлов треугольника a, b, c (рисунок 8.1).
I
А
= I
АВ
– I
СА
;
I
В
= I
ВС
– I
АВ
; (8.2)
I
С
= I
СА
– I
ВС
.
Симметричная система – это система, у которой фазные сопротивления нагрузки равны по величине и одинаковы по характеру, то есть
 (8.3) (8.3)
Для такой системы справедливы равенства
IAB
=IBC
=ICA
=IФ
;
IA
= IB
= IC
= I^
(8.4)
Из векторной диаграммы (рисунок 8.4) можно определить зависимость между величиной линейных и фазных токов, рассмотрев равнобедренный треугольник, состоящий из вектора линейного тока и двух векторов фазных токов. Тогда
I^
=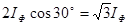 (8.5) (8.5)
Эта зависимость справедлива только для симметричной нагрузки. При несимметричной нагрузке фазные токи определяются
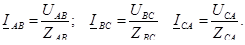 (8.6) (8.6)

Рисунок 8.4
где фазные напряжения, токи и сопротивления выражены в комплексной форме. Линейные токи находят из выражения (8.2). векторная диаграмма для несимметричной нагрузки при активном характере, то есть угол сдвига фаз между фазным током и напряжением равен нулю, приведена на рисунке 8.5.

При обрыве одного линейного провода (например, провода А), при равномерной нагрузке и активном характере фаз, схема соединения нагрузки в треугольник превращается в однофазную разветвленную цепь, в которой две фазы АВ и СА соединены последовательно к фазе ВС (рисунок 8.6).
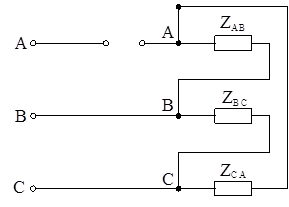
Рисунок 8.6
Нагрузка фазы ВС находится в прежних условиях, то есть под напряжением UBC
. Напряжение приходящееся на фазу АВ и СА в два раза меньше, чем в нормальном режиме и равно половине линейного напряжения UBC
.
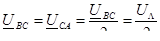 (8.7) (8.7)
Ток в фазе ВС сохраняет свою величину, а в фазе АВ и СА токи уменьшились в два раза, то есть
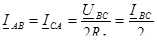 (8.8) (8.8)
Векторная диаграмма для этого случая показана на рисунке 8.7.

Рисунок 8.7
Если в качестве нагрузки применялись лампы накаливания, то при обрыве одного линейного провода накал в последовательно соединенных фазах резко уменьшится.
При обрыве фазы нагрузки, например фазы АВ, 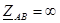 . Тогда токи в линейных проводах: . Тогда токи в линейных проводах:
I
А
= – I
СА
; I
В
= I
ВС
; I
С
= I
СА
– I
ВС
(8.9)
При этом сохраняется условие
I
А
+ I
В
+ I
С
= 0 (8.10)
Независимо от режима фазы АВ напряжение на фазах нагрузки zBC
и zCA
остаются неизменными. Векторная диаграмма для такого случая приведена на рисунке 8.8.

  Рисунок 8.8
Активная мощность трехфазной системы определяется выражением
P=PАВ
+РВС
+РСА
(8.11)
Активные мощности фаз определяются:
Р=UAB
IAB
cosjAB
;
P=UBC
IBC
cosjBC
; (8.12)
P=UCA
ICA
cosjCA
,
где cosjAB
, cosjBC
, cosjCA
– фазные коэффициенты мощности, зависящие от характера нагрузки.
Для симметричной нагрузки
Р= 3РФ
= 3UФ
IФ
cosj =  U^
I^
cosj U^
I^
cosj
Объект и средства исследования
Объектом исследования служит трехфазная цепь при соединении приемника по схеме треугольник (рисунок 8.9).
Для проведения исследования используют:
1) трехфазный источник переменного тока;
2) магазин сопротивлений R;
3) амперметры с пределом измерения от 0 до 2 А;
4) вольтметр с пределом измерения от 0 до 100 В;
5) провода соединительные.
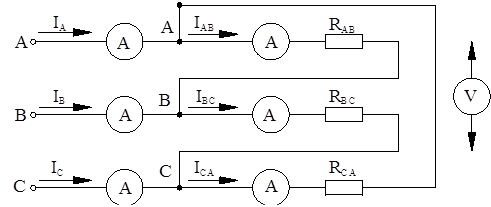
Рисунок 8.9
Рабочее задание
1 Собрать электрическую схему, изображенную на рисунке 8.9.
2 Произвести измерения величин, указанных в таблице 8.1 при активной нагрузке в следующих режимах:
а) режим неравномерной нагрузки – сопротивления в фазах нагрузки различны по величине;
б) обрыв линейного провода;
в) обрыв фазы нагрузки АВ.
Данные измерений для трех режимов работы занести в таблицу 8.1.
Таблица 8.1
| Режим нагрузки
|
Данные измерений
|
Результаты вычислений
|
| UAB
|
UBC
|
UCA
|
IA
|
IB
|
IC
|
IA
В
|
IB
С
|
IC
А
|
РА
|
РВ
|
РС
|
Р
|
| Неравно
мерная
|
| Обрыв линейного провода
|
| Обрыв фазы
|
3 В соответствии с данными измерений построить векторные диаграммы напряжений и токов для всех перечисленных выше режимов работы.
4 Определить мощность каждой фазы и трехфазной системы.
Контрольные вопросы
1. Как соединить электроприемники однофазного тока треугольником?
2. Какая нагрузка в цепи трехфазного тока называется равномерной?
3. Какие существуют соотношения между фазными и линейными электрическими величинами при соединении электроприемников треугольником?
4. Что понимают под трехфазной симметричной системой?
5. Каков вид выражений мощности для трехфазного тока для случая равномерной и неравномерной нагрузок?
6. В чем преимущество приемников, соединенных треугольником?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника : Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова. – 3-е изд., перераб. и доп. – М. : Высшая школа, 1985. - с.110-122.
2 Иванов И.И., Равдоник В.С. Электротехника : Учебное пособие для неэлектрических специальностей вузов. – М. : Высшая школа, 1984. - с. 101-110.
3 Касаткин А.С., Немцов М.В. Электротехника : Учебное пособие для вузов. – 4-е изд., перераб. – М. : Энергоатомиздат, 1983. - с.112-123.
Лабораторная работа № 9 Измерение потери напряжения в проводах
Цель работы: измерение потери напряжения в проводах. Расчет сопротивления проводов и определение материала по потерям напряжения.
Теоретические сведения
При передаче электрической энергии по проводам длиною больше 10 м приходится считаться с их сопротивлением, на котором происходит заметное падение напряжения.
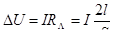 (9.1) (9.1)
При заданном напряжении U1
на выходе линии, приведенной на рисунке 9.1, напряжение на нагрузке при номинальном токе нагрузки будет равно
U2
= U1
– ΔU (9.2)
Падение напряжения ΔU не должно превышать определенных значений, предусмотренных ГОСТом. Отклонения напряжения в сторону уменьшения для осветительных приборов ограничены 2,5-5%, так как при уменьшении напряжения резко уменьшается световой поток приборов. Увеличение напряжения ограничено величиной 5%, так как дальнейшее увеличение напряжения сокращает срок службы ламп накаливания. Недопустимы значительные отклонения напряжения от номинального и для двигателей, так как при больших отклонениях может иметь место ненормальная работа и даже выход из строя двигателя. Поэтому для двигателей установлены допустимые отклонения напряжения в пределах ±5% номинального.
При расчете цепей возможны следующие 4 задачи:
1) определение потерь напряжения при наименьшей и наибольшей нагрузках;
2) определение потерь и отклонения напряжения для данной линии при заданных сечениях проводов и нагрузке;
3) выбор или проверка сечения проводов линии, исходя из того, чтобы провода не перегревались при протекании по ним тока;
4) проверка имеющихся проводов определенного сечения на отсутствие перегрева.
Как следует из (9.1) величина потерь напряжения в линии зависит не только от сопротивления, но и от силы тока, протекающего по ней. Определим потери напряжения в линии с учетом характера нагрузки. На рисунке 9.2 приведена векторная диаграмма. Ее построение выполнено на комплексной плоскости в следующем порядке. Направим вектор напряжения U
2
по действительной оси и под углом j2
к нему проведем вектор тока I
. к концу вектора U
2
прибавим векторы активного и реактивного (индуктивного) JxL
I
напряжения. Треугольник, катетами которого является активное и индуктивное напряжения проводов линии, а гипотенузой – вектор ΔU=I
z , называют треугольником падения напряжения. Вектор U
1
первичного напряжения является замыкающим векторов U2
и ΔU . Разность модулей векторов напряжения в начале и конце линии |U1
| - |U2
| = ΔU называют потерей напряжения. Потеря напряжения в линии передачи показывает, на сколько вольт напряжение в конце линии меньше, чем напряжение в начале линии. Под падением напряжения в линии передачи понимают модуль геометрической разности векторов напряжений в начале и в конце линии, оно равно  . .
Как правило, падение напряжения больше потери напряжения. Лишь только для цепи, состоящей из одних активных сопротивлений, когда cosj1
= cosj2
= I , а следовательно, и для цепи постоянного тока термины «падение» и «потеря напряжения» выражают одну и ту же величину, которую можно определить по формуле (9.1).
Возможен также случай равенства потери и падения напряжения в линии с индуктивностью, если гипотенуза треугольника падения напряжения совпадает по направлению с вектором U
2
. векторная диаграмма для данного случая приведена на рисунке 9.3.
В практике инженерных расчетов потерю напряжения выражают аналитически и часто приближенно. В нашем случае для схемы (рисунок 9.1) это приближение оказывается в том, что вместо отрезка АВ векторной диаграммы (рисунок 9.2), выражающего потерю напряжения, берут отрезок ДВ. Последний в свою очередь заменяется суммой двух отрезков СВ и ДС, являющихся проекциями векторов падения напряжения rI
и jxL
I
на прямую ОА. В этом случае потеря напряжения может быть выражена соотношением:
ΔU= r I cosj2
+xL
I sinj2
или ΔU = I (r cosj2
+xL
sinj2
) (9.3)
Передача энергии на большие расстояния однофазным током не производится, а индуктивность местных распределительных сетей незначительна. Поэтому их индуктивностью пренебрегают и потерю напряжения определяют по формуле
ΔU=I r cosj2
(9.4)

Рисунок 9.1 – Схема замещения линии электропередачи
Из (9.3) следует, что ΔU зависит не только от сопротивлений линии, но и от соотношений активного и реактивного xL
сопротивлений приемника
cosj2
=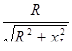 и sinj2
= и sinj2
=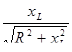

Рисунок 9.2 – Векторная диаграмма линии при индуктивной нагрузке

Рисунок 9.3 – Векторная диаграмма индуктивной нагрузки при равенстве падения и потери напряжения
Используем эту формулу для выбора сечения проводов линии, передающей мощность P2
при напряжении U2
. для этого формулу (9.4) представим в виде выражений
ΔU=I r cosj2
= (9.5) (9.5)
Из (9.5) найдем сечение проводов
S= или S= или S=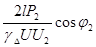 (9.6) (9.6)
В случае активной нагрузки (cosj2
= I) или при постоянном токе сечение проводов определяется по формулам
SПОСТ
=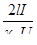 или SПОСТ
= или SПОСТ
=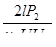 (9.7) (9.7)
Из сравнения (9.6) и (9.7) видно, что при одинаковых расстояниях, напряжениях и передаваемых мощностях сечение проводов, рассчитанных по потере напряжения для постоянного и одновременного и однофазного тока, получаются одинаковыми. Но потери мощности в проводах при этом будут различны.
При постоянном токе
 (9.8) (9.8)
При переменном токе
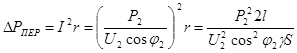 (9.9) (9.9)
При равенстве потерь мощности в проводах
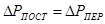 ; ; 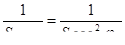
Откуда
 (9.10) (9.10)
Из (9.10) следует, что чем меньше cos j2
, тем больше сечение проводов необходимо иметь для передачи одной и той же мощности потребителю, чтобы сохранить неизменной потерю энергии в проводах сечения проводов, определенных по потери напряжения согласно формулам (9.6) и (9.7), округляются до ближайшего большего стандартного сечения и потом проверяются на нагрев по таблицам длительно допустимых токов нагрузки. Величина допустимых токов для проводов приводится в справочниках. Для примера приведем величины допустимых токов голых алюминиевых проводов при температуре окружающего воздуха 20°С.
| Сечение провода, мм2
|
10
|
16
|
25
|
35
|
50
|
70
|
95
|
120
|
| Допустимый ток, А
|
75
|
105
|
135
|
170
|
215
|
265
|
325
|
375
|
При расчете проводов трехфазного тока под потерей напряжений понимают разность линейных напряжений в начале и в конце линии. Приняв систему напряжений и нагрузки симметричными, расчет проводят для одной фазы, используя при этом векторную диаграмму для одной цепи.
Тогда
 или или 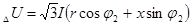 (9.11) (9.11)
При расчете линий электропередач большой протяженности в выражении (9.11) вместо r и x представляют справочные данные r0
и x0
– активное и индуктивное сопротивление 1 км линии
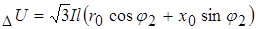 (9.12) (9.12)
Основными материалами, применяемыми в электротехнике для изготовления проводов различного назначения, являются металлы с высокой удельной проводимостью и сплавы с большим удельным сопротивлением, свойства которых приведены в таблице 9.1.
Таблица 9.1 – Свойства проводниковых материалов при t = 20°С
| Материал
|
Удельное сопротивление ρ, 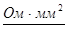
|
Удельная проводимость
γ, 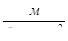
|
Температур-ный коэффициент
α
, град-
I
|
Предель-ная рабочая темпе-ратура
tmax
, °
C
|
| Серебро
|
0,0162
|
62
|
0,0036
|
-
|
| Медь
|
0,0175
|
57
|
0,0041
|
-
|
| Алюминий
|
0,0294
|
34
|
0,0042
|
-
|
| Сталь
|
0,13
|
7,7
|
0,0057
|
-
|
| Чугун
|
0,8
|
1,25
|
0,0010
|
400
|
| Никелин
|
0,42
|
2,4
|
0,0003
|
300
|
| Манганин
|
0,48
|
2,1
|
0,00001
|
500
|
| Константан
|
0,5
|
2,0
|
0,00005
|
1000
|
| Нихром
|
1,0
|
1,0
|
0,00017
|
850
|
| Фехраль
|
1,2
|
0,83
|
0,00008
|
1350
|
| Хромаль
|
1,4
|
0,72
|
0,00004
|
Объект и средства исследования
Объектом исследования служит электрическая цепь приведенная на рисунке 9.4.

Рисунок 9.4 – Электрическая цепь постоянного тока
В процессе исследования используются:
1) источник постоянного тока – 30 В;
2) реостат R = 10 Ом;
3) амперметр PAI с пределом измерения от 0 до 2 А;
4) вольтметр V1
(0-30 В);
5) милливольтметр V2
((≤15 мВ);
6) набор проводников из различных материалов длиной l ≤ 1 м.
Рабочее задание
1 Ознакомиться с размещением приборов на лабораторном стенде рисунок 9.4.
2 Определить цену деления приборов.
3 Собрать электрическую схему, приведенную на рисунке 9.4
4 При отключенном ключе S , включить автомат постоянного тока. Установить с помощью реостата заданное преподавателем напряжение. При этом ток в цепи не должен превышать 2 А, а R ≥ 15 Ом.
5 Измерить ток в цепи и падение напряжения на участке АВ. Измерения сделать для n значений проводов длиною l. Данные измерения занести в таблицу 9.2.
6 По измеренным данным определить согласно закона Ома сопротивления проводов.
7 По полученным данным определить удельное сопротивление каждого провода и по его значениям определить материал по таблице 9.1.
8 Сделать выводы.
Таблица 9.2
| №
|
Измерить
|
Вычислить
|
Определить
|
| |
Δ
U,
|
I,
|
l,
|
S,
|
ρ
,
|
γ
,
|
R,
|
Материал провода
|
| |
B
|
F
|
м
|
мм2
|
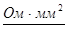
|
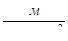
|
Ом
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Контрольные вопросы
1. Что понимают под падением и потерей напряжения?
2. Какие инженерные задачи возникают при расчете проводов линий электропередачи?
3. Назовите допустимые отклонения напряжения для различных видов нагрузки.
4. Как влияет характер нагрузки на величину падения напряжения?
5. Что понимают под треугольником падения напряжения?
6. В каком случае падение и потеря напряжения равны между собой?
7. какие факторы влияют на величину сопротивления?
8. Приведите соотношение сечения проводов при передаче одинаковой мощности на постоянном и переменном токе.
9. Как определить потери напряжения в цепи трехфазного тока?
10.Для изготовления каких электрических устройств используют материалы с большим удельным сопротивлением?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника : Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова – М. : Высшая школа, 1985.
2 Иванов И.И., Равдоник В.С. Электротехника : Учебное пособие для неэлектрических специальностей вузов. – М. : Высшая школа, 1984.
3 Касаткин А.С., Немцов М.В. Электротехника : Учебное пособие для вузов. – 4-е изд., перераб. – М. : Энергоатомиздат, 1983.
Лабораторная работа № 10. Повышение
cosφ
Цель работы: экспериментальное и аналитическое определение коэффициента мощности.
Теоретические сведения
На современных промышленных предприятиях большинство потребителей электрической энергии переменного тока представляют собой индуктивно-активную нагрузку. Это асинхронные двигатели, силовые, сварочные и другие специальные трансформаторы, катушки контакторов и реле и т.п. Активная мощность таких потребителей помимо заданной нагрузки зависит также и от cosφ . Если для потребителя задаются его напряжение U и активная мощность Р , то с изменением cosφ изменится и ток потребителя. С уменьшением cosφ потребителя его ток возрастает
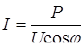 (10.1) (10.1)
Увеличение тока потребителя при снижении cosφ не должно превышать определенных пределов, так как питающие их генераторы рассчитываются на определенную номинальную мощность
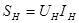 , ВА(10.2) , ВА(10.2)
При заданном напряжении UH
они могут быть нагружены током, не превышающим номинальное значение. Поэтому увеличение тока потребителя вследствие снижения его cosφ не должно превышать определенных пределов. Чтобы ток генератора не был выше номинального при снижении cosφ потребителя, необходимо снижать его активную мощность . В этом случае генератор будет полностью нагружен по току и недогружен по активной мощности.
Для сохранения неизменной активной мощности потребителя при снижении cosφ можно было установить генератор на большую номинальную мощность с тем, чтобы увеличение тока вследствие снижения cosφ не превышало его номинального значения. В этом случае активная мощность
Р=SH
cosφ (10.3)
которой будет нагружен генератор, составляет только часть номинальной SH
. Например, при снижении cosφ от 1 до 0,5 нагрузка генератора составляет только 50% от его номинальной мощности. Таким образом, cosφ характеризует, как используется номинальная мощность источника, и поэтому его называют коэффициентом мощности.
Работа источника питания в целом характеризуется к.п.д. генератора и первичного двигателя. Работа первичного двигателя определяется в основном активной мощностью генератора. Поэтому недогрузка генератора активной мощностью влечет за собой недогрузку и снижение к.п.д. первичного двигателя и всей энергетической установки. Себестоимость электроэнергии от этого повышается.
Работа потребителя с малым коэффициентом мощности, кроме ухудшения условий экономического использования источника питания, приводит к увеличению мощности потерь в лини передачи электрической энергии от источника к потребителю. Если сопротивление проводов этой лини r , то мощность потерь в ней
 (10.4) (10.4)
Мощность потерь, как видно из этого выражения, тем больше, чем ниже cosφ установки. Следовательно, чем ниже cosφ потребителя, тем дороже будет обходиться передача к нему электроэнергии. При номинальном режиме потребители имеют довольно высокий коэффициент мощности, достигающий значения 0,7 – 0,9. Но при малой нагрузке их коэффициент мощности очень мал, что может привести к снижению cosφ энергетической установки в целом.
Чтобы повысить экономичность энергетических установок, принимают меры к повышению коэффициента мощности потребителей. Существует три основных способа увеличения коэффициента мощности:
1 Рациональное использование электрооборудования, заключающееся в следующем:
а) систематическое наблюдение за работой и нагрузкой двигателей, замена малонагруженных двигателей двигателями меньшей мощности;
б) ограничение времени холостого хода двигателей, для чего необходимо применять автоматический пуск и остановку на расстоянии, блокировки и сигнализацию;
в) нормальная нагрузка двигателей путем улучшения технологического процесса, повышения загрузки оборудования;
г) отключение неработающих трансформаторов от сети;
д) применение высокоскоростных двигателей с короткозамкнутым ротором по возможности открытого исполнения;
е) качественный ремонт оборудования.
Проведение указанных мероприятий приводит к значительному увеличению естественного cosφ до 0,7-0,8. естественным называется коэффициент мощности, получающийся без применения специальных технических средств.
2 Технические мероприятия, заключающиеся в замене асинхронных двигателей синхронными, использование синхронных двигателей в качестве компенсаторов (то есть двигателей, работающих в холостую и вырабатывающих реактивную мощность) и в установке конденсаторов. Применение этих мероприятий приводит к искусственному повышению cosφ.
3 Тарифно-экономические мероприятия, которые заключаются в предоставлении предприятию скидки или взиманию надбавки к тарифу на электроэнергию в зависимости от величины коэффициента мощности.
При cosφ < 0,9 предприятие платит надбавку к тарифу по специальной шкале: при cosφ > 0,92 предприятие получает соответствующую скидку. Коэффициент мощности от 0,9 до 0,92 называется нейтральным, так как не оказывает влияния на стоимость электроэнергии.
Идея искусственного повышения cosφ заключается в следующем: общий ток потребителя рассматривают состоящим из активной и реактивной составляющих. Активная мощность потребителя при данном напряжении определяется активной составляющей тока
Р = U Ia
(10.5)
поэтому при заданном значении активной мощности, активная составляющая тока должна оставаться неизменной. Снизить ток потребителя можно только за счет уменьшения реактивной составляющей тока потребителя. Последнее можно осуществить только путем параллельного подключения к нагрузке какого-либо приемника с емкостным током. Таким приемником может быть или синхронный компенсатор, или батарея специальных конденсаторов. Обычно при помощи батареи конденсаторов повышают cosφ до 0,9-0,95.
Объект и средства исследования
Объектом исследования служит электрическая цепь, состоящая из параллельно соединенных катушки индуктивности и емкости (рисунок 10.1).

Рисунок 10.1
Для проведения исследования используют:
1) источник электрической энергии переменного тока – 30 в;
2) ваттметр с пределом измерения 0-1200 Вт;
3) вольтметр – 0-100 В;
4) амперметры – 0-2 А;
5) катушка индуктивности;
6) магазин емкостей;
7) ключ К.
В работе используется ваттметр с пределами измерения по току 2,5 и 5 А и по напряжению 30 В, 75 в, 150 в, 30 в, 450 в и 60 в. Токовая катушка ваттметра включается последовательно в цепь, катушка напряжения – параллельно.
Рабочее задание
1 Собрать электрическую цепь (рисунок 10.1). Ключ К – разомкнут. Включить автомат переменного тока и записать показания приборов в таблицу 10.1 в графу «до компенсации».
Таблица 10.1
| Режим работы цепи
|
Данные измерений
|
Результаты вычислений
|
| U
|
I
|
I1
|
I2
|
P
|
cos
j
|
j
|
С
|
| До компенсации
|
| После компенсации
|
2 Замкнуть ключ К, то есть параллельно катушке индуктивности подключить емкость (рисунок 10.1). включить автомат переменного тока, записать показания приборов в таблицу 10.1 в графу «после компенсаци2.
ВНИМАНИЕ: после окончания каждого опыта автомат переменного тока отключать.
По данным измерений определить cosφ и угол сдвига фаз между током и напряжением φ до и после компенсации. Построить векторную диаграмму, на которой указать угол φ до и после компенсации (рисунок 10.2).

Рисунок 10.2
φ – угол сдвига фаз до компенсации; φ|
- угол сдвига фаз после компенсации; I=I1
– ток в цепи до компенсации; I’
– ток в цепи после компенсации; I2
– ток в цепи с емкостью.
Контрольные вопросы
1. Что называется коэффициентом мощности?
2. В чем состоит экономическое значение коэффициента мощности?
3. В чем состоят меры повышения коэффициента мощности?
4. Как коэффициент мощности влияет на эффективность работы электрооборудования?
Рекомендуемая литература
1 Зайдель Х.Э. и др. Электротехника : Учебник для неэлектрических специальностей вузов / Х.Э.Зайдель, В.В.Коген-Далин, В.В.Крымов и др.; Под редакцией В.Г.Герасимова. – 3-е изд., перераб. и доп. – М. : Высшая школа, 1985. - с.119-122.
2 Касаткин А.С., Немцов М.В. Электротехника : Учебное пособие для вузов. – 4-е изд., перераб. – М. : Энергоатомиздат, 1983. - с.92-94.
Лабораторная работа № 11 Измерение сопротивлений на постоянном токе методом амперметра и вольтметра
Цель работы: измерение малого и большого сопротивления на постоянном токе методом двух приборов.
Теоретические сведения
Сопротивление – один из важнейших параметров электрической цепи. Одни сопротивления сохраняют свои значения в различных условиях, другие, наоборот, изменяются во времени, от температуры, от влажности и т. п. Поэтому при изготовлении электрических машин, аппаратов, приборов, при монтаже электроустановок необходимо производить измерение сопротивлений.
По значениям сопротивления делят на три группы: малые (10 Ом и меньше), средние (10-0,1 Мом) и большие (от 0,1 Мом и выше).
При измерении малых сопротивлений на результат измерения влияют сопротивления соединительных проводов, контактов и т.д. При измерении больших сопротивлений необходимо считаться с объемными и поверхностными сопротивлениями.
Измерение сопротивлений твердых проводников производят на постоянном токе, так как при этом, с одной стороны, исключаются погрешности, связанные с влиянием емкости и индуктивности объекта измерения, с другой стороны, появляется возможность применять приборы магнитоэлектрической системы, имеющие высокую чувствительность и точность.
Магнитоэлектрическая система
Приборы магнитоэлектрической системы применяются для измерения постоянных токов и напряжений (амперметры, вольтметры), сопротивлений (омметры) и т.д. На рисунке 11.1 показано устройство магнитоэлектрического измерительного механизма с подвижной катушкой.

Рисунок 11.1 – Устройство магнитоэлектрического измерительного механизма
На рисунке 11.1: 1 – постоянный магнит, 2 – магнитопровод, 3 – полосные наконечники, 4 – неподвижный сердечник, 5 – спиральная пружина, 6 – подвижная катушка, 7 – магнитный шунт, 8 – указатель.
Ток к подвижной катушке подводится через две спиральные пружинки. Вращающий момент возникает в результате взаимодействия магнитного поля постоянного магнита и магнитного поля катушки с током и определяется
M = B S W I (11.1)
где I – ток в рамке;
B – магнитная индукция в зазоре;
S – площадь рамки;
W – количество витков катушки.
Установившееся положение подвижной части определяется равенством вращающего и противодействующего момента, которое можно записать
I B S W = в α (11.2)
где в – удельный противодействующий момент;
α – угол поворота подвижной части.
Отсюда угол поворотной части:
α =  (11.3) (11.3)
Он пропорционален току, и, следовательно, прибор имеет равномерную шкалу.
Электромагнитная система
Приборы электромагнитной системы применяются для измерения переменных и постоянных токов и напряжений (амперметры, вольтметры). Из-за относительно низкой стоимости и удовлетворительных характеристик электромагнитные приборы составляют большую часть всего парка щитовых приборов.
Электромагнитный измерительный механизм с плоской катушкой включает: ось, указательную стрелку, катушку, эксцентрически укрепленный на оси ферромагнитный сердечник, пружины для создания противодействующего момента, воздушный успокоитель.
При протекании тока I через катушку сердечник намагничивается и втягивается в зазор катушки. Вращающий момент определяется:
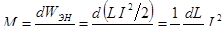 (11.4) (11.4)
где WЭН
– энергия электромагнитного поля катушки с сердечником;
L – индуктивность катушки, зависящая от положения сердечника.
Положение равновесия подвижной части определяется равенством моментов
М = МАР
= в α (11.5)
отсюда угол поворота подвижной части
α = 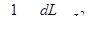 (11.6) (11.6)
Угол будет пропорционален квадрату действующего значения тока и будет одинаков как при постоянном, так и при переменном токе.
Все электроизмерительные приборы подразделяются по следующим признакам: по роду тока (приборы постоянного и переменного тока), по принципу действия в зависимости от системы (таблица11.1), по степени точности, по степени защищенности от внешних полей и т.д.
Кроме обозначения системы прибора, на его шкале указываются следующие технические данные: 1,5 – класс точности при нормировании погрешности в процентах диапазона измерения; |, __ – вертикальное и горизонтальное положение шкалы; * - измерительная цепь изолирована от корпуса и испытана напряжением, например 2 кВ.
Измерение сопротивлений методом двух приборов
Измерив ток I в проводнике и напряжение U на его зажимах, определим согласно закону Ома для участка цепи сопротивление проводника
Rx
= 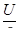
Таблица 11.1 – Условные обозначения, наносимые на электроизмерительные приборы
| Наименование прибора
|
Условное обозначение
|
| Прибор магнитоэлектрический с подвижной рамкой
|

|
| Прибор магнитоэлектрический с подвижным магнитом
|

|
| Прибор электромагнитный
|

|
| Прибор электродинамический
|

|
| Прибор ферродинамический
|

|
| Прибор индукционный
|

|
Отсюда название метода «амперметра-вольтметра», относящегося к косвенным измерениям. Применяются две схемы включения амперметра и вольтметра (рисунок 11.3 и 11.4).
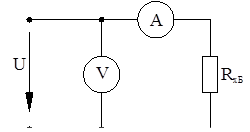
Рисунок 11.3 – Схема для измерения большого сопротивления
При измерениях по схеме рисунка 11.3 показания вольтметра UV
равны сумме напряжений на сопротивления RU
и на амперметре UA
UV
= UA
+ IA
Rx
В этом случае измеряемое сопротивление Rx
равно

где RA
– сопротивление амперметра.
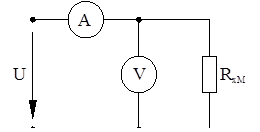
Рисунок 11.4 – Схема для измерения малого сопротивления
Отсюда видно, что появляется погрешность измерения, равная RA
. Поэтому схему по рисунку 11.3 применяют для измерений сопротивлений, больших по сравнению с сопротивлением амперметра, что позволяет пренебречь значениями RA
, то есть считать

При использовании второй схемы (рисунок 11.4) показание амперметра IA
равно сумме токов в сопротивлении Rx
и вольтметре IV
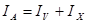
Отсюда 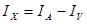 , следовательно, измеряемое сопротивление , следовательно, измеряемое сопротивление
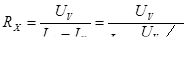
Эту схему применяют для измерений сопротивлений, меньших по сравнению с сопротивлением вольтметра. В этом случае током в вольтметре можно пренебречь, то есть считать
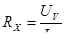
Анализ показывает, что при использовании метода двух приборов, если соблюдается соотношение Rx
< 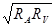 , то следует пользоваться схемой на рисунке 11.3, а в противном случае – схемой на рисунке 11.4. Достоинство этих схем заключается в том, что по измеряемому сопротивлению можно пропускать такой же ток, как и в условиях его будущей эксплуатации. , то следует пользоваться схемой на рисунке 11.3, а в противном случае – схемой на рисунке 11.4. Достоинство этих схем заключается в том, что по измеряемому сопротивлению можно пропускать такой же ток, как и в условиях его будущей эксплуатации.
Объект и средства исследования
Объектом исследования служит электрическая цепь приведенная на рисунке 11.5
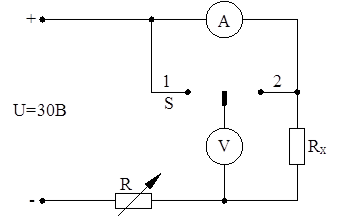
Рисунок 11.5
В процессе исследования используются:
1) источник постоянного тока, U = 30 В;
2) амперметр с пределом измерения от 0 до 2 А;
3) вольтметр с пределом измерения от 0 до 30 В;
4) магазин сопротивлений;
5) набор проводников.
Рабочее задание
1 Собрать электрическую цепь (рисунок 11.5). Для измерения малого сопротивления RxM
(до 10 Ом) ключ S поставить в положение «2». Измерение RxM
производить при трех значениях сопротивления R (указывается преподавателем). Результаты измерений занести в таблицу 11.2.
2 Для измерения большого сопротивления Rx
Б
(300 Ом) ключ S поставить в положение «1». Измерение Rx
Б
также производить при трех значениях сопротивления R . Результаты измерения занести в таблицу 11.2.
3 По данным измерений вычислить приближенные и истинные значения измеряемых сопротивлений, а также абсолютные и относительные погрешности измерений. Результаты вычислений свести в таблицу 11.2.
Таблица 11.2
| Номер по порядку
|
Положение ключа
|
Измерено
|
Вычислено
|
| I, A
|
U, B
|
RI
xM(
d
)
,
Ом
|
RxM(
d
)
,
Ом
|
Δ
RxM(
d
)
|
b
, %
|
| 1
|
«2»
|
| 2
|
| 3
|
| 1
|
«1»
|
| 2
|
| 3
|
Обработка результатов измерений
1 Приближенное значение измеряемого сопротивления R|
xM
(
d
)
R|
xM
(
d
)
=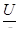
2 Истинное значение измеряемого сопротивления
RxM
= 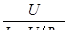
где RV
– сопротивление вольтметра, равное 60 кОм.
3 Истинное значение измеряемого сопротивления Rx
Б
 Rx
Б
= Rx
Б
=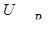
где RA
– сопротивление амперметра, равное 3 Ом.
4 Абсолютная погрешность измерения Δ
RxM
(Б)
Δ
RxM
(Б)
= R|
xM
(Б)
- RxM
(Б)
5 Относительная погрешность измерения b
b = 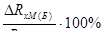
Контрольные вопросы
1. Принцип действия приборов магнитоэлектрической системы, вывод формулы угла поворота подвижной части.
2. Принцип действия приборов электромагнитной системы, вывод формулы угла поворота подвижной части.
3. Схема измерения малого сопротивления RM
, вывод формулы для определения этого сопротивления.
4. Схема для измерения большого сопротивления RБ
, вывод формулы для определения этого сопротивления.
5. Условные обозначения, наносимые на шкалы приборов, их объяснение.
Рекомендуемая литература
1 Душин Е.М., Авдеев Б.Я., Антонюк Е.М. и др. Основы метрологии и электрические измерения: Учебник для вузов. Под редакцией Душина Е.М. – 6-е издание, перераб. и доп. – Л. : Энергоатомиздат, 1987. - с.116-120, 136-140.
2 Попов В.С., Электрические измерения : Учебник для техникумов. Издание 2-е перераб. и доп. - М. : Энергия, 1974. - с.28-32.
|