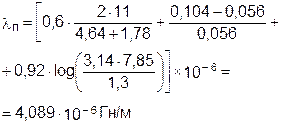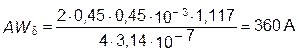Реферат: Методическое руководство по расчету машины постоянного тока МПТ
|
Название: Методическое руководство по расчету машины постоянного тока МПТ Раздел: Остальные рефераты Тип: реферат | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Министерство образования Российской Федерации Пермский государственный технический университет Е.Ф.Беляев РАСЧЕТ И ПРОЕКТИРОВНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН ПОСТОЯННОГО ТОКА МАЛОЙ МОЩНОСТИ Утверждено Редакционно-издательским советом университета в качестве учебно-методического пособия по курсовому проектированию Пермь 2001 УДК 621.313 Б44 Рецензент канд. техн. наук, доц. А.И. Судаков Беляев Е.Ф. Б44 Расчет и проектирование электрических машин постоянного тока малой мощности: Учебно-метод. пособие по курсовому проектированию / Перм. гос. техн. ун-т. Пермь, 2000. 72 с. Изложены методы расчета геометрии конструктивных элементов, параметров и рабочих характеристик машин постоянного тока, выполняемые вручную и на ЭВМ. Приведена методика расчета оптимальных размеров магнита постоянного тока для возбуждения машин, а также упрощенный тепловой расчет. Теоретические вопросы проиллюстрированы примерами расчета. Предназначено для студентов заочных отделений вузов специальности “Электромеханика”, занимающихся изучением вопросов проектирования электрических машин. УДК 621.313 Ó Пермский государственный технический университет, 2000 ВВЕДЕНИЕ Проектирование электрических машин (ЭМ) включает расчёт и конструирование. Расчёт машины представляет математически неопределённую задачу, т.к. число неизвестных, подлежащих определению, превышает число уравнений. Поэтому в процессе расчёта приходится задаваться некоторыми величинами, используя опыт проектирования подобных машин и экспериментальные данные. В процессе расчёта, как правило, рассматривают несколько вариантов, окончательно принимая наиболее выгодный. Проектирование электрических машин включает в себя следующие этапы: 1. Составление технического задания. Выясняются основные требования, предъявляемые заказчиком к электрической машине, соответствие техническим условиям или стандартам, если таковые имеются. 2. Предварительный расчёт основных размеров электрической машины и их соответствие техническому заданию. 3. Предварительный расчёт характеристик машины и оценка её нагрева. Анализируются результаты расчётов различных вариантов и производится выбор наиболее соответствующего выбранному критерия оптимальности. 4. Уточнение конструкции электрической машины, исходя из результатов предыдущего этапа. Полученные материалы являются основой для составления эскизного проекта машины. 5. Изготовление и испытание опытных образцов электрической машины. 6. Корректировка расчётов, размеров и параметров машины с учётом результатов испытаний и составление технического проекта. 7. Выпуск опытной партии электрических машин и составление соответствующей технической документации. Одновременно с указанными этапами работы производится разработка технологической документации, определяются требования к используемым материалам и комплектующим изделиям. При этом технологический отдел конструкторского бюро осуществляет привязку технологического процесса к существующему оборудованию или разрабатывает задание на технологическое оборудование. Результаты расчёта ЭМ достаточно хорошо согласуются с опытом лишь при проектировании машин средней и большой мощностей. В этом случае расхождение расчётных и экспериментальных данных в среднем не превышает 10%. Для машин малой мощности эти погрешности значительно больше и расхождение между расчётными и опытными данными может достигать 40% . Исходными данными для проектирования являются следующие данные: полезная мощность Р н , Вт; номинальное напряжение U н , В; частота вращения n н , об/мин; способ возбуждения - последовательное, параллельное, постоянные магниты; режим работы - продолжительный, кратковременный, повторно-кратковременный; исполнение - закрытое, защищённое. Расчётный формуляр проектируемой машины должен содержать: исходные данные для проектирования, данные расчётов и графическую часть. Последняя включает в себя общий вид и разрез машины, эскиз листа статора и якоря, эскиз паза в разрезе с обмоткой и изоляцией, развёрнутую схему обмотки якоря, рабочие характеристики ЭМ. Расчёт габаритов, параметров и величин, характеризующих МПТ, производится с использованием системы СИ. 1. ОСНОВНЫЕ РАЗМЕРЫ МАШИНЫ Для уменьшения магнитных потерь магнитопровод якоря МПТ малой мощности набирается из штампованных листов электротехнической стали толщиной 0,2, 0,35 и 0,5 мм. Размеры якоря определяются мощностью машины, частотой вращения и режимом её работы. 1. Для определения размеров якоря используют расчётную (электромагнитную) мощность, которая зависит от ЭДС обмотки якоря. Для двигателя постоянного тока
где Е , I a - ЭДС и ток якорной обмотки; U - напряжение, подводимое к двигателю; DU щ - падение напряжения в щётках; Р н - номинальная мощность двигателя; hн - номинальный КПД двигателя; DР м ,DР щ - потери в якорной цепи и щётках двигателя при номинальном токе. Потери в обмотке якоря и щётках для длительного режима можно принять равными 2/3 общих потерь двигателя:
где DРS - суммарные потери двигателя. В этом случае расчётная мощность двигателя определяется следующим выражением:
В электродвигателях повторно-кратковременного или кратковременного режимов работы потери в меди обмотки и щётках составляют в среднем около 3/4 общих потерь. Поэтому для определения расчётной мощности используется формула
В генераторах постоянного тока продолжительного режима потери в обмотке якоря и щётках составляют в среднем около половины общих потерь. Расчётная мощность для этих машин может быть рассчитана по формуле
где I в - ток возбуждения генератора. Это выражение обычно преобразовывают к виду
Значения КПД двигателя и генератора в зависимости от мощности и режима работы представлены в табл. 1. Таблица 1 Значения КПД машин постоянного тока, %
Приведённые величины КПД являются ориентировочными и слабо влияют на габариты МПТ. Более точные значения КПД получаются после полного её расчёта. 2. Величина тока якоря рассчитывается по следующим выражениям: а) для двигателя последовательного возбуждения
б) для двигателя параллельного возбуждения
в) для генератора параллельного возбуждения
Предварительное значение тока возбуждения может быть принято равным 10 - 20% от величины полного тока, причём большее значение - для машин меньшей мощности. ЭДС обмотки якоря рассчитывается через ранее найденную расчётную мощность:
3. Машинную постоянную рассчитывают по уравнению
где a- коэффициент полюсной дуги, a = 0,6 - 0,7; В d - магнитная индукция в воздушном зазоре, Тл; AS - линейная нагрузка якоря, А/м. Величины магнитной индукции и линейной нагрузки зависят от мощности и скорости вращения якоря машины. Ориентировочные значения этих величин представлены в табл. 2. Магнитная индукция и линейная нагрузка определяют габариты машины: чем больше эти величины, тем меньше её размеры. Однако при чрезмерных значениях магнитной индукции происходит сильное насыщение участков магнитопровода машины, возрастает МДС обмотки возбуждения и, следовательно, увеличиваются размеры машины. Кроме того, происходит интенсивный нагрев магнитопровода и снижение КПД машины. Таблица 2Магнитная индукция и линейная нагрузка для машин постоянного тока малой мощности
При чрезмерных значениях линейной нагрузки увеличивается реактивная ЭДС коммутируемых секций, что вызывает ухудшение коммутации МПТ. Помимо этого значительно возрастает поток поперечной реакции якоря, вследствие чего может произойти перемагничивание полюса. Для исключения этого явления приходится увеличивать воздушный зазор машины и габариты обмотки возбуждения. Для крупных МПТ значения магнитной индукции составляют 0,5-1,0 Тл, линейной нагрузки - до 10000 - 60000 А/м. Отношение длины якоря lo к его диаметру Da изменяется в широком диапазоне:
Если рассчитывается серия машин с одним и тем же диаметром, то величина этого отношения может достигать 2,0 - 2,5. Чаще всего x принимается равным 0,8 - 1,2. При выборе величины x необходимо учитывать, что в коротких машинах уменьшается величина реактивной ЭДС и, следовательно, улучшаются условия коммутации. Однако, исходя из экономических соображений, относительную длину якоря стремятся увеличить, так как стоимость коллектора и подшипников практически не зависит от длины машины, а минимум меди якорной обмотки достигается при приближении x к 1,5. Если же машина должна иметь пониженный момент инерции якоря, то относительную длину приходится принимать выше указанного значения. Выбрав величину x, рассчитывают диаметр якоря:
Тогда длина якоря
Полученные значения округляют до ближайшего стандартного типоразмера (прилож., табл. 1). 4. Окружная скорость вращения якоря
Окружная скорость якоря МПТ малой мощности может достигать 20 - 25 м/с. 5. Полюсное деление
В машинах малой мощности число полюсов принимается, как правило, равным двум. При мощностях Р н ³ 200 Вт магнитную систему выгоднее выполнять четырёхполюсной. При этом уменьшается поток полюса, и, следовательно, сечение, и масса магнитопровода машины. Уменьшается также масса меди якоря из-за уменьшения длины лобовых частей якорной обмотки. В результате этого снижается расход активных материалов машины. Вместе с тем с увеличением числа полюсов возрастает трудоёмкость изготовления машины вследствие уменьшения размеров её деталей. Кроме того, увеличивается напряжение между коллекторными пластинами, что обусловливает необходимость увеличения числа коллекторных пластин и диаметра коллектора. Тем не менее, в настоящее время наметилась тенденция к выполнению четырёхполюсных машин даже при сравнительно малых мощностях. Расчётная полюсная дуга
Увеличение коэффициента расчётной полюсной дуги a приводит к уменьшению габаритов машины. При этом, однако, уменьшается межполюсное расстояние, что может привести к увеличению магнитного поля от главных полюсов в зоне коммутации и ухудшению процесса коммутации. 6. Частота перемагничивания стали якоря
7. Воздушный зазор МПТ малой мощности выбирается минимально возможным. Однако для того чтобы магнитное поле не изменяло знака на протяжении полюсной дуги, необходимо выполнение следующего условия:
где F d н и F z н - МДС воздушного зазора и зубцовой зоны МПТ при номинальном токе. Принимая ориентировочно
и учитывая соотношения, связывающие МДС и магнитную индукцию в воздушном зазоре, получим: для электродвигателей с продолжительным режимом работы
для электродвигателей с кратковременным режимом работы
для генераторов
2. ПАРАМЕТРЫ ОБМОТКИ ЯКОРЯ В МПТ малой мощности применяются простые петлевые обмотки при 2р = 2 и простые волновые при 2р = 4. Кроме того, для машин малой мощности весьма перспективно применение постоянных магнитов, позволяющих уменьшить потребляемую из сети мощность за счёт отсутствия тока возбуждения, повысить КПД, а в ряде случаев уменьшить габариты машины. 8. Полезный поток одного полюса машины
9. Число проводников обмотки якоря
где а - число параллельных ветвей якорной обмотки машины (для машин малой мощности обычно, а = 1). 10. При выборе числа пазов необходимо руководствоваться следующим. Слишком малое число пазов приводит к значительным пульсациям ЭДС машины, а слишком большое число - к уменьшению ширины зубцов и их насыщению. Необходимо учитывать также, что увеличение числа зубцов приводит к нерациональному использованию площади паза, так как при уменьшении размеров пазов площадь, занимаемая изоляцией, остаётся прежней. Предпочтение отдаётся нечётному числу, в этом случае уменьшаются пульсации поля под полюсами, вызывающие появление переменной ЭДС, ухудшающей коммутацию. Однако при нечётном числе пазов становится затруднительной машинная намотка якоря. Для МПТ малой мощности число пазов якоря Z = (3 ¸ 4) D a , (2.3) где диметр якоря измерен в сантиметрах. 11. Число коллекторных пластин выбирается равным числу элементарных пазов исходя из соотношения: K = Z Э = u П Z , (2.4) где u П - число элементарных пазов в реальном пазу, выбирается таким образом, чтобы среднее напряжение между коллекторными пластинами не превышало допустимого значения:
Обычно u П = 2 - 3. В случае волновой обмотки при нечётном числе пазов якоря u П должно быть числом нечётным, так как только при этом условии возможно выполнение симметричной обмотки с целым шагом. 12. Число витков в секции обмотки якоря
Число витков в секции должно быть целым. Поэтому рассчитанное по (2.5) значение округляется, а число проводников обмотки якоря соответствующим образом корректируется. Окончательные значения u П и W с принимаются после проверки коммутации, т.к. величина реактивной ЭДС, определяющей характер процесса коммутации, пропорциональна числу Wс . 13. Для простой петлевой обмотки шаги обмотки якоря
для простой волновой обмотки
После определения параметров якорной обмотки составляется таблица обхода и вычерчивается её схема. 14. Линейная нагрузка якоря принимается с учётом скорректированного числа проводников обмотки якоря
Полученная величина линейной нагрузки не должна отличаться от ранее принятой более чем на 5%. В противном случае в качестве исходного значения AS принимается найденное по (2.7) и производится повторный расчёт. 3. РАЗМЕРЫ ЗУБЦОВ, ПАЗОВ И ПРОВОДНИКОВ ОБМОТКИ ЯКОРЯ В МПТ малой мощности часто используются пазы круглой, овальной и трапецеидальной формы. Наиболее технологичны и просты в изготовлении пазы круглой формы. Поэтому, если площадь круглого паза соответствует расчёту, то при всех прочих равных условиях предпочтение отдаётся круглому пазу. Овальная и трапецеидальная формы паза увеличивают его площадь по сравнению с пазом круглой формы при том же диаметре якоря. Площадь паза якоря зависит от количества и сечения проводников обмотки якоря. В свою очередь, сечение проводника определяется величиной тока якоря и его допустимой плотностью, которая зависит от режима работы машины, способа охлаждения, класса изоляции, коэффициента теплоотдачи. 15. Интенсивность нагрева МПТ определяется удельной тепловой нагрузкой (Вт/м2 ), которая для продолжительного режима записывается в виде q = QM a (1 + 0,1 V ), (3.1) где QM - предельно допустимое превышение температуры корпуса над температурой окружающей среды, определяемое классом изоляции. Температура окружающей среды принимается при расчётах равной 400 С; a- коэффициент теплоотдачи поверхности якоря в неподвижной среде, составляющий в среднем 14 - 18 Вт/(К м2 ) для машин закрытого исполнения без вентилятора и 36 - 44 Вт/(К м2 ) для машин защищённого исполнения с встроенным вентилятором; V - окружная скорость якоря в машинах без вентилятора, V = V a . Работа встроенного вентилятора приводит к увеличению потока охлаждающего воздуха и, следовательно, к увеличению скорости его движения V : V = (V a 2 + V в 2 )1/2 , (3.2) где V в - окружная скорость лопаток вентилятора, V в = pD в n н / 60; (3.3) D в - диаметр колеса центробежного вентилятора, D в = (1,25 ¸ 1,4) D a . Удельная тепловая нагрузка для кратковременного режима работы
здесь t р - время работы двигателя, с; T р - постоянная времени нагрева вращающегося якоря, с ,
Для МПТ, работающих в повторно-кратковременном режиме,
где функция Y(t р /T р ) определена зависимостью времени работы машины и паузы: Y(t р /T р ) = 1+ exp ( -а 1 t р / T р ) + exp ( -2 а 1 t р / T р ) +¼ + ¼ exp[- (n -1) а 1 t р / T р ], (3.8) где n - число циклов работы;
Т П - постоянная времени охлаждения неподвижного якоря, с; t П - время паузы, с. 16. Выражая потери в якорной цепи машины через линейную нагрузку и плотность тока в проводниках обмотки, можно получить выражение плотности тока при заданной линейной нагрузке и допустимом превышении температуры QM : а) для МПТ при 2р = 2 и n < 5000 об/мин
при 5000 £n £ 10000 об/мин
при 10000 £n £ 15000 об/мин
б) для МПТ при 2р = 4 и при n < 5000 об/мин
при 5000 £n £ 10000 об/мин
при 10000 £n £ 15000 об/мин
17. Предварительное сечение проводников обмотки якоря
По полученному сечению рассчитывается диаметр провода (выбирается ближайшее его значение), марка и необходимый класс изоляции (прилож., табл. 2). Для выбранного провода определяется сечение и реальная плотность тока в якорной обмотке. 18. Предварительная величина площади паза якоря
где N п - число проводников в пазу якоря, N п = N / Z ; (3.18) S a .из - сечение изолированного проводника якорной обмотки, S a .из = pd из 2 / 4, (3.19) d из - диаметр изолированного проводника обмотки якоря; К з.п - коэффициент заполнения паза, предварительное значение которого принимается равным 0,30 - 0,46. При меньших значениях К з.п заполнение паза будет ²рыхлым², т.е. проводники обмотки будут подвижными. При больших значениях К з.п выполнение обмотки становится невозможным, т.е. в пазу не удаётся разместить необходимое число проводников. 19. Размеры паза и зубцов. Рассчитав площадь паза, необходимо определить его размеры. Поскольку наиболее технологичным является круглый паз, проверяется возможность его реализации. Диаметр круглого паза d п = (4 S п / p )0,5 . (3.20) Кроме того, необходимо учесть наличие щели паза, через которую производится укладка проводников обмотки. Высота щели h щ обычно не превышает 1,0 - 1,5 мм, а её ширина b щ = (2 - 8)d из , причём больший размер для более тонких проводов. Приняв указанные размеры и определив число пазов и их диаметр, рисуют в масштабе эскиз листа якоря (рис.1). Если необходимое число пазов удаётся разместить на листе якоря, то определяют размеры зубцов для трёх сечений. Зубцовое деление якоря tZ = pD a / Z . (3.21) Максимальная ширина зубца bZ 1 = tZ -b щ . (3.22) Ширина зубца в основании паза
Рис.1. Пазы якоря круглой формы Ширина паза в среднем сечении
Минимальную ширину зубца желательно проверить по величине магнитной индукции в этом сечении, исходя из того, что весь поток зубцового деления проходит через зубец:
где K з.с - коэффициент заполнения стали. Его величина зависит от толщины листа и вида изоляции. Для современных сталей величина K з.с =0,95-- 0,97 (прилож., табл. 4). Максимальная величина магнитной индукции в зубцах МПТ малой мощности не превышает 1,8 Тл, а ширина зубцов якоря по технологическим условиям штамповки должна быть не менее 1,5 мм.
На практике чаще всего реализовать круглый паз необходимой площади не удаётся. Поэтому наиболее распространены пазы якоря овальной или трапецеидальной формы (рис.2), позволяющие получать значительные площади паза при небольшой его ширине. Важным достоинством пазов указанной формы является постоянная ширина зубцов якоря, которая, как и в предыдущем случае, должна быть не менее 1,5 мм. Рис.2. Пазы якоря трапецеидальной формы Ширина зубца может быть рассчитана исходя из допустимых значений магнитной индукции Bz по выражению (3.25). Для определения размеров паза в крупном масштабе изображается лист якоря. При известном числе пазов окружность якоря разбивается на соответствующее число секторов, по осям которых в том же масштабе изображаются зубцы якоря необходимой ширины. Ориентировочная высота паза рассчитывается по выражению h п = (D а -d в - 2 h a ), (3.26) h п = (0,22 ¸ 0,3) D а . Диаметр вала МПТ d в = (0,18 ¸ 0,24) D а . Высота спинки якоря выбирается из допустимых значений магнитной индукции на этом участке:
где Ва - магнитная индукция в спинке якоря, максимальная величина которой не должна превышать 1,5 Тл. Таким образом, задаваясь величинами диаметра вала, спинки якоря и зная диаметр якоря, можно уточнить высоту паза h П . Максимальная и минимальная ширина овального паза может быть приближённо рассчитана по следующим выражениям:
а высота средней части паза h
12
= h
п
-h
щ
- По рисунку паза рассчитывается его площадь, которая корректируется исходя из условия размещения проводников в пазу. Так для трапецеидального паза
После этого можно уточнить размеры зубца якоря, в частности его ширину. Увеличение ширины зубца приводит к уменьшению его магнитной индукции, следовательно, уменьшению потерь в стали зубцов, уменьшению МДС обмотки возбуждения, её веса и габаритов. 20. При 2р =2 средняя длина проводников обмотки якоря l a = l 0 + 1,2 D a ; (3.32) при 2р =4 l a = l 0 + 0,8 D a . (3.33) 21. В нагретом состоянии сопротивление обмотки якоря
В этом выражении gM = 57 × 106 (Ом×м)-1 - электропроводность меди при температуре окружающей среды. Температурный коэффициент меди K Q = 1 + 0,004 (Q-Qокр ), (3.35) где Q- рабочая температура; Qокр - температура окружающей среды, Qокр = 20 0 С. 22. Падение напряжения в обмотке якоря DU a = I a R a . (3.36) Величина DU a составляет обычно 10 - 20% от номинального напряжения. Меньшие значения относятся к машинам с высокими номинальными напряжениями U ан >110 В, работающим в длительном режиме. 4. КОЛЛЕКТОР И ЩЁТОЧНЫЙ АППАРАТ В настоящее время коллекторы машин малой мощности выполняются чаще всего с пластмассовой изоляцией. Коллекторные пластины изготовляются из твёрдотянутой меди трапецеидального сечения с впадинами в виде «ласточкина гнезда» (рис. 3). В некоторых конструкциях коллекторные пластины изолируются друг от друга миканитовыми прокладками толщиной 0,6 - 0,8 мм, чаще для изоляции используется та же пластмасса, что и для крепления коллекторных пластин. Более совершенными технологиями изготовления коллекторов являются малоотходные, с использованием цельных заготовок из листов меди или медного порошка. Толщина кольца коллектора выбирается с учётом износа коллектора и дальнейшей его проточки и составляет DК = (0,1¸0,2) D K .
Рис.3. Коллектор машины постоянного тока Коллектор должен быть изолирован от вала машины. Для этой цели также используется изолирующая пластмасса. Щётки и прижимные пружины размещаются в трубчатых или коробчатых щёткодержателях. Различают радиальные и реактивные щёткодержатели. В радиальных щёткодержателях щётка располагается перпендикулярно поверхности коллектора, в реактивных - под некоторым углом по ходу вращения коллектора, обеспечивая при этом более надёжный контакт. Реактивные щёткодержатели обычно применяются в нереверсивных МПТ, имеющих одно направление вращения. 23. Предварительный диаметр коллектора D K = (0,5 ¸ 0,9) D a . 24. В машинах малой мощности ширина коллекторной пластины b K принимается равной 2-5 мм. Толщина изоляции между коллекторными пластинами b из = 0,6 -0,8 мм. Коллекторное деление
Для правильно спроектированного коллектора должно выполняться соотношение t к = b к + b из . (4.2) Ширина коллекторной пластины при этом должна соответствовать ГОСТ 4134-75. Определив t к , уточняют диаметр коллектора, используя выражение (4.1). Окружная скорость коллектора V к = pD к n / 60. (4.3) 25. В МПТ малой мощности для улучшения коммутации наиболее часто используются твёрдые медно-графитовые или электрографитированные щётки, которые меньше подвержены износу, что увеличивает надёжность работы машины. Размеры щёток выбираются исходя из допустимой для каждого типа щёток плотности, которая лежит в широких пределах: 4,0 - 20,0 А/см2 (наиболее часто 10,0 -15,0 А/см2 ). Тогда, выбрав тип щёток и определив допустимую для них плотность тока J щ , можно рассчитать площадь щётки:
С другой стороны, S щ = а щ b щ , (4.5) где a щ - осевая ширина щётки; b щ - ширина щётки по окружности коллектора, ориентировочно принимает- ся b щ = (2 ¸ 3) b к . Выбрав стандартный размер ширины щётки b щ (ГОСТ 122322.1-77), определяют осевой размер щётки а щ , удовлетворяющий необходимой площади. Осевая длина щётки также должна соответствовать указанному стандарту. После определения размеров щёток уточняют получаемую при этом плотность тока, используя выражение (4.4). Величина плотности не должна превосходить допустимого значения для выбранного типа щёток. 26. Активная длина коллектора по оси вала l ¢к = (1,5 ¸ 2,0) ащ . Полная длина коллектора l к = l ¢к + (3 ¸ 5) da , где da - диаметр проводника обмотки якоря без изоляции. 27. Проверка коммутации. В МПТ малой мощности добавочные полюса не выполняются, а щётки устанавливаются строго на линии геометрической нейтрали. Вследствие этого в коммутируемых секциях наводится реактивная ЭДС еR и ЭДС от поля реакции якоря е а , которая также замедляет процесс коммутации. Наличие этих ЭДС приводит к увеличению плотности тока под сбегающим краем щёток и, следовательно, к повышенному искрению. Интенсивность искрения зависит от величины суммарной ЭДС в коммутируемой секции
которая не должна превосходить определённого значения. Среднее значение реактивной ЭДС в коммутируемой секции определяется выражением еR = 2 WС lAS l 0 V a . (4.6) Удельная магнитная проводимость потоков рассеяния l для пазов овальной и трапецеидальной формы определяется выражением
где b П1 и b П2 - максимальная и минимальная ширина паза. ЭДС от реакции якоря при установке щёток на линии геометрической нейтрали
где da - средняя длина магнитной силовой линии в межполюсном пространстве,
Для благоприятной коммутации МПТ малой мощности необходимо, чтобы величина результирующей ЭДС е р в коммутируемой секции не превышала 1,5 В. В случае невыполнения этого условия необходимо либо уменьшить число витков в секции, либо уменьшить величину линейной нагрузки, сохранив при этом габариты машины за счёт увеличения магнитной индукции в воздушном зазоре. На процесс коммутации может оказывать влияние магнитное поле полюсов, величина которого в зоне коммутации теоретически должна быть равной нулю. Однако если ширина зоны коммутации близка к расстоянию между полюсными наконечниками соседних полюсов, то в зоне коммутации будет ощущаться влияние их магнитного поля. Для того чтобы исключить это влияние, необходимо ограничить ширину коммутационной зоны b к до определённых размеров:
где b ¢ щ - ширина щётки, приведённая к окружности якоря,
t ¢ к - коллекторный шаг, приведённый к диаметру якоря,
Для благоприятной коммутации необходимо b к £ 0,8 (t-b 0 ). (4.13) 5. МАГНИТНАЯ СИСТЕМА МАШИНЫ ПОСТОЯННОГО ТОКА Магнитопровод МПТ малой мощности изготовляется чаще всего шихтованным из электротехнической стали, причём полюса выполняются заодно с ярмом статора. Значительно реже магнитопровод статора изготовляется сплошным из труб малоуглеродистой стали. Полюса машины в этом случае изготовляются отдельно, также из мягкой малоуглеродистой стали. В последнее время полюса прессуются из порошковых ферромагнитных материалов. Магнитопровод якоря для уменьшения потерь во всех случаях выполняется шихтованными из малокремнистых электротехнических сталей. 28. Определение геометрических размеров. Воздушный зазор: d¢ = К d d, (5.1) где K d - коэффициент воздушного зазора (коэффициент Картера),
Высота сердечника полюса h пл предварительно принимается равной (0,24 ¸ 0,4) D а . Полученное значение h пл должно быть уточнено после расчёта обмотки возбуждения исходя из необходимой площади окна для размещения обмотки. Осевая длина полюса для МПТ малой мощности обычно равна длине якоря: l пл = l 0 . Магнитная индукция в сердечнике полюсов принимается равной 1,2 - 1,5 Тл для машин, работающих в длительном режиме, и 1,4 - 1,6 Тл для машин с кратковременным режимом работы. Исходя из этих значений, рассчитывается сечение сердечника полюса
где s- коэффициент рассеяния магнитного потока с учетом того, что помимо основного магнитного потока по сердечнику полюса проходит поток рассеяния. Величина этого коэффициента составляет 1,08 - 1,12. Рассчитав площадь сердечника полюса, определяют его ширину:
Если полюс выполнен сплошным, то коэффициент заполнения стали K з.с = 1,0. Сечение магнитопровода станины рассчитывается исходя из допустимых значений магнитной индукции B
ст
на этом участке, которые принимаются равными 1,2 - 1,4 Тл для длительного режима работы машины и до 1,5 Тл для кратковременного режима.
Большие значения индукции рекомендуются для машин с кратковременным режимом работы. Высота сердечника станины
Длина станины l ст принимается равной длине якоря для машин с шихтованной станиной и l ст = l 0 + (3 - 5) мм для машин с отъёмными полюсами. Для станин из литой стали K з.с = 1,0.
29. Расчёт МДС машины постоянного тока. МДС воздушного зазора
МДС зубцовой зоны рассчитывается исходя из предположения,что весь магнитный поток зубцового деления проходит через зубец. Если при этом использованы пазы прямоугольной формы, то ширина зубцов оказывается переменной и магнитная индукция в различных сечениях различна. В этом случае расчёт МДС производится для трёх различных сечений зубца - максимального, среднего и минимального:
Рассчитав значения магнитных индукций, по кривым намагничивания выбранного сорта электротехнической стали (прилож., табл. 5 - 13) определяют соответствующие значения напряжённостей магнитного поля При расчёте МДС зубцов необходимо скорректировать их ширину таким образом, чтобы максимальная величина магнитной индукции МДС зубцовой зоны определяется по формуле Симпсона:
Здесь принято, что высота зубца равна высоте паза. Для машин малой мощности чаще всего используются пазы овальной или трапецеидальной формы. В этом случае ширина зубца во всех сечениях одинакова и расчёт значительно упрощается, так как магнитная индукция и напряжённость магнитного поля в любом сечении зубца оказываются одинаковыми:
AWZ = 2 HZ h п . (5.13) МДС сердечника якоря. Уточнённое значение магнитной индукции в сердечнике якоря
По рассчитанному значению магнитной индукции и кривой намагничивания электротехнической стали определяется величина напряжённости магнитного поля в спинке якоря и МДС этого участка: AW a = H a L a , (5.15) где средняя длина магнитной силовой линии
Величина магнитной индукции в сердечнике полюса уточняется по выражению:
По кривой намагничивания материала полюсов и полученному значению магнитной индукции определяется напряжённость магнитного поля и рассчитывается величина МДС полюсов машины: AW пл = 2 H пл h пл . (5.18) МДС станины . Магнитная индукция в станине
Средняя длина магнитной силовой линии в станине
По рассчитанному значению магнитной индукции В ст и кривой намагничивания материала станины определяется напряжённость магнитного поля H ст и соответствующая МДС: AW ст = H ст L ст . (5.21) Если полюса выполнены отъёмными, то между станиной и сердечником полюса существует воздушный зазор dст = (0,035 ¸0,05) мм. В этом случае необходимо определить МДС этого зазора:
Результирующая МДС машины на пару полюсов в режиме холостого хода AW в = AW d + AW z + AW a + AW пл + AW ст + AW d ст . (5.23) 30. Характеристика холостого хода (х.х.х) МПТ - это зависимость ЭДС обмотки якоря от МДС возбуждения (или тока возбуждения) при неизменной частоте вращения и отсутствии тока якоря. Расчёт х.х.х производится в такой последовательности: - задаются произвольными значениями ЭДС якорной обмотки Е ; - рассчитываются соответствующие значения магнитного потока
- рассчитываются соответствующие значения магнитной индукции в воздушном зазоре с использованием выражения (2.1); - рассчитываются значения МДС для всех участков магнитной цепи и суммарная МДС возбуждения на пару полюсов в соответствии с выражениями п.29. Производимые расчёты сводятся в таблицу (табл. 3, по данным которой строится зависимость Е = f (AW в ) - х.х.х.). 31. МДС реакции якоря. При работе МПТ под нагрузкой по обмотке якоря протекает ток и вокруг проводников обмотки создаётся магнитное поле, называемое полем якоря. Рабочие характеристики МПТ определяются результирующим магнитным полем в зазоре машины, т.е. зависят и от поля якоря. Воздействие магнитного поля якоря на основное поле машины, создаваемое обмоткой возбуждения, называют реакцией якоря. Для учёта магнитного поля якоря его МДС представляют в виде суммы двух составляющих МДС поперечной и продольной реакции якоря. Таблица 3Расчёт характеристики холостого хода МПТ
Кроме того, на магнитное поле машины оказывают действие коммутационные токи, протекающие в секциях якоря при переключении их из одной параллельной ветви в другую. МДС коммутационных токов проявляется при замедленной или ускоренной коммутации и носит продольный характер. Поперечная МДС при ненасыщенной машине искажает магнитное поле, не изменяя его величины. При насыщении машины МДС поперечной реакции якоря ослабляет магнитное поле. Поскольку МПТ работают, как правило, с той или иной степенью насыщения, можно считать, что поперечная реакция якоря имеет размагничивающий характер независимо от режима работы МПТ (двигательный или генераторный). При установке щёток строго на линии геометрической нейтрали продольная МДС якоря теоретически равна нулю. Однако в реальных машинах установить щётки на линии геометрической нейтрали не удаётся; они оказываются смещёнными по ходу вращения машины. Вследствие этого появляется незначительная продольная МДС, которая, как правило, носит намагничивающий характер в двигателях и размагничивающий в генераторах. Процесс коммутации в МПТ без добавочных полюсов оказывается замедленным, коммутационная МДС носит продольный характер, т.е. намагничивает машину в режиме двигателя и размагничивает в режиме генератора. Поскольку обмотка возбуждения должна скомпенсировать поле реакции якоря,то МДС реакции якоря рассчитывается следующим образом: для двигателей: AWR = AW аq -AW ad - АW к , (5.25) для генераторов AWR = AW аq + AW ad +АW к , (5.26) где AW аq - МДС поперечной реакции якоря; AW ad - МДС продольной реакции якоря; АW к - коммутационная МДС. Так как поперечный магнитный поток замыкается через зубцовую зону и воздушный зазор машины, для определения поперечной реакции якоря используется переходная кривая намагничивания (рис. 5): В d = f (AW d + AW z ) / 2, которая строится по данным табл. 3. На этой кривой по оси ординат откладывается номинальная величина магнитной индукции в воздушном зазоре (точка а) и определяется соответствующая номинальная МДС (точка б). Влево и вправо от этой точки в масштабе МДС откладываются отрезки бв и бг, изображающие МДС поперечной реакции якоря:
Рис.5. Переходная характеристика машины постоянно- го тока Так как величины отрезков бв и бг пропорциональны величине расчётной полюсной дуги, а ординаты пропорциональны магнитной индукции, то площади криволинейных треугольников аде и аgк представляют соответственно уменьшение магнитного потока от реакции якоря под одним краем полюса и его возрастание - под другим. Разница площадей этих треугольников определяет уменьшение магнитного потока машины вследствие действия поперечной реакции якоря. Для компенсации этого размагничивающего действия необходимо увеличить МДС обмотки возбуждения на определённую величину, которая определяется следующим образом. Прямоугольник сдвигается вправо таким образом, чтобы площади полученных криволинейных треугольников амf и аpn стали равными. Тогда величина МДС на пару полюсов, компенсирующая поперечную реакцию якоря, определяется выражением AW aq = 2 mn . Эта величина может быть найдена и другим способом. Выражая площади криволинейных треугольников и приращений потоков по формуле Симпсона и приравнивая полученные выражения, можно определить величину МДС поперечной реакции якоря:
МДС продольной реакции якоря зависит от сдвига щёток с линии геометрической нейтрали и определяется выражением A W аd = 2 b b AS , (5.29) где b b - сдвиг щёток с линии геометрической нейтрали вследствие неточности изготовления машины, b b = 0,15 - 0,3 мм. Продольная коммутационная МДС, возникающая при замедленной коммутации, определяется величиной коммутирующего тока, индуктивностью коммутируемых секций, переходным сопротивлением щёток и угловой скоростью якоря. Величина коммутационной МДС при номинальном токе машины и номинальной частоте вращения может быть приближённо рассчитана по следующей формуле:
где b к - ширина коллекторной пластины; AS н - линейная токовая нагрузка при номинальном токе якоря; К к - коэффициент, учитывающий падение напряжения в щётках
Полная МДС возбуждения МПТ при нагрузке AW
å
НАГР
= AW
d
+ AW
z
+ AW
a
+ AW
пл
+ AW
ст
+ Для двигателей и генераторов параллельного возбуждения вначале определяется ЭДС якоря для электродвигателей Е = U -DU a -DU щ (5.33) и для генераторов Е = U +DU a + DU щ . (5.34) По кривой холостого хода определяется результирующая МДС -AW ’ S НАГР соответствующая найденному значению ЭДС, после чего рассчитывается полная МДС с учётом реакции якоря: AW S НАГР = AW S НАГР + AWR . (5.35) 6. РАСЧЁТ ОБМОТКИ ВОЗБУЖДЕНИЯ 6.1. Электродвигатель последовательного возбуждения 32. Число витков обмотки возбуждения на один полюс
33. Предварительное сечение обмоточного провода для обмотки возбуждения S в = I a / j в , (6.2) где jВ - плотность тока в обмотке возбуждения, выбираемая в зависимости от номинального момента Мн по данным табл. 4. Мн = 9,55 Р н /n н . (6.3) Рассчитав сечение провода, выбирают номинальное сечение и диаметр провода в соответствии с ГОСТом, а затем уточняют реальную величину плотности тока возбуждения: j в = I a / S в . (6.4) 34. Сопротивление обмотки возбуждения в нагретом состоянии
где l ср - средняя длина витка обмотки возбуждения, которая определяется по эскизу расположения обмотки на сердечнике полюса.При неотъёмных полюсах машины среднюю длину витка необходимо увеличить на величину (b 0 -b пл ), с тем чтобы была возможность надеть катушку обмотки возбуждения на сердечник полюса через полюсный наконечник. 35. Падение напряжения в обмотке возбуждения DU в = I a R в . (6.6) 36. Величина ЭДС якоря двигателя последовательного возбуждения при нагрузке E = U H -DU a -DU щ -DU в . (6.7) Таблица 4 Плотность тока в обмотке возбуждения МПТ малой мощности (´106 А/м2 )
Полученная величина ЭДС не должна отличаться от предварительно выбранного значения более чем на 3%. При большей разнице необходимо скорректи- ровать число витков обмотки возбуждения. Для этого определяют МДС обмотки возбуждения по характеристике холостого хода и найденному значению ЭДС, прибавляют МДС реакции якоря при номинальной нагрузке, уточняют число витков обмотки возбуждения, её сопротивление, падение напряжения и новое значение ЭДС машины E a . 37. Площадь окна для размещения обмотки возбуждения
где f о - технологический коэффициент, учитывающий промежутки между проводниками и изоляцию провода, f о = 0,8 - 0,84. Фактическая площадь окна для обмотки возбуждения должна быть увеличена на 10 - 20 % для учёта возможных неточностей намотки. Исходя из полученного значения площади окна уточняют высоту сердечника полюса и определяют ширину стороны катушки возбуждения с таким расчётом, чтобы обмотка возбуждения свободно размещалась в окне между станиной и полюсным наконечником. 6.2. МПТ с независимым возбуждением Расчёт обмотки возбуждения в этом случае производится в такой последовательности: 38. Задаются величиной тока возбуждения I в » (5 ¸ 10)% I a . Большие значения тока принимаются для машин меньшей мощности. Исходя из режима работы МПТ и её исполнения, по данным табл. 4 выбирается величина допустимой плотности тока в обмотке возбуждения j в . После этого рассчитывают сечение провода обмотки возбуждения по выражению S ¢ в = I в / j в . (6.9) По найденному значению S ¢ в выбирается марка, сечение и диаметр провода обмотки возбуждения, соответствующего ГОСТу. 39. Зная МДС возбуждения для номинального режима работы AW å НАГР , рассчитывают число витков обмотки возбуждения на один полюс:
40. По выражению (6.5) рассчитывается сопротивление обмотки возбуждения в нагретом состоянии, а исходя из номинального напряжения сети - уточнённые значения тока возбуждения и его плотности, которая должна быть близкой к принятому ранее значению. Площадь окна, необходимую для размещения обмотки возбуждения, рассчитывают так же, как и для машин с последовательным возбуждением. 7. ПОТЕРИ И КПД МАШИНЫ ПОСТОЯННОГО ТОКА В МПТ различают следующие виды потерь: - потери в обмотках якоря и возбуждения; - потери в щётках; - потери в стали якоря; - механические потери; - добавочные потери. 41. Потери в обмотках якоря и возбуждения рассчитываются следующим образом: для МПТ с последовательным возбуждением DР ма = I а 2 R a ; (7.1) DР мв = I а 2 R в ; (7.2) для машин с параллельным возбуждением DР мв = U H I в . (7.3) 42. Потери в щётках DР щ = DU щ I а . (7.4) 43. Потери в стали якоря включают в себя потери в сердечнике якоря и потери в зубцах якоря. Масса стали якоря G с.а = 7800 [p (D а -2 h п )2 l о ]/ 4. (7.5) Масса зубцов якоря G с. z = 7800 Z b Z .CP h П l o . (7.6) Потери в стали сердечника якоря DP с.a = p уд B а 2 f 1,3 G с.а . (7.7) Потери в зубцах якоря DP с. z = p уд B z 2 f 1,3 G с. z . (7.8) В этих выражениях удельные потери для данного сорта стали принимаются увеличенными в 1,5 - 1,8 раза. Потери в стали статора DP с = DP с.a + DP с. z . (7.9) 44. Полные механические потери включают в себя потери на трение щеток о коллектор, потери на трение в шарикоподшипниках и потери на трение о воздух. Потери на трение щёток о коллектор DР тр.щ = 9,81 К тр Р щ S щ V к , (7.10) где К тр - коэффициент трения щёток о коллектор,К тр = 0,2 - 0,25. Р щ - удельное нажатие щёток,Р щ = 1,96 - 2,35 Н/м2 для угольных и угольно-графитовых щёток; Р щ = 2,0 - 4,0 Н/м2 для электрографитированных щёток; Р щ = 1,5 - 2,0 Н/м2 для медно-графитовых щёток; Р щ = 1,7 - 2,2 Н/м2 для бронзо-графитовых щёток. S щ - поверхность всех щёток; V к - окружная скорость коллектора. Потери на трение в шарикоподшипниках DР тр.под = К ш G а n × 10-3 . (7.11) Для машин малой мощности с шарикоподшипниками К ш = 1 - 3. Большие значения относятся к машинам меньшей мощности. Масса якоря G а может быть рассчитана по приближённой формуле G а = 1000 p (D a 2 l o ga + D к 2 l к gк ) / 4. (7.12) В этом выражении средняя объёмная масса якоря ga = 7800 кг/м3 , объемная масса коллектора gK = 8900 кг/м3 . Потери на трение о воздух могут быть рассчитаны для машин малой мощности с частотой вращения до 12000 об/мин по формуле DР тр.в = 2 D a 3 n 3 l о 10-6 ; (7.13) при n > 12000 об/мин DР тр.в = 0,3 D a 5 (1 + l o / D a ) n 3 × 10-6 . (7.14) Полные механические потери DР мех = DР тр.щ + DР тр.под + DР тр.в . (7.15) 45. Полные потери в машине DР å = zo (DР ма + DР мв + DР щ + DР с + DР мех ), (7.16) где коэффициент zo = 1,1 - 1,2 учитывает добавочные потери. 46. При номинальной нагрузке КПД для двигателя
КПД для генератора
В выражениях (7.17), (7.18) I Н = I а - для электродвигателей последовательного возбуждения; I Н = I а + I В - для электродвигателей параллельного возбуждения; I Н = I а -I В - для генераторов параллельного возбуждения. Если номинальная мощность электродвигателя Р Н = U H I Н -DР å отличается от заданной, то необходимо пересчитать величину номинального тока якоря: I а = 0,5 А - (0,25 А 2 -В ). (7.19) Для электродвигателей последовательного возбуждения
для электродвигателей параллельного возбуждения
После определения нового значения токанеобходимо пересчитать величины потерь DР ма ,DР МВ ,DР Щ ,DР å , а также рассчитать новое значение КПД двигателя. 47. Рабочие характеристики двигателя постоянного тока. Рабочими характеристиками называются зависимости I = f (M );P 1 = f (M );P 2 = f (M );n = f (M );h = f (M ). Расчёт рабочих характеристик рационально вести в виде таблицы, заполняемой по мере вычисления отдельных величин. Величина электромагнитного момента рассчитывается по выражению
Заполнение таблицы следует начинать с номинального значения тока I H . Суммарную величину реакции якоря принимают пропорциональной току якоря, а величину магнитного потока определяют по кривой намагничивания для каждого значения тока якоря и результирующей МДС с учётом реакции якоря. По данным табл. 5 строятся рабочие характеристики электродвигателя в общих координатных осях (рис. 6). Таблица 5Расчёт рабочих характеристик двигателя постоянного тока
48. Для генератора постоянного тока параллельного возбуждения строится внешняя характеристика - зависимость напряжения от тока нагрузки U = f (I ) при R B = const. Для построения внешней характеристики генератора параллельного возбуждения необходимо иметь характеристику холостого хода Е = f (I B ), которая строится по кривой Е = f (AW B ) при известном числе витков обмотки возбуждения. Совместно с характеристикой холостого хода в тех же осях строится вольт-амперная характеристика цепи возбуждения U B = I B R B . В точке пересечения этих характеристик (рис.7) имеем режим холостого хода, когда ток якоря I a равен нулю, а напряжение равно напряжению холостого хода U 0 . Указанная точка является первой точкой внешней характеристики генератора. С ростом тока якоря возрастает падение напряжения в якорной цепи DU a = I a R a + DU щ и МДС реакции якоря. Эти величины являются катетами прямоугольного треугольника DАВС , называемого характеристическим. Одна из его вершин (точка А ) лежит на характеристике холостого хода, а другая вершина (точка С ) - на вольт-амперной характеристике цепи возбуждения и, кроме того, определяет величину напряжения генератора при заданном токе якоря.
Рис.6. Рабочие характеристики двигателя последователь- ного возбуждения
Рис.7. Внешняя характеристика генератора параллельного возбуждения Внешнюю характеристику строят таким образом: - для номинального тока якоря определяется падение напряжения в якорной цепи DU a = I a R a + DU Щ и ток возбуждения, эквивалентный реакции якоря: AW R / (2 W B ), т.е. катеты характеристического треугольника; - полученный треугольник размещают между кривыми холостого хода и вольт-амперной характеристикой так, чтобы его вершины лежали на этих кривых; - откладывая по координатной оси токов якоря его номинальную величину, а по оси ординат - величину напряжения, равную ординате нижней вершины треугольника, получают следующую точку внешней характеристики, соответствующую номинальному току; - точки внешней характеристики, соответствующие другим значениям тока, находят аналогичным образом при построении характеристических треугольников, стороны которых пропорциональны данным значениям токов. 8. УПРОЩЕННЫЙ ТЕПЛОВОЙ РАСЧЁТ МАШИНЫ ПОСТОЯННОГО ТОКА МАЛОЙ МОЩНОСТИ Потери, выделяемые в элементах электрических машин, превращаются в тепло, которое вызывает их нагрев и рассеивается в окружающее пространство. По мере увеличения температуры деталей машины увеличивается их теплоотдача, в результате чего температура не возрастает до бесконечности, а принимает установившееся значение. В этом случае выделившееся в машине тепло полностью отдаётся в окружающую среду. Величина установившейся температуры определяется мощностью потерь, габаритами машины и должна соответствовать температурной устойчивости изоляции. Поскольку точный учёт всех факторов нагрева и условий теплоотдачи в машинах малой мощности затруднителен, то расчёт превышений температуры элементов машины над окружающей средой производится приближёнными методами. 49. Превышение температуры якоря. При расчётах считается, что всё тепло, выделяющееся в обмотке якоря, передаётся через пазовую изоляцию стали якоря. Поэтому суммарные потери якоря, определяемые потерями в обмотке, стали якоря и потерями от трения о воздух, снимаются охлаждающим воздухом с его поверхности. Среднее превышение температуры обмотки якоря при установившемся режиме определяется выражением
здесь aa - результирующий коэффициент теплоотдачи наружной поверхности якоря, Вт/(м2 × К), aa = a¢ (1 + 01 V a ), (8.2) a’ -коэффициент теплоотдачи наружной поверхности неподвижного якоря, для машин закрытого исполнения a¢ = 14 - 18 Вт/(м2 × К); для машин защищённого исполнения с вентиляцией a¢ = 36 - 44 Вт/(м2 × К); b Z 1 - ширина вершины зубца якоря; b- общая толщина изоляции от меди до стенки паза, b = b1 +b2 , (8.3) где b1 - толщина пазовой изоляции плюс односторонняя толщина изоляции проводника; b2 - эквивалентная межвитковая изоляция проводников в пазу,
здесь m a - число проводников в ряду по средней ширине паза; d a .из - диаметр изолированного проводника; K с - коэффициент, определяемый выражением K с = 1 + 4 (d a / d a .из - 0,4); (8.5) l¢ - коэффициент теплопроводности междувитковой и пазовой изоляции, l¢ = (0,12 - 0,13) Вт/(м ×К); П - периметр паза; w м.a - удельные потери в меди обмотки якоря на единицу длины,
w с.a - удельные потери в стали якоря на единицу его длины,
w ТР.В - удельные потери трения якоря о воздух на единицу длины якоря,
50. Превышение температуры коллектора. Полные потери в коллекторе DР К = DР Щ + DР ТР.Щ . (8.9) Поверхность охлаждения коллектора S К.ОХ = pD К l К . (8.10) Среднее превышение температуры коллектора над температурой окружающей среды
где aк - коэффициент теплоотдачи коллектора,aк = 40 - 70 Вт/(м2 × К). 51. Превышение температуры обмотки возбуждения. Потери в одной катушке обмотки возбуждения w M.B = DP M.B / 2p . (8.12) Поверхность охлаждения одной катушки обмотки возбуждения для машины с отъёмными полюсами S В.ОХ = 2 (b ПЛ + lПЛ + 4 dК ) h К + 2 (b ПЛ + 2 dК ) dК , (8.13) для машины с шихтованной станиной S В.ОХ = (b 0 + b ПЛ + 2lПЛ + 8 dК ) h К + (b 0 + b ПЛ + 4 dК ) dК . (8.14) В этих выражениях: b ПЛ и lПЛ - ширина и длина сердечника полюса; dК и h К - ширина и высота катушки обмотки возбуждения. Среднее превышение температуры обмотки над температурой окружающей среды
где a0 ¢ - коэффициент теплоотдачи катушек обмотки возбуждения, для машин закрытого исполнения a0 ¢ = 26 - 30 Вт/(м2 × К); для машин защищённого исполнения с вентиляцией a0 ¢ = 52 - 60` Вт/(м2 × К). Рассчитанные значения превышений температуры элементов электрических машин над температурой окружающей среды (QОКР = 400 С) не должны превышать допустимых для выбранного класса изоляции. 9. РАСЧЁТ ПОСТОЯННЫХ МАГНИТОВ ДЛЯ ВОЗБУЖДЕНИЯ МАШИН ПОСТОЯННОГО ТОКА 9.1. Кривые размагничивания постоянных магнитов В МПТ малой мощности перспективно использование постоянных магнитов, позволяющих уменьшить габариты машин и увеличить их КПД. Расчёт МПТ с постоянными магнитами производится теми же методами, что и машин с обмотками возбуждения. Особенностью расчёта является правильный выбор габаритов магнита при известных его параметрах.
ляется между зазором и сердечником магнита. Наличие воздушного зазора эквивалентно размагничивающему действию обмотки с током. Рабочая точка постоянного магнита с зазором оказывается смещённой, занимая положение точки 3 на кривой размагничивания. При повторном намагничивании в силу необратимых процессов, произошедших в магните, намагничивание происходит не по основной кривой, а по частному циклу (точки 3,4). Для расчётов частные циклы заменяются прямой линией, называемой линией возврата (ЛВ). Характер процессов размагничивания магнита определяется величиной МДС размагничивания. При малых значениях МДС размагничивание происходит по линии возврата до точки 3. Если же МДС значительна, то процесс размагничивания вначале происходит по линии возврата до точки 3, а затем - по основной кривой размагничивания (точка 5). Последующие режимы намагничивания в этом случае будут происходить по новой линии возврата, проходящей через точку 5. Магнитная цепь МПТ рассчитывается так, чтобы рабочая точка лежала на середине прямой возврата, а возможные колебания МДС не выводили её за пределы данной линии возврата. Наклон линии возврата определяется магнитной проницаемостью возврата mВ = DВ /DН . (9.1) Значения mВ с достаточной точностью определяются наклоном касательной к кривой размагничивания в точке (В r , 0). Различным точкам на кривой размагничивания соответствуют различные величины удельной энергии магнита: W M = 0,5 B H . (9.2) Зависимость удельной энергии от напряжённости магнита представлена на рис.9. Как видно из рисунка, при некотором значении напряжённости Н о наблюдается максимум удельной энергии в точке А с координатами (В о ,Н о ). Магнитная система должна проектироваться так, чтобы рабочий режим магнита находился вблизи точки максимума. Для расчётов магнитных систем с постоянными магнитами необходимо иметь аналитическое описание кривой размагничивания. Наиболее часто эта зависимость представляется в виде гиперболы:
В этом выражении коэффициент а зависит от формы кривой размагничивания и выражается через коэффициент формы g следующим образом:
где
Рис.9. Удельная энергия постоянного магнита В о и Н о - координаты точки, соответствующие максимуму энергии постоянного магнита на кривой размагничивания. Величина коэффициента формы кривой размагничивания постоянных магнитов 0,25 £g£ 0,9. При g = 0,25 коэффициент а = 0 и гипербола вырождается в прямую
показанную на рис. 10 (кривая 1). При g = 1 коэффициент а = 1 и уравнение гиперболы принимает вид В = В r , т.е. имеем горизонтальную прямую, касательную к кривой размагничивания. При g = 0,5 коэффициент а = 0,8 и гипербола становится близкой к окружности (кривая 3 на рис.10). Коэффициент формы кривой размагничивания определяется материалом постоянного магнита, и для бариевых магнитов g = 0,316 - - 0,390, для метоллокерамики g = 0,36 - 0,64, для сплавов ЮНДК g = 0,5 - 0,9, для магнитов на основе редкоземельных элементов g = 0,27 - 0,3. 9.2. Совместная работа постоянных магнитов с внешней магнитной цепью Простейшая магнитная цепь состоит из постоянного магнита, двух воздушных зазоров и внешнего магнитопровода. Магнитный поток, создаваемый постоянным магнитом, состоит из основного потока, проходящего через воздушные зазоры и внешний магнитопровод, и потока рассеяния, замыкающегося по воздуху, между полюсами магнита. Эти потоки по отношению к магниту являются внешними, и их сумма должна быть равной потоку постоянного магнита ФМ = ФВН = Фd + Фs . (9.7) Величина потока рассеяния принимается пропорциональной МДС магнита: Фs = ls F M . (9.8) Согласно закону полного тока для магнитной цепи справедливо соотношение 2 H M l M + 2 H d d + 2 H CT l CT = 0, (9.9) где l M и l CT - половина длины магнита внешнего магнитопровода. В этом случае F M = - (F d + F CT ) или по модулю ½F M ½ =½F d + F CT ½. (9.10) Поскольку магнитный поток пропорционален магнитной индукции, а напряжённость магнитного поля - МДС, то кривую размагничивания постоянного магнита можно изобразить в координатных осях (Ф,F ). В этих же осях можно построить зависимости Фd = f (F ВН ) и Фs = f (F м ):
Для последовательно включенных участков ФСТ = Фd ,поэтому указанное выражение записывается в виде
отсюда
Полученная зависимость нелинейна, так как по мере увеличения магнитной индукции материала внешнего магнитопровода его магнитная проницаемость падает (кривая Фd (F ВН ) на рис.11). При выполнении условия (9.7) поток рассеяния пропорционален внешней МДС: Фs = ls F м = ls F BH , (9.14) и эта зависимость может быть построена в тех же координатных осях (кривая Фs (F BH ) на рис.11). Просуммировав ординаты указанных кривых, построим ту же зависимость (9.7) с учётом нелинейности
 ФBH = Фd + Фs = f (F BH ). Совместная работа постоянного магнита и внешней магнитной цепи возможна согласно (9.7) и (9.10) при равенстве магнитных потоков и МДС, т.е. в точке пересечения линии возврата магнита и вебер-амперной характеристики внешней магнитной цепи (точка А на рис.11). В тех случаях, когда внешняя магнитная цепь не насыщена, вебер-амперная характеристика изображается прямой, проведённой относительно оси абсцисс под углом
где lВН - магнитная проводимость внешней магнитной цепи. Совместная работа магнита и внешней цепи соответствует рабочей точке 1 с координатами (Н 1 ,В 1 ). Если магнитная цепь имеет обмотку, по которой протекает ток, то к МДС магнита будет добавляться МДС обмотки -DF . Эта МДС не влияет на характеристики внешней магнитной цепи. Поэтому для учёта её влияния достаточно сместить вебер-амперную характеристику внешней цепи ФВН = f (F ВН ) параллельно самой себе на величину DF в зависимости от её полярности. Случай размагничивания показан на рис. 11. Для того чтобы МДС обмотки не вызывала размагничивания постоянного магнита, необходимо ограничить её величину: DF <F РАЗМ . Подмагничивание магнита не вызывает ухода рабочей точки с линии возврата, и величина МДС обмотки в этом случае не ограничивается. Таким образом, задача расчёта магнитной цепи заключается в том, чтобы, зная характеристики постоянного магнита, внешней магнитной цепи и величину размагничивающей МДС обмотки, выбрать положение рабочей точки, обеспечивающей максимум энергии, или, другими словами, минимальный объем магнита. 9.3. Расчёт оптимальных параметров постоянного магнита Пусть задана кривая размагничивания постоянного магнита
с известными параметрами B r , H c , a . Введём относительные величины:
где в качестве масштабов выбраны m B = B r ; m H = H c ; m m = B r / H C ; m Ф = B r S M ; m F = H C l M ; m l = m Ф / m F ; m W = B r H C / 2. Кривая размагничивания в относительных единицах записывается в виде
Допустим, что рабочая точка магнита, положение которой необходимо определить, изображается на рис. 12 точкой 1. Положение этой точки, как было показано выше, соответствует точке пересечения линии возврата и вебер-амперной характеристики внешней цепи. При отсутствии насыщения наклон последней определяется выражением tg a = lВН . (9.17) Линия возврата проходит под углом
причём относительная проницаемость возврата связана с формой кривой размагничивания соотношением
Положим, что задана максимальная размагничивающая МДС и соответствующая ей напряжённость магнитного поля DHM . Выражая координаты рабочей точки 1 через координаты точки 2, лежащей на кривой размагничивания, подставляя полученные выражения в уравнение кривой размагничивания (9.16) и решая его относительно индукции, в окончательном виде получим
Определим удельную энергию магнита в рабочей точке:
Рис.12. К расчёту оптимальных размеров магнита постоянного тока Подставляя (9.20) в (9.21) и исследуя полученную функцию на экстремум, определим оптимальную магнитную проводимость внешней цепи, соответствующую максимуму энергии магнита:
Используя выражение (9.13), выразим lВН.ОПТ через параметры внешней магнитной цепи:
Отсюда при известной площади магнита находят его длину:
Если пренебречь падением магнитного потенциала во внешнем магнитопроводе, т.е. считать mСТ = ¥, то полученное выражение упрощается и принимает вид:
При равенстве площадей магнитного зазора и магнита будем иметь
Величина относительной магнитной индукции при оптимальном режиме постоянного магнита записывается в виде
а относительная напряжённость магнитного поля при этом
Пример № 1
. Постоянный магнит из сплава ЮНДК имеет следующие характеристики: B
r
= 1,02 Тл; H
c
= 110 кА/м; g = 0,6417. Величина относительной напряжённости размагничивающего магнитного поля Определить отношение длины магнита к длине воздушного зазора для оптимально выбранной рабочей точки. Р е ш е н и е. Коэффициент, характеризующий форму кривой размагничивания,
Относительная проницаемость возврата
Оптимальная проводимость внешней цепи в относительных единицах
Масштаб магнитной проницаемости m m = B r / H C = 1,02 / (110 × 103 ) = 9,2727 × 10-6 Гн/м. Магнитная проницаемость воздушного зазора в относительных единицах
Отношение длины магнита к длине воздушного зазора:
Относительная магнитная индукция:
Относительная напряжённость магнитного поля
Относительная удельная энергия магнита
Графическое построение решения задачи представлено на рис. 13 . При заданной величине внешнего размагничивания
Уменьшение магнитной проводимости внешней цепи недопустимо, так как при этом уменьшается величина
Рис. 13. Графическое построение решения примера № 1 Пример №2. Внешняя магнитная цепь и внешнее размагничивание имеют те же, что в примере1, параметры и величины. Определить отношение длины магнита к длине воздушного зазора, если использовать магнит на основе редкоземельных элементов типа КС 37А с параметрами: B r = 0,82 Тл; H с = 560 kA; g = 0,28. Р е ш е н и е. Коэффициент, характеризующий форму кривой размагничивания,
Относительная магнитная проницаемость возврата
Оптимальная магнитная проводимость внешней цепи
Относительная магнитная проницаемость воздушного зазора
Отношение длины магнита к длине воздушного зазора
Сравнивая между собой магниты ЮНДК с магнитами на основе редкоземельных элементов, видим, что объём последних при прочих равных условиях в »11 раз меньше. Такое положение объясняется значительно большими удельными энергиями последних. 10. ПРИМЕР РАСЧЁТА МАШИНЫ ПОСТОЯННОГО ТОКА Исходные данные для расчёта: машина постоянного тока - генератор; полезная мощность -Р Н = 80 Вт; номинальное напряжение -U Н = 230 В; частота вращения -n Н , об/мин; возбуждение - параллельное; режим работы -S 1, продолжительный; исполнение - закрытое. 10.1. Основные размеры машины
10.2. Расчёт обмотки якоря
10.3. Расчёт проводников якорной обмотки, размеров зубцов, пазов якоря
10.4. Коллектор и щёточный аппарат
10.5. Проверка коммутации
10.6. Расчёт магнитной цепи
Таблица 3 Расчёт кривой холостого хода генератора постоянного тока
10.7. Расчёт обмотки возбуждения
10.8. Потери и КПД генератора
10.9. Тепловой расчёт
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Eрмолин Н.П. Электрические машины малой мощности. М.: Высшая школа,1967. 2.Сергеев П.С., Виноградов Н.В., Горяинов Ф.А. Проектирование электрических машин М.: Энергия, 1969. 3.Проектирование электрических машин / И.П. Копылов, Ф.А. Горяинов, Б.К.Клоков и др.; Под ред. И.П.Копылова. M.:Высшая школа, 1980. 4. Проектирование электрических машин / О.Д. Гольдберг, Я.С. Гурин, И.С. Свириденко; Под ред. О.Г. Гольдберга. М.: Высшая школа, 1984. 5. Никулин Н.В. Справочник по электротехническим материалам и изделиям. Свердловск: Средне-Уральское книжное издательство, 1979. 6. Мишин Д.Д. Магнитные материалы. М.: Высшая школа, 1991. 7. Кекало И.Б., Самарин Б.А. Физическое металловедение прецизионных сплавов. М.:Металлургия, 1989. 8. Справочник по электротехническим материалам. Т.3. Л.: Энергоатомиздат,1988. 9. Юферов Ф.М. Электрические машины автоматических устройств. M.: Высшая школа, 1988. 10. Бут Д.А. Бесконтактные электрические машины. М.: Высшая школа, 1985. ПРИЛОЖЕНИЕ Таблица 1 Номинальные диаметры и длины рядов R 5a ,R 10a,R 20a,R 40a
Таблица 2 Характеристики обмоточных проводов
Таблица 3 Номинальные диаметры и сечения медных эмалированных проводов
Таблица 4 Коэффициенты заполнения пакета магнитопровода сталью в зависимости от способа изоляции листов
Таблица 5 Характеристики литой стали для монолитных станин машин постоянного тока (Ст. 3)
Таблица 6 Характеристики чугуна для монолитных станин машин постоянного тока
Таблица 7 Характеристика намагничивания горячекатаных слаболегированных электротехнических сталей 1211, 1212, 1311
Таблица 8 Характеристика намагничивания высоколегированных горячекатаных электротехнических сталей 1511, 1512, 1513
Таблица 9 Характеристика намагничивания холоднокатаных электротехнических сталей 2011, 2013
Таблица 10 Характеристика намагничивания холоднокатаных электротехнических сталей 2311, 2312
Таблица 11 Характеристика намагничивания холоднокатаных электротехнических сталей 2411, 2412,2413
Таблица 12 Характеристика намагничивания холоднокатаной текстурованной электротехнической стали 3411, 3412
Таблица 13 Характеристика намагничивания холоднокатаных текстурованных электротехнических сталей 3413, 3414
Окончание табл. 13
Таблица 14 Номинальные размеры щёток, мм
Окончание табл. 14
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ........................................................................................…..… 3 1. ОСНОВНЫЕ РАЗМЕРЫ МАШИНЫ...........................................………..4 2. ПАРАМЕТРЫ ОБМОТКИ ЯКОРЯ............................................………….8 3. РАЗМЕРЫ ЗУБЦОВ, ПАЗОВ И ПРОВОДНИКОВ ОБМОТКИ ЯКОРЯ…...................................................................………..10 4. КОЛЛЕКТОР И ЩЁТОЧНЫЙ АППАРАТ……….............................……..15 5. МАГНИТНАЯ СИСТЕМА МАШИНЫ ПОСТОЯННОГО ТОКА............................................................…………..19 6. РАСЧЁТ ОБМОТКИ ВОЗБУЖДЕНИЯ….....................................………..26 7. ПОТЕРИ И КПД МАШИНЫ ПОСТОЯННОГО ТОКА................………….28 8. УПРОЩЕННЫЙ ТЕПЛОВОЙ РАСЧЁТ МАШИНЫ ПОСТОЯННОГО ТОКА МАЛОЙ МОЩНОСТИ..............……………….33 9. РАСЧЁТ ПОСТОЯННЫХ МАГНИТОВ ДЛЯ ВОЗБУЖДЕНИЯ МАШИН ПОСТОЯННОГО ТОКА..............………35 10. ПРИМЕР РАСЧЁТА МАШИНЫ ПОСТОЯННОГО ТОКА ……………. 44 БИБЛИОГРАФИЧЕСКИЙ СПИСОК ………………………………..………. 56 ПРИЛОЖЕНИЕ..................................................…….........…………….…. 57 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 . (1.3)
. (1.3) . (1.6)
. (1.6) ; (1.7)
; (1.7)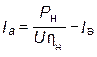 ; (1.8)
; (1.8) (1.12)
(1.12) (3.4)
(3.4) (3.9)
(3.9)
 (3.25)
(3.25)
 . (3.31)
. (3.31)
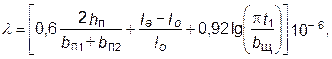 (4.7)
(4.7) (4.10)
(4.10)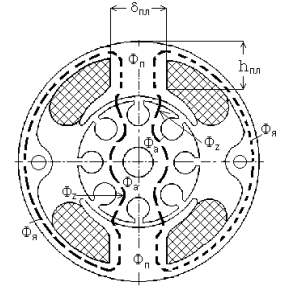
 (5.9)
(5.9)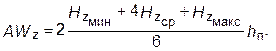 (5.11)
(5.11) ½бв½ = ½бг½= AS
b
0
/ 2. (5.27)
½бв½ = ½бг½= AS
b
0
/ 2. (5.27) (5.30)
(5.30) (6.1)
(6.1) (6.5)
(6.5) (6.8)
(6.8)

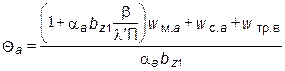 , (8.1)
, (8.1)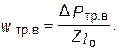 (8.8)
(8.8) Постоянный магнит характеризуется кривой размагничивания, снимаемой для образцов с замкнутым магнитопроводом, вид которой представлен на рис.8.
Постоянный магнит характеризуется кривой размагничивания, снимаемой для образцов с замкнутым магнитопроводом, вид которой представлен на рис.8. 

 , (9.12)
, (9.12) . (9.13)
. (9.13)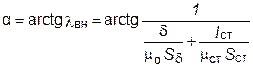 , (9.15)
, (9.15)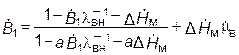 . (9.20)
. (9.20)
 . (9.22)
. (9.22) . (9.23)
. (9.23) . (9.24)
. (9.24) .
.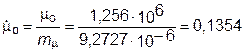 .
.

 .
.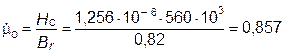 .
.