| Министерство высшего и профессионального образования
Российской Федерации
Иркутский Государственный Технический Университет
Курсовая работа
По электротехнике и электронике
Анализ сложных электрических цепей постоянного тока и однофазного переменного тока
Выполнил:
Проверила:
Василевич М.Р.
Иркутск 2006г
Содержание:
1. Анализ электрических цепей постоянного тока
Расчёт токов с помощью законов Кирхгофа
Расчёт токов методом контурных токов
Расчёт токов методом узлового напряжения
Исходная таблица расчётов токов
Потенциальная диаграмма для контура с двумя Э.Д.С
Баланс мощности
Определение показания вольтметра
2. Анализ электрических цепей переменного тока
Расчёт токов с помощью законов Кирхгофа
Расчёт токов методом контурных токов
Расчёт токов методом узлового напряжения
Исходная таблица расчётов токов
Векторная диаграмма токов и топографическая диаграмма напряжений на комплексной плоскости
Определение показания вольтметра
1. Анализ электрических цепей постоянного тока

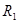 =9 Ом =9 Ом
 =7,5 Ом =7,5 Ом
 =12 Ом =12 Ом
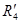 =22,5 Ом =22,5 Ом
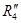 =315 Ом =315 Ом
 =10,5 Ом =10,5 Ом
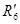 =0 =0
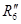 =12 Ом =12 Ом
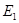 =- =-
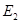 =15 В =15 В
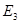 =33 В =33 В
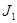 =- =-
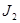 =2 В =2 В
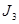 =0 В =0 В
В предложенной электрической цепи заменяем источники тока на источники ЭДС.
 2)Выбираем условно положительное направление токов. 2)Выбираем условно положительное направление токов.
3)Выбираем направление обхода независимых контуров.
Находим эквиваленты:
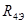 = =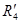 * *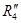 / ( / (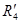 + +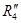 ) = ) =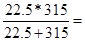 21 21
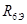 = =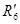 + +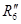 =0+12=12 Ом =0+12=12 Ом
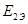 = =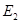 + +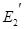 =15+2=17 =15+2=17
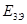 = =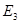 + +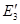 =33+0=33 =33+0=33
1.1 Расчёт токов с помощью законов Кирхгофа
Записываем систему уравнений для расчета электрических цепей с помощью законов Кирхгофа. По 1 закону составляем (у-1) уравнение, где у количество узлов. По 2 закону Кирхгофа составляем [b-(y-1)] уравнение, где b – количество ветвей.
a) 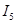 + +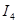 + +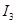 =0 =0
b) 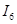 - -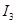 + +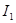 =0 =0
c)- 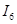 - -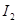 - -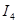 =0 =0
I) 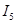  - -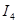 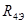 + +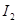  = =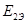
II) 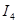 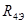 - -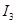  - -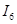 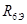 =- =-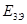
III)- 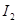  + + 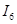 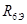 - -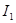 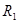 =- =-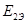
Рассчитываем систему уравнений с помощью ЭВМ, векторы решения находятся в приложении 1.
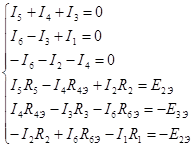
 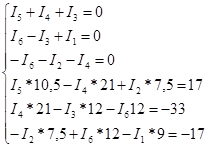

(Данные расчета находятся в приложении 1)
После расчета на ЭВМ записываем:
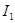 =1.29 A =1.29 A 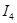 =-0.80 A =-0.80 A
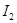 =0.77 A =0.77 A 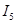 =-0.52 A =-0.52 A
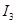 =1.32 A =1.32 A 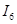 =0.03 A =0.03 A
1.2 Расчёт токов методом контурных токов
Находим действующие в цепи токи с помощью метода контурных токов. Предполагается, что каждый контурный ток имеет свое собственное контурное сопротивление, которое равно арифметической сумме всех сопротивлений входящих в контур. Контурное ЭДС равно сумме всех ЭДС входящих в контур.
В каждом независимом контуре рассматривают независимые и граничащие ветви. В каждой граничащей ветви находят общее сопротивление, которое равно сопротивлению этой ветви. Составляют систему уравнений, количество которых равно количеству контурных токов. В результате расчета находят контурные токи и переходят к действующим.
1) Предположим, что в каждом независимом контуре течет свой контурный ток 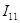 , ,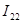 , ,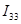 . Выберем произвольно положительное направление обхода токов в одно направление. . Выберем произвольно положительное направление обхода токов в одно направление.
2)Находим полно контурное сопротивление всех контурных токов.
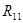 = = + +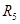 + +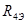 =7,5+10,5+21=39 Ом =7,5+10,5+21=39 Ом
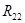 = =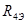 + +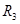 + + =21+12+12=45 Ом =21+12+12=45 Ом
 = =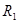 + + + + =9+7,5+12=28,5 Ом =9+7,5+12=28,5 Ом
Находим общее сопротивление
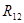 = =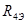 = =
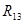 = =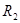 = =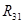
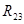 = =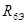 = =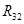
Находим полные контурные ЭДС
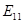 = =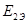
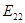 = =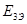
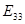 =- =-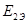
Составляем систему уравнений для нахождения контурных токов
Согласно второму закону Кирхгофа
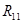 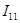 - -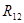 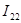 - -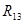 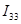 = =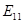
-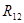 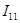 + +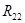 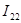 - -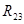 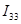 = =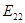
-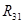 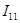 - -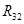 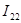 + + 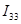 = =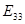
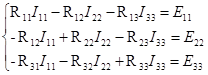
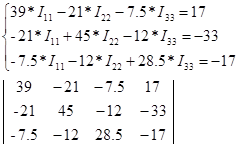
(Данные расчета находятся в приложении 2)
После расчета на ЭВМ записываем:
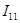 =-0.52455258749889799877 (А) =-0.52455258749889799877 (А)
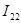 =-1.3224896411883981310 (А) =-1.3224896411883981310 (А)
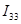 =-1.2913691263334214934 (А) =-1.2913691263334214934 (А)
4.Ток в независимой цепи равен контурному току с учетом знаков, а ток в зависимой цепи равен алгебраической сумме.
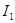 =-I33=1.29 A =-I33=1.29 A
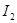 =I11-I33=-0.52455258749889799877-(-1.2913691263334214934) =0,77 A =I11-I33=-0.52455258749889799877-(-1.2913691263334214934) =0,77 A
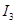 =-I22=1.32 A =-I22=1.32 A
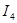 =I22-I11=-1.3224896411883981310-(-0.52455258749889799877) -0,8 A =I22-I11=-1.3224896411883981310-(-0.52455258749889799877) -0,8 A
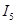 =I11=-0.52 A =I11=-0.52 A
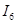 =I33-I22=-1.2913691263334214934-(-1.3224896411883981310) =0,03 A =I33-I22=-1.2913691263334214934-(-1.3224896411883981310) =0,03 A
В результате токи равны:
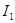 =1.29 A =1.29 A
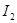 =0,77 A =0,77 A
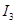 =1.32 A =1.32 A
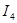 = -0,8 A = -0,8 A
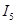 = -0.52 A = -0.52 A
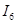 = 0,03 A = 0,03 A
1.3 Расчёт токов методом узлового напряжения
Проверяем правильность нахождения токов в заданной электрической цепи методом узловых потенциалов. Согласно этому методу предполагается, что в каждом узле схемы имеется свой узловой ток который равен алгебраической сумме всех токов за счет проводимости ветвей. Этот метод основан на первом законе Кирхгофа и законе Ома.
Заземляем узел 3, φ
3=0
Если в электрической схеме заземляется один из узлов, потенциал этой точки равен 0, а тока распределение не меняется.
Находим собственные проводимости ветвей присоединенных к оставшимся узлам 1,2,4. Собственная проводимость ветвей равна арифметической сумме проводимостей ветвей присоединенных к соответствующим узлам.
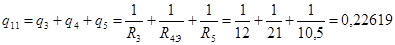 
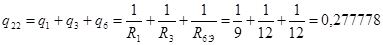 
 
Находим взаимные проводимости, которые равны проводимости общих ветвей между соседними узлами.
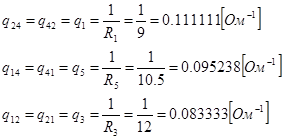
Находим полный узловой ток, который равен сумме произведений ЭДС на соответствующую проводимость.

Составляем уравнение в соответствии с первым законом Кирхгофа.
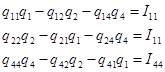
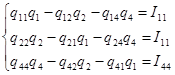
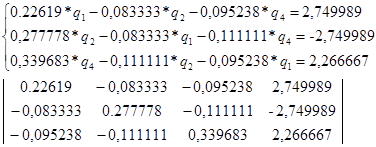
(Данные расчета находятся в приложении 3)
После расчета на ЭВМ записываем:
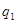 =16,756645482734525139 =16,756645482734525139 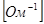
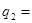 -0,37345273475483642976 -0,37345273475483642976
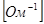
 11,248845822938816704 11,248845822938816704 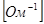
1. По закону Ома находим искомые токи.
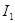 =( =( - -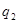 )/ )/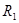 =(11,248845822938816704-( -0,37345273475483642976))/9=1,291367 A =(11,248845822938816704-( -0,37345273475483642976))/9=1,291367 A
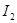 =( =(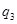 - - + +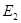 )/ )/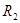 =((0,083333-11,248845822938816704)+17)/7,5=0,777932 A =((0,083333-11,248845822938816704)+17)/7,5=0,777932 A
 =( =(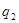 - -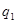 + +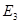 )/ )/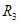 =(0-,37345273475483642976-16,756645482734525139+33)/12= 1,322492 A =(0-,37345273475483642976-16,756645482734525139+33)/12= 1,322492 A
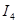 =( =(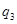 - -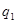 )/ )/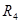 =(0,083333-16,756645482734525139)/21=-0,79397 A =(0,083333-16,756645482734525139)/21=-0,79397 A
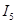 =( =(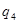 - -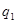 )/ )/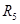 =(11,248845822938816704-16,756645482734525139)/10,5=-0,52455 A =(11,248845822938816704-16,756645482734525139)/10,5=-0,52455 A
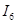 =( =(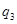 - -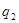 )/ )/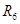 =(0,083333-( -0,37345273475483642976))/12=0,038065 A =(0,083333-( -0,37345273475483642976))/12=0,038065 A
Округляем искомые токи до сотых долей:
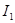 =1,29 A =1,29 A
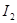 =0,78 A =0,78 A
 =1,32 A =1,32 A
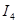 =-0,79 A =-0,79 A
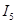 =-0,52 A =-0,52 A
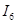 =0,04 A =0,04 A
1.4
Исходная таблица расчётов токов
V Составляем исходную таблицу расчетов токов всеми методами
| I токи
Метод
|
I1,A
|
I2,A
|
I3,A
|
I4,A
|
I5,A
|
I6,A
|
| Закон Кирхгофа
|
1,29
|
0,77
|
1,32
|
-0,8
|
-0,52
|
0,03
|
| Контурных Токов
|
1,29
|
0,77
|
1,32
|
-0,8
|
-0,52
|
0,03
|
| Узловых Потенциалов
|
1,29
|
0,78
|
1,32
|
-0,79
|
-0,52
|
0,04
|
1.5 Потенциальная диаграмма для контура с двумя Э.Д.С
VI Строим потенциальную диаграмму

∑R=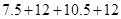 =42 Ом =42 Ом
1.6
Определение показания вольтметра

VII Находим показания вольтметра по второму закону Кирхгофа
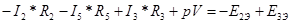
pV=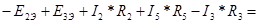 -17+33+0,77*7.5+(-0,52)*10.5-1,32*12= -17+33+0,77*7.5+(-0,52)*10.5-1,32*12=
=0.475 В
1.7
Баланс мощности
XIII Составляем баланс мощности
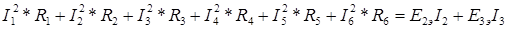
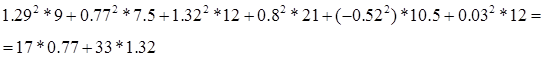
56.62Вт=56.65Вт
2. Анализ электрических цепей переменного тока
1) Начертим электрическую цепь без ваттметра и записать данные.

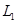 =40.5 мГн =40.5 мГн
 =0 мГн =0 мГн
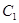 =35.4 мкФ =35.4 мкФ
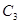 =53 мкФ =53 мкФ
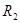 =25 Ом =25 Ом
f=150 Гц
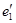 =70.5 cos(ωt+275) =70.5 cos(ωt+275)
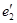 ’=68.5 cos(ωt-174) ’=68.5 cos(ωt-174)
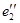 ’=56 sin(ωt-170) ’=56 sin(ωt-170)
2)Найдем сопротивление элементов входящих в цепь.
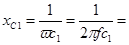 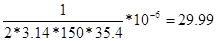 Ом Ом
  Ом Ом
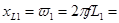  Ом Ом
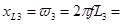 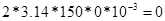 Ом Ом
3)
Находим комплексы ЭДС, входящие в цепь.
Ė= Ė’+ Ė’’

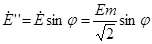
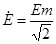
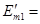 70.5 В 70.5 В
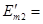 68.5 В 68.5 В
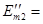 =56 В =56 В
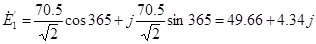
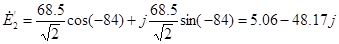
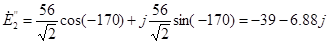
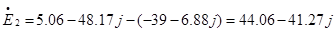
2.1 Расчёт токов с помощью законов Кирхгофа
4)Производим расчет предложенной схемы методом законов Кирхгофа.
Выбираем условно положительное направление токов. Рассчитываем искомые токи.

Записываем систему уравнений для мгновенных значений токов и напряжений в соответствии с первым и вторым законами Кирхгофа в интегро-дифференциальной форме, причем по первому закону Кирхгофа составляем (у-1) –уравнений, а по второму закону Кирхгофа –[b-(y-1)]-уравнений.
(у-1)=1
[b-(y-1)]=2
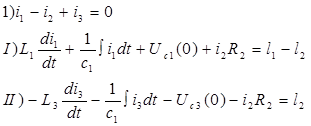
Или в комплексной форме:
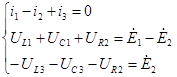
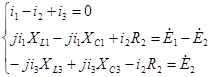
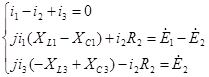

Решаем данную систему уравнений с помощью ЭВМ.
(Данные расчета находятся в приложении 4)
После расчета на ЭВМ записываем значения комплексных токов:
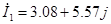 [A] [A]
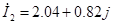 [A] [A]
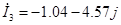 = =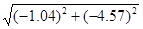 =4.69 [A] =4.69 [A]
Находим действующие значения токов:
 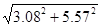 =6.37 [A] =6.37 [A]
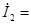 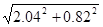 =2.2 [A] =2.2 [A]
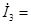 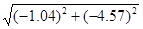 =4.69 [A] =4.69 [A]
2.2 Расчёт токов методом контурных токов
5. Производим расчет данной схемы методом контурных токов.
Находим полные контурные сопротивления:
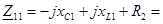 j(38.15-29.99)+25=25+8.16j [Ом] j(38.15-29.99)+25=25+8.16j [Ом]
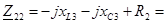 j(0-20.03)+25=25-20.03j [Ом] j(0-20.03)+25=25-20.03j [Ом]
Находим взаимное сопротивление:
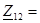 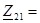 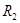 =25 [Ом] =25 [Ом]
Находим комплексы полных контурных ЭДС:
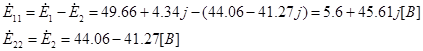
Записываем систему уравнений:
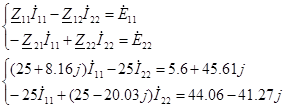
Решаем систему уравнений с помощью ЭВМ.
(Данные расчета находятся в приложении 5)
После расчета на ЭВМ Записываем значения контурных токов:
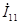 =3.08+5.57j [A] =3.08+5.57j [A]
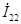 =1.04+4.75j [A] =1.04+4.75j [A]
Причем контурный ток 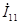 равен току в независимой ветви, т.е. току равен току в независимой ветви, т.е. току 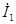 . Контурный ток . Контурный ток 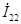 равен току равен току 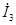 в независимой ветви, но направлен навстречу. Искомый ток в независимой ветви, но направлен навстречу. Искомый ток 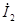 = =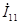 - -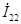 . .
Таким образом:
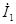 =3.08+5.57j [A] =3.08+5.57j [A]
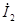 =0.24+0.82j [A] =0.24+0.82j [A]
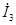 =-1.04-4.75j [A] =-1.04-4.75j [A]
2.3Расчёт токов методом узлового напряжения
6) Проверяем правильность нахождения расчета методом узловых потенциалов.
Для этого узел 2 заземляем, а для остальных составляем систему уравнений.
φ2=0
Находим полную комплексную проводимость узла.
 = =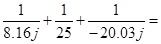 0.04-0.07j 0.04-0.07j 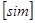
(Данные расчета находятся в приложении 6)
Находим комплекс узлового тока.
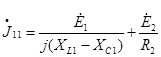 = =
= 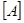
(Данные расчета находятся в приложении 7)
Находим комплексный потенциал:

В результате решения этого уравнения находим комплекс потенциала
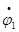 и по закону Ома находим искомые токи. и по закону Ома находим искомые токи.
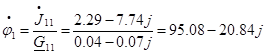
(Данные расчета находятся в приложении 8)
По закону Ома находим искомые токи:
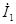 = =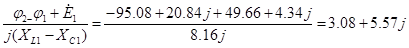 [A] [A]
(Данные расчета находятся в приложении 9)
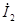 = =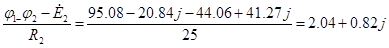 [A] [A]
(Данные расчета находятся в приложении 10)
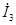 = = [A] [A]
(Данные расчета находятся в приложении 11)
2.4 Исходная таблица расчётов токов
7)Составляем сводную таблицу искомых токов:
| токи
Метод
|
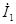 ,A ,A
|
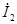 ,A ,A
|
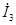 ,A ,A
|
| Законы Кирхгофа
|
3,08+5,57j
|
2.04+0.82j
|
-1.04-4.75j
|
| Контурных Токов
|
3,08+5,57j
|
2.04+0.82j
|
-1.04-4.75j
|
| Узловых Потенциалов
|
3,08+5,57j
|
2.04+0.82j
|
-1.04-4.75j
|
2.5 Векторная диаграмма токов и топографическая диаграмма напряжений на комплексной плоскости
8) Строим на комплексной плоскости векторную диаграмму токов и топографическую диаграмму напряжений и график изменения тока в неразветвленной части цепи.
1. 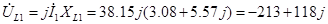 [B] [B]
 [B] [B]
2. 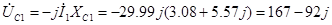 [B] [B]
3. 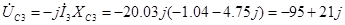 [B] [B]
4. 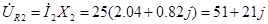 [B] [B]
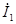 = =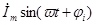
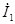 =3.08+5.57j=6.36 =3.08+5.57j=6.36 [A] [A]
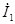 = =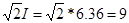 [A] [A]
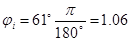 рад рад
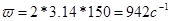
(Данные расчета находятся в приложении 12)
2.6
Определение показания вольтметра
9)Определяем показания вольтметра по второму закону Кирхгофа:

pV-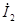 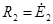
pV= + +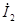 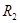 =44.06-41.27j+(2.04+0.82j)*25=95.06-20.77j =44.06-41.27j+(2.04+0.82j)*25=95.06-20.77j
pV=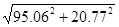 =97 B =97 B
Приложения
Приложение 1:
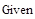
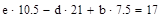
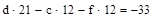
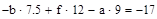

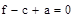
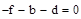
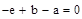

Приложение 2:
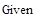
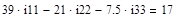
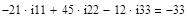
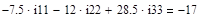

Приложение 3:
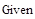
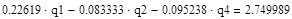
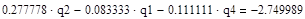
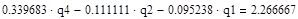
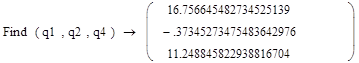
Приложение 4:
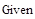

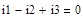
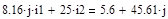
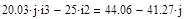

Приложение 5:
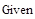

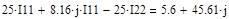
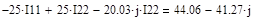
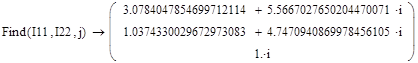
Приложение 6:
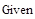

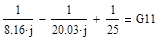
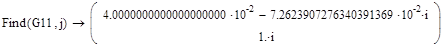
Приложение 7:
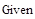

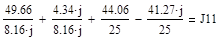
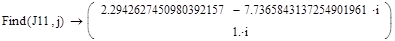
Приложение 8:
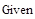

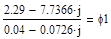
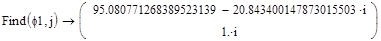
Приложение 9:
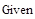

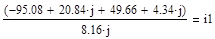
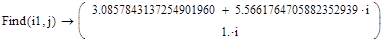
Приложение 10:
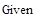

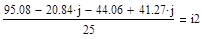
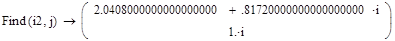
Приложение 11:
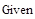

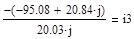
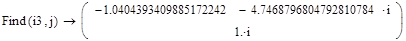
Приложение 12:
График изменения тока в неразветвленной части цепи 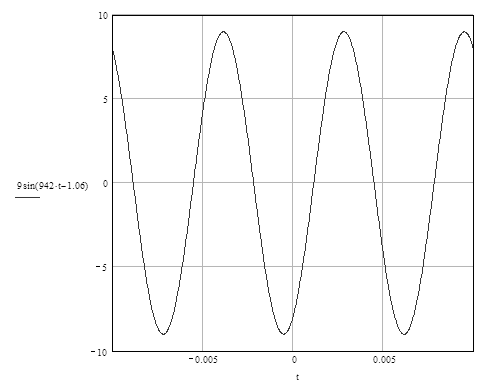
|