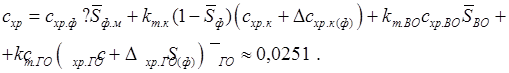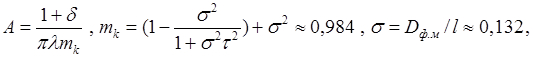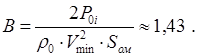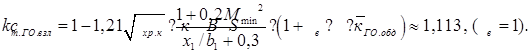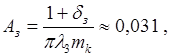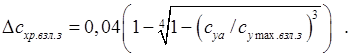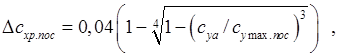Курсовая работа: Расчёт аэродинамических характеристик самолёта T-30 KATANA
|
Название: Расчёт аэродинамических характеристик самолёта T-30 KATANA Раздел: Рефераты по физике Тип: курсовая работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Содержание Введение 1. Подготовка исходных данных 2. Расчёт и построение зависимостей cya (α) для различных режимов полёта 2.1 Расчёт и построение зависимости критического числа Маха от коэффициента подъёмной силы Мкр (суа ) 2.2 Расчёт и построение вспомогательной зависимости cya (α) 2.3 Расчёт и построение взлётных кривых cya (α) 2.4 Расчёт и построение посадочных кривых cya (α) 2.5 Расчёт и построение крейсерских зависимостей cya (α) 3. Расчёт и построение поляр самолёта 3.1 Расчёт и построение вспомогательной поляры 3.2 Расчёт и построение взлётных поляр 3.3 Расчёт и построение посадочных поляр 3.4 Расчёт и построение крейсерских поляр Библиографический список Введение В данной работе рассматривается лёгкий спортивный самолет «T-30 Katana», представляющий собой одноместный одномоторный свободнонесущий среднеплан с закрытой кабиной и неубирающимся шасси. Вычисляются основные геометрические и аэродинамические параметры этого самолёта, на основании которых строятся теоретические зависимости коэффициента подъёмной силы от угла атаки и от коэффициента сопротивления (поляры) для взлетного, крейсерского и посадочного режимов полёта. 1. Подготовка исходных данных Аэродинамические характеристики самолёта зависят от его геометрических параметров. Поэтому сначала по чертежу летательного аппарата (рисунок 1) узнаём необходимые размеры из заносим их в таблицу 1. В эту же таблицу заносим основные лётно-технические характеристики самолёта. Далее на основании имеющихся данных вычисляются прочие необходимые геометрические характеристики и также включаются в таблицу вместе с формулами, по которым они были вычислены. Таблица 1.
2. Расчёт и построение зависимостей cya (α) для различных режимов полёта 2.1 Расчёт и построение зависимости критического числа Маха от коэффициента подъёмной силы Мкр (суа ) Эта зависимость задаётся формулой:
Рисунок 2 — Зависимость критического числа Маха от режима полёта 2.2 Расчёт и построение вспомогательной зависимости суа (α) Эта зависимость строится для полёта на нулевой высоте при отсутствии экранного эффекта с убранными средствами механизации крыла на минимальной скорости полёта, которая находится по следующей формуле:
Ей соответствует число Маха:
Удлинение крыла данного самолёта достаточно велико (λ>4), и поэтому для нахождения теоретического наибольшего значения коэффициента подъёмной силы можно применить формулу:
Определяем три точки для построения графика суа (α):
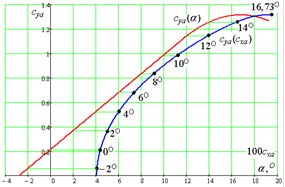
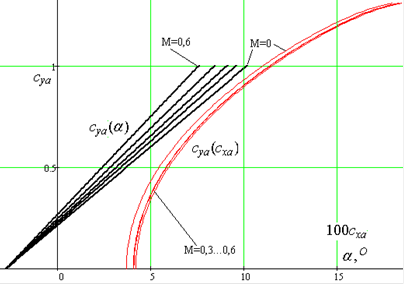
И строим по этим трём точкам график зависимости коэффициента подъёмной силы от угла атаки, аппроксимируя её параболой в области больших углов атаки (рисунок 3 и рисунок 4, кривая 1).
Рисунок 3 — Вспомогательная зависимость коэффициента подъёмной силы от угла атаки. 2.3 Расчёт и построение взлётных кривых суа (α) 1) Во взлётном режиме закрылки выпущены под углом:
Зная данную величину, а также относительную хорду закрылков
То есть на взлёте этот угол равняется:
Теперь можно найти приращение максимального значения коэффициента подъёмной силы из-за выпущенных закрылков по формуле:
где
Зная данную величину, а также относительную площадь крыла, обдуваемую винтом, Теперь можно вычислить максимальное значение коэффициента подъёмной силы во взлётной конфигурации без учёта экранного эффекта земли:
Исходя из найденных значений 2) Учтём теперь влияние экрана земли, которое вносит такую поправку в коэффициент подъёмной силы:
А максимальное значение коэффициента подъёмной силы во взлётной конфигурации с учётом экранного эффекта земли равно:
Находим фиктивное удлинение крыла, учитывающее влияние земли:
Тогда производная коэффициента подъёмной силы по углу атаки с учётом экранного эффекта равна:
Используя найденные значения 2.4 Расчёт и построение посадочных кривых суа (α) 1) Во время посадки закрылки выпущены под углом:
Зная данную величину, а также относительную хорду закрылков
То есть на посадке этот угол равняется:
Теперь можно найти приращение максимального значения коэффициента подъёмной силы из-за выпущенных закрылков по формуле:
На посадке винт не влияет на подъёмную силу крыла. Тогда максимальное значение коэффициента подъёмной силы во взлётной конфигурации без учёта экранного эффекта земли равно:
Исходя из найденных значений
А максимальное значение коэффициента подъёмной силы в посадочной конфигурации с учётом экранного эффекта земли равно:
Используя найденные значения 2.5 Расчёт и построение крейсерских зависимостей cya (α) Высота полёта расчётная Н=2500 м, скорость звука на этой высоте равна аН =330,6 м/с . Скорость полёта расчётная V=101,4 м/с , при этом число Маха равно: Мрасч =V/аН =0,31. Самолёт находится в полётной конфигурации, то есть закрылки убраны. При этом для различных чисел Маха зависимость cya (α) задаётся формулой:
Сводим в таблицу 2 параметры этой зависимости для нескольких чисел Маха. Таблица 2.
И по этим данным строим крейсерские зависимости cya (α) (рисунок 5). 3. Расчёт и построение поляр самолёта 3.1 Расчёт и построение вспомогательной поляры 1) При построении данной поляры принимают, что закрылки убраны, высота полёта нулевая, экранный эффект отсутствует, скорость полёта минимальна (М=Мmin ). 2) Для нахождения профильного сопротивления фюзеляжа, сначала вычислим его число Рейносльдса:
Поскольку воздушный винт находится спереди, то весь фюзеляж обдувается турбулентным потоком, т.е.
Коэффициенты, учитывающие вклад сил давления и эффекта сжимаемости в профильное сопротивление, вычисляются так:
Профильное сопротивления фюзеляжа как тела вращения определяют по формуле:
Далее учитываются конструктивные особенности фюзеляжа путём определения приращения коэффициента профильного сопротивления:а) из-за сужения кормовой части:
б) из-за её скошенности:
в) под влиянием фонаря кабины:
г) от установленного в носовой части ПД воздушного охлаждения:
Итак, коэффициент профильного сопротивления фюзеляжа равен:
Вычислив его для М=Мmin и Н=0, получаем: 3) Для расчёта профильного сопротивления крыла найдём сначала его число Рейнольдса:
Коэффициенты, учитывающие вклад сил давления и эффекта сжимаемости в профильное сопротивление, вычисляются так:
Коэффициент профильного сопротивления крыла находится так:
и равен 4) Для расчёта профильного сопротивления стабилизатора найдём сначала его число Рейнольдса:
Коэффициенты, учитывающие вклад сил давления и эффекта сжимаемости в профильное сопротивление, вычисляются так:
Коэффициент профильного сопротивления стабилизатора находится так:
и равен 5) Для расчёта профильного сопротивления киля найдём сначала его число Рейнольдса:
Коэффициенты, учитывающие вклад сил давления и эффекта сжимаемости в профильное сопротивление, вычисляются так:
Коэффициент профильного сопротивления киля находится так:
и равен 6) Рассматриваемый самолёт является среднепланом. Коэффициент интерференции для крыла и фюзеляжа среднеплана равен
для М=Мmin и Н=0 7) Стабилизатор установлен вверху кормовой части фюзеляжа, а значит, коэффициент их интерференции равен
для М=Мmin и Н=0 .8) Учтя вклад всех местных источников сопротивления: антенны, выхлопных патрубков, стыков между листами обшивки, щелей между крылом (оперением) и управляющими поверхностями - получаем следующее приращение к коэффициенту сопротивления, не зависящее от М, Н, и α:
9) Вспомогательная поляра строится при отсутствии тяги двигателя. При этом коэффициенты торможения потока для крыла, стабилизатора и киля равны:
Итак, коэффициент профильного сопротивления равен:
Коэффициент сопротивления при нулевой подъёмной силе равен:
11) Рассчитаем теперь индуктивное сопротивление самолёта, для чего найдём коэффициент отвала поляры:
При М=Мmin
: Коэффициент индуктивного сопротивления зависит от коэффициента подъёмной силы следующим образом: 12) Приращение коэффициента сопротивления с увеличением угла атаки (подъёмной силы) оценивается следующим выражением:
Итак, теперь можно найти коэффициент лобового сопротивления:
Шасси данного самолёта является неубирающимся, поэтому его воздушное сопротивление (по статистике По данным этой таблицы строятся график вспомогательной зависимости Таблица 3.1.
Рисунок 3.1 — построение вспомогательной поляры 3.2 Расчёт и построение взлётных поляр 1) При построении данных поляр принимают, что закрылки выпущены под углом 20О , высота полёта нулевая, скорость полёта минимальна (М=Мmin ). 2 — 8) Все промежуточные величины, вычисленные в пунктах 2 — 8 при построении вспомогательной поляры (раздел 3.1), вычисляются по тем же формулам и имеют то же численное значение и во взлётном режиме.9) Для учёта вклада обдувки самолёта винтом в лобовое сопротивление найдём коэффициент нагрузки винта по тяге во взлётном режиме:
При этом коэффициенты торможения потока для крыла, киля и стабилизатора равны:
Коэффициент дополнительного сопротивления из-за обдува части крыла винтом определяется по формуле:
Итак, коэффициент профильного сопротивления равен:
Коэффициент сопротивления при нулевой подъёмной силе равен:
11) Без учёта экрана земли коэффициент отвала поляры рассчитывается по тем же формулам и имеет то же численное значение, что и при расчёте вспомогательной поляры (раздел 3.1, пункт 11):
Итак, коэффициент индуктивного сопротивления без учёта и с учётом экранного эффекта ищется по формулам:
12) Приращение коэффициента сопротивления с увеличением угла атаки (подъёмной силы) оценивается следующим выражениями (без учёта и с учётом экранного эффекта):
13) Выпущенные на 20О при взлёте закрылки увеличивают коэффициент сопротивления на величину:
где
Вычислим Таблица 3.2.1
Вычислим Таблица 3.2.2
3.3 Расчёт и построение посадочных поляр 1) При построении данных поляр принимают, что закрылки выпущены под углом 40О , высота полёта нулевая, скорость полёта минимальна (М=Мmin ). 2 — 10) При посадке двигатель работает на очень слабом или холостом ходу, и поэтому вкладом обдувки от воздушного винта в сопротивление можно пренебречь. Поэтому все промежуточные величины, вычисленные в пунктах 2 — 10 при построении вспомогательной поляры (раздел 3.1), вычисляются по тем же формулам и имеют то же численное значение и в посадочном режиме. В итоге:
11) Индуктивное сопротивление и с учётом, и без учёта экранного эффекта задается одними и теми же формулами в посадочном и во взлётном (раздел 3.2, пункт 11) режимах. 12) Приращение коэффициента сопротивления с увеличением угла атаки (подъёмной силы) оценивается следующим выражениями (без учёта и с учётом экранного эффекта):
13) Выпущенные на 40О при посадке закрылки увеличивают коэффициент сопротивления на величину:
где
Вычислим Таблица 3.3.1
Вычислим Таблица 3.3.2
Рисунок 4 — Вспомогательные, взлётные и посадочные зависимости суа (α) и поляры самолёта. 3.4 Расчёт и построение крейсерских поляр 1) Высота полёта расчётная Н=2500 м , скорость звука на этой высоте равна аН =330,6 м/с , кинематическая вязкость воздуха равна νН =1,79*10-5 м2 /с . Самолёт находится в полётной конфигурации, то есть закрылки убраны. 2 — 8, 11, 12) Все промежуточные величины, вычисленные в пунктах 2 — 8, 11, 12 раздела 3.1, и здесь вычисляются по тем же формулам для различных чисел Маха. А при М=0 числа Рейнольдса, входящие в эти формулы, вычисляются для расчётной скорости V=101 м/с . 9,10) В крейсерском режиме полёта коэффициент нагрузки винта по тяге равен:
Величины, вычисленные в пунктах 9, 10 раздела 3.2, и здесь вычисляют по тем же формулам, подставляя в них данное значение B(V), для различных чисел Маха (скоростей).Результаты расчёта для различных чисел Маха и суа сводим в таблицу: Таблица 3.4
Рисунок 5 — Крейсерские поляры и зависимости суа (α). БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Остовлавский И.В. Аэродинамика самолёта. - М.: Оборонгиз, 1957. 2. Меньшиков В.И. Аэродинамические характеристики самолётов: Учебное пособие. - Харьков: Харьк. Авиац. Ин-т, 1984. 3. Мхитарян А.М. Аэродинамика. - М.: Машиностроение, 1976. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



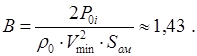

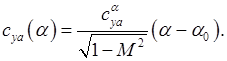



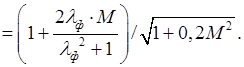
 ;
;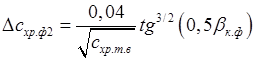 ;
; 10)
10)