Імітаційне моделювання
Машинна імітація випадкових параметрів
Методичні вказівки
щодо виконання лабораторної роботи
Зміст роботи
Методи генерування послідовності рівномірно розподілених випадкових чисел
Завдання
Перевірка якості псевдовипадкових чисел
Завдання
Приклади використання методу Монте Карло в імітаційному моделюванні
Обчислення числа
Обчислення визначеного інтегралу методом Монте-Карло
Для построения последовательности равномерно распределенных случайных чисел используются следующие методы.
Мультипликативно-конгруэнтный метод,
или метод степенных вычетов:
xi
=axi-1
(mod m), i=l,2,...
x0
=b.(1)
где a, m -
неотрицательные целые числа.
Согласно (1) необходимо взять последнее случайное число, умножить его на a
и взять модуль полученного числа по т
(т.е. разделить на т
и взять остаток в качестве следующего xi
).
Последовательность равномерно распределенных на отрезке [О, 1] псевдослучайных чисел получается при делении остатка на т.
В качестве модуля обычно выбирают 2Ь
или 10d
.
На основе конгруэнтной формулы было создано множество генераторов.
Смешанные генераторы Томпсона
основываются на следующей формуле
xi+1
=axi
+ C (mod m)
Аддитивный конгруэнтный метод (Грин, Смит, Клем)
использует рекуррентную формулу
xi+1
=(xi
+ xi-1
)C (mod m)
Примеры построения последовательности псевдослучайных равномерно распределенных на отрезке [0; 1] чисел с помощью приведенных алгоритмов.
Пусть а=111, т=256, b
=10.
Тогда с помощью мультипликативно-конгруэнтного метода получается
x0
=b = 10, r0
= = x0
/m = 10/256=0,039.
Далее получается
x1
=ax0
(mod
m) = 111*10 (mod
256) = 1110 mod
256 = 86,
r1
=x1
/m=86/256=0,336
При тех же параметрах а, m и параметре С=347 с помощью смешанного генератора Томпсона получаем:
x1
=ax0
+C(
mod
m) =
111*10 +347 (mod
256) = 1457 mod
256 = 177,
r1
=x1
/m=177/256=0,691.
Наконец, аддитивно-когруэнтным методом при х0
=100, x1
=183 получаем
х2
=x0
+xl
(
mod
m) = (100 + 183) (mod
256) = 283 mod
256 = 27,
r2
=x2
/m=27/256= 0,105.
В табл. 1 приведены результаты расчетов для первых 10 псевдослучайных чисел, полученных всеми перечисленными способами.
Переваги програмного методу:
- займає мало місця в оперативній пам"яті (близько десяти команд);
- можна поворити спроби;
- забезпечується одноразова первірка якості випадкових чисел;
- не потрібні зовнішні пристрої.
Недоліки програмного методу:
- швідкість утворення випадкових чисел відносно невелика;
- обмежений запас чисел.
Таблица 1
Последовательности псевдослучайных чисел
| i
|
Мультипликативно-конгруэнтный метод |
Смешанный генератор Томпсона |
Аддитивно - конгруэнтный метод |
| xi
|
ri
|
xi
|
ri
|
xi
|
ri
|
| 0 |
10 |
0,039 |
10 |
0,039 |
100 |
0,391 |
| 1 |
86 |
0,336 |
177 |
0,691 |
183 |
0,715 |
| 2 |
74 |
0,289 |
26 |
0,102 |
27 |
0,105 |
| 3 |
22 |
0,086 |
161 |
0,629 |
16 |
0,063 |
| 4 |
138 |
0,539 |
42 |
0,164 |
75 |
0,293 |
| 5 |
214 |
0,836 |
145 |
0,566 |
224 |
0,875 |
| 6 |
202 |
0,789 |
58 |
0,227 |
123 |
0,480 |
| 7 |
150 |
0,586 |
129 |
0,504 |
176 |
0,688 |
| 8 |
10 |
0,039 |
74 |
0,289 |
171 |
0,668 |
| 9 |
86 |
0,336 |
113 |
0,441 |
128 |
0,500 |
| 10 |
74 |
0,289 |
90 |
0,352 |
219 |
0,855 |
Построить последовательности псевдослучайных чисел, используя табличный процессор MS Excel. Получить таблицу, аналогичную таблице 1.
Для вычисления остатка от деления рекомендуется использовать функцию ОСТАТ.
Выполнить форматирование.
Описание функции ОСТАТ
Назначение: Возвращает остаток от деления аргумента число на делитель. Результат имеет такой же знак, как и делитель.
Синтаксис
ОСТАТ
(число
;делитель
)
Число - это число, остаток от деления которого определяется.
Делитель - это число, на которое нужно разделить (делитель). Если делитель равен 0, то функция ОСТАТ возвращает значение ошибки #ДЕЛ/0!
Замечания
Функция ОСТАТ может быть выражена через функцию ЦЕЛОЕ:
ОСТАТ(n; d) = n - d*ЦЕЛОЕ(n/d)
Застосовувати псевдовипадкові числа, утворювані з допомогою програмних генераторів РВП [0, 1], правомірно в тому разі, коли статистичні характеристики їх збігаються з властивостями чисел, породжених деяким ідеальним генератором, що вибирає значення на відрізку [0, 1] рівноймовірно і незалежно одне від одного згідно із законом
| 0 |
при x<0 |
| f(x)= |
1 |
при 0 <= x<= 1 |
| 0 |
при x>1 |
Тому успішне застосування методу Монте-Карло можливе лише тоді, коли створювані генератором числа будуть випадковими
, рівномірно розподіленими на відрізку
[0, 1] і незалежними
. Зрозуміло, що за своїми конструктивними особливостями програмні датчики не можуть відтворювати випадкові числа, які повністю задовольняють перелічені вимоги. Проте для практичних цілей буває достатньо, щоб послідовність РВП [0, 1] приблизно відповідала вимогам ідеального генератора. Таке припущення перевіряється з допомогою спеціальних статистичних тестів. При цьому виконуються дві передумови.
1.Генератор псевдовипадкових чисел вважається придатним для використання, якщо він витримує набір наперед установлених тестів.
2.Якість випадкових чисел перевіряється лише один раз на попередньому етапі побудови імітаційної моделі.
Розроблено чимало тестів, котрі дають змогу оцінювати якість випадкових чисел. Серед них є загальновідомі статистичні методи перевірки гіпотез (перевірка відповідності розподілів за критеріями Пірсона або Колмогорова, виявлення кореляційної залежності між серіями випадкових чисел — автокореляції
), а також і спеціально розроблені для методу Монте-Карло критерії.
Розглянемо кілька спеціальних тестів
перевірки якості випадкових чисел. Особливість їх застосування полягає в тому, що генератор РВП [0,1] вважають за можливе використовувати лише в тому разі, коли він одночасно відповідає всім вибраним тестам (перевірка датчика припиняється, тільки-но він не відповідає черговому тесту). При цьому багато рішень щодо відповідності датчика тому чи іншому тесту експериментатор приймає на інтуїтивному рівні, спираючись на власний досвід таких досліджень.
Перевірка за моментами розподілу
Для ідеального генератора рівномерно розподілених випадкових чисел математичне сподівання
їх дорівнює Ѕ, а дисперсія дорівнює 1/12.
Перевірка на рівномірність за гистограмою
Розіб"ємо відрізок [0,1] на n рівних частин. Кожне з чисел xi
потрапить на один з таких відрізків. Нехай m1
– кількість випадкових чисел, що потрапили на перший відрізок, m1
– на другий і т.д. При цьому
m1
+m2
+... +mn
= N/
Обчислимо відносні частоти потрапляння випадкових чисел на кожний із відрізків
p1
=m1
/N; p2
=m2
/N; … pn
=mn
/N,
а далі для перевірки рівномірності псевдовппадкових чисел будується гістограма.
Якщо випадкові числа рівномірні, то для достатньо великих N гістограма (ламана лінія) має наближатися до теоретичної прямої у = 1/n.
Число розбиттів n
має бути не дуже малим, щоб можна було перевірити локальну рівномірність. Водночас і дуже велике n
нас не задовольняє, оскільки потрібно буде багато випадкових чисел (N
на два — три порядки більше за n
). На практиці n
беруть таким, що задовольняє нерівність 20 <= n
<= 50.
Перевірка зa посередніми ознаками
Дивись [1, с. 55].
Перевірка на періодичність
Якщо серед множини програмне утворюваних випадкових чисел x0
,x1
,x2
, ....xl-1
немає однакових, а xl
збігається з одним зі створених раніше чисел, то L називається відрізком
аперіодичності
. Очевидно, що L<=2k
. При дослідженні генератора випадкових чисел необхідно установити довжину відрізка аперіодичності. Якщо число необхідних для експериментів випадкових чисел менше за довжину відрізка аперіодичності L, то датчик можна використовувати. У противному разі довжину відрізка аперіодичності слід збільшити, застосувавши різні штучні прийоми, зокрема змінивши початкове число x0
або використавши інший генератор.
Перевірка на випадковість
Дивись [1, с. 57].
Перевірка генератора в "роботі"
Досить надійним методом установлення якості випадкових чисел е перевірка генератора РВП [0,1] в «роботі». Згідно з цим методом складають імітаційну модель, результат роботи якої може бути передбачений теоретично. Порівнюючи експеріментальний, здобутий за допомогою ЕОМ, і теоретичний результати, можна зробити висновки щодо придатності генератора випадкових чисел.
Для ілюстрації такого підходу перевірки якості випадкових чисел розглянемо описану далі гру. Стрілець стріляє по мішені. Якшо він у неї влучить, то отримає виграш 9 грн., а якщо промахнеться — заплатить штраф у розмірі 1 грн. Імовірність влучити в мішень становить 0,05.
Величина виграшу с випадковою величиною з таким розподілом:
| Виграш |
9 |
- 1 |
| Імовірність |
0,05 |
0,95 |
Математичне сподівання виграшу за один постріл подається у вигляді
mx
=9*0,05 + (-1)*0,95=-0,5.
Перевіримо якість випадкових чисел, наведених у табл.Д1. ([3] Таблиця випадкових цифр). Для цього, склавши імітаційну модель гри, математичне сподівання виграшу оцінюватимемо за допомогою середнього арифметичного значення виграшу 440 пострілів.
Умовимося, що влучення в ціль імітується відношенням x<=0,05, а промах — x >0,95. Із 440 пострілів (440 випадкових чисел таблиці) маємо 21 влучення. Середній виграш
xср
=(21*9+(-1)*419)/440=230/440=-0,522.
Точність оцінки математичного сподівання e = 0,022 для такого відносно невеликого числа випробувань вважається задовільною. Звідси можна дійти висновку, шо перевірений генератор випадкових
чисел придатний для розв'язування задач методом Монте-Карло.
1. Выполнить проверку правильности генерации случайных чисел по тесту "Перевірка за моментами розподілу". Результаты поместить в таблицу следующего вида. Проанализировать результаты. Сделать выводы.
| Количество испытаний |
Мультипликативно - конгруэнтный метод |
Смешанный генератор Томсона |
| Математическое ожидание |
Дисперсия |
Математическое ожидание |
Дисперсия |
| 10 |
| 50 |
| 100 |
| 200 |
| 300 |
3.
4.Выполнить проверку правильности генерации случайных чисел по тесту "Перевірка на рівномірність за гистограмою". Создать две гистограммы распределения РВП: для мультипликативно - конгруэнтного метода и для смешанного генератора Томсона.
Перед построением диаграмм рекомендуется создать две таблицы следующего вида.
| Мультипликативно - конгруэнтный метод |
Смешанный генератор Томсона |
| Карманы |
Частота |
Карманы |
Частота |
| 0,05 |
0,05 |
| 0,10 |
0,10 |
| 0,15 |
0,15 |
| 0,20 |
0,20 |
| 0,25 |
0,25 |
| 0,30 |
0,30 |
| 0,35 |
0,35 |
| 0,40 |
0,40 |
| 0,45 |
0,45 |
| 0,50 |
0,50 |
| 0,55 |
0,55 |
| 0,60 |
0,60 |
| 0,65 |
0,65 |
| 0,70 |
0,70 |
| 0,75 |
0,75 |
| 0,80 |
0,80 |
| 0,85 |
0,85 |
| 0,90 |
0,90 |
| 0,95 |
0,95 |
| 1,00 |
1,00 |
Рекомендуется следующее оформление диаграммы.
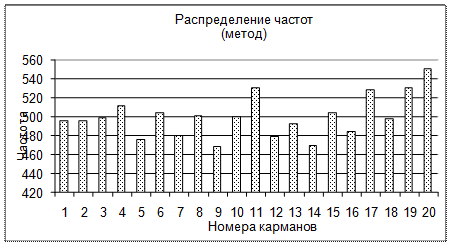
5.Выполнить проверку правильности генерации случайных чисел также по гистограмме, используя программу на языке Паскаль (Смотри Приложение 1).
С помощью программы построить три гистограммы. Проанилизировать результаты. Сделать выводы.
В отчет скопировать гистограммы и текст программы.
Цель работы - ознакомление с возможностями практического применения метода Монте-Карло (1949) – численного метода моделирования случайных величин.
Для примера взяты две задачи: вычисление числа p и вычисление определённого интеграла.
Обчислення числа p
Расчёт числа p проводится путём набрасывания случайных чисел на квадрат со сторонами равными 1, в который вписана единичная окружность. Общее число случайных точек (на отрезке [0;1) принимается за N, а число точек, попавших в круг – за М.
Число p рассчитывается как:
Чем больше проводится экспериментов, тем точнее получается результат.
Практическое задание
Провести моделирование с целью исследования зависимости точности вычисляемого значения p от числа испытаний N.
Для моделирования разработать программное средство. Провести моделирование и результаты внести в таблицу. Проанализировать результат. Сделать выводы.
Для проведения моделирования студент должен создать программу на любом из алгоритмических языков или создать электроннную таблицу. Ниже предлагается один из возможных вариантов решения задачи в табличном процессоре. таблицу отформатировать. Снабдить комментариями.
| X |
Y |
X^2+Y^2 |
Попадание в круг
(1 или 0)
|
Приближенное значение числа p |
| 4*M/N |
Вычисление
количества испытаний (N)
|
Вычисление суммы попаданий (M) |
Обчислення визначенного інтегралу методом Монте-Карло
Вычисление определенного интеграла вида
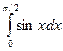
производится по приближенной формуле:
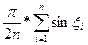 , ,
где xi
- случайная величина, xi
=p/2×g, 0<=g<=1.
Точность результата также зависит от количества испытаний
Практическое задание
Провести моделирование с целью исследования зависимости точности вычисляемого значения интеграла от числа испытаний N.
Для моделирования разработать программное средство. Провести моделирование и результаты внести в таблицу. Проанализировать результат. Сделать выводы.
Для проведения моделирования студент должен создать программу на любом из алгоритмических языков или создать электронную таблицу. Ниже предлагается один из возможных вариантов решения задачи в табличном процессоре. Таблицу отформатировать. Снабдить комментариями.
| гамма |
кси |
sin() |
Сумма |
Количество испытаний |
Интеграл |
| 0,162 |
0,255 |
0,252 |
0,669 |
12 |
0,088 |
Литература
1. Курицкий Б.Я. Поиск оптимальных решений средствами Ехсеl 7.0. - СПб.: ВНV, 1997. - 384 с.
2. Методические рекомендации к выполнению практических заданий по курсу "Имитационное моделирование" для студентов специальности 7.050102 заочной формы обучения / Сост. О.Ю.Полякова. — Харьков: Изд. ХГЭУ, 2002. — 28с.
3. Ситник В.Ф., Орленко Н.С. Імітаційне моделювання.- К.: КНЕУ, 1998.- 232c.
4. Ж.-П. Ламуатье. Упражнения по программированию на Фортране IV. Пер. с франц., под ред. Ю.М.Баяковского. – М.: Мир. 1978. с. 167.
5. Соболь И. М. Метод Монте-Карло. — 4-е изд. — М.: Наука. Главная редакция физико-математической литературы, 1985.— 80 с. — (Популярные лекции по математике).
Контрольные вопросы:
1. В чем сущность метода статистического моделирования?
2. Предельные теоремы теории вероятностей.
3. Какие способы генерации последовательностей случайных чисел используются при компьютерном моделировании?
4. Почему генерируемые на компьютере последовательности чисел называются псевдослучайными?
5. Что собой представляют конгруэнтные процедуры генерации последовательностей чисел?
6. Какие существуют методы проверки качества генераторов случайных чисел?
7. Какие существуют способы генерации последовательностей случайных чисел с заданным законом распределения на компьютере?
8. Моделирование дискретных случайных величин.
9. Чем определяется эффективность компьютерного моделирования систем?
10. Проблемы моделирования систем.
11. Особенности непрерывно-детерминированного подхода к построению математических моделей систем.
12. Особенности дискретно-детерминированного подхода к построению математических моделей систем.
13. Особенности дискретно-стохастического подхода к построению математических моделей систем.
14. Особенности непрерывно-стохастического подхода к построению математических моделей систем.
15. Параметры Q-схемы имитационного моделирования.
16. Определение однородного и неоднородного потоков событий.
17. Определение одинарного и стационарного потоков событий.
18. Определение многоканального и многофазного обслуживания.
Анализ генератора случайных чисел
В системе Турбопаскаль имеется функция random, которая дает случайное число в интервале [0,1] в соответствии с равномерным законом распределения. Можно разделить этот интервал на р
меньших интервалов одинаковой длины и найти, как случайные числа распределяются в этих р
интервалах.
Рассмотрим конкретный пример. Пусть значения случайной величины находятся в интервале: А=0; В=1. Этот интервал будем делить на 20 интервалов: р=20. Генерируются N=10 000 чисел.
Результат работы программы имеет вид гистограммы, где около каждого столбца отображается номер интервала (кармана) и значение частоты.
Ниже приведен пример гистограммы.
Histogram
1 502 **************************************************
2 456 **********************************************
3 470 ***********************************************
4 528 *****************************************************
5 468 ***********************************************
6 498 **************************************************
7 528 *****************************************************
8 534 *****************************************************
9 476 ************************************************
10 521 ****************************************************
11 503 **************************************************
12 503 **************************************************
13 491 *************************************************
14 498 **************************************************
15 451 *********************************************
16 508 ***************************************************
17 516 ****************************************************
18 529 *****************************************************
19 525 *****************************************************
20 495 **************************************************
Замечание
Кроме рассматриваемого здесь теста "по гистограмме" известны и другие, более совершенные статистические тесты для проверки качества генератора случайных чисел [*].
*) Кнут. искусство программирования. Т.2.
Пояснение к алгоритму
При составлении программы авторам [5, с. 103-107] предстояло преодолеть одно затруднение - определить, к какому интервалу относится получаемое случайное число.
Один из возможных методов состоит в выполнении последовательности проверок, которые позволяли бы определить, в какой интервал попадает число. Этот метод легко программируется, но программа получается длинной и медленной.
Самый быстрый метод заключается в определении целой переменной J
, соответствующей номеру интервала, к которому относится число. Например, для интервала [0,1], разделенного на 20 классов длиной 0.05, можно получить значение J
следующим образом:
J=
целое (20 х) +1
х=0.03®целое(0.6)+1
х=0.06®целое(1.2)+2
Чтобы подсчитать число элементов в каждом классе, можно действовать следующим образом:
1) получить случайное число х,
2) вычислить J
,
3) установить T(J)=T(J)+1, где Т – массив из р элементов и каждый элемент T(J) служит счетчиком для класса J.
Программа
uses Crt;
Var
a,b,p,n,i,j: integer;
Var
t: array [1..20] of integer;
Var
h1,x:Real;
Var
rp,y:Real;
Var
aa: array [1..72] of string[1];
Var
k: integer;
Begin
clrscr;
randomize
;
{ writeln('a=0,b=20');
readln(a,b);
writeln('p=20');
readln(p);
writeln('n=10000');
readln(n);}
a:=0;b:=20;p:=20;n:=10000;
for i:=1 to p do t[i]:=0;
h1:=p/(b-a);
for i:=1 to n do
begin
x:=random(b)
;
j:=trunc((x-a)*h1)+1;
t[j]:=t[j]+1
end;
clrscr;
for i:=1 to p do
writeln(i:3,t[i]:10);
readln;
rp:=p;
for i:=1 to p do t[i]:=0;
for i:=1 to n do
begin
y:=random
;
j:=trunc(rp*y)+1;
t[j]:=t[j]+1;
end;
Clrscr;
Writeln('*******');
for i:=1 to p do writeln(i:3,t[i]:10);
readln;
Clrscr;
writeln('Histogram');
for i:=1 to 72 do aa[i]:='*';
for i:=1 to p do
begin
k:=trunc((t[i]+5)/10);
write(i:2,t[i]:4,' ');
{writeln ('k=',k:3);}
for j:=1 to k do write(aa[j]);writeln;
end;
readln
end.
|