| Министерство Образования Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кафедра Телекоммуникационных Систем
Курсовая работа по ТЭС
Расчет системы передачи дискретных сообщений
Вариант 9.
Выполнил: ст. гр. МКС-311 Котов Д.
Проверил: Комиссаров А.М.
Уфа 2004 г.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ по курсу
"ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ"
Рассчитать основные характеристики системы передачи сообщений (рис.1), включающий в себя источник сообщений (ИС), дискретизатор (Д), кодирующее устройство (Кодер), модулятор (Мод), линия связи, демодулятор (Дем), декодер (Дек) и фильтр-восстановитель (ФВ).
   
            
Рис. 1
Исходные данные
amin
= –6,4 B;
amax
= 6,4 B;
Fc
= 15*103
Гц;
j = 79;
i = 5;
Вид модуляции АМ;
N0
= 1,09·10-7
B2
/Гц;
Способ приема когерентный.
Источник сообщений
Источник сообщений выдает сообщение а(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале а min
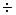 a max
распределены равномерно, а мощность сосредоточена в полосе частот от 0 до Fc
. a max
распределены равномерно, а мощность сосредоточена в полосе частот от 0 до Fc
.
Требуется:
1. 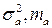 Записать аналитические выражения и построить график одномерной плотности вероятности мгновенных значений сообщения а(t). Записать аналитические выражения и построить график одномерной плотности вероятности мгновенных значений сообщения а(t).
2. Найти мат. ожидание и дисперсию сообщения а(t)
3. Построить график случайного процесса и на графике обозначить max значение сигнала, математическое ожидание и среднеквадратичное отклонение.
1) Для непрерывных процессов Х(t) распределение вероятностей в заданный момент времени t1
характеризуется одномерной плотностью вероятности (ПВ):
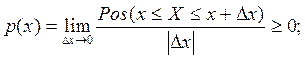
выражающей отношение вероятности того, что случайная величина Х(t) примет значения в интервале 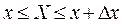 , к величине интервала , к величине интервала  . .
Вероятность того, что случайная величина Х примет значение в интервале
(x1,
х2
) определяется выражением:
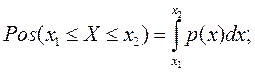
Из условия нормировки для достоверного события имеем:
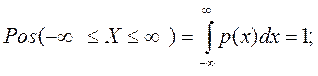
В нашем случае ПВ имеет вид равнобедренного треугольника.
 

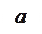 
 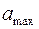
ПВ при треугольном распределении на интервале (аmin
,amax
) изменяется по определенному закону и равна 0 вне этого интервала.
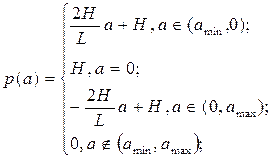
Где L длина основания треугольника:
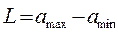 ; ;
L=12.8 В;
Высота треугольника H можно найти из условия нормировки т.к. площадь треугольника равна 1, то

Зная, что 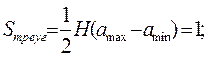
Найдем высоту H:
 ; ;
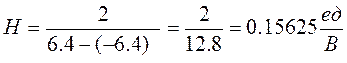 ; ;
Аналитическое выражение для треугольного закона распределения вероятности:
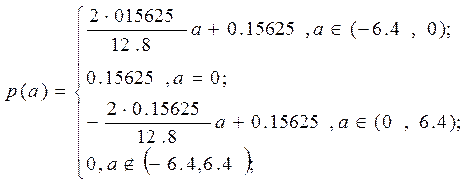
2) Математическое ожидание (МО) определяет среднее значение случайной величены
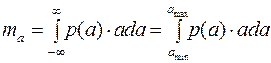 ; ;
и для треугольного распределения ПВ имеет вид:


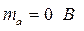 . .
Дисперсия 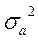 характеризует разброс случайной величены относительно ее среднего значения (физический смысл - средняя мощность отклонения от некоторой средней величины). характеризует разброс случайной величены относительно ее среднего значения (физический смысл - средняя мощность отклонения от некоторой средней величины).
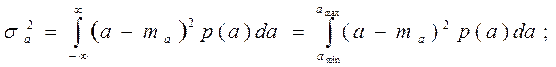
Для треугольного распределения ПВ:

Т.к.  , получим: , получим:
 В итоге В итоге 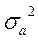 =6.827 В2
. =6.827 В2
.
Величину  называют стандартным или среднеквадратическим отклонением (СКО). называют стандартным или среднеквадратическим отклонением (СКО).
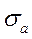 =2.613 В. =2.613 В.
3)

amin
= –6,4 B, amax
= 6,4 B, 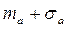 =2,613 В, =2,613 В, 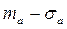 =-2,613 В, =-2,613 В, 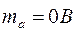 . .
Дискретизатор
Передача непрерывного процесса осуществляется дискретными методами. Для этого сообщение а(t) дискретизируется по времени и квантуется по уровню с равномерным шагом. Шаг квантования по уровню Dа= 0,1В.
Требуется:
1. Определить шаг дискретизации по времени (Dt).
2. Определить число уровней квантования (L).
3. Рассчитать среднюю мощность шума квантования.
4. Рассматривая дискретизатор как источник дискретного сообщения с объемом алфавита L, определить его энтропию и производительность (Н, Н’
), отсчеты, взятые через интервал Dt считать независимыми.
1) По теореме Котельникова, в полосе частот [0 , Fc
] Гц шаг дискретизации по времени; 
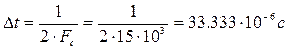 . .
2) Число уровней квантования L при равномерном шаге определяется как частное от деления размаха сигнала на шаг квантования Dа. Число уровней квантования L равно:
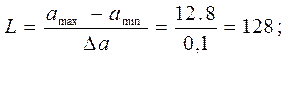
3)Поскольку квантование по уровню производится с равномерным шагом , то закон распределения шума квантования  также будет равномерным и не будет зависеть от номера интервала квантования. Тогда на интервале также будет равномерным и не будет зависеть от номера интервала квантования. Тогда на интервале
МО (среднее значение шума квантования ) будет равно нулю, а средняя мощность (дисперсия шума квантования):

4)Энтропия – это средняя информативность источника на один символ, определяющая ‘неожиданность’ или ‘непредсказуемость’ выдаваемых им сообщений. Полностью детерминированный источник, выдающий лишь одну, заранее известную последовательность, обладает нулевой информативностью. Наоборот, наиболее ‘хаотический’ источник, выдающий
взаимно независимые и равновероятные символы, обладает максимальной информативностью.
Для источника, не обладающего памятью с алфавитом А энтропия записывается следующим образом:

Где L – объем алфавита ,  , i=1,2,3,…,L-вероятности выдачи источником символов , i=1,2,3,…,L-вероятности выдачи источником символов  , причем они не зависят от номера элемента последовательности, т.к. источник является стационарным. , причем они не зависят от номера элемента последовательности, т.к. источник является стационарным.
Для треугольного распределения ПВ
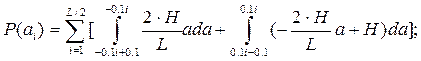
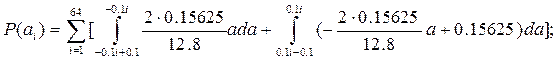
Таким образам энтропия равна:
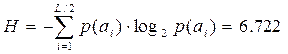 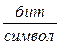 ; ;
Если источник сообщения имеет фиксированную скорость  символ/с, то производительность источника можно определить, как энтропию в единицу времени, (секунду): символ/с, то производительность источника можно определить, как энтропию в единицу времени, (секунду):

Кодер
Кодирование осуществляется в два этапа.
Первый этап:
Производится примитивное кодирование каждого уровня квантованного сообщения k– разрядным двоичным кодом.
Второй этап:
К полученной k– разрядной двоичной кодовой комбинации добавляются проверочные символы, формируемые в соответствии с правилами кодирования по коду Хэмминга.
В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют символу «0», а отрицательные – символу «1» кодовой комбинации.
Требуется:
1. Определить число разрядов кодовой комбинации примитивного кода k, необходимое для кодирования всех L уровней квантованного сообщения.
2. Определить избыточность кода при использовании кодирования Хэмминга.
3. Записать двоичную кодовую комбинацию, соответствующую передаче j-го уровня, считая, что при примитивном кодировании на первом этапе j-му уровню ставится в соответствии двоичная кодовая комбинация, представляющая собой запись числа j в двоичной системе счисления. В полученной кодовой комбинации указать информационные и проверочные разряды.
4. Определить число двоичных символов, выдаваемых кодером в единицу времени Vn
и длительность двоичного символа T.
1)Для кодирования L =128 уровней квантованного сообщения число разрядов двоичной кодовой комбинации:
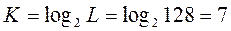 ; ;
Число проверочных разрядов r для исправления однократной ошибки должно удовлетворять неравенству:
 ; ;
В итоге решение неравенства получаем r =4. Тогда длина всей кодовой комбинации:

2)Определим избыточность кода при использовании кодирования Хэмминга.
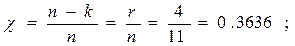
3) j=79 Его двоичная комбинация (занимающая К=7 разрядов). Проверочные символы располагаются 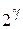 позициях, где позициях, где  =0,1,2,… =0,1,2,…
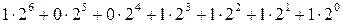
1 0 0 1 1 1 1
  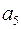   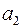 
b11
b10
b9
b7
b6
b5
b3
Определим проверочные символы (они располагаются на 1,2,4,8 позициях):
b1
= b3
 b5 b5
 b7 b7
 b9 b9
 b11
r1
=b1 b11
r1
=b1
 b3 b3
 b5 b5
 b7 b7
 b9 b9
 b11 b11
b2
= b3
 b6 b6
 b7 b7
 b10 b10
 b11
r2
= b2 b11
r2
= b2
 b3 b3
 b6 b6
 b7 b7
 b10 b10
 b11 b11
b4
= b5
 b6 b6
 b7
r3
= b4 b7
r3
= b4
 b5 b5
 b6 b6
 b7 b7
b8
= b9
 b10 b10
 b11
r4
=b8 b11
r4
=b8
 b9 b9
 b10 b10
 b11 b11
b8
b4
b2
b1
Проверочные символы:
1 0 0 0 1 b1
=0 r1
=0
2 0 0 1 0 b2
=0 r2
=0
3 0 0 1 1 b4
=1 r3
=0
4 0 1 0 0 b8
=1 r4
=0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1
В итоге получим кодовую комбинацию, содержащую информационные и проверочные разряды:
1 0 0 1 1 1 1 1 1 0 0
4) Число двоичных символов Vn
, выдаваемых кодером в единицу времени,
определяется числом отсчетов в секунду ( ) и числом двоичных символов ) и числом двоичных символов 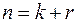 , приходящихся на один отсчет: , приходящихся на один отсчет:
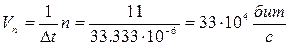 ; ;
Длительность T двоичного символа определяется как :
 ; ;
Модулятор
В модуляторе синхронная двоичная случайная последовательность биполярных импульсов b(t) осуществляет модуляцию гармонического переносчика
Um
= cos(2πft), (Um
=1В, f = 100 ×Vn
Гц)
При АМ «0» соответствует сигнал U1
(t) = 0,
символу «1» - U2
(t) = Um
cos(2πft).
Требуется:
1. Записать аналитическое выражение модулированного сигнала U(t)=φ(b(t)).
2. Изобразить временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передачи j-го уровня сообщения a(t).
3. Привести выражение и начертить график корреляционной функции модулирующего сигнала В(τ).
4. Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала Gb
(f).
5. Определить ширину энергетического спектра модулирующего сигнала ∆Fb
из условия ∆Fb
=αVk
(где α выбирается в пределах от 1 до 3). Отложить полученное значение ∆Fb
на графике Gb
(f).
6. Привести выражение и построить график энергетического спектра Gu
(f) модулированного сигнала.
7. Определить ширину энергетического спектра ∆Fu
модулированного сигнала и отложить значение ∆Fu
на графике Gu
(f).
1) Модуляция – изменение по заданному закону во времени величин, характеризующих какой-либо регулярный физический процесс. Под модуляцией колебаний понимают изменение амплитуды, частоты, фазы и т. д. В случае амплитудной модуляции (АМ) несущее колебание промодулировано по закону изменения амплитуды первичного сигнала. Несущее колебание – это синусоидальное колебание высокой (несущей) частоты, амплитуда которого модулируется передаваемым сигналом.
Модулятор, составная часть передатчика в каналах электросвязи, с помощью которой осуществляется управление параметрами гармонических электромагнитных колебаний, т. е. модуляцией колебаний. Управляющий элемент модулятора – транзистор, электронная лампа, клистрон, ячейка Керра и т. д.
Аналитическое выражение для АМ модулированного сигнала:
 ; ;
 ; ;
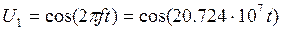 . .
2) Временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передачи j-го уровня сообщения a(t).

3) Корреляция, в математической статистике – вероятностная или статистическая зависимость. Корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов.
Корреляционная функция дает качественное представление о линейной зависимости между значениями одной или двух случайных функций в выбранные моменты времени.
Свойства корреляционной функции:
- Корреляционная функция четна:

- Абсолютное значение автокорреляционной функции при любых
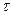 не может превышать значения при не может превышать значения при 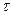 =0. =0.

· корреляционная функция имеет максимум при 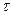 =0. =0.
· абсолютное значение корреляционной функции ограничивается значением дисперсии.
- Случайные процессы, наблюдаемые в стационарно устойчиво работающих системах имеют конечное время корреляции:
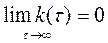
Корреляционная функция случайного синхронного телеграфного биполярного сигнала с единичной высотой импульсов имеет следующий вид:
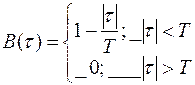 , где T длительность импульсов. , где T длительность импульсов.
 


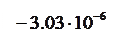   
4) Спектральная плотность величины – предел отношения величины (напряжения, мощности и др.), соответствующий узкому участку оптического спектра, к ширине этого участка.
Для нахождения спектральной плотности мощности Gb
(f) сигнала b(t) необходимо воспользоваться теоремой Хинчина - Винера, которая устанавливает связь между энергетическим спектром корреляционной функцией случайного процесса.
Спектральная плотность мощности модулирующего сигнала Gb
(f):
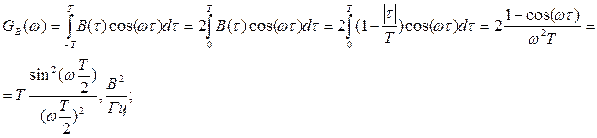
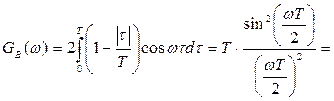
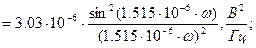
График спектральной плотности мощности модулирующего сигнала Gb
(f):
| Gb
(f),B2
/Гц
|
3.03×10-6
|
9.743×10-9
|
1.335×10-7
|
9.395×10-9
|
4.373×10-8
|
2.962×10-10
|
| f,Гц
|
1
|
3.5×105
|
5×105
|
7×105
|
8.5×105
|
106
|
  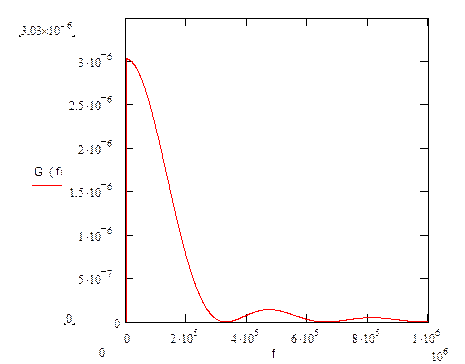
5) На графике видно , что вся энергия модулирующего сигнала сосредоточена в полосе ∆Fb
Гц.
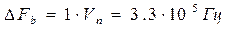
6) График спектральной плотности мощности модулированного сигнала Gb
(f).:
       
В результате модуляции исходный спектр сдвигается на частоту модулируемого колебания. Если известен спектр модулирующего сигнала , можно найти спектр амплитудно-модулированного сигнала. Энергетический спектр амплитудно-модулированного сигнала  содержит содержит 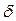 -функцию на частоте f=f0
верхнюю и нижнюю боковые полосы. Наличие -функцию на частоте f=f0
верхнюю и нижнюю боковые полосы. Наличие 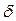 -функции в энергетическом спектре отражает наличие несущей частоты при амплитудной модуляции. Форма верхней боковой полосы энергетического спектра АМ сигнала совпадает с формой энергетического спектра модулирующего сигнала b(t), а форма нижней – совпадает с зеркальным спектром сигнала b(t). -функции в энергетическом спектре отражает наличие несущей частоты при амплитудной модуляции. Форма верхней боковой полосы энергетического спектра АМ сигнала совпадает с формой энергетического спектра модулирующего сигнала b(t), а форма нижней – совпадает с зеркальным спектром сигнала b(t).
7) Ширина энергетического спектра при АМ будет в два раза больше ширины энергетического спектра модулирующего сигнала.
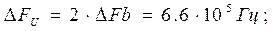
Канал связи
Передача сигнала U(t) осуществляется по каналу с постоянными параметрами и аддитивным флуктуационным шумом n(t) с равномерным энергетическим спектром N0
/2 (белый шум).
Сигнал на выходе такого канала можно записать следующем образом:
z(t) = U(t) + n(t) , U(t)- полезный сигнал, n(t)- аддитивная помеха.
Требуется:
1. Определить мощность шума в полосе частот Fk
= ∆Fu
;
2. Найти отношение сигнал – шум Рс
/Рш
;
3. Найти пропускную способность канала С;
4. Определить эффективность использования пропускной способности канала Кс
, определив ее как отношение производительности источника Н’
к пропускной способности канала С.
1) В каналах связи аддитивные помехи возникают по различным причинам и могут принимать различные формы, индивидуальные реализации которых трудно учесть. Такие помехи чаще вызывают необратимые изменения передаваемых сигналов. Аддитивные помехи по своей структуре разделяют на три основных класса: распределенные по частоте и времени (флуктуационные), сосредоточенные по частоте (квазигармонические) и сосредоточенные во времени (импульсные).
Флуктуационные помехи порождаются в системах связи случайными отклонениями тех или иных физических величин (параметров) от их средних значений. Источником такого шума в электрических цепях могут быть флуктуации тока, обусловленные дискретной природой носителей зарядов.
Наиболее распрастраненной причиной шума в аппаратуре связи являются флуктуации, обусловленные тепловым движением.
Зная спектральную плотность мощности N0
можно определить мощность шума Рш
в полосе ∆Fu
(промодулированного сигнала).
 ; ;
2) При определенном отношении 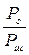 , для двоичных равновероятных сигналов U1
(t) и U2
(t) их средняя мощность будет ровна: , для двоичных равновероятных сигналов U1
(t) и U2
(t) их средняя мощность будет ровна:
 , В2
; , В2
;
где  и и 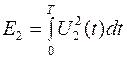 , где T- длительность сигналов. , где T- длительность сигналов.
Символу “0” cоответствует сигнал  ; ;
Символу “1” cоответствует сигнал 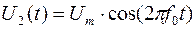 ; ;
Если передается “0” то  ; ;
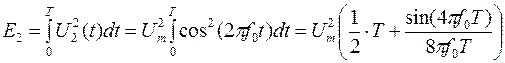 ; ;
Так как  , поэтому , поэтому  ; ;
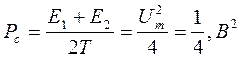 ; ;
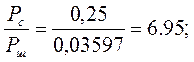
3) Под пропускной способностью понимают количество, данных которое может быть передано по каналу за 1 секунду.
 ; ;
4) Эффективность использования пропускной способности канала Кс
:
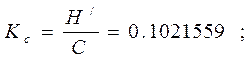
Демодулятор
В демодуляторе осуществляется оптимальная когерентная или некогерентная (в зависимости от варианта) обработка принимаемого сигнала z(t) = U(t) + n(t)
Требуется:
1. Записать алгоритм оптимального приема по критерию минимума средней вероятности ошибки при равновероятных символах в детерминированном канале с белым гауссовским шумом.
2. Нарисовать структурную схему оптимального демодулятора для заданного вида модуляции и способа приема.
3. Вычислить вероятность ошибки рш
оптимального демодулятора.
4. Определить, как нужно изменить энергию сигнала, чтобы при других видах модуляции и заданном способе приема обеспечить найденное значение вероятности ошибки рш
.
1)Канал с аддитивным гауссовским шумом отображается линейной цепью с постоянной передаточной функцией, сосредоточенной в определенной полосе частот. Допустимы любые входные сигналы, спектр которых лежит в определенной полосе частот Fc
, имеющие ограниченную среднюю мощность Рс
(либо пиковую мощность Рпик
).
Предположим , что все искажения в канале строго детерминированы и случайным является только гауссовский белый аддитивный шум со спектральной плотностью N0
. Это значит что при передаче символа “1”
принимаемое колебание можно записать математической моделью z(t) = U2
(t) + n(t) , где U2
(t)- известный переносчик для символа “1”. Передаче символа “0” соответствует известный переносчик U1
(t): z(t) = U1
(t) + n(t).
Неизвестна реализация помехи и позиция (индекс 1 или 2), переданного сигнала , который и должна распознать решающая схема. Распознавание осуществляется на основе метода идеального наблюдателя (Котельникова).
Для когерентного приемника границы начала и конца принимаемого сигнала
точно известны, т.е. передаваемые сигналы финитны и имеют одинаковую длительность, а в канале нет ни многолучевого распространения, ни линейных искажений, вызывающих увеличение длительности сигнала (либо они скорректированы).
В таком случае алгоритм приема, который осуществляет оптимальный приемник над входным колебанием, имеет вид:
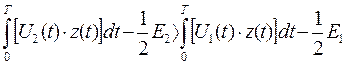
Если неравенство выполняется , то приемник регистрирует “1”, в противном случае “0”.
Т.к. сигнал  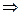  , следовательно , следовательно
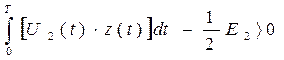
 (*) (*)
2) Структурная схема оптимального когерентного демодулятора, реализующего неравенство *.
На схеме Х-перемножитель,  интегратор, интегратор,  вычитающее устройство, вычитающее устройство,
РУ-решающее устройство, определяющее в моменты времени кратные Т
максимальный сигнал.

             1 1
0
3) Вероятность ошибки рш
оптимального когерентного демодулятора для канала с аддитивным нормальным белым шумом при передаче двоичных сообщений вычисляется следующим выражением:
рш
= 1/2 (1-Ф(х)) ,
где Ф(х) – функция Крампа или интеграл вероятностей
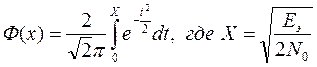
Еэ
– эквивалентная энергия сигналов, определяется следующим образом:
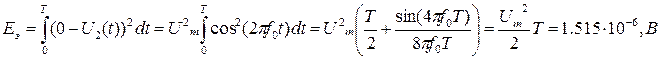

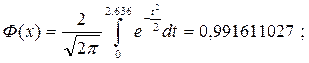
рш
=0.5×(1-0,991611027) =0,004194486;
4) ФМ является наиболее помехоустойчивым видом модуляции при равных энергетических затратах по сравнению АМ и ЧМ. Энергетический выигрыш ее составляет в четыре раза по сравнению с АМ и в два раза по сравнению с ЧМ.
Таблица сравнения.
| Вид модуляции
|
По средней мощности
|
По пиковой мощности
|
| ЧМ
|
1
|
2
|
| ФМ
|
2
|
4
|
| АМ
|
1
|
1
|
Декодер
В декодере декодирование осуществляется в два этапа. На первом этапе производится обнаружение и исправление ошибки в кодовой комбинации. Считать, что ошибка произошла в i-ом разряде. На втором этапе из нее выделяются информационные символы, а затем k – разрядная двоичная кодовая комбинация преобразуется в элемент квантованного сообщения.
Требуется:
1. Оценить обнаруживающую способность q0
кода Хэмминга.
2. Записать алгоритм обнаружения ошибок.
3. Определить вероятность не обнаружения ошибки.
1) По теореме Хемминга для того чтобы код позволял исправлять все ошибки в z (или менее) позициях , необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было:

Наш код исправляет одну ошибку  и обнаруживает и обнаруживает
 ошибки. ошибки.
2) Декодер получает от демодулятора некоторую последовательность двоичных символов b1
, b2
,b3
,…, bi
,…, bn
. В ней может быть ошибка.
Декодер позволяет исправить однократную ошибку и определить наличие
двукратной ошибки.
В декодере формируется т.н. проверочный синдром. По коду синдрома с помощью проверочной матрицы можно определить местоположение ошибки.
Кодовая последовательность: 10011111100 (j=79).
i=5  кодовая последовательность с ошибкой: 10011101100 . кодовая последовательность с ошибкой: 10011101100 .
Определим код синдрома.
1 0 0 1 1 1 0 1 1 0 0
b11
b10
b9
b8
b7
b6
b5
b4
b3
b2
b1
r1
=b1
 b3 b3
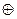 b5 b5
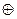 b7 b7
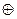 b9 b9
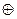 b11
r1
=1 b11
r1
=1
r2
= b2
 b3 b3
 b6 b6
 b7 b7
 b10 b10
 b11
r2
= 0 b11
r2
= 0
r3
= b4
 b5 b5
 b6 b6
 b7
r3
= 1 b7
r3
= 1
r4
=b8
 b9 b9
 b10 b10
 b11
r4
=0 b11
r4
=0
r1
r2
r3
r4
=1010=510
Т.о. разряд №5 является ошибочным. его инвертируем и получаем:
1 0 0 1 1 1 1 1 1 0 0
3) Вероятность не обнаружения ошибки определяется по формуле:
 ; ; ; где ; где
n – число разрядов, 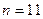 ; ;
q-обнаруживающая способность кода Хэмминга, q=2.
р – вероятность ошибки в одном разряде, р=0,004194486 .
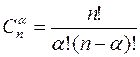 -общее число различных выборок объема -общее число различных выборок объема 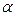 . .
 . .
Фильтр – восстановитель.
Фильтр–восстановитель – фильтр нижних частот с частотой среза Fc
.
Требуется:
1. Указать величину Fc
.
2. Изобразить идеальные АЧХ и ФЧХ фильтра – восстановителя.
3. Найти импульсную характеристику g(t) идеального фильтра – восстановителя и начертить ее график.
1)Частота среза связана с временем дискретизации 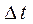 .Из теоремы Котельникова: .Из теоремы Котельникова:
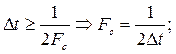
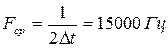 ; ;
2)Передаточная функция идеального ФНЧ:
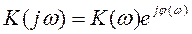 , где , где
j= , ,
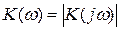 -АЧХ. -АЧХ.
 -ФЧХ. -ФЧХ.
Идеальная АЧХ фильтра – восстановителя имеет вид:

ФЧХ для идеального фильтра.

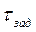 - время задержки (величина порядка 10-4
– 10-5
с). - время задержки (величина порядка 10-4
– 10-5
с).

3) Импульсная переходная характеристика берется как обратное преобразование Фурье:
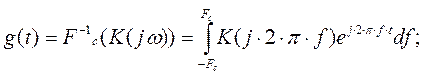
Будем считать, что фильтр работает на низких частотах и время задержки достаточно малая величина.
Если 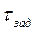 =0, то =0, то 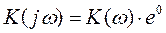 , тогда , тогда
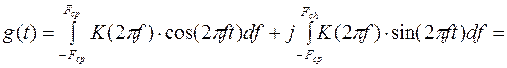
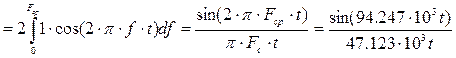 . .
Таблица.
| t,c
|
1
|
0.00002
|
0.000005
|
0.00006
|
0.00007
|
0.000075
|
0.000085
|
| g(t)
|
0
|
1.009
|
1.926
|
-0.207
|
0.0936
|
0.2
|
0.246
|
График импульсной характеристики g(t).

Таблица результатов.
| H (высота),
|
 , В , В
|
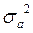 , В2 , В2
|
 , с , с
|
L (число уровней)
|
| 0,15625
|
0
|
6.827
|
33.333·10-6
|
128
|
| Ршк
, В2
|
Н, 
|
Н’,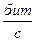
|
n, (число разрядов)
|
 ,(избыточность кода) ,(избыточность кода)
|
| 8,33·10-4
|
6,722
|
201662.0166
|
11
|
0,3636
|
| Vn
, 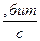
|
Т, с
|
f, Гц
|
 , Гц , Гц
|
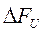 , Гц , Гц
|
| 33·104
|
3.03·10-6
|
33·106
|
3.3·105
|
6.6·105
|
| Рс
, В2
|
Рш
, В2
|
С, 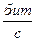
|
рш
|
рно
|
| 0.25
|
0.03597
|
1974060
|
0.004194486
|
0,00001187
|
|