| Медико-биологический лицей г. Саратова.
Предмет:
математика.
ОПРЕДЕЛИТЕЛИ И ИХ ПРИМЕНЕНИЕ В АЛГЕБРЕ И ГЕОМЕТРИИ.
Выполнили:
Дёмин Дмитрий,
Грачёв Денис ученики 11 «б» класса МБЛ.
Руководитель:
Винник Нина Дмитриевна
Учитель математики.
Саратов 2007 г.
Содержание
Введение.
Глава 1 Определители.
1. Определения.
2. Пример вычисления определителя второго порядка в общем виде.
3. Свойства определителя.
4. Доказательства свойств определителя.
5. Пример применения правила Крамера для решения систем из n уравнений с n неизвестными.
Глава 2 Векторное произведение.
1. Определения.
2. Свойства векторного произведения.
3. Доказательства свойств векторного произведение.
4. Смешанное произведение.
5. Векторное произведение векторов заданных проекциями.
6. Примеры решение задач (с использованием определителей).
Вывод.
Список литературы.
Введение
В алгебре существует широкий класс задач, решение которых является громоздким и трудным методами элементарной математики. Например, решение системы n линейных уравнений, с n неизвестными методом Жордана – Гаусса требует длительных вычислений и, как правило, часто ведёт к ошибке.
Теория определителей позволяет решать и исследовать системы с малыми затратами используя правило Крамера, рассматриваемое в этой работе.
(данную часть работы приготовил ученик 11 «б» класса Медико-биологического лицея Дёмин Дмитрий).
При вычислении площадей, объёмов в пространстве часто удобно пользоваться векторным и смешанным произведениями векторов, вычисляя определитель координат векторов, что представлено в работе.
(данную часть работы приготовил ученик 11 «б» класса Грачёв Денис).
Глава 1. Определители
1.
Определения
Опр.
Матрица – прямоугольная таблица, составленная из элементов произвольной природы. Элементы матрицы располагаются в строки и столбцы (иногда их называют колонками). Строки и столбцы часто называют собирательным термином «ряды матрицы». Элементы матрицы часто обозначают двойными индексами – aij
; первый индекс i означает номер строки матрицы, в которой стоит элемент aij
, а второй индекс j означает номер столбца матрицы, в котором стоит aij
. Матрицы символически обозначают заключёнными в круглые или квадратные скобки, или двойные вертикальные черточки. (Кратко: (aij
) или IIaij
II).
Каждой квадратной матрице, элементами которой являются числа, ставится в соответствие число, называемое определителем матрицы
.
Опр.
Определитель (детерминант) n-го порядка – алгебраическая сумма n! слагаемых членов из элементов квадратной матрицы (таблицы), которое вычисляется по следующему закону: каждое слагаемое есть произведение n элементов взятых по одному и только по одному из каждой строки и из каждого столбца матрицы. Каждый член определителя берётся со знаком (-1)t
, где t – число инверсий во вторых индексах члена, когда первые индексы члена расположены в натуральном порядке.
2. Пример вычисления определителя второго порядка в общем виде
Пусть матрица A=  , тогда ее определитель будет содержать 2!=2 слагаемых: , тогда ее определитель будет содержать 2!=2 слагаемых:
a11
a22
и + a21
a12
, так как в перестановке  нет инверсий, следовательно, (-1)0
= -1, а в перестановке нет инверсий, следовательно, (-1)0
= -1, а в перестановке 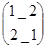 есть одна инверсия есть одна инверсия  и (-1)1
= -1. и (-1)1
= -1.
Значит, 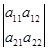 = a11
a22
– a21
a12 = a11
a22
– a21
a12
Минором или алгебраическим дополнением элемента aij
квадратной матрицы или ее определителя, называется определитель порядка n-1, который получается из исходного вычеркиванием i – той строки и j – того столбца.
3. Свойства определителя
Определитель обладает рядом свойств:
1) Определитель не изменяется при транспортировании матриц (строк и столбцов).
2) Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.
3) Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.
4) Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.
5) Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.
6) Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).
7) Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.
4. Доказательства свойств определителя
Свойство №1:
Определитель не изменяется при транспортировании матриц (строк и столбцов).
Доказательство:
Опр.
Матрицы Aji
называется транспонированной матрицей Aij
   = det A = det A 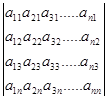 = det AT = det AT
det A = det AT
Выберем любое слагаемое из суммы определителя.
a1i
a2j
… ank
  
ai1
aj2
… akn
сумме det AT

Следовательно определители равны.
Свойство №2:
Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.
Доказательство:
Пусть дана матрица, один столбец которой равен 0.
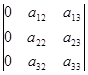 =detA подсчитаем определитель данной матрицы. =detA подсчитаем определитель данной матрицы.
Подсчитаем определитель данной матрицы, используя правило равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям.
        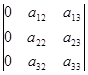 =0*а22
*а33
+а12
*а23
*0+а32
*а13
*0 = 0 =0*а22
*а33
+а12
*а23
*0+а32
*а13
*0 = 0
     =-(а13
*а22
*0+а12
*а33
*0+а23
*а32
*0)=0 =-(а13
*а22
*0+а12
*а33
*0+а23
*а32
*0)=0
Свойство доказано.
Свойство №3:
Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.
Доказательство:
Возьмём матрицу определитель которой равен detA и переставим в ней 2 столбца. Получим:
 ,
после перестановки получим: ,
после перестановки получим: 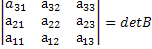 . .
Посчитаем определители обеих матриц. Получим:
det A=(-1)0
*((a11
*a22
*a33
+a12
*a23
*a31
+a21
*a32
*a13
)-(a13
*a22
*a31
+a21
*a12
*a33
+a32
*a23
*a11
))
det B=(-1)2
*((a31
*a22
*a13
+a21
*a12
*a33
+a32
*a23
*a11
)-(a33
*a22
*a11
+a12
*a23
*a31
+a21
*a32
*a13
))
(a11
*a22
*a33
+a12
*a23
*a31
+a21
*a32
*a13
)-(a13
*a22
*a31
+a21
*a12
*a33
+a32
*a23
*a11
) +(a31
*a22
*a13
+a21
*a12
*a33
+a32
*a23
*a11
)-(a33
*a22
*a11
+a12
*a23
*a31
+a21
*a32
*a13
)=0
Получили, что det A=-det B.
Свойство доказано.
Свойство №4:
Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.
Доказательство:
Возьмём матрицу, в которой элементы первого столбца равны aij
+bj
и посчитаем её определитель.

 . .
Раскроем скобки и приведём подобные слагаемые.
      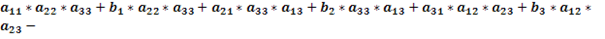
     
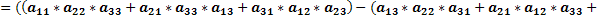
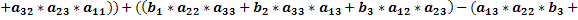
 . .
То есть:  . .
Свойство доказано.
Свойство №5:
Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.
Доказательство:
Пусть дан определитель detA≠0, содержащий две равные строки.
  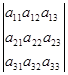 = detA ; = detA ;  = = 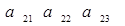
Поменяем местами эти равные строки. Получим новый определитель.
 . .
Так как данный определитель получен из определителя detA перестановкой строк, то из предыдущего свойства следует, что полученный определитель принимает значение –detA. В то же время, количество слагаемых и модуль значений определителей detA и –detA равны, то справедливо будет равенство detA=-detA. Из данного равенства следует что detA
=0
. Свойство доказано.
Свойство №6:
Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).
Доказательство:
Возьмём матрицу коэффициентов и посчитаем её определитель.


Прибавим к первому столбцу третий. Получим новую матрицу.
 . .
Посчитаем её определитель.


  
  
 

 . .
Свойство №7:
Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.
Доказательство:
Возьмём матрицу и посчитаем её определитель.


То есть. 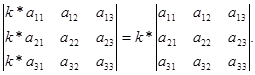
Свойство доказано.
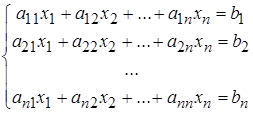
 
5. Пример применения правила Крамера для решения систем
n
уравнений с
n
неизвестными
Определители очень широко используются при решении и исследовании систем линейных n уравнений с n неизвестными. Правило решения такой системы с помощью определителей называется правилом Крамера.
Покажем это правило на примере.
Правило Крамера:
правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных  , где , где  - определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а - определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а  I
– определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений. I
– определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.
Пусть дана система из трех уравнений с тремя неизвестными:
 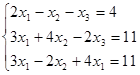
Посчитаем определитель матрицы системы, составленной из коэффициентов при неизвестных:
 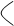          
После подсчета определителя системы, подсчитаем определители неизвестных. Для этого вырезаем из 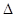 столбец данной переменной, а на его место ставим столбец свободного члена. столбец данной переменной, а на его место ставим столбец свободного члена.
       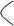    = =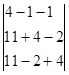 = = = 6 = 6  = 6 = 6 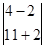 = 6*(4*2-(-2)*11)=180 = 6*(4*2-(-2)*11)=180
Согласно правилу Крамера значение неизвестной переменной равно частному от определителя данной неизвестной и определителя системы. Значит переменная x1=
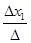 ;
x1
=
;
x1
= . .
Действуя по тому же алгоритму, найдем значения переменных x2
и x3
:
По правилу равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям матрицы получим:
      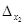 = =  2*11*4+3*11*(-1)+4*(-2)*3= 88-33-24=31 =60 2*11*4+3*11*(-1)+4*(-2)*3= 88-33-24=31 =60
    -2*(-2)*11-3*4*4 – (-1)*11*3= 44-48+33=29 -2*(-2)*11-3*4*4 – (-1)*11*3= 44-48+33=29
   Значит x2
= Значит x2
=
                      
Значит x3
=
Для доказательства истинности правила Крамера, проверим полученные значения переменных, подставив полученные значения в систему:
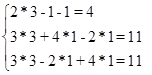 
После подстановки мы получили верное числовое равенство, значит, правило Крамера истинно для решения системы n уравнений с n неизвестными. Ответ: (3;1;1)
Глава 2.
Векторное произведение
1. Определения
Опр.
Векторным произведением двух векторов А и В называется новый вектор С длина которого численно равна площади параллелограмма построенного на векторах А и В перпендикулярный к плоскости этих векторов и направленный в такую сторону, чтобы кратчайший поворот от А к В вокруг полученного вектора С представляется происходящим против часовой стрелки, если смотреть из конца С.
Из этого определения следует, что длина вектора С равна:  . .
Следствие.
Векторное произведение равно нулевому вектору в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым, или если эти векторы параллельны (коллинеарны).

2. Свойства векторного произведения
1. При перестановке сомножителей векторное произведение умножается на (-1). То есть ВxА=-(АxВ).
2. Векторное произведение обладает свойством сочетательности относительно числового множителя:  и и  , т.е. чтобы умножить векторное произведение векторов на число, достаточно умножить на это число один из сомножителей. , т.е. чтобы умножить векторное произведение векторов на число, достаточно умножить на это число один из сомножителей.
3. Векторное произведение подчиняется распределительному закону, то есть 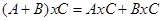 . .
4. Длина векторного произведения неколлинеарных векторов А и В численно равна площади параллелограмма, построенного на приведённых к общему началу векторах А и В, как на сторонах.
3. Доказательства свойств
1. В самом деле, площадь параллелограмма, построенного на векторах А и В, а также и его плоскость не меняются при перестановке А и В. Поэтому векторы А*В и В*А имеют одинаковые длины и коллинеарны. Направления же этих векторов противоположны; действительно, если смотреть на плоскость векторов А и В с конца вектора А*В, то кратчайший поворот от В к А будет казаться происходящим по часовой стрелке. Следовательно, вектор В*А будет направлен в противоположную сторону.
Заметим ещё, что в случае коллинеарности векторов А и В равенство АxВ=-(ВxА) очевидно, так как тогда АxВ и ВxA – нулевые векторы.
2. Обе формулы доказываются аналогично. Докажем, например, первую из них. Ограничимся случаем  >0. >0.
Для доказательства равенства векторов  (АxВ) и (АxВ) и  АxВ заметим прежде всего, что длины этих векторов одинаковы: АxВ заметим прежде всего, что длины этих векторов одинаковы:

 . .
Направления же векторов  (А*В) и (А*В) и  А*В совпадают, так как при умножении вектора на положительное число его направление не меняется. А*В совпадают, так как при умножении вектора на положительное число его направление не меняется.
3. Для доказательства заметим сначала, что произведение АxС0
, где С0
– единичный вектор, можно построить так (рис. 1).
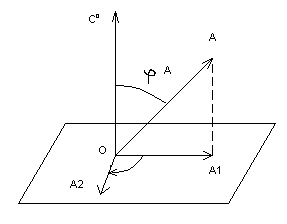
рис. 1.
Спроектируем вектор А= на плоскость, перпендикулярную к С0
, и полученную вектор-проекцию на плоскость, перпендикулярную к С0
, и полученную вектор-проекцию  1
повернём в этой плоскости вокруг точки О по часовой стрелке на 900
(если смотреть на плоскость с конца вектора С0
). 1
повернём в этой плоскости вокруг точки О по часовой стрелке на 900
(если смотреть на плоскость с конца вектора С0
).
Полученный вектор  2
и равен А*С0
. В самом деле, 2
и равен А*С0
. В самом деле,
1) ОА2
=ОА1
=Аcos(900
-φ)=Asinф, где ф – угол между векторами А и С0
;
2) Вектор  2
перпендикулярен к векторам А и С0
представляется совершающимся против часовой стрелки. Итак, 2
перпендикулярен к векторам А и С0
представляется совершающимся против часовой стрелки. Итак,  2
=А*С0
. 2
=А*С0
.
Пусть теперь даны единичный вектор С0
, перпендикулярная к нему плоскость р
и треугольник ОА1
В1
(рис. 2.), в котором  1
=А, 1
=А,  =В и =В и  1
=А+В. 1
=А+В.

рис. 2.
Спроектируем треугольник ОА1
В1
на плоскость р
и повернём против проекцию ОА2
В2
в плоскости р
по часовой стрелке на 900
.
Получим треугольник ОА3
В3
, в котором по предыдущему
 3
=(А+В)*С0
, 3
=(А+В)*С0
,  3
=В*С0
, 3
=В*С0
,  =В*С0
. =В*С0
.
Так как  = = 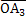 + +  , то (А+В)*С0
=А*С0
+ В*С0
.(1) , то (А+В)*С0
=А*С0
+ В*С0
.(1)
Заметив, что С=С*С0
, умножим теперь обе части равенства (1) на скаляр С. Применив свойство 2 векторного произведения, получим:
(А+В)*СС
4. Справедливость этого утверждения основана на том, что площадь параллелограмма равна произведению длин его смежных сторон и синуса угла между ними, что, в свою очередь, следует непосредственно из определения векторного произведения векторов А и В. (рис. 3,4)

рис. 3
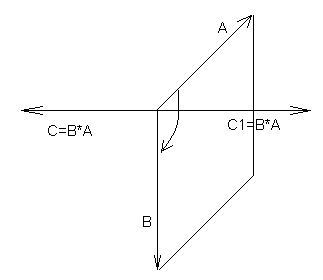
Рис. 4
4. Смешанное произведение
Сме́шанное произведе́ние 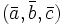 векторов векторов 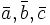 — скалярное произведение вектора — скалярное произведение вектора  на векторное произведение векторов на векторное произведение векторов  и и  : :
 . .
Иногда его называют тройным скалярным произведением
векторов.
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения.
Смешанное произведение 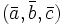 в правой декартовой системе координат равно определителю матрицы, составленной из векторов в правой декартовой системе координат равно определителю матрицы, составленной из векторов  и и  : :
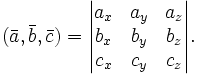
В частности,
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
Смешанное произведение 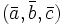 по абсолютному значению равно объёму параллелепипеда, образованного векторами по абсолютному значению равно объёму параллелепипеда, образованного векторами  и и  знак зависит от того, является ли эта тройка векторов правой или левой. знак зависит от того, является ли эта тройка векторов правой или левой.
Теорема:
векторно-скалярное произведение (АВС)=(А*В)С трёх некомпланарных векторов есть число, абсолютная величина которого выражает объём параллелепипеда, построенного на векторах А, В и С, как на рёбрах. Знак произведения положителен, если векторы А, В и С образуют систему, одноимённую с основной
5. Векторное произведение векторов, заданных проекциями
Обозначим через x1
,y1
,z1
проекции вектора А, а через x2
,y2
,z2
проекции вектора В. Выразим через них векторное произведение А*В:
АxВ=(ix1
+jy1
+kz1
)*(ix2
+jy2
+kz2
).
По распределительному свойству суммы векторов умножаются как многочлены:
АxВ=(i*i)x1
x2
+(j*i)y1
x2
+(k*i)z1
x2
+(i*j)x1
y2
+(j*j)y1
y2
+(k*j)z1
y2
+(i*k)x1
z2
+(j*k)y1
z2
+(k*k)z1
z2
. (1)
Так как I, j, k являются тремя взаимно перпендикулярными единичными векторами и вращение от j к k представляется с конца вектора i совершающимся против часовой стрелки, то:
 . .
Следовательно в полученном выражении (1) для АВ пропадут три слагаемых, остальные же соединятся попарно, и окончательная формула будет:
АxВ=i(y1
z2
-y2
z1
)+j(z1
x2
-z2
x1
)+k(x1
y2
-x2
y1
).
Последнюю формулу можно также записать в символический, лёгко запоминаемой форме, если воспользоваться понятием определителя 3-го порядка.
 . .
Вектор 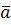 имеет координаты имеет координаты  . Вектор . Вектор 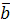 имеет координаты имеет координаты 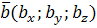 . Тогда . Тогда 
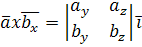

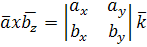
Так как верна формула  , то и следующая формула верна , то и следующая формула верна

6. Примеры решение задач (с использованием определителей)
Пример 1.
Найти площадь треугольника АВС с вершинами в точках А(x1
; y1
; z1
), B(x2
; y2
; z2
), C(x3
; y3
; z3
).
Решение:
Так как вектор  имеет проекции x2
-x1
, y2
-y1
, z2
-z1
а вектор имеет проекции x2
-x1
, y2
-y1
, z2
-z1
а вектор 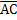 имеет проекции x3
-x1
, y3
-y1
, z3
-z1
, то площадь треугольника имеет проекции x3
-x1
, y3
-y1
, z3
-z1
, то площадь треугольника
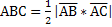 = =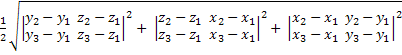 . .
Пример 2.
Определить синус угла А треугольника АВС с вершинами А(1,2,3), В(3,4,5), С(2,4,7).
Решение:
Так как векторы  и и 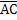 имеют соответственно проекции 2,2,2 и 1,2,4, то имеют соответственно проекции 2,2,2 и 1,2,4, то

угол следует взять острым, если 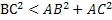 , и тупым, если , и тупым, если 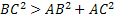 . В данном случае угол А острый. . В данном случае угол А острый.
Вывод
Таким образом мы рассмотрели теорию определителей и выяснили, что, действительно, данная теория очень помогает при решение задач с системами n линейных уравнений с n неизвестными.
Также мы рассмотрели как теория определителей применяется в аналитической геометрии, в частности, в векторном и смешанном произведениях и задач, связанных с ними.
Список используемой литературы
1. Привалов И. И. Аналитическая геометрия Москва Государственное издательство технико-теоретической литературы 1956
2. www.wikipedia.ru
|