Курсовая работа: Свойства многоугольников и их применение в решении задач
|
Название: Свойства многоугольников и их применение в решении задач Раздел: Рефераты по математике Тип: курсовая работа | |||||||
| Учреждение образования «Брестский государственный университет Кафедра алгебры и геометрии Свойства многоугольников и их применение в решении задач Курсовая работа студентки 3 курса Руководитель преподаватель кафедры алгебры и геометрии Брест 2007 ВВЕДЕНИЕ Многими математическими знаниями люди пользовались уже в глубокой древности – тысячи лет назад. Эти знания были необходимы древним купцам и строителям храмов, дворцов и пирамид, воинам и землемерам, жрецам и путешественникам. Знания постепенно накапливались и систематизировались. Около 4 тыс. лет назад возникла наука об измерении расстояний, площадей и объёмов, о свойствах различных фигур. Так как речь в основном шла о земельных участках, то древние греки, узнавшие об этой науке от египтян, назвали её геометрией (по-гречески «гео» - земля, а «метрео» - измеряю. Значит, «геометрия» буквально означает «землемерие». Греческие учёные узнали много новых свойств геометрических фигур, и уже тогда геометрией стали называть науку о геометрических фигурах, а для науки об измерении Земли ввели другое название – «геодезия» (происходит от греческих слов «деление земли»). Древние люди знали, что немаловажное значение имеют такие фигуры как многоугольники. Например, древнегреческие математики (Антифон, Бризон, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга. В данной работе мне предстоит изучить некоторые свойства многоугольников и их особенности при решении задач, а также научиться применять полученные знания на практике. 1.1.МНОГОУГОЛЬНИКИ. СВОЙСТВА МНОГОУГОЛЬНИКОВ Многоугольник — это геометрическая фигура, обычно определяется как замкнутая ломаная без самопересечений (простой многоугольник (рис.1а) ), однако иногда самопересечения допускаются (тогда многоугольник не является простым (рис.1б) )
Углом (или внутренним углом) выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, при этом угол считается со стороны многоугольника. В частности угол может превосходить 180° если многоугольник невыпуклый. Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разница между 180° и внутренним углом. Из каждой вершины Многоугольник с тремя вершинами называется треугольником, с чётырьмя — четырёхугольником, с пятью — пятиугольником и т. д. Многоугольник с n вершинами называется n- угольником. Плоским многоугольником называется фигура, которая состоит из многоугольника и ограниченной им конечной части площади. Многоугольник называют выпуклым, если выполнено одно из следующих (эквивалентных) условий: 1. он лежит по одну сторону от любой прямой, соединяющей его соседние вершины. (т. е. продолжения сторон многоугольника не пересекают других его сторон); 2. он является пересечением (т. е. общей частью) нескольких полуплоскостей; 3. любой отрезок с концами в точках, принадлежащих многоугольнику, целиком ему принадлежит. Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны, например равносторонний треугольник, квадрат и пентагон. Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности. Выпуклый многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности Правильный многоугольник — это многоугольник, у которого все углы и все стороны равны между собой. Свойства многоугольников: 1 Каждая диагональ выпуклого 2 Сумма всех углов выпуклого Д-во: Теорему докажем методом математической индукции. При
3 Около любого правильного многоугольника можно описать окружность, и притом только одну.
доказывается, что О
Докажем теперь, что описанная окружность только одна. Рассмотрим какие-нибудь три вершины многоугольника, например, 4 В любой правильный многоугольник можно вписать окружность и притом только одну. 5 Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. 6 Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. 7 Симметрия: Говорят, что фигура обладает симметрией (симметрична) , если существует такое движение (не тождественное), переводящее эту фигуру в себя. 7.1. Треугольник общего вида не имеет осей или центров симметрии, он несимметричен. Равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии: серединный перпендикуляр к основанию. 7.2. Равносторонний треугольник имеет три оси симметрии (серединные перпендикуляры к сторонам) и поворотную симметрию относительно центра с углом поворота 120 ° . 7.3 У любого правильного n-угольника есть n осей симметрии, все они проходят через его центр. Он также имеет поворотную симметрию относительно центра с углом поворота При четном n одни оси симметрии проходят через противоположные вершины, другие - через середины противоположных сторон. При нечетном n каждая ось проходит через вершину и середину противоположной стороны. Центр правильного многоугольника с четным числом сторон является его центром симметрии. У правильного многоугольника с нечетным числом сторон центра симметрии нет. 8 Подобие: При подобии и Теорема: Если стороны и углы выпуклых многоугольников
то эти многоугольники подобны. 8.1 Отношение периметров двух подобных многоугольников равно коэффициенту подобия. 8.2. Отношение площадей двух выпуклых подобных многоугольников равно квадрату коэффициента подобия. 2.ТРЕУГОЛЬНИКИ 2.1. СВОЙСТВА ПРОИЗВОЛЬНОГО ТРЕУГОЛЬНИКА В геометрии выделяют следующие основные свойства треугольников: 1. Во всяком треугольнике: · Против равных сторон лежат равные углы; · Против большей стороны лежит больший угол; · Против большего угла лежит большая сторона. 2. Сумма внутренних углов треугольника равна 180° . 3. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой. 4. Любой внешний угол треугольника больше любого внутреннего угла, не смежного с ним. 5. Любой внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. 6. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. 7. Длина любой стороны треугольника меньше суммы и больше модуля разности длин двух других сторон: |AC-CB|<AB<AC+CB (2.1) 8. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон. 9. Два не совпадающих ни с одной из сторон треугольника отрезка, поведённых из двух разных вершин треугольника до противолежащих этим вершинам сторон, пересекаются. 10. Прямая, проходящая через вершину треугольника и пересекающая противолежащую вершине сторону, делит данный треугольник на два треугольника, площади которых соответственно пропорциональны отрезкам, отсекаемым прямой на стороне данного треугольника. 11. Множеством вершин треугольников с одними и теми же основанием ВС и высотой h является множество точек двух прямых, параллельных прямой ВС и проходящих на расстоянии h от нее. 12. Если а, b , с - положительные числа, то треугольник со сторонами а, b , с существует в том и только в том случае, если одновременно выполняются неравенства: а + b >с, b +с>а, а + с> b (2.2) Эта система неравенств равносильна двойному неравенству | a - b |<2 c < a + b (2.3). 13.Площадь треугольника равна половине произведения его основаниям на высоту 14.Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. 15.Любой треугольник можно вписать в окружность. 16.Около любого треугольника можно описать только одну окружность. 17.Любой треугольник имеет три вневписанные окружности. Каждая сторона треугольника касается одной и только одной из этих окружностей. 2.2. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК. ОПРЕДЕЛЕНИЕ. ПРИЗНАК И СВОЙСТВА Пример равнобедренного треугольника
Рис. 2.1. Признак равнобедренного треугольника: Если в треугольнике два угла равны, то он равнобедренный. Свойства равнобедренного треугольника: Для равнобедренного треугольника справедливы все свойства произвольного треугольника. Кроме того, имеют место следующие свойства: 1) В равнобедренном треугольнике углы при основании равны. 2) В равнобедренном треугольнике биссектриса, проведенная к основанию, является одновременно медианой и высотой. 3) В равнобедренном треугольнике медианы (а также высоты или биссектрисы), проведенные к боковым сторонам, равны. 2.3. СВОЙСТВА РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА Пример равностороннего треугольника
Рис. 2.2. Свойства равностороннего треугольника: 1) У равностороннего треугольника все углы равны между собой и составляют 60°. 2) В равностороннем треугольнике любая биссектриса является одновременно медианой и высотой. 3) В равностороннем треугольнике все медианы (а также высоты или биссектрисы) равны между собой. 4) Точка пересечения медиан (высот, биссектрис) равностороннего треугольника, называемая его центром, является центром вписанной и описанной окружностей. 2.4. ОПРЕДЕЛЕНИЕ. ПРИЗНАКИ И СВОЙСТВА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА Пример прямоугольного треугольника
Признаки прямоугольного треугольника: 1) Если квадрат одной из сторон треугольника равен сумме квадратов двух других его сторон, то такой треугольник прямоугольный. 2) Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный. Свойства прямоугольного треугольника: Для прямоугольного треугольника справедливы все свойства произвольного треугольника. Кроме того, имеют место следующие свойства: 1) У прямоугольного треугольника только один прямой угол, два других его угла острые. 2) Сумма острых углов прямоугольного треугольника равна 90°. 3) В прямоугольном треугольнике гипотенуза больше любого катета. 4) В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°. 5) Катет, лежащий против угла 30°, равен половине гипотенузы. 6) Гипотенуза вписанного в окружность прямоугольного треугольника совпадает с диаметром этой окружности. 7) Высота прямоугольного прямоугольника, опущенная из вершины прямого угла, делит этот треугольник на два треугольника, подобных исходному. 8) Биссектриса прямого угла в прямоугольном треугольнике лежит между медианой и высотой и делит угол между ними пополам. 9) Площадь равна половине произведения его катетов. 3. ЧЕТЫРЕХУГОЛЬНИКИ Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
Четырехугольники бывают выпуклые (как ABCD) и невыпуклые (A1 B1 C1 D1 ). Свойства четырехугольника: 1. Четырехугольник является выпуклым тогда и только тогда, когда его диагонали пересекаются. 2. В любом четырехугольнике какие-то две противолежащие вершины лежат по разные стороны от прямой, проходящей через две другие вершины. 3. Прямые, содержащие диагонали любого четырехугольника, пересекаются. 4. Каждая сторона четырехугольника меньше суммы трех других сторон:
5. Площадь произвольного выпуклого четырехугольника:
S = 6 Около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов этого четырехугольника равна, 180°. 7 В четырехугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон(Теорема Птолемея). 8 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны. 3.1. ПАРАЛЛЕЛОГРАММ. ЕГО СВОЙСТВА И ПРИЗНАКИ Параллелограммом называется четырехугольник, у которого 1) противолежащие стороны равны; 2) 3) диагонали точкой пересечения делятся пополам; 4) сумма углов, прилежащих к одной стороне, равна 180°; 5) сумма квадратов диагоналей равна сумме квадратов всех сторон: d1 2 +d2 2 =2(a2 +b2 ). (3.3) 6) Около параллелограмма можно описать окружность тогда и только тогда, когда этот параллелограмм является прямоугольником. 7) Если параллелограмм вписан в окружность, то он является ромбом. Признаки параллелограмма: Четырехугольник является параллелограммом, если: 1. Две его противоположные стороны равны и параллельны. 2. Противоположные стороны попарно равны. 3. Противоположные углы попарно равны. 4. Диагонали точкой пересечения делятся пополам. 3.2. ТРАПЕЦИЯ. СВОЙСТВА И ПРИЗНАКИ ТРАПЕЦИИ Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции:1 ее средняя линия параллельна основаниям и равна их полусумме; 2 если трапеция равнобокая, то ее диагонали равны и углы при основании равны; 3 если трапеция равнобокая, то около нее можно описать окружность; 4 если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. 5 Площадь трапеции: 6 Около трапеции можно описать окружность тогда и только тогда, когда эта трапеция равнобедренная. Признаки трапеции:Четырехугольник является трапецией, если его параллельные стороны не равны 3.3. ПРЯМОУГОЛЬНИК. ЕГО СВОЙСТВА И Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольника:
2 диагонали равны. 3 площадь равна: S = ab (3.5) S
=
4 если прямоугольник вписан в окружность, то он является квадратом. Признаки прямоугольника:Параллелограмм является прямоугольником, если: 1. Один из его углов прямой. 2. Его диагонали равны. 3.4. РОМБ. ЕГО СВОЙСТВА И ПРИЗНАКИ Ромбом называется параллелограмм, у которого все стороны равны.
|
|||||||
 Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями. Пусть
Пусть Д-во: Пусть
Д-во: Пусть 



 Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными.
Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. d1
, d2
—
диагонали;
d1
, d2
—
диагонали;  противолежащие стороны попарно параллельны.
противолежащие стороны попарно параллельны. непараллельны.
непараллельны. ПРИЗНАКИ
ПРИЗНАКИ Свойства ромба:
Свойства ромба: стороны равны.
стороны равны.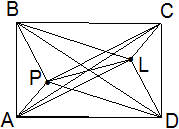 Точка Р
лежит внутри прямоугольника ABCD
.
Докажите, что
Точка Р
лежит внутри прямоугольника ABCD
.
Докажите, что  AC
– наибольшая сторона треугольника ABC
. На АС
выбираются точки А1
и С1
так, что АС1
=АВ
и СА1
=СВ
. Затем на стороне АВ
берется точка А2
так, что АА1
=АА2
, а на стороне CD
– точка С2
так, что СС1
=СС2
. Докажите, что точки А1
, А2
, С1
, С2
лежат на одной окружности.
AC
– наибольшая сторона треугольника ABC
. На АС
выбираются точки А1
и С1
так, что АС1
=АВ
и СА1
=СВ
. Затем на стороне АВ
берется точка А2
так, что АА1
=АА2
, а на стороне CD
– точка С2
так, что СС1
=СС2
. Докажите, что точки А1
, А2
, С1
, С2
лежат на одной окружности. Кроме того, из равенства углов n
-угольника следует, что треугольники A
n
OA
1
A
2
OA
1
— равнобедренные. Поэтому
Кроме того, из равенства углов n
-угольника следует, что треугольники A
n
OA
1
A
2
OA
1
— равнобедренные. Поэтому 
 Пусть A
1
A
2
...A
12
— правильный 12-угольник. Рассмотрим треугольник A
2
A
4
A
8
. Прямые A
2
A
6
, A
3
A
8
и A
4
A
11
— биссектрисы его углов. Точно так же прямые A
3
A
8
, A
5
A
1
и A
11
A
4
— биссектрисы углов треугольника A
3
A
5
A
11
. Отсюда следует, что диагонали A
1
A
5
, A
2
A
6
, A
3
A
8
и A
4
A
11
проходят через одну точку.
Пусть A
1
A
2
...A
12
— правильный 12-угольник. Рассмотрим треугольник A
2
A
4
A
8
. Прямые A
2
A
6
, A
3
A
8
и A
4
A
11
— биссектрисы его углов. Точно так же прямые A
3
A
8
, A
5
A
1
и A
11
A
4
— биссектрисы углов треугольника A
3
A
5
A
11
. Отсюда следует, что диагонали A
1
A
5
, A
2
A
6
, A
3
A
8
и A
4
A
11
проходят через одну точку.  РЕШЕНИЕ:
РЕШЕНИЕ: Пусть Xk
—
образ точки X
при повороте относительно центра O
данного n-
угольника, переводящем Ak
в A1
.
При этом повороте отрезок Ak
X
переходит в A1
Xk
.
Следовательно, A1
X + ... + An
X = A1
X1
+ ... + A1
Xn
.
А так как n-
угольник X1
...Xn
правильный, то
Пусть Xk
—
образ точки X
при повороте относительно центра O
данного n-
угольника, переводящем Ak
в A1
.
При этом повороте отрезок Ak
X
переходит в A1
Xk
.
Следовательно, A1
X + ... + An
X = A1
X1
+ ... + A1
Xn
.
А так как n-
угольник X1
...Xn
правильный, то  Пусть XYZ
— данный треугольник, KLM
— треугольник, получаемый при продолжении сторон AB
, CD
и EF
шестиугольника ABCDEF
(рис.). Пусть O
— центр треугольника XYZ
, докажем, что он является центром треугольника KLM
.
Пусть XYZ
— данный треугольник, KLM
— треугольник, получаемый при продолжении сторон AB
, CD
и EF
шестиугольника ABCDEF
(рис.). Пусть O
— центр треугольника XYZ
, докажем, что он является центром треугольника KLM
.  Пусть М
и N
– середины сторон АВ
и CD
.
Опустим из точки D
перпендикуляр DP
на прямую MN
, а из точки М перпендикуляр MQ
на СВ
. Тогда Q
– точка касания прямой CD
и окружности с диаметром AB
. Прямоугольные треугольники PDN
и QMN
подобны, поэтому DP
=
ND
*
MQ
/
MN
=
ND
*
MA
/
MN
. Аналогично расстояние от точки А
до прямой MN
равно ND
*
MA
/
MN
. Следовательно, AD
||MN
. Аналогично BC
||
MN
.
Пусть М
и N
– середины сторон АВ
и CD
.
Опустим из точки D
перпендикуляр DP
на прямую MN
, а из точки М перпендикуляр MQ
на СВ
. Тогда Q
– точка касания прямой CD
и окружности с диаметром AB
. Прямоугольные треугольники PDN
и QMN
подобны, поэтому DP
=
ND
*
MQ
/
MN
=
ND
*
MA
/
MN
. Аналогично расстояние от точки А
до прямой MN
равно ND
*
MA
/
MN
. Следовательно, AD
||MN
. Аналогично BC
||
MN
.
 РЕШЕНИЕ: Будем считать, что N
лежит на AB,
а K
лежит на AF
(рис.4.11). Заметим, что FK = AN.
Выберем точку P
на BC
, точку R
на CD
, точку S
на DE
и точку T
на EF
РЕШЕНИЕ: Будем считать, что N
лежит на AB,
а K
лежит на AF
(рис.4.11). Заметим, что FK = AN.
Выберем точку P
на BC
, точку R
на CD
, точку S
на DE
и точку T
на EF