МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ УНИВЕРСИТЕТ
Экономический факультет. Государственное и муниципальное управление.
Курсовая работа
На тему: «Статистическое изучение социально-экономического явления.»
Вариант №7.
Выполнила студентка
заочного отделения
группа 21
Живаева К.М.
Москва, 2008
Оглавление
Введение
Формирование исходной выборки
Статистические распределения рядов признаков-факторов и результирующего признака
Проверка однородности и нормальности
Вывод зависимостей результирующего-признака от факторов-признаков
Группировка
Определение доверительного интервала
Вычисление линейных коэффициентов корреляции, вывод уравнения регрессии
Заключение
Список источников
Введение
Целью данной работы является статистическое исследование взаимосвязей стоимости автомобиля марки «Хонда-Сивик» с факторными признаками: пробегом и временем эксплуатации; а также, на основании исследования выявления первичных факторов, влияющих на стоимость и вывод зависимости целевого параметра(стоимости) от первичного фактора.
Для построения исходной выборки был выбран сайт www.auto.ru.
Формирование исходной выборки
Используя сайт auto.ru проводим выборочное исследование 50 автомобилей марки Хонда-Сивик.
Исследуемые признаки:
Y ‑ цена автомобиля, тыс.руб.;
Х1 ‑ время эксплуатации, лет;
Х2 ‑ пробег, тыс. км.
| № п/п |
Марка |
Y |
Х1
|
Х2
|
| 1 |
Civic VII |
379 |
5 |
121 |
| 2 |
Civic VII |
399 |
4 |
74 |
| 3 |
Civic VII |
429 |
4 |
88 |
| 4 |
Civic VII |
393 |
3 |
95 |
| 5 |
Civic VII |
397 |
3 |
60 |
| 6 |
Civic VII |
430 |
3 |
54 |
| 7 |
Civic VII |
459 |
3 |
46 |
| 8 |
Civic VIII |
455 |
2 |
107 |
| 9 |
Civic VIII |
467 |
2 |
47 |
| 10 |
Civic VIII |
468 |
2 |
97 |
| 11 |
Civic VIII |
552 |
2 |
60 |
| 12 |
Civic VIII |
565 |
2 |
41 |
| 13 |
Civic VIII |
570 |
2 |
57 |
| 14 |
Civic VIII |
579 |
2 |
30 |
| 15 |
Civic VIII |
597 |
2 |
150 |
| 16 |
Civic VIII |
441 |
1 |
75 |
| 17 |
Civic VIII |
466 |
1 |
30 |
| 18 |
Civic VIII |
500 |
1 |
15 |
| 19 |
Civic VIII |
524 |
1 |
26 |
| 20 |
Civic VIII |
530 |
1 |
22 |
| 21 |
Civic VIII |
539 |
1 |
32 |
| 22 |
Civic VIII |
555 |
1 |
62 |
| 23 |
Civic VIII |
560 |
1 |
14 |
| 24 |
Civic VIII |
575 |
1 |
30 |
| 25 |
Civic VIII |
575 |
1 |
88 |
| 26 |
Civic VIII |
600 |
1 |
18 |
| 27 |
Civic VIII |
600 |
1 |
18 |
| 28 |
Civic VIII |
615 |
1 |
40 |
| 29 |
Civic VIII |
680 |
1 |
14 |
| 30 |
Civic VIII |
510 |
0 |
18 |
| 31 |
Civic VIII |
533 |
0 |
0 |
| 32 |
Civic VIII |
533 |
0 |
0 |
| 33 |
Civic VIII |
541 |
0 |
0 |
| 34 |
Civic VIII |
541 |
0 |
0 |
| 35 |
Civic VIII |
561 |
0 |
0 |
| 36 |
Civic VIII |
570 |
0 |
29 |
| 37 |
Civic VIII |
585 |
0 |
0 |
| 38 |
Civic VIII |
590 |
0 |
0 |
| 39 |
Civic VIII |
606 |
0 |
0 |
| 40 |
Civic VIII |
616 |
0 |
0 |
| 41 |
Civic VIII |
640 |
0 |
0 |
| 42 |
Civic VIII |
640 |
0 |
0 |
| 43 |
Civic VIII |
640 |
0 |
0 |
| 44 |
Civic VIII |
643 |
0 |
0 |
| 45 |
Civic VIII |
650 |
0 |
10 |
| 46 |
Civic VIII |
650 |
0 |
0 |
| 47 |
Civic VIII |
661 |
0 |
0 |
| 48 |
Civic VIII |
661 |
0 |
0 |
| 49 |
Civic VIII |
683 |
0 |
0 |
| 50 |
Civic VIII |
600 |
0 |
13 |
Статистические распределения рядов признаков-факторов и результирующего признака
Исследуем статистическое распределение признаков Х1
с помощью интервального вариационного ряда:
| Интервальный ряд для Х 1
|
| Х 1
|
F 1
|
Ср. цена тыс.руб. |
| 0-1 |
21 |
603 |
| 1-2 |
14 |
554 |
| 2-3 |
8 |
532 |
| 3-4 |
4 |
420 |
| 4-5 |
2 |
414 |
| 5-6 |
1 |
379 |
Приведем графическое отображение ряда для Х1
в виде гистограммы и кумуляты:
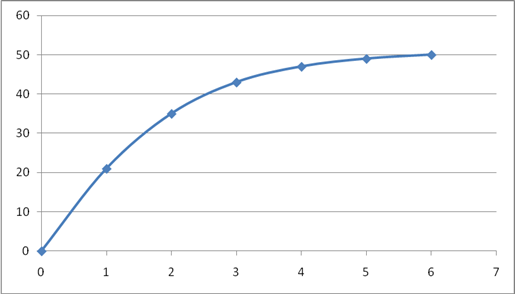
Вычислим среднюю арифметическую, моду и медиану интервального ряда распределения для X1
. Формула для вычисления среднего арифметического:
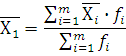
где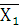 – средняя по ряду распределения; – средняя по ряду распределения;
 – средняя по i-му интервалу; – средняя по i-му интервалу;
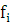 – частота i-го интервала (число автомобилей в интервале). – частота i-го интервала (число автомобилей в интервале).
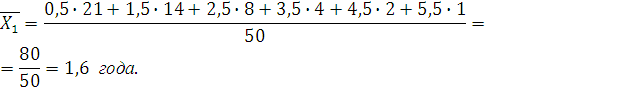
Мода – это наиболее часто встречающееся значение признака. Для интервального ряда мода определяется по формуле:
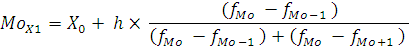
где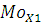 – значение моды; – значение моды;
X0
– нижняя граница модального интервала;
h – величина модального интервала (1 год);
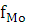 – частота модального интервала; – частота модального интервала;
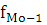 – частота интервала, предшествующая модальному; – частота интервала, предшествующая модальному;
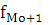 – частота послемодального интервала. – частота послемодального интервала.
Модальный интервал определяется по наибольшей частоте. Для ряда X1 наибольшее значение частоты равно 21, т.е. это будет интервал 0 лет , тогда значение моды:
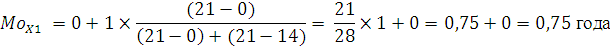
Медиана – значение признака, лежащее в середине упорядоченного ряда распределения.
Номер медианы определяется по формуле:
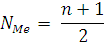
где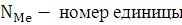
n – число единиц в совокупности
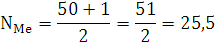
т.к. медиана с дробным номером не бывает, то полученный результат указывает, что медиана находится между 25-й и 26-й величинами совокупности.
Значение медианы можно определить по формуле:
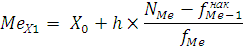
где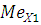 – значение медианы; – значение медианы;
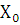 – нижняя граница медианного интервала; – нижняя граница медианного интервала;
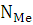 - номер медианы; - номер медианы;
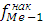 - накопленная частота интервала, предшествующая медианному; - накопленная частота интервала, предшествующая медианному;
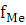 - частота медианного интервала. - частота медианного интервала.
По накопленной частоте определяем, что медиана будет находиться в интервале от 1 года до 2-х лет , тогда значение медианы:
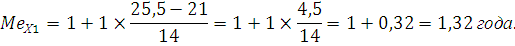
Для вычисления дисперсии воспользуемся следующей формулой:
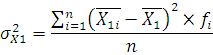
где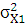 – дисперсия; – дисперсия;
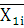 – среднее по i-му интервалу; – среднее по i-му интервалу;
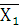 – среднее по ряду распределения; – среднее по ряду распределения;
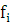 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
Среднее квадратическое отклонение вычислим по следующей формуле:
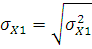
где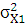 – дисперсия; – дисперсия;
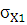 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
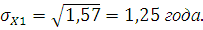
Вычислим коэффициент вариации
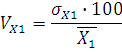
где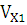 – коэффициент вариации; – коэффициент вариации;
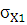 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
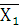 - среднее по ряду распределения. - среднее по ряду распределения.
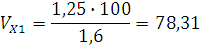
Вычислим значения коэффициента ассиметрии:
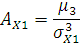
где 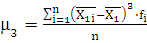 ; ;
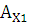 – коэффициент ассиметрии; – коэффициент ассиметрии;
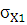 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
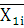 – среднее по i-му интервалу; – среднее по i-му интервалу;
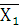 – среднее по ряду распределения; – среднее по ряду распределения;
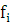 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
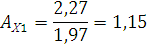
Вычислим значения коэффициента эксцесса:
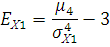
где 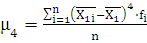
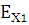 - коэффициент эксцесса; - коэффициент эксцесса;
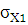 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
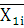 – среднее по i-му интервалу; – среднее по i-му интервалу;
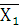 – среднее по ряду распределения; – среднее по ряду распределения;
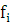 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
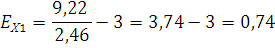
Исследуем статистическое распределение признаков Х2
с помощью интервального вариационного ряда.
Для построения ряда распределения необходимо определить число групп и величину интервала. Для определения числа групп воспользуемся формулой Стерджесса:
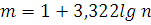
гдеm – число групп (всегда целое);
n – число единиц в выборке, в нашем случае n= 50.
Вычислим m:
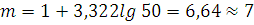
Величину интервала определим по формуле:
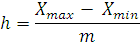
где Хmax – максимальное значение признака;
Хmin - минимальное значение признака;
m – число групп.
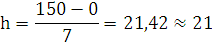
На основании полученных данных построим интервальный ряд для Х2
:
| Интервальный ряд для Х 2
|
| Х 2
|
F 2
|
Ср. цена тыс.руб. |
| 0 - 21 |
25 |
601 |
| 21 - 42 |
9 |
551 |
| 42 - 63 |
7 |
490 |
| 63 - 84 |
2 |
420 |
| 84 - 105 |
4 |
466 |
| 105 - 126 |
2 |
417 |
| 126 - 150 |
1 |
597 |
Приведем графическое отображение ряда для Х2
в виде гистограммы и кумуляты:
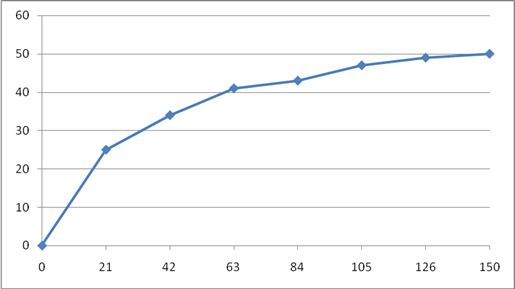
Вычислим среднюю арифметическую, моду и медиану интервального ряда распределения для X2
. Формула для вычисления среднего арифметического:
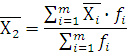
где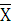 – средняя по ряду распределения; – средняя по ряду распределения;
 – средняя по i-му интервалу; – средняя по i-му интервалу;
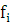 – частота i-го интервала (число автомобилей в интервале). – частота i-го интервала (число автомобилей в интервале).
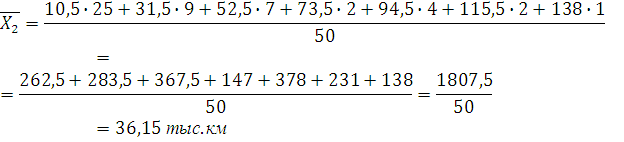
Мода – это наиболее часто встречающееся значение признака. Для интервального ряда мода определяется по формуле:
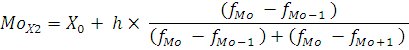
где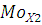 – значение моды; – значение моды;
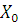 – нижняя граница модального интервала; – нижняя граница модального интервала;
h – величина модального интервала (1 год);
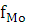 - частота модального интервала; - частота модального интервала;
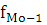 - частота интервала, предшествующая модальному; - частота интервала, предшествующая модальному;
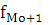 - частота послемодального интервала. - частота послемодального интервала.
Модальный интервал определяется по наибольшей частоте. Для ряда X1
наибольшее значение частоты равно 25, т.е. это будет интервал 0 до 21 тыс. км., тогда значение моды:
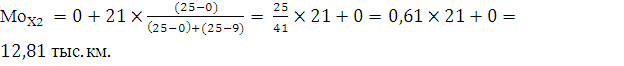
Медиана – значение признака, лежащее в середине упорядоченного ряда распределения.
Номер медианы определяется по формуле:
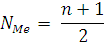
где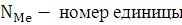
n – число единиц в совокупности
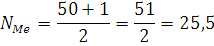
т.к. медиана с дробным номером не бывает, то полученный результат указывает, что медиана находится между 25-й и 26-й величинами совокупности.
Значение медианы можно определить по формуле:
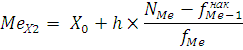
где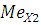 – значение медианы; – значение медианы;
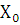 – нижняя граница медианного интервала; – нижняя граница медианного интервала;
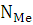 - номер медианы; - номер медианы;
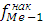 - накопленная частота интервала, предшествующая медианному; - накопленная частота интервала, предшествующая медианному;
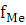 - частота медианного интервала. - частота медианного интервала.
По накопленной частоте определяем, что медиана будет находиться в интервале от 21 до 42 тыс. км., тогда значение медианы:
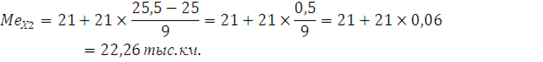
Для вычисления дисперсии воспользуемся следующей формулой:
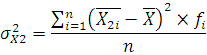
где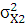 – дисперсия; – дисперсия;
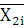 – среднее по i-му интервалу; – среднее по i-му интервалу;
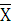 – среднее по ряду распределения; – среднее по ряду распределения;
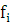 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
Среднее квадратическое отклонение вычислим по следующей формуле:
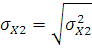
где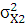 – дисперсия; – дисперсия;
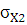 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
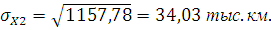
Вычислим коэффициент вариации
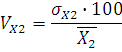
где – коэффициент вариации; – коэффициент вариации;
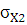 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
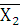 - среднее по ряду распределения. - среднее по ряду распределения.
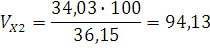
Вычислим значения коэффициента ассиметрии:
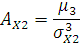
где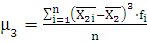
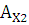 – коэффициент ассиметрии – коэффициент ассиметрии
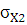 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
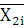 – среднее по i-му интервалу; – среднее по i-му интервалу;
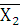 – среднее по ряду распределения; – среднее по ряду распределения;
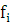 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).

Вычислим значения коэффициента эксцесса:
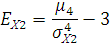
где ; ;
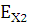 - коэффициент эксцесса; - коэффициент эксцесса;
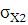 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
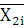 – среднее по i-му интервалу; – среднее по i-му интервалу;
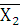 – среднее по ряду распределения; – среднее по ряду распределения;
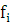 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
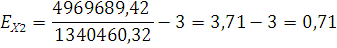
Исследуем статистическое распределение признаков Y с помощью интервального вариационного ряда.
Величину интервала определим по формуле, используя полученное ранее значение m:

где Хmax – максимальное значение признака;
Хmin - минимальное значение признака;
m – число групп.
На основании полученных данных построим интервальный ряд для Y:
| Интервальный ряд для Y |
| Y |
Fy
|
Ср. цена тыс.руб. |
| 379 - 422 |
4 |
400,5 |
| 422 - 465 |
5 |
443,5 |
| 465 - 508 |
4 |
486,5 |
| 508 - 551 |
8 |
529,5 |
| 551 - 594 |
12 |
572,5 |
| 594 - 637 |
7 |
615,5 |
| 637 - 683 |
10 |
660 |
Приведем графическое отображение ряда для Y в виде гистограммы и кумуляты:
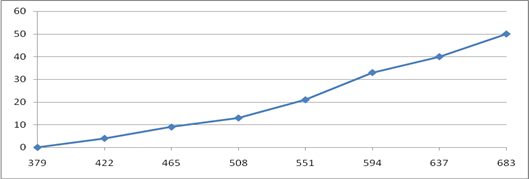
Вычислим среднюю арифметическую , моду и медиану интервального ряда распределения для Y. Формула для вычисления среднего арифметического:
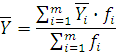
где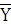 – средняя по ряду распределения; – средняя по ряду распределения;
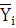 – средняя по i-му интервалу; – средняя по i-му интервалу;
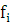 – частота i-го интервала (число автомобилей в интервале). – частота i-го интервала (число автомобилей в интервале).
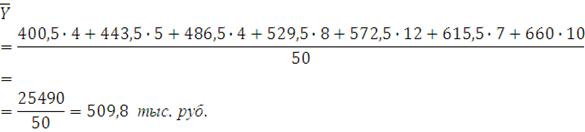
Мода – это наиболее часто встречающееся значение признака. Для интервального ряда мода определяется по формуле:
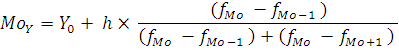
где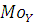 – значение моды; – значение моды;
Y0
– нижняя граница модального интервала;
h– величина модального интервала;
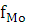 - частота модального интервала; - частота модального интервала;
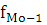 - частота интервала, предшествующая модальному; - частота интервала, предшествующая модальному;
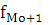 - частота послемодального интервала. - частота послемодального интервала.
Модальный интервал определяется по наибольшей частоте. Для ряда Y наибольшее значение частоты равно 12, т.е. это будет интервал 551-594, тогда значение моды:
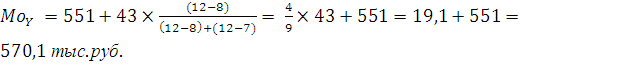
Медиана – значение признака, лежащее в середине упорядоченного ряда распределения.
Номер медианы определяется по формуле:
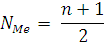
где 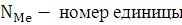 ; ;
n – число единиц в совокупности;
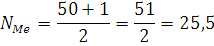
т.к. медиана с дробным номером не бывает, то полученный результат указывает, что медиана находится между 25-й и 26-й величинами совокупности.
Значение медианы можно определить по формуле:
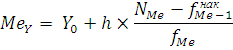
где 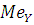 – значение медианы; – значение медианы;
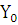 – нижняя граница медианного интервала; – нижняя граница медианного интервала;
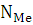 – номер медианы; – номер медианы;
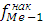 – накопленная частота интервала, предшествующего медианному; – накопленная частота интервала, предшествующего медианному;
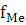 - частота медианного интервала; - частота медианного интервала;
По накопленной частоте определяем, что медиана будет находиться в интервале 551-594 , тогда значение медианы:
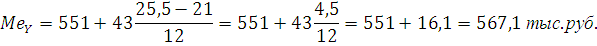
Для вычисления дисперсии воспользуемся следующей формулой:
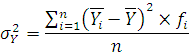
где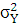 – дисперсия; – дисперсия;
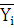 – среднее по i-му интервалу; – среднее по i-му интервалу;
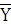 – среднее по ряду распределения; – среднее по ряду распределения;
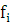 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
Среднее квадратическое отклонение вычислим по следующей формуле:
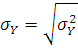
где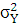 – дисперсия; – дисперсия;
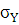 – среднее квадратическое отклонение; – среднее квадратическое отклонение;

Вычислим коэффициент вариации
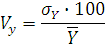
где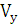 – коэффициент вариации; – коэффициент вариации;
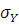 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
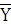 - среднее по ряду распределения. - среднее по ряду распределения.

Вычислим значения коэффициента ассиметрии:
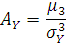
где 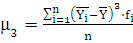
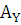 – коэффициент ассиметрии; – коэффициент ассиметрии;
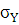 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
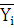 – среднее по i-му интервалу; – среднее по i-му интервалу;
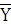 – среднее по ряду распределения; – среднее по ряду распределения;
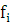 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
Подставив значения, получим, что:
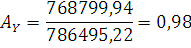
Вычислим значения коэффициента эксцесса:
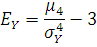
где 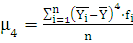 ; ;
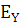 - коэффициент эксцесса; - коэффициент эксцесса;
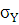 – среднее квадратическое отклонение; – среднее квадратическое отклонение;
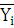 – среднее по i-му интервалу; – среднее по i-му интервалу;
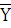 – среднее по ряду распределения; – среднее по ряду распределения;
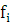 – частота i-го интервала; – частота i-го интервала;
n – размер выборки (n=50).
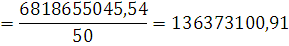

Проверка однородности и нормальности
Проверим интервальные распределения на однородность:
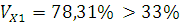
следовательно, совокупность для Х1
является неоднородной.
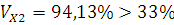
следовательно, совокупность для Х2
является неоднородной.
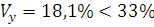
следовательно, совокупность для Y является однородной.
Исследуем нормальность распределения факторного признака Х1
:
| Интервалы значений признака-фактора |
Число единиц, входящих в интервал |
Удельный вес единиц, входящих в интервал, в общем их числе, % |
Удельный вес единиц, входящих в интервал, при нормальном распределении, % |
| 1 |
2 |
3 |
4 |
(1,6-1,25)-(1,6+1,25)
0,35 – 2,85
|
22 |
44 |
68,3 |
(1,6-2×1,25) - (1,6+2×1,25)
-0,9 – 4,1
|
49 |
98 |
95,4 |
(1,6-3×1,25) - (1,6+3×1,25)
-2,15 – 5,35
|
50 |
100 |
99,7 |
Таким образом, сопоставляя гр.3 и гр.4 делаем вывод: распределение Х1
относительно близко к нормальному, но не подчиняется ему.
Исследуем нормальность распределения факторного признака Х2
:
| Интервалы значений признака-фактора |
Число единиц, входящих в интервал |
Удельный вес единиц, входящих в интервал, в общем их числе, % |
Удельный вес единиц, входящих в интервал, при нормальном распределении, % |
| 1 |
2 |
3 |
4 |
(36,15-34,03)-(36,15+34,03)
2,12 – 70,18
|
24 |
48 |
68,3 |
(36,15-2×34,03) - (36,15+2×34,03)
-31,91 – 104,21
|
47 |
94 |
95,4 |
(36,15-3×34,03) - (36,15+3×34,03)
-65,94 – 138,24
|
49 |
98 |
99,7 |
Таким образом, сопоставляя гр.3 и гр.4 делаем вывод: распределение Х2
близко к нормальному, но не подчиняется ему.
Таким образом, проведя анализ на нормальность распределения мы можем отобрать данные не попадающие в диапазон 3х σ. Для ряда Х1
таких значений нет. Для ряда Х2
исключаем значение с пробегом 150 тыс. км.
С учетом отфильтрованных по правилу 3х сигм составим интервальные ряды для Х1
, Х2
, Y.
| Интервальный ряд для Х 1
|
| Х 1
|
F 1
|
Ср. цена тыс.руб. |
| 0-1 |
21 |
603 |
| 1-2 |
14 |
554 |
| 2-3 |
7 |
522 |
| 3-4 |
4 |
420 |
| 4-5 |
2 |
414 |
| 5-6 |
1 |
379 |
| Интервальный ряд для Х 2
|
| Х 2
|
F 2
|
Ср. цена тыс.руб. |
| 0 - 21 |
25 |
601 |
| 21 - 42 |
9 |
551 |
| 42 - 63 |
7 |
490 |
| 63 - 84 |
2 |
420 |
| 84 - 105 |
4 |
466 |
| 105 - 126 |
2 |
417 |
| Интервальный ряд для Y |
| Y |
F y
|
Ср. цена тыс.руб. |
| 379 - 422 |
4 |
400,5 |
| 422 - 465 |
5 |
443,5 |
| 465 - 508 |
4 |
486,5 |
| 508 - 551 |
8 |
529,5 |
| 551 - 594 |
12 |
572,5 |
| 594 - 637 |
6 |
615,5 |
| 637 - 683 |
10 |
660 |
Проведем аналитические группировки продаваемых автомобилей по времени эксплуатации и пробегу и определим групповые средние.
Построим график Y(X1
)
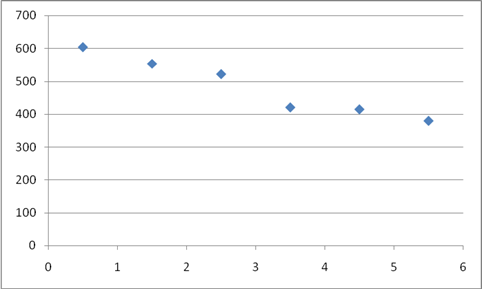
Зависимость цены от времени эксплуатации существует и носит линейный характер, чем больше время эксплуатации, тем дешевле автомобиль.
Построим график Y(X2
)
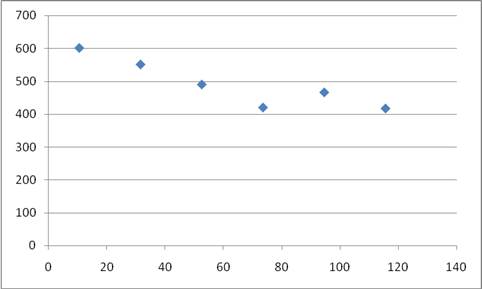
Зависимость цены от пробега существует и носит линейный характер, чем больше пробег автомобиля, тем дешевле автомобиль.
Группировка
На основанииданных статистического наблюдения выделим три типа автомобилей:
· по времени эксплуатации:
o новые автомобили от 0 до 1 года – 34 шт.
o средние автомобили от 2 до 3 лет – 13 шт.
o старые автомобили от 3 до 5 лет – 3 шт.
· по пробегу:
o новые автомобили от 0 до 50 тыс. км. – 36 шт.
o средние автомобили от 50 до 100 тыс.км. – 11 шт.
o старые автомобили от 100 до 150 тыс.км. – 3 шт.
· по цене:
o новые автомобили от 581 до 683 тыс. руб. – 19 шт.
o средние автомобили от 480 до 581 тыс. руб. – 12 шт.
o старые автомобили от 379 до 480 тыс. руб. – 12 шт.
Определение доверительного интервала
Определим доверительный интервал, в котором заключена средняя цена всех продаваемых автомобилей, с вероятностью 0,9.
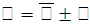
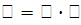
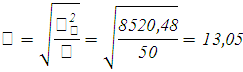
При вероятности 0,9 t = 1,64
Следовательно: 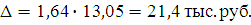
Таким образом, с вероятностью 0,9 можно утверждать, что средняя цена автомобиля равна:
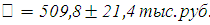
Определим доверительный интервал, в котором заключена средняя цена всех продаваемых автомобилей, с вероятностью 0,95.
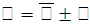
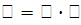
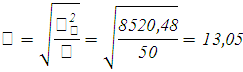
При вероятности 0,95 t = 1,96
Следовательно: 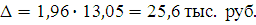
Таким образом, с вероятностью 0,95 можно утверждать, что средняя цена автомобиля равна:
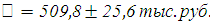
Определим необходимую численность выборки при определении средней цены продаваемых автомобилей, чтобы с вероятностью 0,95 предельная ошибка выборки не превышала 10 тыс.руб.
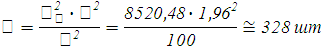
Вычисление линейных коэффициентов корреляции, вывод уравнения регрессии
На основании выборочного наблюдения оценим степень тесноты связи и проведем оценку ее существенности:
Для определения степени тесноты парной линей зависимости используем линейный коэффициент корреляции(r) :
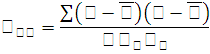
Для вычисления линейных коэффициентов корреляции составим вспомогательную таблицу:
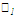 |
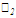 |
 |
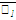 |
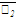 |
 |
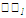 |
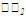 |
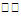 |
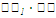 |
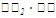 |
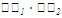 |
| 5 |
121 |
379 |
1,6 |
36,15 |
509,8 |
3,4 |
84,85 |
-130,8 |
-444,72 |
-11098,4 |
288,49 |
| 4 |
74 |
399 |
1,6 |
36,15 |
509,8 |
2,4 |
37,85 |
-110,8 |
-265,92 |
-4193,78 |
90,84 |
| 4 |
88 |
429 |
1,6 |
36,15 |
509,8 |
2,4 |
51,85 |
-80,8 |
-193,92 |
-4189,48 |
124,44 |
| 3 |
95 |
393 |
1,6 |
36,15 |
509,8 |
1,4 |
58,85 |
-116,8 |
-163,52 |
-6873,68 |
82,39 |
| 3 |
60 |
397 |
1,6 |
36,15 |
509,8 |
1,4 |
23,85 |
-112,8 |
-157,92 |
-2690,28 |
33,39 |
| 3 |
54 |
430 |
1,6 |
36,15 |
509,8 |
1,4 |
17,85 |
-79,8 |
-111,72 |
-1424,43 |
24,99 |
| 3 |
46 |
459 |
1,6 |
36,15 |
509,8 |
1,4 |
9,85 |
-50,8 |
-71,12 |
-500,38 |
13,79 |
| 2 |
107 |
455 |
1,6 |
36,15 |
509,8 |
0,4 |
70,85 |
-54,8 |
-21,92 |
-3882,58 |
28,34 |
| 2 |
47 |
467 |
1,6 |
36,15 |
509,8 |
0,4 |
10,85 |
-42,8 |
-17,12 |
-464,38 |
4,34 |
| 2 |
97 |
468 |
1,6 |
36,15 |
509,8 |
0,4 |
60,85 |
-41,8 |
-16,72 |
-2543,53 |
24,34 |
| 2 |
60 |
552 |
1,6 |
36,15 |
509,8 |
0,4 |
23,85 |
42,2 |
16,88 |
1006,47 |
9,54 |
| 2 |
41 |
565 |
1,6 |
36,15 |
509,8 |
0,4 |
4,85 |
55,2 |
22,08 |
267,72 |
1,94 |
| 2 |
57 |
570 |
1,6 |
36,15 |
509,8 |
0,4 |
20,85 |
60,2 |
24,08 |
1255,17 |
8,34 |
| 2 |
30 |
579 |
1,6 |
36,15 |
509,8 |
0,4 |
-6,15 |
69,2 |
27,68 |
-425,58 |
-2,46 |
| 2 |
150 |
597 |
1,6 |
36,15 |
509,8 |
0,4 |
113,85 |
87,2 |
34,88 |
9927,72 |
45,54 |
| 1 |
75 |
441 |
1,6 |
36,15 |
509,8 |
-0,6 |
38,85 |
-68,8 |
41,28 |
-2672,88 |
-23,31 |
| 1 |
30 |
466 |
1,6 |
36,15 |
509,8 |
-0,6 |
-6,15 |
-43,8 |
26,28 |
269,37 |
3,69 |
| 1 |
15 |
500 |
1,6 |
36,15 |
509,8 |
-0,6 |
-21,15 |
-9,8 |
5,88 |
207,27 |
12,69 |
| 1 |
26 |
524 |
1,6 |
36,15 |
509,8 |
-0,6 |
-10,15 |
14,2 |
-8,52 |
-144,13 |
6,09 |
| 1 |
22 |
530 |
1,6 |
36,15 |
509,8 |
-0,6 |
-14,15 |
20,2 |
-12,12 |
-285,83 |
8,49 |
| 1 |
32 |
539 |
1,6 |
36,15 |
509,8 |
-0,6 |
-4,15 |
29,2 |
-17,52 |
-121,18 |
2,49 |
| 1 |
62 |
555 |
1,6 |
36,15 |
509,8 |
-0,6 |
25,85 |
45,2 |
-27,12 |
1168,42 |
-15,51 |
| 1 |
14 |
560 |
1,6 |
36,15 |
509,8 |
-0,6 |
-22,15 |
50,2 |
-30,12 |
-1111,93 |
13,29 |
| 1 |
30 |
575 |
1,6 |
36,15 |
509,8 |
-0,6 |
-6,15 |
65,2 |
-39,12 |
-400,98 |
3,69 |
| 1 |
88 |
575 |
1,6 |
36,15 |
509,8 |
-0,6 |
51,85 |
65,2 |
-39,12 |
3380,62 |
-31,11 |
| 1 |
18 |
600 |
1,6 |
36,15 |
509,8 |
-0,6 |
-18,15 |
90,2 |
-54,12 |
-1637,13 |
10,89 |
| 1 |
18 |
600 |
1,6 |
36,15 |
509,8 |
-0,6 |
-18,15 |
90,2 |
-54,12 |
-1637,13 |
10,89 |
| 1 |
40 |
615 |
1,6 |
36,15 |
509,8 |
-0,6 |
3,85 |
105,2 |
-63,12 |
405,02 |
-2,31 |
| 1 |
14 |
680 |
1,6 |
36,15 |
509,8 |
-0,6 |
-22,15 |
170,2 |
-102,12 |
-3769,93 |
13,29 |
| 0 |
18 |
510 |
1,6 |
36,15 |
509,8 |
-1,6 |
-18,15 |
0,2 |
-0,32 |
-3,63 |
29,04 |
| 0 |
0 |
533 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
23,2 |
-37,12 |
-838,68 |
57,84 |
| 0 |
0 |
533 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
23,2 |
-37,12 |
-838,68 |
57,84 |
| 0 |
0 |
541 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
31,2 |
-49,92 |
-1127,88 |
57,84 |
| 0 |
0 |
541 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
31,2 |
-49,92 |
-1127,88 |
57,84 |
| 0 |
0 |
561 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
51,2 |
-81,92 |
-1850,88 |
57,84 |
| 0 |
29 |
570 |
1,6 |
36,15 |
509,8 |
-1,6 |
-7,15 |
60,2 |
-96,32 |
-430,43 |
11,44 |
| 0 |
0 |
585 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
75,2 |
-120,32 |
-2718,48 |
57,84 |
| 0 |
0 |
590 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
80,2 |
-128,32 |
-2899,23 |
57,84 |
| 0 |
0 |
606 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
96,2 |
-153,92 |
-3477,63 |
57,84 |
| 0 |
0 |
616 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
106,2 |
-169,92 |
-3839,13 |
57,84 |
| 0 |
0 |
640 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
130,2 |
-208,32 |
-4706,73 |
57,84 |
| 0 |
0 |
640 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
130,2 |
-208,32 |
-4706,73 |
57,84 |
| 0 |
0 |
640 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
130,2 |
-208,32 |
-4706,73 |
57,84 |
| 0 |
0 |
643 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
133,2 |
-213,12 |
-4815,18 |
57,84 |
| 0 |
10 |
650 |
1,6 |
36,15 |
509,8 |
-1,6 |
-26,15 |
140,2 |
-224,32 |
-3666,23 |
41,84 |
| 0 |
0 |
650 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
140,2 |
-224,32 |
-5068,23 |
57,84 |
| 0 |
0 |
661 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
151,2 |
-241,92 |
-5465,88 |
57,84 |
| 0 |
0 |
661 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
151,2 |
-241,92 |
-5465,88 |
57,84 |
| 0 |
0 |
683 |
1,6 |
36,15 |
509,8 |
-1,6 |
-36,15 |
173,2 |
-277,12 |
-6261,18 |
57,84 |
| 0 |
13 |
600 |
1,6 |
36,15 |
509,8 |
-1,6 |
-23,15 |
90,2 |
-144,32 |
-2088,13 |
37,04 |
| Итого: |
-4829,8 |
-98283,3 |
1894,15 |
Тогда

Таким образом, значение линейного коэффициента корреляции = -0,84 свидетельствует о наличии обратной и тесной связи между временем эксплуатации и ценой автомобиля.
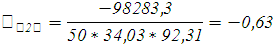
Таким образом, значение линейного коэффициента корреляции = -0,63 свидетельствует о наличии обратной и тесной связи между пробегом и ценой автомобиля.
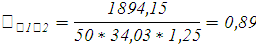
Таким образом, значение линейного коэффициента корреляции = 0,89 свидетельствует о наличии прямой и тесной связи временем эксплуатации и пробегом автомобиля.
Проведем анализ матрицы парных коэффициентов корреляции:
Составим матрицу парных коэффициентов корреляции:
| Y |
X1 |
X2 |
| Y |
1 |
-0,84 |
-0,63 |
| X1 |
-0,84 |
1 |
0,89 |
| X2 |
-0,63 |
0,89 |
1 |
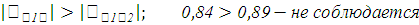
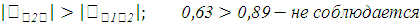
Так как оба условия не соблюдаются, то для составления уравнения регрессии будем использовать наиболее значимый (весомый) факторный признак, т.е. – X1 (время эксплуатации), т.к. 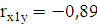 . .
Составим уравнение регрессии:
В качестве регрессионной модели выберем линейную модель, которая имеет вид:
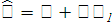
Вычислим коэффициенты регрессионного уравнения:
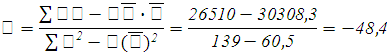

Таким образом, уравнение регрессии примет вид:
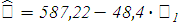
В ходе исследования были выявлены следующие характеристики взаимосвязи стоимости автомобиля с факторными признаками:
· Стоимость автомобиля линейно зависит от пробега и времени эксплуатации причем эта зависимость обратная для обоих случаев. При увеличении пробега (времени эксплуатации) стоимость автомобиля уменьшается;
· Основным фактором, влияющим на конечную стоимость, является время эксплуатации;
· Выявлена зависимость стоимости автомобиля от времени эксплуатации, которая имеет следующий вид:
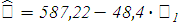
1) Сайт www.auto.ru.
2) Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: Учеб. пособие. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – 336 с: ил. ISBN 5-279-02555-0.
|