Обробка результатів прямих багатократних рівно точних статистичних вимірювань
Хід роботи
I. Схема вимірювань та початкові дані.
1) Схема вимірювань:
2) Початкові дані:
– номінальне значення частоти генератора – 270 Гц
;
– точність установки частоти генератора – ± 1,5%;
– початковий статистичний ряд:
Табл. 1
| Номер вимірювання |
Значення частоти, Гц
|
Номер вимірювання |
Значення частоти, Гц
|
| 1 |
269,508 |
24 |
269,597 |
| 2 |
269,441 |
25 |
269,550 |
| 3 |
269,627 |
26 |
269,517 |
| 4 |
269,442 |
27 |
269,417 |
| 5 |
269,520 |
28 |
269,442 |
| 6 |
269,604 |
29 |
269,476 |
| 7 |
269,627 |
30 |
269,535 |
| 8 |
269,522 |
31 |
269,521 |
| 9 |
269,476 |
32 |
269,623 |
| 10 |
269,451 |
33 |
269,583 |
| 11 |
269,515 |
34 |
269,457 |
| 12 |
269,439 |
35 |
269,441 |
| 13 |
269,509 |
36 |
269,487 |
| 14 |
269,508 |
37 |
269,516 |
| 15 |
269,508 |
38 |
269,528 |
| 16 |
269,526 |
39 |
269,499 |
| 17 |
269,572 |
40 |
269,453 |
| 18 |
269,523 |
41 |
269,518 |
| 19 |
269,580 |
42 |
269,556 |
| 20 |
269,511 |
43 |
269,543 |
| 21 |
269,520 |
44 |
269,445 |
| 22 |
269,528 |
45 |
269,536 |
| 23 |
269,588 |
II. Обчислення оцінок основних статистичних характеристик.
Найчастіше на практиці описують оцінки таких характеристик:
1)
оцінка середнього значення Ā:
 Гц Гц
Ā – характеризує найбільш очікуване значення фізичної величини.
2)
оцінка середнього квадратичного відхилення результатів вимірювання від середнього значення:
 Гц Гц
S – міра розсіювання (розкиду) результатів вимірювань від середнього значення.
3)
оцінка дисперсії розсіювання результатів вимірювань:
 Гц2 Гц2
4)
оцінка коефіцієнта асиметрії:

A – характеризує несиметричність розподілу результатів вимірювань відносно середнього значення.
5)
оцінка коефіцієнта асиметрії:

E – характеризує плосковершинність кривої розподілу.
Всі обчислення подаємо у вигляді таблиці:
Табл. 2
| Номер вимірювання |
ai |
(ai – Ā) |
(ai – Ā)² |
(ai – Ā)³ |
(ai – Ā) |
| 1 |
269,508 |
-0,009 |
0,000081 |
-0,000000729 |
0,000000007 |
| 2 |
269,441 |
-0,076 |
0,005776 |
-0,000438976 |
0,000033362 |
| 3 |
269,627 |
0,110 |
0,012100 |
0,001331000 |
0,000146410 |
| 4 |
269,442 |
-0,075 |
0,005625 |
-0,000421875 |
0,000031641 |
| 5 |
269,520 |
0,003 |
0,000009 |
0,000000027 |
0,000000000 |
| 6 |
269,604 |
0,087 |
0,007569 |
0,000658503 |
0,000057290 |
| 7 |
269,627 |
0,110 |
0,012100 |
0,001331000 |
0,000146410 |
| 8 |
269,522 |
0,005 |
0,000025 |
0,000000125 |
0,000000001 |
| 9 |
269,476 |
-0,041 |
0,001681 |
-0,000068921 |
0,000002826 |
| 10 |
269,451 |
-0,066 |
0,004356 |
-0,000287496 |
0,000018975 |
| 11 |
269,515 |
-0,002 |
0,000004 |
-0,000000008 |
0,000000000 |
| 12 |
269,439 |
-0,078 |
0,006084 |
-0,000474552 |
0,000037015 |
| 13 |
269,509 |
-0,008 |
0,000064 |
-0,000000512 |
0,000000004 |
| 14 |
269,508 |
-0,009 |
0,000081 |
-0,000000729 |
0,000000007 |
| 15 |
269,508 |
-0,009 |
0,000081 |
-0,000000729 |
0,000000007 |
| 16 |
269,526 |
0,009 |
0,000081 |
0,000000729 |
0,000000007 |
| 17 |
269,572 |
0,055 |
0,003025 |
0,000166375 |
0,000009151 |
| 18 |
269,523 |
0,006 |
0,000036 |
0,000000216 |
0,000000001 |
| 19 |
269,580 |
0,063 |
0,003969 |
0,000250047 |
0,000015753 |
| 20 |
269,511 |
-0,006 |
0,000036 |
-0,000000216 |
0,000000001 |
| 21 |
269,520 |
0,003 |
0,000009 |
0,000000027 |
0,000000000 |
| 22 |
269,528 |
0,011 |
0,000121 |
0,000001331 |
0,000000015 |
| 23 |
269,588 |
0,071 |
0,005041 |
0,000357911 |
0,000025412 |
| 24 |
269,597 |
0,080 |
0,006400 |
0,000512000 |
0,000040960 |
| 25 |
269,550 |
0,033 |
0,001089 |
0,000035937 |
0,000001186 |
| 26 |
269,517 |
0,000 |
0,000000 |
0,000000000 |
0,000000000 |
| 27 |
269,417 |
-0,100 |
0,010000 |
-0,001000000 |
0,000100000 |
| 28 |
269,442 |
-0,075 |
0,005625 |
-0,000421875 |
0,000031641 |
| 29 |
269,476 |
-0,041 |
0,001681 |
-0,000068921 |
0,000002826 |
| 30 |
269,535 |
0,018 |
0,000324 |
0,000005832 |
0,000000105 |
| 31 |
269,521 |
0,004 |
0,000016 |
0,000000064 |
0,000000000 |
| 32 |
269,623 |
0,106 |
0,011236 |
0,001191016 |
0,000126248 |
| 33 |
269,583 |
0,066 |
0,004356 |
0,000287496 |
0,000018975 |
| 34 |
269,457 |
-0,060 |
0,003600 |
-0,000216000 |
0,000012960 |
| 35 |
269,441 |
-0,076 |
0,005776 |
-0,000438976 |
0,000033362 |
| 36 |
269,487 |
-0,030 |
0,000900 |
-0,000027000 |
0,000000810 |
| 37 |
269,516 |
-0,001 |
0,000001 |
-0,000000001 |
0,000000000 |
| 38 |
269,528 |
0,011 |
0,000121 |
0,000001331 |
0,000000015 |
| 39 |
269,499 |
-0,018 |
0,000324 |
-0,000005832 |
0,000000105 |
| 40 |
269,453 |
-0,064 |
0,004096 |
-0,000262144 |
0,000016777 |
| 41 |
269,518 |
0,001 |
0,000001 |
0,000000001 |
0,000000000 |
| 42 |
269,556 |
0,039 |
0,001521 |
0,000059319 |
0,000002313 |
| 43 |
269,543 |
0,026 |
0,000676 |
0,000017576 |
0,000000457 |
| 44 |
269,445 |
-0,072 |
0,005184 |
-0,000373248 |
0,000026874 |
| 45 |
269,536 |
0,019 |
0,000361 |
0,000006859 |
0,000000130 |
На практиці оцінюється значущість коефіцієнтів вимірювань.
Для цього обчислюємо дисперсії коефіцієнтів A і E:
 , ,

Якщо виконується умова, що
 і і  , ,
то робиться висновок, що коефіцієнти незначущі, а значить ними можна знехтувати. В протилежному випадку коефіцієнти є значущі, а значить вони повинні бути враховані при виборі математичної моделі для опису розподілу результатів вимірювань.
Висновок: для нормального закону розподілу результатів вимірювань коефіцієнти A і E рівні нулю, тому якщо на практиці ми отримали А 0 і Е 0 і Е 0 або ними можна знехтувати, то з великою достовірністю можна говорити, що наші результати розподіляються за нормальним законом. В нашому випадку А і Е не дорівнюють нулю, тому, що ми маємо дуже мало вимірювань проте вони є незначущі (0,227 0 або ними можна знехтувати, то з великою достовірністю можна говорити, що наші результати розподіляються за нормальним законом. В нашому випадку А і Е не дорівнюють нулю, тому, що ми маємо дуже мало вимірювань проте вони є незначущі (0,227 1,049 і 0,717 1,049 і 0,717 3,277), а значить ними можна знехтувати. Звідси слідує, що дійсно наші результати розподіляються за нормальним законом розподілу. 3,277), а значить ними можна знехтувати. Звідси слідує, що дійсно наші результати розподіляються за нормальним законом розподілу.
Грубі похибки та промахи повинні бути виявленні і відкинуті з результатів вимірювань. З цією метою використовується спеціальний статистичний критерій – критерій Стьюдента.
В роботі використовуємо критерій – правило трьох у.
Початковий статистичний ряд представимо у вигляді такого графіка:

статистичний коефіцієнт середній стьюдент
На графік наносимо середнє значення і межі (границі):
– верхню Ā+3S;
– нижню Ā-3S.
Висновок: грубих похибок і промахів не виявлено; початковий ряд є однорідним; приведемо його характеристики: n=45, Ā=269.517 Гц, S=0.055 Гц
Додатково перевіримо наявність грубих похибок використовуючи коефіцієнти Стьюдента. Для цього знаходимо на графіку максимальне і мінімальне значення і обчислюємо квантиль t1
і t2:


Для n = 45 при p = 0.98 tдоп.
= 2,4
t1
 tдоп.
, t2 tдоп.
, t2
 tдоп. tдоп.
За допомогою коефіцієнтів Стьюдента ми ще раз підтвердили, що грубі похибки і промахи відсутні, статистичний ряд є однорідним.
Експериментальний розподіл отримують у вигляді гістограми.
Порядок побудови гістограми:
1) однорідний ряд розміщуємо в порядку зростання;
2) обчислюємо розмах значень:
 ; ;
3) відрізок  розділяємо на розділяємо на  рівних інтервалів: рівних інтервалів:
 ; ;
4) обчислюємо ширину інтервалу гістограми:
 ; ;
5) обчислюємо межі кожного інтервалу, результати записуємо у таблицю 3.
Табл. 3
| Номер вимірювання |
Межі інтервалів |
nj
|
pj
|
| 1 |
269,417 ч 269,447 |
7 |
0.155556 |
| 2 |
269,447 ч 269,477 |
5 |
0.111111 |
| 3 |
269,477 ч 269,507 |
2 |
0.044444 |
| 4 |
269,507 ч 269,537 |
19 |
0.422222 |
| 5 |
269,537 ч 269,567 |
3 |
0.066667 |
| 6 |
269,567 ч 269,597 |
5 |
0.111111 |
| 7 |
269,597 ч 269,627 |
4 |
0.088889 |
6) підраховуємо число попадання результатів вимірювань в кожен інтервал nj
;
7) обчислюємо імовірності попадань результатів вимірювань в кожен інтервал  ; ;
8) будуємо гістограму:
Для цього на кожному інтервалі будуємо прямокутник площа якого дорівнює pj
.

Гістограма – це експериментальний аналог густини розподілу.
Крім гістограми є ще інші варіанти представлення експериментальних розподілів:
– у вигляді полігону розподілу;
– у вигляді функції накопичених частот.
Вибір математичної моделі проводиться з урахуванням:
Враховуючи сказане і вигляд гістограми вибір математичної моделі розпочинаємо з функції Гауса:
 . .
На практиці використовують нормований варіант задання нормального закону розподілу.
Умови нормування:
- m = 0;
- у = 1.
Після нормування функція Гауса має такий вигляд:

Гістограму також треба представити у нормованому вигляді. Тобто  і і . .
| Номер інтервалу |
Нормовані межі інтервалів |
Експериментальні імовірності (р
j
) |
Теоретичні імовірності (pj
*
)
|
| 1 |
-1,818 ч -1,273 |
0.15556 |
0,067 |
| 2 |
-1,273 ч -0,727 |
0.11111 |
0,132 |
| 3 |
-0,727 ч -0,182 |
0.04444 |
0,194 |
| 4 |
-0,182 ч 0,364 |
0.42222 |
0,214 |
| 5 |
0,364 ч 0,909 |
0.06667 |
0,176 |
| 6 |
0,909 ч 1,445 |
0.11111 |
0,109 |
| 7 |
1,445 ч 2 |
0.08889 |
0,05 |
 , , 

Для вирішення цієї задачі використаємо критерій, який так і називається, критерій узгодженості.
Серед них найчастіше використовуються:
- критерій Пірсона (критерій ч2
);
- критерій Колмогорова;
- критерій щ2
та інші.
В роботі використовуємо критерій Пірсона.
| pj
|
pj
*
|
(pj
 pj
*
) pj
*
)
|
(pj
 pj
*
)2 pj
*
)2
|
(pj
 pj
*
)2
/ pj
* pj
*
)2
/ pj
*
|
| 0.15556 |
0.067 |
0.089 |
0.00792 |
0.118 |
| 0.11111 |
0.132 |
-0.021 |
0.00044 |
0.003 |
| 0.04444 |
0.194 |
-0.150 |
0.0225 |
0.116 |
| 0.42222 |
0.214 |
0.208 |
0.04326 |
0.202 |
| 0.06667 |
0.176 |
-0.109 |
0.01188 |
0.068 |
| 0.11111 |
0.109 |
0.002 |
0.000004 |
0.00004 |
| 0.08889 |
0.050 |
0.039 |
0.00152 |
0.03 |
| ∑ = 0.537 |
Величина  служить мірою розбіжності експериментального розподілу і вибраної математичної моделі. служить мірою розбіжності експериментального розподілу і вибраної математичної моделі.
Вибираємо довірчу імовірність  . .
Обчислюємо рівень значимості  . .
Обчислюємо число вільності 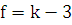 , де k – кількість інтервалів гістограми , де k – кількість інтервалів гістограми  . .
За цими даними із таблиці розподілу Пірсона  . . 
Висновок: математична модель (функція Гауса) не описує експериментальний розподіл, потрібно вибрати наступну математичну модель, наприклад, якщо експериментальний розподіл є симетричним трикутноподібну, або іншу.
|