ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ
Задачи № 1-10.
Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.
9) 
Решение
Задача № 1.
Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.
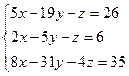
1-й способ (метод Крамера).
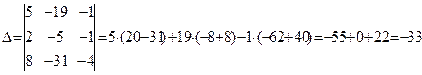
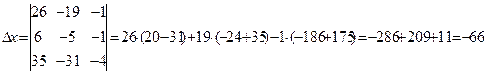
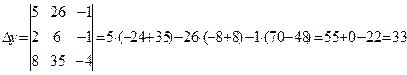
По формулам Крамера, найдем решение:
2 способ (решение с помощью обратной матрицы).
Перепишем систему уравнений в виде AX =
B
, где
 ,  ,  .
Решение матричного уравнения имеет вид X
=
A
-1
B
. Найдем обратную матрицу A
-1
.
Имеем следующий главный определитель системы:
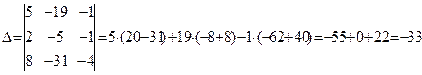
Вычислим алгебраические дополнения элементов транспонированной матрицы:
 ,  ,  ,  ,
 ,  ,  ,  ,
 .
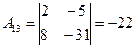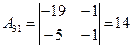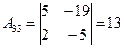Тогда обратная матрица имеет вид:
 , следовательно,
 .
Ответ: x
= 2; y
= -1;z
= 3.
3 способ (метод Гаусса).
 .
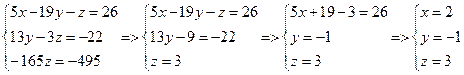Из последнего уравнения имеем z
= 3; подставляя это значение во второе уравнение, получаем y
= -1 и тогда из первого уравнения находим x
= 2.
Задачи № 11 - 20.
Найти производные функций:
15)
а) 
; б) 
.
Решение
Задачи № 21-30.
Найти общее и частное частное решение линейного однородного дифференциального уравнения второго порядка, соответствующего начальным условиям:
при 
, 
, 
.
21) 
;
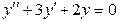Решение
Составим характеристическое уравнение имеет вид:
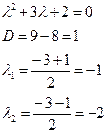
Следовательно, общее решение уравнения без правой части таково:
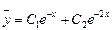
Так как n=1 не является корнем характеристического уравнения, то ищем частное решение уравнения с правой частью в виде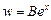 
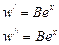
Подставляя эти выражения в наше неоднородное уравнение, получим
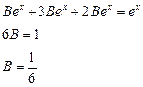
Итак, частное решение уравнения с правой частью есть
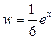
Общее же решение этого уравнения на основании предыдущей теоремы имеет вид:
Найдем частные решения:
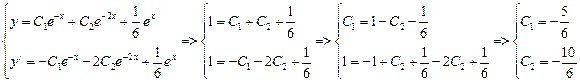
Задачи № 31-40
38) В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 путевок. Найти вероятность того, что среди обладателей путевок окажутся две девушки.
Решение
Задача решается с помощью классической формулы для вычисления вероятностей:
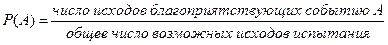
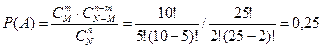
Ответ: 
Задачи № 41-50
Закон распределения дискретной случайной величины Х задан в таблице. Найти: 1)математическое ожидание, дисперсию и среднее квадратическое отклонение; 2) вычислить математическое ожидание и дисперсию случайной величины 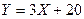 , пользуясь свойствами математического ожидания и дисперсии.
| Номер задачи
|
Условие задачи
|
| 4
1
|
xi
|
2 |
4 |
6 |
8 |
10 |
| pi
|
0,2 |
0,3 |
0,1 |
0,2 |
0,2 |
Решение
Расчет ведем по формулам для числовых характеристик дискретных случайных величин.
Математическое ожидание:
Дисперсия:
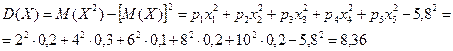
Среднее квадратическое отклонение:
Для вычисления характеристик случайной величины Y=3X+20 воспользуемся свойствами математического ожидания и дисперсии:
Ответ: 
Аудиторная контрольная работа по дисциплине «Математика»
Вариант № 1
1. Решить систему уравнений:  .
Решение
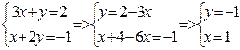
Ответ: х=1, у=-1.
Найти производную:  .
Решение
В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5 отличников.
Решение
Задача решается с помощью классической формулы для вычисления вероятностей:
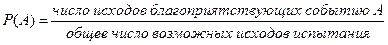
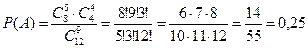
Ответ:
4. Задан закон распределения дискретной случайной величины Х:
| xi
|
-4 |
6 |
10 |
| pi
|
0,2 |
0,3 |
0,5 |
Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение
Расчет ведем по формулам для числовых характеристик дискретных случайных величин.
Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение:
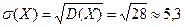
Ответ: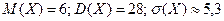 
|