ЦЕНТРОСОЮЗ РОССИЙСКОЙ ФЕДЕРАЦИИ
СИБИРСКИЙ УНИВЕРСИТЕТ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ
Контрольная работа
ЛИНЕЙНАЯ АЛГЕБРА И МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Новосибирск 2009
Задачи 1–10. Показать, что система линейных уравнений имеет единственное решение, и найти его двумя способами: а) по правилу Крамера; б) матричным способом
8. 
Решение
Используя формулы Крамера
Вычислим определитель системы линейных уравнений
Д = 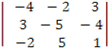 = (-4)(-5)1 + 3(5)3 + (-2)(-2)(-4) – (-2)(-5)(3) – (-4)(5)(-4) -3(-2)(1) = = (-4)(-5)1 + 3(5)3 + (-2)(-2)(-4) – (-2)(-5)(3) – (-4)(5)(-4) -3(-2)(1) =
= 20 + 45 – 16 – 30 – 80 + 6 = - 55
Так как Д # 0, то система линейных уравнений невырожденная и имеет единственное решение.
Вычислим определители Д1, Д2, Д3
Д1 =  = (31)(-5)1 + (-6)(5)3 + (-11)(-2)(-4) – (-11)(-5)(3) – (31)(5)(-4) – (-6)(-2)(1) = - 155 – 90 – 88 – 165 + 620 – 12 = 110 = (31)(-5)1 + (-6)(5)3 + (-11)(-2)(-4) – (-11)(-5)(3) – (31)(5)(-4) – (-6)(-2)(1) = - 155 – 90 – 88 – 165 + 620 – 12 = 110
Д2 = 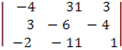 = (-4)(-6)1 + 3(-11)3 + (-2)(31)(-4) – (-2)(-6)(3) – (-4)(-11)(-4) – 3(31)(1) = 24 – 99 + 248 – 36 + 176 - 93 = 220 = (-4)(-6)1 + 3(-11)3 + (-2)(31)(-4) – (-2)(-6)(3) – (-4)(-11)(-4) – 3(31)(1) = 24 – 99 + 248 – 36 + 176 - 93 = 220
Д3 =  = (-4)(-5)(-11) + (3)(5)31 + (-2)(-2)(-6) – (-2)(-5)(31) – (-4)(5)(-6) – 3(-2)(-11) = - 220 + 465 – 24 – 310 – 120 – 66 = - 275 = (-4)(-5)(-11) + (3)(5)31 + (-2)(-2)(-6) – (-2)(-5)(31) – (-4)(5)(-6) – 3(-2)(-11) = - 220 + 465 – 24 – 310 – 120 – 66 = - 275
Отсюда, X1
= 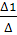 = =  = - 2, X2
= = - 2, X2
=  = = 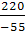 = - 4, X3
= = - 4, X3
=  = =  = 5 = 5
Проверка:
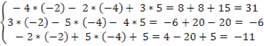  , ,
что подтверждает правильность найденного решения системы линейных уравнений.
· Решение матричным способом
A * X = B X = 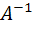 * В * В
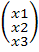 = =  * * 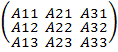 * *  . Д = . Д = 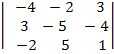 = - 55 = - 55
здесь  - алгебраические дополнения, которые и вычислим: - алгебраические дополнения, которые и вычислим:
A11 = = (-5)1 – 5(-4) = 15 = (-5)1 – 5(-4) = 15
A12 = = -(3(1) –(-2)(-4)) = 5 = -(3(1) –(-2)(-4)) = 5
A13 = = 3(5) – (-2)(-5) = 5 = 3(5) – (-2)(-5) = 5
A21 =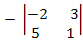 = -( (-2)1 – 5(3) ) = 17 = -( (-2)1 – 5(3) ) = 17
A22 =  = (-4)1 – (-2)3 = 2 = (-4)1 – (-2)3 = 2
A23 = = - ( (-4)5 – (-2)(-2) ) = 24 = - ( (-4)5 – (-2)(-2) ) = 24
A31 = = (-2)(-4) – (-5)3 = 23 = (-2)(-4) – (-5)3 = 23
A32 =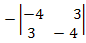 = - ( (-4)(-4) – 3(3) ) = - 7 = - ( (-4)(-4) – 3(3) ) = - 7
A33 = = (-4)(-5) – 3(-2) = 26 = (-4)(-5) – 3(-2) = 26
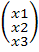 = =  * * 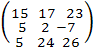 * * 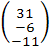 = =  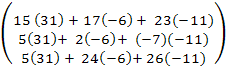
=  = = 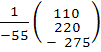 = = 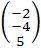
Ответ: X1
= - 2, X2
= - 4, X3
= 5
Задачи 11–20. Пользуясь методом Гаусса, найти общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное.
18. 
Решение
Составим расширенную матрицу (А|B)
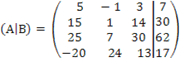
Приведем матрицу (А|B) к ступенчатому виду.
Оставив без изменения первую строку и умножая её соответственно на -3, -5, 4, прибавим полученное к строкам 2, 3 и 4

Оставив без изменения первую и вторую строки и умножая последнюю соответственно на -3, -5, прибавим полученное к строкам 3 и 4
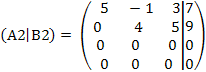
По виду этой матрицы заключаем, что система совместная и неопределенная (имеет бесконечно много решений). Система, соответствующая полученной матрице, имеет вид
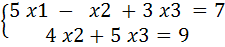
Так как эта система состоит из двух уравнений, но содержит три переменные, одну из переменных можно выбрать произвольно, например, положим х3
. Перенося слагаемые с х3
в правую часть, получим систему

Решая ее, находим: x2
=  , x1
= , x1
=  где х3
– любое действительное число. где х3
– любое действительное число.
Общим решением системы линейных алгебраических уравнений называется такая их запись, в которой часть ее переменных, называемых базисными, выражены через оставшиеся переменные, называемые свободными. В данном примере переменные х1
и х2
– базисные, а х3
– свободная. И запись

называется общим решением системы.
Частные решения получаются из общего, если задать произвольно свободные переменные. Например, если 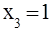 , то X1
= 1, X2
= 2. Это частное решение системы. , то X1
= 1, X2
= 2. Это частное решение системы.
Базисным решением системы линейных алгебраических уравнений называют такое частное решение, при котором свободные переменные равны нулю. Например, если 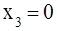 , то X1
= , то X1
= 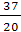 , X2
= , X2
= . Это базисное решение системы линейных алгебраических уравнений . Это базисное решение системы линейных алгебраических уравнений
Задачи 21–30. Решить графически задачу линейного программирования.
23. 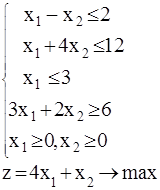
Решение
Построим область допустимых решений. Для этого наносим на чертеж границы области допустимых решений. Каждое из неравенств системы ограничений задачи линейного программирования определяет прямую, которая делит всю числовую плоскость на две полуплоскости. Знак - будет обозначать ту полуплоскость, которая соответствует выполнению неравенства. Область допустимых решений представляет собой многоугольник ABCDE.
 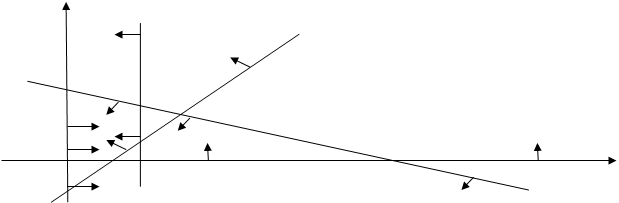 X2 X2
4х1
+ х2
= 0
 5 X1
≤ 3 5 X1
≤ 3
4 X1
- X2
≤ 2
B(0,3) 3 C(3, ) )
2
1 D(3,1) X1
+ 4 X2
≤ 12
 E(2,0) X2
≥ 0 E(2,0) X2
≥ 0
A(0,0) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 X1
X1
≥ 0
Найдем координаты точек A, B, C, D, E. Для этого последовательно решим несколько систем уравнений, образуемых из неравенств системы ограничений задачи линейного программирования.
Для точки А:
 Отсюда, Отсюда,  , т.е. А(0,0). , т.е. А(0,0).
Для точки В: 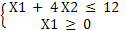 отсюда, отсюда, 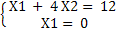 , Х2
= 3, т.е. В(0,3). , Х2
= 3, т.е. В(0,3).
Для точки C: 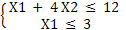 отсюда, отсюда,  , Х2
= , Х2
=  , т.е. С(3, , т.е. С(3, ). ).
Для точки D:  отсюда, отсюда, 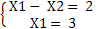 , Х2
= 1, т.е. D(3,1). , Х2
= 1, т.е. D(3,1).
Для точки E:  отсюда, отсюда,  , Х1
= 2, т.е. E(2,0). , Х1
= 2, т.е. E(2,0).
Координаты точек: A(0,0) , B(0,3), C(3, ), D(3,1), E(2,0) ), D(3,1), E(2,0)
В соответствии с коэффициентами целевой функцией
z = 4 x1
+ x2
 max max
построим вектор  ( 4, 1) и прямую 4х1
+ х2
= 0. ( 4, 1) и прямую 4х1
+ х2
= 0.
Перемещаем прямую по направлению вектора. Точкой выхода из области допустимых решений является точка С(3, Точкой выхода из области допустимых решений является точка С(3, ). ).
В точке С(3, ) и будет оптимальное решение (максимальное), то есть при х1
= 3; х2
= ) и будет оптимальное решение (максимальное), то есть при х1
= 3; х2
=  значение целевой функции будет максимальным значение целевой функции будет максимальным
Zmax= 4 * 3 +  = 14 = 14 . .
Проверка:
В соответствии с одной из теорем теории линейного программирования линейная функция z = 4 x1
+ x2
достигает максимального значения в вершинах многогранника, т.е. в точках A(0,0) , B(0,3), C(3, ), D(3,1), E(2,0). ), D(3,1), E(2,0).
Вычислим значения z = 4 x1
+ x2
в этих точках:
· z (A(0,0)) = 4*0 + 0 = 0
· z (B(0,3)) = 4*0 + 3 = 3
· z (D(3,1)) = 4*3 + 1 = 13
· z (E(2,0)) = 4*2 + 0 = 8
· z (C(3, )) = 4*3 + )) = 4*3 + = 14 = 14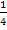 . , что и подтверждаем максимальность значения целевой функции. . , что и подтверждаем максимальность значения целевой функции.
Задачи 31–40. На трех базах А1
, А2
, А3
имеется однородный груз в количестве а1
, а2
, а3
единиц. Этот груз нужно перевезти в пять пунктов В1, В2, В3, В4, В5 в количестве b1, b2, b3, b4, b5 единиц соответственно. Затраты на перевозку груза между пунктами поставок и потребления заданы матрицей тарифов С:
 . .
Спланировать перевозки так, чтобы их общая стоимость была минимальной.
40. 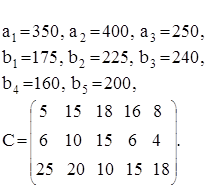
Решение:
Вычислим y =  = 350 + 400 + 250 = 1000, = 350 + 400 + 250 = 1000,
к = 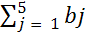 = 175 + 225 + 240 + 160 + 200 = 1000, так как к = y , то решаемая транспортная задача является закрытой. = 175 + 225 + 240 + 160 + 200 = 1000, так как к = y , то решаемая транспортная задача является закрытой.
Обозначим через  количество груза, перевозимого из пункта количество груза, перевозимого из пункта 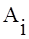 в пункт в пункт  . .
Рассмотрим закрытую транспортную задачу. Ее условия запишем в распределительную таблицу, которую будем использовать для нахождения решения.
Математическая модель закрытой транспортной задачи имеет вид
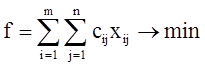
при ограничениях 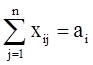 , ,
 , ,
X ij ≥ 0 , i = 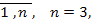 j = j =  , m = 5. , m = 5.
Оптимальным решением задачи является матрица Xopt = ( Xij )3x5, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.
Условия задачи и ее исходное решение будем записывать в распределительную таблицу. Клетки, в которые поместим грузы, называются занятыми, остальные клетки – незанятыми, или пустыми. В верхнем правом углу каждой клетки будем записывать тарифы. Существует несколько способов нахождения исходного решения.
Рассмотрим один из них – метод минимального тарифа (элемента). Согласно этому методу, грузы распределяются в первую очередь в те клетки, в которых находится минимальный тариф перевозок Cij. Далее поставки распределяются в незанятые клетки с наименьшими тарифами с учетом оставшихся запасов у поставщиков и удовлетворения спроса потребителей.
Процесс распределения продолжается до тех пор, пока все грузы от поставщиков не будут вывезены, а потребители не будут удовлетворены. При распределении грузов может оказаться, что количество занятых клеток меньше, чем m + n -1 = 5 + 3 – 1 = .
В этом случае недостающее их число заполняется клетками с нулевыми поставками, такие клетки называют условно занятыми.
Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетке.
Найдем исходное решение по методу минимального тарифа. Для этого составим следующую распределительную таблицу:
 bi bi
ai
|
1 |
2 |
3 |
4 |
5 |
| 175 |
225 |
240 |
160 |
200 |
| 1 |
350 |
5
175
|
15
175
|
18
|
16
|
8
|
| 2 |
400 |
6
|
10
40
|
15
|
6
160
|
4
200
|
| 3 |
250
|
25
|
20
10
|
10
240
|
15
|
18
|
Число занятых клеток в таблице, приведенной выше, равно m + n – 1 = 5 + 3 – 1 = 7, то есть условие невырожденности выполнено. Получили исходное решение, которое запишем в виде матрицы
Х1
=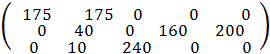
Стоимость перевозки при исходном решении составляет
f1
= 175 * 5 + 175 * 15 + 40 * 10 + 160 * 6 + 200 * 4 + 10 * 20 + 240 * 10 = 8260.
Проверим найденное решение транспортной задачи на оптимальность
Найденное исходное решение проверяется на оптимальность методом потенциалов по следующему критерию: если решение транспортной задачи является оптимальным, то ему соответствует система m+n ( 5 + 3 = 8 ) действительных чисел 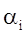 и и  , удовлетворяющих условиям , удовлетворяющих условиям  для занятых клеток и для занятых клеток и  – для свободных клеток. – для свободных клеток.
Числа 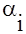 и и  называются потенциалами. В распределительную таблицу добавляют столбец называются потенциалами. В распределительную таблицу добавляют столбец 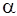 и строку и строку 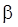 . .
Потенциалы  и и  находят из равенства находят из равенства 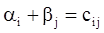 , справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например , справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например  , тогда остальные потенциалы определяются однозначно. Так, если известен потенциал , тогда остальные потенциалы определяются однозначно. Так, если известен потенциал  , то , то  ; если известен потенциал ; если известен потенциал  , то , то  . .
Обозначим 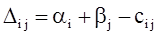 . Эту оценку называют оценкой свободных клеток. Если . Эту оценку называют оценкой свободных клеток. Если 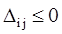 , то опорное решение является оптимальным. Если хотя бы одна из оценок , то опорное решение является оптимальным. Если хотя бы одна из оценок 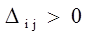 , то решение не является оптимальным и его можно улучшить, перейдя от одного решения к другому. , то решение не является оптимальным и его можно улучшить, перейдя от одного решения к другому.
Проверим найденное решение на оптимальность, добавив в распределительную таблицу, приведенную ниже, столбец  и строку и строку  . .
Полагая 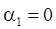 , запишем это значение в последнем столбце , запишем это значение в последнем столбце
таблицы.
 bi bi
ai
|
1 |
2 |
3 |
4 |
5 |
| 175 |
225 |
240 |
160 |
200 |
𝛼i
|
1
|
350
|
5
175
|
15
175
|
18
|
16
|
8
|
0
|
2
|
400
|
6
|
10
40
|
15
|
6
160
|
4
200
|
-5
|
3
|
250
|
25
|
20
10
|
10
240
|
15
|
18
|
0
|
| 𝛽i
|
5 |
15 |
10 |
11 |
9 |
Для клетки (1,1) :  1 + 1 +  1 = 5, 1 = 5,  1 = 0, 1 = 0,  1 = 5 1 = 5
Для клетки (1,2) :  1 + 1 +  2 = 15, 2 = 15,  1 = 0, 1 = 0,  2 = 15 2 = 15
Для клетки (2,2) :  2 + 2 +  2 = 10, 2 = 10,  2 = -5, 2 = -5,  2 = 15 2 = 15
Для клетки (2,4) :  2 + 2 + 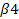 = 6, = 6,  2 = -5, 2 = -5,  4 = 11 4 = 11
Для клетки (2,5) :  2 + 2 +  = 4, = 4,  2 = -5, 2 = -5,  5 = 9 5 = 9
Для клетки (3,3) : 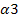 + + 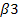 = 10, = 10,  3 = 0, 3 = 0,  3 = 10 3 = 10
Найденные значения потенциалов заносим в таблицу. Вычисляем оценки свободных клеток:
Δ13 =  1 + 1 +  3 – с 13 = 0 + 10 – 18 = - 8 3 – с 13 = 0 + 10 – 18 = - 8 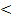 0 0
Δ14 =  1 + 1 + 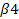 – с 14 = 0 + 11 – 16 = - 5 – с 14 = 0 + 11 – 16 = - 5 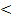 0 0
Δ15 =  1 + 1 +  – с 15 = 0 + 9 – 8 = 1 – с 15 = 0 + 9 – 8 = 1 0 0
Δ21 =  + +  – с 21 = -5 + 5 – 6 = -6 – с 21 = -5 + 5 – 6 = -6 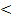 0 0
Δ23 =  + + 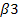 – с 23 = -5 + 10 – 15 = -10 – с 23 = -5 + 10 – 15 = -10 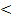 0 0
Δ31 = 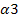 + +  – с 31 = 0 + 5 – 25 = -20 – с 31 = 0 + 5 – 25 = -20 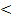 0 0
Δ34 = 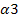 + + 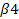 – с 34 = 0 + 11 – 15 = -4 – с 34 = 0 + 11 – 15 = -4 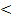 0 0
Δ35 = 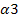 + +  – с 35 = 0 + 9 – 18 = -9 – с 35 = 0 + 9 – 18 = -9 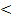 0 0
Получили одну оценку Δ15 = 1 0 следовательно, исходное решение не является оптимальным и его можно улучшить. 0 следовательно, исходное решение не является оптимальным и его можно улучшить.
Переход от одного решения транспортной задачи к другому.
Наличие положительной оценки свободной клетки (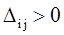 ) при проверке решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной. ) при проверке решения на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.
Для свободной клетки Δ15 = 1 0 строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новое решение. Это решение проверяем на оптимальность, и так далее до тех пор, пока не получим оптимальное решение. 0 строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (-) и (+). У вершин со знаком (-) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (-). В результате перераспределения груза получим новое решение. Это решение проверяем на оптимальность, и так далее до тех пор, пока не получим оптимальное решение.
Х2
=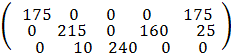
Стоимость перевозки при исходном решении составляет
f2
= 175 * 5 + 215 * 10 + 10 * 20 + 240 * 10 + 160 * 6 + 175 * 8 + 25 * 4 = 8085.
Проверим полученное решение на оптимальность. Для этого запишем его в распределительную таблицу, приведенную ниже, найдем потенциалы занятых и оценки свободных клеток.
 bi bi
ai
|
1 |
2 |
3 |
4 |
5 |
| 175 |
225 |
240 |
160 |
200 |
𝛼i
|
| 1 |
350 |
5
175
|
15
|
18
|
16
|
8
175
|
0 |
| 2 |
400 |
6
|
10
215
|
15
|
6
160
|
4
25
|
-4 |
| 3 |
250
|
25
|
20
10
|
10
240
|
15
|
18
|
0 |
| 𝛽i
|
5 |
14 |
10 |
10 |
8 |
Для клетки (1,1) :  1 + 1 +  1 = 5, 1 = 5,  1 = 0, 1 = 0,  1 = 5 1 = 5
Для клетки (1,5) :  1 + 1 +  5 = 8, 5 = 8,  1 = 0, 1 = 0,  5 = 8 5 = 8
Для клетки (2,5) :  2 + 2 +  = 4, = 4,  = -4, = -4,  = 8 = 8
Для клетки (2,4) :  2 + 2 + 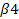 = 6, = 6,  2 = -4, 2 = -4,  4 = 10 4 = 10
Для клетки (2,2) :  2 + 2 + 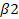 = 10, = 10,  2 = -4, 2 = -4, 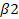 = 14 = 14
Для клетки (3,3) : 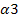 + + 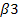 = 10, = 10,  3 = 0, 3 = 0,  3 = 10 3 = 10
Найденные значения потенциалов заносим в таблицу. Вычисляем оценки свободных клеток:
Δ12 =  1 + 1 + 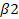 – с 12 = 0 + 14 – 15 = - 1 – с 12 = 0 + 14 – 15 = - 1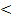 0 0
Δ13 =  1 + 1 + 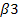 – с 13 = 0 + 10 – 18 = - 8 – с 13 = 0 + 10 – 18 = - 8 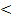 0 0
Δ14 =  1 + 1 + 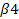 – с 14 = 0 + 10 – 16 = - 6 – с 14 = 0 + 10 – 16 = - 6 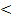 0 0
Δ21 =  + +  – с 21 = -4 + 5 – 6 = - 5 – с 21 = -4 + 5 – 6 = - 5 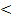 0 0
Δ23 =  + + 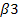 – с 23 = - 4 + 10 – 15 = - 9 – с 23 = - 4 + 10 – 15 = - 9 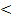 0 0
Δ31 = 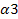 + +  – с 31 = 0 + 5 – 25 = - 20 – с 31 = 0 + 5 – 25 = - 20 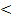 0 0
Δ34 = 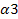 + + 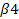 – с 34 = 0 + 10 – 15 = - 5 – с 34 = 0 + 10 – 15 = - 5 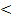 0 0
Δ35 = 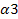 + +  – с 35 = 0 + 8 – 18 = - 10 – с 35 = 0 + 8 – 18 = - 10 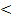 0 0
Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Итак,
Хорт =
Стоимость транспортных расходов равна
Fmin
= 175 * 5 + 215 * 10 + 10 * 20 + 240 * 10 + 160 * 6 + 175 * 8 + 25 * 4 = 8085.
По сравнению с исходным решением, транспортные расходы уменьшились на 175 усл.ед. (8260 – 8085 = 175).
Задачи 41–50. Составить экономико-математическую модель. Найти решение задачи линейного программирования при помощи средств Excel на ПК.
48. В суточном рационе кормления крупного рогатого скота должно быть не менее 20 кормовых единиц, не менее 2000 г белков и не менее 100 г кальция. Для кормления используют сено, силос, корнеплоды и концентраты. Содержание питательных веществ в 1 кг каждого вида корма, а также его себестоимость представлены в таблице. Составить кормовой рацион минимальной стоимости.
| Содержание питательных веществ в 1 кг корма |
Корм |
| Сено |
Силос |
Корнеплоды |
Концентрат |
| Кормовая единица |
0,5 |
0,2 |
6 |
0,8 |
| Белки, г |
40 |
10 |
12 |
200 |
| Кальций, г |
5 |
4 |
3 |
1 |
| Себестоимость 1 кг корма, ден. ед. |
2 |
1 |
2 |
4 |
Решение
Обозначим через
· х1
– количество сена,
· х2
- количество силоса,
· х3
- количество корнеплодов,
· х4
- количество концентрата.
Ограничения можно выразить соотношением:
ограничения по кормовой единице-
0,5 * х1
+ 0,2 * х2
+ 6 * х3
+ 0,8 х4
≥ 20. (1)
ограничения по белкам –
40* х1
+ 10 * х2
+ 12 * х3
+ 200 * х4
≥ 2000. (2)
ограничения по кальцию –
5 * х1
+ 4 * х2
+ 3 * х3
+ х4
≥ 100. (3)
Очевидно, что
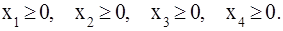 (4) (4)
Требование составить кормовой рацион минимальной стоимости определяет целевую функцию:
F = 2 * х1
+ х2
+ 2 * х3
+ 4 * х4
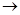 ( min) ( min)
Требуется найти х1
, х2
, х3
, х4
, минимизирующие целевую функцию и удовлетворяющие ограничениям (1)–(4).

F = 2 * х1
+ х2
+ 2 * х3
+ 4 * х4
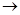 ( min) ( min)
Решаем задачу линейного программирования, использую EXCEL.
Порядок выполнения работы:
1 Загрузили Excel
2 Объединив ячейки А1:В1, пишем текст «Задание № 48»
3 Объединив ячейки А3:G3, пишем текст «Расчет кормового рациона минимальной стоимости»
4 В ячейку А4 пишем текст «Питательные вещества в 1 кг корма»
5 В ячейку А5 пишем текст «кормовая единица»
6 В ячейку А6 пишем текст «Белки, г»
7 В ячейку А7 пишем текст «Кальций, г»
8 В ячейку А8 пишем текст «Себестоимость 1 кг корма, ден.ед.»
9 В ячейку А8 пишем текст «Себестоимость 1 кг корма, ден.ед.»
10 Объдинив ячейки А9:А12, пишем текст «Количество»
11 В ячейку В4 пишем текст «Сено»
12 В ячейку С4 пишем текст «Силос»
13 В ячейку D4 пишем текст «Корнеплоды»
14 В ячейку E4 пишем текст «Корнеплоды»
15 В ячейку F4 пишем текст «функции ограничения»
16 В ячейку G4 пишем текст «Минимальный суточный рацион»
17 В ячейку G4 пишем текст «Минимальный суточный рацион»
18 В ячейку B9 пишем текст «Х1 - сена»
19 В ячейку B10 пишем текст «Х2 - силоса»
20 В ячейку B11 пишем текст «Х3 - корнеплодов»
21 В ячейку B12 пишем текст «Х4 - концентрата»
22 Объдинив ячейки А13:B13, пишем текст «Целевая функция F»
23 В ячейки B5: В7 пишем числа 0,5; 40; 5
24 В ячейки С5: С7 пишем числа 0,2; 10; 4
25 В ячейки D5: D7 пишем числа 6; 12; 3
26 В ячейки E5: E7 пишем числа 0.8; 200; 1
27 В ячейки G5: G7 пишем числа 200; 2000; 100
28 В ячейки B8: E8 пишем числа 2; 1; 2; 4
29 В ячейку F5 пишем формулу =B5*C9+C5*C10+D5*C11+E5*C12
30 В ячейку F6 пишем формулу =B6*C9+C6*C10+D6*C11+E6*C12
31 В ячейку F7 пишем формулу=B7*C9+C7*C10+D7*C11+E7*C12
32 В ячейку С13 пишем формулу =B8*C9+C8*C10+D8*C11+E8*C12
33 Сервис – Поиск решения
34 Установить целевую функцию $C$13
35 Минимальному значению
36 Изменяя ячейки $C$9 : $C$12
36 Ограничения : $C$9 ≥ 0, $C$10 ≥ 0, $C$11 ≥ 0, $C$11 ≥ 0,
$F$5 ≥ $G$5 , $F$6 ≥ $G$6 , $F$7 ≥ $G$7
37 Выполнить
38 Читаем результат : С9 = 0 (х1), С10 = 21,72 (х2),
С11 = 1,43 (х3), С12 = 8,83 (х4),
С13 = 59,9 (F – целевая функция)
Ниже приводится расчетная таблица, полученная в EXCEL:
Задание № 48
| Расчет кормового рациона минимальной стоимости |
| Питательные вещества в 1 кг корма |
Сено |
Силос |
Корнеплоды |
Концент рат |
функции ограничения |
Минимальный суточный рацион |
| кормовая единица |
0,50 |
0,20 |
6,00 |
0,80 |
20,00 |
20,00 |
| Белки, г |
40,00 |
10,00 |
12,00 |
200,00 |
2000,00 |
2000,00 |
| Кальций, г |
5,00 |
4,00 |
3,00 |
1,00 |
100,00 |
100,00 |
| Себестоимость 1 кг корма, ден.ед. |
2,00 |
1,00 |
2,00 |
4,00 |
| Количество |
Х1 - сена |
0 |
| Х2 - силоса |
21,72 |
| Х3 - корнеплодов |
1,43 |
| Х4 - концент рата |
8,83 |
| Целевая функция F |
59,90 |
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
2. Красс М.С. Математика для экономических специальностей. – М.: Инфа-М, 1998.
3. Кузнецов Ю.Н. Математическое программирование. – М.: Высшая школа, 1980.
4. Общий курс высшей математики для экономистов: Учебник/Под ред. В.И. Ермакова. – М.: ИНФРА-М, 2002.
5. Высшая математика для экономистов/Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 1997.
|