Міністерство освіти і науки України
Дніпропетровський національний університетімені Олеся Гончара
МАГІСТЕРСЬКА РОБОТА
Порушення основних припущень лінійного регресійного аналізу
Виконавець:
студентка групи МС-08-1м
Черемісіна В.О.
«__»________2009р.
Керівник роботи:
__________________ «__»________2009р.
Рецензент:
__________________ «__»________2009р.
Дніпропетровськ2009
Реферат
Магістерська робота містить 85 сторінок, 38 рисунків, 13 таблиць, 4 джерела.
Об’єктом дослідження є основні припущення лінійного регресійного аналізу.
Мета роботи – вивчення наслідків порушення основних припущень лінійного регресійного аналізу.
Методика дослідження – оцінювання параметрів лінійної регресії МНК-методом, перевірка статистичних гіпотез, побудова простої лінійної регресії та лінійної регресії з двома незалежними змінними.
Результати досліджень можуть бути використані при розв’язанні задач та при подальшому вивченні порушень припущень лінійного регресійного аналізу.
Перелік ключових слів: ПОРУШЕННЯ ПРИПУЩЕНЬ, ЛІНІЙНА РЕГРЕСІЯ, ЗАЛИШКИ, РОЗПОДІЛ, НЕКОРЕЛЬОВАНІСТЬ, ЗНАЧУЩІСТЬ, АДЕКВАТНІСТЬ.
ЗМІСТ
ВСТУП
РОЗДІЛ І Проста лінійна регресія
1.1 Постановка задачі
1.2 Метод найменших квадратів
1.3 Точність оцінки регресії
1.4 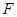 -критерій значущості регресії -критерій значущості регресії
1.5 Геометрична інтерпретація коефіцієнтів регресії
1.6 Довірчий інтервал для 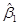 . Стандартне відхилення кутового коефіцієнта . Стандартне відхилення кутового коефіцієнта 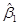
1.7 Довірчий інтервал для 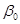 . Стандартне відхилення вільного члена . Стандартне відхилення вільного члена
1.8 Довірча смуга для регресії
1.9 Повторні спостереження. Неадекватність і “чиста помилка”
1.10 Деякі відомості з математичної статистики
1.10.1 Критерій 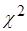 (гіпотетичний розподіл визначений) (гіпотетичний розподіл визначений)
1.10.2.Критерій 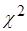 (гіпотетичний розподіл невизначений) (гіпотетичний розподіл невизначений)
1.10.3 Критерій Бартлетта
1.11 Аналіз залишків
1.12 Лінійна регресія з двома незалежними змінними
РОЗДІЛ ІІ Дослідження порушень основних припущень лінійного регресійного аналізу
2.1 „Ідеальна” модель лінійної регресії
2.2 Модель лінійної регресії, в якій дисперсія спостережень  величина змінна величина змінна
2.3 Модель лінійної регресії, в якій спостереження  величини залежні величини залежні
2.4 Модель лінійної регресії, в якій спостереження  рівномірно розподілені величини рівномірно розподілені величини
2.5 Модель лінійної регресії, в якій спостереження  показниково розподілені величини показниково розподілені величини
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Нехай  – результат спостереження, який описується лінійною моделлю виду – результат спостереження, який описується лінійною моделлю виду
 (1) (1)
де 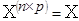 – регресійна матриця розміру – регресійна матриця розміру 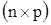 , , 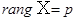 , ,
 – вектор невідомих параметрів, – вектор невідомих параметрів,
 – вектор похибок спостережень. – вектор похибок спостережень.
Припущення відносно вектора спостережень  позначатимемо позначатимемо  : :
 .(2) .(2)
Або, що те ж саме, припущення відносно вектора похибок  мають вигляд: мають вигляд:
 (3) (3)
Вихідні припущення (2) або (3) регресійного аналізу виконуються далеко не завжди. Виникає низка питань: як виявити порушення цих припущень? В яких випадках і які порушення можна вважати припустимими? Що робити, якщо порушення виявляються неприпустимими?
Метою роботи є вивчення наслідків порушення основних припущень (3) лінійного регресійного аналізу, а саме:
1) припущення про незміщеність похибок  ; ;
2) припущення про однакову дисперсію і некорельованість похибок  ; ;
3) припущення про нормальний розподіл похибок  ; ;
4) припущення про незалежність спостережень 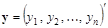 . .
РОЗДІЛ І
П
РОСТА ЛІНІЙНА РЕГРЕСІЯ
1.1
Постановка задачі
Нехай  – вибірка, утворена незалежними нормально розподіленими випадковими величинами з однією і тією ж дисперсією – вибірка, утворена незалежними нормально розподіленими випадковими величинами з однією і тією ж дисперсією і середніми, про які відомо, що вони лінійно залежать від параметрів, тобто мають вигляд і середніми, про які відомо, що вони лінійно залежать від параметрів, тобто мають вигляд
 ,(1.1.1) ,(1.1.1)
де – відомі невипадкові величини; – відомі невипадкові величини; – невідомі параметри. – невідомі параметри.
Кожну з випадкових величин  можна подати у вигляді можна подати у вигляді
 , (1.1.2) , (1.1.2)
де  називають похибкою спостережень. Похибка називають похибкою спостережень. Похибка  змінюється від спостереження до спостереження, змінюється від спостереження до спостереження,  ( ( ) - незалежні випадкові величини. Відносно ) - незалежні випадкові величини. Відносно  будемо припускати, що будемо припускати, що
1) 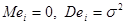
2)  , , некорельовані при некорельовані при 
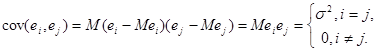
(з незалежності  , ,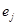 випливає їх некорельованість) випливає їх некорельованість)
3)  розподілені нормально з параметрами розподілені нормально з параметрами 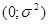 . .
Отже, нехай 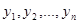 – результати спостережень, які описуються моделлю виду – результати спостережень, які описуються моделлю виду
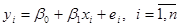 (1.1.3) (1.1.3)
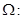 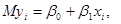 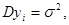 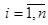
Параметри 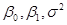 невідомі, і їх необхідно оцінити за вибіркою невідомі, і їх необхідно оцінити за вибіркою 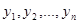 . .
Для оцінки невідомих параметрів 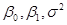 використовують метод максимальної правдоподібності або метод найменших квадратів. використовують метод максимальної правдоподібності або метод найменших квадратів.
1.2
Метод найменших квадратів
Означення 1.2.1. МНК-оцінкою параметрів  будемо називати точку будемо називати точку  , в якій функція , в якій функція
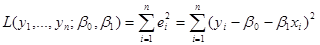 (1.2.1) (1.2.1)
досягає найменшого значення.
Здиференцюємо 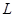 по по 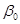 , а потім по , а потім по 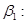
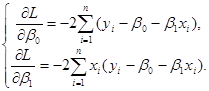
Прирівнюємо похідні нулеві:
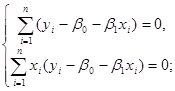
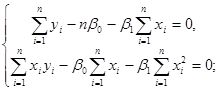
 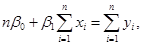 (1.2.2) (1.2.2)
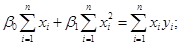 (1.2.3) (1.2.3)
Останню систему називають системою нормальних рівнянь. Із (1.2.2) маємо:
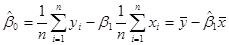 (1.2.4) (1.2.4)
Підставляємо  в (1.2.3): в (1.2.3):

 (1.2.5) (1.2.5)
Оскільки
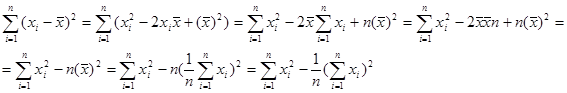
і, крім того,
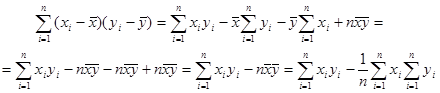
то (1.2.5) запишеться у вигляді

Тоді рівняння простої лінійної регресії має вигляд

Перевіримо, що в точці  функція функція 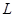 дійсно досягає мінімуму. дійсно досягає мінімуму.
Візьмемо другі похідні:

Складаємо дискримінант:
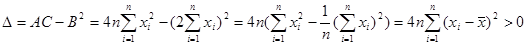
Отже, 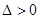 і і  . Тоді в точці . Тоді в точці  функція функція 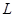 досягає мінімального значення. досягає мінімального значення.
Зауваження 1. Якщо в рівнянні регресії
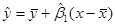
обрати 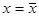 , то , то  . Це означає, що точка . Це означає, що точка 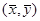 лежить на підібраній прямій. лежить на підібраній прямій.
Зауваження 2. Сума всіх залишків 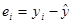 дорівнює нулю, дійсно, дорівнює нулю, дійсно,
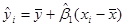 в кожній точці. в кожній точці.
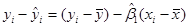
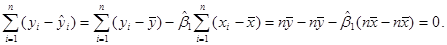
1.3
Точність оцінки регресії
Тепер розглянемо питання про те, яка точність може бути приписана лінії регресії, коефіцієнти якої були оцінені. Розглянемо таку тотожність:
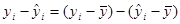
 (1.3.1) (1.3.1)
Розглянемо доданок

Підставляємо останнє в (1.3.1):
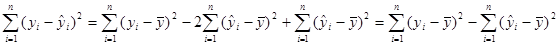
Звідки
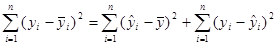 (1.3.2) (1.3.2)
Означення 1.3.1. Величина 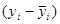 – це відхилення – це відхилення  -го спостереження від загального середнього, тому суму -го спостереження від загального середнього, тому суму 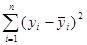 називають сумою квадратів відхилень відносно середнього значення. називають сумою квадратів відхилень відносно середнього значення.
Означення 1.3.2. Величина 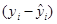 – це відхилення – це відхилення  -го спостереження від його передбаченого значення, тому суму -го спостереження від його передбаченого значення, тому суму  називають сумою квадратів відхилень відносно регресії. називають сумою квадратів відхилень відносно регресії.
Означення 1.3.3. Величина 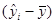 – це відхилення – це відхилення  -го передбаченого значення від загального середнього, тому суму -го передбаченого значення від загального середнього, тому суму  називають сумою квадратів, обумовленою регресією. називають сумою квадратів, обумовленою регресією.
Тоді (1.3.2) можна переписати в еквівалентній формі
      сума квадратів сума квадратів сума квадратів сума квадратів сума квадратів сума квадратів
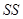 = = 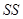 + + 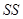
відносно обумовлена відносно (1.3.3)
середнього регресією регресії
З останнього випливає, що розсіювання 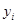 відносно відносно 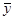 можна приписати у деякій мірі тому факту, що не всі спостереження знаходяться на лінії регресії. можна приписати у деякій мірі тому факту, що не всі спостереження знаходяться на лінії регресії.
Якщо це було б не так, то 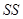 відносно регресії дорівнювала б нулю відносно регресії дорівнювала б нулю

З цих міркувань зрозуміло, що придатність лінії регресії  з метою прогнозування залежить від того, яка частина суму квадратів відносно середнього приходиться на суму квадратів, обумовлену регресією, і яка на суму квадратів відносно регресії. з метою прогнозування залежить від того, яка частина суму квадратів відносно середнього приходиться на суму квадратів, обумовлену регресією, і яка на суму квадратів відносно регресії.
Задовільним вважається випадок, коли сума квадратів, обумовлена регресією, буде набагато більша, ніж сума квадратів відносно регресії.
Кожна сума квадратів пов’язана з числом, яке називають її ступенем вільності.
Число ступенів вільності – це число незалежних елементів, які складаються з 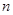 незалежних чисел незалежних чисел 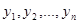 , необхідних для утворення даної суми квадратів. , необхідних для утворення даної суми квадратів.
Розглянемо суму квадратів відхилень відносно середнього значення 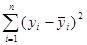 . .
Серед величин  незалежними є тільки незалежними є тільки  величина, оскільки останній елемент знаходиться як лінійна комбінація інших величина, оскільки останній елемент знаходиться як лінійна комбінація інших
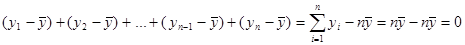
Число ступенів вільності цієї суми квадратів дорівнює  . .
Розглянемо суму квадратів, обумовлену регресією  . .
Єдиною функцією від 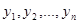 є оцінка є оцінка 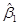 , оскільки, , оскільки, 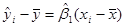 . Тому число ступенів вільності цієї суми квадратів дорівнює . Тому число ступенів вільності цієї суми квадратів дорівнює  . .
Число ступенів вільності суми квадратів  дорівнює дорівнює  . .
Отже, згідно з (1.3.3) ми можемо розкласти ступені вільності суми квадратів так:
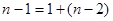 (1.3.4) (1.3.4)
За допомогою (1.3.3) та (1.3.4), побудуємо таблицю дисперсійного аналізу.
Таблиця 1.3.1. Таблиця дисперсійного аналізу
1.4
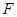 -критерій значущості регресії -критерій значущості регресії
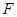 -критерій. Якщо гіпотезу -критерій. Якщо гіпотезу 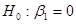 відхиляти при відхиляти при
 (1.4.1) (1.4.1)
і не відхиляти в супротивному разі, то з імовірністю 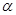 гіпотеза гіпотеза 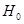 відхиляється, коли вона справедлива. відхиляється, коли вона справедлива.
Якщо гіпотеза 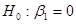 відхиляється, то регресія значуща, тобто між змінними відхиляється, то регресія значуща, тобто між змінними 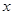 та та 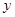 існує лінійна залежність. існує лінійна залежність.
Якщо ж гіпотеза 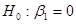 не відхиляється, то регресія незначуща, між змінними не відхиляється, то регресія незначуща, між змінними 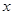 та та 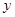 лінійної залежності немає. лінійної залежності немає.
На практиці для перевірки гіпотези 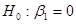 також можна використовувати також можна використовувати 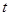 -критерій, який еквівалентний -критерій, який еквівалентний 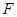 -критерію, оскільки -критерію, оскільки

А
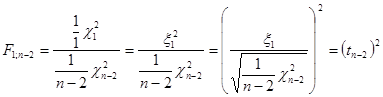
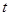 -критерій. Якщо гіпотезу -критерій. Якщо гіпотезу 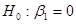 відхиляти при відхиляти при
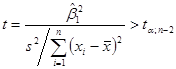 (1.4.2) (1.4.2)
і не відхиляти в супротивному разі, то з імовірністю 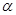 гіпотеза гіпотеза 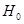 відхиляється, коли вона справедлива. відхиляється, коли вона справедлива.
1.5
Геометрична інтерпретація коефіцієнтів регресії
Коефіцієнт 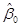 визначає точку перетину прямої регресії з віссю ординат, а коефіцієнт визначає точку перетину прямої регресії з віссю ординат, а коефіцієнт 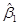 характеризує нахил прямої регресії до вісі абсцис. характеризує нахил прямої регресії до вісі абсцис.
   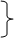  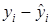
      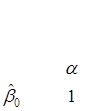    
 1 1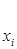 
Нехай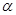 – кут, утворений прямою регресії з віссю абсцис, тоді – кут, утворений прямою регресії з віссю абсцис, тоді
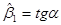
Отже, 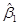 – це міра залежності – це міра залежності 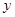 від від 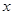 . .
Згідно з  оцінка оцінка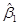 показує на скільки змінюється показує на скільки змінюється 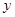 при зміні при зміні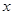 на одиницю. Знак на одиницю. Знак 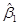 визначає напрям цієї зміни. визначає напрям цієї зміни.
Оцінки параметрів регресії  не безрозмірні величини. Оцінка не безрозмірні величини. Оцінка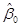 має розмірність змінної має розмірність змінної 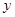 , а оцінка , а оцінка 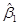 має розмірність, яка дорівнює відношенню розмірності має розмірність, яка дорівнює відношенню розмірності 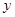 до розмірності до розмірності 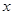 . .
1.6 Довірчий інтервал для
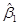 . Стандартне відхилення кутового коефіцієнта
. Стандартне відхилення кутового коефіцієнта
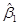
Введемо основні припущення (постулати) про те, що в лінійній моделі
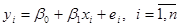
1. Похибка  – випадкова величина з середнім – випадкова величина з середнім 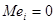 і невідомою дисперсією і невідомою дисперсією  . .
2. Похибки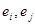 некорельовані при некорельовані при 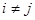 , тобто , тобто
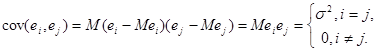
Тому
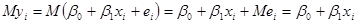
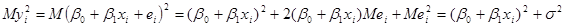

3.  некорельовані при некорельовані при 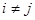 , тобто , тобто
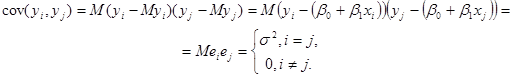
4. Похибка нормально розподілена з параметрами нормально розподілена з параметрами  , отже, , отже, 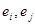 стають не тільки некорельованими, але й незалежними. стають не тільки некорельованими, але й незалежними.
В підрозділі 1.2 за допомогою МНК-метода знайдено оцінку параметра 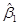 : :
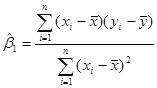
Перепишемо цю оцінку у вигляді
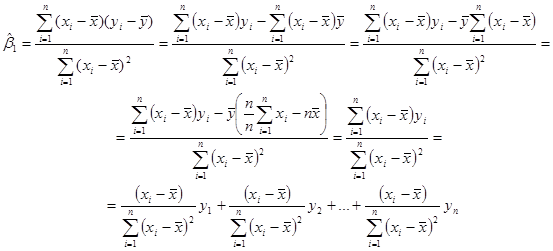
Далі розглянемо функцію

Порахуємо дисперсію цієї функції
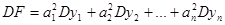 , ,
Якщо  – попарно некорельовані ( – попарно некорельовані (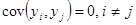 ), ),  – константи, крім того, – константи, крім того,  , отже, , отже,

У виразі для 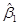 константи константи  , оскільки , оскільки 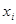 можна розглядати як величини. можна розглядати як величини.
Отже, дисперсія оцінки 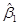 дорівнює дорівнює
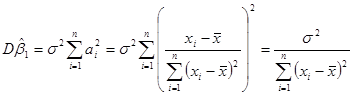 (1.6.1) (1.6.1)
Стандартне відхилення оцінки 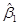 – це корінь квадратний з дисперсії – це корінь квадратний з дисперсії
 (1.6.2)
(1.6.2)
Оскільки 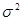 невідома, то заміть неї використовується оцінка невідома, то заміть неї використовується оцінка  , припускаючи, що модель коректна. , припускаючи, що модель коректна.
Нагадаємо, що середній квадрат  дорівнює дорівнює

Тоді оцінка стандартного відхилення 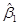 дорівнює дорівнює
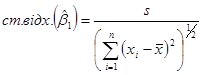 (1.6.3) (1.6.3)
Перепишемо її у вигляді
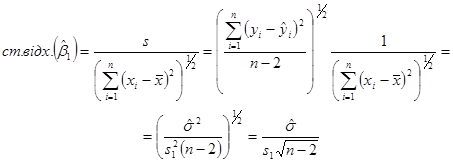
Якщо розсіювання спостережень відносно лінії регресії нормальне, тобто, всі похибки  розподілені нормально з параметрами розподілені нормально з параметрами  , то , то 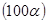 %-вий довірчий інтервал для параметра %-вий довірчий інтервал для параметра 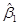 має вигляд має вигляд
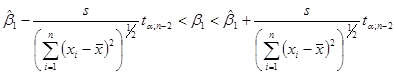 (1.6.4) (1.6.4)
і містить невідомий параметр з імовірністю 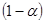 . .
З іншого боку, якшо це доцільно, то ми можемо перевірити гіпотезу  ( (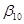 – const) проти альтернативи – const) проти альтернативи  . .
 -критерій. Якщо гіпотезу -критерій. Якщо гіпотезу  відхиляти при відхиляти при
 (1.6.5) (1.6.5)
і не відхиляти в супротивному разі, то з імовірністю 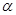 гіпотеза гіпотеза 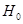 відхиляється, коли вона справедлива. відхиляється, коли вона справедлива.
Після того, як ми знайшли довірчий інтервал для 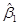 , немає необхідності знаходити величину , немає необхідності знаходити величину 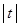 для перевірки гіпотези за допомогою t-критерію. Дійсно, досить дослідити довірчий інтервал для для перевірки гіпотези за допомогою t-критерію. Дійсно, досить дослідити довірчий інтервал для 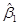 і подивитись, чи містить він значення і подивитись, чи містить він значення  . Якщо довірчий інтервал містить . Якщо довірчий інтервал містить 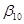 , то гіпотеза , то гіпотеза 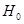 не відхиляється, і відхиляється у супротивному разі. не відхиляється, і відхиляється у супротивному разі.
Отже, гіпотеза  відхиляється, якщо відхиляється, якщо
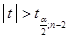
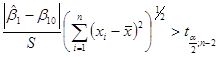 , ,
 , ,
тобто 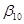 лежить за межами, які відповідають (1.6.4). лежить за межами, які відповідають (1.6.4).
1.7 Довірчий інтервал для 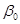 . Стандартне відхилення вільного члена . Стандартне відхилення вільного члена
В підрозділі 1.2 за допомогою МНК-метода знайдено оцінку параметра 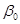

Порахуємо дисперсію оцінки 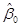 : :

  (1.7.1) (1.7.1)
Тоді стандартне відхилення оцінки  дорівнює: дорівнює:
 (1.7.2) (1.7.2)
Оскільки дисперсія 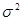 невідома, то замість неї використовується оцінка невідома, то замість неї використовується оцінка 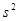 , припускаючи, що модель коректна , припускаючи, що модель коректна
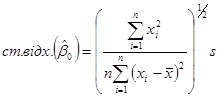 (1.7.3) (1.7.3)
 %-ий довірчий інтервал для параметра %-ий довірчий інтервал для параметра  має вигляд має вигляд
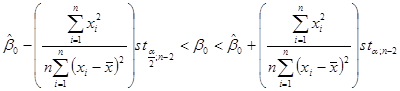
і містить невідомий параметр з імовірністю  . .
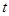 -критерій. Якщо гіпотезу -критерій. Якщо гіпотезу  ( ( – const) відхиляти при – const) відхиляти при
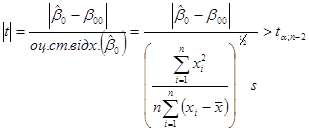
і не відхиляти в супротивному разі, то з імовірністю  гіпотеза гіпотеза  відхиляється, коли вона справедлива. відхиляється, коли вона справедлива.
Перевірити гіпотезу 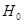 можна й за допомогою довірчого інтервалу для можна й за допомогою довірчого інтервалу для  . .
Необхідно записати довірчий інтервал для  і подивитись, чи містить він значення і подивитись, чи містить він значення  . Якщо довірчий інтервал містить . Якщо довірчий інтервал містить  , то , то  не відхиляється, і відхиляється у супротивному разі. не відхиляється, і відхиляється у супротивному разі.
1.8
Довірча смуга для регресії
Спочатку розглянемо лінійні комбінації
 , де , де  – const, – const, 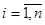
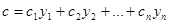 , де , де 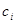 – const, – const, 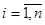
В припущеннях некорельованості  при при 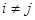 ( ( при при 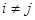 ) ) 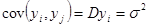 , обчислимо , обчислимо  . .
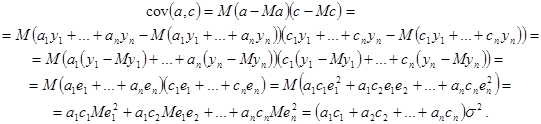
В підрозділі 1.2 було знайдено рівняння простої лінійної регресії:
 . .
Нехай  , тоді , тоді 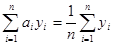 , звідси , звідси  . .
А  , тоді , тоді  , звідси , звідси 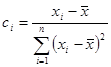 . .
Отже,

тобто 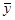 і і  некорельовані випадкові величини. некорельовані випадкові величини.
Порахуємо дисперсію 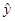 (або (або 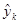 при заданому при заданому 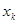 ). ).
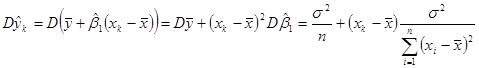 (1.8.1) (1.8.1)
Стандартне відхилення оцінки 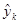 при заданому при заданому 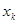 є є
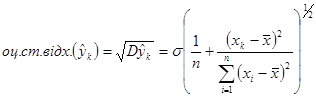 (1.8.2) (1.8.2)
Оскільки 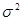 невідома, то замість неї використовують оцінку невідома, то замість неї використовують оцінку 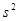 , припускаючи, що модель коректна. , припускаючи, що модель коректна.
Оцінка стандартного відхилення має вигляд:
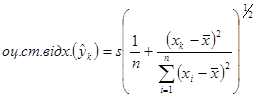 (1.8.3) (1.8.3)
Ця величина досягає мінімального значення, коли 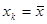 , і зростає при віддаленні , і зростає при віддаленні 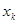 від від 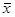 в будь-якому напрямі. в будь-якому напрямі.
 %-ві довірчі інтервали для регресії мають вигляд: %-ві довірчі інтервали для регресії мають вигляд:
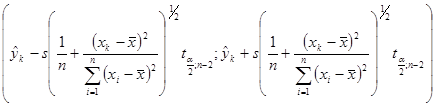
або, що те ж саме,
 Чим більша різниця між Чим більша різниця між 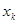 та та 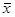 , тим більше відхилення між , тим більше відхилення між 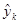 та та 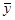 (довжина довірчого інтервалу). Останнє означає, що точність прогнозу різна в різних точках (довжина довірчого інтервалу). Останнє означає, що точність прогнозу різна в різних точках 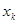 . .
Дві криві по обидві сторони від лінії регресії визначають 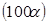 %-ві довірчі границі й показують, як змінюються границі в залежності від зміни %-ві довірчі границі й показують, як змінюються границі в залежності від зміни 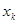 . Ці криві – гіперболи. . Ці криві – гіперболи.
Для того, щоб одержати ці криві, необхідно з’єднати неперервною лінією всі значення  при всіх при всіх  (нижня гіпербола) та (нижня гіпербола) та  при всіх при всіх  (верхня гіпербола). (верхня гіпербола).
1.9
Повторні спостереження. Неадекватність і “чиста” помилка
Побудована лінія регресії – це розрахункова лінія, яка базується на деякій моделі або припущеннях. Але припущення потрібно розглядати як попередні. При деяких обставинах (умовах) можна перевірити, чи коректна (адекватна) побудована модель.
Розглянемо випадок, коли в даних містяться повторні спостереження. Введемо додаткові позначення для множини спостережень при одному й тому ж значенні  . .
Нехай
 – – 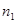 спостережень при спостережень при 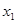 , ,
 – –  спостережень при спостережень при  , ,
. . . . . . . . .
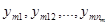 – – 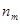 спостережень при спостережень при 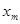 , ,
при цьому  . .
Якщо спостереження повторюються (два рази або більше) при однакових значеннях  , то ми можемо використати ці повторення для знаходження оцінки для дисперсії , то ми можемо використати ці повторення для знаходження оцінки для дисперсії 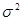 . Про таку оцінку говорять, що вона представляє “чисту помилку”, оскільки, якщо . Про таку оцінку говорять, що вона представляє “чисту помилку”, оскільки, якщо  однакові, наприклад, для двох спостережень, то тільки випадкові варіації можуть впливати на результати однакові, наприклад, для двох спостережень, то тільки випадкові варіації можуть впливати на результати 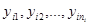 і створювати розсіювання між ними. Такі відмінності, як правило, забезпечують одержання надійної оцінки для і створювати розсіювання між ними. Такі відмінності, як правило, забезпечують одержання надійної оцінки для 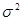 . Тому при плануванні експериментів має сенс ставити експерименти з повтореннями. . Тому при плануванні експериментів має сенс ставити експерименти з повтореннями.
Оцінка величини 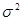 , пов’язана з “чистою помилкою”, знаходиться так. , пов’язана з “чистою помилкою”, знаходиться так.
Сума квадратів, пов’язана з “чистою помилкою” при 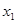 дорівнює дорівнює
 , де , де 
Число ступенів вільності цієї суми 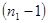 . .
Сума квадратів, пов’язана з “чистою помилкою” при  дорівнює дорівнює
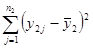 , де , де 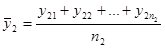
Число ступенів вільності цієї суми  і т. д. і т. д.
Загальна сума квадратів, пов’язана з “чистою помилкою”дорівнює
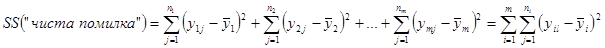 з загальним числом ступенів вільності з загальним числом ступенів вільності
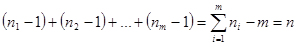
Звідси середній квадрат для “чистої помилки” дорівнює
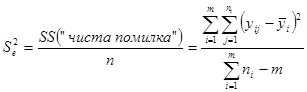 (1.9.1) (1.9.1)
і є оцінкою для 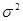 . .
Покажемо, що сума квадратів, пов’язана з “чистою помилкою”, є частиною суми квадратів залишків (суми квадратів відносно регресії).
Залишок для 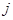 -того спостереження при -того спостереження при 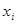 можна записати у вигляді: можна записати у вигляді:
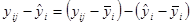
Піднесемо праву та ліву частини рівності до квадрату.
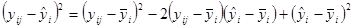
Візьмемо суму по кожному з індексів  та та  . .
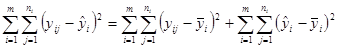 (1.9.2) (1.9.2)
при цьому 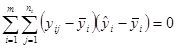 . .
Суму (1.9.2) можна записати так
      Сума Сума квадратів Сума Сума Сума квадратів Сума
квадратів = “чистих + квадратів (1.9.3.)
залишків помилок” неадекватності
Число ступенів вільності:
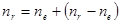
Отже, суму квадратів “чистих помилок” можна ввести в таблицю дисперсійного аналізу.
Таблиця 1.9.1. Таблиця дисперсійного аналізу
Критерій для перевірки адекватності моделі регресії можна сформулювати так.
Якщо
 (1.9.4) (1.9.4)
то відношення є значущим (лінійна модель неадекватна), при цьому, чим обумовлена неадекватність можна вивчити, дослідивши залишки; в супротивному випадку:
 (1.9.5) (1.9.5)
відношення є незначущим (лінійна модель адекватна), при цьому як 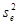 , так і , так і  можна використовувати як оцінки для можна використовувати як оцінки для 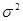 . .
Об’єднана оцінка для 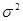 може бути знайдена з суми квадратів “чистої помилки” і суми квадратів “неадекватністі” шляхом їх об’єднання у суму квадратів залишків і поділу її на число ступенів вільності може бути знайдена з суми квадратів “чистої помилки” і суми квадратів “неадекватністі” шляхом їх об’єднання у суму квадратів залишків і поділу її на число ступенів вільності  . .
Якщо виявлено неадекватність моделі, то необхідно будувати іншу модель (нелінійну).
1.10
Деякі відомості з математичної статистики
1.10.1 Критерій  (гіпотетичний розподіл визначений) (гіпотетичний розподіл визначений)
Постановка задачі. Нехай  – реалізація вибірки з невідомого розподілу – реалізація вибірки з невідомого розподілу  , відносно якого висувається гіпотеза , відносно якого висувається гіпотеза 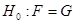 , де , де  належить заданому класу розподілів (зокрема, належить заданому класу розподілів (зокрема,  може бути повністю визначеним розподілом). Гіпотезу може бути повністю визначеним розподілом). Гіпотезу  можна сформулювати і так: можна сформулювати і так:  є вибіркою з розподілу є вибіркою з розподілу  із заданими властивостями. із заданими властивостями.
Необхідно за реалізацією вибірки  дійти висновку: відхиляти гіпотезу дійти висновку: відхиляти гіпотезу  чи ні. чи ні.
Відхилення емпіричного розподілу від гіпотетичного. Незалежно від того, справджується гіпотеза  чи ні, емпіричний розподіл чи ні, емпіричний розподіл  , побудований за вибіркою , побудований за вибіркою  з з  , а саме, для кожного фіксованого , а саме, для кожного фіксованого  значення емпіричної функції розподілу значення емпіричної функції розподілу  є незміщеною і спроможною оцінкою є незміщеною і спроможною оцінкою 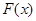 . Тому, якщо ввести відхилення . Тому, якщо ввести відхилення  емпіричного емпіричного  розподілу від гіпотетичного розподілу від гіпотетичного  , причому так, щоб воно набирало малих значень, коли гіпотеза , причому так, щоб воно набирало малих значень, коли гіпотеза  справджується, і великих, коли гіпотеза справджується, і великих, коли гіпотеза  не справджується (а це видається цілком можливим, оскільки не справджується (а це видається цілком можливим, оскільки  мало відрізняється від мало відрізняється від 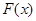 ), то гіпотезу ), то гіпотезу  природно відхиляти або не відхиляти залежно від того, якого значення набрало відхилення природно відхиляти або не відхиляти залежно від того, якого значення набрало відхилення  - великого чи малого. - великого чи малого.
Відхилення Пірсона емпіричного розподілу  від гіпотетичного від гіпотетичного  . Відхилення між двома розподілами: . Відхилення між двома розподілами:  - емпіричним, побудованим за вибіркою - емпіричним, побудованим за вибіркою  , і , і  –гіпотетичним, заданими на множині –гіпотетичним, заданими на множині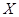 вибіркових значень вибіркових значень  (на вибірковому просторі), можна будувати різними способами. Далі описано відхилення (на вибірковому просторі), можна будувати різними способами. Далі описано відхилення  від від  , запропоноване Пірсоном. Воно будується так. Ділимо , запропоноване Пірсоном. Воно будується так. Ділимо 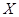 на скінчене число на скінчене число  неперетинних множин неперетинних множин  : :
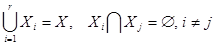 . .
І як відхилення  від від  розглядаємо розглядаємо
 (1.10.1.1) (1.10.1.1)
де  - імовірність того, що вибіркове значення - імовірність того, що вибіркове значення  потрапить до множини потрапить до множини  , обчислена за гіпотетичним розподілом , обчислена за гіпотетичним розподілом  (тобто (тобто 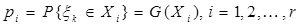 )); ));  – імовірність вибірковому значенню потрапити до множини – імовірність вибірковому значенню потрапити до множини 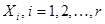 , обчислена за емпіричним розподілом , обчислена за емпіричним розподілом  ; чисельно ця ймовірність дорівнює частоті вибірковому значенню потрапити до множини ; чисельно ця ймовірність дорівнює частоті вибірковому значенню потрапити до множини  , знайденій за вибіркою , знайденій за вибіркою 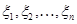 ( ( – кількість вибіркових значень з – кількість вибіркових значень з 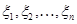 , що потрапили до , що потрапили до  ). ).
Далі, якщо 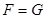 , то , то  є ймовірність вибірковому значенню потрапити до є ймовірність вибірковому значенню потрапити до  , обчислена за розподілом , обчислена за розподілом  , з якого добуто вибірку , з якого добуто вибірку 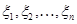 , а тому для кожного , а тому для кожного  частоти частоти 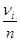 вибіркового значення потрапити до вибіркового значення потрапити до  є незміщеними і спроможними оцінками ймовірностей є незміщеними і спроможними оцінками ймовірностей  . І отже, відхилення . І отже, відхилення  є малим порівняно з відхиленням є малим порівняно з відхиленням 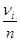 від від 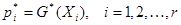 , обчисленими за розподілом , обчисленими за розподілом  , відмінним від , відмінним від  . А разом із ними малим є відхилення . А разом із ними малим є відхилення 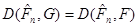 порівняно з відхиленням порівняно з відхиленням 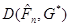 , коли розподіл , коли розподіл  відмінний від відмінний від  (більш того, (більш того, 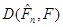 – мінімально можливе відхилення). – мінімально можливе відхилення).
Таким чином, для перевірки гіпотези  : : 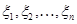 є вибірка з розподілу є вибірка з розподілу  , обчислюємо відхилення , обчислюємо відхилення  . Якщо при цьому . Якщо при цьому 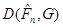 набрало малого значення, то гіпотезу набрало малого значення, то гіпотезу  не відхиляємо , у супротивному разі – відхиляємо. не відхиляємо , у супротивному разі – відхиляємо.
Межі, що відокремлюють великі значення відхилення 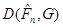 від малих, установлюються на підставі того факту, що для вибірки від малих, установлюються на підставі того факту, що для вибірки 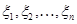 з розподілу з розподілу  при великих при великих  розподіл розподіл 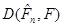 (розподіл мінімально можливого відхилення) мало відрізняється від розподілу (розподіл мінімально можливого відхилення) мало відрізняється від розподілу  з з 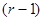 ступенями вільності. ступенями вільності.
Критерій  (гіпотетичний розподіл не залежить від невідомих параметрів). Нехай (гіпотетичний розподіл не залежить від невідомих параметрів). Нехай  – вибірка із розподілу – вибірка із розподілу  і і 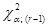 – верхня α-межа – верхня α-межа  - розподілу з - розподілу з 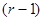 ступенями вільності. ступенями вільності.
Якщо гіпотезу  : : 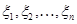 є вибірка з розподілу є вибірка з розподілу  відхиляти при відхиляти при
 (1.10.1.2) (1.10.1.2)
і не відхиляти в супротивному разі, то з імовірністю α гіпотеза  буде відхилятися, коли вона справджується. буде відхилятися, коли вона справджується.
1.10.2 Критерій  (гіпотетичний розподіл невизначений) (гіпотетичний розподіл невизначений)
Нехай  – вибірка з невідомого розподілу – вибірка з невідомого розподілу  , стосовно якого висувається гіпотеза , стосовно якого висувається гіпотеза
 . .
Розподіл  залежить від параметрів залежить від параметрів 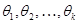 , які невідомо, причому єдиним джерелом інформації про значення цих параметрів є вибірка , які невідомо, причому єдиним джерелом інформації про значення цих параметрів є вибірка  . Іншими словами, гіпотеза . Іншими словами, гіпотеза  полягає в тому, що полягає в тому, що  є вибіркою із розподілу, який належить до класу розподілів є вибіркою із розподілу, який належить до класу розподілів 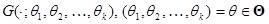 . .
Необхідно за реалізацією вибірки  дійти висновку: відхиляти гіпотезу дійти висновку: відхиляти гіпотезу  чи ні. чи ні.
Природно діяти так. Визнаємо за значення невідомих параметрів 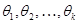 їхні оцінки їхні оцінки  , знайдені за вибіркою , знайдені за вибіркою 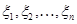 , і, отже, за гіпотетичний приймемо розподіл , і, отже, за гіпотетичний приймемо розподіл  . Відхилення . Відхилення 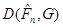 будуємо так само, як і раніше: будуємо так само, як і раніше:
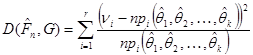 (1.10.2.1) (1.10.2.1)
де 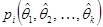 – імовірність того, що вибіркове значення потрапить до множини – імовірність того, що вибіркове значення потрапить до множини 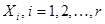 , обчислена за гіпотетичним розподілом. Фішер встановив, що коли гіпотеза , обчислена за гіпотетичним розподілом. Фішер встановив, що коли гіпотеза  справджується і оцінки справджується і оцінки  знайдено за методом максимальної правдоподібності, то розподіл відхилення знайдено за методом максимальної правдоподібності, то розподіл відхилення  між між  і і  , коли , коли  , збігається до розподілу , збігається до розподілу  з з  ступенями вільності, де ступенями вільності, де  – кількість параметрів, оцінених за вибіркою – кількість параметрів, оцінених за вибіркою 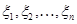 . .
Таким чином, коли параметри оцінюються за вибіркою методом максимальної правдоподібності, можна користуватися критерієм  у такому формулюванні. у такому формулюванні.
Якщо гіпотезу  відхиляти при відхиляти при
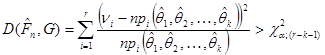 (1.10.2.2) (1.10.2.2)
і не відхиляти в супротивному разі, то з імовірністю α гіпотеза  буде відхилятися, коли вона справджується. буде відхилятися, коли вона справджується.
1.10.3
Критерій Бартлетта
Доволі поширеним є випадок, в якому вважається відомим, що дисперсії похибок 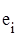 всередині певних груп рівні. Припустимо, що ми хочемо перевірити гіпотезу всередині певних груп рівні. Припустимо, що ми хочемо перевірити гіпотезу  . Тоді, якщо маємо . Тоді, якщо маємо 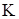 взаємно незалежних статистик взаємно незалежних статистик  ( (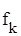 – число ступенів вільності – число ступенів вільності 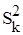 ), то можна перевірити гіпотезу ), то можна перевірити гіпотезу 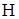 , використовуючи критерій Бартлетта. , використовуючи критерій Бартлетта.
Цей критерій вимагає обчислення статистики
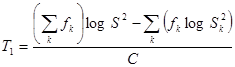 , ,
де
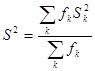
і
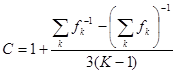 . .
Якщо гіпотеза 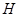 справедлива, то статистика справедлива, то статистика  розподілена приблизно як розподілена приблизно як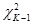 , причому така апроксимація виявляється задовільною і при досить малих вибірках ( , причому така апроксимація виявляється задовільною і при досить малих вибірках (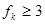 ). На жаль, цей критерій надто чутливий до будь-якого відхилення від нормальності величин, що складають кожне ). На жаль, цей критерій надто чутливий до будь-якого відхилення від нормальності величин, що складають кожне 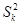 . Значимість статистики . Значимість статистики  може вказувати не на відсутність однорідності дисперсії, а просто на відхилення від нормальності. може вказувати не на відсутність однорідності дисперсії, а просто на відхилення від нормальності.
1.11 Аналіз залишків
Електронні обчислювальні машини дають нам можливість обчислення відхилень кожного серед значень 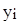 , що спостерігались, від апроксимуючої регресії , що спостерігались, від апроксимуючої регресії 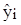 . Ці різниці називаються залишками і позначаються символами . Ці різниці називаються залишками і позначаються символами
 , ,
Критерій Дарбіна-Уотсона.
Нехай нам треба підібрати постульовану лінійну модель
 (1.11.1) (1.11.1)
методом найменших квадратів за спостереженнями 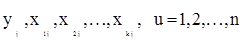 . Зазвичайми повинні припускати, що похибки . Зазвичайми повинні припускати, що похибки  – незалежні випадкові величини з розподілом – незалежні випадкові величини з розподілом  , тобто всі серіальні кореляції , тобто всі серіальні кореляції  . За допомогою критерію Дарбіна-Уотсона можна перевірити гіпотезу . За допомогою критерію Дарбіна-Уотсона можна перевірити гіпотезу 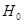 про те, що всі про те, що всі  проти альтернативної гіпотези проти альтернативної гіпотези 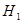 : залишки пов’язані корельовано лінійною залежністю : залишки пов’язані корельовано лінійною залежністю
 , ,
де  . .
Для перевірки гіпотези 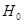 проти альтернативи проти альтернативи 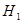 будуємо модель за рівнянням (1.15.1) і знаходимо набір залишків будуємо модель за рівнянням (1.15.1) і знаходимо набір залишків  . Тепер можна побудувати статистику . Тепер можна побудувати статистику
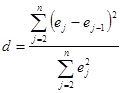 (1.11.2) (1.11.2)
і визначити на її основі, чи можна відхиляти гіпотезу 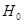 . .
Критичні точки статистики Дарбіна-Уотсона табульовані.
Знаходимо верхню  і нижню і нижню 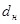 границі (вони залежать від числа границі (вони залежать від числа 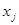 в моделі і кількості спостережень в моделі і кількості спостережень  ). ).
Якщо 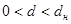 , то залишки додатньо автокорельовані. , то залишки додатньо автокорельовані.
Якщо  , то залишки некорельовані. , то залишки некорельовані.
Якщо 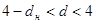 , то залишки від’ємно корельовані. , то залишки від’ємно корельовані.
Якщо  або або 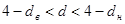 , то необхідно збільшити кількість спостережень. , то необхідно збільшити кількість спостережень.
1.12
Лінійна множинна регресія
з двома
незалежн
ими
змінн
ими
Нехай  – результати спостережень, які описуються моделлю: – результати спостережень, які описуються моделлю:
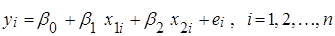 (1.12.1) (1.12.1)
Основні припущення мають вигляд:
  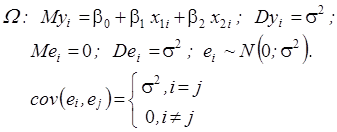
Значення змінних  відомій ці змінні незалежні. Необхідно знайти оцінки невідомих параметрів відомій ці змінні незалежні. Необхідно знайти оцінки невідомих параметрів  . .
Використаємо МНК-метод:
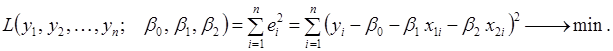 
Отримаємо систему нормальних рівнянь для моделі (1.12.1). Ця система включає систему нормальних рівнянь простої лінійної регресії.
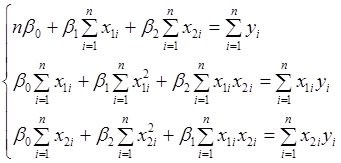 (1.12.2)
(1.12.2)
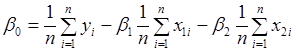
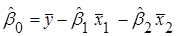
 знаходяться з першого та другого рівнянь останньої системи. знаходяться з першого та другого рівнянь останньої системи.
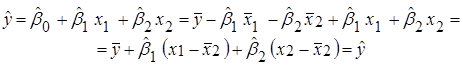
Отримали рівняння регресії:
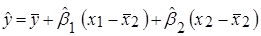
Матричний спосіб знаходження 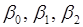 . .
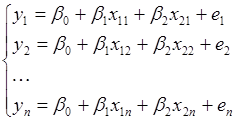
 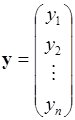 ; ; ; ;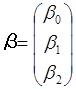 ; ;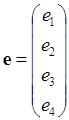 ; ;
 – транспонована матриця. – транспонована матриця.

Систему (1.12.2) перепишемо у вигляді:

Або в матричному виді:
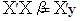
Домножимо праву та ліву частини на  . .

Звідси
 . .
Або, що те ж саме,
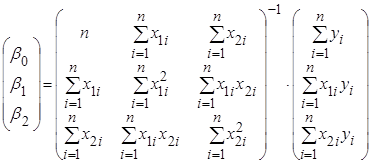 . .
У множинній лінійній регресії на значущість треба перевіряти всю регресію, а також окремі коефіцієнти регресії. В першому випадку використовується загальний 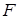 -критерій, а у другому – частинний -критерій, а у другому – частинний 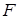 -критерій. -критерій.
Загальний 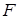 -критерій. -критерій.
Для перевірки гіпотези  використовується використовується 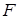 -критерій, в якому -критерій, в якому
Загальна сума квадратів
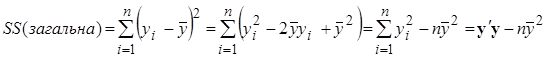 , ,
де 
Сума квадратів залишків

Сума квадратів, обумовлена регресією

| Джерело варіації |
SS |
df |
MS |
F |
Регресія 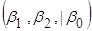 |
 |
2 |
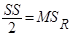 |
 |
| Залишки |
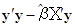 |
 |
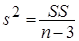 |
| Загальна |
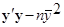 |
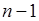 |
 -критерій перевірки значущості. -критерій перевірки значущості.
Гіпотеза 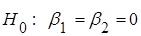 відхиляється, якщо відхиляється, якщо
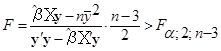 , (1.12.3) , (1.12.3)
і в цьому випадку кажуть, що регресія значуща; і не відхиляється в супротивному разі (регресія незначуща).
Частинний  -критерій. -критерій.
Розглянемо 3 моделі:
1. 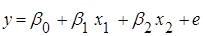 . .
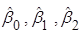 – МНК-оцінки параметрів – МНК-оцінки параметрів 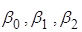 . .
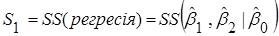 ; ;  . .
2. 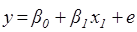 . .
 – МНК-оцінки параметрів – МНК-оцінки параметрів 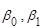 , які не збігаються з оцінками моделі 1. , які не збігаються з оцінками моделі 1.
 ; ; 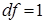 . .
3.  . .
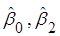 – МНК-оцінки параметрів – МНК-оцінки параметрів 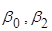 , які не збігаються з оцінками моделей 1, 2. , які не збігаються з оцінками моделей 1, 2.
 ; ; 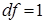 . .
Означення 1. Величину 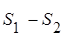 називають додатковою сумою квадратів, обумовленою включенням в модель 2 члена називають додатковою сумою квадратів, обумовленою включенням в модель 2 члена 
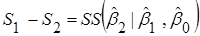 ; ;  . .
Означення 2. Величину 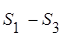 називають додатковою сумою квадратів, обумовленою включенням в модель 3 члена називають додатковою сумою квадратів, обумовленою включенням в модель 3 члена 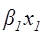
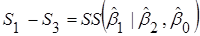 ; ;  . .
Оскільки
 , ,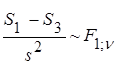 , ,
де  – число ступенів вільності, що відповідають середній сумі квадратів – число ступенів вільності, що відповідають середній сумі квадратів 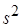 : :
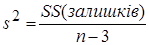 , ,
ми можемо записати 2 частинні  -критерії. -критерії.
Гіпотеза 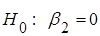 (при умові, що (при умові, що 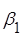 включено в модель) відхиляється, якщо: включено в модель) відхиляється, якщо:
  , ,
і не відхиляється в супротивному разі.
Якщо гіпотеза  відхиляється, то коефіцієнт відхиляється, то коефіцієнт 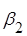 є значущим, і його необхідно включити в модель. є значущим, і його необхідно включити в модель.
Якщо гіпотеза  не відхиляється, то включення коефіцієнта не відхиляється, то включення коефіцієнта 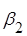 в модель не підвищує значущості регресії, і рівняння можна залишити у вигляді в модель не підвищує значущості регресії, і рівняння можна залишити у вигляді
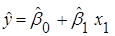 . .
Гіпотеза 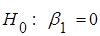 (при умові, що (при умові, що 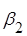 включено в модель) відхиляється, якщо: включено в модель) відхиляється, якщо:
 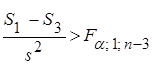 , ,
і не відхиляється в супротивному разі.
Якщо гіпотеза  відхиляється, то коефіцієнт відхиляється, то коефіцієнт 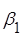 є значущим, і його необхідно включити в модель. є значущим, і його необхідно включити в модель.
Якщо гіпотеза  не відхиляється, то включення коефіцієнта не відхиляється, то включення коефіцієнта 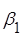 в модель не підвищує значущості регресії, і рівняння можна залишити у вигляді в модель не підвищує значущості регресії, і рівняння можна залишити у вигляді
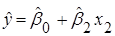 . .
РОЗДІЛ ІІ ДОСЛІДЖЕННЯ ПОРУШЕНЬ ОСНОВНИХ ПРИПУЩЕНЬ ЛІНІЙНОГО РЕГРЕСІЙНОГО АНАЛІЗУ
2.1 „Ідеальна” модель лінійної регресії
Нехай  – незалежні нормально розподілені випадкові величини з однаковою дисперсією – незалежні нормально розподілені випадкові величини з однаковою дисперсією  та середніми та середніми 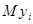 , лінійними за параметрами , лінійними за параметрами 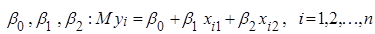 , де , де  – невідомі параметри, – невідомі параметри,  – відомі невипадкові величини. Кожну випадкову величину – відомі невипадкові величини. Кожну випадкову величину 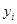 можна подати у вигляді можна подати у вигляді 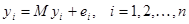 , де , де  – похибки спостережень, і вони змінюються від спостереження до спостереження. Відносно похибок – похибки спостережень, і вони змінюються від спостереження до спостереження. Відносно похибок  висуваються припущення: висуваються припущення:
1) 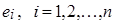 , – незалежні випадкові величини; , – незалежні випадкові величини;
2) 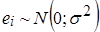 . .
За спостереженнями  , які описуються моделлю , які описуються моделлю
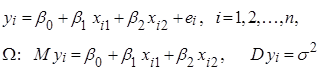 (2.1.1)
(2.1.1)
необхідно оцінити невідомі параметри  . .
Означення 2.1.1. «Ідеальною» моделлю лінійної регресії з двома незалежними змінними називатимемо модель виду
 (2.1.2)
(2.1.2)
«Ідеальна» модель лінійної регресії – це модель (2.1.1) з коефіцієнтами 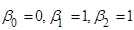 . .
Означення 2.1.2. «Ідеальною» моделлю простої лінійної регресії називатимемо модель виду
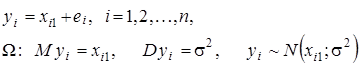 (2.1.3) (2.1.3)
«Ідеальна» модель простої лінійної регресії – це модель (2.1.1) з коефіцієнтами 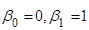 та змінною та змінною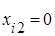 . .
Стохастичний експеримент. Проведемо стохастичний експеримент, який полягає в моделюванні вибірок  з нормальних розподілів з параметрами з нормальних розподілів з параметрами  відповідно, де відповідно, де  а середні а середні  обирались так. обирались так.
Квадрат 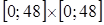 розіб’ємо на 16 однакових квадратів розміром розіб’ємо на 16 однакових квадратів розміром  . В кожному з них оберемо 4 точки, які виступають вершинами квадратів розміром . В кожному з них оберемо 4 точки, які виступають вершинами квадратів розміром  . Ці 64 вершини квадратів і обрані за значення, які набувають невипадкові змінні . Ці 64 вершини квадратів і обрані за значення, які набувають невипадкові змінні  . .

Рис. 2.1.1. Вибір значень
 , які набувають невипадкові змінні
, які набувають невипадкові змінні

«Ідеальна» модель простої лінійної регресії. Знайдемо МНК – оцінки параметрів 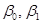 та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 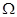 в „ідеальній” моделі. в „ідеальній” моделі.
Результати стохастичного експерименту, за умов, що змінна  , наведено на рисунку 2.1.2. , наведено на рисунку 2.1.2.
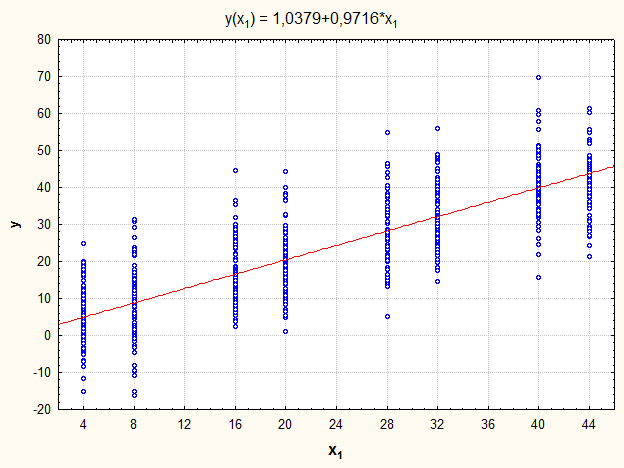 Рис. 2.1.2. „Ідеальна” модель простої лінійної регресії
Рис. 2.1.2. „Ідеальна” модель простої лінійної регресії
Результати перевірки адекватності та значущості „ідеальної” моделі простої лінійної регресії наведено в таблиці 2.1.1.
Таблиця 2.1.1. Результати перевірки адекватності та значущості „ідеальної” моделі простої лінійної регресії
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
111167 |
1 |
111167 |
1411,53 |
| Відносно регресії |
50246,7 |
638 |
78,8 |
| Відносно середнього |
161413,7 |
639 |
| Неадекватність |
828,5 |
6 |
138,1 |
1,77 |
| "Чиста помилка" |
49418,2 |
632 |
78,2 |
F1 = 1,77 < 2,11 = F0,05;6;632, „ідеальна” модель адекватна.
F2 = 1411,53 > 3,86 = F0,05;1;638, „ідеальна” модель значуща. значуща.
Перевіримо гіпотези 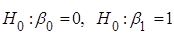 за допомогою критерію Стьюдента. за допомогою критерію Стьюдента.
Якщо 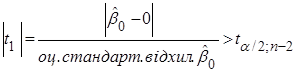 , то гіпотеза , то гіпотеза 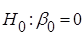 відхиляється, і не відхиляється у супротивному випадку. відхиляється, і не відхиляється у супротивному випадку.
Якщо  , то гіпотеза , то гіпотеза 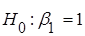 відхиляється, і не відхиляється у супротивному випадку. відхиляється, і не відхиляється у супротивному випадку.
|t1| = 1,46 < 1,96 = t0,025;638, гіпотеза 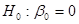 не відхиляється. не відхиляється.
|t2| = 1 < 1,96 = t0,025;638, гіпотеза  не відхиляється. не відхиляється.
Перевіримо припущення про некорельованість залишків 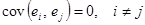 за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію
 . .
Оскільки 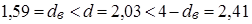 , то залишки , то залишки  „ідеальної” моделі некорельовані. „ідеальної” моделі некорельовані.
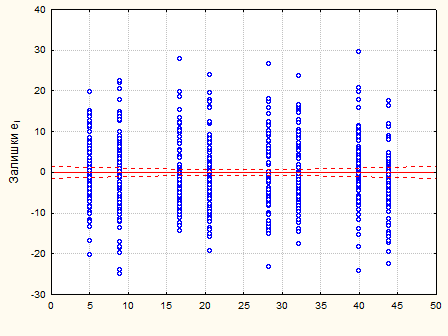

Рис. 2.1.3. Графік залишків – смуга постійної ширини
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію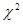 . .

Рис.2.1.4. Нормальний розподіл залишків 
Статистика , тому залишки можна вважати нормально розподіленими з параметрами , тому залишки можна вважати нормально розподіленими з параметрами 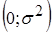 . .
Статистика Бартлетта 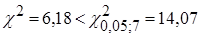 , тому дисперсія залишків , тому дисперсія залишків  постійна. постійна.
Отже,
1) „ідеальна” модель адекватна;
2) регресія  значуща (гіпотеза значуща (гіпотеза 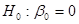 не відхиляється; гіпотеза не відхиляється; гіпотеза 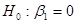 відхиляється, а гіпотеза відхиляється, а гіпотеза  не відхиляється); не відхиляється);
3) залишки 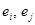  , „ідеальної” моделі некорельовані; , „ідеальної” моделі некорельовані;
4) залишки  „ідеальної” моделі нормально розподілені випадкові величини з параметрами „ідеальної” моделі нормально розподілені випадкові величини з параметрами 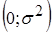 ; ;
5) дисперсія залишків  „ідеальної” моделі величина постійна. „ідеальної” моделі величина постійна.
«Ідеальна» модель лінійної регресії з двома незалежними змінними. Знайдемо МНК – оцінки параметрів  та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 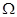 в „ідеальній” моделі. в „ідеальній” моделі.
Результати стохастичного експерименту, за умов, що незалежні змінні  обрані згідно з рис. 2.1.1, наведено на рисунку 2.1.5. обрані згідно з рис. 2.1.1, наведено на рисунку 2.1.5.
 Рис. 2.1.5. „Ідеальна” модель лінійної регресії з двома незалежними змінними Рис. 2.1.5. „Ідеальна” модель лінійної регресії з двома незалежними змінними
Результати перевірки адекватності та значущості „ідеальної” моделі лінійної регресії наведено в таблиці 2.1.2.
Таблиця 2.1.2. Результати перевірки адекватності та значущості „ідеальної” моделі лінійної регресії
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
232687,1 |
2 |
116343,5 |
1399,4 |
| Відносно регресії |
52960,7 |
637 |
83,1 |
| Відносно середнього |
285647,7 |
639 |
| Неадекватність |
3965,6 |
61 |
65 |
0,76 |
| "Чиста помилка" |
48995,1 |
576 |
85,1 |
F1 = 0,76 < 1,34= F0,05;61;576, „ідеальна” модель адекватна.
F2 = 1399,4 > 3,01= F0,05;2;637, регресія значуща. значуща.
Перевіримо гіпотези 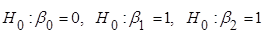 за допомогою критерію Стьюдента. за допомогою критерію Стьюдента.
Якщо 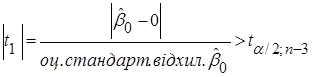 , то гіпотеза , то гіпотеза 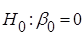 відхиляється, і не відхиляється у супротивному випадку. відхиляється, і не відхиляється у супротивному випадку.
Якщо  , то гіпотеза , то гіпотеза 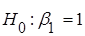 відхиляється, і не відхиляється у супротивному випадку. відхиляється, і не відхиляється у супротивному випадку.
Якщо 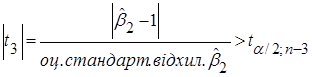 , то гіпотеза , то гіпотеза 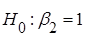 відхиляється, і не відхиляється у супротивному випадку. відхиляється, і не відхиляється у супротивному випадку.
|t1| = 0,04 < 1,96 = t0,025;637, гіпотеза  не відхиляється. не відхиляється.
|t2| = 0,3 < 1,96 = t0,025;637, гіпотеза 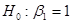 не відхиляється. не відхиляється.
|t3| = 0,7 < 1,96 = t0,025;637, гіпотеза  не відхиляється. не відхиляється.
Перевіримо припущення про некорельованість залишків 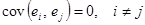 за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію
 . .
Оскільки 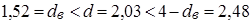 , то залишки , то залишки  „ідеальної” моделі некорельовані. „ідеальної” моделі некорельовані.
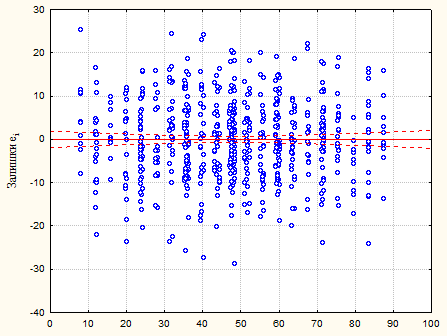

Рис. 2.1.6. Графік залишків – смуга постійної ширини
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію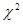 . .

Рис.2.1.6. Нормальний розподіл залишків 
Статистика , тому залишки можна вважати нормально розподіленими з параметрами , тому залишки можна вважати нормально розподіленими з параметрами 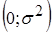 . .
Статистика Бартлетта 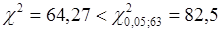 , тому дисперсія залишків , тому дисперсія залишків  постійна. постійна.
Отже,
1) „ідеальна” модель адекватна;
2) регресія 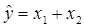 значуща (гіпотеза значуща (гіпотеза 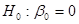 не відхиляється; гіпотеза не відхиляється; гіпотеза 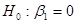 відхиляється, гіпотеза відхиляється, гіпотеза  не відхиляється, гіпотеза не відхиляється, гіпотеза  не відхиляється); не відхиляється);
3) залишки 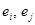  , „ідеальної” моделі некорельовані; , „ідеальної” моделі некорельовані;
4) залишки  „ідеальної” моделі нормально розподілені випадкові величини з параметрами „ідеальної” моделі нормально розподілені випадкові величини з параметрами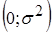 ; ;
5) дисперсія залишків  „ідеальної” моделі величина постійна. „ідеальної” моделі величина постійна.
2.2 Модель лінійної регресії, в якій дисперсія спостережень  величина змінна величина змінна
Нехай  – незалежні нормально розподілені випадкові величини з середніми – незалежні нормально розподілені випадкові величини з середніми  , лінійними за параметрами , лінійними за параметрами 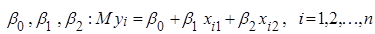 та дисперсією та дисперсією  , що змінюється від спостереження до спостереження. , що змінюється від спостереження до спостереження.
Параметри 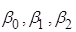 невідомі, невідомі,  – відомі невипадкові величини. – відомі невипадкові величини.
За спостереженнями  , які описуються моделлю , які описуються моделлю
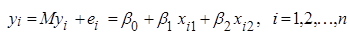 , (2.2.1) , (2.2.1)
необхідно оцінити невідомі параметри 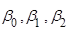 , перевірити адекватність лінійної моделі (2.2.1), значущість лінійної регресії , перевірити адекватність лінійної моделі (2.2.1), значущість лінійної регресії 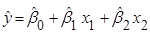 , а також з’ясувати, чи виконуються основні припущення , а також з’ясувати, чи виконуються основні припущення  лінійного регресійного аналізу. лінійного регресійного аналізу.
Стохастичний експеримент. Проведемо стохастичний експеримент, який полягає в моделюванні вибірок з нормальних розподілів з середніми, що дорівнюють сумі координат точок квадрата, і змінними дисперсіями:

Проста лінійна регресія. Знайдемо МНК – оцінки параметрів 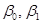 та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 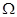 в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що змінна 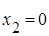 , наведено на рисунку 2.2.1. , наведено на рисунку 2.2.1.
 Рис. 2.2.1. Модель простої лінійної регресії, в якій дисперсія спостережень Рис. 2.2.1. Модель простої лінійної регресії, в якій дисперсія спостережень
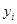 величина змінна
величина змінна
Результати перевірки адекватності та значущості цієї моделі простої лінійної регресії наведено в таблиці 2.2.1.
Таблиця 2.2.1. Результати перевірки адекватності та значущості моделі простої лінійної регресії, в якій дисперсія спостережень
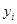 величина змінна
величина змінна
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
124615,2 |
1 |
124615,2 |
166,26 |
| Відносно регресії |
478200,8 |
638 |
749,5 |
| Відносно середнього |
602816 |
639 |
| Неадекватність |
3025,8 |
6 |
504,3 |
0,67 |
| "Чиста помилка" |
475175 |
632 |
751,9 |
F1 = 0,67 < 2,11 = F0,05;6;632, лінійна модель адекватна.
F2 = 166,26 > 3,86 = F0,05;1;638, регресія  значуща. значуща.
|t1| = 0,04 < 1,96 = t0,025;638, гіпотеза 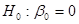 не відхиляється. не відхиляється.
|t2| = 0,38 < 1,96 = t0,025;638, гіпотеза  не відхиляється. не відхиляється.
Перевіримо припущення про некорельованість залишків 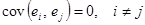 за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію  . Оскільки . Оскільки  , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.
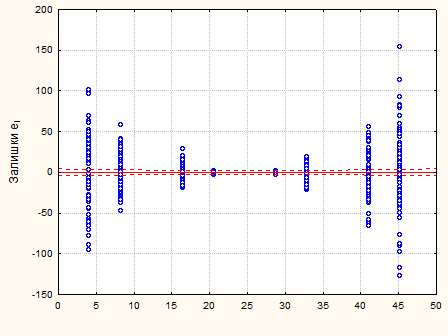

Рис. 2.2.2. Графік залишків – дисперсія змінюється
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію . .

Рис.2.2.3. Нормальний розподіл залишків 
Статистика  ,тому залишки ,тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта  , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія  значуща (гіпотеза значуща (гіпотеза 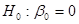 не відхиляється; гіпотеза не відхиляється; гіпотеза 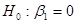 відхиляється, а гіпотеза відхиляється, а гіпотеза  не відхиляється); не відхиляється);
3) залишки   некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
Лінійна регресія з двома незалежними змінними. Знайдемо МНК – оцінки параметрів  та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення  в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що незалежні змінні  обрані згідно з рис. 2.1.1, наведено на рисунку 2.2.4. обрані згідно з рис. 2.1.1, наведено на рисунку 2.2.4.
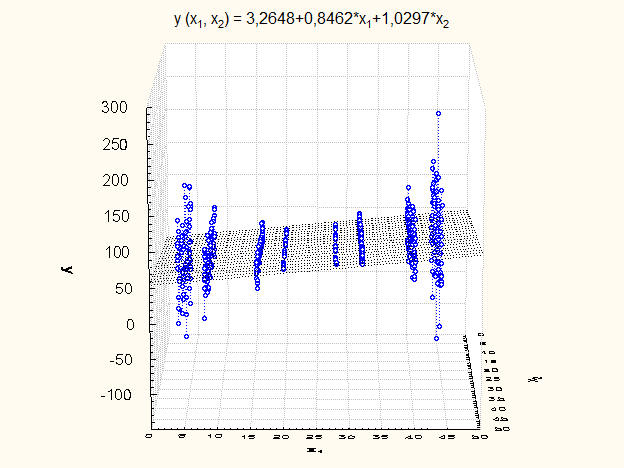 Рис. 2.2.4. Модель лінійної регресії, в якій дисперсія спостережень
Рис. 2.2.4. Модель лінійної регресії, в якій дисперсія спостережень
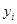 величина змінна
величина змінна
Результати перевірки адекватності та значущості цієї моделі лінійної регресії наведено в таблиці 2.2.2.
Таблиця 2.2.2. Результати перевірки адекватності та значущості моделі лінійної регресії, в якій дисперсія спостережень
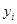 величина змінна
величина змінна
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
209188,2 |
2 |
104594,1 |
132,29 |
| Відносно регресії |
503614,7 |
637 |
790,6 |
| Відносно середнього |
712802,9 |
639 |
| Неадекватність |
32906,7 |
61 |
539,5 |
0,66 |
| "Чиста помилка" |
470708,0 |
576 |
817,2 |
F1 = 0,66 < 1,34= F0,05;61;576, лінійна модель адекватна.
F2 = 132,29 > 3,01= F0,05;2;637, регресія 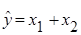 значуща. значуща.
|t1| = 1,09 < 1,96 = t0,025;637, гіпотеза 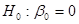 не відхиляється. не відхиляється.
|t2| = 1,88 < 1,96 = t0,025;637, гіпотеза  не відхиляється. не відхиляється.
|t3| = 0,38 < 1,96 = t0,025;637, гіпотеза  не відхиляється. не відхиляється.
Перевіримо припущення про некорельованість залишків 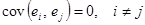 за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію 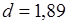 . Оскільки . Оскільки 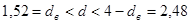 , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.
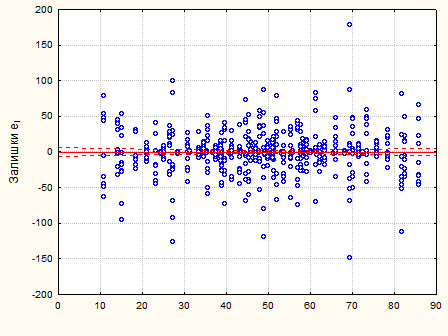

Рис. 2.2.5. Графік залишків – смуга постійної ширини
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію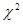 . .
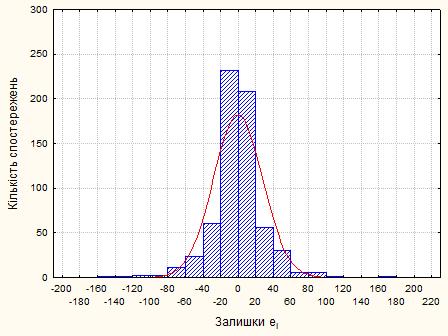
Рис. 2.2.6. Нормальний розподіл залишків 
Статистика 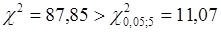 ,тому залишки ,тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта 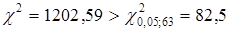 , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія  значуща (гіпотеза значуща (гіпотеза 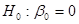 не відхиляється; гіпотеза не відхиляється; гіпотеза 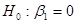 відхиляється, гіпотеза відхиляється, гіпотеза  не відхиляється, гіпотеза не відхиляється, гіпотеза  не відхиляється); не відхиляється);
3) залишки 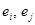  некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
2.3 Модель лінійної регресії, в якій спостереження  величини залежні величини залежні
Нехай  – залежні нормально розподілені випадкові величини з однаковою дисперсією – залежні нормально розподілені випадкові величини з однаковою дисперсією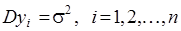 та середніми та середніми  , лінійними за параметрами , лінійними за параметрами  . .
Параметри 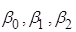 невідомі, невідомі,  – відомі невипадкові величини. – відомі невипадкові величини.
За спостереженнями  , які описуються моделлю , які описуються моделлю
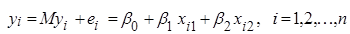 , (2.3.1) , (2.3.1)
необхідно оцінити невідомі параметри 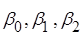 , перевірити адекватність лінійної моделі (2.3.1), значущість лінійної регресії , перевірити адекватність лінійної моделі (2.3.1), значущість лінійної регресії 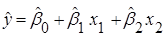 , а також з’ясувати, чи виконуються основні припущення , а також з’ясувати, чи виконуються основні припущення  лінійного регресійного аналізу. лінійного регресійного аналізу.
Стохастичний експеримент. Проведемо стохастичний експеримент, який полягає в моделюванні вибірки  з нормального розподілу з параметрами 0 та 1. з нормального розподілу з параметрами 0 та 1.
Наступні 7 вибірок рахуються за формулою
 , ,
де сталі 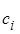 – елементи послідовності Фібоначчі, а саме: – елементи послідовності Фібоначчі, а саме: 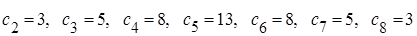 . .
Проста лінійна регресія. Знайдемо МНК – оцінки параметрів  та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення  в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що 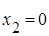 , наведено на рисунку 2.3.1. , наведено на рисунку 2.3.1.
 Рис. 2.3.1. Модель лінійної регресії, в якій спостереження
Рис. 2.3.1. Модель лінійної регресії, в якій спостереження  величини залежні величини залежні
Результати перевірки адекватності та значущості цієї моделі простої лінійної регресії наведено в таблиці 2.3.1.
Таблиця 2.3.1. Результати перевірки адекватності та значущості моделі простої лінійної регресії, в якій спостереження  величини залежні величини залежні
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
0,97 |
1 |
0,97 |
0,03 |
| Відносно регресії |
22892,15 |
638 |
35,88 |
| Відносно середнього |
22893,13 |
639 |
| Неадекватність |
9,81 |
6 |
1,64 |
0,05 |
| "Чиста помилка" |
22893,13 |
632 |
36,21 |
F1 = 0,05 < 2,11 = F0,05;6;632, лінійна модель адекватна.
F2 = 0,03 < 3,86 = F0,05;1;638, регресія 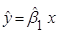 незначуща. незначуща.
|t1| = 0,29 < 1,96 = t0,025;638, гіпотеза 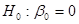 не відхиляється. не відхиляється.
|t2| = 100 > 1,96 = t0,025;638, гіпотеза  відхиляється. відхиляється.
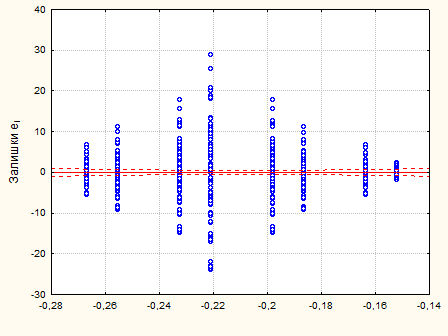

Рис. 2.3.2. Графік залишків – дисперсія змінюється
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію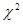 . .
Рис.2.3.3. Нормальний розподіл залишків 
Статистика 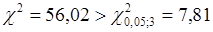 ,тому залишки ,тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта  , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія  незначуща (гіпотеза незначуща (гіпотеза 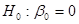 не відхиляється; гіпотеза не відхиляється; гіпотеза 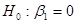 не відхиляється, а гіпотеза не відхиляється, а гіпотеза  відхиляється); відхиляється);
3) залишки 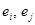  некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
Лінійна регресія з двома незалежними змінними. Знайдемо МНК – оцінки параметрів  та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 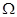 в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що незалежні змінні 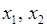 обрані згідно з рис. 2.1.1, наведено на рисунку 2.3.4. обрані згідно з рис. 2.1.1, наведено на рисунку 2.3.4.
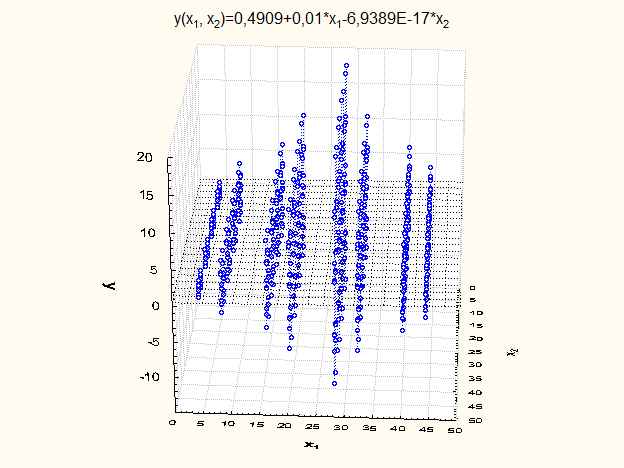 Рис. 2.3.4. Модель лінійної регресії, в якій спостереження
Рис. 2.3.4. Модель лінійної регресії, в якій спостереження  величини залежні величини залежні
Результати перевірки адекватності та значущості цієї моделі лінійної регресії наведено в таблиці 2.3.2.
Таблиця 2.3.2. Результати перевірки адекватності та значущості моделі лінійної регресії, в якій спостереження  величини залежні величини залежні
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
11,83 |
2 |
5,92 |
0,25 |
| Відносно регресії |
15256,05 |
637 |
23,95 |
| Відносно середнього |
15267,88 |
639 |
| Неадекватність |
119,56 |
61 |
1,96 |
0,07 |
| "Чиста помилка" |
15136,49 |
576 |
26,28 |
F1 = 0,07 < 1,34= F0,05;61;576, лінійна модель адекватна.
F2 = 0,25 < 3,01= F0,05;2;637, регресія 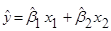 незначуща. незначуща.
|t1| = 0,94 < 1,96 = t0,025;637, гіпотеза 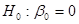 не відхиляється. не відхиляється.
|t2| = 99 > 1,96 = t0,025;637, гіпотеза  відхиляється. відхиляється.
|t3| = 100 > 1,96 = t0,025;637, гіпотеза  відхиляється. відхиляється.
Перевіримо припущення про некорельованість залишків 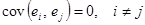 за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію  . Оскільки . Оскільки 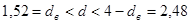 , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.


Рис. 2.3.5. Графік залишків – дисперсія змінюється
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію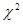 . .

Рис. 2.3.6. Нормальний розподіл залишків 
Статистика  ,тому залишки ,тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта 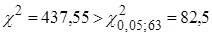 , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія  значуща (гіпотеза значуща (гіпотеза 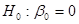 не відхиляється; гіпотеза не відхиляється; гіпотеза 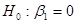 відхиляється, гіпотеза відхиляється, гіпотеза  відхиляється, гіпотеза відхиляється, гіпотеза  відхиляється); відхиляється);
3) залишки 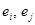  некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
2.4 Модель лінійної регресії, в якій спостереження  рівномірно розподілені величини рівномірно розподілені величини
Нехай  – незалежні рівномірно розподілені випадкові величини. – незалежні рівномірно розподілені випадкові величини.
За спостереженнями  , які описуються моделлю , які описуються моделлю
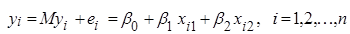 , (2.4.1) , (2.4.1)
необхідно оцінити невідомі параметри 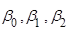 , перевірити адекватність лінійної моделі (2.4.1), значущість лінійної регресії , перевірити адекватність лінійної моделі (2.4.1), значущість лінійної регресії 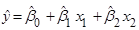 , а також з’ясувати, чи виконуються основні припущення , а також з’ясувати, чи виконуються основні припущення  лінійного регресійного аналізу. лінійного регресійного аналізу.
Стохастичний експеримент. Проведемо стохастичний експеримент, який полягає в моделюванні спостережень 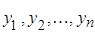 з рівномірного на відрізку з рівномірного на відрізку 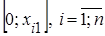 розподілу. розподілу.
Проста лінійна регресія. Знайдемо МНК – оцінки параметрів 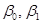 та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 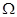 в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що 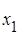 обирається згідно рис. 2.1.1, наведено на рисунку 2.4.1. обирається згідно рис. 2.1.1, наведено на рисунку 2.4.1.
 Рис. 2.4.1. Модель простої лінійної регресії, в якій спостереження
Рис. 2.4.1. Модель простої лінійної регресії, в якій спостереження  рівномірно розподілені рівномірно розподілені
Результати перевірки адекватності та значущості цієї моделі простої лінійної регресії наведено в таблиці 2.4.1.
Таблиця 2.4.1 Результати перевірки адекватності та значущості моделі простої лінійної регресії, в якій спостереження  рівномірно розподілені рівномірно розподілені
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
28061,45 |
1 |
28061,45 |
437,88 |
| Відносно регресії |
40886,36 |
638 |
64,09 |
| Відносно середнього |
68947,81 |
639 |
| Неадекватність |
414 |
6 |
69 |
1,07 |
| "Чиста помилка" |
40472,36 |
632 |
64,04 |
F1 = 1,07 < 2,11 = F0,05;6;632, модель адекватна.
F2 = 437,88 > 3,86 = F0,05;1;638, регресія 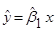 значуща. значуща.
|t1| = 0,16 < 1,96 = t0,025;638, гіпотеза 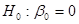 не відхиляється. не відхиляється.
|t2| = 25,5 > 1,96 = t0,025;638, гіпотеза  відхиляється. відхиляється.
Перевіримо припущення про некорельованість залишків 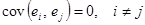 за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію  . Оскільки . Оскільки  , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.

Рис.2.4.2. Графік залишків – дисперсія залишків змінюється
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію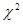 . .
Рис. 2.4.3. Нормальний розподіл залишків 
Статистика, 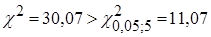 ,тому залишки ,тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта 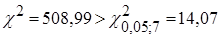 , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія 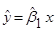 значуща (гіпотеза значуща (гіпотеза 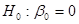 не відхиляється; гіпотеза не відхиляється; гіпотеза 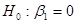 відхиляється, гіпотеза відхиляється, гіпотеза  відхиляється); відхиляється);
3) залишки 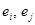  некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
Лінійна регресія з двома незалежними змінними. Знайдемо МНК-оцінки параметрів 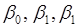 та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 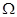 в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що значення 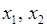 обираються згідно рис. 2.1.1, наведено на рисунку 2.4.4. обираються згідно рис. 2.1.1, наведено на рисунку 2.4.4.
 Рис. 2.
4
.4. Модель лінійної регресії, в якій спостереження Рис. 2.
4
.4. Модель лінійної регресії, в якій спостереження  рівномірно розподілені рівномірно розподілені
Результати перевірки адекватності та значущості цієї моделі лінійної регресії наведено в таблиці 2.4.2.
Таблиця 2.4.2. Результати перевірки адекватності та значущості моделі лінійної регресії, в якій спостереження  рівномірно розподілені рівномірно розподілені
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
28171,07 |
2 |
14085,54 |
220,04 |
| Відносно регресії |
40776,74 |
637 |
64,01 |
| Відносно середнього |
68947,81 |
639 |
| Неадекватність |
3539,39 |
61 |
58,02 |
0,89 |
| "Чиста помилка" |
37237,35 |
576 |
64,65 |
F1 = 0,89 < 1,34 = F0,05;61;576, модель адекватна.
F2 = 220,04 > 3,01 = F0,05;2;637, модель значуща.
|t1| = 0,74< 1,96 = t0,025;637, гіпотеза 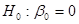 не відхиляється. не відхиляється.
|t2| = 25,5 > 1,96 = t0,025;637, гіпотеза  відхиляється. відхиляється.
|t3| = 48,5 > 1,96 = t0,025;637, гіпотеза 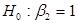 відхиляється. відхиляється.
Перевіримо припущення про некорельованість залишків 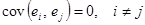 за допомогою критерію Дарбіна-Уотсона. Статистика критерія за допомогою критерію Дарбіна-Уотсона. Статистика критерія  . Оскільки . Оскільки 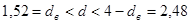 , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.
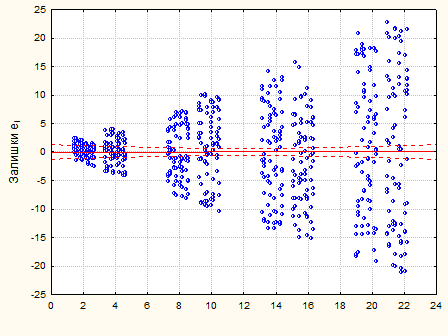

Рис.2.
4
.5. Графік залишків – дисперсія залишків змінюється
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію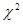 . .

Рис. 2.4.5. Нормальний розподіл залишків 
Статистика, 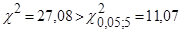 ,тому залишки ,тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта 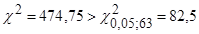 , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія  значуща (гіпотеза значуща (гіпотеза 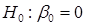 не відхиляється; гіпотеза не відхиляється; гіпотеза 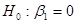 відхиляється, гіпотеза відхиляється, гіпотеза  відхиляється, гіпотеза відхиляється, гіпотеза 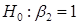 відхиляється); відхиляється);
3) залишки 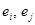  некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
2.5 Модель простої лінійної регресії, в якій спостереження  показниково розподілені величини показниково розподілені величини
Нехай  – незалежні показниково розподілені випадкові величини з параметром – незалежні показниково розподілені випадкові величини з параметром 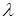 . .
За спостереженнями  , які описуються моделлю , які описуються моделлю
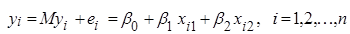 , (2.5.1) , (2.5.1)
необхідно оцінити невідомі параметри 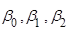 , перевірити адекватність лінійної моделі (2.5.1), значущість лінійної регресії , перевірити адекватність лінійної моделі (2.5.1), значущість лінійної регресії 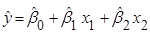 , а також з’ясувати, чи виконуються основні припущення , а також з’ясувати, чи виконуються основні припущення  лінійного регресійного аналізу. лінійного регресійного аналізу.
Стохастичний експеримент. Проведемо стохастичний експеримент, який полягає в моделюванні вибірки  з показникового розподілу з параметром з показникового розподілу з параметром 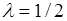 . .
Проста лінійна регресія. Знайдемо МНК – оцінки параметрів 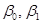 та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 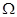 в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що 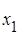 обирається згідно рис. 2.1.1, наведено на рисунку 2.5.1. обирається згідно рис. 2.1.1, наведено на рисунку 2.5.1.
 Рис. 2.5.1. Модель простої лінійної регресії, в якій спостереження
Рис. 2.5.1. Модель простої лінійної регресії, в якій спостереження  показниково розподілені показниково розподілені
Результати перевірки адекватності та значущості цієї моделі простої лінійної регресії наведено в таблиці 2.5.1.
Таблиця 2.5.1. Результати перевірки адекватності та значущості моделі простої лінійної регресії, в якій спостереження  показниково розподілені показниково розподілені
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
6,6 |
1 |
6,6 |
2,11 |
| Відносно регресії |
1992,5 |
638 |
3,12 |
| Відносно середнього |
1999,1 |
639 |
| Неадекватність |
16,04 |
6 |
2,67 |
0,85 |
| "Чиста помилка" |
1976,46 |
632 |
3,13 |
F1 = 0,85 < 2,11 = F0,05;6;632, модель адекватна.
F2 = 2,11 < 3,86 = F0,05;1;638, тому регресія  незначуща. незначуща.
|t1| = 12,29 > 1,96 = t0,025;498, гіпотеза 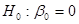 відхиляється. відхиляється.
|t2| = 99 > 1,96 = t0,025;498, гіпотеза 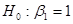 відхиляється. відхиляється.
Перевіримо припущення про некорельованість залишків  за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію 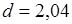 Оскільки Оскільки  , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.
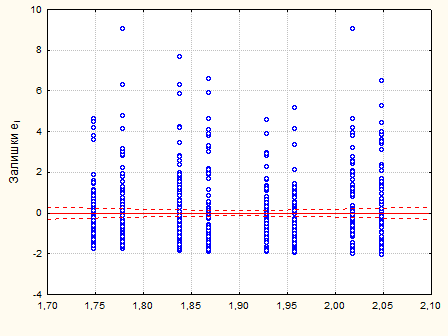
Рис. 2.5.2. Графік залишків – смуга постійної ширини
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію . .
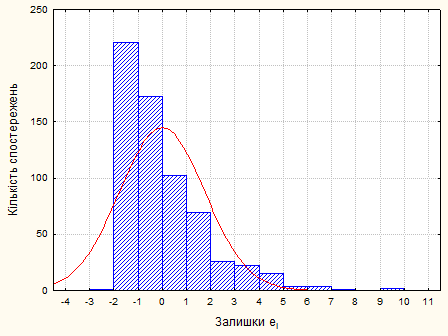
Рис. 2.5.3. Нормальний розподіл залишків 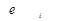
Статистика  , тому залишки , тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта 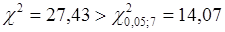 , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) модель 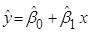 незначуща (гіпотеза незначуща (гіпотеза 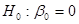 відхиляється; гіпотеза відхиляється; гіпотеза 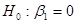 не відхиляється, гіпотеза не відхиляється, гіпотеза 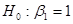 відхиляється); відхиляється);
3) залишки  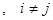 некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
Лінійна регресія з двома незалежними змінними. Знайдемо МНК – оцінки параметрів  та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення та перевіримо гіпотези про адекватність та значущість лінійної моделі регресії. Також з’ясуємо, чи виконуються припущення 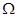 в цій моделі. в цій моделі.
Результати стохастичного експерименту, за умов, що значення  обиралися згідно рис.2.1.1, наведено на рисунку 2.5.4. обиралися згідно рис.2.1.1, наведено на рисунку 2.5.4.
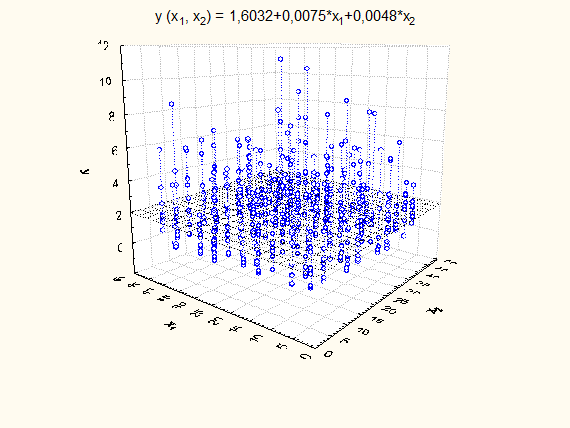
Рис. 2.
5
.4. Модель лінійної регресії, в якій спостереження  показниково розподілені показниково розподілені
Результати перевірки адекватності та значущості цієї моделі простої лінійної регресії наведено в таблиці 2.5.2.
Таблиця 2.
5
.2. Результати перевірки адекватності та значущості моделі простої лінійної регресії, в якій спостереження  показниково розподілені показниково розподілені
| Джерело варіації |
SS |
df |
MS |
F |
| Обумовлена регресією |
9,3 |
2 |
9,3 |
1,49 |
| Відносно регресії |
1989,79 |
637 |
3,12 |
| Відносно середнього |
1999,09 |
639 |
| Неадекватність |
176,57 |
61 |
2,89 |
0,92 |
| "Чиста помилка" |
1813,22 |
576 |
3,15 |
F1 = 0,92 < 1,34 = F0,05;61;576, лінійна модель адекватна.
F2 = 1,49 < 3,01 = F0,05;2;637, регресія 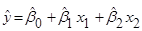 незначуща. незначуща.
|t1| = 8,42 > 1,96 = t0,025;637, гіпотеза 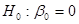 відхиляється. відхиляється.
|t2| = 99 > 1,96 = t0,025;637, гіпотеза 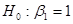 відхиляється. відхиляється.
|t3| = 100 > 1,96 = t0,025;637, гіпотеза  відхиляється. відхиляється.
Перевіримо припущення про некорельованість залишків  за допомогою критерію Дарбіна-Уотсона. Статистика критерію за допомогою критерію Дарбіна-Уотсона. Статистика критерію  . Оскільки . Оскільки  , то залишки , то залишки  цієї моделі некорельовані. цієї моделі некорельовані.
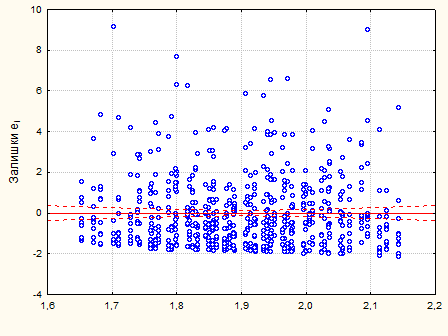
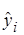
Рис. 2.
5
.5. Графік залишків – смуга постійної ширини
Гіпотезу про нормальний розподіл залишків  перевіримо за допомогою критерію перевіримо за допомогою критерію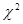 . .

Рис. 2.5.6. Нормальний розподіл залишків 
Статистика 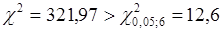 , тому залишки , тому залишки  не можна вважати нормально розподіленими. не можна вважати нормально розподіленими.
Статистика Бартлетта 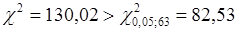 , тому дисперсія залишків , тому дисперсія залишків  змінна величина. змінна величина.
Отже,
1) лінійна модель адекватна;
2) регресія 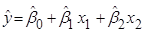 незначуща (гіпотеза незначуща (гіпотеза 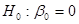 відхиляється; гіпотеза відхиляється; гіпотеза 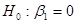 не відхиляється, гіпотеза не відхиляється, гіпотеза 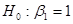 відхиляється, гіпотеза відхиляється, гіпотеза 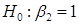 відхиляється); відхиляється);
3) залишки  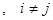 некорельовані; некорельовані;
4) залишки  не можна вважати нормально розподіленими; не можна вважати нормально розподіленими;
5) дисперсія залишків  змінна величина. змінна величина.
ВИСНОВКИ
Нехай 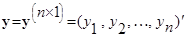 – результат спостереження, який описується лінійною моделлю виду – результат спостереження, який описується лінійною моделлю виду
 (1) (1)
де 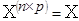 – регресійна матриця розміру – регресійна матриця розміру 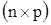 , ,  , ,
 – вектор невідомих параметрів, – вектор невідомих параметрів,
 – вектор похибок спостережень. – вектор похибок спостережень.
Припущення відносно вектора спостережень  позначатимемо позначатимемо 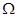 : :
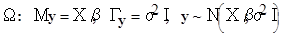 .(2) .(2)
Або, що те ж саме, припущення відносно вектора похибок 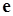 мають вигляд: мають вигляд:
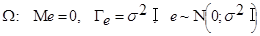 (3) (3)
Вихідні припущення (2) або (3) регресійного аналізу виконуються далеко не завжди. Виникає низка питань: як виявити порушення цих припущень? В яких випадках і які порушення можна вважати припустимими? Що робити, якщо порушення виявляються неприпустимими?
Метою роботи є вивчення наслідків порушення основних припущень (3) лінійного регресійного аналізу, а саме:
1) припущення про незміщеність похибок  ; (4) ; (4)
2) припущення про однакову дисперсію і некорельованість похибок 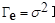 (5) (5)
3) припущення про нормальний розподіл похибок 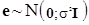 ; (6) ; (6)
4) припущення про незалежність спостережень  . (7) . (7)
Наслідки порушення припущень (4)-(7) розглянемо на прикладі лінійної регресії з двома незалежними змінними.
«Ідеальною» моделлю лінійної регресії з двома незалежними змінними називатимемо модель виду
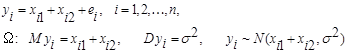 (8) (8)
«Ідеальна» модель – це модель (1) з коефіцієнтами 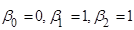 . .
Опишемо вибір невипадкових змінних  . .
Квадрат  розіб’ємо на 16 однакових квадратів розміром розіб’ємо на 16 однакових квадратів розміром  . В кожному з них оберемо 4 точки, які виступають вершинами квадратів розміром . В кожному з них оберемо 4 точки, які виступають вершинами квадратів розміром 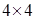 . Ці 64 вершини квадратів і обрані за значення, які набувають невипадкові змінні . Ці 64 вершини квадратів і обрані за значення, які набувають невипадкові змінні 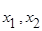 . .

Рис. 1. Вибір значень
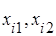 , які набувають невипадкові змінні
, які набувають невипадкові змінні

Проведемо стохастичний експеримент, який полягає в моделюванні спостережень згідно з моделлю (8).
Результати експерименту наведено на рисунку 2.

Рис. 2
За допомогою критеріїв математичної статистики ми будемо перевіряти не тільки, чи виконуються припущення регресійного аналізу, але й гіпотези про адекватність лінійної моделі, про значущість регресії, про значущість коефіцієнтів регресії. Отже, модель (8) узгоджується з результатами експерименту, жодне з вихідних припущень 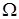 не порушено. не порушено.
1) „ідеальна” модель  адекватна (модель лінійна); адекватна (модель лінійна);
2) „ідеальна” регресія  значуща; значуща;
3) гіпотези  , , 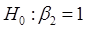 не відхиляються; не відхиляються;
4) дисперсія залишків  постійна; постійна;
5) залишки  некорельовані; некорельовані;
6) залишки  нормально розподілені нормально розподілені  . .
Розглянемо модель лінійної регресії, в якій дисперсія спостережень  величина змінна, тобто припущення (5) місця не має. величина змінна, тобто припущення (5) місця не має.
Проведемо стохастичний експеримент, який полягає в моделюванні спостережень згідно з моделлю
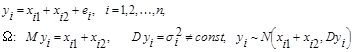 (9) (9)
Результати експерименту наведено на рисунку 3.
Рис. 3
В порівнянні з ідеальною моделлю залишки  не мають не мають  . .
Отже, разом з порушенням припущення про постійну дисперсію залишків порушується й припущення про нормальний розподіл залишків.
Якщо залишки  не мають нормального розподілу, то використовувати МНК-метод для оцінки параметрів регресії неприпустимо (МНК-оцінки не збігаються з ММП-оцінками). не мають нормального розподілу, то використовувати МНК-метод для оцінки параметрів регресії неприпустимо (МНК-оцінки не збігаються з ММП-оцінками).
Розглянемо модель лінійної регресії, в якій спостереження  величини залежні, тобто припущення (7) місця не має. величини залежні, тобто припущення (7) місця не має.
Проведемо стохастичний експеримент, який полягає в моделюванні спостережень згідно з моделлю
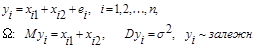 (10) (10)
Результати експерименту наведено на рисунку 4.
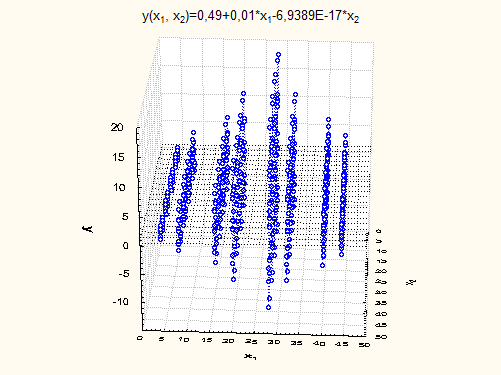
Рис. 4
В порівнянні з ідеальною моделлю
1) регресія  незначуща; незначуща;
2) гіпотези  , ,  відхиляються; відхиляються;
3) дисперсія залишків  змінна величина; змінна величина;
4) залишки  не мають не мають  . .
Отже, разом з порушенням припущення про незалежність спостережень  , порушуються й припущення про постійність дисперсії залишків і припущення про нормальний розподіл залишків. Такі порушення неприпустимі. , порушуються й припущення про постійність дисперсії залишків і припущення про нормальний розподіл залишків. Такі порушення неприпустимі.
Розглянемо модель лінійної регресії, в якій спостереження  рівномірно розподілені, тобто припущення (6) місця не має. рівномірно розподілені, тобто припущення (6) місця не має.
Проведемо стохастичний експеримент, який полягає в моделюванні спостережень згідно з моделлю
 (11) (11)
Результати експерименту наведено на рисунку 5.

Рис. 5
В порівнянні з ідеальною моделлю
1) гіпотези  , , 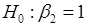 відхиляються; відхиляються;
2) дисперсія залишків  змінна величина. змінна величина.
Отже, разом з порушенням припущення про нормальний розподіл залишків, порушується й припущення про постійність дисперсії залишків.
Розглянемо модель лінійної регресії, в якій спостереження  показниково розподілені, тобто припущення (6) місця не має. показниково розподілені, тобто припущення (6) місця не має.
Проведемо стохастичний експеримент, який полягає в моделюванні спостережень згідно з моделлю
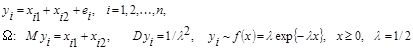 (12) (12)
Результати експерименту наведено на рисунку 6.

Рис. 6
В порівнянні з ідеальною моделлю,
1) лінійна регресія  незначуща; незначуща;
2) гіпотези 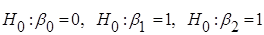 відхиляються; відхиляються;
3) дисперсія залишків  змінна величина. змінна величина.
Отже, разом з порушенням припущення про нормальний розподіл залишків, порушується й припущення про постійність дисперсії залишків.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Дрейпер Н., Смит Г. Прикладнойрегрессионный анализ. – М.: Статистика, 1973.
2. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2-е изд. – М.: Физматгиз, 1962.
3. Рао С.Р. Линейные статистические методы и их применение. – М.: Наука, 1968.
4. Себер Дж. Линейный регрессионный анализ. – М: Мир, 1980.
|