Курсовая работа: Проявление сил инерции на Земле

Тема данного исследования на сегодняшний день актуальна в силу того, что ряд авторов признают силу инерции, как существующую, а не фиктивную. Введение сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения. Следует отчетливо понимать, что силы инерции нельзя ставить в один ряд с такими силами, как упругие, гравитационные силы и силы трения, т.е. силами, обусловленными воздействием на тело со стороны других тел. Силы инерции обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. В этом смысле их можно назвать фиктивными силами. Введение в рассмотрение сил. инерции не является принципиально необходимым. В принципе любое движение можно всегда рассмотреть по отношению к инерциальной системе отсчета. Однако практически часто представляет интерес как раз движение тел по отношению к неинерциальным системам отсчета, например по отношению к земной поверхности. Использование сил инерции дает возможность решить соответствующую задачу непосредственно по отношению к такой системе отсчета, что часто оказывается значительно проще, чем рассмотрение движения в инерциальной системе.

Что касается вопроса, о включении в курс физики средней школы понятия "неинерциальные системы отсчета", то он рассматривался в середине семидесятых годов, однако, в то время методической поддержки он не получил. Считалось, что изучение этих понятий недоступно для школьников. В последние годы были проведены исследования, которые позволили подойти к решению проблемы формирования понятий "неинерциальные системы отсчета" и "силы инерции" с новых позиций. Поэтому своевременность обращения к этой проблеме обусловлена теми противоречиями, которые присущи современному процессу обучения:

между необходимостью формирования у учащихся целостного представления о современной физической картине мира и ограничением объема учебного материала;

между расширенной информационной средой (телевидение, научно-популярная литература и др.), окружающей школьников и создающей условия для изучения понятий "неинерциальные системы отсчета" и "силы инерции", и недостаточностью разработки соответствующих методических основ для введения этих понятий в курс физики средней школы;

между требованиями к отбору содержания курса физики по вопросу формирования современной физической картины мира и недостаточной разработкой соответствующих учебных технологий обучения.

Преодоление этих противоречий может способствовать включение в учебный материал понятий "неинерциальные системы отсчета" и "силы инерции".

Таким образом, актуальность исследования обусловлена тем, что в настоящее время появляется возможность для разработки методики изучения понятий "неинерциальные системы отсчета" и "силы инерции" в курсе физики средней школы, что позволит повысить уровень систематизации знаний и даст возможность рассматривать с более глубоких научных позиций происходящие физические явления, а это, в свою очередь, будет способствовать формированию у школьников целостных представлений о современной физической картине мира.

Объектом исследования является процессы проявления сил инерции на Земле.

Предмет исследования - изучения понятий "неинерциальные системы отсчета" и "силы инерции".

Цель исследования - обоснование формирования понятий "неинерциальные системы отсчета" и "силы инерции", а так же обоснование проявления данных сил на Земле.

Неинерциальные системы отсчета

Неинерциальными называют такие системы отсчета, в которых не выполняются законы Ньютона. Не выполняется закон инерции, ибо в таких системах отсчета тело, на которое не действуют другие тела, не сохраняет своего состояния покоя или равномерного прямолинейного движения. Не выполняется второй закон Ньютона, так как тело может иметь ускорение, не испытывая действия со стороны другого тела. Наконец, не выполняется и третий закон Ньютона, ибо тело, испытывая действие некоторой силы инерции, не оказывает противодействия (нет тела, к которому должно быть приложено это противодействие). Системы отсчета, движущиеся равномерно и прямолинейно относительно инерциальной системы, являются инерциальными. Неинерциальными же будут все те системы отсчета, которые движутся с ускорением относительно какой-либо инерциальной системы. Различают два вида неинерциальных систем отсчета: системы, движущиеся относительно инерциальной системы отсчета поступательно с постоянным или переменным ускорением, и системы, вращающиеся с постоянной или переменной угловой скоростью относительно некоторого центра или некоторой оси. Произвольное движение системы всегда можно представить в виде суммы указанных двух движений.

Неинерциальные системы отсчета, движущиеся поступательно

Силы инерции . На горизонтальном прямолинейном участке железнодорожного пути находится железнодорожный вагон. На полу вагона лежит неподвижный шар (рис.1.1), могущий перемещаться на полу без трения. Выберем две системы отсчета: одну систему (К) свяжем с поверхностью земли, а другую (К') - со стенками вагона. Систему отсчета, связанную с землей, можно с известным приближением считать инерциальной. Система же, связанная с вагоном, будет инерциальной только тогда, когда вагон покоится или движется равномерно и прямолинейно. Рассмотрим "поведение" шара относительно систем К и К'.

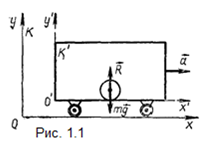
Вагон покоится. В этом случае шар неподвижен в обеих системах отсчета. Наблюдатели, находящиеся в системах К и К', объяснят покой шара одинаковым образом в соответствии с первым законом Ньютона: шар находится в покое, так как сумма действующих на него сил (сила тяжести и сила реакции пола) равна нулю.

Вагон движется с ускорением а. В этом случае наблюдатели, находящиеся в системах отсчета К и К' воспримут движение шара по-разному. Наблюдатель в системе К отметит, что шар в полном согласии с законами Ньютона покоится, так как между шаром и полом вагона трения нет; нет и причин для изменения состояния покоя шара. Изменение относительного расстояния между шаром и стенкой вагона наблюдатель в системе К объяснит тем, что вагон уходит, а шар остается на месте. Этому наблюдателю будет понятно и то, что если вагон движется с ускорением а , то движение шара относительно стен вагона (в системе К') будет происходить с тем же ускорением, но направленным в противоположную сторону. Это ускорение, естественно, будет одинаково для всех тел независимо от их массы. Наблюдатель, находящийся в системе К' (в вагоне), отметит, что в этой системе шар движется с ускорением а' . Если он измерит это ускорение, то обнаружит, что оно по модулю равно ускорению вагона а (об ускорении вагона ему может сообщить, например, по радио наблюдатель с земли). Заменяя шар другими телами, также способными перемещаться по полу без трения, наблюдатель в системе К' придет к выводу (который был очевиден и наблюдателю в системе К), что ускорение тел не зависит от их массы; оно одинаково для всех тел и равно ускорению, с которыми движется система отсчета К', взятому с обратным знаком:

где а' - ускорение, измеренное в системе К'; а - ускорение самой системы К' относительно инерциальной системы К. (Это справедливо только для рассматриваемого случая, когда сумма ньютоновских сил равна нулю.) Исходя из законов Ньютона, наблюдатель в системе К' скажет, что на шар массой mдействует сила, равная mа' , и начнет искать тело, которое своим действием создает эту силу. Однако такого тела он, естественно, не найдет. Тогда наблюдатель в системе К' придет к заключению, что в этой системе отсчета не выполняются законы Ньютона: не выполняется закон инерции, ибо шар не сохраняет состояния покоя или равномерного прямолинейного движения, хотя никакие тела на него не действуют; шар имеет ускорение, которое не вызвано силой в ньютоновском понимании. Таким образом, наблюдатель в системе отсчета К' отнесет эту систему к классу неинерциальных. Из разобранного примера видно, что, находясь внутри системы отсчета и наблюдая за поведением свободных тел (тел, для которых сумма действующих на них ньютоновских сил равна нулю), можно установить, к какому классу относится данная система отсчета: к классу инерциальных или к классу неинерциальных систем. Более того, измеряя ускорение свободного тела, можно даже установить, с каким ускорением и в какую сторону движется данная система отсчета относительно некоторой (заданной) инерциальной системы. Напомним, что никакими опытами, проведенными внутри инерциальной системы, нельзя установить, движется или покоится эта система.

Силы инерции . Было бы неудобно создавать для неинерциальных систем отсчета другую механику, отличную от ньютоновской. Поэтому вполне логично поставить такой вопрос: нельзя ли внести такие дополнения или изменения в механику Ньютона, чтобы сделать выполнимыми основные законы динамики и в неинерциальных системах? Оказывается, это сделать можно. Нужно только расширить понятие силы: считать, что в неинерциальных системах отсчета, кроме обычных (ньютоновских) сил, на все тела действуют еще такие, не совсем обычные силы, которые не вызваны взаимодействием тел друг с другом, а являются результатом ускоренного движения самой системы отсчета. Эти силы, получившие название сил инерции, способны оказывать на тела динамическое и статическое действие, подобно обычным ньютоновским силам. Учитывая это, наблюдатель, находящийся в системе отсчета К' (рис.1.1), объяснит ускоренное движение шара как результат действия на шар силы инерции. В данном примере сумма ньютоновских сил (сила тяжести и сила реакции пола) равна нулю. Поэтому наблюдатель в системе К' запишет для шара второй закон Ньютона в обычной форме:

(1.1)

Пользуясь этим уравнением, наблюдатель, зная силу F_ин и начальные условия, сможет установить закон движения шара. Остается выяснить, как подсчитывается сила инерции. Если сумма ньютоновских сил равна нулю, шар в системе К' движется с ускорением а', которое равно по модулю и противоположно по направлению ускорению самой системы К' относительно инерциальной системы К:

Умножим обе части этого равенства на массу шара m. Сравнивая полученное выражение с выражением (1.1), найдем, что

(1.2)

Таким образом, получается следующее правило: в ускоренно движущейся системе отсчета на все тела действует сила инерции, равная произведению массы тела на ускорение системы отсчета, взятому с противоположным направлением. Если система отсчета движется с постоянным ускорением, то сила инерции постоянна. Если же система движется с изменяющимся ускорением, то и сила инерции непостоянна; ее мгновенное значение определяется соотношением (1.2). Обратим внимание на одну важную особенность силы инерции: эта сила пропорциональна массе тела, на которое она действует. Это роднит силу инерции с силой тяжести. Как и сила тяжести, сила инерции относится к категории массовых сил, оказывающих свое действие на каждый элемент тела.

Свойства сил инерции. Хотя силы инерции и не вызваны действием тел друг на друга, они для наблюдателя, находящегося в ускоренно движущейся системе отсчета, вполне реальны. В их реальности любой может убедиться на собственном опыте каждый раз, когда, будучи пассажиром какого-либо транспорта, испытывает ее действие в момент резкого торможения или рывка вперед. В эти моменты все ощущают силу, которая заставляет наклониться вперед или назад. Ощущение этой силы напоминает ощущение веса. И это происходит потому, что силы инерции, как и вес, - массовые силы; они действуют на все элементы нашего тела. Для наблюдателя, находящегося на земле, т.е. в инерциальной системе отсчета, сил инерции не существует. Отклонение тел при торможении или рывке вперед он объясняет в соответствии с первым законом Ньютона - стремлением тел сохранять свое состояние движения или покоя. Можно поставить в движущейся с ускорением системе отсчета К' и другие опыты, которые покажут реальность сил инерции, не связывая это с личным ощущением наблюдателя. Обратимся вновь к ускоренно движущемуся вагону. Если наблюдатель, находящийся в вагоне (системе К'), присоединит шар А к легкой ("невесомой") пружине, скрепленной с передней стенкой вагона, а шар В подвесит к потолку на тонкой ("невесомой") нити (рис.1.2), то он отметит, что оба шара через некоторое время после начала ускоренного движения будут неподвижны.

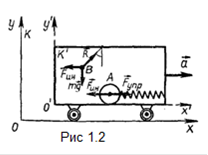
При этом пружина окажется растянутой на некоторую величину (Δx'), а нить - отклоненной от вертикали на некоторый угол α. Но пружина может растянуться, а подвешенное тело может отклониться от вертикали только в том случае, если на шары действуют реальные силы. Этими силами в ускоренно движущемся вагоне являются силы инерции. Видно, что силы инерции, как и обычные ньютоновские силы, могут вызывать деформацию тел, отклонение подвешенных тел от вертикали. Они "делают" все то, что "делают" обычные силы. Наблюдатель в системе "земля" объяснит растяжение пружины тем, что шар в его системе движется с ускорением а , а для этого нужна сила. Этой силой является сила упругости растянутой пружины. Отклонение шара В от вертикали он объяснит тем, что для ускоренного движения тела В нужна сила, которая появится как результирующая силы натяжения нити и силы тяжести, действующей на шар.

Законы сохранения. Известно, что в ньютоновской механике закон сохранения импульса системы материальных точек справедлив для замкнутых систем. Выполняется ли указанный закон в неинерциальных системах отсчета? Чтобы получить замкнутую систему тел, надо было бы включить в эту систему и то тело, которое порождает силу инерции. Но такого тела нет. Поэтому ни одна система тел в ускоренно движущейся системе отсчета не может быть замкнутой. Отсюда следует неприменимость закона сохранения импульса в неинерциальной системе отсчета.

Поле сил инерции. Силы инерции, действующие в неинерциальной системе отсчета, образуют силовое поле. Очевидно, для систем, движущихся поступательно, поле сил инерции будет однородным. Такое поле образуется, например, в системе отсчета, связанной с ускоренно движущимся вагоном. Поле сил инерции будет во всех точках пространства и вне вагона, если это пространство рассматривать в системе К'.

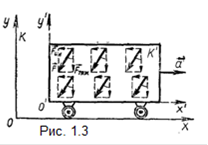
Однако в движущемся вагоне, кроме поля сил инерции, существует также поле сил тяжести, которое можно считать однородным ввиду незначительных размеров вагона по сравнению с Землей. На рисунке (1.3) оба поля показаны пунктирными стрелками. В соответствии с принципом суперпозиции оба поля накладываются одно на другое и образуют новое, результирующее поле, которое действует на точку массой mс силой

(1.3)

На рис. (1.3) результирующее поле показано сплошными стрелками. Наблюдатель, находящийся в вагоне, воспримет результирующее поле как измененное поле тяготения.

Вращающиеся системы отсчета. Связывая систему отсчета с вращающимся телом, получим вращающуюся систему отсчета. Поскольку вращающиеся системы суть системы, движущиеся относительно инерциальной с некоторым (радиальным) ускорением, то в них должны также действовать силы инерции.

Нахождение сил инерции в общем случае представляет собой сложную задачу. Поэтому ограничимся только частным случаем, когда система вращается относительно неподвижной (инерциальной системы) с постоянной угловой скоростью. В отличие от случая поступательного движения системы, рассмотренного выше, во вращающейся системе отсчета проявляются два рода сил инерции: центробежные силы, определяемые только положением тела в системе отсчета и не зависящие от скорости тела в этой системе, и кориолисовы силы, которые, наоборот, зависят от скорости движения тела, но не зависят от его положения в системе отсчета. На покоящееся во вращающейся системе отсчета тело действует только центробежная сила, на движущееся тело - и центробежная и кориолисова. С действием этих сил можно ознакомиться на примере аттракциона "карусель". Кому приходилось кататься на карусели, хорошо помнят действие силы, стремящейся выбросить человека наружу. По личному ощущению покоящийся на карусели наблюдатель может заметить, что эта сила направлена по радиусу к периферии, а модуль ее тем больше, чем дальше

наблюдатель находится от оси вращения. Кому приходилось ходить по полу вращающейся карусели, знает, как трудно удержаться в равновесии. Эта трудность возникает из-за того, что на движущегося человека, кроме центробежной силы, направленной по радиусу, действует еще одна сила - сила кориолиса, которая, будучи перпендикулярна направлению движения человека, "валит" его на бок и, чтобы не упасть, он должен идти, "переплетая" ноги. Но разберем подробнее обе эти силы.

Центробежная сила инерции

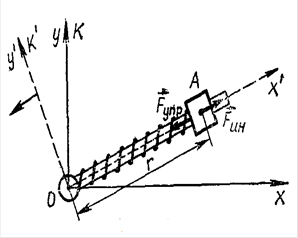
Рис. 1.4

Обратимся к следующему эксперименту.

На стержне, способном вращаться в горизонтальной плоскости, около одного своего конца (точка О на рисунке 1.4) посажена муфта А, скрепленная (невесомой) пружиной с центром О. Муфта может перемещаться по стержню без трения. Опишем движение муфты и состояние пружины относительно двух систем отсчета: неподвижной (она же инерциальная) х, у (К) и вращающейся х', у' (К'), скрепленной осью х' со стержнем. Когда стержень неподвижен относительно инерциальной системы отсчета, то муфта в обеих системах отсчета К и К' покоится, а пружина находится в нерастянутом состоянии, что согласуется с законами Ньютона. Если же стержень приведен в равномерное вращение с угловой скоростью ω, оба наблюдателя (в системах К и К') отметят растяжение пружины на величину Δх'. Но объяснят они это по-разному. Наблюдатель в инерциальной системе объяснит растяжение пружины тем, что в начальные моменты времени (когда стержень только начал вращаться) муфта получает импульс Р_а в направлении, перпендикулярном стержню (рис.1.5). Этот импульс, согласно закону инерции, муфта стремится сохранить, перемещаясь по прямой аа' . Удаление муфты от центра и, следовательно, растяжение пружины приводит к появлению силы, направленной к центру (под углом α₁ > 90° к вектору скорости муфты). Появившаяся сила F_ynp изменит направление движения, и муфта попадет в точку b. Двигаясь далее по прямой bb', муфта удалится от центра еще больше, что приведет к увеличению растяжения пружины и возрастанию силы F_yпp (α₂ > 90°, но α₂ < α₁ ).

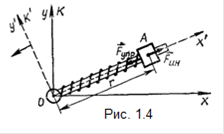
Под действием силы F_ynp направление движения муфты изменяется более резко, и муфта попадет в точку с. Вскоре наступит момент, когда угол α станет равным 90° (точка d), а сила упругости достигнет такого значения, которое необходимо для обеспечения равномерного движения муфты массой mпо окружности радиуса r:

Таким образом, для наблюдателя в системе отсчета К муфта начнет двигаться по окружности, так как на нее действует сила, перпендикулярная скорости и направленная к центру О. Для наблюдателя в системе отсчета К' стержень находится в покое. Растяжение пружины этот наблюдатель объяснит тем, что с началом вращения стержня на муфту стала действовать некоторая сила, стремящаяся удалить ее от центра; но удаляясь от центра, муфта растягивает пружину.

Наблюдатель в системе отсчета К' может установить, что появившаяся сила не является результатом взаимодействия муфты с каким-либо телом системы и поэтому она по природе своей принадлежит к силам инерции, обусловленным ускоренным движением самой системы отсчета.

Установившееся состояние покоя муфты в системе отсчета К' наблюдатель в этой системе объяснит тем, что сила упругости пружины в конце концов уравновесит действие силы инерции:

(1.4)

Так как в инерциальной системе отсчета сила упругости пружины выполняет роль центростремительной силы (F_yпp = F_ц.с.) , то из (1.4) получаем:

Сила инерции направлена от центра вращения системы наружу. Это и послужило поводом называть ее центробежной. Поскольку центростремительная сила определяется соотношением F_ц.с. = - mω² r (где ω - угловая скорость движения материальной точки по окружности радиуса г; r - радиус-вектор, соединяющий центр вращения с движущейся точкой), то центробежная сила в системе отсчета, в которой это тело покоится, будет определяться таким равенством: (1.5)

Однако величины ω и rприобретают иной смысл: со - угловая скорость вращения системы отсчета, а r - радиус-вектор, соединяющий центр вращения с покоящейся в системе отсчета К' точкой, в нашем примере - муфтой.

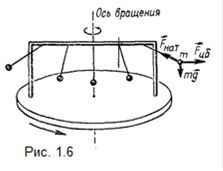
Выражение (1.5) является наиболее общим определением центробежной силы: центробежная сила пропорциональна массе тела, квадрату угловой скорости вращения системы отсчета и расстоянию точки от оси вращения. Зависимость центробежной силы от расстояния материальной точки до оси вращения (формула 1.5) можно наглядно проиллюстрировать на опыте, смысл которого ясен из рисунка 1.6. На шарик, подвешенный к стойке, укрепленной на вращающемся диске, действуют в системе отсчета К' три силы. Отклонение шарика от вертикали обусловлено действием центробежной силы. Очевидно, чем больше эта сила, тем больше угол а отклонения шарика от вертикали.

Кориолисовы силы инерции. Проявление кориолисовых сил в некоторых опытах. Возьмем диск, могущий вращаться около вертикальной оси, и проведем на нем радиальную прямую от центра к точке А (рис.1.7, а).

Запустим вдоль этого направления шарик со скоростью v₀ (трение отсутствует). Если диск не вращается, то шарик будет двигаться вдоль прочерченной линии со скоростью v₀ . Если же диск привести в равномерное вращение, то движение шарика будет восприниматься различными наблюдателями по-разному. Для наблюдателя, находящегося на земле, шарик по-прежнему движется прямолинейно с той же скоростью, ибо ввиду отсутствия трения не возникает причин к изменению скорости шарика (диск проходит под шариком, не увлекая его). Для наблюдателя, находящегося на диске, движение шарика будет криволинейным с возрастающей скоростью v относительно диска. Для этого наблюдателя шарик отклонится от первоначального положения вправо (рис.1.7) и придет в точку В.

Положение точки В зависит от начальной скорости v₀ (при данной угловой скорости вращения диска). Если v₀ велико, то за время движения шарика от оси к краю диска последний повернется на малый угол (рис.1.7, а) и точка В окажется вблизи точки А. Если скорость шарика v₀ невелика, то за время движения шарика от оси к А краю диска диск повернется на значительный угол (рис.1.7,6) или успеет сделать несколько оборотов (рис.1.7, б). В этом случае вращающийся наблюдатель увидит, что шарик движется вокруг центра по раскручивающейся спирали. Но известно, что движение тела по криволинейной траектории возникает только тогда, когда действующая на тело сила имеет составляющую, направленную нормально к вектору скорости. Поэтому наблюдатель, находящийся на диске, объяснит криволинейность движения шарика тем, что на шарик перпендикулярно к его скорости действует какая-то сила, которая, однако, не вызвана взаимодействием шарика с каким-либо телом. Это - сила инерции, названная кориолисовой силой.

В отличии от центробежной силы, значение которой зависит от расстояния до оси вращения, сила Кориолиса не зависит от положения тела. Она определяется скоростью движения тела, и при этом не только значением скорости, но и ее направлением по отношению к оси вращения. Если тело движется вдоль оси вращения, то сила Кориолиса равно нулю. Чем больше угол между вектором скорости и осью вращения, тем больше сила Кориолиса; максимальное значение Сила примет при движении тела под прямым углом к оси.

Земля как неинерциальная (вращающаяся) система отсчета

Относительно инерциальной системы отсчета Земля совершает суточное вращение около оси с угловой скоростью

По этой причине связанная с Землей система отсчета будет неинерциальной. В этой системе приобретают вполне реальное значение центробежные и кориолисовы силы инерции.

Проявление центробежных сил . Центробежные силы оказывают влияние на силу тяжести, ускорение свободного падения и вес тел. Кроме того, действие их оказывает влияние также и на форму самой Земли. Тело массой mна поверхности Земли испытывает действие двух массовых сил: силы тяготения

и центробежной силы

где r - расстояние тела от оси вращения.

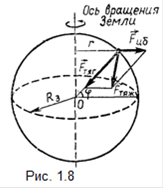
На рисунке 1.8 показаны обе силы на широте φ. Равнодействующая этих сил, называемая силой тяжести, равна

(1.6)

Если тело свободно, оно получит ускорение g_φ и

Поэтому

Следовательно, наблюдаемое ускорение свободного падения на широте φ равно:

(1.7)

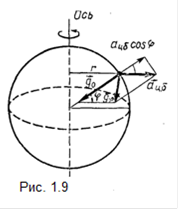
Таким образом, ускорение свободного падения (рис.1.9) не направлено к центру Земли и не равно тому ускорению g₀ , которое имело бы тело, если бы Земля не вращалась.

Наибольшее различие между g_φ и g₀ имеется на экваторе:

Оно составляет приблизительно ¹ /₃₀₀ от наблюдаемого ускорения на средних широтах (9,81 м/с² ).

Из расчета видно, что вектор а_ц.б. на рисунке 1.9 сильно преувеличен и что направление g_φ очень мало отличается от направления вектора g_{0. Е} сли пренебречь этим отклонением, то можно вычислить величину g_φ .

Проецируя а_ц.б. на продолжение радиуса и вычитая эту проекцию из g₀ , получим:

Так как

то

(1.8)

Вес тела на поверхности Земли. По определению весом называют силу, с которой тело действует на подвес или опору, удерживающие тело от падения. Вес, следовательно, есть сила упругости, ибо взаимодействие тела с опорой осуществляется через силы упругости. Однако вес тела можно выразить через силу тяготения и центробежную силу. На покоящееся тело действует сила

С такой же силой покоящееся тело действует на удерживающую его опору. Поэтому вес тела Р на поверхности Земли равен:

(1.9)

Вес тела отличается от действующей на него силы тяготения F_тяг как по модулю, так и по направлению (хотя и незначительно). Поскольку F_ц.б. зависит от географической широты, то и вес тела будет зависеть от широты. Вес тела можно представить в виде произведения массы на ускорение свободного падения:

Эта формула верна лишь в том случае, когда тело и опора неподвижны относительно земли. Если же тело и опора движутся с некоторым ускорением а, то вес тела не будет равен mg_φ . Действительно, в движущейся с ускорением а системе отсчета на тело действуют, кроме сил тяготения, силы инерции, связанные с вращением Земли (F_ц.б. и F_кop ), и силы инерции F_ин.nocт , обусловленные поступательным движением системы отсчета К':

Результирующая этих сил равна:

С такой силой тело, покоящееся в системе отсчета К', действует на удерживающую опору. Тогда

Учитывая, что

получаем:

(1.10)

Таким образом, вес тела в системе отсчета, движущейся относительно земли с ускорением, отличается от произведения mg_φ , т.е. от веса тела на поверхности земли. Если сила Кориолиса невелика (при малой скорости движения тела относительно земли), то ее можно не учитывать. Тогда

(1.11)

где g* - напряженность результирующего поля сил тяготения и инерции в системе отсчета К'.

Формула (1.10) определяет вес тела в самом общем случае, а формула (1.11) - при условии, что силой Кориолиса можно пренебречь. Для величины g_φ берут среднее значение ускорения свободного падения g_φ = g = 9,81 м/с² . Формула (1.11) справедлива для опоры или подвеса любого вида.

Перегрузки и невесомость . Если модуль веса тела |Р| в (1.11) превосходит вес тела, покоящегося на земле (mg), то говорят, что внутри движущейся системы отсчета (например, самолета или космического корабля) установилось состояние перегрузки. Количественно перегрузка nвыражается так:

Десятикратная (n= 10) кратковременная перегрузка является пределом для человека (тренированного космонавта). Допустимое значение длительных перегрузок меньше. Имеющиеся для человека ограничения в перегрузках создают серьезные затруднения в использовании космических пилотируемых кораблей для исследования других (даже самых близких) звездных систем.

Чтобы космонавт мог в течение своей жизни (60 лет) достигнуть самой близкой к нам звезды α-Центавра, удаленной от Земли на расстояние, равное четырем световым годам, космический корабль должен как можно быстрее набрать скорость, соизмеримую со скоростью света. Расчет показывает, что необходимое для этого ускорение создает такую перегрузку, которую человек не сможет вынести, если не будут разработаны специальные защитные меры.

Если система отсчета (космический корабль, например) движется с ускорением а = g, то вес тела согласно (1.11) равен нулю (Р = 0), т.е. тело в этом случае не действует на опору; значит, напряженность результирующего поля сил гравитации и сил инерции в движущейся системе равна нулю (g*=0). Такое состояние и называют состоянием невесомости. Внешним проявлением этого состояния является отсутствие веса у тел. Однако дело не только в этом. При невесомости все тела находятся в особом, недеформированном состоянии. Это обусловлено тем, что в условиях невесомости нет ни массовых сил (g* = 0), ни сил реакции со стороны опоры, т.е. тех сил, которые создают деформацию покоящихся тел.

Для наблюдателя, находящегося в неподвижной (инерциальной) системе отсчета, все тела внутри ракеты и сама ракета или космический корабль свободно "падают" с одинаковым ускорением g. Именно поэтому они находятся друг относительно друга в покое и не оказывают давления друг на друга. По этой же причине частицы одного и того же тела не смещаются относительно друг друга и тело не деформируется. Таким образом, чтобы в ракете была невесомость, она должна двигаться свободно с ускорением g.

Этим способом создают "бассейн" невесомости при тренировках космонавтов. Просторный самолет сначала разгоняют до максимально допустимой скорости v₀ , образующей с горизонтом некоторый угол α, а затем выключают двигатели. При этом самолет совершает свободный полет по кривой, близкой к параболе. Отличие от параболы обусловлено наличием сопротивления воздуха. Чтобы движение происходило точно по параболе, двигатели выключают не полностью: они должны создавать тягу, которая компенсирует сопротивление воздуха. Так удается получить невесомость в течение малого промежутка времени.

Деформация Земли . На вращающейся Земле центробежная сила действует не только на тело, лежащее на Земле, но и на каждую частицу самой Земли. Действие этих сил привело к тому, что Земля оказалась деформированной, сжатой у полюсов. Сжатие шарообразного тела у полюсов можно проиллюстрировать на следующей модели. Два круговых обруча из тонких полосок стали насажены на вертикальный стержень (рис.1.10, а). В нижней части обручи скреплены со стержнем. В верхней (В) они свободно могут скользить по стержню. Если привести обручи во вращение, то под действием центробежных сил они сожмутся в направлении оси вращения (рис.1.10,6).

В результате сплюснутости Земли ее полярная ось почти на ¹ /₃₀₀ долю короче диаметра экватора. А это приводит к тому, что и сила тяготения вблизи поверхности Земли становится зависящей от широты: она наибольшая на полюсе и наименьшая на экваторе. Поэтому фактическая зависимость g_φ от φ будет более сложной, чем это выражено соотношением (1.8), в котором ускорение g_o . сообщаемое телу силой тяготения, принималось не зависящим от широты. Измерения на различных широтах привели к следующей эмпирической формуле:

(1.12)

Здесь g_φ выражается в метрах на секунду в квадрате (м/с² ). Поправочный член достигает наибольшей величины при φ= 0, т.е. на экваторе, и достигает значения 0,052 м/с² . Ввиду малости этой величины ее влиянием в ряде случаев можно пренебрегать. При расчетах часто берут значение g_φ на уровне моря для широты φ = 45° (g_45° = 9,81 м/с² ).

Проявление сил Кориолиса . На любое тело, движущееся по поверхности Земли, действует кориолисова сила

На рисунке 1.11 показаны силы Кориолиса для различных движений. В точке А тело движется с севера на юг. На него действует сила Кориолиса F_ко _p , направленная на запад - вправо относительно направления v'. Если бы тело двигалось с юга на север, то F_к _op была бы направлена на восток - снова вправо относительно v'. В точке В , находящейся также в северном полушарии, тело движется на восток, а кориолисова сила направлена на юг - опять вправо относительно v'. В точке С, находящейся в южном полушарии, сила Кориолиса направлена влево относительно скорости v'.

Если тело движется на экваторе и с юга на север или с севера на юг, то F_кор = 0, так как ω|| v'. Если же тело на экваторе движется с запада на восток (точка D), то сила Кориолиса направлена вертикально вверх; при движении с востока на запад эта - сила направлена вертикально вниз. Таким образом, силы Кориолиса в северном полушарии Земли стремятся сместить движущееся тело вправо, а в южном полушарии - влево по отношению к скорости движения тела v'.

По этой причине в северном полушарии правые берега рек более размытые, чем левые, а в южном полушарии, наоборот, более размыты левые берега; в северном полушарии большую нагрузку испытывает правый рельс железной дороги, а в южном - левый рельс.

Силы Кориолиса оказывают действие на движущиеся корабли и самолеты. Они особенно значительны для самолетов, движущихся с большими скоростями, для ракет, спутников Земли и т.д. Кориолисовы силы оказывают отклоняющее действие на воздушные течения в атмосфере и водные течения в океанах. Эти силы вызывают поворот плоскости колебания маятника (опыт Фуко).

Действием силы Кориолиса объясняются многие интересные явления на Земле. Земля - шар, а не диск. Поэтому проявления сил Кориолиса сложнее. Эти силы будут сказываться как на движении вдоль земной поверхности, так и при падении тел на Землю.

Падает ли тело строго по вертикали? Не вполне. Только на полюсе тело падает строго по вертикали. Направление движения и ось вращения Земли совпадают, поэтому сила Кориолиса отсутствует. Иначе обстоит дело на экваторе; здесь направление движения составляет прямой угол с земной осью. Если смотреть со стороны северного полюса, то вращение Земли представится нам против часовой стрелки. Значит, свободно падающее тело должно отклониться вправо по ходу движения, т.е. на восток. Величина восточного отклонения, наибольшего на экваторе, уменьшается до нуля с приближением к полюсам.

Должны ли учитывать силу Кориолиса артиллеристы? Пушка Берта, из которой немцы вели обстрел Парижа во время первой мировой войны, находилась в 110 км от цели. Отклонение Кориолиса достигает в этом случае 1600 м. Это уже не маленькая величина.

Если летающий снаряд будет отправлен на большое расстояние без учета силы Кориолиса, то он значительно отклонится от курса. Этот эффект велик не потому, что велика сила (для снаряда в 10 т, имеющего скорость 1000 км/ч, сила Кориолиса будет около 25 кгс), а потому, что сила действует непрерывно длительное время.

Конечно, влияние ветра на неуправляемый снаряд может быть не менее значительным. Поправка к курсу, которая дается пилотом, обусловлена действием ветра, эффектом Кориолиса и несовершенством самолета.

Какие специалисты, кроме авиаторов и артиллеристов, должны принять эффект Кориолиса во внимание? К ним относятся, как ни странно, и железнодорожники. На железной дороге один рельс под действием кориолисовой силы истирается изнутри заметно больше другого. Даже ясно какой именно: в северном полушарии это будет правый рельс (по ходу движения), в южном - левый. Лишены хлопот по этому поводу лишь железнодорожники экваториальных стран.

Известно, что в район пониженного давления направляются потоки воздуха. Но почему такой ветер называется циклоном? Ведь корень этого слова указывает на круговое (циклическое) движение.

Так оно и есть - в районе пониженного давления возникает круговое движение воздушных масс. Причина заключается в действии силы Кориолиса. В северном полушарии все устремляющиеся к месту пониженного давления воздушные потоки отклоняются вправо по своему движению. Это приводит к отклонению дующих в обоих полушариях от тропиков к экватору ветров к западу.

Почему же такая небольшая сила играет такую большую роль в движении воздушных масс?

Это объясняется незначительностью сил трения. Воздух легко подвижен, и малая, но постоянно действующая сила приводит к важным следствиям.

Маятник Фуко . Представим себе маятник, помещенный над Северным полюсом Земли (рис.1.12) на длинном, свободно вращающемся подвесе. Отведем его от положения равновесия и дадим возможность свободно качаться. Маятник движется под действием силы тяжести и силы натяжения подвеса. Обе они лежат в плоскости качания маятника, следовательно,

плоскость качания должна сохранять свое положение в пространстве. Земля же поворачивается под маятником. Проекция плоскости качания на поверхность Земли у полюса поворачивается в направлении, противоположном вращению Земли, со скоростью 15° в час. Таким образом, в неподвижной системе отсчета поворот проекции плоскости качания маятника есть результат постоянства положения плоскости качания и вращения относительно нее Земли.

Рассматривая движение маятника в системе координат, связанной с Землей, к указанным выше силам нужно добавить силу Кориолиса. На полюсе скорость маятника v' при большой длине подвеса можно считать перпендикулярной оси вращения Земли и, следовательно, вектору угловой скорости ω. Сила Кориолиса, действующая на маятник, будет равна

F_K = 2mv' ω

Будучи перпендикулярна к плоскости, включающей векторы v' и ω, она лежит в горизонтальной плоскости и в соответствии с правилом буравчика направлена вправо от направления движения маятника. Плоскость качания

маятника должна поворачиваться по часовой стрелке (так как сила Кориолиса никакой другой силой не уравновешена) и совершать один оборот в сутки. На рисунке 1.13 показана розетка, которую очерчивает на горизонтальном листе бумаги перо, прикрепленное к маятнику.

Если опыт производится не на полюсе, а на широте φ, то, чтобы получить горизонтальную составляющую силы Кориолиса, надо взять составляющую угловой скорости в направлении вертикали данного места: ω_φ = ω sin φ. Тогда

F_Кφ = mv' ω sinφ

В этом случае плоскость качания повернется за сутки на угол 2л sinφ радиан.

Опыт Фуко, произведенный им в 1850 г. в Париже, явился непосредственным доказательством вращения Земли вокруг своей оси.

Другие проявления вращения Земли . Рассмотрим как наиболее простой случай движение поезда. Положим, поезд движется с юга на север вдоль меридиана в северном полушарии. Он переходит от точек Земли, имеющих большую окружную скорость v₁ (слева направо по движению поезда), к точкам, имеющим меньшую скорость v₂ . Сохраняя по инерции некоторое время скорость v₁ поезд ребордой колеса давит на правый рельс и этим способствует быстрому его снашиванию.

В системе отсчета, связанной с Землей, на поезд действует сила Кориолиса. Величину ее горизонтальной составляющей можно найти, взяв проекцию угловой скорости вращения Земли на вертикаль данного места:

F_K = 2mv' ω sin φ

Направлена сила всегда вправо по ходу поезда. Поэтому на двухколейных железных дорогах износ правого рельса происходит быстрее, чем левого. Заметим, что сила Кориолиса проявляется при движении и под углом к меридиану или вдоль параллели. При движении вдоль параллели кориолисова сила направлена от оси вращения Земли, если поезд движется на восток, и к оси, если он движется на запад. Проекция силы на горизонтальную плоскость в этом случае:

F_K = 2mv' ω sinφ

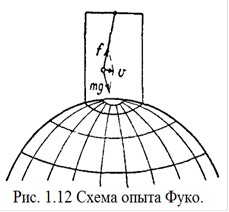
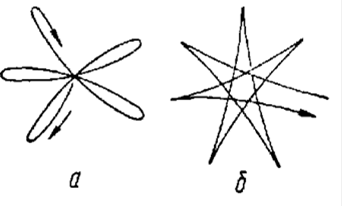
Рис. 1.13 Розетка, полученная при записи качаний маятника во вращающейся системе: а – запись начинается при движении от положения равновесия; б – запись начинается при движении от положения наибольшего отклонения.

Отклоняющее влияние кориолисовой силы заставляет мощное океаническое течение Гольфстрим, выходящее из Мексиканского залива через Флоридский пролив в направлении, близком к меридиональному, отойти от берегов

Америки, пересечь Атлантический океан и выйти в Баренцево море у берегов Скандинавии.

Так называемые дрейфовые (ветровые) течения вследствие отклоняющего влияния силы Кориолиса всегда образуют некоторый угол с направлением вызвавшего их ветра.

Сильно нагретый в зоне экватора воздух поднимается вверх и движется к полюсам. Охлаждаясь на высоте, воздух на широтах 25-30° устремляется вниз, образуя так называемые субтропические области высокого давления. От этих областей по направлению к экватору дуют постоянные ветры, называемые пассатами. Под влиянием силы Кориолиса они отклоняются от меридионального направления и дуют в северном полушарии с северо-востока на юго-запад, а в южном - с юго-востока на северо-запад.

Во всех приведенных выше примерах рассматривается влияние на движение тел в системе отсчета, связанной с Землей, вращения Земли вокруг собственной оси. Строго говоря, нужно было бы еще рассмотреть и влияние движения Земли по орбите вокруг Солнца. Однако это влияние настолько мало, что им вполне можно пренебречь даже в описании явлений таких масштабов, как атмосферные и океанические течения.

Спираль Экмана. Течение Гольфстрим

В 1893-1896 годах норвежский исследователь Арктики Ф. Нансен во время дрейфа во льдах Северного океана на судне "Фрам" заметил, что при постоянном ветре дрейф происходит не в направлении ветра, а под углом 20-40° направо от него. Нансен сам дал качественное объяснение этому явлению: кроме ветрового напряжения на течение действует и ускорение Кориолиса. Напомним, оно вызвано вращением Земли с угловой скоростью ω = 7,3 *10^-5 с^-1 , направлено перпендикулярно скорости направо в Северном полушарии и налево в Южном, а по величине равно 2ωvsin ϕ.

В 1905 году шведский ученый В. Экман создал теорию ветрового течения в открытом глубоком океане. Как удивительно поворачивается течение в глубине (рис.1.13) под действием силы Кориолиса" Вот формулы, описывающие эту спираль Экмана. Если ветер направлен по оси у, то вектор скорости течения (V_x , V_y ) на глубине z равен:

Нижний знак относится к Южному полушарию.

Поверхностная скорость v₀ по величине примерно такая же, как и в случае мелкой воды, но направлена она под углом 45° к направлению ветра, направо в Северном полушарии и налево в Южном. Вектор скорости при углублении поворачивается. На глубине z= З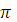/4kон направлен уже против ветра! Скорость течения там равна V₀ ехр {-Зπ/4} = 0,095 v₀ . На глубине π/k вода течет в сторону, противоположную поверхностному течению со скоростью V₀ ехр {-π} = 0,043 V₀

Параметр kопределяет характерную глубину, на которой происходит поворот течения и затухание его скорости. Он зависит от географической широты ϕ и численно равен

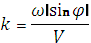
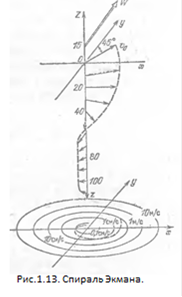
При скорости ветра W=10 м\с поверхностная скорость течения в океане порядка 0,1 м/с, а глубина, на которой течение поворачивает вспять, порядка 100 м. Число Рейнольдса океанической турбулентности при такой скорости ветра порядка 10⁷ . Турбулентность эффективно перемешивает океан в поверхностном слое глубиной около ста метров, в этом же слое происходит перенос водных масс течениями.

Достоинство теории Экмана в том, что она дает разумную физическую картину и верную оценку характерных скоростей и глубин. Но это, конечно, очень идеализированная схема. Она не применима, в частности, вблизи экватора, где ускорение Кориолиса, а вместе с ним и параметр kобращаются в нуль.

Если просуммировать по глубине потоки жидкости в спирали Экмана, то окажется, что полный поток направлен по оси х, прямо перпендикулярно направлению ветра! И полный поток каждого из пассатных течений, поток, просуммированный по глубинам, тоже направлен не точно на запад, но имеет составляющую, направленную от экватора. Для компенсации этих оттоков на экваторе происходит подъем глубинных вод. Поскольку на глубине вода холодная, то температура поверхностных вод на экваторе оказывается на 2-3 градуса холоднее, чем температура со - соседних тропических вод. Экваториальная область океанов - относительно холодное место нашей планеты! Медленный подъем океанских вод в специальной литературе называют апвеллингом, опускание-даунвеллингом, не переводя соответствующие английские слова upwelling и downwelling. Кроме экваториального апвеллинга, подъем или опускание вод происходит у берегов больших водоемов при касательном к берегу направлении ветра. Примеры таких течений показаны на рис.1.15.

Это тоже проявление кориолисовых сил, направляющих полный поток жидкости, как и в спирали Экмана, перпендикулярно направлению ветра. Когда пассатные течения подходят к шельфу - подводному краю континентов - им приходится и у поверхности поворачивать от экватора. Так начинаются мощные течения средних широт: Гольфстрим (англ.”течение залива”) и Бразильское течения в Атлантике, Куросио и Восточно-Австралийское течения Тихого океана, Мадагаскарское течение Индийского океана. Основная движущая сила этих течений уже не ветер, а напор воды у континентов. Уровень воды океана в Атлантике в Мексиканском заливе на 60 см выше, чем у Африки, а в Тихом океане разница уровней между западным и восточным его берегами достигает 70 см. Создается такой нагон пассатными ветрами. Но структура течений средних широт уже не ветровая: они прослеживаются в океане до глубины в полтора-два километра и только еще глубже можно обнаружить слабое противотечение.

Но и ветры, особенно на широтах 40-50°, тоже подгоняют, усиливают эти течения. К тридцатиградусным широтам они расположением континентов и силами Кориолиса отворачиваются на северо-запад, а на широтах 40-50° начинают течь и прямо на запад. Вот тут-то их снова усиливают ветры, дующие с юго-востока в Северном полушарии и с северо-востока в Южном. Особенно мощным становится направленное на запад Антарктическое циркумполярное течение - вбирающее в себя течения средних широт всех океанов, почти не имеющее на своем пути континентальных препятствий и подгоняемое северо-западными ветрами. Наконец, в Северном Ледовитом океане под действием северо-восточных ветров третьей, полярной ячейки Хэдли возникает почти круговое Западное Арктическое течение. В Южном полушарии у него есть слабый аналог у самого побережья Антарктиды.

Такова глобальная картина океанских течений, она логично следует из карты ветров и карты континентов. Но вот какой еще вопрос тревожит. И ветры Земли, и течения океана значительно отклоняются вращением планеты, силами Кориолиса. Спрашивается, ну а ветры и течения сами как влияют на вращение Земли, не тормозят ли его? Вопрос кажется очень сложным. Но ответ на него прост, - нет. И ветры, и течения вызваны падающим на Землю излучением Солнца. Оно дает энергию движениям атмосферы и океана. Эта энергия диссипируется, переходит в тепло, при этом действительно возникают силы трения. Однако эти силы - внутренние. Для каждой такой силы, замедляющей вращение планеты, по третьему закону Ньютона найдется равная и противоположно направленная сила, вращение Земли ускоряющая. Суммарный момент всех внутренних сил равен нулю. Солнечное излучение не изменяет момента количества движения Земли - ветры и течения в среднем не замедляют Землю и не ускоряют ее.

Заключение

Введение сил инерции вызывает различные толкования, и при изучении их возникают трудности, поэтому приводятся основные рассуждения.

1. Нет сил инерции. В неинерциальной системе отсчета несправедливы первый и второй законы динамики, силы взаимодействия тел еще не определяют ускорение тела. Поэтому необходимо, сначала произвести динамический анализ движения данного тела относительно инерциальной системы отсчета. После того, как найдено движение тела относительно этой системы, можно по законам кинематики определить его движение и в неинерциальной системе отсчета.

2. Есть силы инерции. В этом случае формально справедливы первый и второй законы динамики, поэтому можно произвести динамический анализ движения тела прямо относительно неинерциальной системы отсчета, для этого необходимо к силам взаимодействия, действующим на данное тело, прибавить еще силы инерции. При поступательном движении неинерциальной системы силы инерции одинаковы во всех точках этой системы отсчета и не зависят от скорости движения тела относительно нее. Во вращающейся системе отсчета силы инерции различны в разных точках неинерциальной системы (центробежные силы) и зависят от относительной скорости движения (кориолисовьг силы).

Физический смысл сил инерции только в том, что они учитывают ускорение тела, равномерно и прямолинейно движущегося относительно неинерциальной системы отсчета, - ускорение, имеющее место вследствие ускоренного движения системы отсчета. Прибавление сил инерции к внешним силам, действующим на тело, равносильно вычитанию из суммы внешних сил той их части, которая определяет центростремительное и кориолисово ускорение тела (в случае вращающейся системы отсчета) или ускорение неинерциальной системы отсчета (при поступательном ее движении). Оставшаяся часть внешних сил определяет ускорение относительно неинерциальной системы отсчета.

Проявление сил инерции на Земле играет важнейшую роль, как в построении физической картины мира, так и в жизни самих жителей нашей планеты. Из проделанной работы становится ясно понятно, что силы инерции не стоит оставлять без внимания, их необходимо учитывать в различных сферах деятельности. А также необходимо включить в курс средней школы понятия "неинерциальной системы отсчета" и "силы инерции", что позволит повысить уровень систематизации знаний и даст возможность рассматривать с более глубоких научных позиций происходящие физические явления, а это, в свою очередь, будет способствовать формированию у школьников целостных представлений о современной физической картине мира.

Список литературы

1. Александров, В.Н. Курс общей физики. Механика /В.Н. Александров, А.Я. Яшкин. - М.: Просвещение, 1978. - 210 с.

2. Архангельский, М.М. Курс физики. Механика / М.М. Архангельский. - М.: Просвещение, 1965. - 123 с.

3. Детлаф, А.А. Курс физики. Механика. Основы молекулярной физики и термодинамики / А.А. Детлаф, Б.М. Яворский, Л.Б. Милковская. - 4-е изд. испр. и допл. - М.: Высшая школа, 1973. - 135 с.

4. Сивухин, Д.В. Общий курс физики. Механика / Д.В. Сивухин. - М.: Просвещение, 1979. - 357 с.

5. Стрелков, С.П. Общий курс физики. Механика / С.П. Стрелков. - М.: Наука, 1975. - 152 с.

6. Ландау, Л.Д. Физика для всех. Физические тела / Л.Д. Ландау, Ф.И. Китайгородский. - М.: Наука, 1984. - 73 с.

7. Бялко, А.В. Наша планета - Земля / А.В. Бялко. - М. : Наука, 1983. - 150 с.