Міністерство освіти і науки України
Національний авіаційний університет
Інститут аеропортів
Кафедра комп’ютерних технологій будівництва
Розрахунково-графічна робота №1
Виконав: ст. групи ІАП 308
Шепа В. В.
Перевірив: Яковенко І. А.
Київ 2010р.
Задача №1
Визначення об’ємного напруженого стану в точці тіла
Для напруженого стану в точці тіла задано 6 компонентів:
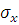 =65 кН; =65 кН;  кН; кН;
 кН; кН;  кН; кН;
 ; ;  кН; кН;
Необхідно знайти зн-ня головних напружень та положення головних площадок.
Рішення:
 (1.1) (1.1)
1.З р-ня (1.1) коефіцієнти є інваріантами перетвор. Координат

Р-ня (1.1) підстановкою  зводимо до наступного вигляду: зводимо до наступного вигляду:
 ; (1.3) ; (1.3)
У р-ні (1.3) нові коефіцієнти відповідно дорівнюють:
P= (1.4) (1.4)
q= - 

Корені кубічного рівняння (1.3) виражаємо через допоміжний кут  , який визначаємо з р-нь: , який визначаємо з р-нь:
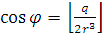 = = r= r= =78,12; =78,12;

 (1.4) (1.4)

Перевірка:
 =0; =0;
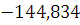 + + + +
2. Визначимо головні напруження за формулою:

 (1.7) (1.7)

Цим трьом головним напруженням в подальшому робимо наступне позначення  : :  . .
 кН, кН,
 кН, кН,
 кН, кН,
Контроль якості вирішення кубічного рівняння (1.1) проводимо, використовуючи інваріантність коефіцієнтів  так щоб: так щоб:

 

3.З системи 1.9 з трьох рівнянь тільки 2 невідомих  і і  із рішення двох рівнянь третє використовується для перевірки знайдених відношень. Запишемо рішення системи 1.9 в загальному вигляді: із рішення двох рівнянь третє використовується для перевірки знайдених відношень. Запишемо рішення системи 1.9 в загальному вигляді:




Значення співвідношення
 ; ; 
і з цього рівняння знаходимо 2 корені 
Перевірка:
-65(-1,42608)+65(-0,751526)+(65-144,83)=0.
З р-ня 1.1 маємо:

 . .
Тоді:



 м. м.

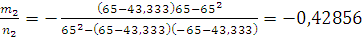 ; ;


Тоді:  




Тоді:  
Перевірка напрямних косинусів:
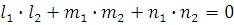 ; ;
-0,75183+(-0,3962)

Рис.1.3
На рисунку 1.3 зображено нормалі до головних площадок  , ,  головні площадки та головні напруження головні площадки та головні напруження  . .
Задача №2
Плоска задача теорії пружності
Нехай задано прямокутну балку довжиною l, висотою h та товщиною, що дорівнює 1.
Необхідно:
· Перевірити можливість використовувати ф-ї f=(x, y) для рішення плоскої задачі теорії пружності.
· Знайти вирази для напружень 
· Побудувати епюри напружень  для перерізів x= для перерізів x=
· Визначити внутрішні сили (нормальні та дотичні, які прикладені до всіх чотирьох граней балки, дати їх зображення на рисунку.
· Виконати статичну перевірку для знайдених сил (зовнішні).
Теоретичні відомості:
Ф-я f=(x, y) повинна задовольняти наступне дегармонічне рівняння.
 (2.1) (2.1)
З цього рівняння вирази для напружень  знаходимо за формулою: знаходимо за формулою:

 (2.2) (2.2)
Для визначення зовнішніх сил нормальних та дотичних, які прикладені до всіх чотирьох граней балки, використовуєм умови на поверхні тіла (умови на контурі тіла або статичні і граничні умови).
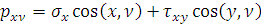 (2.2) (2.2)

У рівнянні (2.3 )  - проекції на вісі Ox і Oy внутрішніх сил, що діють на грані балки. - проекції на вісі Ox і Oy внутрішніх сил, що діють на грані балки.
 - нормаль до грані, - нормаль до грані,  - напрямні косинуси нормалі - напрямні косинуси нормалі 
Для перевірки знайдених зовнішніх сил можна використовувати умови рівноваги балки під їх дією:



Рішення:
1.Нехай задана балка з ф-ю напруження:

a=2, b=1, l=5, 

 2ay; 2ay;

 0; 0;
 ; ;
 ; ;


2. ; ;
 2ay; 2ay; 
3. Побудуємо епюри напружень в перерізах.

При x= =2,5 м. =2,5 м. 
 2ay=4y; 2ay=4y; 
4. Визначимо зовнішні сили (нормальні та дотичні).
Верхня грань:
y= 
 ; ;
 ; ;
 ; ;
2. Нижня грань:
y= 
 ; ;
 ; ;
 ; ;
l=0; l=5.
Ліва грань: x=0;
 
 ; ;
 ; ;
 ; ;
l=- ; l= ; l= . .
Права грань:x=l=5 м
 
 ; ;
 ; ;
 ; ;
l= - ; l= ; l=

5. Перевіримо умови рівноваги балки:


 + + + + =0. =0.
Отже, умови рівноваги балки зберігаються, а значить зовнішні сили та напруження в перерізах знайдені правильно.
Для визначення зовнішніх сил нормальних та дотичних, які прикладені до всіх чотирьох граней балки, я використала умови на поверхні тіла (умови на контурі тіла або статичні і граничні умови).
Побудувала епюри напружень в перерізах, визначила зовнішні сили (нормальні та дотичні). Перевірила умови рівноваги балки.
Міністерство освіти і науки України
Національний авіаційний університет
Інститут аеропортів
Кафедра комп’ютерних технологій будівництва
Розрахунково-графічна робота №2
Виконав: ст. групи ІАП 308
Шепа В. В.
Перевірив: Яковенко І. А
Київ 2010р.
Задача №1
Изгиб прямоугольной пластинки
Прямоугольная пластинка изгибается под действием поперечной нагрузки интенсивности q (x, y):
 ; ;

Задано уравнение упругой поверхности пластинки
 ; ;
C=const; a=4 м, b=2 м,  =0,21. =0,21.
Жесткость пластинки D=const. Требуется: установить, каким граничным условиям удовлетворяет предложенное уравнение упругой поверхности w(x,y); определить постоянный коэффициент C; составить выражения моментов и поперечных сил, построить эпюры моментов и поперечных сил в сечении 
Решение:
1. Определяем условия на контуре пластинки (граничные условия):
При x= a w=0; a w=0;
y= w=0; w=0;
Следовательно, пластинка оперта по всем четырем краям. Выясним, как она оперта: шарнирно или жостко. Уравнение углов поворота в направлении, паралельном Ox,
 =C =C
При x=
Это значит, что левый и правый края защемлены.
Уравнение углов поворота в направлении, параллельном  , ,
 =-C =-C ; ;
При y=
Получаем, что верхний и нижний края тоже защемлены. Итак, пластинка жестко защемлена по всем четырем краям.
2. Определяем постоянную С. Для этого воспользуемся уравнением и составим соответствующие производные:
 ; ;
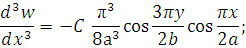
 ; ;
 =C =C ; ;
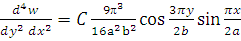 ; ;
 ; ;
 ; ;
 ; ;
 ; ;

Левая часть уравнения принимает следующий вид
D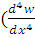 +2 +2 ; ;
DC ; (4.2) ; (4.2)
Подставив в уравнение левую и правую части, после сокращений получаем

3. Составляем выражение для внутренних усилий по формулам:
Изгибающие моменты:


Крутящий момент:

Поперечные силы:




 ; ;

 ( (
Выражения для внутренних усилий с учетом найденного значения С имеют вид



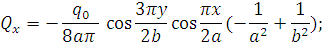


Отже, я побудував епюри моментів і поперечних сил, знайшов граничне значення напруги, що задовольняє рівнянням пружної поверхні  , ,  визначив постійний коефіцієнт C; склав вираз моментів і поперечних сил , побудував епюри моментів і поперечних сил в розрізі визначив постійний коефіцієнт C; склав вираз моментів і поперечних сил , побудував епюри моментів і поперечних сил в розрізі  Склав вираз для внутрішніх зусиль. Склав вираз для внутрішніх зусиль.
|