Дипломная работа: Линейные дифференциальные уравнения
|
Название: Линейные дифференциальные уравнения Раздел: Рефераты по математике Тип: дипломная работа |
Содержание 1.1 Предварительные определения и обозначения 1.2 Линейные однородные системы 1.3 Неоднородные линейные системы 1.4 Линейные системы с постоянными коэффициентами 1.5 Линейные системы с периодическими коэффициентами 2. Линейные дифференциальные уравнения 2.1 Линейные дифференциальные уравнения порядка n 2.2 Линейные уравнения с аналитическими коэффициентами 2.3 Асимптотическое поведение решений некоторых линейных систем ВведениеПри изучении физических явлений часто не удается непосредственно найти законы, связывающие физические величины, но сравнительно легко устанавливается зависимость между теми же величинами, их производными или дифференциалами. Таким образом, большинство физических явлений описывается на языке дифференциальных уравнений, содержащих неизвестные функции под знаком производной или дифференциала. В работе рассматриваются понятия простейших дифференциальных уравнений, а также линейных дифференциальных уравнений произвольного порядка и систем таких уравнений. Особое внимание уделяется изучению линейных дифференциальных уравнений с постоянными коэффициентами и систем линейных уравнений. Решением дифференциального уравнения называется n раз дифференцируемая функция Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительные условие: например, потребовать, чтобы решение принимало в данной точке данное значение. Задача нахождения решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений, удовлетворяющего некоторым начальным условиям, называется задачей Коши. Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для обыкновенных дифференциальных уравнений, методы решения простейших обыкновенных дифференциальных уравнений , качественное исследование решений обыкновенных дифференциальных уравнений без нахождения их явного вида. Цель дипломной работы – изучить понятие линейных дифференциальных уравнений. В связи с поставленной целью необходимо выполнить следующие задачи: 1) Рассмотреть понятие линейных систем; 2) Изучить линейные дифференциальные уравнения различных порядков, в том числе с аналитическими коэффициентами; 3) Решить предложенные практические задания. 1. Линейные системы1.1 Предварительные определения и обозначенияПусть А = (aij ) – квадратная матрица порядка n, где aij – комплексные числа. Определим норму А следующим образом:
Если n-мерный вектор х представлять как матрицу с n строками и одним столбцом, то норма вектора совпадает с нормой x, определенной по формуле (1). Легко видеть, что норма обладает следующими свойствами: (I) |A+B| (II) |AB| (III) |Ax| где А и В – матрицы, х – n-мерный вектор. По определению, расстояние между двумя матрицами А и В равно |A-B|, и это расстояние удовлетворяет обычным свойствам метрики. Нулевая матрица будет обозначаться через О, единичная – через Е. В случае опасности смешения размерностей эти квадратные матрицы порядка n будут обозначаться соответственно через Оn и Еn . Заметим, что | Оn | = 0 и | Еn | = n, а не 1. Комплексно сопряженной матрицей для А = (aij
) называется матрица Если det А = 0, то матрица А называется особой. Не особая матрица имеет обратную матрицу А-1 , которая удовлетворяет соотношениям А А-1 = А-1А = Е. Многочлен det (λЕ-А) степени n от λ называется характеристическим многочленом для матрицы А, а его корни – характеристическими корнями А. Если эти корни обозначены λi (i = 1, …, n), то det (λЕ-А) = Две квадратные матрицы А и В порядка n называются подобными, если существует Неособая квадратная матрица Р порядка n, такая что В = РАР-1. Если А и В подобны, то они имеют один и тот же характеристический многочлен, ибо det (λЕ-В) = det (Р(λЕ-А)Р-1 )= det Р* det (λЕ-А)* det Р-1 = det (λЕ-А). В частности, коэффициенты многочлена det (λЕ-А) при степенях λ инвариантны относительно преобразования подобия. Два наиболее важных инварианта - det А и sp A – определитель и след А соответственно. Приведем следующий фундаментальный результат о канонической форме матрицы. Теорема 1.1 Каждая квадратная матрица А порядка n и подобная матрица вида
где J0 – диагональная матрица с элементами λ1 , λ2 ,…, λq и
Здесь λj , j = 1, …, q+s, - характеристические корни А, не обязательно различные. Если λj – простой корень, то он встречается в J0 и поэтому, если все корни различны, А подобна диагональной матрице
Из теоремы 1.1 непосредственно следует, что det А = где произведение и сумма распространены на все корни, причем каждый корень считается столько раз, каков а его кратность. Матрицы Ji имеют вид Ji = λq + i Еri +Zi , где Ji – квадратная матрица порядка ri и
Матрицы Ji можно представить также в виде λq + i Еri +γZi , где γ – любая постоянная, отличная от нуля. Последовательность матриц {Аm } имеет своим пределом А, если для любого ε > 0 существует такое целое число N, что при p, q > N |Aq - Ap | <ε. Очевидно, что последовательность {Аm } сходится в том и только в том случае, когда сходится каждая из последовательностей компонент, а отсюда следует, что {Аm } сходится в том и только в том случае, когда существует предельная матрица, к которой и сходится эта последовательность. Бесконечный ряд
называется сходящимся, если сходится последовательность частных сумм, а суммой ряда называется предельная матрица для частных сумм. Важное значение при изучении линейных уравнений имеет специальный ряд, который называется экспонентной матрицей А, а именно:
где Аm есть m-я степень А. Ряд, определяющий еА , сходится для всех А, июо для любых положительных целых p и q
а последнее выражение есть разность Коши для ряда еА , сходящегося для всех конечных |A|. Далее, |еА
| Для матриц, вообще говоря, равенство еА+В = еА еВ неверно. Это равенство верно, если А и В коммутируют. Далее будет показано, что det еА = еsp А , (1.4) и поэтому еА есть неособая матрица для всех А. Так как –А коммутирует с А, то е-А = (еА )-1 . Каждая матрица А удовлетворяет своему характеристическому уравнению det (λЕ-А) = 0, и это замечание часто бывает полезно для эффективного вычисления еА . Пусть В – неособая матрица. Покажем, что существует матрица А (называемая логарифмом В), такая, что еА = В. В самом деле, если в имеет каноническую форму J теоремы 1, то А, очевидно, можно представить в виде
при условии, что еА i = Jj , j = 0, 1, …, s. Легко также проверить, что А0 можно представить в виде
Далее,
где Zj – нильпотентная матрица, определенная в теореме 1.1. так как высшие степени Zj равны нулю, то ряд
содержит лишь конечное число членов и поэтому сходится. Положим, по определению, сумму этого ряда, который на самом деле является многочленом от
Таким образом,
есть многочлен от
(|x| < 1) следует после приведения справа подобных членов, коэффициенты при хk
, k
Отсюда легко получаем, что Аj можно представить в виде
Пользуясь тем, что для каждой матрицы М (PMP-1 )k = PMk P-1 (k = 1, 2, …), нетрудно видеть, что
Отсюда следует, что результат, полученный для канонической матрицы В, переносится на произвольную неособую матрицу В. В самом деле, если J = eA
и B = PJP-1
, то В = Если Ф – произвольная квадратная матрица порядка n из функций, определенная на действительном i-интревале I (элементы матрицы могут быть действительными или комплексными функциями), то Ф называется непрерывной, дифференцируемой ли аналитической на I, если все элементы Ф соответственно непрерывны, дифференцируемы или аналитичны на I. Если Ф на I дифференцируема, то через
и, вообще говоря, Если в точке t производная матрица
где
Если матрица А на t-интервале Iнепрерывна и Ф удовлетворяет уравнению
а в интегральной форме
1.2 Линейные однородные системыПусть А – непрерывная квадратная матрица порядка n, элементами которой служат непрерывные комплексные функции, определенные на t-интервале I. Линейная система
Называется линейной однородной системой порядка n. Для любого ξ и для τ
где m интегрируема по Лебегу на I, то существует единственное решение φ системы (ЛО), удовлетворяющее условию φ(τ) = ξ. В дальнейшем будем полагать, что для А выполняется по крайней мере условие (*). Нулевая вектор-функция на I является решением системы (ЛО). Это решение называется тривиальным. Если решение системы (ЛО) равно нулю для некоторого Теорема 2.1. Множество всех решений системы (ЛО) на интервале I образует n-мерное векторное пространство над полем комплексных чисел. Доказательство. Если φ1 и φ2 – решения (ЛО) и с1 , с2 – комплексные числа, то с1 φ1 + с2 φ2 также является решением (ЛО). Это показывает, что решения образуют векторное пространство. Чтобы доказать, что это пространство n-мерно, следует показать, что существует n линейно зависимых решений φ1
, φ2
, …, φn
, таких, что каждое другое решение системы (ЛО) есть линейная комбинация (с комплексными коэффициентами) этих φi
. Пусть ξi
, i=1, 2, …, n – линейно независимые векторы n-мерного х-пространства. Например, за ξi
можно взять вектор со всеми компонентами, равными нулю, кроме i-й, которая равна 1. Тогда, по теореме существования, если Если бы решения φi были линейно зависимы, то существовали бы n комплексных чисел , не равных одновременно нулю и таких, что
Отсюда следует равенство
противоречащее предположению о том, что векторы ξi линейно независимы. Если φ – некоторое решение (ЛО) на I, такое, что φ(τ)=ξ , то можно найти (единственным образом определенные) постоянные сi , удовлетворяющие равенству
ибо векторы ξi образуют базис n-мерного х-пространства. Поэтому функция
есть решение (ЛО), принимающее при t = τ значение ξ, и, следовательно, в силу теоремы единственности
Итак, каждое решение φ есть (единственная) линейная комбинация φi и теорема 2.1 полностью доказана. Всякое множество φ1 , φ2 , …, φn линейно зависимых решений системы (ЛО) называется базисом или фундаментальным множеством решений системы (ЛО). Если Ф – матрица, n столбцов которой являются n линейно независимыми решениями (ЛО) на I, то Ф называется фундаментальной матрицей системы (ЛО). Очевидно, Ф удовлетворяет матричному уравнению
Под матричным дифференциальным уравнением, соответствующим системе (ЛО) на I, подразумевается задача отыскания квадратной матрицы Ф порядка n, столбцы которой являются решениями системы (ЛО) на I. Эта задача обозначается так:
Матрица Ф называется решением задачи (2.2) на I, и Ф удовлетворяет уравнению (2.1). Из теоремы 2.1. следует, что зная фундаментальную матрицу системы (ЛО), которая является, разумеется, частным решением уравнения (2.2), мы будем знать полную систему решений системы (ЛО). Теорема 2.2. Для того, чтобы решение-матрица уравнения (2.2) была фундаментальной матрицей, необходимо и достаточно, чтобы det Ф(t) Замечание. Если det Ф(t) Доказательство теоремы 2.2. Пусть Ф – фундаментальная матрица, столбцами которой являются векторы φj , и пусть φ – некоторое нетривиальное решение системы (ЛО). В силу теоремы 2.1 существуют единственным образом определенные постоянные с1 , с2 , …, сn , не равные все нулю и такие, что
или, выражая при помощи матрицы Ф,
где с – вектор-столбец с элементами с1
, с2
, …, сn
. Это соотношение при каждом Наоборот, пусть Ф – матрица-решение уравнения (2.2) и пусть det Ф(t) Матрица из векторов-столбцов может иметь определитель, тождественно равный нулю на интервале I, даже при линейно независимых векторах. Например, пусть
для каждого действительного интервала I. Содержание теоремы 2.2 состоит в том, что этого не может случиться для векторов, которые являются решениями системы (ЛО). Теорема 2.3. Если Ф – фундаментальная матрица для системы (ЛО) и С – (комплексная) постоянная неособая матрица, то ФС также является фундаментальной матрицей системы (ЛО). Каждая фундаментальная матрица системы (ЛО) может быть представлена в такой форме при помощи некоторой неособой матрицы С. Доказательство. Из (2.1), если Ф – фундаментальная матрица, вытекает, что
Или
и, следовательно, ФС есть матрица-решение уравнения (2.2). Так как det (ФС)=( det Ф)( det С) то ФС – фундаментальная матрица. Наоборот, если Ф1
и Ф2
– две фундаментальные матрицы , то Ф2
= Ф1
С, где С – некоторая постоянная неособая матрица. Для доказательства этого положим Ф1
-1
Ф2
= Ψ(t). Тогда Ф2
= Ф1
Ψ. Дифференцируя это равенство, получим, что Замечания. Если предполагать, что Ф2 – решение, то матрица С может быть особой. Заметим, что если Ф – фундаментальная матрица системы (ЛО) и С – постоянная неособая матрица, то СФ, вообще говоря, не является фундаментальной матрицей. Две различные однородные системы не могут иметь одну и ту же фундаментальную матрицу, ибо из уравнения (ЛО) следует, что Сопряженные системы. Если Ф - фундаментальная матрица для системы (ЛО), то
или, переходя к сопряженным матрицам,
Поэтому
Система (2.3) называется сопряженной для системы (ЛО) и матричное уравнение
называется сопряженным для уравнения (2.2.). Это соответствие симметрично, ибо (ЛО) и (2.2) сопряжены (2.3) и (2.4) соответственно. Теорема 2.4. Если Ф - фундаментальная матрица для системы (ЛО), то Ψ есть фундаментальная матрица для сопряженной системы (2.3) в том и только в том случае, когда
где С – постоянная неособая матрица. Доказательство. Если Ф - фундаментальная матрица для системы (ЛО) и Ψ есть фундаментальная матрица системы (2.3), то так как
где в – некоторая постоянная неособая матрица (теорема 2.3). Поэтому
и можно принять С = D* . Наоборот, если Ф - фундаментальная матрица для сопряженной системы (ЛО) и удовлетворяет (2.5), то Если А = - А*
, то
где С – постоянная неособая матрица. Из уравнения (2.6), в частности, следует, что эвклидова длина каждого вектора-решения системы (ЛО) постоянна. Понижение порядка однородной системы. Если известно m (0<m<n) линейно зависимых решений системы (ЛО), то можно понизить порядок системы на m единиц, и следовательно, дело сведется к решению линейной системы порядка n-m. Предположим, что φ1
, φ2
, …, φm
- m линейно независимых векторов, которые являются решениями системы (ЛО) на интервале I. Пусть вектор φj
имеет компоненты φij
(i = 1, …, n). Тогда ранг прямоугольной матрицы с элементами φij
(i = 1, …, n; j = 1, …, m) для каждого Пусть матрица U имеет своими первыми m столбцами векторы φ1
, φ2
, …, φm
и своими n-m столбцами – векторы еm+1
, …, en
, где ej
– вектор-столбец со всеми нулевыми элементами, кроме j-го, который равен 1. Очевидно, что U – неособая матрица на x = Uy. (2.7) Заметим, что решениям х = φj (j = 1, …, m) при подстановке (2.7) соответствуют решения y = ej (j = 1, …, m). Поэтому подстановку (2.7) можно рассматривать как систему относительно y, которая должна иметь решения ej (j = 1, …, m). Подставляя (2.7) в систему (ЛО), получаем
или в координатах,
Выражая то обстоятельство, что векторы φj с компонентами φi j являются решениями системы (ЛО), получаем
откуда следует, что
Так как det Фm
т.е. линейную систему порядка n-m. Рассуждая в обратном порядке, предположим, что
(i = 1, …, m; p = m+1, …, n). Пусть Ф=U Ψ, то Ф есть матрица-решение (ЛО) на I. U – неособая матрица. Так как det Теорема 2.5. Пусть φ1
, φ2
, …, φm
(m < n) – m известных линейно независимых решений системы (ЛО), причем φj
(j = 1, …, m) имеют компоненты φi
j
(i = 1, …, n). Предположим, что определитель матрицы с элементами φi
j
(i, j = 1, …, m) на некотором подинтервале Избавимся теперь от ограничения, что матрица Фm
неособая на некотором интервале. Ясно, что прямоугольная матрица с элементами φi
j
(i = 1, …, n; j = 1, …, m) имеет ранг m в силу независимости решений φj
(j = 1, …, m). Таким образом, для каждого t = t0
существует неособая квадратная матрица порядка m, которую мы получим, выбирая m строк i1
, …, im
из прямоугольной матрицы с n строками и m столбцами. В силу непрерывности эта матрица неособая на некотором интервале Хорошо известно и легко доказывается, что существует такая постоянная неособая матрица Т, применив которую к любому вектору х с n компонентами, получим матрицу Тх, имеющую своим m первыми компонентами компоненты вектора х с номерами i1
, …, im
. Полагая 1.3 Неоднородные линейные системыПусть А – неособая квадратная матрица порядка n из непрерывных функций, определенных на действительном t-интервале I и b – непрерывный вектор на I, не равный тождественно нулю. Система уравнений
называется линейной неоднородной системой порядка n. Если элементы А и b непрерывны и даже измеримы и мажорируются суммируемой функцией на I, то существует единственное решение φ системы (ЛН), для которого φ(τ) = ξ , где Если известна фундаментальная матрица Ф системы (ЛО), то легко найти решение системы (ЛН). Теорема 3.1. Если Ф - фундаментальная матрица для системы (ЛО), то функция
есть решение системы (ЛН), удовлетворяющее начальному условию φ(τ) = 0 ( Доказательство получается непосредственно при помощи прямой проверки. Интуитивные соображения, с помощью которых можно получить выражение (3.1), заключаются в следующем6 для каждого постоянного вектора с функция Фс является решением системы (ЛО). Метод состоит в том, что мы рассматриваем с как функцию, определенную на I, и находим, какой должна быть с (если она существует), для того, чтобы функция φ = Фс была решением неоднородной системы (ЛН). Пусть φ = Фс – решение системы (ЛН). Тогда
где последнее равенство следует из (ЛН). Поэтому Ф
Последнее уравнение всегда разрешимо, причем если с(τ) = 0, то
Итак, φ определяется по формуле (3.1). Легко видеть, что в условиях теоремы 3.1 решение системы (ЛН), удовлетворяющее условию φ(τ) = ξ (
где φh (τ) = ξ . Формула (3.1) (или (3.2)) называется формулой вариации постоянных для системы (ЛН). Заметим, что формулу (3.1) можно записать в виде
где Ψ – фундаментальная матрица системы
сопряженной системе (ЛО). Другая форма записи формулы (3.1) такова:
однако здесь необходимо ограничение 1.4 Линейные системы с постоянными коэффициентамиПусть А – постоянная квадратная матрица порядка n и рассмотрим соответствующую однородную систему
Если n = 1, то (4.1) имеет очевидное решение еt А , и решение, которое при t = τ равно ξ , имеет вид е( t -τ)А ξ . Оказывается, что решение имеет эту форму и в том случае, когда х, ξ являются векторами произвольной конечной размерности и А – квадратная матрица порядка n. Теорема 4.1. Фундаментальная матрица Ф системы (4.1) дается формулой Ф(t) = еt
А
(|t| < и решение φ системы (4.1), удовлетворяющее условию φ(τ) = ξ (|τ | < имеет вид φ(t) = е(
t
-τ)А
ξ (|t| < Доказательство. Так как е( t -Δ t )А = еt А еΔ t А , то из определения производной легко получаем, что
Поэтому Ф(t) = еt А есть решение системы (4.1). Так как Ф(0) = Е, то из (1.8) следует, что det Ф(t) = еtsp А . Итак, Ф – фундаментальная матрица. Теперь формула (4.3) очевидна. Замечание. Заметим, что выражение Интересно исследовать структуру фундаментальной матрицы (4.2). пусть J – каноническая форма матрицы А, указанная в теореме 1.1, и предположим, что Р – неособая постоянная матрица, такая, что АР = PJ. Тогда
и J имеет вид
где J0 – диагональная матрица с элементами λ1 , λ2 ,…, λq и
Далее,
и легкое вычисление показывает, что
Так как
где Другая фундаментальная матрица системы (4.1) такова: Ψ(t) = еt А P = P еtJ . (4.10) Пусть матрица Р имеет своими столбцами векторы р1 , …, рn . Столбцы матрицы Ψ. Которые мы обозначаем через ψ1 , ψ 2 , …, ψn , образуют совокупность n линейно независимых решений системы (4.1) и из (4.10) и вида матрицы J получаем
Так как АР = PJ, то векторы р1 , …, рn удовлетворяют соотношениям Ар1 = λ1 р1 ,…, Арq = λq рq , Арq +1 = λq +1 рq +1 , Арq +2 = рq +1 + λq +1 рq +2 , Арn - rs +1 = λq + s рn - rs +1 , Арn - rs +2 = рn - rs +1 +λq + s рn - rs +2 , Арn = рn -1 +λq + s рn . Решения ψj выражаются посредством независимых векторов р1 , …, рn из предыдущей последовательности уравнений. Формула вариации постоянных (3.1) в применении к неоднородной системе
где А – постоянная матрица, дает для решения φ системы (4.11), удовлетворяющего условию φ(τ) = 0,
Решение φ системы (4.11), удовлетворяющее условию φ(τ) = ξ , где
1.5 Линейные системы с периодическими коэффициентамиРассмотрим линейную однородную систему
где А – матрица элементами которой служат непрерывные комплексные функции, и
для некоторой постоянной ω Теорема 5.1. Если Ф – фундаментальная матрица для системы (5.1), то тем же свойством обладает матрица Ψ(t) = Ф(t+ω) Каждой такой матрице Ф соответствует периодическая неособая матрица Р с периодом ω и постоянная матрица R, такие, что Ф(t) = P(t)etR . (5.3) Доказательство. Так как
то в силу (5.2)
Поэтому Ψ есть матрица-решение системы (5.1), и эта матрица фундаментальная, так как det Ψ(t) = det Ф(t+ω) Следовательно, существует постоянная матрица С, такая что Ф(t+ω) = Ф(t)С, (5.4) и, сверх этого, существует постоянная матрица R, такая что С = еωR . (5.5) Из (5.4) и (5.5) получаем Ф(t+ω) = Ф(t) еωR . (5.6) Определим матрицу Р по формуле Р(t) = Ф(t) е- tR . (5.7) Тогда, используя (5.6), получаем Р(t+ω) = Ф(t+ω) е-( t + ω ) R = Ф(t) еωR е-( t + ω ) R = Ф(t) е- tR =Р(t). Так как матрицы Ф(t) и е-
tR
для Значение теоремы 5.1 состоит в том, что значение фундаментальной матрицы Ф на интервале длины ω, например Если Ф1 – некоторая другая фундаментальная матрица системы (5.1), для которой выполняется (5.2), то Ф = Ф1 Т, где Т – некоторая постоянная неособая матрица. Из (5.6) следует, что Ф1 (t+ω)Т = Ф1 (t)ТеωR , или Ф1 (t+ω) = Ф1 (t)(ТеωR Т-1 ). (5.8) Таким образом, в силу (5.8) каждая фундаментальна матрица Ф1
определяет матрицу ТеωR
Т-1
, подобную еωR
. Наоборот, если Т – любая постоянная неособая матрица, то существует фундаментальная матрица Ф1
системы (5.1), такая, что выполняется (5.8). Следовательно, хотя Ф не определяет R однозначно, множество всех фундаментальных матриц системы (5.1), а следовательно матрица А, определяет однозначно все связанные с Rвеличины, инвариантные относительно подобных преобразований. В частности, множество всех фундаментальных матриц системы (5.1) определяет однозначно множество характеристических корней, а именно характеристические корни матрицы С = еωR
. Обозначим эти корни через λ1
, λ2
,…, λn
и назовем их мультипликаторами, соответствующими матрице А. Ни один из мультипликаторов не равен нулю, ибо Интересно выяснить явный вид множества n линейно независимых векторов-решений системы (5.1). Пусть Т – постоянная неособая матрица, такая что матрица Т-1 RТ = J имеет каноническую форму, указанную в теореме 1.1, и положим Ф1 = ФТ, Р1 = РТ. Тогда из (5.3) следует Ф1 (t) = Р1 (t) еtJ , Р1 (t+ω) = Р1 (t). (5.9) Поэтому, если ρi – характеристические корни R, то матрица еtJ имеет вид
где
и
Очевидно, что λi = еωρi , и поэтому, хотя сами корни ρi определяются неоднозначно, но их действительные части определяются однозначно. Из (5.9) следует, что столбцы φ1 , φ2 , …, φn матрицы Ф1 , которые образуют множество n линейно независимых решений системы (5.1), имеют вид:
В этих формулах р1 , р2 , …, рn - периодические векторы-столбцы матрицы Р1 . Из (5.10) очевидно, что если Reρi
< 0 или, что эквивалентно, | λi
| < 1, то при Из (5.6) следует, что Ф(ω) = Ф(0)еωR , и поэтому λi можно рассматривать как характеристические корни матрицыФ-1 (0)Ф(ω). В частности, если Ф(0) = Е, то еωR = Ф(ω) и λi являются характеристическими корнями матрицы Ф(ω). Так как
то n-й корень можно определить из (5.11), если известны n-1 корней λi . Действительная неособая матрица С не обязана иметь действительный логарифм, т.е. не всегда существует действительная матрица В, такая что еВ = С. В самом деле, матрица с одной строкой и одним столбцом С = -1 доставляет соответствующий пример. Однако справедливо утверждение, что для действительной матрицы С существует действительная матрица В, такая, что С2 = еВ . Используя это при доказательстве теоремы 5.1, нетрудно получить следующий результат6 если в системе (5.1) матрица А (t) действительная периодическая с периодом ω, то каждой действительной фундаментальной матрице Ф соответствует действительная матрица Р периода 2ω и действительная постоянная матрица R, такие, что Ф(t) = Р(t)еtR . 2. Линейные дифференциальные уравнения2.1 Линейные дифференциальные уравнения порядка nПредположим, что n+1 коэффициентов а0 , а1 , …, аn представляют собой непрерывные (комплексные) функции, определенные на действительном t-интервале I, и пусть Ln обозначает формальный дифференциальный оператор
это означает, что если функция g имеет n производных на I, то
Далее предположим, что а0
(t)
(в подробной записи
оно называется линейным однородным дифференциальным уравнением порядка n. Соответствующая этому уравнению система есть векторное уравнение
где
Так как (6.1) – линейная система с непрерывной на I матрицей коэффициентов А, то существует единственный вектор-решение φ на I системы (6.1), удовлетворяющий условию
где
Так как φ1
– решение уравнения Применим теперь остальные результаты, полученные ранее для линейных систем, к уравнению Если φ1
, …, φn
– n решений уравнения
есть матрица-решение для (6.1). Определитель этой матрицы называется вронскианом уравнения
следует (замечая из (6.2), что spA = - а1 /а0 ) W(φ1
, …, φn
)(t) = W(φ1
, …, φn
)(τ) Теорема 6.1. Необходимое и достаточное условие того, чтобы n решений φ1
, …, φn
уравнения W(φ1
, …, φn
) Каждое решение уравнения Доказательство. Если решения φ1 , …, φn на I линейно зависимы. То существуют постоянные с1 , …, сn , не все равные нулю, такие, что
Отсюда следует тождество
и поэтому векторы Так как каждый вектор-решение задачи (6.1), (6.2) есть линейная комбинация nлинейно независимых векторов-решений, то каждое решение уравнения Ввиду свойства, указанного в теореме 6.1, множество nлинейно независимых решений уравнения Теорема 6.2. Пусть φ1
, …, φn
- n функций, имеющих на интервале I непрерывные производные порядка n, и пусть W(φ1
, …, φn
)(t)
Замечание. Вронскиан W(х, φ1 , …, φn ) представляет собой определитель матрицы, первая строка которой состоит из элементов х, φ1 , …, φn , а последующие строки являются последовательными производными первой строки до порядка n включительно. Доказательство. Очевидно, что W(φi
, φ1
, …, φn
) = 0 (i = 1, …, n), ибо в этом определителе имеются два одинаковых столбца. Разложение числителя W(х, φ1
, …, φn
) левой части уравнения (6.6) по элементам первого столбца показывает, что (6.6) есть дифференциальное уравнение порядка n. Коэффициент при х(
n
)
в W(х, φ1
, …, φn
) равен (-1)n
W(φ1
, …, φn
), т.е. в (6.6) при х(
n
)
равен единице. Так как W(φ1
, …, φn
) Единственность уравнения (6.6) следует из того, что соответствующие векторы Если одно или более из решений уравнения Сопряженные уравнения. С формальным оператором Ln
тесно связан другой линейный оператор
Иначе говоря, если g – функция на I, для которой произведение
Уравнение
(в подробной записи
называемое сопряженным для Ln
х = 0 на I, определяется как задача отыскания функции φ (решения), на I, такой, что произведение
Если
разделив на Рассмотрим тот специальный случай оператора Ln х когда а0 = 1. Для системы (6.1), (6.2), ассоциированной с уравнением
сопряженная система имеет вид
где в силу (6.2)
Записывая (6.8) в компонентах, получаем в силу (6.9)
Таким образом, если φ1
, …, φn
– решение системы (6.10), для которого
существуют, то дифференцируя k-е равенство (6.10) k-1 раз и решая относительно
Поэтому φn удовлетворяет уравнению
которое является сопряженным к (6.7). Важность оператора Теорема 6.3. (Тождество Лагранжа). Предположим, что в Ln
где [uv] – форма относительно величин (u,
Доказательство. Пользуясь правилом дифференциального произведения, имеем для m = 0, 1, …, n
Таким образом, получаем
что доказывает формулу (6.11). Следствие (Формула Грина). Если ак
вLn
и u, v такие же как и в теореме 6.3, то для любых
где [u, v](ti ) – значение [u, v] при t = ti . Доказательство. Следует проинтегрировать тождество (6.11) в пределах от t1 до t2 . Если ψ – известное решение уравнения
Неоднородное линейное уравнение порядка n. Предположим, что на действительном t-интервале Iа0
которое совпадает с уравнением
Это уравнение (в случае b(t)
где А – матрица (6.2) и Теорема 6.4. Если φ1 , …, φn – фундаментальное множество для однородного уравнения
то решение ψ неоднородного уравнения Ln
х = b(t) ( удовлетворяющее условию
имеет вид
где Доказательство. В силу (3.1) первая компонента ψ = ψ1
вектора-решения
где
где
где Wk
(φ1
, …, φn
)(s) определен в формуле теоремы. Таким образом, решение ψ уравнения Ln
х = b(t) , удовлетворяющее условию
и очевидно, что (6.15) дает решение, удовлетворяющее условию Линейное уравнение порядка n с постоянными коэффициентами. Рассмотрим тот случай, когда в Ln все коэффициенты а0 = 1, а1 , …, аn – постоянные. В этом случае можно предполагать, что I есть вся числовая ось. Далее, уравнению
соответствует система
где А – постоянная матрица
Можно предполагать, что для (6.16) можно указать фундаментальное множество решений, и точный вид этих функций зависит от характеристического многочлена f(λ) = det (λE - A) постоянной матрицы А в (6.18). Лемма. Характеристический многочлен для матрицы А в (6.18) имеет вид f(λ) = λn + а1 λn -1 +…+ аn . (6.19) Заметим, что f(λ) может быть получено из Ln (х) формальной заменой х( k ) на λk. Доказательство проводится по индукции. Для n = 1 А = - а1 ; значит det(λE1 - A) = λ + а1 и, следовательно, (6.19) верно для n = 1. Предположим, что результат справедлив для n – 1. Разложим определитель det(λEn
- A) = по элементам первого столбца и заметим, что коэффициент при λ есть определитель (n-1)-го порядка, именно det(λEn -1 – A1 ), где
Поэтому λdet(λEn -1 – A1 ) = λn + а1 λn -1 +…+ аn --1 λ. Единственный другой ненулевой элемент в первом столбце есть аn и его алгебраическое дополнение равно 1. Поэтому det(λEn – A) = λn + а1 λn -1 +…+ аn --1 λ + аn , что и требовалось доказать. Теорема 6.5 (без доказательства). Пусть λ1 , …, λn - различные корни характеристического уравнения f(λ) = λn + а1 λn -1 +…+ аn = 0 и пусть кратность корня λi равна mi (i = 1, …, s ). Тогда фундаментальное множество для (6.16) дается n функциями tk eλi (k = 0, 1,…, mi – 1; i = 1, 2,…, s). (6.20) 2.2 Линейные уравнения с аналитическими коэффициентамиПредположим, что А – квадратная матрица порядка n и b – n-мерный вектор, определенные и аналитические в односвязной области в z-плоскости, и пусть
при условии
имеет в в единственное аналитическое решение В самом деле, пусть
причем интеграл берется вдоль С, так что приближения
Очевидно, эти оценки справедливы для всех точек z в D, достижимых из z0
другой длины L, на которой |A(z)| и |
Это доказывает утверждение для R и, следовательно, для D. Кроме того, все теоремы, доказанные в пп. 1.2 и 1.3, будучи существенно алгебраической природы, справедливы для системы (7.1). Соответственно этому, если n+1 функций а1 , …, аn , b аналитичны в D, то линейное уравнение порядка n
имеет в в единственное решение, удовлетворяющее условиям
где w1 , …, wn – n данных комплексных чисел. Наконец, все результаты п. 2.1 распространяются очевидным образом на случай (7.2). 2.3 Асимптотическое поведение решений некоторых линейных системЕсли коэффициенты линейной системы дифференциальных уравнений при Здесь рассматривается проблема для действительного переменного. Рассмотрим пример
где v – действительная дифференцируемая функция, для которой
для некоторого t0
. (На самом деле достаточно, чтобы функция v имела в интервале
при Этот результат показывает, что функция r нисколько не влияет на грубую асимптотику. Однако случай
убеждает нас в том, что влияние v существенно. Эти асимптотические формулы показывают также, что если положить в уравнении функцию r(t) равной нулю, а 1 + v(t) – постоянной, то результат будет отличаться от точного только членом о(1) при В дальнейшем будет рассматриваться линейная система
которая включает как частный случай предыдущий пример. Теорема 8.1. Пусть А – постоянная матрица с различными характеристическими корнями μj , j = 1, …, n. Пусть матрица V дифференцируема и удовлетворяет условию
и пусть
Обозначим корни уравнения det (A + V(t) - λE) = 0 через λj
(t), j = 1, …, n. Очевидно, что можно, если это необходимо, переставить μj
так, чтобы
Допустим, что все j, 1
и
здесь kфиксировано и К – постоянная. Пусть pk – характеристический вектор А, соответствующий μk , так что Аpk = μk pk . (8.6) Тогда существует решение φk
системы (8.1) и число t0
, 0
Доказательство. Если условия теоремы выполняются для всех k, 1 Предположим в начале, что А + V(t) для t
Пусть Ψ(t) – диагональная матрица: Ψ(t) = так что
Пусть еК - вектор-столбец со всеми нулевыми элементами, за исключением k-го, который равен 1, и ψk – вектор, определенный равенством
При фиксированном k и I1 , I2 , определенных согласно неравенствам (8.4), (8.5), положим Ψ = Ψ1 + Ψ2 , где диагональные матрицы Ψ1 и Ψ2 содержат элементы Ψ, соответствующие столбцам с индексами j, принадлежащим соответственно I1 и I2 . Тогда
Рассмотрим теперь уравнение
Можно непосредственно проверить, что если уравнение (8.11) имеет решение φ, то
Последнее уравнение имеет рассматриваемый нами вид (8.1) Пусть φ0 (t) = 0 и
Тогда φ1
(t) = ψk
(t) и для t
Каждый элемент диагональной матрицы
или равен нулю. Но для t0
Поэтому для t0
Точно также для τ
Используя эти неравенства, получаем из (8.13)
Из (8.8) и (8.14) теперь по индукции следует
Отсюда следует равномерная сходимость последовательности {φj
} на каждом конечном подинтервале интервала [t0
,
Покажем теперь, что
Это будет установлено, если мы покажем, что при t→ ∞
И
Доказательство соотношения (8.18) сразу получается из (8.15) и (8.5). Доказательство соотношения (8.17) основывается на равенстве
которое является следствием (8.4). Каково бы ни было ε > 0, можно подобрать такое t1 , что
Поэтому, обозначая левую часть (8.17) через J(t), получаем
Из (8.19) следует, что
Так как ε произвольно, то (8.17) доказано. Таким образом, теорема доказана для случая A+ V(t) = A(t), если за φ взята φk . Доказательство теоремы 8.1 вытекает из следующей леммы. Лемма. Пусть A и V удовлетворяют условиям теоремы 8.1. Тогда существует матрица S(t), которая при t → ∞ стремится к постоянной неособой матрице Т, такая что S(A + V) = ΛS, (8.20) где Λ(t) – диагональная матрица с диагональными элементами λj (t), j = 1, 2, …, n. При t → ∞ λj (t) → μj , где μj – характеристические корни матрицы А. Кроме того, для некоторого t0
Доказательство теоремы 8.1. Так как S(t) → T при t → ∞ и Т – неособая матрица, то S(t) – неособая матрица для всех достаточно больших t. Выберем t0
настолько большим, чтобы не только (8.21) выполнялось, но и S-1
(t) существовала для t
Пусть
Поэтому (8.1) имеет решение S-1 θk = φk . Так как S-1 (t) → T-1 , то Аpk = μk pk . Это завершает доказательство теоремы 8.1. 3. Решение задачЗадача 1. Пусть матрица А и вектор b – интегрируемые функции от t на интервале [a, c]. Пусть |A(t)| |b(t)|
Пусть τ
Доказать, что существует решение φ на [a, c] в том смысле, что
Доказательство. Используем последовательные приближения. Пусть φ0 (t) = ξ и
Тогда
Пусть
Значит,
Следовательно, последовательность {φj } сходится равномерно на [a, c]. Задача 2. Решить систему дифференциальных уравнений 2-го порядка методом Эйлера. Решение: Система дифференциальных уравнений второго порядка имеет вид:
Приведем систему к системе дифференциальных уравнений первого порядка. Сделаем замену:
Пусть заданы начальные условия
и выбран шаг h по оси x. Метод Эйлера для решения системы дифференциальных уравнений 2-го порядка в общем виде:
где j – номер шага. ЗаключениеВ дипломной работе рассмотрены вопросы решения линейных дифференциальных уравнений и систем уравнений. Можно сделать вывод, что многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Задача нахождения решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений, удовлетворяющего некоторым начальным условиям, называется задачей Коши. Решением будет функция, график которой касается каждой своей точкой соответствующего отрезка. Каждое отдельное решение называется частным решением дифференциального уравнения; если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение. Частное решение представляет собой одну функцию, в то время как общее – целое их семейство. Решить дифференциальное уравнение – это значит найти либо его частное, либо общее решение. Линейные уравнения – это уравнения «первой степени» – неизвестная функция и ее производные входят в такие уравнения только в первой степени. Таким образом, линейное дифференциальное уравнение первого порядка имеет вид dy/dx + p(x) = q(x), где p(x) и q(x) – функции, зависящие только от x. Его решение всегда можно записать с помощью интегралов от известных функций. Многие другие типы дифференциальных уравнений первого порядка решаются с помощью специальных приемов. Многие дифференциальные уравнения, с которыми сталкиваются физики, это уравнения второго порядка (т.е. уравнения, содержащие вторые производные) Вообще говоря, можно ожидать, что уравнение второго порядка имеет частные решения, удовлетворяющие двум условиям; например, можно потребовать, чтобы кривая-решение проходила через данную точку в данном направлении. В случаях, когда дифференциальное уравнение содержит некоторый параметр (число, величина которого зависит от обстоятельств), решения требуемого типа существуют только при определенных значениях этого параметра. Значения параметра, при которых уравнение имеет особые решения, называются характеристическими или собственными значениями; они играют важную роль во многих задачах. В работе также проведено решение конкретных заданий, связанных с нахождением решения дифференциальных уравнений и систем дифференциальных уравнений. Таким образом, дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому). Список литературы1. Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука, 1966. – 384 с. 2. Бабушка И., Витасек Э., Прагер М. Численные процессы решения дифференциальных уравнений. М.: Мир, 1969. – 428 с. 3. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. М.: Наука, 1967. – 439 с. 4. Дородницын А.А. Численные методы решения дифференциальных и интегральных уравнений и квадратурные формулы. Сборник статей. М.: Наука, 1964. – 386 с. 5. Дьяченко В.Ф. Основные понятия вычислительной математики. М.: Наука, 1972. – 563 с. 6. Ильин В.А., Позняк Э.Г. Основы математического анализа. – ч. 1. М.: Наука, 1973. – 591 с. 7. Карташев А.П., Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М.: Наука, 1976. – 472 с. 8. Коллатц Л. Функциональный анализ и вычислительная математика. М.: Мир, 1969. – 475 с. 9. Марчук Г.И. Методы вычислительной математики. М.: Наука, 1977. – 623 с. 10. Михлин С.Г., Смолицкий X.Л. Приближенные методы решения дифференциальных и интегральных уравнений. М.: Наука, 1965. – 352 с. 11. Островский А.М. Решение уравнений и систем уравнений. М.: ИЛ, 1963. – 349 с. 12. Степанов В.В. Курс дифференциальных уравнений. М.: Гостехиздат, 1963. – 461 с. 13. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977. – 522 с. 14. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М., 1982. – 549 с. 15. Полянин А. Д. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001. – 419 с. 16. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1984. – 463 с. 17. Штеттер X. Анализ методов дискретизации для обыкновенных дифференциальных уравнений. М.: Мир, 1978. – 275 с. 18. Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. М., 1986. – 478 с. 19. Интернет-источник: www.mathematics.ru. 20. Интернет-источник: www.nsu.ru/matlab. 21. Интернет-источник: ru.wikipedia.org. 22. Интернет-источник: www.matclub.ru. |
 . (1.1)
. (1.1)

 (i = 1, …, s).
(i = 1, …, s).

 (1.2)
(1.2)











 ,
,



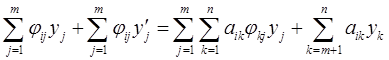 (i = 1, …, m),
(i = 1, …, m),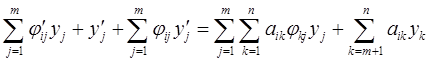 (i = m+1, …, n).
(i = m+1, …, n). (i = 1, …, n; j = 1, …, m),
(i = 1, …, n; j = 1, …, m),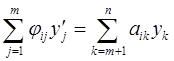 (i = 1, …, m),
(i = 1, …, m),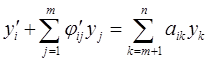 (i = m+1, …, n). (2.8)
(i = m+1, …, n). (2.8)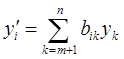 (i = m+1, …, n), (2.9)
(i = m+1, …, n), (2.9)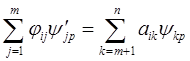 (2.10)
(2.10)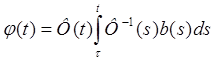
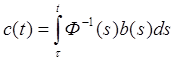

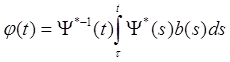
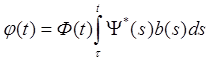 ,
, не обязано быть решением системы
не обязано быть решением системы 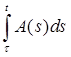 не коммутируют. Они коммутируют, когда матрица А(t) либо постоянная, либо диагональная.
не коммутируют. Они коммутируют, когда матрица А(t) либо постоянная, либо диагональная.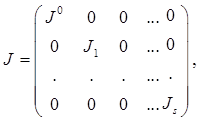 (4.5)
(4.5)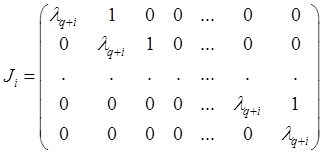 (i = 1, …, s). (4.6)
(i = 1, …, s). (4.6)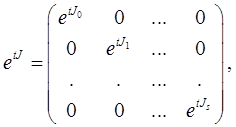 (4.7)
(4.7)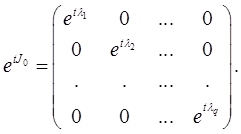 (4.8)
(4.8)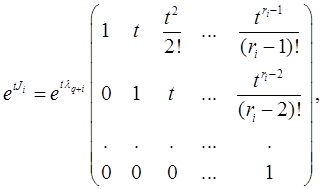 (4.9)
(4.9)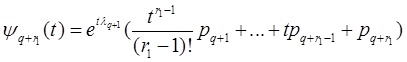 ,
,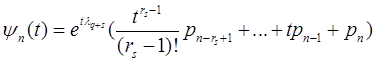 .
.


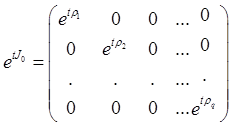
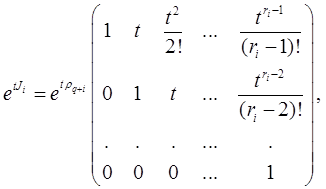 (i = 1, …, s; q+
(i = 1, …, s; q+ ,
,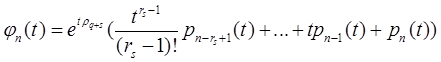 .
.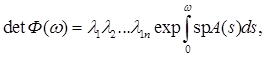 (5.11)
(5.11)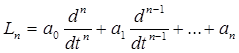 ;
;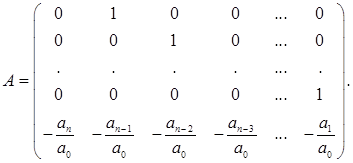 (6.2)
(6.2)  (6.4)
(6.4)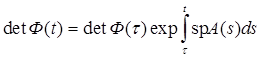
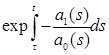

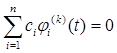 (k = 0, 1, …, n-1),
(k = 0, 1, …, n-1),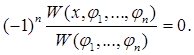 (6.6)
(6.6)
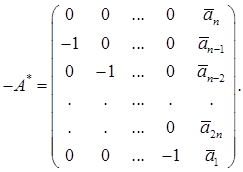 (6.9)
(6.9) (6.12)
(6.12)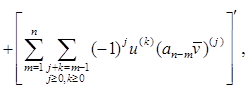
 (6.13)
(6.13)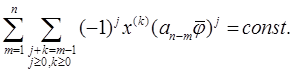
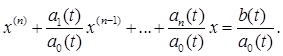
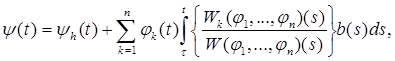 (6.15)
(6.15)
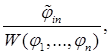
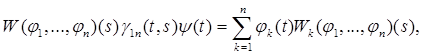

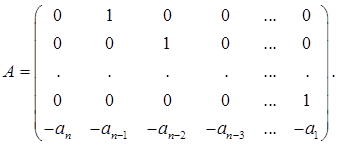 (6.18)
(6.18)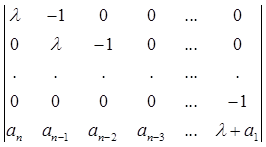
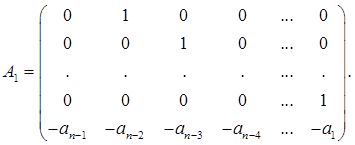


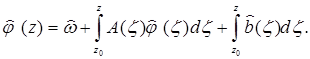
 ,
, 
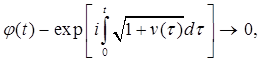
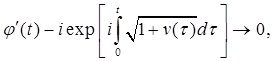
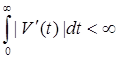 (8.2)
(8.2)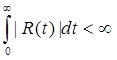 . (8.3)
. (8.3)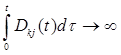 при
при 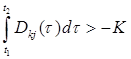
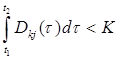
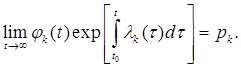 (8.7)
(8.7) (8.8)
(8.8)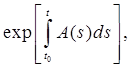
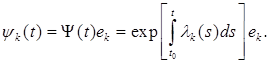
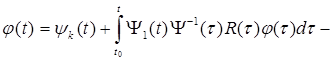
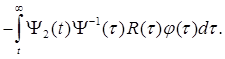 (8.11)
(8.11)
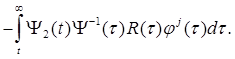 (8.13)
(8.13)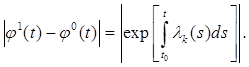 (8.14)
(8.14)

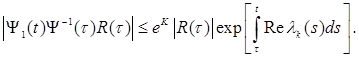
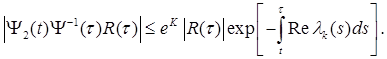

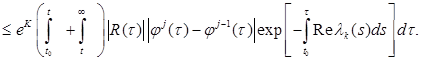

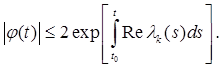 (8.15)
(8.15) (8.16)
(8.16) (8.17)
(8.17)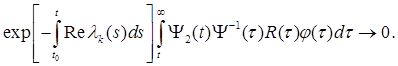 (8.18)
(8.18) (8.19)
(8.19)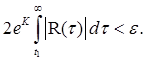

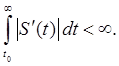 (8.21)
(8.21)
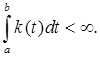
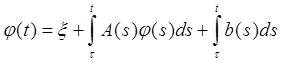 на [a, c].
на [a, c].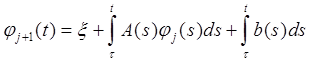 , j
, j 
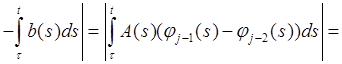
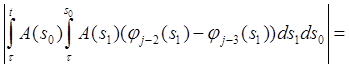
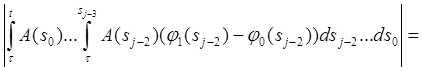
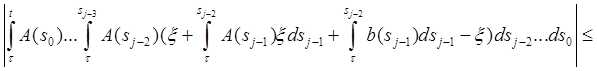


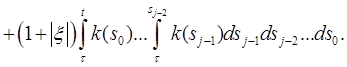
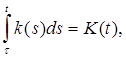 тогда
тогда 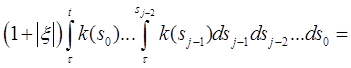
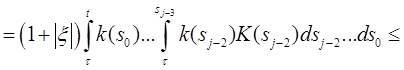
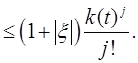
 где
где 