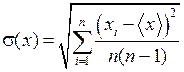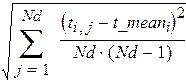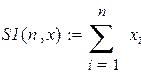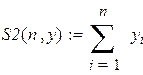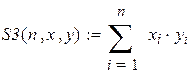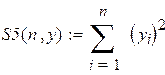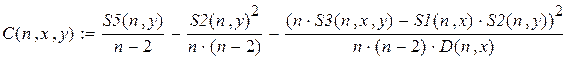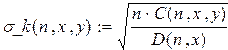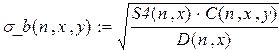Лабораторная работа: Определение момента инерции твердых тел 5
|
Название: Определение момента инерции твердых тел 5 Раздел: Рефераты по физике Тип: лабораторная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Федеральное Агентство по образованию ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра физики ОТЧЕТ Лабораторная работа по курсу "Общая физика" ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ Преподаватель Студент ___________ /____________. / ___________200_ г. 2009 1. ЦЕЛЬ РАБОТЫ Целью настоящей работы является изучение основных законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока и сравнение его с расчетным значением. 2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА Схема экспериментальной установки на основе машины Атвуда приведена на рис. 3.1. На вертикальной стойке 1 крепится массивный блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы, равной 80 г. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. Риска на корпусе среднего кронштейна совпадает с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положение грузов. За начальное, принимают положение нижнего среза груза, за конечное - риску на корпусе среднего кронштейна. Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Опоры 9 используют для регулировки положения установки на лабораторном столе. Принцип работы машины Атвуда заключается в следующем. Когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если же на один из грузов (обычно на правый) положить перегрузок, то система выйдет из равновесия, и грузы начнут двигаться с ускорением. Машина Атвуд а
1 – стойка; 2 – блок; 3 – нить; 4 – грузы; 5 – средний кронштейн; 6 – фотодатчик; 7 – линейка; 8 – миллисекундомер; 9 – регулировочная опора. Рис. 3.1 3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ На рис. 4.1 приведена схема, поясняющая характер движения грузов, а также величины и точки приложения сил. Рассмотрим движение тел в машине Атвуда, используя основные законы динамики вращательного и поступательного движений.
Рис. 4.1 Пусть основные грузы имеют массу М каждый, а перегруз массой m лежит на правом грузе (рис. 4.1). Уравнения движения грузов в проекциях на ось х запишутся следующим образом
где а – ускорение движения грузов, Т1 и Т2 – соответствующие силы натяжения нитей. Вращательное движение блока описывается уравнением
где Согласно рис. 4.1 сумма моментов сил равна
Как следует из системы (4.3), ускорение а
есть величина постоянная в условиях постоянства масс и момента инерции. Т.е. грузы движутся равноускоренно. Ускорение а
может быть определено на основании измерения высоты
Подставляя выражение (4.4) в систему (4.3) и разрешая ее относительно
Выражение (4.5) может быть переписано в виде
где
Формула (4.6) показывает, что в случае адекватности рассмотренной физической модели условиям опыта экспериментальные точки, нанесенные на график в координатах 4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ. Таблица 4.1 – результаты измерений времени прохождения груза
Вычисление погрешностей прямых и косвенных измерений Так как класс точности электронных часов, используемых в лабораторной работе, не указан, то за приборную погрешность принимается единица в младшем разряде часов, т.е
Чтобы вычислить случайную погрешность измерения времени, необходимо определить коэффициент Стьюдента и среднеквадратичное отклонение. определим коэффициент Стьюдента - Определим среднеквадратичное отклонение:
Рассчитаем случайные погрешности измерения времени
Рассчитаем абсолютные погрешности измерения времени:
Найдем абсолютные погрешности вычисления квадратов(
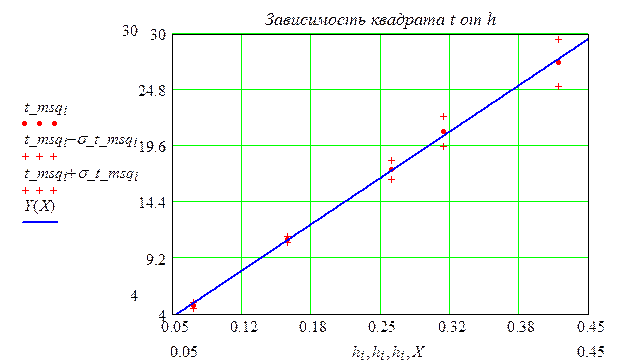
Построение графиков Метод наименьших квадратов для построения прямых по экспериментальным точкам:
5 ВЫВОДЫ: В ходе работы изучены основные законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока. Также мы смогли определить аналитическим и экспериментальным методами момент инерции и сравнить их, получим отличие в 3.185%. 6 КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое момент сил и момент инерции? Момент инерции I материальной точки относительно неподвижной оси вращения - физическая величина, равная произведению массы m материальной точки на квадрат расстояния r между точкой и осью вращения: I = m∙r2. Скалярная величина I = ΣIi = Σ(mi∙ri2) равная сумме моментов инерции всех материальных точек твердого тела и характеризующая инерционность тела по отношению к вращению – есть момент инерции твердого тела относительно выбранной оси вращения. 2. Моменты каких сил действуют на блок? Вращательное движение блока описывается уравнением
Сумма моментов сил равна T1R – T2R. При движении нерастяжимой нити без скольжения по блоку имеет место равенство ε = a/R. Здесь а – линейное ускорение точек на поверхности блока, а, следовательно, и самой нити, R – радиус блока. 3. Как рассчитать момент инерции блока? Сформулировать теорему Штейнера. Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями: I = I0 + ml². 4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными. - физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин; точность вычислений. |
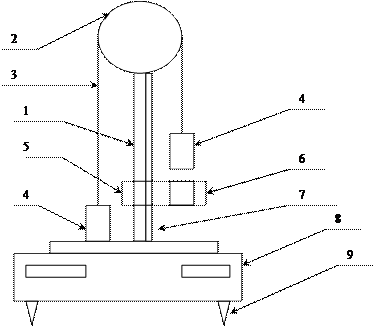
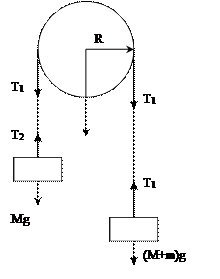 Схема приложения сил
Схема приложения сил
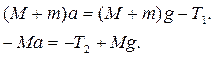 (4.1)
(4.1)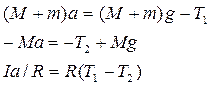 (4.3)
(4.3)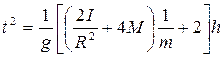 (4.5)
(4.5)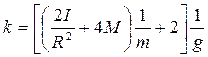 (4.7)
(4.7)