Содержание
Введение
Моделирование линейных непрерывных систем
Численное решение дифференциальных уравнений
Замена непрерывной передаточной функции дискретной
Моделирование линейных замкнутых систем
Заключение
Список литературы
LabVIEW (LaboratoryVirtualInstrumentEngineeringWorkbench) позволяет разрабатывать прикладное программное обеспечение для организации взаимодействия с измерительной и управляющей аппаратурой, сбора, обработки и отображения информации и результатов расчетов, а также моделирования как отдельных объектов, так и автоматизированных систем в целом. Разработчиком LabVIEW является американская компания National Instruments.
LabVIEW является открытой системой программирования и имеет встроенную поддержку всех применяемых в настоящее время программных интерфейсов, таких как Win32 DLL, COM.net, DDE, сетевых протоколов на базе IP, DataSocket и др. В состав LabVIEW входят библиотеки управления различными аппаратными средствами и интерфейсами, такими как PCI, CompactPCI/PXI, VME, VXI, GPIB (КОП), PLC, VISA, системами технического зрения и др. Программные продукты, созданные с использованием LabVIEW, могут быть дополнены фрагментами, азработанными на традиционных языках программирования, например C/С++, Pascal, Basic, FORTRAN. И наоборот можно использовать модули, разработанные в LabVIEW в проектах, создаваемых в других системах программирования. Таким образом, LabVIEW позволяет разрабатывать практически любые приложения, взаимодействующие с любыми видами аппаратных средств, поддерживаемых операционной системой компьютера.
среда программирование дифференциальное уравнение
При цифровом моделировании непрерывных систем необходимо обеспечить близость процессов в моделируемой непрерывной системе и в ее цифровой модели. Несовпадение этих процессов связано с двумя причинами:
1) заменой непрерывного входного процесса цифровым и 2) использованием численных методов анализа. Ошибки, связанные с заменой непрерывного процесса цифровым, были рассмотрены в предыдущей лабораторной работе. Остановимся на второй причине.
Математическая модель непрерывной системы представляет собой или нелинейное дифференциальное уравнение или совокупность соединенных между собой линейных и нелинейных блоков. В зависимости от принятой математической модели используются различные подходы к формированию цифровой модели.
Разработано большое количество методов численного решения дифференциальных уравнений. Рассмотрим, как производится численное решение на примере нелинейного дифференциального уравнения первого порядка
du
/dt
= f
(u,
x,
t
). (1)
Здесь x=
x
(t
) - независимая функция (входной процесс), u=
u
(t
) - решение уравнения (выходной процесс).
Численное решение находится для дискретных значений аргумента t
, отличающихся на шаг интегрирования Dt
. В одношаговых разностных методах для нахождения следующего значения u
к
= u
(t
к
) требуется информация только об одном предыдущем шаге. Из одношаговых методов наибольшую известность получили методы Рунге-Кутта. В основу метода Рунге-Кутта первого порядка, называемого также явным или прямым методом Эйлера, положено разложение функции u
(t
) в ряд Тейлора в окрестности точки A
(t
k-1,
, u
k-1
):
u
(t
) = S0
+ S1
(t - tk -
1
) + S2
(t - tk -
1
) 2
+ …, (5.2)
где S0
= u
(tk -
1
) = uk -
1,
Si
= (
1/i
!) du
(t
) /dt
при t = tk -
1
.
В методах Эйлера (и Рунге-Кутта тоже) ограничиваются только двумя первыми членами разложения в ряд. Запишем значение uk
= u
(tk
), приняв в выражении (5.2) t=
tk
и ограничившись двумя первыми членами ряда:
uk
= uk
-
1
+ S1
(tk
- tk -
1
) = uk
-
1
+ S1
Δt
Учитывая, что производная du
(t
) /dt
равна правой части дифференциального уравнения (1), имеем S1
= f
(uk
-
1
,
xk
- 1
,
tk
- 1
) и окончательно получим:
uk
= uk
-
1
+ Δt
f
(uk
-
1
,
xk
- 1
,
tk
- 1
). (3)
Это выражение является приближенным решением дифференциального уравнения (1) прямым методом Эйлера. Оно рекуррентное и позволяет найти значение выходного процесса uk
по значениям выходного и входного процессов в предыдущем такте.
На рис. 1 а
) проиллюстрировано решение прямым методом Эйлера.
Видим, что при использовании этого метода используется линейная экстраполяция и тангенс угла наклона экстраполирующей прямой равен производной функции u
(t
) в точке А.
Экстраполированное значение uk
отличается от точного на величину ошибки.
Неявный (обратный) метод Эйлера основан на разложении функцииu
(t
) в ряд Тейлора в окрестности точки В
(u
k,
, t
k
) (см. рис.1 б
):
u
(t
) = uk
+ S1
(t - tk
) + S2
(t - tk
) 2
+ …,
Приняв в этом выражении t=
tk
- 1
и ограничившись двумя первыми членами ряда, получим
uk
- 1
= uk
- Δt
f
(uk
,
xk
,
tk
)
.
Откуда
uk
= uk
- 1
+ Δt
f
(uk
,
xk
,
tk
)
. (5.4)
Искомое значение процесса uk
входит и в левую, и в правую части уравнения, и если не удается найти uk
в явном виде, то приходится использовать приближенные методы решения этого уравнения.
Применим методы Эйлера для расчета переходной характеристики интегрирующей цепи. Передаточная функция интегрирующей цепи:
K
(p
) = 1/ (1 + pT
).
Отсюда дифференциальное уравнение в операторной форме:
(pT
+ 1) y
= x
и в канонической форме:
Tdy
/dt
+ y
= x
.
Перепишем его в виде (1):
dy
/dt
= (1/T
) (x -
y
).
Запишем рекуррентную формулу для прямого метода Эйлера в соответствии с (5.3)
yk
=
yk
- 1
+ (Δt
/T
) (xk
- 1
- yk
- 1
), (5.5) или yk
=
(1 - Δt
/T
) yk
- 1
+ Δt
/T
xk
- 1
.
Формула для обратного метода Эйлера запишется в соответствии с (4)
yk
=
yk
- 1
+ (Δt
/T
) (xk
- yk
).
Так как уравнение линейное, то значение yk
вычисляется в явной форме:
yk
=
(yk
- 1
+ (Δt
/T
) xk
) / (1 + Δt
/T
). (6)
Методы Эйлера обладают низкой точностью. В более точных методах используются различные способы определения угла наклона экстраполирующей прямой, чтобы она прошла ближе к точному решению. Хорошей точностью обладает метод Рунге-Кутта четвертого порядка, который обычно и используется. Программы для численного решения дифференциальных уравнений имеются практически в любом пакете прикладных программ, в том числе и в LabVIEW.
Для вычислений по формулам (5.5) и (5.6) используем структуру FormulaNode. Внутри этой структуры запишем точное выражение для переходной характеристики:
z
= 1 - e-
i
Δt
/
T
,
и выражения для переходной характеристики, полученные прямым методом Эйлера:
y=
y
1
+ (Δt
/T
) (1 - y
1
)
и обратным методом Эйлера:
v=
(v
1
+ (Δt
/T
)) / (1 + Δt
/T
)
при нулевых начальных условиях: y (0) = 0, v (0) = 0.
В этих выражениях использованы различные обозначения для выходных переменных и принято x
= 1 (t
) = 1, так как t
> 0.
На рис.2 показана эта структура. В формулах Δt
обозначена как dt
.
 |

|
| Рис.2 |
Рис.3 |
Напомним, что для образования входных и выходных терминалов нужно щелкнуть ПКМ на границе структуры в предполагаемом месте терминала и в раскрывшемся меню выбрать AddInputили AddOutput.
Для формирования массивов выходных переменных структура FormulaNodeпомещается внутрь структуры ForLoop, при этом задержанные на интервал дискретизации отсчеты выходных переменных y
1
и v
1
получаются с помощью регистра сдвига (рис.3).
Прямой метод Эйлера при большом интервале дискретизации может дать неустойчивое решение. Это случится, если отклонение решения от входного процесса xk
- 1
- yk
- 1
(см формулу (5)) даст такое значение yk
. что отклонение на следующем шаге xk
- yk
будет той же величины, что и предыдущее, но обратным по знаку. Решение будет колебательным незатухающим.
| К графическому индикатору |
|
 |
| Рис.4 |
В предыдущих лабораторных работах развертка графического индикатора Graphосуществлялась автоматически в соответствии с типом данных, подаваемых на вход графического индикатора. В этой работе мы сформируем данные так, чтобы по горизонтальной оси откладывалось время. Для этого надо сформировать кластер, куда кроме массива данных будет входить информация о времени. Используем ВП Bundle (Объединить), который находится в подпалитре Cluster (Кластер). На его входы elementподаются (см. рис.4): на верхний - время начала развертки - 0; на средний - интервал дискретизации - Δt; на нижний - массив данных
Если математическая модель системы представляется в виде соединения линейных и нелинейных блоков, то для описания линейных блоков чаще всего используется передаточная функция K
(p
). В этом случае цифровую модель непрерывного линейного блока можно получить, заменив непрерывную передаточную функцию K
(p
) дискретной K
(z
).
Для этого можно использовать связь между непрерывными и дискретными изображениями, устанавливаемую дискретным преобразованием Лапласа (Z
-преобразованием). В таблице 1 приведена эта связь для передаточных функций, используемых в данной лабораторной работе.
Таблица 1
| K
(p
) |
 1 1
p
|
1
 p
2 p
2
|
1
 (1 +pT
) (1 +pT
)
|
| K
(z
) |
Δt z
 (z
- 1) (z
- 1)
|
(Δt
) 2
z
 (z
- 1) 2 (z
- 1) 2
|
(Δt
/T
) z
 (z - e-
Δt
/T
) (z - e-
Δt
/T
)
|
Заметим, что здесь комплексная переменная z
определяется как z
= ep
Δt
и является оператором опережения на интервал дискретизации. Соответственно z
-1
- это оператор задержки на интервал дискретизации.
Другой путь предусматривает непосредственный переход от комплексной переменной p
к комплексной переменной z
заменой операции аналогового интегрирования 1/p
операцией дискретного интегрирования. При дискретном описании аналогового интегрирования можно оперировать только с значениями входного и выходного процессов в моменты дискретизации. На рис.5 показано, как это можно сделать, используя численное интегрирование по методу прямоугольников и по методу трапеций.
Значение выходного процесса yk
интегратора в момент времени t=
k
Δt
отличается от предыдущего значения yk
-1
на величину площади S
под кривой x
(t
) (заштрихованная фигура на рис.5 а
).
|
|
yk
= yk-
1
+ S
|
yk
= yk-1
+ Δt xk-1
|
yk
= yk-
1
+ Δt xk
|
yk
=
yk
-
1
+
+Δt
(xk
+ xk
-
1
) /2
|
| а
) |
б
) |
в
) |
г
) |
| Рис.5 |
По методу прямоугольников площадь можно определить по разному в зависимости от того, какую величину принять за высоту прямоугольника: xk
-
1
или xk
(рис.5.5 б
и рис.5.5 в
). На рис.5.5 г
) показано, как вычисляется эта площадь по методу трапеций. Рекуррентные формулы для интегрирования приведены под рисунками.
По этим формулам можно записать дискретные передаточные функции. Поясним это на примере интегрирования по методу трапеций:
yk
=
yk
-
1
+ Δt
(xk
+ xk
-
1
) /2.
Перенесем yk
-
1
в левую часть и возьмем от полученного выражения Z
-преобразование. Учитывая, что запаздывание на интервал дискретизации в области оригиналов соответствует умножению на z
-1
в области изображений, получим:
Y
(z
) - z-
1
Y
(z
) = (Δt
/2) (X
(z
) + z-
1
X
(z
)).
Дискретная передаточная функция - это отношение Z
-изображений выходной и входной переменных, поэтому
K
(z
) = Y
(z
) /X
(z
) = (Δt
/2) (1 + z
-1
) / (1 - z
-1
) = (Δt
/2) (z
+ 1) / (z
- 1).
В таблице 2 приведены выражения дискретных передаточных функций для различных методов численного интегрирования для одного и двух интеграторов.
Таблица 2
| K
(p
) |
K
(z
) |
| Метод прямоугольников (1) |
Метод прямоугольников (2) |
Метод трапеций |
1
 p p
|
Δt
 z
- 1 z
- 1
|
Δt z
 z
- 1 z
- 1
|
Δt (z
+ 1)
 2 (z
- 1) 2 (z
- 1)
|
1
 p
2 p
2
|
(Δt
) 2
(z
+1)
 2 (z
- 1) 2 2 (z
- 1) 2
|
(Δt
) 2
z
 (z
- 1) 2 (z
- 1) 2
|
(Δt
) 2 (
z
2
+ 4z
+ 1)
 6 (z
- 1) 2 6 (z
- 1) 2
|
Видим, что одно и то же аналоговое устройство может описываться отличающимися дискретными передаточными функциями.
В таблице 1 была приведена дискретная передаточная функция интегрирующей цепи (для которой К
(р
) = 1/ (1 + рТ
)), полученной применением Z
-преобразования. Найдем другие варианты дискретной передаточной функции интегрирующей цепи, отличающиеся методами численного интегрирования.
При использовании метода прямоугольников (1) в передаточную функцию K
(p
) = 1/ (1 + pT
) вместо р
нужно подставить (z
- 1) /Δt
. Тогда получим
 K
(z
) = 1/ (1 + (z
- 1) T
/Δt
) =. K
(z
) = 1/ (1 + (z
- 1) T
/Δt
) =.
Аналогично можно получить дискретные передаточные функции и для других методов численного интегрирования. Они представлены в таблице 3 Принято обозначение Δt
/T
= α
Таблица 3
| Метод |
K
(z
) |
| Z
-преобразование |
α z
 z
- e
-α z
- e
-α
|
| Метод прямоугольников (1) |
α
 z
- (1 - α) z
- (1 - α)
|
| Метод прямоугольников (2) |
(α/ (1 + α)) z
 z
- 1/ (1 + α) z
- 1/ (1 + α)
|
| Метод трапеций |
(α / (2 + α)) (z
+ 1)
 z
- (2 - α) / (2 + α) z
- (2 - α) / (2 + α)
|
Этим передаточным функциям соответствуют следующие рекуррентные формулы.
Для Z
-преобразования
yk
=
e-
α
yk
- 1
+ αxk
. (7)
Для численного интегрирования по методу прямоугольников (1)
yk
= (
1 - α) yk
- 1
+ αxk
- 1
.
Полученная формула совпадает с формулой для прямого метода Эйлера
Для численного интегрирования по методу прямоугольников (2)
yk
=
(1/ (1 + α)) yk
- 1
+ (α/ (1 + α)) xk
. (8)
и по методу трапеций
yk
=
( (2 - α) / (2 + α)) yk
- 1
+ (α/ (2 + α)) (xk
+ xk
- 1
). (9)
В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов.
Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со значением выходного процесса, рассчитанного по предыдущим значениям входного процесса. Это экстраполированное значение не должно значительно отличаться от входного процесса.
В противном случае возникают большие ошибки моделирования, а при большом интервале дискретизации процесс может стать неустойчивым. Выбор интервала дискретизации нужно связывать с полосой пропускания замкнутой системы.
Проводя аналогию с теоремой Котельникова, можно потребовать, чтобы Δf
0,1
Δt
= 5 - 10, где Δf
0,1
- полоса пропускания замкнутой системы по уровню 0,1.
Рассмотрим моделирование непрерывной замкнутой системы на конкретном примере, когда передаточная функция разомкнутой системы
 Кр
(р
) =. (10) Кр
(р
) =. (10)Такая модель часто используется при анализе ошибок в следящей системе.
Запишем дискретную передаточную функцию разомкнутой системы, заменяя интеграторы по методу прямоугольников (2). Для этого преобразуем передаточную функцию разомкнутой системы (5.10), поделив числитель и знаменатель на р
2
:
 Кр
(р
) =. Кр
(р
) =.
Используя соотношения, приведенные в таблице (5.2), получим:
К
(Δt
)2
z
/(z
– 1)2
Т
+ Δt z
/(z
– 1)
|
|
|
  Кр
(z
) = =, (11) Кр
(z
) = =, (11)
где b
1
= K
(Δt
) 2
/ (T+
Δt
), a
1
= - (2T+
Δt
) / (T+
Δt
), a
2
= T
/ (T+
Δt
).
Для моделирования устройства с передаточной функцией (11) используется БИХ-фильтр, коэффициенты числителя которого (ForwardCoefficients) представляются массивом из двух элементов (0,b
1
), а коэффициенты знаменателя - массивом из трех элементов (1, a
1
,a
2
).
Специфика использования БИХ-фильтра заключается в том, что неизвестен целиком входной массив Х
, а известен только текущий элемент, а следующий элемент рассчитывается с учетом значения текущего элемента выходного массива фильтра. В LabVIEWсуществует такой фильтр - IIRFilterPtByPt (IIRFilterPointByPoint - БИХ-фильтр точка за точкой).
 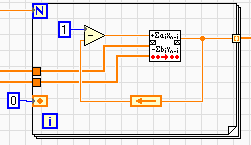 |
| Рис.6 |
Вычисления БИХ-фильтром IIRFilterPtByPtпроизводятся в цикле For
Loop (рис.5.6). В этом же цикле генерируется единичное входное воздействие. Автоматическое появление в цепи обратной связи регистра сдвига обусловлено тем, что рассчитанное значение выходного процесса используется для сравнения с входным только в следующем интервале дискретизации, то есть с запаздыванием на интервал дискретизации. В результате вычислений формируется массив переходной характеристики.
Для точного расчета переходной характеристики воспользуемся ВП ODELinearnthOrderNumeric - “Решение линейного обыкновенного дифференциального уравнения n-го порядка в численном виде” (рис.7).
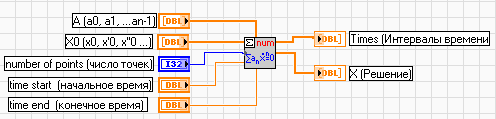 |
| Рис.7 |
ВП находит решение в виде суммы экспонент и вычисляет его для заданных точек. Поэтому решение точное.
Вход А представляет собой массив коэффициентов дифференциального уравнения в порядке увеличения степени производной. Коэффициент при производной самой высокой степени считается равным 1 и не требует ввода.
На вход Х0 подается массив начальных условий - начальные значения решения и его n - 1 - й производных.
Вход “число точек" задает число равноудаленных по времени точек между начальным и конечным временем
Выход Х содержит массив значений решения в равномерно расположенных по оси времени точках. Значение времени в этих точках выводится в массиве Times.
Дифференциальное уравнение замкнутой системы запишем по передаточной функции замкнутой системы:
  Кз
(р
) = = (12) Кз
(р
) = = (12)
Дифференциальное уравнение замкнутой системы
Td
2
y
/dt
2
+ dy
/dt
+ Ky
= Kx
Запишем однородное дифференциальное уравнение, учитывая, что коэффициент при высшей производной должен быть равен 1
d
2
y
/dt
2
+ (1/Т
) dy
/dt
+ (K
/Т
) y
= 0
Для компьютерного решения этого уравнения нужно задать массив А = (К
/Т
, 1/Т
). Чтобы получить переходную характеристику, нужно задать массив Х = ( - 1, 0) и к решению прибавить 1.
Полностью блок-схема программы моделирования замкнутой системы приведена на рис.8.
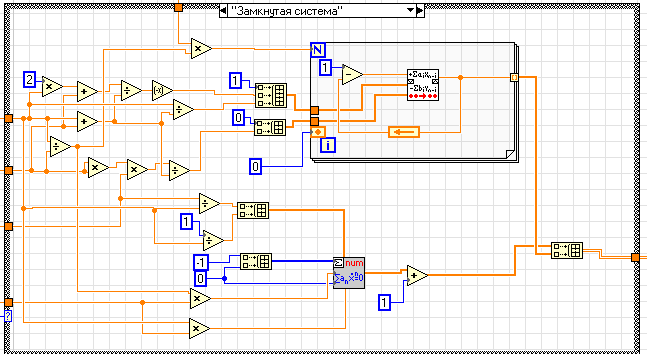 Рис.8
В основе технологии использования LabVIEW лежит комбинированное моделирование систем на ЭВМ, включающее аналитическое, имитационное и натурное.
Для аналитического моделирования характерно то, что алгоритм функционирования системы записывается в виде некоторых аналитических соотношений (алгебраических, интегро-дифференциальных, конечно - разностных и т.п.) или логических условий. При имитационном моделировании алгоритм функционирования системы воспроизводится во времени с сохранением логической структуры и последовательности протекания элементарных явлений, составляющих процесс. В настоящее время имитационное моделирование - наиболее эффективный метод исследования систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.
Натурным моделированием называют проведение исследования на реальном объекте с возможностью вмешательства человека в процесс проведения эксперимента и последующей обработки результатов эксперимента на вычислительной технике.
Отличие модельного эксперимента от реального заключается в том, что в модельном эксперименте могут быть реализованы любые ситуации, в том числе "невозможные" и аварийные, что в силу разных причин бывает недопустимо при работе с реальными объектами. Все представленные виды моделирования могут быть реализованы с использованием системы программирования LabVIEW.
1. Н.А. Виноградова, Я.И. Листратов, Е.В. Свиридов. "Разработка прикладного программного обеспечения в среде LabVIEW". Учебное пособие - М.: Издательство МЭИ, 2005.
2. http://www.automationlabs.ru/
3. http://digital. ni.com/
4. http://www.labview.ru/
5.
http://ru. wikipedia.org/
|