МИНИСТЕРСВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Приборостроительный факультет
Кафедра «Микро- и нанотехника»
Курсовая работа по дисциплине «Физика полупроводников»
''ЭФФЕКТ ПОЛЯ. РАСЧЕТ ЭФФЕКТИВНОЙ ПОДВИЖНОСТИ НОСИТЕЛЕЙ ЗАРЯДА''
Выполнила: студентка ПСФ,
гр. 113416 Ющенко А.А.
Руководитель:
канд. физ. - мат. наук, доц. Сернов С.П.
Минск 2009
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 2
1
. ЭФФЕКТ ПОЛЯ
.. 2
1.1 Зонная диаграмма. 2
2
ЭФФЕКТ ПОЛЯ ПРИ РАЗЛИЧНЫХ ВЗАИМОДЕЙСТВИЯХ
.. 2
2.1Влияние квантово-размерных слоев In(Ga)As на эффект поля в слоях GaAs …………………………………………………………………………….2
2.1.1Методика исследования. 2
2.1.2Экспериментальные результаты.. 2
3 РАСЧЕТ ЭФФЕКТИВНОЙ ПОДВИЖНОСТИ НОСИТЕЛЕЙ ЗАРЯДА
2
ЗАКЛЮЧЕНИЕ. 2
СПИСОК ЛИТЕРАТУРЫ.. 2
Различные электронные процессы, которые несколько условно могут быть объединены названием поверхностных, в значительной мере связаны с наличием приповерхностного слоя пространственного заряда. Свойства этого слоя для данного вида образца полупроводника однозначно характеризуются поверхностным электростатическим потенциалом. Отсюда следует, что возможности исследования и управления величиной и знаком поверхностного электростатического потенциала. Существует множество методов изменения поверхностного электростатического потенциала, но в данной работе рассматривали метод воздействия на поверхностный электростатический потенциал полупроводника. Он заключается в непосредственном приложении внешнего электрического поля, нормального к его поверхности. Этот метод, получивший название «эффекта поля».
В зависимости от процесса релаксации разделяют существование двух принципиально различных механизмов экранировки объема полупроводника от проникновения в него внешнего поперечного поля. Первый из них заключается в захвате индуцированного в полупроводник заряда поверхностными состояниями. Второй механизм экранировки связан с изменением заряда в слое пространственного заряда, и следовательно, с изменением поверхностного электростатического потенциала.
Величину поверхностного потенциала можно изменять не только изменяя окружающую среду, но и создавая у поверхности полупроводника поперечное электрическое поле. Влияние внешнего электрического поля на электропроводность полупроводника получило название эффекта поля.
Существует большое число разнообразных экспериментальных приемов изучения эффекта поля, как в стационарном, так и в нестационарном режимах. Пример стационарного метода показан на рисунке 1.1.

Рисунок 1.1 – Схема наблюдения стационарного эффекта поля.
Пластинка полупроводника П служит одной из обкладок конденсатора, второй обкладкой которого является металлическая пластина М, отделенная от полупроводника тонким слоем изолятора И. К конденсатору прикладывается постоянное напряжение, величину и знак которого можно изменять. Концы пластинки полупроводника имеют низкоомные контакты, с помощью которых она включается мостовую схему (или какую-либо другую) для точного измерения малых измерений проводимости.
Ещё удобнее исследовать эффект поля, прикладывая к пластинам конденсатора переменное напряжение низкой частоты (десятки или сотни герц). Тогда, используя простые схемы и подавая на одну из пар пластин осциллографа сигнал, пропорциональный приложенному напряжению u, а на другую пару пластин – сигнал, пропорциональный ∆G , можно получить на экране всю кривую зависимости ∆G от u. Это позволяет легко определить по формуле 1 значение Ys
при любом напряжении на конденсаторе, и в частности, при u = 0 (в «естественном» состоянии поверхности).
Ya
= Ys
min
+ ∆Ys
, (1.1)
∆Ys
определяется величиной (G – Gmin
).
Такой метод имеет большое преимущество перед использованием различных газовых атмосфер, так как эти последние могут не только искривлять энергетические зоны, но и изменять концентрацию поверхностных уровней энергии вследствие адсорбции атомов газов.
Исследование эффекта поля позволяет получить ценную информацию о поверхностных состояниях (энергетических уровнях и их концентрациях). Эта возможность основана на следующем. Электроны и дырки под каждой единицей поверхности создают заряд
Q = Qv
+ Qs
= e( Гp
– Гn
) + Qs
(1.2)
где Qv
– подвижный заряд в объеме приповерхностного слоя
Qs
– связанный заряд на поверхностных уровнях
Гp
и Гn
– полные количества избыточных дырок и электронов, определяемые формулой (1.3)


Кроме того, имеется ещё заряд, создаваемый ионами в объеме полупроводника (заряженными донорами и акцепторами), и ионами, адсорбированными на внешней поверхности окисла. В отсутствие внешнего поля заряд ионов равен по величине и противоположен по знаку заряду Q.
Во многих случаях можно считать, что в эффекте поля ионный заряд не изменяется. Это справедливо, если доноры и акцепторы в объеме полупроводника полностью ионизированы. Адсорбированные же ионы обмениваются электронами с полупроводником очень медленно (часто за многие секунды и минуты), и за время измерения их заряд остается постоянным. Поэтому индуцированный заряд равен
δQ = δQv
+ δQs
= e( δГp
– δГn
) + δQs
(1.4)
Так как Гp
и Гn
– известные функции поверхностного потенциала Ys
, а этот последний тоже определяется из эффекта поля, то величину δQv
можно легко найти. С другой стороны, суммарный индуцированный заряд (отнесенный к единице площади) равен
δQ = Cu (1.5)
где С – емкость конденсатора на единицу площади, которая непосредственно определяется на опыте. Поэтому оказывается возможным определить δQs
и найти, какая доля иногда выражают с помощью эффективной подвижности. Она, по определению, равна
(1.6)
где δG – изменение проводимости в эффекте поля.
Эта величина имеет особенно простой физический смысл, если искривление зон невелико и проводимость везде можно считать монополярной. Тогда получаем для дырочного полупроводника
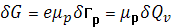 ,(1.7) ,(1.7)
а следовательно,
В этом случае μэф
определяет, какая доля полного заряда поверхности находится в подвижном состоянии.
Исследуя зависимость Qs
от Ys
, можно определить энергетическое положение поверхностных уровней энергии и их концентрацию. Действительно, при изменении Ys
поверхностные уровни, так же как и края зон у поверхности, перемещаются относительно уровня Ферми F. При прохождении какого-либо уровня Es
через F зарядное состояние уровня изменяется. При наличии уровней только одного типа это проявляется на кривых зависимости Qs
от Ys
возникновением ступени.
Чтобы охарактеризовать энергетический спектр поверхностных состояний, отсчитываем Es
при неискривленных зонах (Ys
=0) от положения уровня Ферми в собственном полупроводнике Fi
, обозначая εs
≡ Es
– Ei
. Тогда
Es
– F = εs
– (F – Fi
) – kTYs
.
Для невырожденных (в объеме ) полупроводников получаем
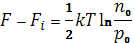
Поэтому можно найти, что вероятность заполнения уровня Es
при данном Ys
есть
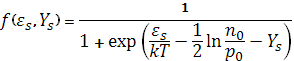
Если рассматриваемые уровни акцепторные и их поверхностная концентрация равна ν, то заряд поверхности буде равен
Qs
= –eνf(εs
, Ys
). (1.8)
Для донорных уровней получаем
Qv
= eν(1 – f(εs
, Ys
)). (1.9)
Из формул (1.8) и (1.9) видно, что в обоих случаях на кривых зависимости Qs
от Ys
появляется ступень, а также точка перегиба. Последняя соответствует поверхностному потенциалу
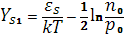
Значит, определяя по данным эффекта поля Ys
1
, можно найти εs
. Величина ступени равна eν.
В случае нескольких дискретных уровней энергии получилось бы не одна, а несколько точек перегиба.
Если имеется непрерывный энергетический спектр поверхностных состояний, то Q, получается суммированием выражений типа. Так, например, для акцепторных уровней получаем:
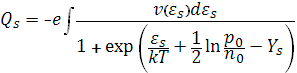
Где интегрирование производится по всей запрещенной зоне энергий. Здесь ν(εs
) есть поверхностная плотность уровней, рассчитанная на единичный интервал энергии. В этом случае задача определения энергетического спектра поверхностных состояний ν(εs
) по экспериментальной зависимости Qs
от Ys
становится гораздо более сложной и требует либо дополнительных данных, либо дополнительных предположений.
Экспериментальное исследование зависимости Qs
от Ys
(«кривых захвата») показывает, что кривые захвата, как правило, оказываются плавными и не обнаруживают ясно выраженных ступеней и точек перегиба. Пример таких кривых для германия приведен на рисунке 1.2

Рисунок 1.2 – Пример зависимости заряда поверхности от поверхностного потенциала для образца германия
Это показывает, что энергетический спектр поверхностных состояний, ответственных за захват носителей заряда, является казинепрерывным. Анализ кривых захвата приводит также к заключению, что ν(εs
) имеет обычно минимальное значение вблизи середины запрещенной зоны и увеличивается по мере приближения к краям разрешенных зон энергии.
Важные данные о свойствах поверхностных уровней можно получить, исследуя изменение ∆G во времени. Для этого разработаны различные методы. Одна из схем показана на рисунке 1.3

где П – полупроводник; М – металлическая обкладка; И – изолятор; Г – генератор прямоугольных импульсов; О – осциллограф; Б – источники постоянного тока
Рисунок 1.3 – Наблюдение релаксации проводимости в эффекте поля.
Здесь на обкладках конденсатора полупроводник – металл подается прямоугольный импульс напряжения с крутым передним фронтом. Об изменении проводимости полупроводника судят по изменению падения напряжения на нем, возникающего от протекания слабого постоянного тока от батареи Б. Это напряжение регистрируется осциллографом О, развертка которого синхронизована с генератором импульсов Г.
В подобных импульсных методах, однако, всегда необходимо тщательно исключать наводку в измерительной схеме, возникающую при наложении напряжения на конденсатор (вследствие неполной симметрии схемы), которая может быть намного больше измеряемого сигнала. Для ее исключения образец включают в схему моста R
-
C
и подбирают сопротивления r1
, r2
и емкости С1
, С2
таким образом, чтобы при выключенной батарее Б сигнал наводки был минимальным.
Наблюдаемая зависимость ∆G от времени обычно имеет вид, показанный схематически на рисунке 1.4

Рисунок 1.4 – Зависимость изменения проводимости ∆G в эффекте поля от времени (схематически)
После подачи напряжения, соответствующего обогащению поверхностного слоя основными носителями, G быстро увеличивается и через короткое время, порядка максвелловского времени релаксации, ∆G достигает наибольшего значения. За эти времена поверхностные уровни ещё не успевают заметно изменить свое зарядовое состояние, и весь индуцированный заряд находится в свободном состоянии. Затем начинается перераспределение заряда между объемом и поверхностными уровнями и G уменьшается. Это изменение имеет сложный, неэкспоненциальный характер. Сначала G изменяется быстро на некоторую величину ∆G1
. Эту стадию процесса можно условно охарактеризовать некоторым временем релаксации τ1
, в течение которого G уменьшается на определенную долю в e раз. Значения τ1
зависят от рода полупроводника и состояния его поверхности и обычно лежат в интервале 10-2
– 102
мкс. Затем электропроводность изменяется ещё на величину ∆G2
, однако гораздо более медленно, и в конце концов достигает стационарного состояния. Характерное время для второй стадии процесса может измеряться многими секундами и минутами. Такой характер кинетики показывает, что поверхностные уровни можно разделить на две группы: «быстрые» уровни, которые легко обмениваются электронами с объемом, и «медленные» уровни, обменивающиеся электронами с объемом гораздо хуже.
Другой прием исследования эффекта поля показан на рисунке 1.5.

где О – образец; И – изолятор; М – металлическая обкладка; Г – гальванометр.
Рисунок 1.5 – Измерение частотной зависимости эффективной подвижности.
Здесь к конденсатору и к торцам образца прикладываются переменные напряжения одинаковой частоты
u = u0
cos(ωt), u1
= u10
cos(ωt) (1.10)
Эффект поля вызывает модуляцию проводимости образца, которую при малых напряжениях можно считать тоже гармонической:
G = G0
+ (∆G)0
cos(ωt – φ) = G0
+ (∆G)0
(cosωt∙cosφ + sinωt∙sinφ).
Поэтому сила тока через через образец есть
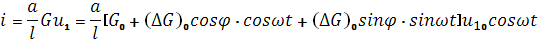
где 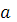 - ширина пластинки, а - ширина пластинки, а 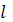 – её длина. – её длина.
Усредняя это выражение по периоду колебаний, мы находим, что вследствие эффекта поля возникает постоянная составляющая тока
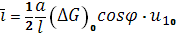
С другой стороны, амплитуда индуцированного заряда на единице поверхности есть (∆Q)0
= Cu0
. Поэтому для эффективной подвижности получается
Пользуясь комплексным описанием гармонических колебаний, можно сказать, что формула дает вещественную часть Re μэф
.
Определение фазового сдвига φ требует дополнительных измерений. Однако уже исследование Re μэф
дат много данных. На рисунке 1.6 приведен пример зависимости Re μэф
от частоты для германия p-типа, поверхность которого была протравлена кислотами (смесь уксусной, азотной и фтористоводородной) в различных газовых атмосферах.
 \ \
Рисунок 1.6 – Пример зависимости эффективной подвижности от частоты. Германий p-типа.
Из рисунка видно, что при адсорбции дипольных молекул воды Re μэф
при низких частотах оказывается отрицательной, что означает существование инверсионного слоя. Однако при увеличении частоты Re μэф
становится положительной. В других газах (сухой кислород, озон ) инверсионный слой не возникает. Исследование зависимости μэф
от частоты подтверждает существование быстрых и медленны поверхностных уровней и позволяет оценить их характерные времена релаксации.
Имеющиеся данные показывают, что поверхностные состояния характеризуются сложным и, как правило, непрерывным энергетическим спектром. Часть поверхностных уровней лежит в верхней половине запрещенной зоны, а часть – в нижней половине.
Эти уровни могут быть акцепторными и донорными. Их концентрация зависит от обработки поверхности (шлифовка, химическое травление и др.) и, например, в германии может достигать порядка 1014
– 1015
см-2
.
Основная часть быстрых поверхностных состояний является по-видимому, состоянием Тамма, уровни которых на реальной поверхности локализованы вблизи раздела полупроводник – окисел. Медленные же состояния обычно связывают с адсорбированными атомами, так как электронный обмен между ними и объемом полупроводника сильно затрудняется наличием слоя окисла. Однако некоторые из состояний Тамма могут оказаться тоже медленными, если соответствующие им сечения захвата электронов (дырок) малы.
Поверхностные состояния особого типа возникают при достаточно сильном изгибе зон. Если, например, Ys
>0, то зоны изгибаются вниз и у поверхности возникает потенциальная яма для электронов (рисунок 1.7)

Рисунок 1.7 – Потенциальная яма для электрона при Ys
>0. Штрихами обозначен один из уровней электрона в яме.
Форма её зависит от степени однородности поверхности. Если свойства последней всюду одинаковы, то яма, очевидно, имеет вид желоба с острым дном, вытянутого вдоль поверхности. При достаточной глубине и ширине ямы в ней могут образоваться связанные состояния, находясь в которых, электроны локализованы вблизи поверхности. Это явление называется поверхностным квантованием. В одномерном случае указанным состояниям отвечали бы дискретные уровни в запрещенной зоне; в трехмерной задаче с однородной поверхностью получаем поверхностные энергетические зоны.
Вблизи границы раздела полупроводника с другой средой можно создать условия для реализации квантового размерного эффекта, ограничивая движение носителей в слое, толщина которого сравнима с их дебройлевской длиной волны. Так, если в полупроводнике p-типа, например, с помощью эффекта поля создать на поверхности достаточно большой изгиб зон вниз, то около границы раздела с диэлектриком в полупроводнике можно образовать узкий потенциальный желоб с размерно-квантовыми электронами (рисунок 1.7). Поскольку электроны «заквантованы» только в направлении х, то их спектр имеет вид двумерных подзон, а состояние определяется номером подзоны и двумерным квазиимпульсом с компонентами py
, pz
. При достаточно низких температурах все электроны оказываются в самой нижней подзоне и образуют двумерный электронный газ.
Аналогичная ситуация имеет место в гетеропереходе GaAs – GaAlx
As1-
x
,
когда из специально легированного донорами полупроводника GaAlx
As1-
x
с широкой запрещенной зоной электроны переходят в GaAs и образуют в нем около границы раздела канал с двумерным электронным газом. Благодаря селективному легированию и хорошему согласованию решеток компонент гетероперехода носители в двумерном канале обладают очень высокой подвижностью. На основе подобных структур созданы сверхбыстродействующие транзисторы.
Тонкий слой полупроводника, ограниченного с обеих сторон полупроводником с большей шириной запрещенной зоны, представляет собой кантовую яму (рисунок 1.8)

Рисунок 1.8 – Схематическое изображение квантовой ямы
А периодическая последовательность таких слоев образует макроскопическую квантовую сверхрешетку (рисунок 1.9)

Рисунок 1.9 – Схематическое изображение сверхрешетки GaAs – GaAlAs
Реальные поверхности полупроводников, обработанные в травителе и находящиеся в атмосфере, обычно бывают покрыты аморфным и пористым слоем оксида толщиной (2 – 7) нм. Концентрация поверхностных состояний на таких поверхностях может быть порядка 1011
– 1012
см-2
, т.е. значительно меньшей, чем концентрация на атомарно-чистых поверхностях. Это может быть связано с уменьшением концентрации собственных поверхностных состояний при окислении поверхности. Неоднородность поверхности приводит к тому, что полной аналогии между поверхностными и объемными зонами нет. Состояния в поверхностных зонах вблизи неоднородной поверхности или границы раздела могут оказаться локализованными не только вдоль оси Ох, но и в плоскости yz; в результате электропроводность по поверхностным зонам может не проявляться[1].
Будем считать, что электрическое поле создается заряженной металлической плоскостью с поверхностной плотностью зарядов σ. Поскольку силовые линии электрического поля должны быть замкнуты, то на поверхности полупроводника возникает равный по величине, но противоположный по знаку электрический заряд. В зависимости от знака заряда на металлической плоскости (положительной или отрицательной) экранирующий это поле заряд в приповерхностной области полупроводника также будет различных знаков. На рисунке 1.1.1 приведены ситуации положительно и отрицательно заряженной плоскости.
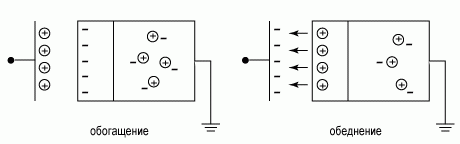
Рисунок 1.1.1 – Изменение концентрации свободных носителей в приповерхностной области полупроводника при наличии вблизи поверхности заряженной металлической плоскости
Случай, когда в приповерхностной области возрастает концентрация свободных носителей, носит название обогащение, а когда в приповерхностной области уменьшается концентрация свободных носителей - обеднение.
Если концентрация доноров в объеме полупроводника ND
=1015
см-3
, то среднее расстояние между свободными электронами (и ионизированными донорами) в квазинейтральном объеме полупроводника будет равно, а = ND
-1/3
= 10-5
см = 1000 Å. При поверхностной плотности заряда 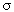 = 1012
см-2
толщина слоя пространственного заряда ионизованных доноров будет равна 1011
/ 1015
= 10-4
см или 1 микрон. Отсюда следует, что электрическое поле в полупроводник может проникать на значительные расстояния. = 1012
см-2
толщина слоя пространственного заряда ионизованных доноров будет равна 1011
/ 1015
= 10-4
см или 1 микрон. Отсюда следует, что электрическое поле в полупроводник может проникать на значительные расстояния.
Изменение концентрации свободных носителей в приповерхностной области полупроводника под действием внешнего электрического поля получило название эффекта поля.
При наличии внешнего поля приповерхностная область в полупроводнике не будет электронейтральной. Заряд, возникший в этой области, обычно называется пространственным зарядом, а сама область - областью пространственного заряда. Наличие электрического поля E(z) в области пространственного заряда меняет величину потенциальной энергии электрона. Если поле направлено от поверхности вглубь полупроводника, то электроны в этом случае будут иметь минимальную энергию у поверхности, что соответствует наличию потенциальной ямы для электронов там же.
Изменение потенциальной энергии электронов:
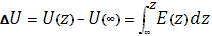
где U(∞)-потенциальная энергия электронов в квазинейтральном объеме полупроводника. Поскольку на дне зоны проводимости кинетическая энергия электронов равна нулю, то изменение потенциальной энергии по координате должно точно так же изменить энергетическое положение дна зоны проводимости Ec
, (а соответственно и вершины валентной зоны Ev
.) На зонных диаграммах это выражается в изгибе энергетических зон[5].
Величина разности потенциалов между квазинейтральным объемом и произвольной точкой ОПЗ получила название электростатического потенциала:
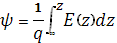
Значение электростатического потенциала на поверхности полупроводника называется поверхностным потенциалом и обозначается символом ψs
.
Знак поверхностного потенциала ψs
соответствует знаку заряда на металлическом электроде, вызывающего изгиб энергетических зон. ψs
> 0, зоны изогнуты вниз, ψs
< 0, зоны изогнуты вверх (рис. 11).
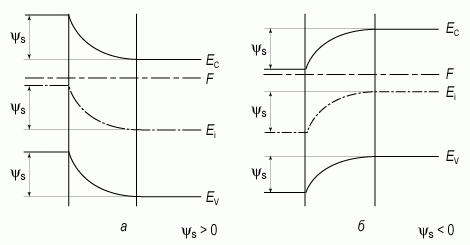
Рисунок 1.1.2 – Энергетические зоны на поверхности полупроводника n-типа:а) в случае обеднения; б) в случае обогащения
2
ЭФФЕКТ ПОЛЯ ПРИ РАЗЛИЧНЫХ ВЗАИМОДЕЙСТВИЯХ
2.1 Влияние квантово-размерных слоев
In(Ga)As на эффект поля в слоях GaAs
Квантово-размерные гетеронаноструктуры (ГНС) с квантовыми точками (КТ) и квантовыми ямами (КЯ) In(Ga)As/GaAs играют важную роль в современной электронике. Исследование эффекта поля в этих структурах представляет интерес в связи с разработкой новых методик диагностики электронных параметров этих структур. При встраивании квантово-размерного слоя In(Ga)Asв приповерхностную область пространственного заряда (ОПЗ) матрицы GaAs эти слои должны проявлять себя в эффекте поля аналогично поверхностным состояниям (ПС) как электронные или дырочные ловушки для инжектированных носителей. В связи с конкуренцией квантово-размерных и поверхностных состояний за захват носителей высокая поверхностная концентрация поверхностных состояний в GaAs создает определенные трудности в выделении вклада квантово-размерных состояний на характеристиках эффекта поля. Для определения электронных параметров квантово-размерных слоев, в частности плотности состояний, высоты эмиссионного барьера и др., обычно используется емкостная диагностика барьеров Шоттки или p
-n
-
переходов в квантово-размерных гетеронаноструктурах. В данной работе изучалась возможность использования эффекта поля для диагностики гетеронаноструктур In(Ga)As/GaAs.
2.1.1 Методика исследования
Исследовались гетеронаноструктуры с одиночными слоями квантовых точек InAsи квантовых ям In0.2
Ga0.8
As шириной 3 нм, встроенными в область пространственного заряда на разных расстояниях dc
= 5, 20, 100 и 300 нм от поверхности буферного слоя GaAsn
-типа, который предварительно наносилсяна подложку полуизолирующего GaAs. Благодаря закреплению (пиннингу) уровня Ферми на поверхностных состояниях в приповерхностной области слоя n-GaAs возникает обедненный электронами слой с высотой барьера около 0.6 эВ. Ширина области пространственного заряда при уровне легирования буферного слоя ~ 1016
см-3
составляла обычно 200-250 нм. Изменение толщины покровного слоя dc
позволяло менять положение слоя квантовых точек или квантовых ям в области пространственного заряда почти от границы с поверхностью до границы с квазинейтральной областью структуры. Структуры выращивались методом газофазной эпитаксии из металлорганических (МОС) соединений при атмосферном давлении водорода - газа-носителя паров МОС.
Эффект поля исследовался на разборных МДП структурах металл-диэлектрик-полупроводник (МДП) типа полевых транзисторов с пластинкой слюды толщиной порядка 20 мкм в качестве диэлектрика. Разборная конструкция МДП структуры обеспечивает простоту реализации методики эффекта поля и удобна в том отношении, что ее емкость Cg
определяется емкостью слюдяного конденсатора и практически не зависит от емкости ОПЗ. На управляющий электрод (затвор) подавалось однополупериодное синусоидальное напряжение Vg
(
t
)
положительной полярности с амплитудой до 800 В (рис. 1), инжектирующее в гетеронаноструктуре основные носители (электроны). К омическим контактам на поверхности гетеронаноструктур (ширина контактов и расстояние между ними = 5 мм) прикладывалось постоянное напряжение Vd
около 10 В. Динамическая зависимость квазиповерхностной проводимости ∆
σs
(
t
)
от переменного напряжения на затворе Vg
(
t
)
после аналого-цифрового преобразования анализировалась на компьютере. При постоянной емкости Cg
и отсутствии захвата инжектированных электронов на какие-либо ловушки динамическая зависимость ∆
σs
(
Vg
(
t
))
должна быть линейной (рисунок 2.1.1.1, кривая 1), и определенная по ее наклону подвижность в эффекте поля
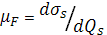
где dQs
=
Cg
dVg
,
должна быть равна дрейфовой подвижности электронов в области пространственного заряда μn
.
Захват инжектированных в эффекте поля электронов на поверхностные и объемные ловушки, а также в квантово-размерные состояния приводят к уменьшению наклона динамической зависимости ∆
σs
(
Vg
(
t
))
и появлению на ней петли гистерезиса на частотах измерения f ~ (27πτ)-1
, где τ - время релаксации процесса захвата.

Рисунок 2.1.1.1 – Динамическая зависимость удельной поверхностной проводимости от переменного напряжения на затворе. При отсутствии захвата на ловушки, 2 - для гетеронаноструктур со слоем квантовых точек InAs, встроенным вблизи границы области пространственного заряда с квазинейтральной областью. На вставке показана форма переменного напряжения на затворе.
На рисунке 2.1.1.1 приведена типичная кривая динамического эффекта поля (ДЭП) при наличии захвата на ловушки (кривая 2). Верхняя ветвь этой кривой ∆
σsi
(
Vg
(
t
))
определяет изменение поверхностной проводимости при инжекции электронов в полупроводник, нижняя ветвь ∆
σs
е
(
Vg
(
t
)) -
изменение проводимости при их экстракции. Для количественной характеристики гистерезиса определялась ширина петли гистерезиса по оси напряжений ∆
Vgh
между одинаковыми значениями проводимости: на кривой инжекции ∆
σsi
(0)
и на кривой экстракции ∆
σs
е
(0).
Равенство этих значений проводимости означает, что инжектированные электроны с поверхностной концентрацией
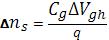
где 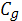 – удельная емкость МДП конденсатора, не участвуют в проводимости, т.к. связаны на ловушках и не успевают перейти в зону проводимости при уменьшении напряжения Vg
(
t
). – удельная емкость МДП конденсатора, не участвуют в проводимости, т.к. связаны на ловушках и не успевают перейти в зону проводимости при уменьшении напряжения Vg
(
t
).
Процесс захвата инжектированных носителей на ловушки характеризуют также величины ∆
σsi
(0)
и наклон кривой инжекции 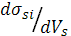 Отклонение ∆
σsi
(0)
от равновесного нулевого значения при действии периодического монополярного напряжения обусловлено захватом и накоплением инжектированных электронов на глубоких ловушках, с которых эмиссия в зону проводимости не успевает произойти на частоте измерения. Это приводит к увеличению исходного отрицательного заряда на ПС на величину Отклонение ∆
σsi
(0)
от равновесного нулевого значения при действии периодического монополярного напряжения обусловлено захватом и накоплением инжектированных электронов на глубоких ловушках, с которых эмиссия в зону проводимости не успевает произойти на частоте измерения. Это приводит к увеличению исходного отрицательного заряда на ПС на величину
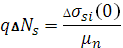
Производная 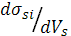 определяет подвижность в эффекте поля μF
(1) Фактор захвата θ = μF
/μn
характеризует долю инжектированных электронов, которые участвуют в проводимости[4]. определяет подвижность в эффекте поля μF
(1) Фактор захвата θ = μF
/μn
характеризует долю инжектированных электронов, которые участвуют в проводимости[4].
На частотах измерения ДЭП f << (2πτ)-1
и f >> (2πτ)-1
гистерезис должен отсутствовать: на низких частотах - из-за того, что за время действия напряжения успевает завершиться процесс релаксации захваченных носителей, на высоких частотах - из-за отсутствия самого захвата. Такой квазистационарный режим измерения ДЭП обычно используется для определения изгиба зон по минимуму квазиповерхностной проводимости. Он применим к относительно узкозонным полупроводникам (Ge, Si), но в GaAs из-за большой ширины запрещенной зоны и высокой концентрации ПС, приводящей к закреплению уровня Ферми на поверхности, минимум квазиповерхностной проводимости обычно не наблюдается. В данной работе этот метод в условиях нестационарного ДЭП, т.е. при наличии гистерезиса, развивается для исследования процесса захвата инжектированных носителей в ГНС. Измерения ДЭП проводились на частоте f= 60 Гц.
Для получения дополнительной информации о релаксации эффекта поля исследовалась также частотная зависимость малосигнального ЭП в диапазоне частот 20-106
Гц по методу. Этим методом также определялись подвижность μ
F
(
f
)
и фактор захвата
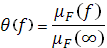
где 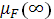 - подвижность в электронном поле на достаточно высокой частоте, когда захват отсутствует и - подвижность в электронном поле на достаточно высокой частоте, когда захват отсутствует и 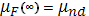
Частота f
1/2
,на которой  ,где ,где 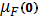 - подвижность на низкой частоте при завершившемся захвате на ловушки, определяет время релаксации эффекта поля - подвижность на низкой частоте при завершившемся захвате на ловушки, определяет время релаксации эффекта поля 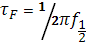 . .
2.1.2 Экспериментальные результаты
Рассмотрим сначала особенности ДЭП в однородном (буферном) слое GaAs и влияние на ДЭП освещения слоя, которое уменьшает высоту поверхностного барьера. В темноте (рисунок 2.1.2.1, кривая 1) гистерезис ДЭП относительно мал (ΔVgh
< 10 В), а подвижность в эффекте поля (1) в начале кривой инжекции μ
F
≈
4500 см2
/В∙с близка к значению холловской подвижности электронов и подвижности μ
F
в малосигнальном эффекте поля, которая не имеет дисперсии во всем диапазоне измерения частотной зависимости. Очевидно, на начальном участке кривой инжекции, когда напряжение Vg
(
t
)
мало, а скорость его изменения относительно велика, захвата инжектированных электронов на ПС практически не происходит, что объясняется большой высотой препятствующего захвату поверхностного барьера в GaAs (приблизительно 0.6 эВ).

Рисунок 2.1.2.1. Влияние освещения на ДЭП в однородном слое GaAs. Интенсивность освещения: 1 - в темноте, 2 -10%, 3 - 100%

Рисунок 2.1.2.2. Влияние встраивания слоя КТ на ДЭП. 1 - однородный слой GaAs. 2 - 5 - ГНС с КТ. Толщина покровного слоя dc
:
кривая 2 соответствует 5 нм, 3 - 20 нм, 4 -100 нм, 5 - 300 нм.
Однако в установившемся режиме ДЭП некоторый захват электронов на ПС все же происходит. На это указывает уменьшение наклона на кривой инжекции и уширение петли гистерезиса при больших значениях Vg
(
t
),
а также ярко выраженный эффект накопления, который проявляется в значительном отрицательном значении Δσsi
(0). Уменьшение 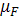 и увеличение ΔVgh
связаны с относительно быстро релаксирующим захватом на ПС, а накопление - с медленно релаксирующим захватом. Оценка увеличения концентрации отрицательно заряженных ПС по эффекту накопления (2) дает ΔNS
=
8-109
см-2
. Это значение составляет около 1% от равновесной концентрации отрицательного заряда на ПС (
Ns
~ 1012
см-2
), определяющего изгиб зон на реальной поверхности GaAs. и увеличение ΔVgh
связаны с относительно быстро релаксирующим захватом на ПС, а накопление - с медленно релаксирующим захватом. Оценка увеличения концентрации отрицательно заряженных ПС по эффекту накопления (2) дает ΔNS
=
8-109
см-2
. Это значение составляет около 1% от равновесной концентрации отрицательного заряда на ПС (
Ns
~ 1012
см-2
), определяющего изгиб зон на реальной поверхности GaAs.
Даже слабое освещение слоя GaAsизлучением от лампы накаливания сильно увеличивает захват на ПС. При максимальной интенсивности освещения (рисунок 2.1.2.1, кривая 3) ДЭП становится очень мал: подвижность 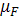 уменьшается, а ширина петли гистерезиса увеличивается в 20-30 раз, и полностью исчезает эффект накопления. Это обусловлено значительным уменьшением высоты поверхностного барьера в результате возникновения поверхностной фотоэдс Vф
, зависимость которой от интенсивности освещения L
имеет вид: Vф
=(kT/q)ln(l+BL),
где В -
некоторая постоянная. При максимальной интенсивности освещения, как показали измерения фотоэдс, Vф
достигает 0.4-0.5 В, и, следовательно, высота поверхностного барьера уменьшается приблизительно до 0.2 эВ. Было установлено, что величина Δσsi
(0) уменьшается, а ΔVgh
увеличивается также пропорционально InL в диапазоне, по крайней мере, двух порядков изменения интенсивности. Это определенно свидетельствует о том, что захват и накопление электронов на ПС происходит в результате их термического заброса через поверхностный барьер. уменьшается, а ширина петли гистерезиса увеличивается в 20-30 раз, и полностью исчезает эффект накопления. Это обусловлено значительным уменьшением высоты поверхностного барьера в результате возникновения поверхностной фотоэдс Vф
, зависимость которой от интенсивности освещения L
имеет вид: Vф
=(kT/q)ln(l+BL),
где В -
некоторая постоянная. При максимальной интенсивности освещения, как показали измерения фотоэдс, Vф
достигает 0.4-0.5 В, и, следовательно, высота поверхностного барьера уменьшается приблизительно до 0.2 эВ. Было установлено, что величина Δσsi
(0) уменьшается, а ΔVgh
увеличивается также пропорционально InL в диапазоне, по крайней мере, двух порядков изменения интенсивности. Это определенно свидетельствует о том, что захват и накопление электронов на ПС происходит в результате их термического заброса через поверхностный барьер.
Рисунок 2.1.2.2. показывает влияние встраивания слоя КТ и изменения его положения в области пространственного заряда на ДЭП. Чтобы не загромождать рисунок, кривые разнесены по вертикали, и поэтому положение точки Δσsi
(0) не связано с эффектом накопления, а задано произвольно. Видно, что встраивание слоя КТ по мере удаления его от поверхности приводит к закономерному уменьшению наклона кривой инжекции и к увеличению ширины петли гистерезиса (показана стрелкой на каждой кривой). Оба эффекта, очевидно, обусловлены снижением при увеличении dc
высоты поверхностного барьера, препятствующего захвату электронов на локализованные состояния в слое КТ. Особенно ярко эти эффекты проявляются при dc
=300
нм (кривая 5), когда слой КТ встроен вблизи границы ОПЗ с квазинейтральной областью структуры и барьер практически исчезает. По сравнению с ДЭП в буферном слое (кривая 1) начальный наклон кривой 5 уменьшился почти в 5 раз, а ширина петли гистерезиса увеличилась почти в 30 раз.
Заметим, что на кривых ДЭП при dc
=300
нм практически исчезает эффект накопления, ярко выраженный в однородных слоях GaAs (как уже говорилось, на рисунке 2.1.2.2. это не отражено). Отсутствие эффекта накопления обусловлено тем, что из-за сильного захвата инжектированных электронов в слой КТ не остается свободных электронов для захвата на ПС, с которым связан эффект накопления. Интересно, что кривая 5 очень похожа на кривую ДЭП для однородного слоя GaAs при сильном освещении (рисунок 2.1.2.1, кривая 3), когда из-за уменьшения высоты поверхностного барьера сильно возрастает захват на ПС. В обоих случаях на частотной зависимости малосигнального эффекта μ
F
(
f
)
появляется ярко выраженная дисперсия на частоте f
1/2
~
1 кГц, которой соответствует время релаксации процесса захвата 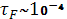 секунды[4]. секунды[4].
Оценка поверхностной концентрации центров захвата в слое КТ по ширине петли гистерезиса (2) дает для кривой 5 на рис. 4 Δns
≈ 1∙1011
см-2
. Это значение определяет нижний предел концентрации центров захвата в слое КТ, т.к. по величине ΔVgh
определяются только центры, из которых захваченные электроны не успевают перейти в зону проводимости при уменьшении напряжения Vg
от амплитудного значения до значения ΔVgh
на частоте измерения ДЭП. Однако и это значение на порядок превышает поверхностную концентрацию КТ в исследованных структурах (0.5 – 1.5)∙1010
см-2
, определенную методом атомно-силовой микроскопии. Более полный учет центров захвата в слое КТ за все время инжекции дает оценка их концентрации по фактору захвата Qm
при амплитудном значении Vg
(
t
)=
Vga
по формуле 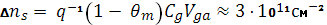
Это расхождение можно объяснить тем, что встраивание слоя КТ в GaAs генерирует вблизи КТ атмосферу дефектов - ловушек для электронов - с разной глубиной залегания. Если предположить, что некоторые из этих ловушек расположены на туннельно-близком расстоянии от КТ, то захват на них может происходить через захват в основное состояние КТ с последующим упругим или неупругим туннелированием на уровни ловушек. Заметим, что поскольку времена жизни электронно-дырочных пар в КТ по отношению к процессам излучательной рекомбинации электронов и дырок в КТ и эмиссии их из КТ на 4-5 порядков меньше времени релаксации захвата на ловушки, этот захват непосредственно не влияет на интенсивность фотолюминесценции и значение фоточувствительности от КТ. Он проявляется в эффекте поля на относительно низких частотах благодаря монополярной инжекции только основных носителей. Эти ловушки могут существенно влиять на вольтамперные и вольтемкостные характеристики барьеров Шоттки и р-п
-переходов в гетеронаноструктурах.
На рисунке 2.1.2.3. приведены кривые ДЭП для гетероструктур с одиночной КЯ при разном удалении КЯ от поверхности. В отличие от структур с КТ в структурах с КЯ гистерезис очень мал. Причем кривая ДЭП линейна, ее наклон имеет минимальное значение и гистерезис практически полностью отсутствует при dc
=
300 нм (кривая 4), когда КЯ находится вблизи границы области пространственного заряда и квазинейтральной области, т.е. когда почти все инжектированные электроны захватываются в КЯ. При этом подвижность в эффекте поля μ
F
≈ 1500 см2
/В∙с оказывается примерно в три раза меньше холловской подвижности электронов. При приближении КЯ к поверхности наклон кривой ДЭП увеличивается и появляется заметный гистерезис, однако при dc
=
5 нм наклон снова уменьшается. По-видимому это связано с появлением захвата носителей из КЯ на ПС.

Рисунок 2.1.2.3. – Влияние встраивания слоя КЯ на ДЭП. Толщина покровного слоя dc
:
кривая 1 соответствует 5 нм, 2 -20 нм, 3 - 100 нм, 4 - 300 нм.
Энергетический спектр КЯ, в отличие от дискретного спектра КТ, квазинепрерывный. Поэтому захват электронов в слой КТ не должен приводить к их локализации, если, конечно, в этом слое, на его границах с матрицей или на туннельно-близком расстоянии вблизи этих границ нет каких-либо ловушек, на которых может происходить локализация захваченных в КЯ электронов. Поскольку состав КЯ In0,2
Ga0,8
As меньше отличается от состава матрицы GaAs, чем состав слоя КТ InAs, и упругие напряжения в псевдоморфном слое КЯ относительно невелики. Генерация таких ловушек-дефектов, которую мы предполагаем при встраивании слоев КТ, в этом случае маловероятна. Мы полагаем поэтому, что подвижность μ
F
для структур с КЯ, расположенной на внутренней границе области пространственного заряда, характеризует дрейфовую подвижность электронов в самой КЯ (около 1500 см2
/В∙с) в условиях отсутствия захвата на ловушки. Холловская подвижность μН
характеризует с точностью до холловского отношения r
н
≈ 1 дрейфовую подвижность электронов в квазинейтральной области структуры (≈ 4500 см2
/В∙с). Меньшее значение дрейфовой подвижности электронов в КЯ связано с наличием дополнительных механизмов рассеяния электронов, возможно, на мелкомасштабных флуктуациях ширины и состава КЯ. Увеличение подвижности μ
F
при приближении КЯ к поверхности связано с уменьшением доли захваченных в КЯ электронов из-за увеличения высоты барьера, препятствующего захвату. При этом увеличивается доля свободных электронов в области пространственного заряда с более высокой дрейфовой подвижностью, по-видимому, близкой к холловской. Инжектированный на единице площади заряд электронов Qs
=
Cg
∆
Vg
=
Qss
+ Qw
+ Qv
,
где Qss
и Qw
-
заряды, захваченные на ПС и в квантовые ямы соответственно, Qv
-
свободный заряд в олбласти пространственного заряда. Изменение поверхностной проводимости создается зарядами Qw
и Qv
: ∆
σs
=
Qs
μ
F
=
Qw
μ
nw
+ Qv
μ
nv
,
где μ
nw
и μ
nv
– дрейфовые подвижности электронов в квантовых ямах и в области пространственного заряда соответственно. Если Qss
<< (
Qw
+
Qv
),
эффективная подвижность в эффекте поля μ
F
= (
Qw
μ
nw
+ +
Qv
μ
nv
)/(
Qw
+ Qv
).
В результате проведенных исследований разработана новая методика исследования нестационарного динамического эффекта поля. Ее применение к квантово-размерным гетеронаноструктурам In(Ga)As/GaAs с квантовыми точками и квантовыми ямами позволяет получить информацию о наличии дефектов, связанных с встраиванием этих слоев в матрицу, и оценить их концентрацию, а также о дрейфовой подвижности электронов в одиночных квантовых ямах. Представляется перспективным дальнейшее развитие этой методики диагностики квантово-размерных гетеронаноструктур, в частности измерение температурной зависимости ДЭП[4].
3 РАСЧЕТ ЭФФЕКТИВНОЙ ПОДВИЖНОСТИ НОСИТЕЛЕЙ ЗАРЯДА
При малых электрических полях дрейфовая скорость носителей Vd
пропорциональна напряженности электрического поля ε
Vd
= µε(3.1)
Коэффициент пропорциональности есть подвижность µ [см2
·В-1
·с-1
]. В неполярных полупроводниках, таких, как Ge и Si, основными механизмами, определяющими подвижность носителей, являются рассеяние на акустических фононах и рассеяние на ионизированных примесных атомах. Значения подвижности, определяемой рассеянием на акустических фононах, задаются следующим выражением:
 (3.2) (3.2)
где С11
— средний продольный модуль упругости полупроводника,
Eds
— смещение края зоны на единицу деформации кристаллической решетки,
m* — эффективная масса электрона проводимости.
Согласно выражению (3.2), подвижность уменьшается с ростом температуры и при увеличении эффективной массы.
Подвижность, обусловленная рассеянием на ионизированных примесях, определяется выражением
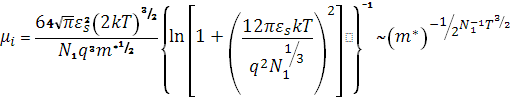 (3.3) (3.3)
где N1
— концентрация ионизированных примесей,
εs
— диэлектрическая проницаемость.
Видно, что в этом случае подвижность также уменьшается с ростом эффективной массы m*, но cростом температуры она увеличивается. Результирующая подвижность
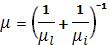

Рисунок 3.1 – Дрейфовая подвижность в Ge, Si и GaAs при T = 300К в зависимости от концентрации легирующей примеси
В полярных полупроводниках, таких, как GaAs, определяющую роль играет рассеяние на оптических фононах. В этом случае
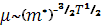
Кроме названных выше механизмов, влияющих на подвижность носителей, следует отметить междолинное рассеяние, когда электрон при рассеянии переходит из одного энергетического минимума в другой, испуская или поглощая при этом соответствующий коротковолновый фонон.
На рисунке. 3.1 приведены экспериментальные зависимости подвижности в Ge, Si и GaAs при комнатной температуре от концентрации примеси. Видно, что с ростом концентрации примеси (при комнатной температуре большая часть примесных атомов ионизирована) подвижность уменьшается, что соответствует выражению (3.3). Поскольку при увеличении эффективной массы m* подвижность уменьшается, в этих важнейших полупроводниковых материалах при той же концентрации примеси электронная подвижность больше дырочной.

Рисунок 3.2 – Температурная зависимость подвижности электронов и дырок в Si.
На рисунок 3.2приведены температурные зависимости подвижности в кремниевых образцах n- и p-типа с различной концентрацией примеси. При малых концентрациях примесных атомов подвижность действительно уменьшается с ростом температуры, как это следует из выражения (3.2).
Однако показатель степени экспериментальной зависимости отличается от теоретического значения – 3/2, что, вероятно, обусловлено влиянием дополнительных механизмов рассеяния. В чистых материалах в области комнатных температур подвижность изменяется по закону Т-1,65
и Т-2,33
для n- и p-кремния; Т-1,0
и Т-2,1
для n- и p-GaAs соответственно.
Другим важным параметром, связанным с подвижностью является коэффициент диффузии Dn
(Dp
) электронов и дырок. Его величина связана с величиной подвижности обобщенным соотношением Эйнштейна
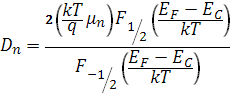
где F1/2
и F-1/2
– интегралы Ферми-Дирака. Это выражение можно записать в виде ряда
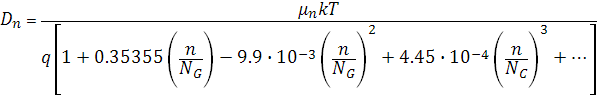
где n – концентрация электронов,
NG
– плотность состояний в зоне проводимости.
В большинстве практических ситуаций достаточно учесть лишь первое и второе слагаемые этого выражения. Аналогичные соотношения связывают коэффициент диффузии и подвижность дырок. В невырожденных полупроводниках, где n << NC
(p << Nv
), выражение переходит в обычное соотношение Эйнштейна
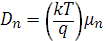
Коэффициенты диффузии при комнатной температуре легко получить из приведенных на рисунке 3.1 значений подвижности. Для этого их надо умножить на kT/q = 0,0259 В (Т = 300К)[2].
В ходе данной курсовой работы был рассмотрен эффект поля. Он применим только в том случае, когда удается обеспечить условия квазиравновесия на поверхности полупроводника. Это квазиравновесное состояние поверхности характеризуется тем, что носители заряда в зонах проводимости и валентной находятся в равновесии и между собой (поскольку рекомбинационно-генерационные процессы успели завершиться), и с быстрыми поверхностными состояниями (так как завершилась и релаксация, связанная с заполнением этих состояний электронами и дырками). При этом поверхностные концентрации носителей заряда в зонах, а также и степень заполнения быстрых поверхностных состояний определяются единым квазиравновесным значением уровня Ферми на поверхности, т.е. так называемым поверхностными потенциалом.
В связи с тем, что заполнение быстрых поверхностных состояний при указанных условиях измерения по методу эффекта поля является равновесным по отношению к измеряемой величине поверхностного потенциала, этот метод предоставляет дополнительную возможность исследования самих поверхностных состояний.
1. Бонч-Бруевич В.Л., Калашников С.Г. Физика полупроводников. М.: Наука; 1977. – 988с
2. С. Зи. Физика полупроводниковых приборов. М: Наука;
3. Ржанов А.В. Электронные процессы на поверхности полупроводников. М: Наука;1971. – 480с
4. Леденцов Н.Н., Устинов В.М., Щукин В.А. и др.// ФТП 1988 Т 32 С.382
5. Овсюк В.Н. Электронные процессы в полупроводниках с областями пространственного заряда. Новосибирск: Наука. Сибирское отделение. 1984. – 233с.
|