| Қазақстан Республикасының білім және ғылым министрлігі
Министерство образования и науки Республики Казахстан
РИИ индустриалды-технологиялық колледжі
Индустриально-технологический колледж РИИ
КОНТРОЛЬНАЯ РАБОТА №1,2
по дисциплине: «Основы технической механики»
по разделам: «Теоретическая механика. Сопротивление материалов»
Выполнил: Шпис И.
Группа ЗЭ-10 2
Шифр 100480
Преподаватель: Семёнова О.Л.
Рудный 2010
Задача №1 Статика
На схеме показаны способы закрепления бруса, ось которого - ломаная линия. Задаваемая нагрузка и размеры указаны в таблице 1.
Требуется определить реакции опор.
Таблица 1 - Исходные данные
| Р, кН
|
М, кН·м
|
q, кН/м
|
| 5
|
10
|
2
|

Решение.
Рассмотрим систему уравновешивающихся сил, приложенных к конструкции. Действие связей на конструкцию заменяем их реакциями ХА
, YА
, МА
. Равномерно распределенную нагрузку интенсивностью q заменяем равнодействующей:
Q = q·2 = 2 ·2 = 4 кН
Рх
= Р·cos450
=5·0,707=3,53 кН
Py
=P·sin450
=5·0,707=3,53 кН
Момент в заделке найдем, не определяя пока остальных реакций
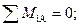 МА
- Р·2 sin 45° + М - Q·5 = 0. МА
- Р·2 sin 45° + М - Q·5 = 0.
Вычисления дают:
МА
= 17,07 кН·м.
Определим остальные опорные реакции для этой схемы:
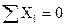 ХА
+РХ
=0 ХА
= -РХ
= -3,53 кН ХА
+РХ
=0 ХА
= -РХ
= -3,53 кН
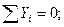 YA
-PY
-Q=0 YA
= PY
+ Q=3,53+4=7,53кН YA
-PY
-Q=0 YA
= PY
+ Q=3,53+4=7,53кН
Проверка:
ΣМВ
=0
-YA
·2+MA
+M-Q·3=0
-7,53·2+17,07+10-12=0
12.01-12=0
-0,01=0
ε=0.01/12.01·100%=0,008% (допускается погрешность до 0,1%)
Задача№2 Растяжение
На короткий чугунный брус круглого поперечного сечения действуют растягивающие и сжимающие усилия. Требуется спроектировать брус равного сопротивления, для чего:
1) разбить брус на участки (пронумеровав их, начиная от свободного конца) и на каждом участке найти внутреннюю продольную силу;
2) построить эпюру внутренних продольных сил;
3) из расчета на прочность определить для каждого участка бруса необходимый диаметр поперечного сечения и подобрать (для каждого участка) окончательную величину диаметра в соответствии с таблицей нормальных размеров;
4) начертить схему бруса с учетом найденных размеров сечений. Для спроектированного бруса:
5) найти на каждом участке напряжения и построить эпюру напряжений
| F
кН
|
[σР
]
МПа
|
[σ
с]
МПа
|
а
м
|
| 55
|
55
|
120
|
0.18
|

1. Построение эпюры N
Решение задачи начинается от свободного конца бруса. Это позволяет начать построение эпюры N без определения реакции опоры. Эпюра N строится методом сечений. Разделяем брус на участки. Границами участков являются точки приложения внешних сил, перемена сечения бруса и опора.
Границы участков обозначим буквами а, b, с, d, e.
I участок (ab)
N1
=-2F= -110 кН (сжатие)
II участок (bс)
N2
=-2F-4F=-6F=-330 кН (сжатие)
III участок (cd)
N3
==-2F-4F+13F=7 F=385кН (растяжение)
IV участок (de)
N4
=2F-4F+13F+5F=12F=660 кН (растяжение)
2. Строим эпюру N начиная от свободного конца бруса. Сначала проводим нулевую горизонтальную линию, далее откладываем значения подсчитанной продольной силы (положительные значения вверх, отрицательные вниз).
3. Определяем диаметр каждого участка
Условие прочности при растяжении:
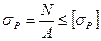 , ,
Условие прочности при сжатии:
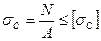
где А – площадь поперечного сечения бруса
Для бруса круглого поперечного сечения:
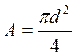
где d- диаметр бруса.
Подставляя в условие прочности и выражая значение диаметра получаем:
Для растяжения:
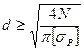
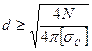
Для участков:
I участок (ab):
d1
= √ 4·110/(3.14·12) = 11.67
По таблице нормальных размеров принимаем d1
=12 мм
II участок (bс):
d2
= √ 4·330/(3.14·12) = 35.03
Принимаем d2
=36 мм
III участок (cd):
d3
= √ 4·385/(3.14·5.5) = 89.17
Принимаем d3
=90 мм.
IV участок (de)
d3
= √ 4·660/(3.14·5.5) = 152.8
Принимаем d4
=153 мм.
4 Строим схему бруса с учетом найденных значений диаметров
Посторенние начинаем с проведения штрихпунктирной линии, изображающей центр бруса, затем по участкам откладываем значения диаметров.
5 Находим на каждом участке напряжения и строим эпюру напряжений
Значение нормальных напряжений на участке определяем по формуле:
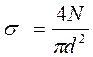
I участок (ab)
σ1
= 4·(-110)/3.14·
(1.2)2
= -97.7
II участок (be)
σ2
= 4·(-330)/3.14·
(3.6)2
= -32.44
III участок (cd)
σ3
= 4·(385)/3.14·
(9)2
= 6.05
IV участок (de)
σ4
= 4·(660)/3.14·
(15.3)2
= 3.59
Строим эпюру нормальных напряжений, руководствуясь правилами построения эпюры продольных сил.
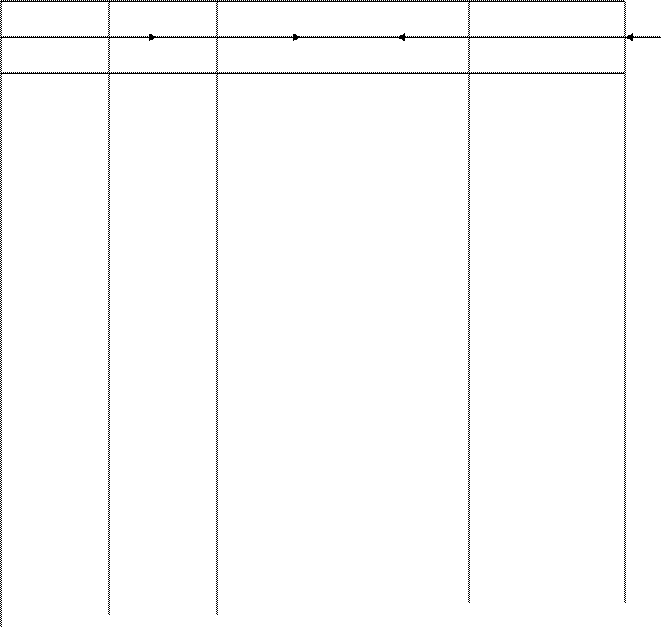
5F 13F 4F 2F
      e в c b a e в c b a
   а а 2а а а а 2а а
    660 660
385
    + +
                      + +
-
  - 110 - 110
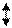         330 330
d4
=153 d3
=90
d1
=12
d2
=36
3.59
       
            + 6.05 + 6.05
                               + +
-
-
32.44
97.7
Задача №3 Кручение
К стальному ступенчатому валу, имеющему сплошное поперечное сечение, приложены четыре момента. Левый конец вала жестко закреплён в опоре, а правый конец – свободен и его торец имеет угловые перемещения относительно левого конца.
Требуется:
- построить эпюру крутящих моментов по длине вала;
- при заданном значении допускаемого напряжения на кручение определить диаметры d1
и d2
вала из расчёта на прочность, полученные значения округлить.
Исходные данные
| Расстояние, м
|
Моменты, кН·м
|
[τ],
МПа
|
| а
|
b
|
с
|
Т1
|
Т2
|
Т3
|
Т4
|
| 1.3
|
1.7
|
1.9
|
5.8
|
2.8
|
1.8
|
0.8
|
45
|

Решение:
1. Построение эпюры Мкр
(крутящего момента)
МкрI
= -Т4
= -0.8 кН·м
МкрII
= -Т4
+Т3
= -0.8+1.8=1кН·м
МкрIII
= -Т4
+Т3
+Т2
= -0.8+1.8+2.8=3.8кН·м
МкрΙV
= -Т4
+Т3
+Т2
+Т1
= -0.8+1.8+2.8+5.8=9.6 кН·м
По этим данным строим эпюру Мкр
2. Определение диаметров вала
Общее условие прочности при кручении:
τкр
=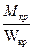 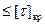
Максимальный крутящий момент для диаметра d1
:
Мкр
=9600 Н·м
Максимальный крутящий момент для диаметра d2
:
Мкр
=1000Н·м
Момент сопротивления при кручении:
Wкр
=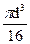
Подставляем значение в общее условие прочности:
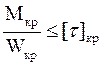
Получаем значение диаметра:
 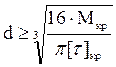
Вычисляем значение диаметров:
d1
=3
√ 16·8200/3.14·45·106
≥ 0.17
d2
= 3
√ 16·1000/3.14·45·106
≥ 0.05 3
√ 16·1000/3.14·45·106
≥ 0.05
Принимаем d1
=115мм, d2
=50мм по таблице нормальных размеров.
ΙV Т1
Т2
                           ΙΙΙ ΙΙΙ
   ΙΙ Т3
Ι ΙΙ Т3
Ι
d1
d2
Т4
а b c a
9.6
3.8
+
+ 1
+
0.8
-
Задача №4 Изгиб
Для заданной схемы балки требуется написать выражение для определения изгибающего момента для каждого участка в общем виде, построить эпюру М, найти Ммах
и подобрать стальную балку двутаврового поперечного сечения при [σ]= 160 МПа.
Таблица 5 – Исходные данные
| а, м
|
b, м
|
с, м
|
l, м
|
М,
кН·м
|
F,
кН
|
q,
кН/м
|
| 2.6
|
4.6
|
2.7
|
11
|
10
|
10
|
15
|

Уравнение прочности при изгибе в общем виде:
σ и
=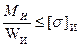
1.Составляем расчётную схему и методами теоретической механики определяем реакции в опорах. Предварительно определяем размер d:
d=l-(a+b+c) =11- (2.6+4.6+2.7) =1.1 м
ΣМА
= 0 , - (2q·а) · (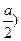 - P·d +RB
· (d+b) +M = 0 - P·d +RB
· (d+b) +M = 0
RB
= 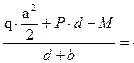
15·3.38+10·1.1-10
RB
=————————— = 29.52
1.1+4.6
ΣМB
=0
- (2q·а)·(b+d+(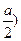 )-RА
(d+b)+P·b+М=0 )-RА
(d+b)+P·b+М=0
RА
=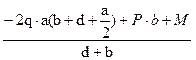
-30·(4.6+1.1+1.3)+10·4.6+10
RА
= ——————————————— = -27.01
1.1.+4.6
т.е. реакция направлена в другую сторону, чем на схеме.
2.Определяем изгибающие моменты, действующие по длине балки, используя правило знаков для изгибающего момента.
Изгибающий момент на участке с координатой Х1
:
МИ1
=2q·Х1
·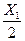
при Х1
=0,МИ
=0
при Х1
=а, МИ
=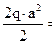 30·6.76/2 = 101.4 30·6.76/2 = 101.4
(кривая на эпюре парабола, т.к. переменная Х1
во второй степени).
Изгибающий момент на участке с координатой Х2
:
МИII
= 2q·а ·(Х2
-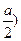 +RA
·(Х2
-а) +RA
·(Х2
-а)
при Х2
=а, МИ
=2q·а· (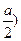 +RА
·(а-а)=101.4 кН·м +RА
·(а-а)=101.4 кН·м
Это значение совпадает со значением момента в этой опоре на предыдущем участке.
при Х2
= а +d, МИ
=2q·а ·(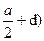 +RA
· (а +d-а)=157.5 кН·м +RA
· (а +d-а)=157.5 кН·м
Изгибающий момент на участке с координатой Х3
:
МИIII
=2q·а·(Х3
-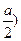 -RА
·(Х3
-а)- Р·(Х3
-а-d) -RА
·(Х3
-а)- Р·(Х3
-а-d)
при Х3
=а+d, МИ
=214.21 кН·м
Это значение совпадает со значением момента в этой точке балки на предыдущем участке.
при Х3
=а+d+b, Ми=6.53 кН·м
Изгибающий момент на участке с координатой Х4
равен моменту М, который задан в условии задачи.
МИIV
=М=7кН·м
На предыдущем участке момент в этой опоре был равен 6.53 кН·м, разница в значениях моментов это погрешность расчёта.
На основании расчётов строим эпюру изгибающих моментов.
3. Определение опасного сечения балки.
Опасным сечением будет являться то сечение, в котором изгибающий момент максимальный. Это сечение в опоре А, изгибающий момент в котором равен 101.4Н·м. Подбираем номер двутавра по формуле:
WХ
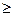 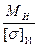
где МИ
-максимальный изгибающий момент, кН·м
WX
- момент сопротивления двутавра, см3
.
[σ]И
- допускаемое напряжение на изгиб, МПа
[σ]И
=160 МПа=16 кН/см3
WX
≥ 101000/16000 = 630 см2
Номер двутавра по моменту сопротивления подбирается по таблице.
Значения момента сопротивления для двутавров
| №
|
Wx
|
№
|
Wx
|
| 10
|
39.7
|
27
|
371
|
| 12
|
58.4
|
27а
|
407
|
| 14
|
81.7
|
30
|
472
|
| 16
|
109
|
30а
|
518
|
| 18
|
143
|
33
|
597
|
| 18а
|
159
|
36
|
743
|
| 20
|
184
|
40
|
953
|
| 20а
|
203
|
45
|
1231
|
| 22
|
232
|
50
|
1589
|
| 24
|
289
|
55
|
2035
|
| 24а
|
317
|
60
|
2560
|
Принимаем двутавр №36 с Wx
=743см2
.
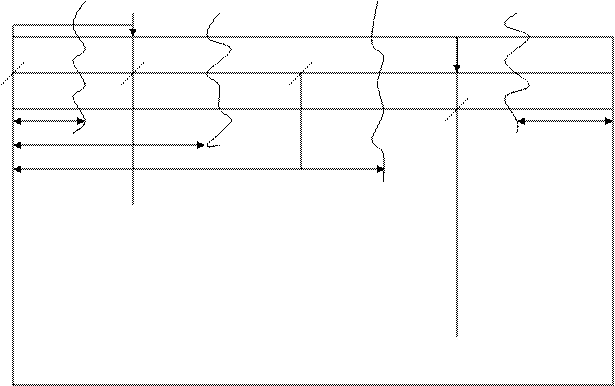
а в b c
e
Х4
Х1
Х2
                       Х3 Х3
214.21
101.4
7
Список использованной литературы.
1. Сборник заданий для курсовых работ по теоретической механике: Учеб. Пособие для техн. вузов/ Яблонский А.А., Норейко С.С., Вольфсон С.А. и др.; М.: Высш. шк., 1985.
2. Стёпин П.А. Сопротивление материалов: Учебник для немашиностроительных специальностей вузов.-7-е изд.-М.: Высш. шк., 1983.
3. Яблонский А.А, Курс теоретической механики часть 1: Учебник для машиностроительных, механических, приборостроительных, электротехнических и строительных специальностей вузов. М.: Высш. шк, 1963.: ил.
|