| Содержание
Введение
1. Расчет моста крана
2. Выбор основных размеров
3. Определение расчетных нагрузок для главной (пролетной) балки
4. Размещение диафрагм жесткости и проверка местной устойчивости
5. Анализ полученных результатов
6. Заключение
Список использованных источников
Введение
Мостовым краном называется грузоподъемная машина, передвигающаяся по рельсам на некотором расстоянии от земли (пола) и обеспечивающая перемещение груза в трех взаимно перпендикулярных направлениях (рис. 1). Мостовые краны являются одним из наиболее распространенных средств механизации различных производств, погрузочно-разгрузочных и складских работ. Перемещаясь по путям, расположенным над землей, они не занимают полезной площади цеха или склада, обеспечивая в тоже время обслуживание практически любой их точки.

Рис. 1. Мостовой кран:
1 - грузовая тележка; 2 - мост; 3 - механизм передвижения крана;
4 - подтележечный рельс; 5 - покрановый рельс.
Мосты мостовых кранов весьма разнообразны по своим возможным конструктивным формам. Они могут быть листовыми и решетчатыми, двухбалочными и однобалочными. Наибольшее распространение в настоящее время получили двухбалочные мосты листовой конструкции с коробчатыми главными и концевыми балками, которые обладают рядом преимуществ.
Коробчатая конструкция поддается механизации изготовления, обладает хорошим сопротивлением усталости, меньшей общей высотой моста и возможностью применения на концевой балке выкатных колес.
Решетчатая конструкция обладает наименьшей массой, наименьшей высотой от головки подкранового рельса до рельса на мосту и хорошей горизонтальной жесткостью. Ее недостатки: большая трудоемкость изготовления, более низкое сопротивление усталости и невозможность применения на концевых балках выкатных колес. В настоящее время мостов такой конструкции изготовляют мало.
В связи с широким применением мостов указанной конструкции, тему данной работы можно считать актуальной.
1. Расчет моста крана
Мост крана состоит из двух пространственно жестких балок, соединенных по концам пролета с концевыми балками, в которых установлены ходовые колеса. Крановая тележка перемещается пo рельсам, уложенным по верхним поясам коробчатых балок. Принятая схема металлоконструкции моста приведена на рис. 2.

Рис. 2. Схема моста крана.
Расчет моста крана выполнен в табличной форме.
В таблице 1 представлены исходные данные проекта, которые вносятся в таблицу из задания на курсовую работу.
2. Выбор основных размеров
Высоту балки назначают в зависимости от размера пролета по соотношению:
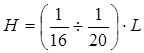 , (1) , (1)
где L – колея крана.
Высоту опорного сечения балки рекомендуется принимать в пределах:
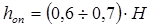 (2) (2)
Длину скоса рекомендуется принимать в пределах:
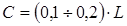 (3) (3)
В таблице 2 приведены значения указанных параметров балки в соответствии с формулами (1; 2; 3). В нижней строке указанной таблицы выбраны значения Н; hоп
; С, которые фигурируют в дальнейших расчетах.
Ширина площадок, как со стороны механизма передвижения, так и со стороны троллеев принята равной Впл
=1 м, а масса рабочей площадки 5250 кг.
Вес грузовой тележки отечественных двухбалочных кранов с листовой конструкцией грузоподъемность 5…100 т. с приемлемой точностью можно оценить по формуле:
 (4) (4)
где Q - грузоподъемность крана, т.
Расчет металлоконструкции моста мостового крана
Таблица 1 – Исходные данные для расчета.
| г/п, Р, т
|
Колея крана, L, м
|
Колея гр. тел., K, м
|
Тип подкранового рельса
|
Группа режима
|
Скорость подъема, м/с
|
Скорость передви -
жения крана, м/с (м/мин)
|
Материал м/к, сталь марки
|
| 50
|
34,5
|
2,5
|
Квадрат 80х80
|
А5
|
0,63
|
1,25 (75)
|
09Г2С
|
| Вес Gпм
полумоста, кН
|
Вес кабины, РК
, кН
|
Вес механизма предвижения, Рмех
, кН
|
Расстояние каб. от опоры,
в, м
|
Расстояние мех. пер. от опоры, а, м
|
Вес рабочих площадок, кН
|
Вес грузовой тележки G3
, кН
|
| 40
|
20
|
10
|
1,5
|
1
|
52,5
|
141,2
|
Таблица 2 – Выбор основных размеров моста крана.
| Высота гл. балки H, мм
|
Высота опорного сечения hоп
, мм
|
Длина скоса С, мм
|
Ширина балки В, мм
|
| От
|
До
|
От
|
До
|
От
|
До
|
От
|
До
|
| 2156
|
1725
|
414
|
483
|
3450
|
6900
|
430
|
470
|
| Приним. предварительно
|
Приним. предварительно
|
Приним. предварительно
|
Приним. предварительно
|
Приним. предварительно
|
Приним. предварительно
|
Приним. предварительно
|
Приним. предварительно
|
| 1620
|
405
|
3523
|
690
|
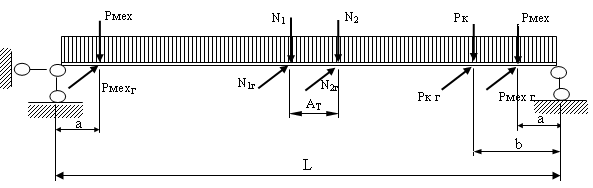
Рис. 3. Расчетная схема главной балки моста крана при действии вертикальных нагрузок.
Определение сечения главной балки
Таблица 3 – Исходные данные.
| L, м
|
a, м
|
P, кН
|
H, м
|
B, м
|
δп, м
|
δст, м
|
| 34,5
|
11,25
|
500
|
1,62
|
0,69
|
0,015
|
0,01
|
Таблица 4 – Геометрические характеристики сечения и ориентировочные значения изгибающего его момента М и нормальных напряжений σ.
| Ix, м4
|
Wx, м3
|
M, Н·м
|
σ, МПа
|
| 0,02
|
0,02
|
3790760
|
189,5
|
Момент инерции площади поперечного сечения определяется по формуле:
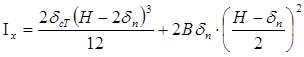
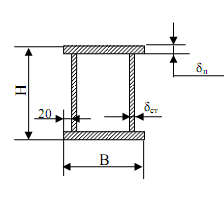
Рис. 4. Сечение балки
Момент сопротивления сечения определяется по формуле:

Изгибающий момент определяется по формуле:
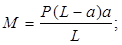
Напряжения определяются по формуле:
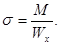
Значение динамического коэффициента для кранов мостового типа общего назначения удобно определять в зависимости от типа привода и скорости механизма подъема:
- двигатель с короткозамкнутым ротором 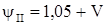 ; ;
- двигатель с фазным ротором  ; ;
- система плавного регулирования скорости 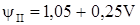 . .
Таблица 5 – Расчетные значения коэффициентов.
| Коэффициент перегрузки для соб. веса металлоконструкции,
n1
|
Коэффициент перегрузки для веса оборудования, n2
= n3
|
Коэффициент перегрузки для веса груза, n4
|
Коэффициент толчков, kт
|
Коэффициент динамичности для груза, ψII
|
| 1,1
|
1,1
|
1,2
|
1,2
|
1,21
|
3. Определение расчетных нагрузок для главной (пролетной) балки
В практике краностроения находят применение два метода расчета металлических конструкций: расчет по методу предельных состояний и по методу допускаемых напряжений. Данная конструкция рассчитывается по методу предельных состояний.
Данная конструкция рассчитывается по второму случаю нагружения при сочетании внешних воздействий IIа и IIb.
Для металлических конструкций кранов должны удовлетворяться два предельных состояния: 1) по потере несущей способности элементов конструкций, по прочности или потере устойчивости при наибольших нагрузках (II и III случаи нагружения) или многократных (различной величины) нагрузках – I случая нагружения за расчетный срок службы крана; 2) по непригодности к нормальной эксплуатации вследствие недопустимых упругих деформаций или колебаний, которые влияют на работу крана и обслуживающего персонала.
Значения коэффициентов перегрузки для отдельных нагрузок следующие для веса металлической конструкции n1
= 1,05 – 1,1; для веса оборудования n2
= n3
= 1,1 –1,3; для веса груза коэффициент перегрузки n4
зависит от назначения крана, его грузоподъемности (для малых грузов он больше, для больших – меньше) и режима работы (для легких режимов он меньше, для тяжелых — больше), его значения колеблются в пределах 1,1 – 1,5 (таблица. 1.59 в [1] стр. 166), а в особых случаях (например, при подъеме электромагнитом стального проката со сплошного металлического основания) – до 1,8; коэффициенты толчков kт
и динамические коэффициенты ψ вводятся в расчет без дополнительных коэффициентов перегрузки.
Нагрузки, действующие на главную балку моста крана, определяются на основе исходных величин таблицы 1.
Нагрузка от собственного веса рабочей площадки является равномерно-распределенной по всей длине балки, приложенной к подтележечному рельсу. Интенсивность распределенной нагрузки от собственного веса рабочей площадки определяется по формуле:
 , (5) , (5)
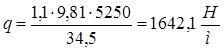
где n1
- коэффициент перегрузки для собственного веса металлоконструкции и элементов крана, принимаем его в соответствии с указанным выше n1
=1,1;
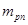 - масса рабочей площадки; - масса рабочей площадки;
 - ускорение свободного падения, 9,81 м/с2
; - ускорение свободного падения, 9,81 м/с2
;
L - пролет крана.
Вес механизма передвижения крана, вес кабины, давление колес грузовой тележки от ее собственного веса, давление поднимаемого груза на колеса тележки определяются в таблице 6 по аналогичным формулам с помощью коэффициентов перегрузки из таблицы 5 и номинальных значений указанных нагрузок из таблицы 1.
Подвижная нагрузка от ходового колеса тележки N1
= N2
(рисунок 3) для комбинации нагрузок IIa определяется по формуле:
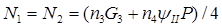 , (6) , (6)
где ψII
– динамический коэффициент, который определяется в таблице 5 на основе данных, характеризующих жесткость конструкции главной балки моста крана;
Р - грузоподъемная сила крана, Н.
Подвижная нагрузка от ходового колеса тележки N1
= N2
(рисунок 3) для комбинации нагрузок IIb определяется по формуле:
 (7) (7)
Горизонтальная инерционная нагрузка при числе приводных колес, составляющих половину от общего числа ходовых колес, принимается равной 0,1 от вертикальных сил веса движущихся масс.
Таблица 6 – Расчетные нагрузки моста крана при расчете по методу предельных состояний
| Вид нагрузки
|
Случаи нагружения
|
| Обозначение, ед изм.
|
IIa
|
IIb
|
| Вес металлической конструкции главной балки с рабочей площадкой, кН
|
q, кН/м
|
25,2
|
30,24
|
| Вес механизма передвижения крана, кН
|
Рмех, кН
|
11
|
13,2
|
| Вес кабины, кН
|
Рк, кН
|
22
|
26,4
|
| Давление колес гр. тел. от ее соб. Веса, кН
|
N1
= N2,
кН
|
253,16
|
219,096
|
| Давление поднимаемого груза на колеса тележки, кН
|
4. Размещение диафрагм жесткости и проверка местной устойчивости
Проверка местной устойчивости элементов балок производится для вертикальных стенок и сжатых поясов. Потеря устойчивости вертикальной стенки возможна под действием следующих факторов:
1) касательных напряжений от изгиба;
2) нормальных (сжимающих) напряжений от изгиба;
3) нормальных (сжимающих) напряжений от нагрузки, приложенной к верхней кромке стенки;
4) нормальных (сжимающих) напряжений от изгиба и осевого сжатия (балки рамных и других конструкций).
Первые два фактора могут действовать как раздельно, так и совместно; третий действует всегда совместно с одним или с обоими первыми. Что бы проверить местную устойчивость стенки необходимо сначала расставить ребра жесткости, исходя из конструктивных рекомендаций, а затем для расчетных отсеков вычислить критические напряжения и сравнить их с расчетными напряжениями.
Стенку можно не проверять на устойчивость, если условная гибкость стенки λ0
не превышает значения 3,2 в балках с односторонними поясными швами, при отсутствии местного напряжения.
Предельное расстояние между поперечными основными ребрами жесткости «а» не должно в стальных конструкциях превышать:
при λ0
> 3,2 – тогда шаг а ≤ 2h0
;
при λ0
≤ 3,2 – тогда шаг а ≤ 2,5h0
.
 , (8) , (8)
где hст
– высота стенки;
Rp
– расчетное сопротивление материала стенки, согласно таблицы 1.5.11 [1],
Rp
=240 МПа;
E – модуль упругости материала стенки, E = 210000 МПа.
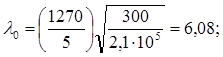 следовательно, шаг равен: а ≤ 2h0
; следовательно, шаг равен: а ≤ 2h0
;
Поперечные ребра следует устанавливать также в местах приложения к верхнему поясу больших неподвижных сосредоточенных грузов.
В главной балке имеется три характерных отсека, на которые она делится основными вертикальными ребрами жесткости (диафрагмами).
Отсек на опоре отличается тем, что в нем действуют максимальные касательные напряжения от поперечной силы, а нормальные напряжения равны нулю, так как на опоре изгибающий момент равен нулю.
Отсек в середине пролета отличается тем, что в нем действуют максимальные нормальные напряжения, а касательные напряжения равны нулю.
И отсек в средней четверти пролета, который отличается тем, что в нем действуют одновременно и касательные и нормальные напряжения, хотя и те и другие не принимают максимальных значений.
Для отсека на опоре критические напряжения определяются по формуле:
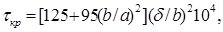 (9) (9)
где “а” и “b” – большая и меньшая стороны прямоугольника (отсека) соответственно, b = h0
;
δ – толщина стенки.
Условие обеспечения местной устойчивости при расчете по методу предельных состояний:
 , (10) , (10)
где τ - напряжение определяется с учетом коэффициентов перегрузки.
В среднем отсеке критическое напряжение определяется по формуле:
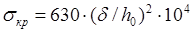 (11) (11)
В том отсеке, где действуют и касательные и нормальные напряжения, для обеспечения устойчивости должно выполняться условие:
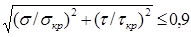 (12) (12)
Кроме вертикальных ребер жесткости для обеспечения местной устойчивости стенок могут потребоваться продольные ребра жесткости.
Если
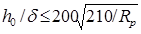 , (13) , (13)
то продольные ребра не требуются.
Если
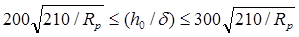 , (14) , (14)
то требуется одно продольное ребро жесткости.
Если
 , (15) , (15)
то требуется 2 продольных ребра жесткости.
Продольное ребро устанавливается на расстоянии (0,20…0,25)h0
, а в случае необходимости второго продольного ребра ставиться на расстоянии(0,15…0,20)h0
, а второе - (0,35…0,40)h0
от сжатого края стенки.
Необходимый момент инерции продольного ребра, образованного, как правило, уголком, следует принимать не менее:
Ix
≥ 1,5h0
δ3
ст
(16)
В рассматриваемой конструкции балки подтележечный рельс устанавливается посередине верхнего пояса главной балки. В таких конструкциях короткие ребра жесткости выполняют еще одну функцию – они являются дополнительными опорами для рельса подтележечного пути.
Ix
= 1,5 · 162 · 0,43
= 15,56 см 4
,
принимаем уголок 40 равнополочный 40×40 с Ix
= 45,9 см 4
,
т.к. Ix
= 45,9 см 4
≥ Ix
= 15,56 см4
.
В нижней строке таблицы 7 и 8 показаны расчетные значения параметров, по которым решается вопрос о постановке дополнительных, коротких, ребер жесткости, исходя из требований устойчивости стенки балки.
Таблица 7 – Проверка местной устойчивости элементов главной балки.
| Толщина стенки δ, мм
|
Высота стенки на опоре h0
, мм
|
Высота стенки h0
, мм
|
Шаг основных ребер жесткости, мм
|
h0
/δ
|
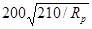
|
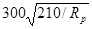
|
σкр
по формуле (11), МПа
|
| 10
|
405
|
1620
|
3000
|
162
|
187
|
281
|
165
|
| τкр
по формуле (9) на опоре, МПа
|
τкр
по формуле (9) в сечении, МПа
|
Левая часть формулы (12)
|
| 125,16
|
51,22
|
0,86
|
В таблице 8 выполнены необходимые расчеты для решения вопроса об установке коротких ребер жесткости для обеспечения прочности рельса пути крановой тележки. Рельс рассматривается как неразрезная балка, изгибающий момент в которой Мр
определяется по формуле:
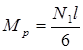 , (17) , (17)
где N1
– давление колеса тележки, см. таблицу ;
l – расстояние между опорами рельса, т.е. между малыми диафрагмами (ребрами жесткости).
Прочность рельса обеспечивается, если выполняется условие:
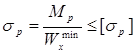 (18) (18)
После несложных преобразований из формул (17) и (18) можно получить формулу для определения расстояния между диафрагмами, которое необходимо для обеспечения условия (19):
 (19) (19)
Высота малых диафрагм принимается равной (0,20…0,25)H.
Геометрические характеристики поперечных сечений крановых и железнодорожных рельсов приведены в таблицах V.2.57., V.2.58. стр. 325 [2].
После определения основных геометрических размеров пролетной балки, поперечного сечения, длины отсеков, шагов расстановки малых диафрагм, продольных ребер жесткости вычерчивается рабочая схема с указанием основных размеров (см. рис. 5), согласно которой осуществляется дальнейшее проектирование.
Таблица 8 – Расчет подтележечного рельса.
| Тип рельса
|
Wx
min
= (bh2
)/6, см3
|
[σp
], МПа
|
l,по формуле(19), мм
|
| Квадрат 80х80
|
85,3
|
270
|
630,7
|
Как видно из таблицы 8, для обеспечения условия прочности рельса, необходимо установить между высокими ребрами жесткости два дополнительных коротких ребра жесткости.

5. Анализ полученных результатов

Рис. 6. Произвольный вид главной балки.
Загружение 0, Множитель собственного веса 1,67
Таблица 9 – Нагрузки на узлы.
Таблица: Нагрузки на узлы Загружение: Загружение 0
| N
|
Тип
|
Номер узла
|
Проекции
|
Модуль
|
| на x
|
на y
|
на z
|
| 0
|
сила , Н
|
1505
|
0.00
|
0.00
|
-205000.00
|
205000.00
|
Нагрузки на стержни Загружение: Загружение 0
Индекс стержня 447 (Rod 887)
Индекс начальной точки 1600
Направление системы координат стержня
x = ( 0.000, 1.000, 0.000) (вдоль оси стержня)
y = ( 0.000, -0.000, 1.000)
z = ( 1.000, -0.000, -0.000)
Радиальные силы
| N
|
Расстояние отлевого конца балки, мм
|
Модуль, Н
|
Угол, град
|
| 0
|
144.30
|
205000.00
|
180.00
|
Таблица 11 – Материалы.
| Название
|
Модуль Юнга [Н/мм^2]
|
Коэф. Пуассона
|
Плотность [кг/кб.мм]
|
Коэф. температурного расширения [°C]
|
Коэф. теплопроводности [Вт/(°C*мм)]
|
| Сталь
|
200000
|
0.30
|
7.8e-006
|
1.2e-005
|
0.001
|
| Бетон
|
19000
|
0.20
|
2.503e-006
|
1e-005
|
0.001
|
Таблица: Расход
| Название
|
Количество
|
Длина [мм]
|
Погонная масса [кг/мм]
|
Масса изделия[кг]
|
Общая масса[кг]
|
Площадь окраски[мм^2]
|
| Сталь
|
| L40x4 ГОСТ 8509-93
|
4
|
230.00
|
0.00
|
0.55
|
2.22
|
143883.114
|
| L40x4 ГОСТ 8509-93
|
4
|
242.80
|
0.00
|
0.58
|
2.34
|
151890.522
|
| L40x4 ГОСТ 8509-93
|
12
|
236.40
|
0.00
|
0.57
|
6.83
|
443660.454
|
| L40x4 ГОСТ 8509-93
|
284
|
214.00
|
0.00
|
0.52
|
146.40
|
9505043.627
|
| L40x4 ГОСТ 8509-93
|
40
|
216.00
|
0.00
|
0.52
|
20.81
|
1351250.114
|
| L40x4 ГОСТ 8509-93
|
2
|
428.00
|
0.00
|
1.03
|
2.06
|
133873.854
|
| квадрат 80*80
|
10
|
236.40
|
0.05
|
11.80
|
118.01
|
756480.000
|
| квадрат 80*80
|
36
|
214.00
|
0.05
|
10.68
|
384.58
|
2465280.000
|
| квадрат 80*80
|
11
|
216.00
|
0.05
|
10.78
|
118.61
|
760320.000
|
| квадрат 80*80
|
117
|
214.15
|
0.05
|
10.69
|
1250.79
|
8017920.000
|
| Всего для сечения
|
| L40x4 ГОСТ 8509-93
|
346
|
75000.00
|
0.00
|
180.67
|
180.67
|
11729601.686
|
| квадрат 80*80
|
174
|
37500.00
|
0.05
|
1871.99
|
1871.99
|
12000000.000
|
| Всего для материала
|
2052.65
|
23729601.686
|
Карта результатов SVM[Н/мм^2]

Рис. 7. Крановый рельс (квадрат 80х80).
Параметры сечения рельса
Параметры сечения
Площадь 6399.95 кв.мм
Центр масс: X= 70.000 Y= 10.000мм
Момент инерции
относит. оси X 3412543.62мм4
относит. оси Y 3411120.44мм4
полярный 6823664.06мм4
Угол наклона главных центральных осей 45.00градус
Карта результатов SVM[Н/мм^2], SVM+[Н/мм^2]

Карта результатов USUM[мм], USUM[мм]

Диаграмма: Момент кручения [Н*мм] (Загружение 0)
Диаграмма: Момент изгиба в пл-ти XY [Н*мм] (Загружение 0)
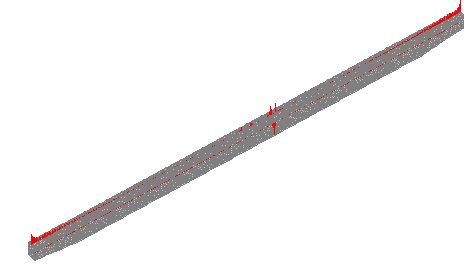
Диаграмма: Момент изгиба в пл-ти XZ [Н*мм] (Загружение 0)

6. Заключение
В результате расчета металлоконструкции главной (пролетной) балки мостового крана с использованием модуля проектирования APM WinMachine, можно сделать вывод о том, что спроектированная конструкция удовлетворяет требованиям прочности и жесткости. Так как расчетные значения напряжений и перемещений в опасном сечении главной балки получились меньше предельных допустимых значений.
Прочность главной балки обеспечивается, т.к выполняется условие:
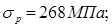
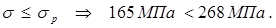
Допускаемый прогиб балки fдоп
в середине пролета обеспечивается, т.к. выполняется условие:
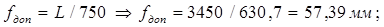
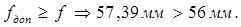
Следовательно, несущая металлоконструкция главная (пролетная) балка мостового крана грузоподъемностью 50 тонн, пригодна к эксплуатации в установленном режиме работы.
Список использованных источников
1. Справочник по кранам, Т1 /Под ред. М.М. Гохберга. Л.: Машиностроение, 1988. 535 с.
2. Справочник по кранам, Т2 /Под ред. М.М. Гохберга. Л.: Машиностроение, 1988. 559 с.
3. Методические указания по выполнению курсовой работы, /Под ред. А.С. Толоконникова. Тула: 2009.
4. Кузнецов, В. А. Петрозаводский государственный университет. Оптимизация на графах (алгоритмы и реализация) : учеб. пособие / В.А. Кузнецов, А.М. Караваев; ПетрГУ.- Петрозаводск : Изд-во ПетрГУ, 2007 .- 184с.
5. Соколов, С.А. Металлические конструкции подъемно-транспортных машин : учебное пособие для вузов / С.А. Соколов.- СПб. : Политехника, 2005 .- 423с.
|